Efficient Core-selecting Incentive Mechanism for Data Sharing in Federated Learning
Abstract
Federated learning is a distributed machine learning system that uses participants’ data to train an improved global model. In federated learning, participants collaboratively train a global model, and after the training is completed, each participant receives that global model along with a payment. Rational participants try to maximize their individual utility, and they will not input their high-quality data truthfully unless they are provided with satisfactory payments based on their contributions. Furthermore, federated learning benefits from the cooperation of participants. Accordingly, how to establish an incentive mechanism that both incentivizes inputting data truthfully and promotes stable cooperation has become an important issue to consider. In this paper, we introduce a data sharing game model for federated learning and employ game-theoretic approaches to design a core-selecting incentive mechanism by utilizing a popular concept in cooperative games, the core. In federated learning, the core can be empty, resulting in the core-selecting mechanism becoming infeasible. To address this issue, our core-selecting mechanism employs a relaxation method and simultaneously minimizes the benefits of inputting false data for all participants. Meanwhile, to reduce the computational complexity of the core-selecting mechanism, we propose an efficient core-selecting mechanism based on sampling approximation that only aggregates models on sampled coalitions to approximate the exact result. Extensive experiments verify that the efficient core-selecting mechanism can incentivize inputting high-quality data truthfully and stable cooperation, while it reduces computational overhead compared to the core-selecting mechanism.
Index Terms:
Federated Learning, Incentive Mechanism, Data Pricing, Game Theory.I Introduction
In recent years, the success in the field of machine learning has been mainly attributed to the collection and use of massive amounts of data. Although the demand for data in machine learning is growing, collecting and using data are still difficult. On the one hand, data owners, or participants in federated learning, have recognized the worth of their data, so they are reluctant to provide it for free. On the other hand, privacy protection regulations such as the General Data Protection Regulation (GDPR) impose strict restrictions on access to private data [1]. To address the problem of privacy protection, federated learning has been proposed, which is a cooperative framework based on collaborative training and model sharing [2]. In federated learning, the data of participants is stored locally and used to train local models. Then these local models are aggregated by a server to create a global model. Since federated learning does not require participants to upload data to the server, it prevents possible privacy leaks during the uploading, saving, and model training processes. In recent years, federated learning has attracted attention in many fields such as healthcare, finance, and the Internet of Things [3, 4, 5].
In federated learning, economic incentives are crucial for motivating participants to cooperatively train a global model [6]. In practice, participants are reluctant to truthfully input their worthy data unless they receive satisfactory payments for their high-quality data. In addition, the global model relies on the stable cooperation of all participants and the server. Therefore, a desirable incentive mechanism should also take into account cooperative contributions and truthfulness. Along with the development of federated learning, research on incentive mechanisms has attracted many scholars’ interests [7, 8, 9]. Many methods are used to design incentive mechanisms for federated learning, including auction [10, 11, 12], contract theory [13], and matching theory [14]. Game theory investigates strategic interactions among players or agents, which provides a framework to analyze the strategic behaviors of participants in federated learning. Therefore, more and more incentive mechanisms have used game-theoretic methods to design incentive mechanisms in federated learning. Such methods include Stackelberg game [15, 16], evolutionary game [17, 18], VCG-based (Vickrey-Clarke-Groves) mechanisms [19, 20, 21, 22, 23], and Shapley value [24, 25, 26, 27].
Many existing studies in federated learning and machine learning focus on designing incentive mechanisms to provide economic incentives for participants. The VCG (Vickrey–Clarke–Groves) mechanism is famous in game theory and mechanism design theory because it satisfies the properties of incentive compatibility and individual rationality. Due to its desirable properties, the VCG mechanism motivates participants to report their private information truthfully. Therefore, the VCG-based incentive mechanism has been widely used in machine learning and federated learning [19, 20, 21, 22, 23]. To reduce computational complexity, a faithful federated learning (FFL) mechanism was proposed to compute the VCG-like payment via an incremental computation [23]. It effectively reduces computational complexity, making it suitable for large-scale training scenarios. The utility of participants under the VCG-based mechanism is equal to their marginal contribution, which motivates them to input high-quality data. In addition to computing the VCG payment, allocating payments or profits based on cooperative contributions to promote stable cooperation is also a challenge in federated learning.
Cooperative game theory offers various solution concepts to determine how benefits should be allocated. The Shapley value is a classic solution in cooperative game theory with desirable properties and interpretability, which has been widely adopted in incentive mechanisms for machine learning and federated learning [24, 28, 29, 26, 27, 25]. These methods allocate payments according to the marginal surplus of each participant, which reflects the combined worth of participants’ data. Except for Shapley value, the core is also a widely used solution concept in cooperative game theory [30, 31, 32]. It represents a stable and fair allocation set that satisfies the properties of individual rationality and coalitional rationality, which is different from Shapley value. The allocation element in the core ensures that no player or coalition has the motivation to deviate from cooperation. Due to its desirable properties, the core has been widely applied in many fields such as spectrum auctions, crowdsourcing, and transportation scenarios [33, 34, 35]. Recently, the core has also been used in federated learning to evaluate the cooperative contributions of participants [36, 37]. These methods fully analyze the existence of the core and provide a fair allocation scheme. Nevertheless, the core is a set solution that cannot provide a unique optimal solution, and the advantages of the VCG payment or marginal contribution have not been fully considered by these methods. Core-selecting mechanisms, often referred to as core-selecting auctions, are designed to ensure that the resulting allocation is in the core of the associated cooperative game [38]. Therefore, we will use the core-selecting mechanism and adopt some improvements to address potential issues that may arise in federated learning. Additionally, it is worth noting that determining the exact core in federated learning also faces computational difficulties because it requires computing additional models [39].
As shown in Table I, we give the comparison table to highlight the differences of existing incentive mechanisms.
|
|
|
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [29, 26, 27] | Shapley value | \ | \ | Yes | ||||||||
| [36, 37] | core | \ | Yes | \ | ||||||||
| [39] | least core | \ | \ | Yes | ||||||||
| [21] | \ | VCG-based | Yes | \ | ||||||||
| [19, 20] | \ | VCG-like | \ | Yes | ||||||||
| [23] | \ | VCG-like | Yes | \ | ||||||||
| This paper | strong -core | VCG-like | Yes | \ |
In this paper, we propose an efficient core-selecting incentive mechanism for federated learning. First, we introduce a data sharing game for federated learning. Then we introduce a core-selecting incentive mechanism that combines the advantages of both the VCG-like payment and the core, which can promote stable cooperation among players and also motivate participants to input their high-quality data. Different from the classical core-selecting mechanism, we adopt a relaxation on the core to deal with the randomness in federated learning. Since the core-selecting incentive mechanism requires exponential time to aggregate and evaluate additional models in federated learning, it is difficult to compute the exact solution. To address this, we propose an efficient core-selecting mechanism based on sampling approximation that significantly reduces computational complexity. This mechanism adjusts the aggregation weight of participants based on their historical contributions to avoid the impact of low-quality data. In addition, we verify the theoretical results of the proposed mechanism in experiments. Further experiments show that the efficient core-selecting mechanism can motivate participants to truthfully input high-quality data and promote stable cooperation, while it reduces computational overhead compared to the core-selecting mechanism.
Our contributions are as follows:
-
1.
We introduce a data-sharing game for federated learning to study participants’ strategic behaviors. Based on the outcomes of this data-sharing game, we define the characteristic function and the core to measure participants’ cooperative contributions.
-
2.
We employ a core-selecting mechanism for federated learning, which aims to find the optimal payment based on the core to incentivize participants’ cooperation. Due to the impact of low-quality data or overfitting on the global model, the core may be empty. To address this issue, our core-selecting mechanism employs a relaxed version of the core, strong -core, and minimizes the benefits of inputting false data.
-
3.
To avoid the core-selecting incentive mechanism implementing in an exponential time to aggregate and evaluate additional models in federated learning, we propose an efficient core-selecting incentive mechanism based on sampling approximation that significantly reduces computational complexity. This incentive mechanism aggregates new global models based on the historical contributions of participants.
The rest of this paper is organized as follows. Section II introduces the background of federated learning and formulates the problem. Section III introduces the truthful incentive mechanism for federated learning. The core-selecting mechanism is proposed in Section IV. The efficient core-selecting mechanism and its theoretical results are proposed in Section V. Experiments are given in Section VI to illustrate the performance of our method. Section VII concludes this paper.
II Background and Problem Formulation
We first introduce the background of federated learning in Section II-A, and then introduce the necessary notions and definitions in Section II-B.
II-A Background of Federated Learning

We introduce a typical federated learning system, as shown in Fig. 1. In this system, participants with data collaboratively train a machine learning model with the help of a server [40]. The training process of federated learning system typically consists of the following four steps.
- Step 1:
- Step 2:
-
Step 3:
The server sends back the aggregated results (gradients information) to participants.
-
Step 4:
Participants update their local model parameters with the gradient results from the server.
The process of above steps will continue until the loss function converges. This system is independent of specific machine learning algorithms (logical regression, deep neural networks, etc.), and all participants will share the final model parameters.
In the above steps, the participant sends gradient information, and the server aggregates the gradient information using a weighted average method. Therefore, this method is called gradient averaging [43, 44]. In addition to sharing gradient information, participants in federated learning can also share models. Participants calculate model parameters locally and send them to the server [45]. The server aggregates the received model parameters (for example, calculates a weighted average) and then sends the aggregated model parameters to the participants. This method is called model averaging, as shown in Algorithm 1. Experiments have shown that model averaging is equivalent to gradient averaging, so both are called federated averaging [43].
It is important to note that federated learning requires stable cooperation among participants and the server. In addition, on the above system, participants are not supervised when training local models, so no one else knows whether participants are using truthful data or generated false data. In order to promote stable cooperation and encourage training with truthful data, it is necessary to design an incentive mechanism for federated learning to determine reasonable payments for participants.

In this paper, we consider an incentive mechanism framework for federated learning, as shown in Fig. 2. The operator sets up a server responsible for coordinating participants to implement a federated learning algorithm, such as the FedAvg algorithm. The server measure each participant’s contribution and provide them with payments when the global model is given at each round. In the following sections, we will study some desirable incentive mechanisms based on this framework.
II-B Problem Formulation
In order to analyze federated learning from the perspective of game theory, a data sharing game environment outlining federated learning algorithm is proposed in this section. We denote the set of all participants as , and each participant’s dataset is denoted as . In each round , each participant updates their local model and the global model using their inputted dataset . We will employ game theory to analyze the strategic behavior of these participants in each round.
-
1.
Players: Participants and the server .
-
2.
Type: Each participant has a dataset to input during the local training process, which can be called player ’s type in game theory. Note that is ’s private information, not known to others.
-
3.
Strategy: Each player selects as its input, which can be truthful, i.e., , or untruthful, i.e., . In addition, each participant can also choose to quit (). We denote as the original dataset, and as the selected dataset.
-
4.
Each player inputs its selected dataset to update its local model , and then a global model is aggregated from these local models, which is denoted as . We can write the accuracy function , where represents a federated learning algorithm that maps an inputted dataset onto a global model and is some accuracy metric applied to the model.
-
5.
As the global model is shared among players during the update process, each participant will receive the parameters of the global model after this round. Each player will gain potential benefits from the global model if it is better than its local model . To characterize the immediate benefits for the current round, we define the valuation function of player as
(1) where is a pricing function for a given model, defined as a monotonically increasing function of the model accuracy. The specific form of is given by the participants and operator. For simplicity, we set , where is a constant number that represents ’s preference for a model. represents player ’s benefits valuation for the global model when player ’s original dataset is .
-
6.
Each player will receive a payment , which is to be determined. Then player ’s utility function is defined as
(2) -
7.
The server has a budget to pay for all participants. Thus, the utility of player is defined as .
Note that the initial update of a participant’s local model is based on its own dataset, while subsequent updates are based on the global model aggregated in the previous round. The valuation function (1) is used to evaluate the potential benefits in each round. For participant , the cumulative valuation of all rounds represents the improvement of the global model compared to ’s initial model.
A cooperative game is determined by a player set and a characteristic function . The characteristic function assigns a numerical value to each subset (also called a coalition) of the player set, representing the total worth that the coalition can obtain.
In order to study the cooperative behavior of players using cooperative game methods, we need to define a characteristic function based on the outcome of the data sharing game.
In federated learning, players gain benefits from the global model. Hence, the worth generated by all players , can be written as
| (3) |
where also holds.
Assuming the model training is restricted to coalition , and coalition gets a global model where , then the worth generated by coalition is
| (4) |
Note that we use the notation instead of , as the cooperation of federated learning definitely requires the server and notation is more convenient to use. Thus, the characteristic function is given as follows.
| (5) |
where represents all subsets of . To compute all characteristic values, the server has to aggregate additional models for all coalitions . By inputting these characteristic values, solutions in cooperative games, such as the core, can determine a payoff allocation scheme, thus incentivizing players’ cooperative behaviors.
The problem studied in this paper is to design a desirable incentive mechanism based on these characteristic values. Based on our previous discussion, this mechanism is designed to incentivize each player to truthfully input its high-quality dataset, with no player willing to deviate from cooperation. In order to design such a mechanism, the following properties will be considered.
-
•
Incentive Compatibility: All players input their dataset truthfully, which is a Nash strategic equilibrium. In other words, any participant has no motivation to deviate from inputting the original dataset because the utility of inputting original dataset is not less than the utility of inputting false dataset:
(6) -
•
Individual Rationality: Any player can get non-negative utility when inputting dataset truthfully:
(7) -
•
Coalitional Rationality: Any coalition has no motivation to split off:
(8) -
•
Computational Efficiency: The incentive mechanism can be implemented in polynomial time.
The first two properties described above are intended to encourage players to input dataset truthfully. The third property is to ensure the stability of cooperation among all players and the server.
III Truthful Incentive Mechanism for Federated Learning
The VCG (Vickrey–Clarke–Groves) mechanism is famous in game theory and mechanism design theory, which satisfies the property of incentive compatibility, i.e., telling the truth is a dominant strategy for all players [46]. The VCG mechanism was previously employed by Nix and Kantarcioglu in the context of distributed machine learning [20], and they have proposed a critical assumption in their work. Meng Zhang et al. have also investigated VCG-based mechanisms in the context of federated learning and proposed a VCG-like payment to approximate VCG payments via an incremental computation. In this section, with minor modifications, we also implement this VCG-based mechanism for our incentive mechanism framework. This truthful incentive mechanism will serve as the foundation for the core-selecting mechanism in the next section.
In federated learning, a commonly used assumption is that each dataset and the test dataset are sampled from a real distribution . During the training process, participant actually inputs an untruthful dataset , where deviates from the real probability distribution and follows a probability distribution with artificial errors, i.e., .
Let and , the expected risks of these two models on distribution are denoted as and where is a per-sample loss function. Generally, holds because model fits the data points under the real distribution , whereas model fits the noisy data points. As a result, on the test dataset , the performance of will be better than that of . Mathematically, this can be expressed as
| (9) |
where is a non-negative, increasing function and is a distance function of the dataset.
This assumption is similar to the assumption proposed by Nix and Kantarcioglu [20]. It means that deviating from a real data will make a bad model’s performance more likely. Obviously, a truthful input will not decrease the model accuracy for each player , and more input of truthful data will improve model performance. Nix and Kantarcioglu also mentioned the possible effects of the overfitting phenomenon. In order to verify the validity of this assumption in the context of federated learning, we will test it by inputting a noisy dataset in Section VI.
The truthful incentive mechanism is easy to operate. Given an input , each player receives a global model and a VCG-like payment, which is defined as
| (10) |
To compute the payments for all participants, additional models need to be aggregated and evaluated. Note that it is not strictly a classic VCG mechanism. The difference between this mechanism and the classical VCG mechanism is that the selection of players is not executed here. The reasons are twofold. Firstly, in order to find the optimal model and achieve a selection of players, times of aggregation and times of evaluation for all potential selection schemes are required, which are computationally expensive. Secondly, only after a participant is selected can we obtain its local model and evaluate it. Thus, the selection of participants is not considered in this paper. Although the selection is not performed by this mechanism, it still satisfies incentive compatibility.
Theorem 1 (Nix and Kantarcioglu [20])
The truthful mechanism satisfies the properties of incentive compatibility and individual rationality.
Proof:
Given any input profile of other players, if inputs , player ’s utility is
| (11) | ||||
Similarly, if inputs truthfully, player ’s utility is
| (12) |
In order for incentive compatibility to exist, this requires that
| (13) |
We assert that always holds, since either the last expression is zero, in which case the first expression is greater than or equal to zero, and the last expression is greater than zero, in which case the first expression is greater than or equal to the last expression due to inequality (9). Therefore, we have and the above inequality holds. ∎
Proof:
To show that the mechanism is individually rational, we only need to show that the mechanism has a utility of at least zero. The utility of player is
| (14) | ||||
Let , according to inequality (9), we have
| (15) |
Hence,
| (16) |
∎
The VCG-like payment measures the difference between the global model, i.e., , and the model without his input, i.e., . In economics, allocating benefits by marginal contributions encourages participants to adopt decisions and behaviors that have a positive impact on team benefits. If participant inputs data truthfully, its utility will be equal to its marginal contribution , which encourages participants to input high-quality data to improve . This truthful incentive mechanism, or the VCG-like payment, meets the requirements of the first two properties mentioned in Section II.
IV Core-selecting Incentive Mechanism for Federated Learning
While the truthful incentive mechanism can motivate players to input their high-quality data, it fails to consider cooperation among all players and the server. The core is a classic set solution in cooperative games. In this section, we define the core based on the outcomes of the proposed data sharing game. The core cannot be guaranteed to be nonempty in federated learning. To address this issue, we adopt a relaxed version of the core, strong -core. Then, we propose a core-selecting mechanism that selects a solution minimizing participants’ benefits of untruthful input within the strong -core.
Let be the observable surplus of player . It does not involve the private information of players and can be computed by the server. Instead of the true utility , the core is defined over surplus because the server does not have any knowledge on the players’ original data , without a guarantee on the incentive compatibility [38]. The true utility and the incentive for participants to input data truthfully will be discussed later. The server’s surplus is defined as .
Definition 1 (Core)
A surplus vector is feasible if , which means that all players completely allocate the worth generated in federated learning. A surplus vector is blocked by coalition if there is another such that for all , and . The core is the set of non-negative surplus vectors that are feasible and not blocked by any coalition, which can be mathematically defined as
| (17) | |||
This implies that when the server selects a vector from the core, there is no motivation for any player to form a coalition with other players to deviate from coalition for any possible improvement of their total utility.
The classical core-selecting mechanism, as shown in quadratic programming (18) and Fig. 3, aims to find a surplus from the core, which is closest to the surplus vector determined by the VCG-like payment, . It combines the advantages of the VCG-based mechanism and the core.
| (18) | |||||
| s.t. | |||||

Theorem 2
The core is nonempty if performs better than for any coalition .
Proof:
We show that the surplus vector determined by the first price rule is in the core. Given any type profile , for each player , we let and then we have for all . For any coalition , we have
| (19) | ||||
and
| (20) | ||||
Therefore, the surplus vector determined by the first price rule is in the core, so the core is nonempty. ∎
Intuitively speaking, with more input, should perform better than and the core should be a nonempty set. However, there are some issues in practice. Firstly, in practical implementation, we cannot repeat training infinitely to accurately approximate the expected value of accuracy. Additionally, model overfitting may also result in and even holding for a coalition . Both two issues result in an empty core, and the core-selecting cannot be used directly. To address this, we employ a non-empty set solution similar to the core, strong -core, which adopts a relaxation to the core [47]. The strong -core is defined as
| (21) | |||
In the concept of strong -core [47], represents a minor perturbation or a threshold for deviation. If a coalition can increase its utility by more than the threshold, i.e., , through deviating from , then the coalition will choose to deviate and not collaborate with the participants in . The strong -core of a game can be interpreted as the set of all allocation vectors that cannot be improved upon by any coalition if one imposes a cost of in all cases where a nontrivial coalition is formed [47].
For convenience, the surplus vector in the strong -core, is called core surplus vector, and the surplus vector determined by the VCG-like payment, is also called VCG surplus vector. The strong -core is a set solution, while the VCG surplus vector is a single point solution. Obviously, increasing can expand the strong -core. A sufficiently large can ensure the VCG surplus vector is in the strong -core.
Theorem 3
Denote for any coalition . Given satisfying , then the VCG surplus vector is in the strong -core.
Proof:
The VCG surplus vector is defined as
| (22) |
For any coalition , we show that the blocking inequality associated with coalition is satisfied.
| (23) | ||||
Hence, the VCG surplus vector is in the strong -core. ∎
The above theorem provides a lower bound on to ensure that the VCG surplus vector is in the strong core. If a very small lower bound can guarantee that the VCG surplus is in the core, we can directly employ the VCG-like payment to incentivize players. In the theorem mentioned above, this lower bound is difficult to calculate. Although we are uncertain whether the VCG surplus is in the -core, we still have another way to comprehensively consider the VCG surplus and the strong -core.
Lemma 1
For any player , the core surplus is not greater than .
Proof:
Given any type profile , for any player , holds, otherwise, there is at least one player , such that
| (24) |
and we have the following inequality
| (25) |
which contradicts the core constraint. ∎
Theorem 4
For the core payment , the amount that player can benefit by deviating from the truthful input strategy is less than or equal to .
Proof:
Suppose not, there is some input such that
| (26) | ||||
where is the payment when the player inputs truthfully.
Next, we have
| (27) | ||||
Note that for any input, we have for all due to Lemma 1. So we can enlarge the left part of the inequality as follows,
| (28) | ||||
The left part of the above inequality is the utility when the player inputs untruthfully, and the right part is the utility when the player inputs truthfully. The inequality contradicts the incentive compatibility property of the VCG-like payments. ∎
Theorem 4 shows that by reducing the distance between and , we can limit the benefits of inputting false data. In other words, although we cannot find a VCG surplus vector in the strong -core, reducing the distance between and as much as possible can still motivate participants to input data truthfully. Eventually, our core-selecting incentive mechanism for federated learning is proposed as follows.
-
Step 1:
Before computing the payments, model is trained and evaluated for each coalition . Meanwhile, the characteristic values are calculated as
(29) -
Step 2:
Next, the VCG surplus is determined as
(30) -
Step 3:
The following quadratic programming is solved to give a solution .
(31) s.t. -
Step 4:
Finally, the payments given to participants are calculated as
(32)
The above procedure determines the observable surplus vector that we want to achieve. In particular, if the VCG surplus vector is in the -core, the solution of the core-selecting incentive mechanism is equal to the VCG surplus vector. Conservative participants are prefer to input data truthfully because the payment under the core-selecting mechanism may be equal to or very close to that under the truthful incentive mechanism. Even if aggressive participants attempt to input false data, Theorem 4 indicates that the additional benefits obtained by inputting false data are also minimized. Since the selected surplus vector is taken from the strong -core and is also reduced in the programming, there is little incentive for any coalition or any participant to deviate from cooperation.
V Efficient Core-selecting Incentive Mechanism based on Sampling Approximation
The proposed core-selecting mechanism is an ideal mechanism for federated learning. However, exact computation of the core-selecting mechanism requires evaluating the additional model with times to obtain the characteristic values before solving the quadratic programming, which is computationally expensive. To address this, our method is to sample a relatively small number of coalitions from a probability distribution, and compute the desired solution on the sampled coalitions.
In our method, a set of coalition is sampled from a probability distribution and the characteristic values of these coalitions are given by aggregating and evaluating additional models. Then, solving the core-selecting quadratic programming over coalitions instead of coalitions gives an approximate core surplus vector, resulting in the following quadratic programming.
| (33) | |||||
| s.t. | |||||
The solution of the above quadratic programming may not satisfy all core constraints. In order to analyze its properties, we consider that satisfies each core constraint with a probability, and similar to [39], we introduce the definition of -probable core as follows.
Definition 2 (-probable core)
A surplus vector is in the -probable core if and only if
| (34) |
Given any coalition drawn from , the core constraint is violated with probability at most . For the exact core-selecting surplus , we have
| (35) |
The definition of -probable core can explain the constraints of approximate quadratic programming (33). The next question we focus on is how to determine the sample size . The following theorem 5 answers this question. Before presenting this theorem, we introduce two known lemmas [48].
Lemma 2
Let be a function class from to , and let be the true value function. If has VC-dimension , then with
| (36) |
i.i.d. samples , we have
| (37) |
for all and with probability .
Lemma 3
The function class has VC-dimension .
Theorem 5
Given a distribution over , and , , solving the programming (33) over coalitions sampled from gives a surplus vector in the -probable core with probability .
Proof:
Given a coalition sampled from , we convert it into a vector where and if and otherwise.
Consider a linear classifier defined by parameter where . If , then we have . Obviously, classifier can identify the core constraint for coalition . If a linear classifier satisfies for all coalitions , then it represents a surplus vector in the -core . This inspires us to define a class of functions to represent the -probable core:
| (38) | |||
This class of functions is a subset of , and it has VC-dimension at most by Lemma 3.
Suppose that we solve quadratic programming (33) on coalition samples , which gives us a solution and the corresponding classifier . Note that holds for .
By Lemma 2, the following inequality holds with probability .
| (39) | ||||
where is a dimensional probability distribution and the second transition holds because and agree on . ∎
Theorem 5 provides a theoretical result for our approximate method. The above incentives reasonably evaluate the contributions of participants. The VCG surplus can be seen as a marginal contribution, and surplus can be seen as a contribution based on the approximate strong -core.
Next, in order to aggregate and obtain a better model, we employ a non-uniform weighted aggregation scheme. Reputation is widely used to measure the reliability of a participant based on its past behavior [49, 50, 8]. The participant with a better reputation will be assigned a greater weight. At each round , the surplus can be determined. We calculate the reputation of each participant based on its contribution from round to round . Let denote participant ’s reputation. It can be computed as
| (40) |
where is a small positive number representing the lower bound. In the next round , we will use to aggregate the new global model as
| (41) |
We implement the efficient core-selecting incentive mechanism by adding additional model evaluation, and the computation process is shown in Algorithm 2.
VI Experiments
The purpose of this section is threefold. First, we empirically demonstrate our theoretical results. In the second part of the experiment, we investigate the influence of inputting untruthful data on the incentive mechanism based on VCG-like payments, core-selecting payments, and efficient core-selecting payments. Moreover, we will test the efficiency of our mechanism.
All tests are performed on a computer with an Intel Xeon 5218 CPU, Nvidia Quadro RTX4000 GPU and 64GB RAM. The optimization problems are solved with Gurobi.
VI-A Validation
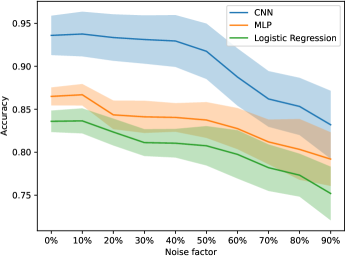
To verify our assumption, a participant is selected, and the participant will input noisy data as shown in Fig. 4. The MNIST dataset is chosen. 10 percent of the dataset is set as an independent test set for the server, and the remaining is divided into 5 parts for 5 participants. Based on Algorithm 1, the logistic regression, multi-layer perceptron (MLP), and convolutional neural network (CNN) models are trained for 10 rounds, respectively. The results are shown in Fig. 5. We can see that the accuracy mainly decreases as the false degree increases. Due to noise causing overfitting, the accuracy increases by around 10 percent. For this phenomenon, we believe that this type of data is also high-quality, as long as it can improve the performance of the global model.

To verify theorem 5, we randomly sample a small fraction of coalitions to implement the efficient core-selecting mechanism for a single round and determine what fraction of all coalitions satisfy the core constraints, which gives us the fraction , referred to as core accuracy. In this experiment, we chose the smaller-scale iris dataset that only has 4 features. This makes it computationally feasible to evaluate all possible models and compute the core-selecting payment exactly. 10 percent of the dataset is set up as an independent test set for the server, and the remaining is divided into 10 parts for 10 participants. Based on Algorithm 2, we will train the logistic regression models and multi-layer perceptron (MLP) models using stochastic gradient descent. The parameters are set as and . The payment, utility, and error will be calculated.
As shown in Fig. 6, even with a small number of sampled coalitions, the resultant surplus vector is still in the -probable core.

Then, as shown in Fig. 7, the errors of decrease as the number of samples increases.

Next, as shown in Fig. 8, we can see that the VCG-like payment cannot satisfy all core constraints, and the efficient core-selecting payment has a higher average accuracy compared to the VCG-like payment.

The above experiments show that the difference between the efficient core-selecting payment and the exact core-selecting payment decreases as the number of samples increases. When the scale of the problem is large, the efficient core-selecting mechanism can improve the computational efficiency by reducing the number of samples.
VI-B Truthfulness
In this experiment, we compare the effects of different inputs on the incentive mechanism based on the VCG-like, core-selecting, and efficient core-selecting payments. Of course, the three payments rule also corresponds to three types of aggregation weights. We still use the MNIST dataset and divide it into 5 parts for 5 participants. The parameter settings from the previous experiment. The logistic regression, multi-layer perceptron (MLP), and convolutional neural network (CNN) models are trained for 10 rounds, respectively. The parameters of the efficient core-selecting are set as and . To simulate the input behavior of participants, we select a participant and design three strategies for the participant to input data untruthfully. Then the selected participant’s accumulated utility is computed. We repeat the entire process 10 times to compute the mean utility.
The first input strategy is adding different proportion of white noise to all training data. The utility of the selected participant is shown in Fig. 9. It is easy to see that the utility decreases with the increase in false degrees. In particular, when the noise is increased to 10 percent, the utility does not decrease but increases slightly. The reason is that adding noise to the data during the training process can prevent overfitting, which is commonly used as a regularization method.

The second input strategy is removing a proportion of data, which is similar to the work of [39]. The third input strategy is inputting some incorrect labels, which is malicious behavior. The results are shown in Fig. 10, and we can see that the utility of the third strategy decreases more significantly than other strategies because it is more malicious than other strategies.


Because rational participants will maximize the utility, the above experiments show that the efficient core-selecting mechanism can prevent participants from inputting low-quality or false data.
Additional experiments are conducted to compare the three mechanisms. As shown in Fig. 11, we can see that there is not much difference between the core-selecting mechanism and the efficient core-selecting mechanism.


VI-C Efficiency
In this experiment, we visualize the run time as the number of people increases. We still use the MNIST dataset. The parameters of the efficient core-selecting mechanism are fixed to sample coalitions ( and ). The main computational overhead is that additional models need to be aggregated and evaluated in each round, so we only compare the running time of a single round. As shown in Fig. 12, as the number of participants increases, the run time of the efficient core-selecting mechanism increases linearly, while the run time of the core-selecting mechanism increases exponentially.

Therefore, the efficient core-selecting mechanism can reduce computational overhead compared to the core-selecting mechanism.
VII Conclusion
In this paper, in order to motivate participants to input truthful data and promote stable cooperation in federated learning, we propose an efficient core-selecting incentive mechanism. First, we introduce a data sharing game for federated learning. Then we used a core-selecting incentive mechanism that combines the advantages of both the VCG-like payment and the core. Different from the classical core-selecting mechanism, this mechanism adopts a relaxation on the core to deal with the randomness in federated learning and minimizes the benefits of inputting false data, which can promote stable cooperation among players and also evaluate the quality of participants’ data. Since the core-selecting incentive mechanism requires exponential time to aggregate and evaluate additional models, we propose an efficient core-selecting mechanism based on sampling approximation. To avoid the impact of low-quality data, the mechanism adjusts the aggregation weight of participants based on their historical contributions. Our experiments demonstrate that the proposed mechanism can prevent participants from inputting false data. In addition, participants will not deviate from cooperation because this mechanism can achieve the desired core accuracy through sampling.
For future work, we wish to continue exploring the connection between federated learning and game theory, and develop more reasonable payments for participants. Additionally, combining reputation and participant selection may improve the performance of global model.
References
- [1] E. Parliament and T. C. of the European Union, “The general data protection regulation (gdpr),” https://eugdpr.org, 2016.
- [2] Q. Yang, Y. Liu, T. Chen, and Y. Tong, “Federated machine learning: Concept and applications,” ACM Transactions on Intelligent Systems and Technology (TIST), vol. 10, no. 2, pp. 1–19, 2019.
- [3] N. Rieke, J. Hancox, W. Li, F. Milletari, H. R. Roth, S. Albarqouni, S. Bakas, M. N. Galtier, B. A. Landman, K. Maier-Hein et al., “The future of digital health with federated learning,” NPJ digital medicine, vol. 3, no. 1, p. 119, 2020.
- [4] Q. Li, Z. Wen, Z. Wu, S. Hu, N. Wang, Y. Li, X. Liu, and B. He, “A survey on federated learning systems: Vision, hype and reality for data privacy and protection,” IEEE Transactions on Knowledge and Data Engineering, vol. 35, no. 4, pp. 3347–3366, 2023.
- [5] Y. Lu, X. Huang, Y. Dai, S. Maharjan, and Y. Zhang, “Blockchain and federated learning for privacy-preserved data sharing in industrial iot,” IEEE Transactions on Industrial Informatics, vol. 16, no. 6, pp. 4177–4186, 2019.
- [6] Y. Zhan, J. Zhang, Z. Hong, L. Wu, P. Li, and S. Guo, “A survey of incentive mechanism design for federated learning,” IEEE Transactions on Emerging Topics in Computing, vol. 10, no. 2, pp. 1035–1044, 2021.
- [7] X. Tu, K. Zhu, N. C. Luong, D. Niyato, Y. Zhang, and J. Li, “Incentive mechanisms for federated learning: From economic and game theoretic perspective,” IEEE Transactions on Cognitive Communications and Networking, 2022.
- [8] Z. Shi, L. Zhang, Z. Yao, L. Lyu, C. Chen, L. Wang, J. Wang, and X.-Y. Li, “Fedfaim: A model performance-based fair incentive mechanism for federated learning,” IEEE Transactions on Big Data, 2022, early access.
- [9] J. Lu, B. Pan, A. M. Seid, B. Li, G. Hu, and S. Wan, “Truthful incentive mechanism design via internalizing externalities and lp relaxation for vertical federated learning,” IEEE Transactions on Computational Social Systems, 2022.
- [10] R. Zeng, S. Zhang, J. Wang, and X. Chu, “Fmore: An incentive scheme of multi-dimensional auction for federated learning in mec,” in 2020 IEEE 40th International Conference on Distributed Computing Systems (ICDCS). IEEE, 2020, pp. 278–288.
- [11] Y. Jiao, P. Wang, D. Niyato, B. Lin, and D. I. Kim, “Toward an automated auction framework for wireless federated learning services market,” IEEE Transactions on Mobile Computing, vol. 20, no. 10, pp. 3034–3048, 2020.
- [12] Y. Deng, F. Lyu, J. Ren, Y.-C. Chen, P. Yang, Y. Zhou, and Y. Zhang, “Fair: Quality-aware federated learning with precise user incentive and model aggregation,” in IEEE INFOCOM 2021-IEEE Conference on Computer Communications. IEEE, 2021, pp. 1–10.
- [13] J. Kang, Z. Xiong, D. Niyato, S. Xie, and J. Zhang, “Incentive mechanism for reliable federated learning: A joint optimization approach to combining reputation and contract theory,” IEEE Internet of Things Journal, vol. 6, no. 6, pp. 10 700–10 714, 2019.
- [14] W. Y. B. Lim, J. Huang, Z. Xiong, J. Kang, D. Niyato, X.-S. Hua, C. Leung, and C. Miao, “Towards federated learning in uav-enabled internet of vehicles: A multi-dimensional contract-matching approach,” IEEE Transactions on Intelligent Transportation Systems, vol. 22, no. 8, pp. 5140–5154, 2021.
- [15] Y. Sarikaya and O. Ercetin, “Motivating workers in federated learning: A stackelberg game perspective,” IEEE Networking Letters, vol. 2, no. 1, pp. 23–27, 2019.
- [16] Y. Zhan, P. Li, Z. Qu, D. Zeng, and S. Guo, “A learning-based incentive mechanism for federated learning,” IEEE Internet of Things Journal, vol. 7, no. 7, pp. 6360–6368, 2020.
- [17] X. Luo, Z. Zhang, J. He, and S. Hu, “Strategic analysis of the parameter servers and participants in federated learning: An evolutionary game perspective,” IEEE Transactions on Computational Social Systems, 2022.
- [18] W. Cheng, Y. Zou, J. Xu, and W. Liu, “Dynamic games for social model training service market via federated learning approach,” IEEE Transactions on Computational Social Systems, vol. 9, no. 1, pp. 64–75, 2021.
- [19] M. Kantarcioglu and R. Nix, “Incentive compatible distributed data mining,” in 2010 IEEE Second International Conference on Social Computing. IEEE, 2010, pp. 735–742.
- [20] R. Nix and M. Kantarciouglu, “Incentive compatible privacy-preserving distributed classification,” IEEE Transactions on Dependable and Secure Computing, vol. 9, no. 4, pp. 451–462, 2011.
- [21] M. Cong, H. Yu, X. Weng, J. Qu, Y. Liu, and S. M. Yiu, “A vcg-based fair incentive mechanism for federated learning,” arXiv preprint arXiv:2008.06680, 2020.
- [22] M. Cong, H. Yu, X. Weng, and S. M. Yiu, “A game-theoretic framework for incentive mechanism design in federated learning,” Federated Learning: Privacy and Incentive, pp. 205–222, 2020.
- [23] M. Zhang, E. Wei, and R. Berry, “Faithful edge federated learning: Scalability and privacy,” IEEE Journal on Selected Areas in Communications, vol. 39, no. 12, pp. 3790–3804, 2021.
- [24] G. Wang, C. X. Dang, and Z. Zhou, “Measure contribution of participants in federated learning,” in 2019 IEEE International Conference on Big Data (Big Data). IEEE, 2019, pp. 2597–2604.
- [25] R. H. L. Sim, Y. Zhang, M. C. Chan, and B. K. H. Low, “Collaborative machine learning with incentive-aware model rewards,” in International Conference on Machine Learning. PMLR, 2020, pp. 8927–8936.
- [26] A. Ghorbani and J. Zou, “Data shapley: Equitable valuation of data for machine learning,” in International Conference on Machine Learning. PMLR, 2019, pp. 2242–2251.
- [27] T. Wang, J. Rausch, C. Zhang, R. Jia, and D. Song, “A principled approach to data valuation for federated learning,” Federated Learning: Privacy and Incentive, pp. 153–167, 2020.
- [28] T. Song, Y. Tong, and S. Wei, “Profit allocation for federated learning,” in 2019 IEEE International Conference on Big Data (Big Data). IEEE, 2019, pp. 2577–2586.
- [29] R. Jia, D. Dao, B. Wang, F. A. Hubis, N. Hynes, N. M. Gürel, B. Li, C. Zhang, D. Song, and C. J. Spanos, “Towards efficient data valuation based on the shapley value,” in The 22nd International Conference on Artificial Intelligence and Statistics. PMLR, 2019, pp. 1167–1176.
- [30] D. B. Gillies, Some theorems on n-person games. Princeton University, 1953.
- [31] H. E. Scarf, “The core of an n person game,” Econometrica, vol. 35, no. 1, pp. 50–69, 1967.
- [32] L. G. Telser, “The usefulness of core theory in economics,” Journal of Economic Perspectives, vol. 8, no. 2, pp. 151–164, 1994.
- [33] Y. Zhu, B. Li, H. Fu, and Z. Li, “Core-selecting secondary spectrum auctions,” IEEE Journal on Selected Areas in Communications, vol. 32, no. 11, pp. 2268–2279, 2014.
- [34] J. Hu, H. Lin, X. Guo, and J. Yang, “Dtcs: An integrated strategy for enhancing data trustworthiness in mobile crowdsourcing,” IEEE Internet of Things Journal, vol. 5, no. 6, pp. 4663–4671, 2018.
- [35] J. James and A. Y. Lam, “Core-selecting auctions for autonomous vehicle public transportation system,” IEEE Systems Journal, vol. 13, no. 2, pp. 2046–2056, 2018.
- [36] B. Ray Chaudhury, L. Li, M. Kang, B. Li, and R. Mehta, “Fairness in federated learning via core-stability,” Advances in Neural Information Processing Systems, vol. 35, pp. 5738–5750, 2022.
- [37] K. Donahue and J. Kleinberg, “Optimality and stability in federated learning: A game-theoretic approach,” Advances in Neural Information Processing Systems, vol. 34, pp. 1287–1298, 2021.
- [38] R. W. Day and P. Cramton, “Quadratic core-selecting payment rules for combinatorial auctions,” Operations Research, vol. 60, no. 3, pp. 588–603, 2012.
- [39] T. Yan and A. D. Procaccia, “If you like shapley then you’ll love the core,” in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 35, no. 6, 2021, pp. 5751–5759.
- [40] Y. Aono, T. Hayashi, L. Wang, S. Moriai et al., “Privacy-preserving deep learning via additively homomorphic encryption,” IEEE Transactions on Information Forensics and Security, vol. 13, no. 5, pp. 1333–1345, 2017.
- [41] M. Abadi, A. Chu, I. Goodfellow, H. B. McMahan, I. Mironov, K. Talwar, and L. Zhang, “Deep learning with differential privacy,” in Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, 2016, pp. 308–318.
- [42] K. Bonawitz, V. Ivanov, B. Kreuter, A. Marcedone, H. B. McMahan, S. Patel, D. Ramage, A. Segal, and K. Seth, “Practical secure aggregation for privacy-preserving machine learning,” in proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, 2017, pp. 1175–1191.
- [43] H. B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. y Arcas, “Communication-efficient learning of deep networks from decentralized data,” in International Conference on Artificial Intelligence and Statistics, 2016.
- [44] C. Yu, H. Tang, C. Renggli, S. Kassing, A. Singla, D. Alistarh, C. Zhang, and J. Liu, “Distributed learning over unreliable networks,” in International Conference on Machine Learning. PMLR, 2019, pp. 7202–7212.
- [45] T. T. Phuong et al., “Privacy-preserving deep learning via weight transmission,” IEEE Transactions on Information Forensics and Security, vol. 14, no. 11, pp. 3003–3015, 2019.
- [46] Y. Narahari, Game theory and mechanism design. World Scientific, 2014.
- [47] T. S. Driessen, Cooperative games, solutions and applications. Springer Science & Business Media, 2013, vol. 3.
- [48] S. Shalev-Shwartz and S. Ben-David, Understanding Machine Learning: From Theory to Algorithms. Cambridge University Press, 2014.
- [49] J. Kang, R. Yu, X. Huang, M. Wu, S. Maharjan, S. Xie, and Y. Zhang, “Blockchain for secure and efficient data sharing in vehicular edge computing and networks,” IEEE Internet of Things Journal, vol. 6, no. 3, pp. 4660–4670, 2018.
- [50] X. Huang, R. Yu, J. Kang, Z. Xia, and Y. Zhang, “Software defined networking for energy harvesting internet of things,” IEEE Internet of Things Journal, vol. 5, no. 3, pp. 1389–1399, 2018.