Effects of valley splitting on resonant-tunneling readout of spin qubits

Device structure— Here, we explain the basic spin qubit system without the valley splitting proposed in Ref. tanaJAP . We utilize the nonlinear current behavior of the resonant-tunneling of the channel-QD to detect the spin states of the qubit-QDs (Fig.1(a)). Figure 1(b) is the single unit which consists of a channel-QD coupled with the qubit-QDs that represents qubits. The qubit is represented by an electron spin confined in the qubit-QD with its lowest energy level. The qubit states $|0\rangle$ and $|1\rangle$ are defined as the $\downarrow$-spin and $\uparrow$-spin states, respectively. The channel-QD coupled to the qubit-QDs is connected to the source and drain electrodes. The drain electrode is connected to a conventional transistor such as metal-oxide-semiconductor field-effect transistors(MOSFETs), which controls the channel current $I_{\rm D}$. The channel-QD plays both roles of the coupling between the qubits, and the readout. The electric potential of the qubit-QDs is controlled by the control gates $V_{\rm cg}$. The electric potential of the channel-QD is also changed by adjusting that of the source and drain voltage $V_{\rm D}$. Static magnetic field $B_{z}$ is applied to generate Zeeman splitting. The both ends of the qubit array are channel-QDs which couple one qubit which corresponds $W_{12}=0$ or $W_{23}=0$ in Fig. 1(b).

Single qubit operation— Single qubit operations are carried out in a conventional way by using the gradient magnetic field method Takeda2 ; Yoneda (local magnets are not shown in Fig. 1).

Qubit-qubit coupling— The coupling between qubits are carried out when there is no applied voltage ($V_{\rm D}=0$). The electron in the channel-QD mediates the coupling between the two qubits (upper-left figure of Fig.1(c)). The coupling between qubits are described as the three QD system which has been already investigated in the literatureFei ; Burkard ; Kandel ; Noiri ; Medford .

Readout process— Readout of the qubit states is carried out by applying $V_{\rm D}$. In order not to directly change the qubit states, the energy level of the qubit-QD(QD₁ or QD₃) is lowered downward as shown in the upper-right figure of Fig.1(c). This situation is realized by applying $V_{\rm cg}$. By adjusting the energy level of the channel-QD(QD₂) to the upper energy-level of the singlet states of the qubits, the channel electrons go back and forth between these energy levels and reflect the qubit states on $I_{\rm D}$, as denoted by the red arrows in the right figures of Fig.1(c).

It is also assumed that the qubit-QD has a large on-site Coulomb energy $U$ Engel . The spin direction of the upper energy levels of the singlet is opposite to that of the lower electron spin. The $I_{\rm D}$ changes when the energy level of the channel-QD resonates with those of the upper energy levels of the singlet states. The backaction of the readout is estimated by comparing the measurement time $t_{\rm meas}$ with a coherence time $t_{\rm dec}$. The ratio $t_{\rm dec}/t_{\rm meas}$ corresponds to the possible number of the readout, which is desirable to exceed more than hundred to realize the surface code. In Ref. tanaJAP , we found the parameter regions in which $t_{\rm dec}/t_{\rm meas}>100$ is satisfied.

Under the applied magnetic field, both the energy levels of the QDs and the source and drain exhibit spin-splitting Sanchez , as illustrated later in Fig. 4. We assume that the up-spin current ($\uparrow$-current) and the down-spin current ($\downarrow$-current) are independent, then, the $\uparrow$-current and $\downarrow$-current can be treated to have different Fermi energies $E_{F\pm}=E_{F}\mp\Delta_{z}/2$. The $\uparrow$ and $\downarrow$-currents are controlled by the transistor which is connected to the channel-QD.

Stacking the three-QD array system will form the surface code, if the forthcoming 2nm-transistor architecture TSMC2023 ; Intel2023 ; IMEC2023 ; Kim ; Ryckaert is used. Two types of stacking forms are discussed in appendix A.

The valley-splitting energy $E_{\rm VS}\equiv E_{V+}-E_{V-}$ between the two valley states $E_{V+}$ and $E_{V-}$ are approximately within the range from 10 $\mu$eV to 2 meVGoswami ; Gamble . The valley splitting can be treated separately into three regions relating with an applied magnetic field described by the Zeeman splitting energy $\Delta_{z}\equiv g\mu_{B}B_{z}$:
(1) $E_{\rm VS}<\Delta_{z}$ (small valley region),
(2) $E_{\rm VS}\approx\Delta_{z}$ (intermediate valley region),
(3) $E_{\rm VS}>\Delta_{z}$ (large valley region).
In this study, the small valley region of $E_{\rm VS}<\Delta_{z}$ is mainly considered. The large valley region of $E_{\rm VS}>\Delta_{z}$ is treated in appendix C. In these two regions, no spin flip can be assumed. The intermediate region $E_{\rm VS}\approx\Delta_{z}$, where the spin flips happen, is not treated here.

In general, the valley energies are randomly distributed in space due to variations in the fabrication process. Consequently, it is possible for the three quantum dots (QDs) depicted in Fig. 1(b) to have different valley energies, indicating a nonuniformity in these energies. In the latter part of this study, we will present the current characteristics for different energy levels among the QDs. The valley splitting is modeled by replacing a single energy level $E_{i}$ in a QD with two energy levels $E_{ia}$ and $E_{ib}$ ($i=1,2,3)$. The source and drain electrodes consist of three-dimensional electrons, and it is assumed that there are no valley splittings in the electrodes, similar to bulk silicon.

Figure 2 shows the change in the energy band diagram when there are small valley splittings for qubit-QDs ($E_{\rm VS}<\Delta_{z}$). Because of the valley splitting, the energy diagram of qubit-QDs changes from Fig. 2(a) to Fig. 2(b). A large on-site Coulomb energy $U$ is assumed ($U\gg\Delta_{z},E_{\rm VS}$).

Figure 3 shows the energy diagram of the relationship between the qubit-QDs (QD₁ or QD₃) and the channel-QD (QD₂). In the readout mode, the bottom of the energy band of the channel-QD is higher than those of the qubits (Fig. 1(c)). Depending on the qubit states ($|0\rangle$ or $|1\rangle$) and currents ($\uparrow$ or $\downarrow$-currents), different distributions of the current characteristics are considered. The readout mechanism is described such that if there is an energy level in the qubit-QDs (circles in Figs. 2 and 3 for the qubit-QDs), electrons with the same spin can tunnel into the qubit-QDs. When there is no corresponding energy for a given $V_{\rm D}$, the tunneling is blocked. This blocked feature is expressed by the no tunneling term in the Hamiltonian shown below ($W_{i\xi,j\xi^{\prime}}=0$ in Eq.(1)).

From Fig. 3, the $\uparrow$-spin electron of the $\uparrow$-current can enter the qubit-QD only when the qubit-QD is in $|0\rangle$, and $\downarrow$-spin electron of the $\downarrow$-current can enter the qubit-QD only when the qubit-QD is in $|1\rangle$. Depending on the spin states of the two-qubit-QD (QD1 or QD3), four qubit states $|00\rangle$(or $|\downarrow\downarrow\rangle$), $|01\rangle$(or $|\downarrow\uparrow\rangle$), $|10\rangle$(or $|\uparrow\downarrow\rangle$), and $|11\rangle$ (or $|\uparrow\uparrow\rangle$) exist. Because $|\downarrow\uparrow\rangle$ has the same effect as $|\uparrow\downarrow\rangle$, only $|\uparrow\downarrow\rangle$ is considered in the following.

The valley splitting energy of $E_{\rm VS}\ll 100\mu$eV is close to the expected operating temperature of approximately 100 mK (which is around 10 $\mu$eV). As a result, the mixing of valley energy levels ($E_{ia}$ and $E_{ib}$($i=1,2,3$)) during the tunneling process must be taken into account, regardless of whether the qubit electron (the first electron) is positioned at the lower ($E_{V-}$) or the upper ($E_{V+}$) of the valley energy level.

In the readout process, the energy levels $E_{ia}$ and $E_{ib}$ ($i=1,2,3)$ are considered as depicted in Fig. 3. Thus, we formulate three QDs each of which have two valley energy levels. Strong uniform magnetic field $B_{z}$ is applied, and there is no gradient magnetic field. Because no spin flip is assumed, the $\uparrow$ and $\downarrow$ spins can be treated separately. Then, the Hamiltonian of the three QDs depicted in Fig. 3 is given by

where $f_{k_{\alpha},s}^{\dagger}$ ($f_{k_{\alpha},s}$) creates (annihilates) an electron of momentum $k_{\alpha}$ and spin $s(=\pm 1/2)$ in the electrodes $(\alpha=S,D)$. $d^{\dagger}_{i\xi s}$ ($d_{i\xi s}$) creates (annihilates) an electron in the QDs ($i=1,2,3$) where $\xi=a$ and $\xi=b$ correspond to the lower and higher valley levels. $E_{k_{\alpha}s}=E_{k_{\alpha}}+sg\mu_{B}B_{z}$ is the energy level of the electrode ($\alpha=S,D$), and $E_{i\xi s}=E_{i}+sg\mu_{B}B_{z}+\Xi_{\xi}$ is the energy level for three QDs ($i=1,2,3$) with $\Xi_{a}=-E_{\rm VS}/2$ and $\Xi_{b}=E_{\rm VS}/2$. $E_{i}$ is an energy level without the valley splitting or magnetic fields.

The coupling coefficients of the electrodes to the channel-QD are given by

($\alpha=S,D$, $\xi=a,b$). Strictly speaking, $\Gamma_{\alpha,s,\xi}(\omega)$ depends on the spin direction through the density of states, and the valley levels. However, for the sake of simplicity, we take $\Gamma_{\alpha}\equiv\Gamma_{\alpha,\uparrow,\xi}(\omega)=\Gamma_{\alpha,\downarrow,\xi}(\omega)(\alpha=S,D,\xi=a,b)$.

Following Ref. Jauho ; Meir1 , the current $I_{S}$ of the source electrode is derived from the time-derivative of the number of the electrons $N_{S}\equiv\sum_{k_{S}s}f_{k_{S}s}^{\dagger}f_{k_{S}s}$ of the source electrode given by

where

and

When the direction of the drain current $I_{\rm D}$ is defined as the increase in the number of electrons in the drain electrode, we can take $I_{\rm S}=I_{\rm D}$. Because we assume that the spin-flip process is neglected, the suffix $s$ is omitted in the following.

The Green functions are derived using the equation of motion method Jauho . For example, the time-dependent behavior of the operator $f_{k_{\alpha},s}$ is derived from $i\frac{df_{k_{\alpha},s}}{dt}=[H,f_{k_{\alpha},s}]$, and we have

The Green functions of the electrodes ($\alpha=S,D$) are the free-particle Green functions given by

where $f_{\alpha}(\omega)=[\exp[(\omega-\mu_{\alpha})/(k_{B}T)]+1]^{-1}$ ($k_{B}$, $\mu_{\alpha}$, and $T$ denote the Boltzmann constant, the chemical potential of the $\alpha$-electrode, and temperature, respectively). As shown in the appendix D, all Green functions are obtained after a long derivation process. Eventually, the current formula is expressed by

where $b_{a}^{r}$, $b^{r}$, $a_{vba}^{r}$, and $a_{vab}^{r}$ are the retarded expressions of the functions given by

Here, we define

with $\gamma_{f}\equiv[\Gamma_{S}+\Gamma_{D}]/2$ ($\Lambda_{i}(\omega)$ is assumed to be constant and included in $E_{i}$ in the following), and $\Sigma_{2a}\equiv 1/(\omega-E_{2a})$ and $\Sigma_{2b}\equiv 1/(\omega-E_{2b})$. $A_{va}$ and $A_{vb}$ are given by

where $\Sigma_{1\xi}\equiv 1/(\omega-E_{1\xi})$ and $\Sigma_{3\xi}\equiv 1/(\omega-E_{3\xi})$ ($\xi=a,b$). $W_{12\xi\xi^{\prime}}$ expresses the coupling between the $1\xi$ state and the $2\xi^{\prime}$ state. We assume that $W_{12ab}=W_{12aa}$, $W_{32ab}=W_{32aa}$, $W_{12ba}=W_{12bb}$, and $W_{32ba}=W_{32bb}$, which means that the tunneling probabilities between different valley energies are the same as those between the same valley energies. Using these formalisms, four distributions can be distinguished as follows. For only the channel-QD without coupling to qubits (no qubit case), $W_{12aa\uparrow}=W_{12aa\downarrow}=W_{32aa\uparrow}=W_{32aa\downarrow}=0$ is taken for the $\uparrow$ and $\downarrow$-currents. For $|\uparrow\downarrow\rangle$, $W_{12aa\uparrow}=W_{32aa\downarrow}=W$ and $W_{12aa\downarrow}=W_{32aa\uparrow}=0$ are taken (for the state $|\downarrow\uparrow\rangle$, the symbols $\uparrow$ and $\downarrow$ are exchanged). For the $|\uparrow\uparrow\rangle$ case, $W_{12aa\uparrow}=W_{32aa\uparrow}=W$ for the $\uparrow$-current and $W_{12aa\downarrow}=W_{32aa\downarrow}=0$ for the $\downarrow$-current are taken. For the $|\downarrow\downarrow\rangle$ case, $W_{12aa\uparrow}=W_{32aa\uparrow}=0$ for the $\uparrow$-current and $W_{12aa\downarrow}=W_{32aa\downarrow}=W$ for the $\downarrow$-current are taken.

In the large valley region, $E_{\rm VS}>\Delta_{z}$ and $E_{\rm VS}>V_{\rm D}$ are assumed, and the effect of the valley splitting is neglected. This is the same situation as that in our previous paper tanaJAP . The current $I_{\rm D}$ for the large valley splitting case is given by

We use the core model for $I_{\rm D}$-$V_{\rm D}$ of the fin field-effect transistor (FinFET), given by BSIM

where $\beta\equiv(\mu{\mathcal{W}}/L)(\epsilon/EOT)$ ($L=1$ µm, ${\mathcal{W}}=80$ nm, $\mu=1000$ cm²V^-1s^-1, $EOT=1$ nm, and $\epsilon=3.9\times 8.854\times 10^{-12}$ F/m represent the gate length, gate width, mobility, oxide thickness, and dielectric constant, respectively BSIM ). The output voltage $V_{\rm out}$ is numerically determined by solving the equations of the QD device and the transistor, given by

where $V_{\rm ds}$ is the bias difference of the source and drain of the transistor. This equation is solved numerically using Newton’s method, assuming $I_{S}=I_{\rm TR}$.

Using the current difference $\Delta I$ depending on different qubit states in Fig. 3, the qubit states are distinguished. The measurement time $t_{\rm meas}$ is estimated using $\Delta I$ and shot noise $S_{N}$, given by Schon

The measurement times of the four cases in Fig. 3 are calculated from the current difference $\Delta I$ from the reference state where there is no coupling to the qubit (no qubit case). Here, the classical form $S_{N}=2eI_{\rm D}$ of the shot noise is used.

Although the decoherence time was calculated using Fermi’s golden rule previously tanaJAP , in this study, we introduce a fixed coherence times $t_{\rm dec}$. This is because it is hard to disassemble the many tunneling processes in the present model, and it is rather beneficial to use a fixed coherence time to directly compare the theory to experiments.

Figure 4 shows the current characteristics of a single QD coupled to the source and drain under a magnetic field. Figure 4(a) shows the $\uparrow$ and $\downarrow$-currents separately. Single peaks are observed for each current element. The electrons of the $\uparrow$ and $\downarrow$-currents have different energy bands, as shown in the upper insets of Fig. 4(a). The switching-on voltage of the $\uparrow$-current is lower than that of the $\downarrow$-current for this parameter region because the energy level of the $\uparrow$-spin is higher than that of the $\downarrow$-current (see upper-left inset of Fig. 4(a)). Meanwhile, the resonant peaks end at the same $V_{\rm D}$ for the $\uparrow$, and $\downarrow$-currents (see middle-right inset of Fig. 4(a)). Figure 4(b) shows the total current $I_{\rm D}$ without the transistor or valley splitting, which is the summation of the $\uparrow$ and $\downarrow$-currents. The step structure is the result of the different switching-on voltages of the $\uparrow$ and $\downarrow$-currents.

The characteristics of the resonant peak can be approximately analyzed by comparing the energy level $E_{2}^{(0)}\pm\Delta_{z}/2$ of channel-QD with those of the two electrodes. The detailed analysis for the resonant peak structure is presented in appendix B. Let us shortly analyze Fig. 4 using Table 2 of appendix B. Because $E_{2}^{(0)}+\Delta_{z}/2=0.88+0.116=0.996$ meV is below $E_{F}$=1 meV, the top row of Table 2 is applied. Then, the switching-on voltages are approximately given by $V_{{\rm D}\uparrow}^{\rm on}\approx 2(E_{F}\!-\!E_{2}^{(0)}\!-\Delta_{z}/2)=0.008$ meV and $V_{{\rm D}\downarrow}^{\rm on}\approx 2(E_{F}\!-\!E_{2}^{(0)}\!+\Delta_{z}/2)=0.472$ meV for the $\uparrow$ and $\downarrow$-currents, respectively. Meanwhile, the switching-off voltages are given by $V_{{\rm D}\downarrow}^{\rm off}\approx 2E_{2}^{(0)}=1.76$ meV. The width of the resonant peaks $4E_{2}^{(0)}+\Delta_{z}-2E_{F}$ are 1.752 and 1.288 meV, respectively. The peak centers $E_{F}-\Delta_{z}/2$ are 0.884 and 1.116 meV. If we compare these values with those in Fig. 4(a), the $V_{{\rm D}\downarrow}^{\rm off}$ is approximately correct. However, the other values are shifted. Thus, it is better to use the analysis for obtaining general trends.

Figure 5 shows $I_{\rm D}$-$V_{\rm D}$ characteristics when two qubits are added to the simple resonant-tunneling structure of Fig. 4(b). Apparently, the current for the pair $\uparrow\downarrow$ or $\downarrow\uparrow$ exists in the middle of the $\uparrow\uparrow$ and $\downarrow\downarrow$ pair. In the present case, as shown in Fig. 4, the switching-on voltage of the $\uparrow$-current is lower than that of the $\downarrow$-current. For the $\downarrow\downarrow$ pair ($|00\rangle$ state), the resonant energy level of the qubits, which matches the energy level of the channel-QD, becomes high, as shown in Figs. 3(a) and 3(c). The resonance occurs around $E_{1}(=E_{3})=E_{2}^{(0)}+V_{\rm D}/2$, which leads to $V_{\rm D}\approx 2(E_{1}-E_{2}^{(0)})=2(1.2-0.88)=0.64$meV. The small peak structure of $\downarrow\downarrow$ pair around $V_{\rm D}\approx 0.6$ meV is the result of this resonance. Meanwhile, for the $\downarrow\downarrow$ pair ($|11\rangle$ state), the resonant energy level of the qubit-QD and the channel-QDs becomes low, as shown in Figs. 3(b) and 3(d). Thus, the corresponding resonance peak is hidden in the original resonant-tunneling peak of Fig. 4(b).

In Fig. 6(a), the $\uparrow$- and $\downarrow$-currents are separately shown as functions of $V_{\rm D}$ for two valley splitting energies ($E_{\rm VS}=10\mu$eV and $E_{\rm VS}=100\mu$eV). The single-peak structures represent the resonant peak by the resonant energy level similar to Fig. 4. In Fig. 6(b), the total current $I_{\rm D}$ by the $\uparrow$- and $\downarrow$-currents are shown. A shoulder structure becomes clear as $E_{\rm VS}$ becomes larger.

The shoulder structure is analyzed in Table 2 of appendix B. The total current is the summation of the currents of $E_{2a}$ and $E_{2b}$ from Eq.(3). From Table 2, the widths of the resonant peak and peak center are approximately estimated by $4E_{2}^{(0)}+\Delta_{z}-2E_{F}$ and $E_{F}-\Delta_{z}/2$, respectively. If we apply $E_{2a}$ and $E_{2b}$ into $E_{2}^{(0)}$, the center of the resonant peak does not change, but the width of the resonant peak depends on the valley energies of $E_{2a}$ and $E_{2b}$. The width of the valley of $E_{2b}$ is wider than that of $E_{2a}$ because $E_{2b}=E_{2a}+E_{\rm VS}$. Then, the shoulder of Fig. 6 is the result of the wide resonant peak added to the narrow resonant peak.

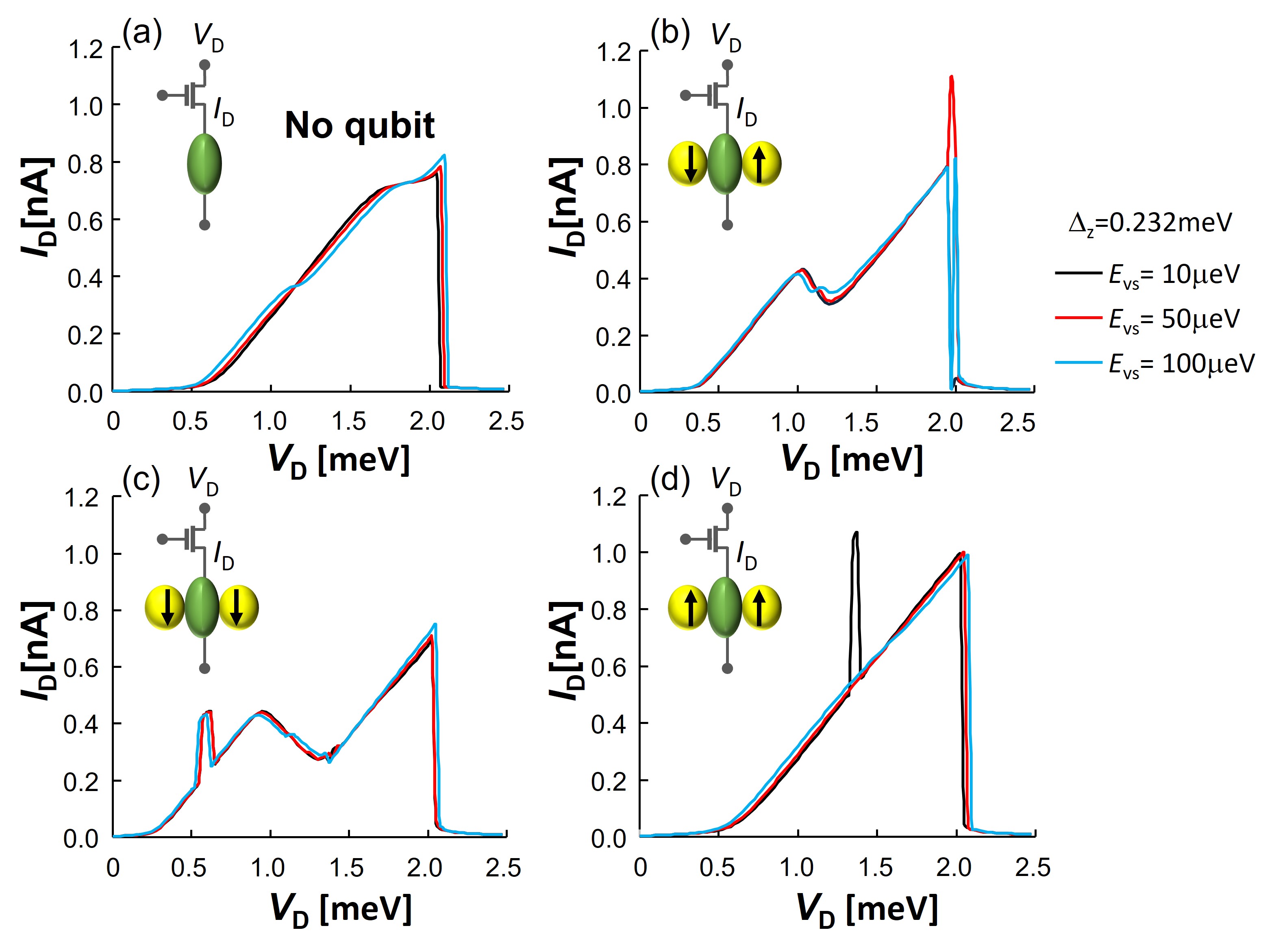
Figure 7 shows $I_{\rm D}$-$V_{\rm D}$ with a connection to the transistor when both sides of the qubit-QDs have the same value of $E_{\rm VS}$. The transistor size $L=10$ µm is determined to increase the different $V_{\rm out}$ values depending on the qubit states. This situation is realized when the resistance of the transistor is comparable to that of the channel-QD. Because the current characteristics of the transistor have less nonlinearity than those of the channel-QD, the $I_{\rm D}$ values of Fig. 7 have gentler slopes than those of Fig. 6(b).

The different $I_{\rm D}$-$V_{\rm D}$ characteristics are explained similarly to Fig. 5. For the $\downarrow\downarrow$ pair ($|00\rangle$ state) of Fig. 7(c), the resonant energy level of the qubit-QDs, which is the upper energy level of the singlet state, becomes high, as shown in Figs. 3(a) and 3(c), resulting in a peak structure at lower $V_{\rm D}$. Meanwhile, for the $\uparrow\uparrow$ pair ($|11\rangle$ state) of Fig. 7(d), the resonant energy level of the qubit-QDs becomes low, as shown in Figs. 3(b) and 3(d). Then, the resonant peak structure is hidden in the original resonant-tunneling peak between the source and drain. The $I_{\rm D}$-$V_{\rm D}$ characteristics of Fig. 7(b) takes the middle properties between Figs. 7(c) and 7(d). Due to the presence of two energy levels in each QD, multiple resonant peaks appear in the current characteristics. The sharp peaks observed in Figs. 7(b-d) can be attributed to the complex resonant structure involving six energy levels across the three QDs (as indicated in the denominator of Eq. (LABEL:current_formula)). Consequently, the presence of valley energy levels enhances the transitions between energy levels, resulting in a greater difference in the $I_{\rm D}$s that reflect the qubit states.

It has been reported that valley splitting energies vary depending on the location in the range of $(100{\rm nm})^{2}$ Losert . Herein, we consider the case where the three QDs have different valley splitting energies. We calculate $E_{\rm VS}=$10, 20, 50, and 100 µeV for QD₁(left qubit) and QD₃(right qubit). Figure 8 shows the $I_{\rm D}$-$V_{\rm D}$ characteristics of the small valley region for $W=0.09$ meV. The shape of the $I_{\rm D}$-$V_{\rm D}$ characteristics is primarily determined by $E_{2}^{(0)}<E_{1},E_{3}$ (Fig. 8(a)) or $E_{2}^{(0)}>E_{1},E_{3}$ (Fig. 8(b)). Because the energy level of QD₂ increases as $V_{\rm D}$ increases, such as $E_{2}=E_{2}^{(0)}+V_{\rm D}/2$, the case of $E_{2}^{(0)}<E_{1},E_{3}$ (Fig. 8(a)) shows clear peak structures as a result of energy crossing between $E_{2}$ and $E_{1}$, $E_{3}$. Meanwhile, for the case of $E_{2}^{(0)}>E_{1},E_{3}$, nonlinear characteristics appear as a result of higher-order tunneling, resulting in a vague peak structure in Fig. 8(b). By the nonuniformity of the valley splitting, $I_{\rm D}$-$V_{\rm D}$ characteristics in Fig. 8 are modified in a more complicated way from those in Fig. 7.

Figure 9 shows the output voltage $V_{\rm out}$ corresponding to Figs. 8(a) and 8(b). For the case of $E_{2}^{(0)}<E_{1},E_{3}$ (Fig. 9(a)), a clear separation among various $V_{\rm out}$ values can be observed. In contrast, for the case of $E_{2}^{(0)}>E_{1},E_{3}$ (Fig. 9(b)), the difference among $V_{\rm out}$ values becomes small. A larger voltage difference is desirable for distinguishing different qubit states, which is conducted by connected circuits, as in a previous study tanaAPL . Thus, the case of $E_{2}^{(0)}<E_{1},E_{3}$ is better for the detection of qubit states.

Figure 10 shows the results for $t_{\rm dec}/t_{\rm meas}$. Regarding $t_{\rm dec}/t_{\rm meas}$, simultaneous peaks of $t_{\rm dec}/t_{\rm meas}>100$ appear around the right end of the resonant peak for the case of $E_{2}^{(0)}<E_{1},E_{3}$. In contrast, for the case of $E_{2}^{(0)}>E_{1},E_{3}$, a large $t_{\rm dec}/t_{\rm meas}$ can be seen around $V_{\rm D}=0$, where the energy levels of the three QDs are close to each other. The region of $t_{\rm dec}/t_{\rm meas}>100$ for $W=0.18$ meV appears to be smaller than that for $W=0.09$ meV (figure not shown). Increased mixing of resonant energy levels appears to increase the nonlinearity of $I_{\rm D}$-$V_{\rm D}$ and increase $t_{\rm dec}/t_{\rm meas}$. The valley splitting energy is closer to $W=0.09$ meV than $W=0.18$ meV, and increased energy level mixing is expected at $W=0.09$ meV. Note that $t_{\rm dec}/t_{\rm meas}$ in Fig. 10 is larger than that in Fig. 18 of appendix C, which is equivalent to no valley splitting case. Therefore, the increased nonlinearity of the current improves the readout in this small nonuniformity of the valley energy levels.

We also calculate $E_{\rm VS1}=10$ µeV, $E_{\rm VS2}=50$ µeV, $E_{\rm VS3}=100$ µeV, and $E_{\rm VS1}=10$ µeV, $E_{\rm VS2}=50$ µeV, $E_{\rm VS3}=10$ µeV, both for $E_{2}^{(0)}<E_{1},E_{3}$. In the former case, we can see the simultaneous peaks $t_{\rm dec}/t_{\rm meas}>100$ around the right end of the resonant peak around $V_{\rm D}\approx 2.0V$ (figures not shown). However, in the latter case, the peaks $t_{\rm dec}/t_{\rm meas}>100$ around $V_{\rm D}\approx 2.0V$ deviate from each other (figures not shown). Therefore, although it is difficult to obtain a unified understanding of these cases, simultaneous peaks with $t_{\rm dec}/t_{\rm meas}>100$ are expected when the valley splitting energies between the nearest QDs are close to each other.

The data supporting the findings of this study are available in this article.

T.T. conceived and designed the theoretical calculations. K.O. discussed the results from the experimentalist viewpoint.

The authors have no conflicts of interest to disclose.