Effects of the non-Markovianity and non-Gaussianity of active environmental noises on engine performance

First, we consider the ‘shot’-noise or ‘white Poisson’-noise model Kanazawa ; entropy . In this model, $\zeta_{i}(t)$ is given by

where $c_{i,n}$ is the noise magnitude determined by a given distribution $p_{i}(c)$ and $t_{i,n}$ is the $n$-th event time of the Possion process with rate $\lambda_{i}$. Note that the time interval of successive Poisson events ($\Delta t_{i,n}=t_{i,n+1}-t_{i,n}$) obeys the distribution $P(\Delta t)=\lambda e^{-\lambda\Delta t}$. The $\delta$-function type impulse of this noise describes a sequence of microscopic discrete events such as random collisions of bacteria Kanazawa ; Pak without any memory in the first approximation entropy . Thus, this shot noise is Markovian with $\tau_{i}\rightarrow 0$ in Eq. (2) and its autocorrelation function is given by Kanazawa ; entropy

where $\langle\cdots\rangle_{p_{i}}$ denotes average over the distribution $p_{i}(c)$ with $\langle c_{i,n}\rangle_{p_{i}}=0$. Though Eq. (4) shows the same $\delta$-correlated property as that of the equilibrium white noise, the shot noise leads to a nonequilibrium steady state as shown in Fig. 1(b) due to the discrete nature of the noise. The equilibrium (Gaussian white) limit is obtained by taking the $\lambda_{i}\rightarrow\infty$ limit with keeping the noise strength constant as $\lambda_{i}\langle c^{2}\rangle_{p_{i}}=2D_{i}/\gamma_{i}^{2}$ Kanazawa . In this limit, we can infer an effective temperature from the noise strength as $D_{i}/\gamma_{i}\equiv T_{i}$ in the Boltzmann constant unit by setting $k_{\textrm{B}}=1$. For finite $\lambda_{i}$ and $\langle c^{2}\rangle_{p_{i}}$, the shot noise is Markovian, but non-Gaussian, which can be checked from the nonzero fourth cumulant of the noise entropy .

The colored-Poisson noise is a generalized version of the white-Poisson noise Pak . In this model, $\zeta_{i}(t)$ is given by

where $c_{i,n}$ and $t_{i,n}$ are defined in Eq. (3), and $H(t)$ is the Heaviside step function: $H(t)=1$ for $t>0$, $0$ for $t<0$, and $1/2$ at $t=0$. With this noise, each $n$-th impulse from the collision at time $t_{i,n}$ exponentially decays with the finite persistence time $\tau_{i}$. Thus, this noise is non-Markovian and the Markovian white-Poisson noise is obtained in the $\tau_{i}\rightarrow 0$ limit. The noise autocorrelation function is

which is explicitly derived in Appendix A.1. By comparing Eq. (6) with Eq. (2), we can identify $D_{i}=\gamma_{i}^{2}\lambda_{i}\langle c^{2}\rangle_{p_{i}}/2$.

The non-Gaussianity of this noise can be checked from the calculation of the fourth cumulant of the noise. For a Poisson noise $\zeta(t)$ with the form $\zeta(t)=\sum_{n}c_{n}H(t-t_{n})h(t-t_{n})$, where $h(t)$ is an arbitrary function of time, its fourth cumulant is given by Manuel

where $\langle\langle\cdots\rangle\rangle$ stands for the cumulant average. Thus, the fourth cumulant of the colored-Poisson noise with $h(t)=e^{-t/\tau}/\tau$ is given by $\lambda\langle c^{4}\rangle_{p_{i}}/(4\tau^{3})$, which may serve as a measure for the non-Gaussianity of the noise. Hence, the colored-Poisson noise model provides a systematic way to study the effect of the non-Markovianity and the non-Gaussianity of an active noise by controlling the two parameters, $\lambda$ and $\tau$.

In this model, the noise $\zeta_{i}(t)$ satisfies the following Ornstein-Uhlenbeck process:

where $\xi_{i}$ is a Gaussian white noise with zero mean and unit variance. It is straightforward to see that the steady state distribution of $\zeta_{i}$ is Gaussian from Eq. (8). Thus, the AOUP noise is Gaussian. Using the general solution of Eq. (8), $\zeta_{i}(t)=e^{-t/\tau_{i}}\zeta_{i}(0)+\sqrt{2D_{i}/\gamma_{i}^{2}}\tau_{i}^{-1}\int_{0}^{t}e^{-(t-s)/\tau_{i}}\xi_{i}(s)ds$, the noise autocorrelation can be calcuated as

In the steady state where $t,t^{\prime}\gg\tau_{i},\tau_{j}$, the autocorrelation function takes the same form in Eq. (2). Thus, the AOUP noise is non-Markovian, but Gaussian. The Gaussian white noise is obtained in the $\tau_{i}\rightarrow 0$ limit.

Consider a self-propelled particle moving in a two-dimensional space. The ABP model describes the motion of the active particle with the self-propulsion speed $v_{0}$ ABP1 ; ABP2 . Its motion can be described by the following overdamped Langevin equation:

where $\textbf{{e}}_{\theta}=(\cos\theta,\sin\theta)^{\textsf{T}}$ is the unit self-propulsion vector, ${\bm{\xi}}=(\xi_{1},\xi_{2})^{\textsf{T}}$ and $\xi_{\theta}$ are the Gaussian white noises with zero mean and unit variance, $\textbf{{f}}(\textbf{{x}},t)=(f_{1}(\textbf{{x}},t),f_{2}(\textbf{{x}},t))^{\textsf{T}}$ is an external force, and $D_{\theta}$ is the noise strength for the rotational angle $\theta$. If we ignore the equilibrium noise $\sqrt{2\gamma T}{\bm{\xi}}$, regard the self-propulsion term as an active noise ${\bm{\zeta}}\equiv v_{0}\textbf{{e}}_{\theta}$, and integrate the angular dynamics, we obtain the same equation as Eq. (1). Then the noise autocorrelation function becomes ABP1

where $\tau=1/D_{\theta}$ and $\langle\cdots\rangle_{\theta}$ denotes an average over the $\theta$ variable. By comparing Eq. (11) with Eq. (2), we can identify $D=\gamma^{2}v_{0}^{2}\tau/2$. For completeness, we present the derivation of Eq. (11) in Appendix A.2. Note that the noise autocorrelation can be also calculated in the three dimensions ABP2 .

Different active-noise models yield different steady states. To illustrate the difference, we perform numerical simulations of the one-dimensional Brownian motion trapped in a harmonic potential, $f(x)=-kx$ with $k=1$ and $\gamma=1$, described by Eq. (1). From the simulations, we obtain the steady-state probability distribution of $x$ for various noise models from $10^{6}$ data, which are shown in Fig. 1. For all these simulations, we set the parameters for the second moment of $x$ being $\langle x^{2}\rangle=1/4$. Parameters of respective models are specified in the caption of Fig. 1.

Figure 1 (a) shows the steady-state distribution when $\zeta$ is an equilibrium noise, i.e., the Gaussian white noise satisfying $\langle\zeta(t)\zeta(t^{\prime})\rangle=2D\delta(t-t^{\prime})$ with temperature $T=D/\gamma=1/4$. As expected, the distribution is exactly Gaussian. The steady-state distribution of the shot-noise model is evidently deviated from the Gaussian as shown in Fig. 1 (b), even though the noise autocorrelation function and the second moment of $x$ are the same as those of the equilibrium noise. Figure 1 (c) shows the steady-state distribution of the colored-Poisson noise model, which is also non-Gaussian. Different from the other active-noise models, the AOUP model results in the Gaussian distribution as shown in Fig. 1 (d), which is due to the Gaussianity of the noise. Finally, Fig. 1 (e) is the steady-state distribution of the two-dimensional ABP model along the $x$ direction. The distribution has two symmetric peaks, which have been usually observed in the ABP systems ABP_bimodal .

First, we consider the case where the total mechanical force is given as a linear force in position such as

where $\textsf{A}(t)$ is a time-dependent force matrix. Then, Eq. (1) can be written as

where $\bm{\zeta}=(\zeta_{1},\cdots,\zeta_{N})^{\textsf{T}}$. Note that the force matrix can be divided into the conservative and nonconservative part as $\textsf{A}(t)=\textsf{A}^{\textrm{c}}(t)+\textsf{A}^{\textrm{nc}}(t)$. The general solution of Eq. (16) is

with the propagator $\textsf{K}^{(b,a)}=\exp\left[-\int_{a}^{b}dt~{}\textsf{A}(t)\right]$. As the active noise $\bm{\zeta}$ is non-Markovian in general, we should be careful in preparing the initial condition. Here we consider the situation that the system and the environment are separated for $t<0$, and then connected for $t\geq 0$. Therefore, there exists no correlation between the initial position $\textbf{{x}}(0)$ and the initial noise $\bm{\zeta}(0)$, i.e., $\langle\textbf{{x}}^{\textsf{T}}(0)\bm{\zeta}(0)\rangle=0$, and then obviously $\langle\textbf{{x}}^{\textsf{T}}(0)\bm{\zeta}(t)\rangle=0$ for $t>0$ with the assumption that $\bm{\zeta}$ is independent of position.

The covariance (correlation) matrix of $x_{i}(t)$ and $x_{j}(t^{\prime})$ can be calculated, using Eq. (17), as

and the covariance matrix of $x_{i}(t)$ and $\eta_{j}(t^{\prime})$ becomes

Equations (18) and (19) show that the covariance function depends only on the two-point correlation function of noise, i.e., $\langle\zeta_{i}(t)\zeta_{j}(t^{\prime})\rangle$, but not on the higher-order multi-point correlations. This means that the covariance function will remain the same even for different active-noise models, as long as their two-point correlations are the same.

We now calculate the average work and heat generated by a linear force in the overdamped dynamics. First, from Eq. (14c),the work done by the nonconservative force can be written as

Note that the Stratonovich product between state variables like $x_{i}$ can be replaced by the Ito product (no extra symbol), but can not be ignored when the $\delta$- correlated noise $\zeta_{i}$ is involved. For example, in case of the shot noise in Eq. (4), we can easily find that $\langle\zeta_{i}(s)\circ x_{j}(s)\rangle=\langle\zeta_{i}(s)x_{j}(s)\rangle+\delta_{ij}\lambda_{i}\langle c^{2}\rangle_{p_{i}}/2$. For the non-Markovian noise with a finite persistence time $\tau$, the Stratonovich product is the same as the Ito product.

Second, for the Jarzynski work, we define the potential as $U(\textit{{x}},\lambda)=\textit{{x}}^{\textsf{T}}\textsf{U}\textit{{x}}$ satisfying $\Gamma\textit{{A}}^{\textrm{c}}(t)\textit{{x}}=\nabla U(\textit{{x}},\lambda)$. Then, from Eq. (14b), the Jarzynski work is given by

Finally, from Eq. (14a), the heat is expressed as

As shown in Eqs. (20), (21), and (22), the average work and heat are fully determined by the covariance matrices, and thus by the two-point correlation function $\langle\zeta_{i}(t)\zeta_{j}(t^{\prime})\rangle$ only. Therefore, for a linear system, the engine performance is not affected by the non-Gaussianity of a noise which is imbedded in higher-order multi-point (more than two) correlation functions, while it depends on the non-Markovianity characterized by the persistence time $\tau$ defining the two-point correlation function. We finally note that, though average values of work and heat are independent of model specifics as long as the two-point correlations of noises are the same, higher order quantities such as skewness of the distribution and fluctuation of work and heat are model-dependent Roy .

In this section, we study an engine driven by a linear force in contact with the (active) reservoirs, of which the noises have the same noise-autocorrelation form in Eq. (2) with two constant parameters; noise strength $D_{i}$ and persistence time $\tau_{i}$. Various noises in Sec. II are considered with the same values of $D_{i}$ and $\tau_{i}$ with the same initial state of the engine. Thus, we expect the same values for work and heat, independent of models from Eqs. (20), (21), and (22).

First, we consider a two-dimensional Brownian particle trapped in a harmonic potential and driven by a nonconservative rotational force. The dynamics is described by Eq. (16) with $\Gamma$ and time-independent $\textsf{A}^{\textrm{c}}$ and $\textsf{A}^{\textrm{nc}}$ given by

The position coordinate ‘$x_{1}$’ and ‘$x_{2}$’ are connected to reservoirs $1$ and $2$ with noises $\zeta_{1}$ and $\zeta_{2}$, respectively. In this example, we take reservoir $1$ as an equilibrium reservoir with temperature $T_{1}$, thus $\langle\zeta_{1}(t)\zeta_{1}(t^{\prime})\rangle=2T_{1}\gamma_{1}^{-1}\delta(t-t^{\prime})$. Reservoir $2$ is an active reservoir of which the noise satisfies $\langle\zeta_{2}(t)\zeta_{2}(t^{\prime})\rangle=D_{2}\tau_{2}^{-1}\gamma_{2}^{-2}\exp(-|t-t^{\prime}|/\tau_{2})$. Note that reservoir $2$ can also be an equilibrium reservoir in the $\tau_{2}\rightarrow 0$ limit with temperature $T_{2}=D_{2}/\gamma_{2}$. In this setup, we can obtain the analytic expressions for the average rates of the work and heat in the steady state from Eqs. (20) and (22). The results are JSLee2020active

where $\langle\cdots\rangle^{\textrm{ss}}$ denotes the steady-state average and $\langle x_{1}\dot{x}_{2}\rangle^{\textrm{ss}}$ is given by

with $\mathcal{B}=1+k\gamma_{2}\tau_{2}/(\gamma_{1}G_{2})+(k^{2}-\delta\epsilon)\tau_{2}^{2}/(\gamma_{1}G_{2})$ and $G_{2}=\gamma_{2}+k\tau_{2}$.

Figure 2 shows the averge rates of work and heat in the steady state for various models as a function of $D_{2}$ for $\tau_{2}=0$, $0.5$, and $1.0$. For these simulations, we set $k=\gamma_{1}=\gamma_{2}=1$, $T_{1}=2$, $\epsilon=0.5$, and $\delta=0.4$. Other parameters of respective models are specified in the caption of Fig. 2. Solid curves denote the analytic results in Eqs. (30) and (31) and dots are simulation results obtained by averaging over $10^{6}$ samples in the steady state. The $\tau_{2}=0$ case corresponds to the $\delta$-correlated noise for reservoir 2, which can be either equilibrium or shot noise reservoir. The results of these two models coincide with each other and are exactly fitted by the analytic curve for $\dot{W}$, $\dot{Q}_{1}$, and $\dot{Q}_{2}$ as shown in Figs.  2(a),  2(b), and  2(c), respectively. The colored-Poisson, the AOUP, and the ABP models belong to the case with finite $\tau$. As seen in Figs.  2(a),  2(b), and  2(c), data points of three different models with the same finite $\tau_{2}$ coincide with each others and are perfectly matched to a single analytic curve. This clearly demonstrates that the work and heat are determined solely by the two-point noise correlation function, regardless of other details of the noise statistics.

The second example is a one-dimensional Brownian particle trapped in a breathing harmonic potential. The motion is described by the following equation:

where $k(t)$ is the time-dependent stiffness with period $\mathcal{T}_{\textrm{p}}$ given by

where the noise autocorrelation function is given by $\langle\zeta(t)\zeta(t^{\prime})\rangle=D\tau^{-1}\gamma^{-2}\exp(-|t-t^{\prime}|/\tau)$. For this simulation, $k_{\textrm{min}}=\gamma=D=\omega=1$ and $\mathcal{T}_{\textrm{p}}=8$ are used and the initial state is set to be $x(0)=0$. With these conditions, we numerically calculate the accumulated Jarzynski work $W$ from Eq. (21) and the accumulated heat $Q$ from Eq. (22).

Figure 3 shows $W$ and $Q$ as a function of time. Similar to the previous example, the $\tau=0$ case corresponds to the equilibrium and the shot noise model. Here, $T=1$ is used for the equilibrium noise and $\lambda=1$ and $\langle c^{2}\rangle_{p}=2$ are used for the shot noise. As expected, the two results are exactly matched to each other. Simulations for the colored-Poisson, the AOUP, and the ABP models are also performed for finite $\tau=0.5,1.0$. In this calculation, $\lambda=1$, $D=1$, and $\alpha=1$ are used. As the figure shows, the same values of $\tau$ and $D$ lead to the same amount of the work and heat regardless of noise models. This again demonstrates that the engine performance for a linear system is affected only by the non-Markovianity, but not by the non-Gaussianity, even for a system driven by an arbitrary time-dependent protocol.

Cyclic protocol of conventional heat engines such as Carnot and Stirling engines is usually accompanied with temporal changes of heat reservoirs. Here, we consider the same temporal changes of active reservoirs. In the recent experiment on the Stirling engine with a bacterial active reservoir Krishnamurthy , the effective temperature of the active reservoir was varied by changing the activity of bacteria by controlling the ambient temperature. As the active particles (bacteria) tend to maintain their motion within a given persistence time, the noise statistics of the active reservoir will not be changed abruptly when external control parameters are changed, but instead have some memory effect originated from its past state. Thus, this reservoir-memory effect should be taken into consideration when an active reservoir changes in time, which has not been recognized and investigated so far in literatures.

To investigate the memory effect on the engine performance, we consider the Stirling engine with an active reservoir. A one-dimensional Brownian particle is trapped in a time-dependent harmonic potential with stiffness $k(t)$ and in contact with a temporal active reservoir with constant persistence time $\tau$ and time-varying noise strength $D(t)$. For simplicity, we take the time-dependent protocol given by Eqs. (32) and (35). The cyclic engine protocol consists of four steps which are shown in Fig. 4; (i) isochoric process $1\rightarrow 2$: $D$ is suddenly switched from $D_{\textrm{h}}$ to $D_{\textrm{c}}$ with fixed $k=k_{\textrm{min}}$ at $t=0$. This process corresponds to the sudden temperature change of the heat bath with fixed volume of the conventional Stirling engine. (ii) isoactive process $2\rightarrow 3$: $k$ changes linearly from $k_{\textrm{min}}$ to $k_{\textrm{max}}\equiv k_{\textrm{min}}+\mathcal{T}_{\textrm{p}}\omega/2$ with fixed $D=D_{\textrm{c}}$ during $0<t<\mathcal{T}_{\textrm{p}}/2$. This process corresponds to the isothermal compression process of the conventional engine. (iii) isochoric process $3\rightarrow 4$: $D$ changes abruptly from $D_{\textrm{c}}$ to $D_{\textrm{h}}$ with fixed $k=k_{\textrm{max}}$ at $t=\mathcal{T}_{\textrm{p}}/2$. (iv) isoactive process $4\rightarrow 1$: $k$ changes linearly from $k_{\textrm{max}}$ to $k_{\textrm{min}}$ with fixed $D=D_{\textrm{h}}$ during $\mathcal{T}_{\textrm{p}}/2<t<\mathcal{T}_{\textrm{p}}$. This process corresponds to the isothermal expansion process of the conventional engine.

Figure 5 shows the accumulated work and heat of this Stirling engine for different noise models and different $\tau$. For this simulation, we set the protocol parameters as $\omega=0.2$, $\mathcal{T}_{\textrm{p}}=10$, $k_{\textrm{min}}=1$ (thus, $k_{\textrm{max}}=2$) with the reservoir parameters as $\gamma=1$, $D_{\textrm{h}}=2$, and $D_{\textrm{c}}=1$. Note that the data for the equilibrium noise and the shot noise (both $\tau=0$) coincide with each other for $W$ and $Q$. In contrast to these cases, $W$ and $Q$ data points of the colored-Poisson, the AOUP, and the ABP models with finite $\tau$ do not agree with the others even though they have the same $\tau$ and the same sequence of $D$. This discrepancy is due to the distinct memory effect for different models, which becomes smaller as the persistence time $\tau$ decreases as shown in Fig. 5. All data eventually collapse on the equilibrium curve in the $\tau\rightarrow 0$ limit.

In Appendix B, we explicitly calculate the noise autocorrelation functions for various active models when $\tau$ and $D$ is changed abruptly at a certain time $t_{\textrm{c}}$. In most cases, the noise autocorrelation function involving a later time than $t_{c}$ does not maintain the simple exponential form in Eq. (2) and becomes more complicated with the memory effect for finite $\tau$, which depends on the details of the model. This model-dependent memory effect leads to the difference of $W$ and $Q$ for the different active-noise models in Fig. 5. As this difference lasts for several persistence times until a noise is relaxed, the discrepancy gets smaller when $\tau$ gets smaller.

One may consider a speed variation of the time-dependent protocol, i.e. varying $\omega$ and $\mathcal{T}_{p}$ while keeping the values of $k_{\textrm{min}}$ and $k_{\textrm{max}}$. For a very slow process (small $\omega$ or large $\mathcal{T}_{p}$), the memory effect can be ignored for $\tau\ll\mathcal{T}_{p}/2$. We confirm this by numerical simulations. Figure 6 shows the plots of $W$ and $Q$ for various protocol speed $\omega=0.2,0.08,0.02$. For relatively high speed ($\omega=0.2$), $W$ and $Q$ of the colored-Poisson, the AOUP, and the ABP models are different from the others, while they almost coincide with each other for a very slow process ($\omega=0.02$). Note that these results can not match the equilibrium data even in the quasistatic limit ($\omega\rightarrow 0$), due to the finite persistent time $\tau$.

When the total mechanical force is nonlinear in position, the work and heat cannot be simply expressed by the two-point noise correlation functions as discussed in Sec. IV, but higher-order correlation functions are necessary in general. Therefore, in this nonlinear case, the non-Gaussianity of a noise should contribute to the work and heat in general.

To investigate the non-Gaussian effect explicitly, we consider a similar steady-state engine studied in Sec. IV.2, i.e. a two-dimensional Brownian particle trapped by an anharmonic potential $U(x_{1},x_{2})=\frac{k}{q}(x_{1}^{q}+x_{2}^{q})$ where $q$ is an even integer, and driven by a linear nonconservative force ${\textit{{f}}^{\textrm{nc}}(\textit{{x}})}^{\textsf{T}}=(\epsilon x_{2},\delta x_{1})$. Thus, the equation of motion can be written as

where $\zeta_{1}$ is the equilibrium noise satisfying $\langle\zeta_{1}(t)\zeta_{1}(t^{\prime})\rangle=2\gamma_{1}^{-1}T_{1}\delta(t-t^{\prime})$ and $\zeta_{2}$ is the active noise satisfying $\langle\zeta_{2}(t)\zeta_{2}(t^{\prime})\rangle=D_{2}\tau_{2}^{-1}\gamma_{2}^{-2}\exp(-|t-t^{\prime}|/\tau_{2})$.

We perform numerical simulations for $q=4$ with the same parameter values used in Sec. IV.2. Figure 7 shows the average rates of the work and heat in the steady state as a function of $D_{2}$ for various values of $\tau_{2}$. Notice a clear distinction between data for the equilibrium noise and the shot noise (both $\tau_{2}=0$), which should be due to the non-Gaussianity of the shot noise for nonlinear systems. For the other active models with the same $\tau_{2}$, the simulation data differ from each other as expected.

It is interesting to study the quasistatic process of the Stirling engine with the shot noise, subject to the breathing anharmonic potential $U(x)=\frac{k(t)}{q}x^{q}$ in one dimension. The equation of motion is given as

where the stiffness protocol is given by Eq. (35) and $\zeta(t)$ is the shot noise.

Due to the nonlinearity of the mechanical force ($q>2$), we expect that the non-Gaussianity of the shot noise should contribute to the work and heat as found in the steady-state engine in Sec. V.1. For example, the Jarzynski work during the process $2\rightarrow 3$ is given from Eq. (14b) as

As the system internal energy is given by $\langle U\rangle=\frac{k(t)}{q}\langle x^{q}\rangle$, the thermodynamic first law guarantees that the heat also depends on $\langle x^{q}\rangle$. Hence, the work and heat obviously include the higher-order correlation functions for $q>2$.

However, in the quasistatic limit, the average $\langle x^{q}\rangle$ is reduced to a constant independent of the higher-order noise correlation functions, and thus the non-Gaussianity of the shot noise does not come into play. In this subsection, we show this interesting result analytically and also perform numerical simulations for $q=4$ and $6$ with various protocol speeds $\omega$.

First, consider the evolution equation of the probability distribution $P(x,t)$, corresponding to Eq. (37) as entropy

where $p(c)$ is the distribution function of the shot-noise magnitude $c$ as explained in Sec. II.1. Multiplying $x^{2}$ to Eq. (39) and integrating it over $x$, one can easily find

In the quasistatic process, the system is almost always in a steady state with the instant value of $k(t)$ at that moment. In this instant steady state at time $t$, we obtain, by setting both sides of Eq. (40) zero,

which clearly shows that the average $\langle x^{q}\rangle$ does not depend on the higher-order noise correlations in the quasistatic process.

For later use, we define effective temperatures of the system with the shot-noise reservoir. From the equipartition relation similar to that in equilibrium, it is reasonable to define for fixed $k$

which converges to the conventional temperature $T$ in the equilibrium limit discussed in Sec. II.1, i.e. $\lambda\langle c^{2}\rangle_{p}=2T/\gamma$ fixed in the $\lambda\rightarrow\infty$ limit. One may define another effective temperature from the diffusive behavior of a particle without any trapping potential ($k=0$) as

where Eq. (40) is used for $k=0$. Notice that these two effective temperatures are the same for the shot noise, whereas they are different for other active noises in general.

We take the Stirling engine protocol in Fig. 4 with the anharmonic potential. For simplicity, we use the temperature notation for the two shot-noise reservoirs with $T_{\textrm{c}}^{\textrm{E}}$ and $T_{\textrm{h}}^{\textrm{E}}$. Then, in the quasistatic process, using Eqs. (38) and (42), we find

which is exactly the same form as the work, Eq. (67), of the equilibrium-reservoir counterpart explained in Appendix C by matching $T_{\textrm{c}}^{\textrm{E}}$ with $T_{\textrm{c}}$. Works and heats for other quasistatic-process segments are also the same as those presented in Eqs. (68) and (69), respectively also by matching $T_{\textrm{h}}^{\textrm{E}}$ with $T_{\textrm{h}}$.

We define the efficiency of the shot-noise Stirling engine in the conventional way as the ratio of the extracted work versus the heat energy flow from the high-temperature reservoir:

Then, in the quasistatic process, we obtain

which is the same as that of the equilibrium Stirling engine $\eta_{\textrm{C}}^{\textrm{Stir}}$ by replacing $T^{\textrm{E}}$ with $T$, see Eq. (70). Note that $\eta_{\textrm{E}}$ is the effective Carnot efficiency defined from the effective temperature $T^{\textrm{E}}$. In the same way, we can define another effective Carnot efficiency $\eta_{\textrm{D}}\equiv 1-T_{\textrm{c}}^{\textrm{D}}/T_{\textrm{h}}^{\textrm{D}}$ from $T^{\textrm{D}}$ defined in Eq. (43). More discussions on the efficiency of active engines are presented in the next subsection V.3.

Figure 8 shows the numerical results with various values of the protocol speed $\omega$ for the equilibrium and the shot noises. Accumulated work and heat for $q=4$ are presented in Figs. 8(a) and 8(b), respectively. For these simulations, we set the protocol speed very small as $\omega=0.01$. Solid curves and data points denote analytic and numerical results, respectively, and they are exactly matched. Figure 8(c) shows the plots of the normalized efficiency $\tilde{\eta}$ as a function of $\omega$ with $\tilde{\eta}_{\textrm{C}}\equiv\eta/\eta_{\textrm{C}}^{\textrm{Stir}}$ for the equilibrium noise and with $\tilde{\eta}_{\textrm{E}}\equiv\eta/\eta_{\textrm{E}}^{\textrm{Stir}}$ for the shot noise. As expected, the two efficiencies are almost identical for small $\omega$, but show a discrepancy for $\omega\gtrsim 1$. We find similar results for $q=6$ in Figs. (8)(d), (8)(e) and (8)(f). Note that the efficiency of the shot-noise engine is higher than that of the equilibrium engine with a fast protocol speed. This indicates that the efficiency can be enhanced soley by the non-Gaussianity of a noise without any non-Markovianity.

We investigate the nonlinear effect on the efficiency of the steady-state active engine introduced in Sec. V.1, where the energy-supplying bath is in equilibrium with temperature $T_{1}$ and the energy-dissipating bath is an active bath with $D_{2}$ and $\tau_{2}$ (effectively low-temperature bath). The efficiency is defined in the conventional way as the ratio of the total work extraction rate and the heat flow rate out of the (high-temperature) equilibrium reservoir.

In our previous study JSLee2020active , we investigated the same steady-state active engine model with $q=2$ (linear force) and the AOUP noise. From the study, it was shown that the efficiency can overcome the two effective Carnot efficiencies $\eta_{\textrm{D}}$ and $\eta_{\textrm{E}}$ when the persistence times of the two reservoirs are different. Note that surpassing the effective Carnot efficiency in an active engine does not mean the violation of the thermodynamic second law since the dissipation into nonequilibrium reservoirs do not account the full entropy production in general JSLee2020active . For the linear engine, the work and heat are not affected by the non-Gaussianity, thus we expect the same efficiency for other types of active reservoirs as long as the two-point noise correlation functions are identical. That is, surpassing the effective Carnot efficiency can be achieved solely by the non-Markovianity.

However, it is clear that, for a system with a nonlinear force, the non-Gaussianity can also give an additional contribution in enhancing the efficiency. We perform numerical simulations for the steady-state engine described by Eq. (36) for $q=4$ with $T_{1}=2$. We use the same values of other parameters as for the linear engine in Sec. IV.2, i.e. $k=\gamma_{1}=\gamma_{2}=1$.

Figures 9(a) and (b) show the simulation results when the reservoir $2$ is also in equilibrium with temperature $T_{2}=1$. The yellow dots in Fig. 9(a) are plotted on the $\epsilon-\delta$ plane when the model system works as an engine, that is, the engine condition $W<0$ (positive work extraction) and $Q_{1}>0$ (heat flow out of the reservoir 1) is satisfied. As expected, the yellow-dotted engine area is restricted in between the two lines: (i) the $\eta=0$ line ($\delta=\epsilon$) and (ii) the $\eta=\eta_{\textrm{C}}$ line ($\delta=(T_{2}/T_{1})\epsilon$) with the Carnot efficiency $\eta_{\textrm{C}}=1-T_{2}/T_{1}$. Thus, the efficiency is bounded from above by $\eta_{\textrm{C}}$ as explicitly shown in Fig. 9(b), which is the plot for the efficiency and the normalized power $\tilde{P}\equiv{P}/P_{\textrm{eq}}^{\textrm{max}}$ as a function of $\epsilon$ with fixed $\delta=0.3$. The global maximum power is given by $P_{\textrm{eq}}^{\textrm{max}}=kT_{1}\eta_{\textrm{CA}}^{2}/(\gamma_{1}+\gamma_{2})$ with $\eta_{\textrm{CA}}=1-\sqrt{T_{2}/T_{1}}$ JSLee2020active .

Figure 9(c) shows the engine area when the noise of the reservoir $2$ is the shot noise with $D_{2}=1$ ($\lambda=1$ and $\langle c^{2}\rangle_{p}=2$), leading to $T_{2}^{\textrm{E}}=1$. Clearly distinct from Fig. 9(a), the engine area is extended over the effective Carnot efficiency line ($\eta=\eta^{\textrm{E}}$ line). This leads to surpassing the effective Carnot efficiency $\eta_{\textrm{E}}$ as presented in Fig. 9(d). This definitely manifests the non-Gaussian effect on engine efficiency through a nonlinear force without any non-Markovianity.

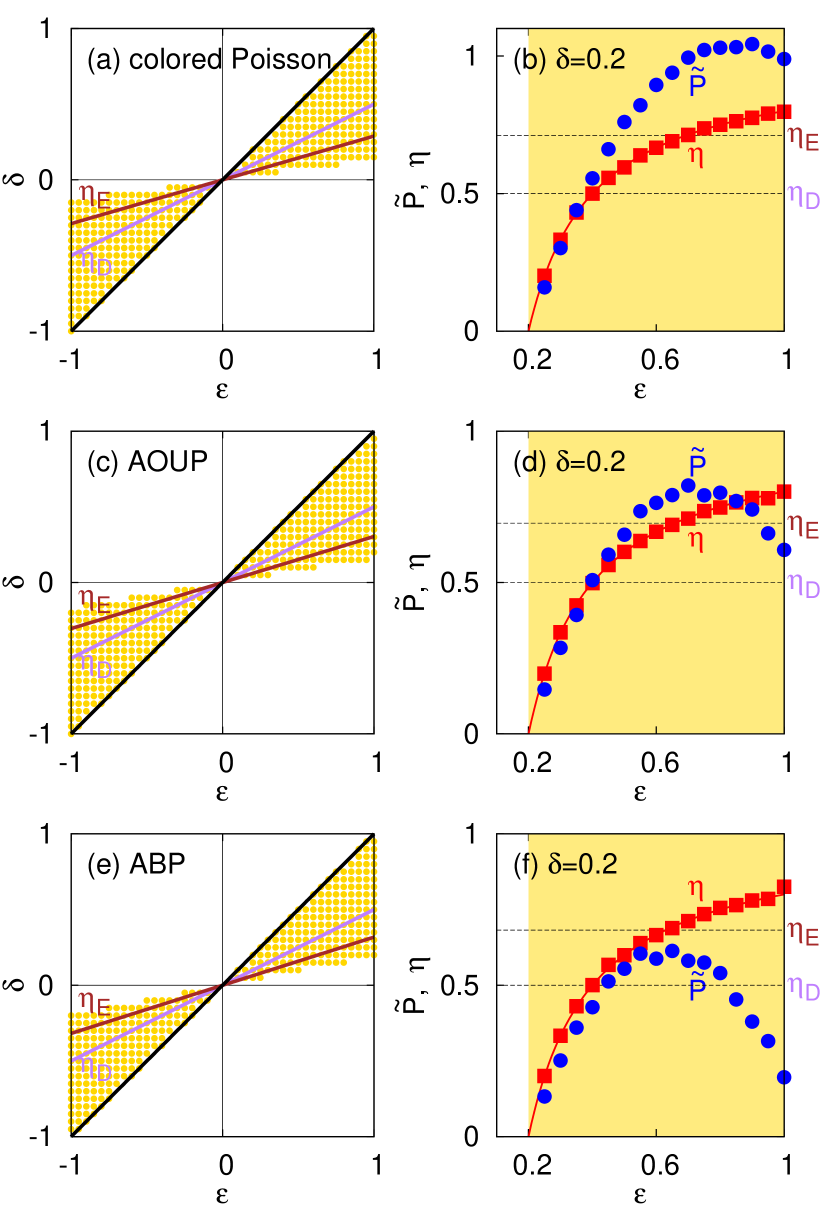
We also perform similar simulations when the reservoir $2$ generates the colored-Poisson, the AOUP, or the ABP noise with $D_{2}=1$ and $\tau_{2}=0.5$. The results are presented in Fig. 10, which show that the efficiency of all active engines with finite $\tau_{2}$ can overcome both $\eta_{\textrm{D}}$ and $\eta_{\textrm{E}}$. Among these three models, only the AOUP noise is Gaussian. Therefore, one can also conclude that the effective Carnot efficiencies can be overcome solely by the non-Markovian noise without any non-Gaussianity.