compat=1.1.0
Effects of Electroweak Symmetry Breaking on Axion Like Particles as Dark Matter
Abstract
Axion like particles (ALPs), the pseudo Nambu-Goldstone bosons associated to the spontaneous breaking of global symmetry, have emerged as promising dark matter candidates. Conventionally, in the context of misalignment mechanism, the non-thermally produced ALPs happen to stay frozen due to Hubble friction initially and at a later stage, they begin to oscillate (before matter-radiation equality) at characteristic frequencies defined by their masses and behaving like cold dark matter. In this work, we study the influence of electroweak symmetry breaking (EWSB), through a higher order Higgs portal interaction, on the evolution of ALPs. Such an interaction is found to contribute partially to the ALP’s mass during EWSB, thereby modifying oscillation frequencies during EWSB as well as impacting upon the existing correlation between the scale of symmetry breaking and their masses. The novelty of the work lies in broadening the relic satisfied parameter space so as to probe it in near future via a wide range of experiments.
I Introduction
Axion like particles (ALPs) are generically classified as the pseudo Nambu-Goldstone bosons (pNGB) associated to the spontaneous breaking of a global symmetry, prevalent in many extensions of the Standard Model (SM) in superstrings theories Svrcek and Witten (2006); Arvanitaki et al. (2010); Demirtas et al. (2020). Though they are analogous to the pNGB of the Peccei Quinn symmetry, originally introduced to solve the strong CP problem of QCD Peccei and Quinn (1977a, b); Weinberg (1978); Wilczek (1978), ALPs belong to a more general class and hence not necessarily be connected to the solution of the strong CP problem. They are typically very light, neutral pseudo-scalar particles having at most a derivative coupling with the Standard Model at an effective level, suppressed by the scale of spontaneous symmetry breaking () of the global symmetry (also referred to as the ALP decay constant), thereby emerging as ideal candidates for explaining the dark matter of the Universe. The mass of an ALP may originate from non-perturbative instanton effect in a strongly interacting hidden sector (analogous to the QCD axion) as well as from explicit symmetry breaking. Correspondingly, contrary to the QCD axion, an ALP does not in general carry any specific relation between its mass and the decay constant. As a result, their mass and decay constant may span over a wide range making them attractive from detection point of view.
Most commonly in the literature, an ALP is considered to be produced non-thermally via the so called mechanism Preskill et al. (1983); Abbott and Sikivie (1983); Dine and Fischler (1983); Turner (1983); Arias et al. (2012). The ALP, considered as a classical field in this context, is expected to have an initial non-zero field value and gets frozen there till the Hubble () induced friction remains larger that its mass (). Once , the ALP starts to oscillate at a temperature about the minimum of a periodic potential characteristics of a pNGB. Such an oscillatory field mimics as cold dark matter as the associated energy density () scales as , hence behaving like ordinary matter ( is the scale factor of the Universe) provided it remains stable over cosmological time scale. The relic density satisfaction of such ALP provides a standard correlation involving and which turns out to be well restricted by several cosmological constraints as well from ALP search experiments as summarised in Arias et al. (2012); Cadamuro and Redondo (2012); Ringwald (2012); Workman et al. (2022); Marsh (2018). Considering all such aspects, it turns out that the ALPs being DM should be very light (below keV).
In this work, we propose to include a higher order shift symmetry breaking Higgs portal interaction of ALPs which contributes to its mass () after the electroweak symmetry breaking (EWSB) on top of its existing mass, , presumably followed from non-perturbative instanton effect. Inclusion of such additional mass is expected to modify the frequency of ALP oscillation after the EWSB. This would have profound effect on the relic density and hence on the ALP parameter space in plane, where . We find that depending upon the onset of conventional ALP oscillation (connected with its mass only) before or after the EWSB and associated modification of it after EWSB, the standard correlation between ALP mass and decay constant can be altered significantly leading to opening up of otherwise excluded (restricted) parameter space ( keV-GeV range) for ALPs.
There are some studies focusing on modification of the PQ axion or ALP potential. For example, in ref. Jeong et al. (2022), the authors examine the effect of tiny (limited by neutron electric dipole moment) explicit Peccei-Quinn (PQ) symmetry breaking on the PQ axion dynamics and its role as DM. In this case, the PQ axion initially starts oscillating about a wrong minimum guided by the explicit PQ breaking term and afterward it oscillates about the true minimum leading to a modification of the conventional PQ parameter space. Ref. Li (2023) recently analyses the effect of introducing a PQ breaking term on axiverse that encompasses the PQ axion, an ALP and a hypothetical mixing between them. In another work, ref. Chatrchyan et al. (2023) discusses the effect of adding a non-periodic potential to ALP and thereby find the possibility of accommodating a large misalignment angles which may change the conventional parameter space of ALPs. Another modification of axion or ALP potential is referred as kinetic misalignment (Co et al. (2020); Chang and Cui (2020); Co et al. (2021)). In this scenario, a higher dimensional explicit PQ breaking potential and a large initial field value for the PQ symmetry breaking field lead to a nonzero initial ALP velocity which in turn, triggers a delayed ALP oscillation bringing modifications in the relic abundance as well as in parameter space of ALPs. A more general treatment of the effect of initial conditions of ALP and its effects on the parameter space can be found in ref. Eröncel et al. (2022). Ref. Chao et al. (2022) discusses about the impact of ALP mass modification on its relic abundance, within the context of the type-II seesaw mechanism.
Our proposal differs from the existing works in a sense that it relies on the electroweak symmetry breaking phase (most natural and unavoidable phase) for modifying the ALP potential, without changing its minimum though. The new mass term for ALP that originates at EWSB may provide a dominant or sub-dominant contribution to the effective final mass of the ALP (). Depending on the onset of ALP oscillation before or at EWSB, the standard misalignment mechanism gets modified so as to obtain a new parameter space, in plane, carrying significant differences with the standard one which might be interesting from ALP search experiments. It turns out that such a Higgs portal interaction of ALPs allows us to probe for light ALPs. Interactions involving ALP and Standard Model (SM) Higgs have also been exercised in few references Im and Jeong (2019); Dev et al. (2019); Oikonomou (2023), however in different contexts. Specifically, a higher dimensional operator consisting of axion and Higgs are discussed in Oikonomou (2023) which is responsible for a new minimum of ALP inducing an epoch of kination and generation of gravitational waves. Contrary to our proposal, the ALP there neither plays the role of DM nor obtains a shift in its mass during EWSB.
The outline of the work is as follows. In the next section, we discuss the standard ALP scenario and following this, we move for studying the evolution of ALPs in our modified scenario. The observation and constraints are elaborated in sections III and IV respectively. Finally we conclude in section VI.
II Standard Misalignment Mechanism and ALP as DM
In this section, we first elaborate on the production of ALPs in the early Universe via misalignment mechanism followed by standard ALP cosmology and the related parameter space. We presume the existence of ALPs prior to the end of primordial inflation as a result of spontaneous breaking of a global symmetry during inflation. After inflation (followed by a reheating era), the ALP field is expected to be spatially homogeneous, hence described by only, and gets frozen at an initial value parametrised by the misalignment angle (with ), as long as the Hubble remains larger compared to its mass . Note that, the ALP being a Nambu Goldstone Boson, the origin of is related to the breaking of shift symmetry which can possibly be connected to the non-perturbative dynamics, (analogous to PQ axion) and independent of temperature. This can be realised if the ALP couples to a hidden sector (the global symmetry is anomalous under such non-abelian group) which may not be thermalised.
The related ALP potential can be parametrised by
| (1) |
where corresponds to the scale of spontaneous symmetry breaking of the global . The ALP field parametrised by follows the classical equation of motion in the background of expanding Universe as given by
| (2) |
and ‘dot’ indicates the derivative with respect to time .
At very early Universe, after inflation, when , the of the axion field remains overdamped and gets stuck at its initial value due to Hubble friction. In a radiation dominated era, at some point when
| (3) |
the field rolls toward its potential minimum and starts to oscillate. The onset of oscillation can be characterised by the temperature . Near the minimum of the potential, and the equation of motion (below ) reduces to
| (4) |
where the ALP field is considered to be a homogeneous one, the spatial variation over Hubble volume, vanishes. Using the expression of the Hubble parameter in a radiation-dominated universe, , and the relation in Eq. 3, we can estimate the conventional oscillation temperature for ALP as
| (5) |
where, is the number of relativistic degrees of freedom () at a temperature and the value of Planck mass, GeV is deployed.
At the conventional oscillation temperature , the total energy density of the ALP is fully embedded in its potential part only since ALP does not have any initial velocity, and is given by
| (6) |
For , Eq. 4 implies that field would perform fast oscillations with slowly decreasing amplitude where the average energy density scales as and the equation of state turns out to be zero implying that it behaves like non-relativistic matter Arias et al. (2012); Marsh (2016). Here, implies averaging over one complete oscillation.
Since the ALP number density in a co-moving volume turns out to be conserved Arias et al. (2012), the present day ALP energy density can be estimated as
| (7) | |||
| (8) |
where eV is the present temperature and a change of ALP mass at different (later) temperature, if any, is included in the form of . However as stated above, unlike QCD Axion, ALP masses are generally considered as temperature independent, . In this case, employing Eq. 8 and considering the adiabatic expansion of the Universe where is the entropy density of the universe given by , the ALP relic density can be expressed as
| (9) |
where (present critical energy density) and (number of relativistic at present temperature) Bauer and Plehn (2019). Using the expression of Eq. 5 into Eq. 9, the ALP relic density can be estimated as
| (10) |
from which a correlation between the two parameters and can easily be obtained. However, once the astrophysical and cosmological bounds are imposed (to be discussed later in section IV), the allowed mass range for the ALPs falls below keV-scale Balázs et al. (2022) only.
III Higgs portal interaction and ALP
In this section, we introduce an explicit higher order shift symmetry breaking term in the ALP potential involving the SM Higgs. As a result, a new contribution toward the mass of ALP originates once the electroweak symmetry breaking takes place. The appearance of such a mass term for ALP at an intermediate phase (during its evolution) in addition to (connected to non-perturbative dynamics) not only enables the effective mass of the ALP () and its decay constant () to treat as independent parameters, but also modifies the frequency of ALP oscillation at EWSB as we observe below.
We first consider the Lagrangian involving a global symmetry breaking complex scalar field , as
| (11) |
where as parametrised in the earlier section. Once the global symmetry is spontaneously broken, the potential for the ALP field is given of Eq. 1. We now introduce additional dimension-6 shift symmetry breaking term involving SM Higgs doublet , as given by
| (12) |
where the phase in Eq. 12 can take values in the range Higaki et al. (2016) and acts as a cut-off scale with , indicating that the explicit breaking of the global symmetry may take place at some high scale () Draper et al. (2022); Cordova et al. (2022). Based on this known possibility that gravity effects explicitly break a global symmetry Giddings and Strominger (1988); Coleman (1988); Rey (1989); Abbott and Wise (1989); Akhmedov et al. (1992) at Planck scale (or even at a scale much smaller than the Planck one, as recently shown by Cordova et al. (2022) in the context of weak-gravity conjecture Arkani-Hamed et al. (2007)), we discuss the origin of such an operator in Appendix-A. The specific construction mentioned there is also capable of disallowing another dimension-6 explicit symmetry breaking term which can be present otherwise. Note that this additional operator can be excluded from a naive consideration too by keeping the order of explicit breaking (by amount of charges) minimal. While we mostly focus on the explicit breaking operator as in Eq. 12 only for the rest of the analysis, we show in Appendix-B that inclusion of the additional dimension-6 operator may lead to an altogether different phenomenology.
The phenomenologically relevant part of the potential for the ALP or the field, after the spontaneous breaking of the PQ-like global symmetry, then turns out to be
| (13) |
At a temperature sufficiently higher than the electroweak scale, 150 GeV, the temperature correction to the SM Higgs potential helps the SM Higgs to have a single minimum at origin Kolb and Turner (1990). Hence the Higgs field is expected to settle at origin as a result of which this term does not contribute till the temperature becomes comparable to when gets a vacuum expectation value (vev), with GeV. After the EWSB, the ALP receives a new contribution to its mass such that its effective mass satisfies the relation
| (14) |
where denotes the newly developed minimum of the ALP potential after EWSB. The value of can be estimated as a solution to the equation,
| (15) |
obtained by minimising the ALP potential. Clearly, the new potential minimum depends on the choice of and other parameters ( and ). We pursue with for the rest of the analysis that results into the effective mass of the ALP given by,
| (16) |
Such a choice of is motivated primarily from the fact that the minimum of the ALP potential () remains unaffected due to the presence of this additional contribution to ALP potential via Eq. 12. However, for conventional QCD axion, such explicitly breaking term should be incorporated very carefully as any alteration of the minimum can spoil the resolution of the strong CP problem, the strong-CP violating angle being heavily constrained by neutron electric dipole moment Abel et al. (2020) (widely referred as Axion quality problem Kamionkowski and March-Russell (1992); Holman et al. (1992); Barr and Seckel (1992)). With a general axion like particles, such a solution of strong CP problem is not necessarily be connected to the solution of the strong CP problem. To investigate the impact of different values on and hence on relic, we incorporate an analysis in the later part of the following sub-section.
Appearance of such a mass term would affect the evolution of the ALP field, in terms of its change in oscillation frequency, immediately after the EWSB. To analyse it further, we divide the study into two cases depending on whether the ALP starts its oscillation at a temperature (due to ) prior to EWSB temperature
or not, as
| (17) | |||||
Note that the demarcation between these two cases is set by the condition
| (18) |
which translates (assuming a radiation dominated universe) into GeV (for case [A]) and GeV (for case [B]) where we use GeV.
III.1 ALP oscillation starts before EWSB
Here the ALP is expected to start its oscillation at a temperature higher than , connected to its mass . So, the evolution of this ALP for the period to is guided by Eq. 4. Near the onset of its oscillation at , it carries an energy density same as of Eq. 6. At , due to the electroweak symmetry breaking, the higher order Higgs portal interaction provides an additional contribution to its mass as specified in Eq. 16. As a result, the evolution of the ALP is now governed by the same form of Eq. 4, however replacing by via Eq. 16,
| (19) |
The shift of ALP mass across the EWSB can be incorporated in estimating the ALP energy density , crucial in determining the ALP relic density, before and after the electroweak phase transition in line with the discussion in the context of Eqs. 7-8 as pursued below. The discontinuity of around EWSB can be guided by an appropriate logistic function (as shown in appendix-C) in case one tries to explore evolution of the field as function of scale factor (normalised by ), depicted in Fig. 1.

Considering the conservation of ALP number density in a co-moving volume across EWSB, the immediately after the EWSB (at ) can be written, via Eq. 7, as
| (20) |
Here is the energy density of the ALP just before the EWSB (at ) given by
| (21) |
where is the scale factor at the onset of oscillation, . While the mass of the ALP before EWSB is , results after EWSB as given by Eq. 16. Here, and are the scale factors of the universe at temperatures and respectively.
The energy density of the ALP today (associated with temperature ) can be written as
| (22) | |||||
where Eqs. 20, 21 are employed and corresponds to today’s scale factor.
Using the expressions of of Eq. 6, as given by Eq. 5 and plugging them in of Eq. 22, we find the ALP relic density today as
| (23) |
Apart from , the dependence relies on the cut-off scale . Unlike the standard dependence of relic on and via Eq. 10, here in case-[A], the final relic density also involves the third parameter , the cut-off scale of the theory which is apparent though the involvement of in Eq. 23 apart from .

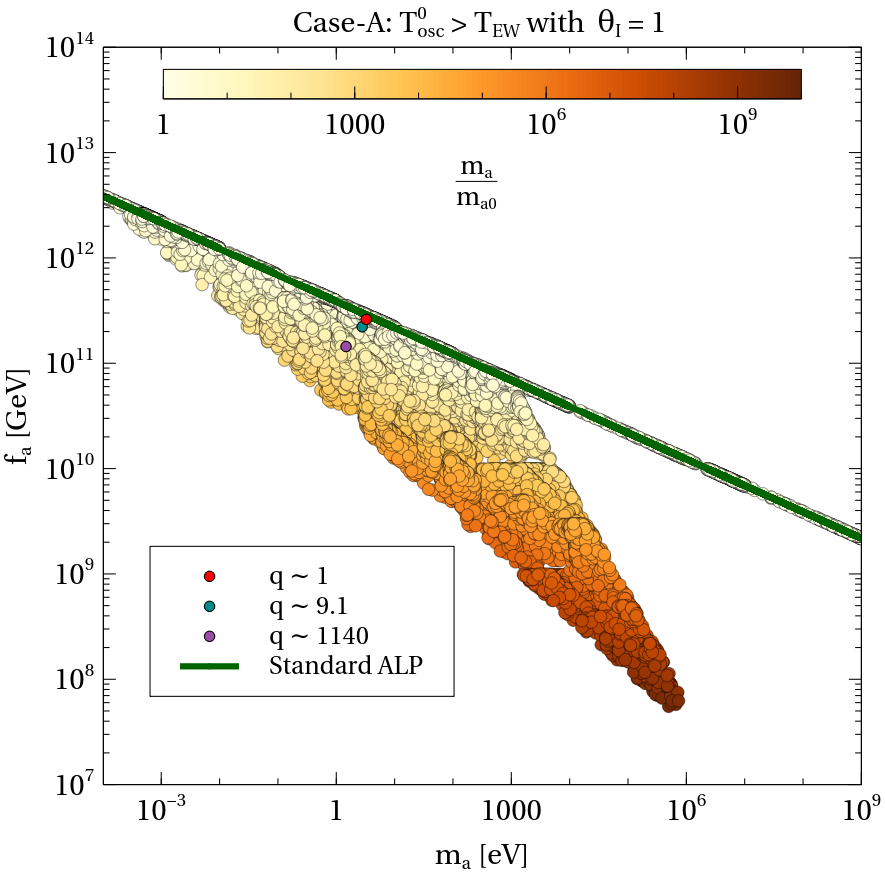
The effective mass being the final mass of the ALP which is phenomenologically more relevant than , we choose to consider the three parameters as and for our phenomenological analysis. To make the parameters dependence of the relic density explicit, we provide the result of the parameter space scan in plane shown in Figs. 2 and 3 where the dependence of and are indicated in the respective color maps maintaining . All the points in and plane satisfy the correct relic density Aghanim et al. (2020). The gradients of the colors inside the color maps ranging from dark red to blue (for Fig. 2) and yellow to brown (for Fig. 3) indicate the one to one correspondence between the set of values with and respectively for case-[A]. The narrow green line (merged with the borderline of the parameter space of Figs. 2 and 3) represents the relic-satisfied parameter space for standard scenario with ALP mass, equivalent to , from the very beginning. To clarify further, for the green line only, the ALP oscillation begins at some other temperature (say ) than satisfying . In terms of the extended parameter space as obtained in our scenario, this green line acts as the borderline of the parameter space implying that on this line, the change in the ALP mass during EWSB (in presence of the Higgs portal interaction) in very negligible , which is clear from Fig. 3. Interestingly, the rest of the extended region allows for a significant gain in ALP mass during EWSB, for GeV, as evident from the top-color-bar of Fig. 3.
Note that, the presence of the higher dimensional Higgs portal coupling of the ALP allows such broadening of parameter space (particularly for ) which would be very significant from experimental perspective clubbed with other constraints which we shall discuss in the next section IV. The broadening of the parameter space is an artefact of intermediate change in ALP oscillation frequency as shown in Fig. 1. Considering the ALP to constitute of dark matter energy density in the universe, the upper part of the parameter space in this case (which is merged with the standard case) is excluded by the overabundance of dark matter while the excluded region below this (the left and right border lines of the allowed parameter space) is due to the consideration: . In terms of ALP mass, the lower limit on is kept as GeV here so as to keep above , the higher side of can even be extended beyond the specified value (1 GeV) of the figure. The other constraint, is only important at the leftmost region of the parameter space in this case as the minimum contribution from dim-6 operator to ALP mass is GeV. However, such a correlation involving and the decay constant deserves a further scrutiny from several astrophysical and cosmological bounds which we will discuss in a subsequent section.
It is perhaps pertinent here to comment on the choice of the phase, . We noted that for the specific choice of , the remains at the origin even after the EWSB. However, for an arbitrary , this may not be the case always, indicating a possible impact on the final relic density of ALP. To investigate this, we first use Eq. 15 to demonstrate the variation of against for some choices of values. For this purpose we pick up three different sets of parameters (corresponding to three different values) from the parameter space of Fig. 2 (or 3): (a) , marked in red dark dot having , (b) , marked in dark cyan dark dot having , and (c) GeV, marked in purple dark dot having . We then employ these three values to obtain as function of for each as depicted in Fig. 4. Firstly we note that with , the potential minimum in terms of depends on the choice of . To be specific, remains at origin for while it becomes for . For non-zero , picks a distinct value. Hence, a correlation between and is noticed in this case as observed in Fig. 4. However, for , turns out to be zero irrespective of , signifying to be an unique choice.
Corresponding to Fig. 4, a variation in relic density with is shown in Fig. 5. It is evident that a maximum relic density results for . This is simply because the relic density being proportional to the effective ALP mass attains its maximum value for as can be seen from Eq. 15 (or 16). Any other choice of obviously produces a reduced relic density as the resulting mass remains smaller than its maximum value. As indicated in Fig. 5, the change in relic density is only significant for . For a sizeable , the variation in relic density is almost negligible with . However, such a decrease in relic density can also be compensated by appropriate scaling of value which is not directly entering in determining the .


III.2 ALP oscillation starts after EWSB
Now we elaborate on the possibility where the ALP is scheduled to start its conventional oscillation (connected to its mass only) after EWSB. As discussed earlier, this can materialise only if GeV. In this case, even if the global symmetry is spontaneously broken during or before inflation, the ALP field got stuck at the misalignment angle . The situation may alter with the presence of dim-6 Higgs portal interaction we include in this work leading to two possibilities: (a) the effective mass after EWSB immediately satisfies the condition , thanks to the Higgs portal contribution toward ; (b) even with the additional contribution to its mass, satisfies the condition with a temperature smaller than and hence ALP oscillation starts later.

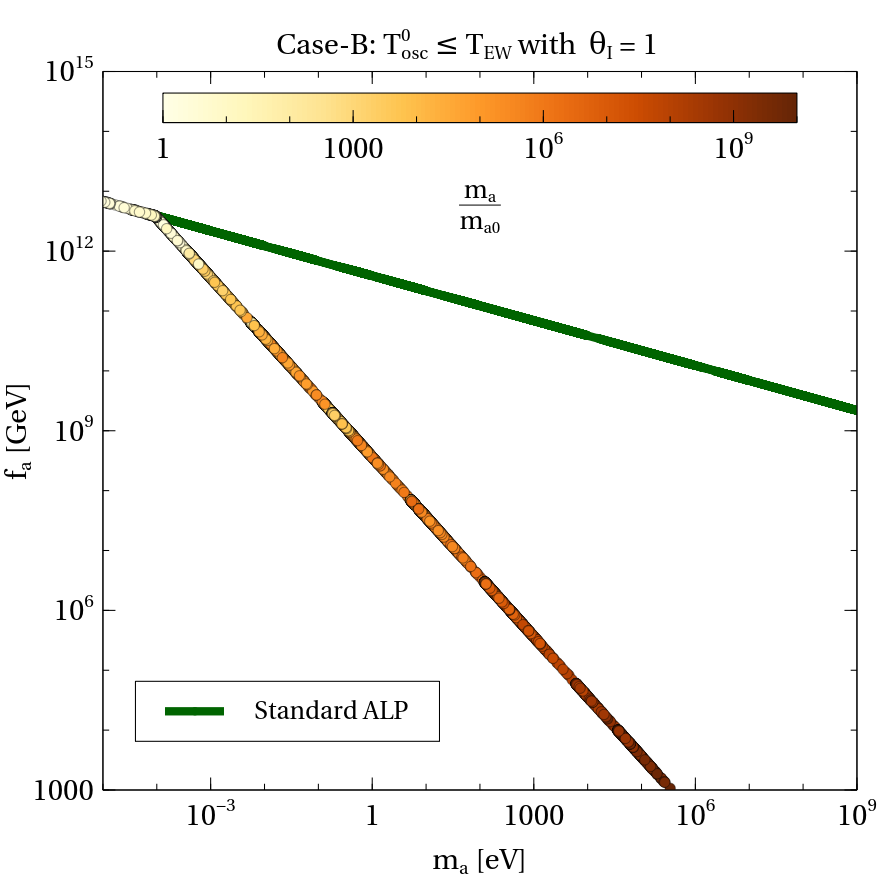
We notice that contrary to case [A], there would not be any abrupt change in ALP oscillation here as the oscillation begins already with the effective mass at or below EWSB. The evolution of ALP then proceeds according to the Eq. 19. The rest of the prescription for evaluating the final relic is similar to the standard case discussed in the section II. The parameter space satisfying the final relic for this case is represented in Figs. 6 and 7 while the corresponding values of parameter and the ratio are shown in top bar, respectively. In the same plot, the standard case ( without Higgs portal coupling) relic satisfied parameter space having ALP mass equivalent of from the beginning is indicated by the green patch for comparison purpose. The relic satisfied parameter space in this case [B] is not broadened (absence of elongated relic satisfied patch as in case [A]) compared to the conventional or standard parameter space as there is no such intermediate change in oscillation frequency. However the standard ALP parameter space for this range of final ALP mass changes its gradient due to a different onset of ALP oscillation era (it starts at related to its mass equivalent of ). It is found that except for large satisfying , the Higgs portal operator provides dominant contribution to ALP final mass, . The minimum contribution to ALP mass obtainable from the dim-6 Higgs portal is of order GeV which sets the boundary of to its lower side. Around this large , both and Higgs portal contributions are comparable (refer to Fig. 7) explaining the overlap of the two parameter space lines near GeV.
IV Constraints on ALP parameter space
In the previous section, we analyse the relic satisfied parameter space of ALP characterized by its final mass and the decay constant . However, such a parameter space can be further constrained from astrophysical and cosmological limits as well as few laboratory and telescope searches provided one considers an ALP-photon coupling Marsh (2016); Jaeckel and Ringwald (2010) of the form
| (24) |
where and are the electromagnetic field strength tensor and its dual respectively. The effective coupling can be written in terms of the ALP decay constant as
| (25) |
Generally, is expected to be and is the fine-structure constant.
Such an ALP-photon coupling opens up several windows of observation on which a considerable effort is being devoted now-a-days. These ALPs might get produced within the searing plasma of stars via interactions with photons. Such process may subsequently impact the stellar evolution leading to an overall energy loss of a star while escaping. Therefore, the non-observance of any unwanted energy loss in stars sets bounds on the parameter Turner (1990); Raffelt (2008). A stringent bound on GeV-1 emerges from the study of evolution of the horizontal branch (HB) stars Ayala et al. (2014). Also, the Sun is a likely source of ALPs (solar ALP), which are detectable on Earth in a telescope with a macroscopic magnetic field via reverse Primakoff process, commonly known as the Sikivie (1983). We have used the latest findings with best sensitivity from the CERN Axion Solar Telescope (CAST) which also puts constraints on similar to those derived from the study of HB stars as, GeV-1 for eV Anastassopoulos et al. (2017). The ALP-photon interaction is also constrained by the measurements of solar neutrino flux as GeV-1 for Gondolo and Raffelt (2009). Other important constraints emerge from the cavity experiments such as Rochester-Brookhaven-Florida and University of Florida (RBF and UF) and Axion Dark Matter Experiment (ADMX) which are sensitive for the ALP mass ranges of eV De Panfilis et al. (1987); Wuensch et al. (1989); Hagmann et al. (1990) and eV Asztalos et al. (2004) respectively. Telescope searches including Visible Multi-Object Spectrograph (VIMOS) and Multi Unit Spectroscopic Explorer (MUSE) further constrain the ALP mass ranges of eV and eV respectively Workman et al. (2022); Regis et al. (2021).


Searches for ALP are also actively done by various laboratory experiments. One such experimental approach is the light shining through a wall (LSW) experiment Redondo and Ringwald (2011) where a laser beam is expected to be converted into axion or ALPs after being exposed to a high magnetic field. Subsequently, these converted particles pass through an opaque wall and upon re-converting into photons via a second magnetic field behind the wall, they provide indirect evidence for the presence of ALPs. The current best limit by such LSW experiments are given by OSQAR (Optical Search for QED Vacuum Birefringence, Axions, and Photon Regeneration) as GeV-1 for meV Isleif (2022).
The cosmological constraint of (with being the age of the Universe and representing the decay width of ALP) serves as a key condition in guaranteeing the stability of the non-thermally produced cosmic ALPs as a viable dark matter over the universe lifetime Balázs et al. (2022). If , the extra radiations impart additional limits on extending to very large ALP masses Masso and Toldra (1995). Additionally, photons from ALP decays can be seen as peaks on top of the known backgrounds in the galactic x-ray spectra and must not surpass the extragalactic background light (EBL) Overduin and Wesson (2004). Also, ALP decaying into photons can lead to the ionization of primordial hydrogen, and the constraint comes from the requirement to prevent this ionization from making a crucial contribution to the optical depth after recombination and hence ensuring the consistency of BBN with observations Masso and Toldra (1995); Cadamuro and Redondo (2012); Depta et al. (2020). Other cosmological constraints comes from the excess photons (when decay occurs during opaque universe) include spectral distortions in the CMB spectrum and increase in (photon temperature) relative to (neutrino temperature), thus modifying the value of inferring from WMAP Depta et al. (2020).
The bounds regarding all these constraints are shown in the Fig. 8 which are taken from the updated online repository AxionLimits O’hare (2020). In Fig. 8, the yellow line acts as the demarkation line below which the ALP may serve as a viable dark matter ( sec). On the other hand, the red line corresponds to the ALP dark matter relic satisfaction contour originating from the standard misalignment mechanism (as discussed in section II) representative of the green line displayed in Figs. 2, 3, 6 and 7 with the consideration of (which is followed throughout the analysis). The obtained parameter spaces in our scenario (Figs. 2 and 6) of cases [A] and [B] are further constrained by these bounds and the residual allowed parameter regions in plane (converted from ) are demonstrated in top and bottom panels of Fig. 8 respectively. Note that as seen from Fig. 8 corresponding to case A, ALP masses
ranging from (keV) to GeV (serves as the lower limit for this case as per our previous discussion) are allowed with larger couplings (by several orders of magnitude) compared to the conventional
picture (red line). Similarly, higher ALP-photon couplings are permitted for case B as well, where the upper limit of allowed ALP mass turns out to be eV while the lower limit is set at GeV, which is the minimum mass contribution arising from the dimension-6 operator. It is important to note that for standard misalignment of ALP (without any higher dimensional soft symmetry breaking term), the lower limit of ALP mass can be extrapolated upto very small values ( eV) Marsh (2016).
V Isocurvature perturbations
In the present scenario, where the PQ-like symmetry is assumed to be broken during inflation, the ALP field should experience quantum fluctuations having an amplitude denoted by , where is the Hubble parameter during inflation. These quantum fluctuations give rise to isocurvature perturbation of the cold dark matter Hamann et al. (2009); Beltran et al. (2007); Kawasaki et al. (2018) which is constrained from the measurements of the CMB anisotropies111These ALP fluctuations however do not play any role in the overall density fluctuations of the universe.. The contribution of ALP to CDM isocurvature perturbation can be expressed as
| (26) |
In our scenario, ALP contributes entirely to relic density of CDM . The spectrum of CDM isocurvature perturbation in the Fourier space is given by
| (27) |
is the comoving wavenumber, to be evaluated at the pivot scale defined by . The limit imposed by Aghanim et al. (2020) on CDM isocurvature perturbation with respect to the adiabatic power, , is expressed as Aghanim et al. (2020)
| (28) |
The ALP density perturbation of Eq. 26 can also be recast as
| (29) |
using which follows from Eq. 6. Considering the misalignment angle to be and employing the fluctuation of the misalignment angle during inflation, , into Eqs. 29 and 27, we obtain
| (30) |
Following the constraint in Eq. 28 and considering as in the previous sections, we obtain an upper bound on the inflationary Hubble scale as
| (31) |
Depending on the specific cases in our scenario, we can derive a few more constraints as a consequence of Eq. 31 Arias et al. (2012) as we discuss in the following.
For case A (), the ALP mass at the onset of oscillation can be constrained by the required condition . Using Eq. 31 and setting in Eq. 23, we obtain the following relation
| (32) |
where is considered.
On the other hand, for case B (), the constraints can appear in two different ways: () when the ALP with effective mass starts to oscillate at only, the criteria along with Eq. 31 leads to
| (33) |
() Secondly, if the oscillation temperature of the ALP with effective mass is itself smaller than (no intermediate change in the ALP mass takes place), we need to utilize the criteria . Here, similar to case A, using Eq. 31 and setting in Eq. 10 (with replaced by ), we obtain
| (34) |
The correlations obtained in Eq. 32 and constraints on as in Eqs. 33-34 are evidently weaker than the other restrictions shown in the previous section and obeyed by the allowed parameter space in the respective cases. The constraint in Eq. 31 is however significant in the context of gravitational wave detection. As inflation can give rise to the generation of gravitational waves through tensor perturbations, the generation of tensor perturbations during inflation is directly correlated with the Hubble parameter Kawasaki et al. (2018) as
| (35) |
which can be translated in our scenario as
| (36) |
which is very small number to be predicted in near future as the current observational constraint on the tensor mode, , is derived from the Planck measurements of the CMB Ade et al. (2016).
VI conclusion
Axion-like particles are well motivated dark matter candidates which are thought to be produced primarily through the misalignment mechanism in the early universe. In this study, we have explored the impact of electroweak symmetry breaking on the evolution of such ALP DM in presence of an explicit shift symmetry breaking dimension-6 Higgs portal interaction of it. We observe that such an operator may significantly contribute to the ALP mass during the EWSB which further initiates a change in the oscillation frequency, thereby deviating from the standard misalignment mechanism in terms of final outcome. We have shown that depending on the standard ALP oscillation temperature (which is determined by the ALP mass originating from non-perturbative dynamics only), the change in the ALP mass across EWSB gives rise to a significant modifications in relic-density allowed parameter space compared to the standard misalignment mechanism.
Our findings can be broadly categorised into two: (a) one in which we obtain an extended parameter space (in plane) compared to the standard misalignment mechanism, applicable when the non-perturbative mass of ALP exceeds GeV and (b) secondly, where we obtain a parameter space with a different slope (in plane) compared to the standard one which applies when falls below GeV.
Finally, taking into account all the existing constraints from several terrestrial experiments, astrophysical and cosmological bounds on the plane (translated from plane) characterising ALP’s interaction with photons, we have identified a significant residue of newly opened up parameter space (from relic satisfaction point of view) in the sub-keV ALP mass regime to be compatible as non-thermal dark matter. These constraints also play a crucial role in restricting the lower limit on the cut-off scale (as evident from Fig. 8), thereby forbidding the other possibility of ALP production via freeze-in from the decay or annihilations of the Higgs, which requires relatively smaller values of . Interestingly, the predicted ALP-photon couplings turn out to be notably larger compared to the case of conventional misalignment, opening up opportunities for exploration through upcoming experiments.
Acknowledgements.
The work of AS is supported by the grants CRG/2021/005080 and MTR/2021/000774 from SERB, Govt. of India.Appendix A Origin of dimension-6 operator
Here, we present a possible origin of dimension-6 global symmetry breaking operator of our kind using the fact that any global symmetry is expected to be explicitly broken by gravity at Giddings and Strominger (1988); Coleman (1988); Rey (1989); Abbott and Wise (1989); Akhmedov et al. (1992). For this purpose, we consider the following Lagrangian (relevant part only)
| (37) |
Here, is our symmetry breaking complex scalar field having charge under while is a heavy (mass ) complex SM singlet scalar field carrying charge -2 such that the first term respects the symmetry. The dimensionful coupling can naturally be of order . The second term being a dimension-5 operator can be thought of a soft symmetry breaking one resulting due to the explicit breaking of the by gravity at . Considering the hierarchy of mass scales as: , integrating out the heavy field at energies below results into the following dimension-6 term Bonnefoy (2023)
| (38) |
Identifying with the scale , we obtain the operator considered in our analysis. Note that such a construction would not allow any other dimension-6 operator such as which could otherwise be present.
Appendix B Phenemenology in presence of two dimension-6 operators
For completeness purpose, we shall briefly discuss here how the phenomenology changes if we include the other possible dimension-6 operator ( without restricting to the possible origin of such operator as outlined in Appendix-A)
| (39) |
where is a dimensionless coupling. With both the explicit breaking terms present (via Eqs. 12 and 39) and considering , ALP will acquire a bigger mass (in comparison to Eq. 16) after EWSB, without altering the potential minimum (), as follows
| (40) |
Apart from inducing a sizeable contribution to the final mass of ALP, the new term (Eq. 39) also allows a dominant production of ALPs through decay (and annihilation) of the Higgs field after EWSB. As a result, a possible freeze-in production of ALPs remains viable in addition to the production through misalignment mechanism. Such a possibility although prevails with the other dimension-6 operator (we comment on this in the conclusion section), here with the additional one via Eq. 39, the freeze-in of ALP may proceed with larger coupling strength (between two ALPs and the Higgs field) proportional to , in contrary to the other case (with Eq. 12 only), where was replaced by the Higgs vev (). Hence, freeze-in can be significantly enhanced by inclusion of the operator in Eq. 39. Additionally, it may lead to the possibility of ALP thermalisation if happens to be of order or more. To alleviate such possibilities, we find that restricting by , ALP can favourably be produced through misalignment mechanism only.

Therefore, considering the presence of both the dimension-6 operators with , we showcase the relic allowed parameter space in Fig. B.1. Here GeV is taken so that the conventional ALP oscillation starts prior to EWSB. As the operator of Eq. 39 adds a substantial contribution to ALP mass via Eq. 40, a lower value of is required to achieve the correct relic density as evident from Eq. 23, which is also observed in Fig. B.1. We notice that with the choice of , the relic allowed parameter space is shifted beyond eV, where the leftmost boundary is dictated by the choice of . Hence it turns out that after imposing all the relevant cosmological and astrophysical bounds (as outlined in section IV), only a tiny fraction of the parameter space remains viable to achieve the correct relic density through misalignment mechanism in this case.
Appendix C Transition of ALP mass across EWSB

In connecting the evolution of the ALP field across , an apparent discontinuity is felt due to the sudden change in the mass of ALP: from at to at (representative of a step function at ). To retain the continuity of the ALP field while passing through the EWPT, we propose to make the transition of to a smooth one by introducing logistic function for the mass Di Bari et al. (2020) defined as
| (41) |
across . Here, is a parameter which controls the abruptness involved in the transition (a large indicates a more sharper transition). Since the EWPT happens within a finite range of temperature , such an approximation is justified provided the the change of ALP mass extends over that period . A schematic presentation of such an approximation is exhibited in Fig. C.1 with is employed. This is for the illustration purpose in case one tries to track the evolution of the field via Eq. 19. While evaluating the energy density of the ALP field, we use the sudden approximation in line with Eq. 20.
References
- Svrcek and Witten (2006) P. Svrcek and E. Witten, JHEP 06, 051 (2006), eprint hep-th/0605206.
- Arvanitaki et al. (2010) A. Arvanitaki, S. Dimopoulos, S. Dubovsky, N. Kaloper, and J. March-Russell, Phys. Rev. D 81, 123530 (2010), eprint 0905.4720.
- Demirtas et al. (2020) M. Demirtas, C. Long, L. McAllister, and M. Stillman, JHEP 04, 138 (2020), eprint 1808.01282.
- Peccei and Quinn (1977a) R. D. Peccei and H. R. Quinn, Phys. Rev. Lett. 38, 1440 (1977a).
- Peccei and Quinn (1977b) R. D. Peccei and H. R. Quinn, Phys. Rev. D 16, 1791 (1977b).
- Weinberg (1978) S. Weinberg, Phys. Rev. Lett. 40, 223 (1978).
- Wilczek (1978) F. Wilczek, Phys. Rev. Lett. 40, 279 (1978).
- Preskill et al. (1983) J. Preskill, M. B. Wise, and F. Wilczek, Phys. Lett. B 120, 127 (1983).
- Abbott and Sikivie (1983) L. F. Abbott and P. Sikivie, Phys. Lett. B 120, 133 (1983).
- Dine and Fischler (1983) M. Dine and W. Fischler, Phys. Lett. B 120, 137 (1983).
- Turner (1983) M. S. Turner, Phys. Rev. D 28, 1243 (1983).
- Arias et al. (2012) P. Arias, D. Cadamuro, M. Goodsell, J. Jaeckel, J. Redondo, and A. Ringwald, JCAP 06, 013 (2012), eprint 1201.5902.
- Cadamuro and Redondo (2012) D. Cadamuro and J. Redondo, JCAP 02, 032 (2012), eprint 1110.2895.
- Ringwald (2012) A. Ringwald, Phys. Dark Univ. 1, 116 (2012), eprint 1210.5081.
- Workman et al. (2022) R. L. Workman et al. (Particle Data Group), PTEP 2022, 083C01 (2022).
- Marsh (2018) D. J. E. Marsh, in 13th Patras Workshop on Axions, WIMPs and WISPs (2018), pp. 59–74, eprint 1712.03018.
- Jeong et al. (2022) K. S. Jeong, K. Matsukawa, S. Nakagawa, and F. Takahashi, JCAP 03, 026 (2022), eprint 2201.00681.
- Li (2023) H.-J. Li (2023), eprint 2307.09245.
- Chatrchyan et al. (2023) A. Chatrchyan, C. Eröncel, M. Koschnitzke, and G. Servant (2023), eprint 2305.03756.
- Co et al. (2020) R. T. Co, L. J. Hall, and K. Harigaya, Phys. Rev. Lett. 124, 251802 (2020), eprint 1910.14152.
- Chang and Cui (2020) C.-F. Chang and Y. Cui, Phys. Rev. D 102, 015003 (2020), eprint 1911.11885.
- Co et al. (2021) R. T. Co, L. J. Hall, and K. Harigaya, JHEP 01, 172 (2021), eprint 2006.04809.
- Eröncel et al. (2022) C. Eröncel, R. Sato, G. Servant, and P. Sørensen, JCAP 10, 053 (2022), eprint 2206.14259.
- Chao et al. (2022) W. Chao, M. Jin, H.-J. Li, and Y.-Q. Peng (2022), eprint 2210.13233.
- Im and Jeong (2019) S. H. Im and K. S. Jeong, Phys. Lett. B 799, 135044 (2019), eprint 1907.07383.
- Dev et al. (2019) P. S. B. Dev, F. Ferrer, Y. Zhang, and Y. Zhang, JCAP 11, 006 (2019), eprint 1905.00891.
- Oikonomou (2023) V. K. Oikonomou, Phys. Rev. D 107, 064071 (2023), eprint 2303.05889.
- Marsh (2016) D. J. E. Marsh, Phys. Rept. 643, 1 (2016), eprint 1510.07633.
- Bauer and Plehn (2019) M. Bauer and T. Plehn, Yet Another Introduction to Dark Matter: The Particle Physics Approach, vol. 959 of Lecture Notes in Physics (Springer, 2019), eprint 1705.01987.
- Balázs et al. (2022) C. Balázs et al., JCAP 12, 027 (2022), eprint 2205.13549.
- Higaki et al. (2016) T. Higaki, K. S. Jeong, N. Kitajima, and F. Takahashi, JHEP 06, 150 (2016), eprint 1603.02090.
- Draper et al. (2022) P. Draper, I. G. Garcia, and M. Reece, in Snowmass 2021 (2022), eprint 2203.07624.
- Cordova et al. (2022) C. Cordova, K. Ohmori, and T. Rudelius, JHEP 11, 154 (2022), eprint 2202.05866.
- Giddings and Strominger (1988) S. B. Giddings and A. Strominger, Nucl. Phys. B 307, 854 (1988).
- Coleman (1988) S. R. Coleman, Nucl. Phys. B 310, 643 (1988).
- Rey (1989) S.-J. Rey, Phys. Rev. D 39, 3185 (1989).
- Abbott and Wise (1989) L. F. Abbott and M. B. Wise, Nucl. Phys. B 325, 687 (1989).
- Akhmedov et al. (1992) E. K. Akhmedov, Z. G. Berezhiani, and G. Senjanovic, Phys. Rev. Lett. 69, 3013 (1992), eprint hep-ph/9205230.
- Arkani-Hamed et al. (2007) N. Arkani-Hamed, L. Motl, A. Nicolis, and C. Vafa, JHEP 06, 060 (2007), eprint hep-th/0601001.
- Kolb and Turner (1990) E. W. Kolb and M. S. Turner, The Early Universe, vol. 69 (1990), ISBN 978-0-201-62674-2.
- Abel et al. (2020) C. Abel et al., Phys. Rev. Lett. 124, 081803 (2020), eprint 2001.11966.
- Kamionkowski and March-Russell (1992) M. Kamionkowski and J. March-Russell, Phys. Lett. B 282, 137 (1992), eprint hep-th/9202003.
- Holman et al. (1992) R. Holman, S. D. H. Hsu, T. W. Kephart, E. W. Kolb, R. Watkins, and L. M. Widrow, Phys. Lett. B 282, 132 (1992), eprint hep-ph/9203206.
- Barr and Seckel (1992) S. M. Barr and D. Seckel, Phys. Rev. D 46, 539 (1992).
- Aghanim et al. (2020) N. Aghanim et al. (Planck), Astron. Astrophys. 641, A6 (2020), [Erratum: Astron.Astrophys. 652, C4 (2021)], eprint 1807.06209.
- Jaeckel and Ringwald (2010) J. Jaeckel and A. Ringwald, Ann. Rev. Nucl. Part. Sci. 60, 405 (2010), eprint 1002.0329.
- Turner (1990) M. S. Turner, Phys. Rept. 197, 67 (1990).
- Raffelt (2008) G. G. Raffelt, Lect. Notes Phys. 741, 51 (2008), eprint hep-ph/0611350.
- Ayala et al. (2014) A. Ayala, I. Domínguez, M. Giannotti, A. Mirizzi, and O. Straniero, Phys. Rev. Lett. 113, 191302 (2014), eprint 1406.6053.
- Sikivie (1983) P. Sikivie, Phys. Rev. Lett. 51, 1415 (1983), [Erratum: Phys.Rev.Lett. 52, 695 (1984)].
- Anastassopoulos et al. (2017) V. Anastassopoulos et al. (CAST), Nature Phys. 13, 584 (2017), eprint 1705.02290.
- Gondolo and Raffelt (2009) P. Gondolo and G. G. Raffelt, Phys. Rev. D 79, 107301 (2009), eprint 0807.2926.
- De Panfilis et al. (1987) S. De Panfilis, A. C. Melissinos, B. E. Moskowitz, J. T. Rogers, Y. K. Semertzidis, W. Wuensch, H. J. Halama, A. G. Prodell, W. B. Fowler, and F. A. Nezrick, Phys. Rev. Lett. 59, 839 (1987).
- Wuensch et al. (1989) W. Wuensch, S. De Panfilis-Wuensch, Y. K. Semertzidis, J. T. Rogers, A. C. Melissinos, H. J. Halama, B. E. Moskowitz, A. G. Prodell, W. B. Fowler, and F. A. Nezrick, Phys. Rev. D 40, 3153 (1989).
- Hagmann et al. (1990) C. Hagmann, P. Sikivie, N. S. Sullivan, and D. B. Tanner, Phys. Rev. D 42, 1297 (1990).
- Asztalos et al. (2004) S. J. Asztalos et al. (ADMX), Phys. Rev. D 69, 011101 (2004), eprint astro-ph/0310042.
- Regis et al. (2021) M. Regis, M. Taoso, D. Vaz, J. Brinchmann, S. L. Zoutendijk, N. F. Bouché, and M. Steinmetz, Phys. Lett. B 814, 136075 (2021), eprint 2009.01310.
- Redondo and Ringwald (2011) J. Redondo and A. Ringwald, Contemp. Phys. 52, 211 (2011), eprint 1011.3741.
- Isleif (2022) K.-S. Isleif (ALPS), Moscow Univ. Phys. Bull. 77, 120 (2022), eprint 2202.07306.
- Masso and Toldra (1995) E. Masso and R. Toldra, Phys. Rev. D 52, 1755 (1995), eprint hep-ph/9503293.
- Overduin and Wesson (2004) J. M. Overduin and P. S. Wesson, Phys. Rept. 402, 267 (2004), eprint astro-ph/0407207.
- Depta et al. (2020) P. F. Depta, M. Hufnagel, and K. Schmidt-Hoberg, JCAP 05, 009 (2020), eprint 2002.08370.
- O’hare (2020) C. O’hare, cajohare/AxionLimits: AxionLimits (2020).
- Hamann et al. (2009) J. Hamann, S. Hannestad, G. G. Raffelt, and Y. Y. Y. Wong, JCAP 06, 022 (2009), eprint 0904.0647.
- Beltran et al. (2007) M. Beltran, J. Garcia-Bellido, and J. Lesgourgues, Phys. Rev. D 75, 103507 (2007), eprint hep-ph/0606107.
- Kawasaki et al. (2018) M. Kawasaki, E. Sonomoto, and T. T. Yanagida, Phys. Lett. B 782, 181 (2018), eprint 1801.07409.
- Ade et al. (2016) P. A. R. Ade et al. (Planck), Astron. Astrophys. 594, A20 (2016), eprint 1502.02114.
- Bonnefoy (2023) Q. Bonnefoy, Phys. Rev. D 108, 035023 (2023), eprint 2212.00102.
- Di Bari et al. (2020) P. Di Bari, D. Marfatia, and Y.-L. Zhou, Phys. Rev. D 102, 095017 (2020), eprint 2001.07637.