Effective non-Hermitian Physics for Degenerate Ground States of non-Hermitian Ising Model with $\mathcal{RT}$-Symmetry

For a class of non-Hermitian quantum systems as dynamic equilibrium steady systems under specific symmetry, their Hamiltonians may exhibit entirely real eigenvalues like Hermitian quantum systems. Since Parity-time ($\mathcal{PT}$)-symmetric non-Hermitian quantum theory was put forward by Bender and BoettcherBender98 ; Bender02 ; Bender07 in the 1990s, it attracts massive researches in different fields in recent years. Many platforms were proposed to realize $\mathcal{PT}$-symmetric non-Hermitian symmetric quantum mechanics, such as optical systems R10 ; Hang13 ; Peng16 ; Zhang16 , electronicsBender13b ; Assawaworrarit17 ; Choi18 , microwavesBittner12 , acousticsZhu14 ; Popa14 ; Fleury15 and single-spin systemWu19 . Some applications associated with $\mathcal{PT}$-symmetric system have been explored including unidirectional transportFeng13 ; Peng14 and single-mode lasersFeng14 ; Hodaei14 . Also $\mathcal{PT}$-symmetric non-Hermitian quantum spin models have been designedKorff07 ; Korff08 ; Giorgi10 ; Song13 ; Ghatak19 , which can well capture the essence of many discrete models. For a (or anti) $\mathcal{PT}$-symmetric non-Hermitian HamiltonianGe13 which is invariant under the combined action of the $\mathcal{P}$ and $\mathcal{T}$ operations, (or anti) $\mathcal{PT}$ spontaneous symmetry breaking (SSB) occurs with adjustable parameters accompanied by a real-to-complex spectral phase transition. The critical point is called, exceptional point (EP), at which two or more eigenvalues, and their corresponding eigenvectors, simultaneously coalesce.

As another typical quantum spin non-Hermitian models, rotation-time ($\mathcal{RT}$)-symmetric non-Hermitian spin models have been studiedSong13 . $\mathcal{RT}$-invariant non-Hermitian Hamiltonians for quantum spin models as a class of pseudo-Hermitian Hamiltonians behave homologous to (or anti) $\mathcal{PT}$-invariant non-Hermitian Hamiltonians. It is naturally conceivable that the spin rotation operator $\mathcal{R}$ might replace the parity operator $\mathcal{P}$ to construct a quantum spin model of non-Hermitian quantum systems. Therefore, $\mathcal{RT}$-invariant non-Hermitian Hamiltonians for quantum spin models can be regarded as a generalization of $\mathcal{PT}$-invariant non-Hermitian Hamiltonians. In addition, the Hamiltonians with $\mathcal{RT}$ $\mathcal{(PT)}$-symmetric complex magnetic fields between spins in quantum spin models Giorgi10 ; Song13 ; Castro09 ; Deguchi09 are also non-Hermitian quantum systems predicted to contain those properties as above mentioned.

In this paper, we investigate a one dimensional (1D) spin modelGiorgi10 ; Song13 ; Castro09 ; Deguchi09 ; Song16 with $\mathcal{RT}$-invariant non-Hermitian term and focus on how Non-Hermitian terms affect the degenerate ground states of this model. we find that the effective Hamiltonian for the degenerate ground states has (or anti) $\mathcal{PT}$-symmetry and there exists (or anti) $\mathcal{PT}$ SSB for the two degenerate ground states with tunable parameters in external fields at EPs. At EPs, the original real eigenvalues turn into the complex ones and their associated eigenvectors simultaneously merge into one. By using high order perturbation methodkou09a ; kou09b ; kou09c to manipulate the quantum tunneling effect between two degenerate ground states, we detect that the energy splitting of two degenerate ground states comes from quantum tunneling in transverse filed and Zeeman splitting in longitudinal field, which is precisely consistent with the numerical calculations of the extent of the energy splitting of two degenerate ground states.

Let us begin with the 1D non-Hermitian Hamiltonian with $\mathcal{RT}$-symmetry for quantum spin model given by

where $\hat{H}_{0}=-g\sum_{i}\tau_{i}^{z}\tau_{i+1}^{z}$ is 1D Ising model without external field and $\hat{H}^{\prime}=\sum_{i}(\alpha\tau_{i}^{x}+\beta\tau_{i}^{z})$ represents the external field term. $\tau_{i}^{x,y,z}$ are Pauli matrices at sites $i$ and satisfy the periodic boundary condition $\tau_{i}^{x,y,z}=\tau_{i+N}^{x,y,z}$.$\ \alpha$ and $\beta$ are the strength of the transverse and longitudinal fields, respectively. As the perturbation term, $\left|\alpha\right|,$ $\left|\beta\right|$ are much smaller than $g$ normally. In this paper, we focus on the case of $g\gg\left|\alpha\right|$, $g\gg\left|\beta\right|$, and the coupling parameter $g$ is set to be unit, $g\equiv 1$. In particular, $\alpha$ or $\beta$ can be real or imaginary tunable parameter.

For a non-Hermitian Hamiltonian with $\mathcal{RT}$-symmetry, we have $\left[\mathcal{R},\hat{H}_{\mathcal{RT}}\right]\neq 0$ and $\left[\mathcal{T},\hat{H}_{\mathcal{RT}}\right]\neq 0$, but $\left[\mathcal{RT},\hat{H}_{\mathcal{RT}}\right]=0.$ Here the time reversal operator $\mathcal{T}$ is defined as $\mathcal{T}i\mathcal{T=-}i$ and the spin rotation operator $\mathcal{R}$ is defined by rotating each spin by $\pi$ about the $a$-axis

where $N$ is the number of lattice sites and $a$ denotes $x$, $y$, $z$ directions.

In this paper, will study the following three cases under periodic boundary condition:

1. 1.

   The non-Hermitian Ising model with $\mathcal{R}^{x}\mathcal{T}$-symmetry: for the case of $\mathcal{R}=\mathcal{R}^{x}\mathcal{(}\pi\mathcal{)}=\Pi_{j=1}^{N}(i\tau_{j}^{x})$, the spin rotation operator $\mathcal{R}^{x}\mathcal{(}\pi\mathcal{)}$ turns into parity operation and the $\mathcal{R}^{x}\mathcal{T}$-symmetry turns into traditional $\mathcal{PT}$-symmetry. Now, $\alpha$ is real and $\beta$ is imaginary, respectively. The Hamiltonian becomes

   $$\hat{H}_{\mathcal{R}^{x}\mathcal{T}}=-g\sum_{i}\tau_{i}^{z}\tau_{i+1}^{z}+\sum_{i}(\pm\left|\alpha\right|\tau_{i}^{x}\pm i\left|\beta\right|\tau_{i}^{z}).$$

   (2)

   This model has been applied to investigate a lattice version of the Yang–Lee modelYang52 ; Lee52 ; Castro09 ; Deguchi09 ; Cardy85 ; Gehlen91a ; Gehlen91b .

2. 2.

   The non-Hermitian Ising model with $\mathcal{R}^{z}\mathcal{T}$-symmetry: for the case of $\mathcal{R}=\mathcal{R}^{z}\mathcal{(}\pi\mathcal{)}=\Pi_{j=1}^{N}(i\tau_{j}^{z})$, the spin rotation operator $\mathcal{R}^{z}\mathcal{(}\pi\mathcal{)}$ turns into anti-parity operation and the $\mathcal{RT}$-symmetry turns into traditional anti-$\mathcal{PT}$-symmetry. Now, $\alpha$ is imaginary and $\beta$ is real, respectively. The Hamiltonian becomes

   $$\hat{H}_{\mathcal{R}^{z}\mathcal{T}}=-g\sum_{i}\tau_{i}^{z}\tau_{i+1}^{z}+\sum_{i}(\pm i\left|\alpha\right|\tau_{i}^{x}\pm\left|\beta\right|\tau_{i}^{z});$$

3. 3.

   The non-Hermitian Ising model with $\mathcal{R}^{y}\mathcal{T}$-symmetry: for the case of $\mathcal{R}=\mathcal{R}^{y}\mathcal{(}\pi\mathcal{)}=\Pi_{j=1}^{N}(i\tau_{j}^{y})=i\mathcal{R}^{x}\mathcal{(}\pi\mathcal{)R}^{z}\mathcal{(}\pi\mathcal{)}$, the spin rotation operator $\mathcal{R}^{y}\mathcal{(}\pi\mathcal{)}$ turns into ”parity” operation. Now, $\alpha$ and $\beta$ are all imaginary. The Hamiltonian becomes

   $$\hat{H}_{\mathcal{R}^{y}\mathcal{T}}=-g\sum_{i}\tau_{i}^{z}\tau_{i+1}^{z}+\sum_{i}(\pm i\left|\alpha\right|\tau_{i}^{x}\pm i\left|\beta\right|\tau_{i}^{z}).$$

   (3)

In the limit of $\alpha,\beta\rightarrow 0$, the Hamiltonian $\hat{H}_{\mathcal{RT}}$ will reduce to 1D Ising model $\hat{H}_{0}$ without external filed. Now the ground states have two-fold degeneracy and becomes Ferromagnetic (FM) states, i.e., $\left|\uparrow\uparrow\cdots\uparrow\uparrow\right\rangle$ and $\left|\downarrow\downarrow\cdots\downarrow\downarrow\right\rangle$. Due to the existence of the external fields, the energies for the FM degenerate ground states split. For the case of $\alpha\neq 0,$ $\beta=0$, the energy splitting for the degenerate ground states comes from quantum tunneling effect. The quantum tunneling process corresponds to the creation of a pair of virtual domain wall with one of them traversing around the chain and annihilating with the other one finally. Under the periodic boundary condition for the Ising chain, the dominant tunneling process is a single virtual domain wall moving from one side to the other with a reduced tunneling splitting obtained by high-order perturbation approach. On the other hand, for the case of $\alpha=0,$ $\beta\neq 0$, the energy splitting for the degenerate ground states comes from Zeeman effect that leads to an energy splitting proportional to external field.

Now, we discuss the energy splitting from imaginary (or real) transverse external field, i.e., the term $\sum_{i}\alpha\tau_{i}^{x}.$

According to high-order perturbation approach, after adding the transverse field $\tau_{i}^{x}$ to the Ising chain, we are able to generate two domain walls and drive one of them hopping around the chain by considering high-order perturbation terms.

We denote the two ground states by $\left|\uparrow\uparrow\cdots\uparrow\uparrow\right\rangle$ and $\left|\downarrow\downarrow\cdots\downarrow\downarrow\right\rangle$. Considering this tunneling process, we obtain the perturbation energy as we may obtain the energy shift $\Delta$ as

where $E_{0}$ is the ground state energy. According to $\hat{H}_{0}\left|\downarrow\downarrow\cdots\uparrow\cdots\downarrow\downarrow\right\rangle=(E_{0}+4g)\left|\downarrow\downarrow\cdots\uparrow\cdots\downarrow\downarrow\right\rangle,$ the energy for the excited state $\left|\downarrow\downarrow\cdots\uparrow\cdots\downarrow\downarrow\right\rangle$ of the two domain walls at the sites $i$ and $i-1$ is $E_{0}+4g$. Then we have

After the domain wall moves step by step around the chain and annihilates with the other, the ground state changes from $\left|\downarrow\downarrow\cdots\downarrow\downarrow\right\rangle$ to $\mid\uparrow\uparrow\cdots\uparrow\uparrow\rangle$ (or from $\mid\uparrow\uparrow\cdots\uparrow\uparrow\rangle$ to $\left|\downarrow\downarrow\cdots\downarrow\downarrow\right\rangle$). As a result, the corresponding energy splitting is obtained as

Next, we consider the energy splitting from imaginary (or real) longitudinal field $\sum_{i}\beta\tau_{i}^{z}$. When we apply the longitudinal external field ($\beta\neq 0$), the corresponding eigenstates of the Hamiltonian are just $\left|\uparrow\uparrow\cdots\uparrow\uparrow\right\rangle$ and $\left|\downarrow\downarrow\cdots\downarrow\downarrow\right\rangle$ with energy shifting. The energy difference between the states $\left|\uparrow\uparrow\cdots\uparrow\uparrow\right\rangle$ and $\left|\downarrow\downarrow\cdots\downarrow\downarrow\right\rangle$ is obtained as

Finally, an effective pseudo-spin Hamiltonian for the (quasi) degenerate ground states is obtained as

where $\Delta=N\frac{(\alpha)^{N}}{(-4g)^{N-1}}$ and $\varepsilon=N\beta$. In thermodynamic limit, $\Delta\rightarrow 0$, we have

that is Hermitian when $\operatorname{Im}\varepsilon=0$ or anti-Hermitian when $\operatorname{Re}\varepsilon=0$.

By diagonalizing the effective Hamiltonian $\mathcal{\hat{H}}_{\mathrm{eff}}$, we get eigenvalues and eigenvectors as

The total energy splitting becomes

Firstly, we consider the case of real $\alpha$ (transverse field) and imaginary $\beta$ (Zeeman filed). The Hamiltonian of the non-Hermitian Ising model becomes

The Hamiltonian has $\mathcal{R}^{x}\mathcal{T}$-symmetry, i.e, $\left[\mathcal{R}^{x},\hat{H}_{\mathcal{R}^{x}\mathcal{T}}\right]\neq 0$ and $\left[\mathcal{T},\hat{H}_{\mathcal{R}^{x}\mathcal{T}}\right]\neq 0,$ but $\left[\mathcal{R}^{x}\mathcal{T},\text{ }\hat{H}_{\mathcal{R}^{x}\mathcal{T}}\right]=0.$ From above discussion, the effective Hamiltonian for the (quasi) degenerate ground states is obtained as

There exists effective $\mathcal{PT}$-symmetry for the effective Hamiltonian for the (quasi) degenerate ground states, i.e., $\left[\mathcal{P}_{\mathrm{eff}},\mathcal{\hat{H}}_{\mathrm{eff}}\right]\neq 0$ and $\left[\mathcal{T},\mathcal{\hat{H}}_{\mathrm{eff}}\right]\neq 0,$ but $\left[\mathcal{P}_{\mathrm{eff}}\mathcal{T},\text{ }\mathcal{\hat{H}}_{\mathrm{eff}}\right]=0$ where $\mathcal{P}_{\mathrm{eff}}=\sigma^{x}$.

For $\left|\Delta\right|$ $>\left|\varepsilon\right|$, both eigenvalues $E_{\pm}$ are real, indicating the system in a phase with effective $\mathcal{PT}$ symmetry. In the region of unbroken effective $\mathcal{PT}$ symmetry, the eigenvectors are eigenstates of the symmetry operator, i.e., $\mathcal{P}_{\mathrm{eff}}\mathcal{T}\psi_{\pm}=\psi_{\pm}$; For $\left|\Delta\right|$ $<\left|\varepsilon\right|$, both eigenvalues become imaginary. In this region $\theta$ is complex and $\psi_{\pm}$ no longer possess the same symmetry as $\mathcal{\hat{H}}_{\mathrm{eff}}$. A spontaneous (effective) $\mathcal{PT}$-symmetry-breaking transition occurs at the exceptional points $\left|\Delta\right|$ $=\left|\varepsilon\right|$ that indicates a relationship

As a result, the two degenerate ground states merge into one at EP.

In Fig. 1, we illustrate the numerical results from the exact diagonalization technique of the Ising model on even and odd lattices with periodic boundary conditions. For case of $N=4$, Fig. 1(a) and (b) show the real part $\operatorname{Re}\left|\delta E\right|$ and the imaginary part $\operatorname{Im}\left|\delta E\right|$ for the ground states energy splitting of the non-Hermitian Ising model with $\left|\alpha\right|=0.3$, respectively. Fig. 1(c) shows the global phase diagram of $\mathcal{PT}$-symmetry-breaking transition for the two degenerate ground states, of which the phase boundary is composed of exceptional points characterized by the relation $\left|\alpha\right|^{4}=(4g)^{3}\left|\beta\right|$. For case of $N=5$, Fig. 1(d) and Fig. 1(e) show the real part $\operatorname{Re}\left|\delta E\right|$ and the imaginary part $\operatorname{Im}\left|\delta E\right|$ for the ground states energy splitting of the non-Hermitian Ising model with $\left|\alpha\right|=0.3$, respectively. Fig. 1(f) shows the global phase diagram of $\mathcal{PT}$-symmetry-breaking transition for degenerate ground states, the phase boundary are exceptional points characterized by the relation $\left|\alpha\right|^{5}=(4g)^{4}\left|\beta\right|$. We can see the numerical results are consistent to our theoretical prediction by this high-order perturbation approach.

Therefore, we found that, quantum properties for $\hat{H}_{\mathcal{R}^{x}\mathcal{T}}$ on a spin chain with even number of lattice sites and those for $\hat{H}_{\mathcal{R}^{x}\mathcal{T}}$ on a spin chain with odd number of lattice sites are similar and even a small imaginary external field applied will drive $\mathcal{PT}$ phase transition by reason of the Pauli matrices non-commutative relation.

Secondly, we consider the case of imaginary $\alpha$ (transverse field) and real $\beta$ (Zeeman filed). The Hamiltonian for the non-Hermitian Ising model becomes

The Hamiltonian has $\mathcal{R}^{z}\mathcal{T}$-symmetry, i.e, $\left[\mathcal{R}^{z},\hat{H}_{\mathcal{R}^{z}\mathcal{T}}\right]\neq 0$ and $\left[\mathcal{T},\hat{H}_{\mathcal{R}^{z}\mathcal{T}}\right]\neq 0,$ but $\left[\mathcal{R}^{z}\mathcal{T},\text{ }\hat{H}_{\mathcal{R}^{z}\mathcal{T}}\right]=0.$ From above discussion, the effective Hamiltonian for the (quasi) degenerate ground states is obtained as

We found that, quantum properties for $\hat{H}_{\mathcal{R}^{z}\mathcal{T}}$ on a spin chain with even number of lattice sites and those for $\hat{H}_{\mathcal{R}^{z}\mathcal{T}}$ on a spin chain with odd number of lattice sites are quite different.

In the case of a system on spin chain with even $N$ sites, the effective Hamiltonian is Hermitian, i.e, $\mathcal{\hat{H}}_{\mathrm{eff}}=\mathcal{\hat{H}}_{\mathrm{eff}}^{\ast}.$ In Fig. 2, we show the numerical results from the exact diagonalization technique of the Ising model with periodic boundary conditions. For $N=4$, the energy splitting $\Delta E$ is always real due to $(\frac{\Delta}{2})^{2}+(\frac{\varepsilon}{2})^{2}>0$, the effective Hamiltonian is Hermitian, no $\mathcal{PT}$ phase transition happens.

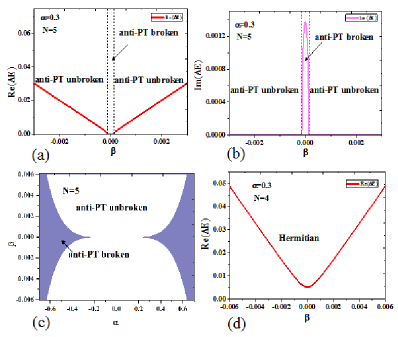
Whereas, in the case of system on a spin chain with odd $N$ sites, the effective Hamiltonian is non-Hermitian, i.e, $\mathcal{\hat{H}}_{\mathrm{eff}}\neq\mathcal{\hat{H}}_{\mathrm{eff}}^{\ast}$. There exists effective anti-$\mathcal{PT}$-symmetry for the effective Hamiltonian for the (quasi) degenerate ground states, i.e., $\left[\mathcal{P}_{\mathrm{anti,eff}},\mathcal{\hat{H}}_{\mathrm{eff}}\right]\neq 0$ and $\left[\mathcal{T},\mathcal{\hat{H}}_{\mathrm{eff}}\right]\neq 0,$ but $\{\mathcal{P}_{\mathrm{anti,eff}}\mathcal{T},$ $\mathcal{\hat{H}}_{\mathrm{eff}}\}=0$ where $\mathcal{P}_{\mathrm{anti,eff}}=\sigma^{x}$. For $\left|\Delta\right|$ $<\left|\varepsilon\right|$, we have effective anti-$\mathcal{PT}$ symmetry. Now, both eigenvalues $E_{\pm}$ are real. In this region of unbroken anti-$\mathcal{PT}$ symmetry, the eigenvectors are eigenstates of the symmetry operator. For $\left|\Delta\right|$ $>\left|\varepsilon\right|$, effective anti-$\mathcal{PT}$ symmetry is broken. A spontaneous (effective) anti-$\mathcal{PT}$-symmetry-breaking transition occurs at the exceptional points $\left|\Delta\right|$ $=\left|\varepsilon\right|$ that indicates a power law relationship

As a result, at EP the two degenerate ground states also merge into one.

In Fig. 2(d), we give the real parts of energy splitting for even lattice $N=4$ , we derive the entirely real energy splitting but no imaginary part of energy splitting due to its pure real effective Hermitian Hamiltonian. Fig. 2(a) and (b) illustrate $\operatorname{Re}\left|\delta E\right|$ and $\operatorname{Im}\left|\delta E\right|$ of the energy splitting for the two degenerate ground states, respectively. In Fig. 2(c), we show the global phase diagram of anti-$\mathcal{PT}$-symmetry-breaking transition for degenerate ground states of the non-Hermitian Ising model with $\left|\alpha\right|=0.3$ on $N=5$ odd lattice. The phase boundary are exceptional points characterized by the relation $\left|\alpha\right|^{5}=(4g)^{4}\left|\beta\right|$. We also find a very small imaginary external field applied will drive anti-$\mathcal{PT}$ phase transition.

Thirdly, we consider the case of imaginary $\alpha$ (transverse field) and imaginary $\beta$ (Zeeman filed). The Hamiltonian for the non-Hermitian Ising model becomes

The Hamiltonian has $\mathcal{R}^{y}\mathcal{T}$-symmetry, i.e, $\left[\mathcal{R}^{y},\hat{H}_{\mathcal{R}^{y}\mathcal{T}}\right]\neq 0$ and $\left[\mathcal{T},\hat{H}_{\mathcal{R}^{y}\mathcal{T}}\right]\neq 0,$ but $\left[\mathcal{R}^{y}\mathcal{T},\text{ }\hat{H}_{\mathcal{R}^{y}\mathcal{T}}\right]=0.$ From above discussion, the effective Hamiltonian for the (quasi) degenerate ground states is obtained as

We found that quantum properties for $\hat{H}_{\mathcal{R}^{y}\mathcal{T}}$ on a spin chain with even $N$ and those for $\hat{H}_{\mathcal{R}^{y}\mathcal{T}}$ on a spin chain with odd $N$ odd lattices are also quite different.

For the case of a system on spin chain with odd number of lattice sites, the effective Hamiltonian is pure imaginary and non-Hermitian, i.e, $\mathcal{\hat{H}}_{\mathrm{eff}}=-\mathcal{\hat{H}}_{\mathrm{eff}}^{\ast}$, resulting in no $\mathcal{PT}$ phase transition.

For the case of system on a spin chain with even number of lattice sites, the effective Hamiltonian is non-Hermitian, i.e, $\mathcal{\hat{H}}_{\mathrm{eff}}\neq\mathcal{\hat{H}}_{\mathrm{eff}}^{\ast}$. There exists effective $\mathcal{PT}$-symmetry for the effective Hamiltonian for the (quasi) degenerate ground states, i.e., $\left[\mathcal{P}_{\mathrm{eff}},\mathcal{\hat{H}}_{\mathrm{eff}}\right]\neq 0$ and $\left[\mathcal{T},\mathcal{\hat{H}}_{\mathrm{eff}}\right]\neq 0,$ but $\left[\mathcal{P}_{\mathrm{eff}}\mathcal{T},\text{ }\mathcal{\hat{H}}_{\mathrm{eff}}\right]=0$ where $\mathcal{P}_{\mathrm{eff}}=\sigma^{x}$. For $\left|\Delta\right|>\left|\varepsilon\right|$, we have effective $\mathcal{PT}$ symmetry, both eigenvalues $E_{\pm}$ are real. In this region of unbroken effective $\mathcal{PT}$ symmetry, the eigenvectors are eigenstates of the symmetry operator, i.e., $\mathcal{P}_{\mathrm{eff}}\mathcal{T}\psi_{\pm}=\psi_{\pm}$. For $\left|\Delta\right|$ $<\left|\varepsilon\right|$, effective $\mathcal{PT}$ symmetry is broken, both eigenvalues become imaginary and correspond to a gain and a loss eigenstate. A spontaneous (effective) $\mathcal{PT}$-symmetry-breaking transition occurs at the exceptional points $\left|\Delta\right|=\left|\varepsilon\right|$ that indicates a relationship $\frac{\left|\alpha\right|^{N}}{(4g)^{N-1}}=\left|\beta\right|.$ At EP the two degenerate ground states also merge into one.

In Fig. 3(a) and (b)  we depict the $\operatorname{Re}\left|\delta E\right|$ and $\operatorname{Im}\left|\delta E\right|$ of energy splitting for the two degenerate ground states of the non-Hermitian Ising model with $\left|\alpha\right|=0.4$ on even lattice $N=4$. In Fig. 3(c) we exhibit the global phase diagram of effective anti-$\mathcal{PT}$-symmetry-breaking transition for degenerate ground states for $N=4$ , the phase boundary is composed of exceptional points characterized by the relation $\left|\alpha\right|^{4}=(4g)^{3}\left|\beta\right|$, Fig. 3(d) shows the imaginary parts of energy splitting for odd lattice $N=5$, we obtain the entirely imaginary energy splitting but no real part of energy splitting due to its pure imaginary non-Hermitian Hamiltonian.

In this paper, we studied non-Hermitian spin Ising model with $\mathcal{RT}$-symmetry. To describe the low energy physics, we introduce an effective pseudo-spin model, of which the (anti) $\mathcal{PT}$-symmetry emerges. In particular, spontaneous (or anti) $\mathcal{PT}$-symmetry breaking may happen in parameters space with tunable external field for special spin chains. As a result, at EPs the two degenerate ground states always merge into one. These results are consistent with those obtained from exact diagnalization numerical technique. Also we find that $\mathcal{PT}$ phase transition is very robust even in a tiny imaginary field although lattice sizes determine its phase boundary. We can expand this conclusion to other spin systems with imaginary external fields for studying their degenerate ground states properties due to the Pauli matrices non-commutative relation.

We give Table. 1 to show the main results – the physics results for non-Hermitian spin Ising model with different $\mathcal{RT}$-symmetries: 1) For the non-Hermitian Ising model with $\mathcal{R}^{x}\mathcal{T}$-symmetry and even/odd number of lattice sites, there exists effective $\mathcal{PT}$-symmetry for the effective Hamiltonian for the (quasi) degenerate ground states. Spontaneous $\mathcal{PT}$-symmetry breaking occurs; 2) For the non-Hermitian Ising model with $\mathcal{R}^{z}\mathcal{T}$-symmetry and even number of lattice sites, effective Hamiltonian for the (quasi) degenerate ground states is Hermitian. However, for the non-Hermitian Ising model with $\mathcal{R}^{z}\mathcal{T}$-symmetry and odd number of lattice sites, effective Hamiltonian for the (quasi) degenerate ground states is non-Hermitian with effective anti-$\mathcal{PT}$-symmetry. Spontaneous anti-$\mathcal{PT}$-symmetry breaking occurs; 3) For the non-Hermitian Ising model with $\mathcal{R}^{y}\mathcal{T}$-symmetry and odd number of lattice sites, effective Hamiltonian for the (quasi) degenerate ground states is non-Hermitian and pure imaginary. However, for the non-Hermitian Ising model with $\mathcal{R}^{y}\mathcal{T}$-symmetry and even number of lattice sites, effective Hamiltonian for the (quasi) degenerate ground states is non-Hermitian with effective $\mathcal{PT}$-symmetry. Spontaneous $\mathcal{PT}$-symmetry breaking occurs.

In the end, we address several relevant issues. The first is the relationship between the non-Hermitian Ising model and the non-Hermitian systems with topological bands. It was known that the quantum transverse Ising model is equivalent to a topological fermionic model after Jordan-Wigner transformation. However, for the 1D non-Hermitian Ising model with both transverse and longitudinal fields, the Jordan-Wigner transformation doesn’t work and the quantum spin model cannot be mapped to a local (Hermitian or non-Hermitian) fermionic model. Another relevant issue is the experimental realization. It is still a challenge to experimentally investigate non-Hermitian Hamiltonian related physics in quantum systems. A possible approach is cold-atom experiments due to spontaneous decayHang2013 ; Lee2014 ; luo . A possible application is to obtain a Schrödinger cat state. The basic idea is to drive the two-level system of degenerate ground states to EPs by adding external field and then remove it slowly. Due to the non-Hermitian term, the degeneracy is reduced into non-Hermitian degeneracy at the exceptional points. As a result, the two ground states merge into one quantum ”steady” state and a pure Schrödinger cat state is obtained.