††thanks: [email protected] ††thanks: [email protected]
Effective minimal model and unconventional spin-singlet pairing in Kagome superconductor CsV3Sb5
Abstract
Recently synthesized Kagome compounds AV3Sb5 attract great attention due to the unusual coexistence of the topology, charge density wave and superconductivity. In this Letter, based on the band structures for CsV3Sb5 in pristine phase, we fit an effective 6-band model for the low-energy processes; utilizing the random phase approximation (RPA) on the effective minimal model, we obtain the momentum-resolved static spin susceptibility; attributing the spin-fluctuation pairing mechanism, we find that the superconducting pairing strengths increase with the lift of the Coulomb correlation, and the superconductive pairing symmetry is singlet, the gap functions are antisymmetric with respect to the x-axis and the y-axis in the intermediate to strong Coulomb correlated regime, indicating the unconventional superconductivity in Kagome compounds AV3Sb5.
Introduction:
Local spins in a Kagome lattice compound was regarded as most probably forming exotic quantum spin liquid Lu et al. (2011); Chen et al. (2021a). Once such Kagome compounds Ortiz et al. (2019) become superconductiveOrtiz et al. (2020); Yin et al. (2021); Ortiz et al. (2021); Chen et al. (2021b); Zhang et al. (2021a); Chen et al. (2021c); Zhu et al. (2021); Yu et al. (2021); Ni et al. (2021); Fu et al. (2021); Xu et al. (2021); Zhao et al. (2021a); Chen et al. (2021d); Jiang et al. (2021); Shumiya et al. (2021); Wang et al. (2021); Mu et al. (2021); Zhao et al. (2021b), the long-term searching relationship between quantum spin liquid phase and unconventional superconductivity seems link with each other; recently found novel Kagome lattice compounds AV3Sb5 (A = K, Rb, Cs) have been attracting great research interestOrtiz et al. (2020); Yin et al. (2021); Ortiz et al. (2021); Chen et al. (2021b); Zhang et al. (2021a); Chen et al. (2021c); Zhu et al. (2021); Yu et al. (2021); Ni et al. (2021); Fu et al. (2021); Xu et al. (2021); Zhao et al. (2021a); Chen et al. (2021d); Jiang et al. (2021); Shumiya et al. (2021); Wang et al. (2021); Mu et al. (2021); Zhao et al. (2021b); Tan et al. (2021); Zhang et al. (2021b); Wu et al. (2021a); LaBollita and Botana (2021); Luo et al. (2021); Li et al. (2021); Liu et al. (2021); Kang et al. (2021); Cho et al. (2021). Through recent great efforts, many physical properties of AV3Sb5, including the electronic structuresOrtiz et al. (2019); Tan et al. (2021); Zhang et al. (2021b); Wu et al. (2021a); LaBollita and Botana (2021), normal-state Ortiz et al. (2019); Li et al. (2021) and superconducting-state propertiesOrtiz et al. (2020); Yin et al. (2021); Ortiz et al. (2021); Chen et al. (2021b); Zhang et al. (2021a); Chen et al. (2021c); Zhu et al. (2021); Yu et al. (2021); Ni et al. (2021); Fu et al. (2021); Xu et al. (2021); Zhao et al. (2021a); Chen et al. (2021d); Jiang et al. (2021); Shumiya et al. (2021); Wang et al. (2021); Mu et al. (2021); Zhao et al. (2021b), pressure effectChen et al. (2021b); Zhang et al. (2021a); Chen et al. (2021c); Zhu et al. (2021), magnetic field effectYu et al. (2021); Ni et al. (2021); Fu et al. (2021), STM results Xu et al. (2021); Zhao et al. (2021a); Chen et al. (2021d); Jiang et al. (2021); Shumiya et al. (2021); Wang et al. (2021) and ARPES dataLiu et al. (2021); Kang et al. (2021); Cho et al. (2021) have gradually become clear. Several theoretical models were also proposed to address the chirality of the charge-density-wave stateFeng et al. (2021); Denner et al. (2021) and superconductivityWu et al. (2021b). Nevertheless, a few of essential features remain not revealed, including the effective low-energy model, superconducting pairing force and the pairing symmetry, etc..
Due to unique crystal structure of Kagome compounds AV3Sb5, the electronic structures of normal-state AV3Sb5 are rather complicated. The band structures of the pristine phase of CsV3Sb5Tan et al. (2021), calculated by the density functional theory (DFT), predicted that seven bands cross the Fermi energy EF and are composed of V 3 orbitals and Sb 5 orbitals, which shows typical multi-orbital character. Since the unit cell of Kagome lattice contains three V sites in the pristine phase, at the same time, the metallic ground state in AV3Sb5 and partial filled V 3 orbitals also imply the multi-orbital character in the low-energy model. These inevitably bring difficulty in constructing an effective multiorbital model for superconducting AV3Sb5. At present the microscopic origin of the charge density wave is generally attributed to the van Hove singularity, whereas, to understand the essential superconductive nature, a proper effective model correctly describing the low-energy processes plays key roles and is highly expected.
So-far experimental data strongly support unconventional superconductive pairing mechanism in AV3Sb5: conventional e-ph coupling mechanism is not enough to account for the superconductive microscopic origin, neither the transition temperatures estimated by the McMillan’s formula for RbV3Sb5 and CsV3Sb5 considerably deviate from the experimental TC Tan et al. (2021), nor the experimental TC violates the expectation of the conventional e-ph mechanism when A varies from K, Rb to Cs. AV3Sb5 superconductors also display many features of unconventional superconductivity: with the increase of hydrostatic pressure, the P-T phase diagram demonstrates two superconductive regions Chen et al. (2021b); Zhu et al. (2021), similar to the two-dome superconductive phase diagrams in iron-based superconductorsSun et al. (2012); Shahi et al. (2018). Though the local magnetic moment was argued to be absent Kenney et al. (2021), the observation of the anomalous Hall effect in CsV3Sb5 Yang et al. (2020) strongly favors of the presence of local magnetic field, hence the local spins. The first-principles electronic structure calculations also suggested there exists local magnetic moments in AV3Sb5 Zhang et al. (2021b); Wu et al. (2021a), implying that the spin-orbital fluctuations mechanism is the possible pairing origin, since not only the system posses local magnetic moments and multiorbital character, but also Kagome lattice structure favors strong spin frustrations and fluctuations. These eager further deep theoretical investigations.
On the other hand, the details of the superconductive nature in AV3Sb5 are not clear. A very recent studyWu et al. (2021b) suggested that the superconducting electrons in CsV3Sb5 are f-wave triplet pairing: i.e. the superconductive Cooper pairs are spatial f-wave, and spin parallel or triplet. Such a prediction was inconsistent with the temperature-dependence Knight shift experimentMu et al. (2021). One also finds that in similar sixfold-symmetric superconductor NaxCoO2.yH2O, an earlier theoretical investigation suggested to be f-wave pairing symmetry Mazin and Johannes (2005), however, the experiments supported that the pairing symmetry of superconducting cobaltates is singlet d-wave Matano et al. (2007). This arises the puzzle whether the Cooper pairs with high angular momentum could stably exist in AV3Sb5. In this Letter, based on our calculated band structures for CsV3Sb5 in the pristine phase, we fit an effective low-energy 6-band model; utilizing the random phase approximation (RPA) on the effective minimal model, we show that the superconducting pairing strengths increase with the increase of Coulomb correlation, and the superconductive pairing symmetry is singlet dxy-wave-like. The present theoretical results favor our understand on the unconventional superconductivity in Kagome compounds AV3Sb5.



Effective minimal model Hamiltonian:
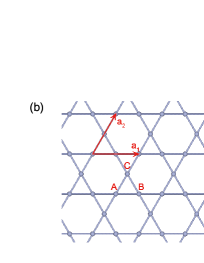
To investigate the many body effects and superconductivity in AV3Sb5, one should first construct an effective low-energy model. To this end, we start to perform the first-principles electronic structures calculations to obtain the band structures of CsV3Sb5. The details of the method and the calculations are given in the Supplementary Materials. Fig. 1(a) shows the crystal structure of the layered CsV3Sb5. Recent resistivity measurement on CsV3Sb5 Ortiz et al. (2020) showed remarkable anisotropy of the -plane to the -axis, indicating that the interlayer V-V hybridization is rather small. Throughout this paper we confine our study on the V-Sb Kagome plane, as seen in Fig. 1(b).
Our band structures and Fermi surfaces are in agreement with available literature LaBollita and Botana (2021); Luo et al. (2021).
There are three distinct Fermi surface sheets at kz=0 :
(i) a central ring sheet around contributed by Sb- orbitals, (ii) a hexagonal sheet composed of V-, V-, and V-, and (iii) two additional sheets composed of V- orbitalsLaBollita and Botana (2021); Luo et al. (2021).
In fitting the band structures with an effective low-energy tight-binding model,
we consider the large hexagonal Fermi pocket (ii) and one of the Fermi surface sheets (iii), to which the corresponding energy bands are hybridized weakly with the orbitals of SbLaBollita and Botana (2021), and then construct a six-band tight-binding (TB) model with two local orbitals on each V site.
By constructing localized Wannier functions, the hopping integrals between different V orbitals and (, ) are zeros, see the TABLE S1 in Supplementary Materials, indicating that interorbital hybridization between the and orbits of vanadiums is vanishing small, so we neglect the interorbital hopping terms in the tight-binding model.
The fitted tight-binding bands and the full electronic structures of CsV3Sb5 are the red and black lines in Fig. 2(a), respectively.
The fitted six pack-band tight-binding model for CsV3Sb5 can be written as
| (1) |
where the inequivalent V sites , the orbital indices , and the hopping matrix elements ,
where denotes the lattice structure factor defined in Supplementary Materials.
The denotes the energy level of the orbital and is the chemical potential. The operator () creates (annihilates) an electron with momentum and spin of sublattice in orbital .
The , and denote intra-orbital hopping integrals for the first, second and third nearest neighbors respectively. The hopping parameters are given in Supplementary Materials, see Table S3. Within the present six-band model, the Fermi surface is plotted in Fig. 2(b). The corresponding electron filling number is to match the chemical potential of CsV3Sb5 .
To investigate the spin fluctuations and superconducting pairing properties in CsV3Sb5, we consider the on-site Coulomb interaction as following
here denote the th unit cell. The on-site intra- and interorbital Coulomb repulsions
are denoted by and . and are the Hund’s rule exchange and pair-hopping term, respectively.
Throughout this paper, we set the Couloub and Hund’s interaction parameters and , which satisfy spin rotational invariance. The fact that the DFT band structures are in good agreement with the angle-resolved photoemission spectroscopy (ARPES) dataOrtiz et al. (2020), demonstrates that the electronic correlation in CsV3Sb5 is not very strong.
Within the random phase approximation (RPA), the singlet (s) and triplet (t) pairing vertices arising from spin and charge fluctuations for the multiorbital case Takimoto et al. (2002, 2003); Kubo (2007) are given by
here and represent the matrices in the V orbital space, and and are the ones RPA spin and orbital (charge) susceptibility matrix given in the Sec. III of Supplementary Materials.
By projecting the zero frequency pairing vertex into the band space Graser et al. (2009); Scalapino (2012), we obtain
| (5) | |||||
The (or ) determines the scatterings of two electrons of opposite (or same) spin from the state on the Fermi surface sheet to the state on the Fermi surface sheet . By means of a mean-field decouping of the interaction, the gap equation in singlet and triplet channels can be obtained and expressed as
| (6) |
with
| (7) | |||||
| (8) | |||||
| (9) |
It is worthy noting that is an even function with respect to k and an odd function. The superconducting instability appears at temperature. When the temperature just below Tc the gap function are expected to be very small, and hence we study the superconducting instability by solving the linearized gap equations Graser et al. (2009); Maier et al. (2019)
| (10) |
Here the eigenvalues are the superconducting pairing strengths and the corresponding eigenfunctions. is the area of a Brillouin zone, and are the band indices of Fermi surface vectors , , respectively, is the magnitude of the Fermi velocity. The largest pairing strength determines the highest transition temperature and the corresponding eigenfunction shows the symmetry of the gap function. Throughout this paper we perform the calculations at temperature of eV.
Momentum-resolved Spin Susceptibility:
The distribution of spin susceptibility in momentum space may not only disclose the spin fluctuation modes or the magnetic order, but also provide the superconductive pairing information. The RPA spin susceptibility of the effective minimal model for pristine CsV3Sb5 shows six peaks near and other five sixfold-symmetric wavevectors, as seen the red points in Fig. 3(a). In the lines connecting these maxima, the magnitude of the spin susceptibility is also very large, as seen the yellow lines in Fig. 3(a). These indicate that there exist multi-mode antiferromagnetic or spin-density-wave fluctuations. We also find that these peaks are enhanced with the increase of the Coulomb correlation U, as seen in Fig. 3(b).
Note that the e-ph coupling mechanism could not account for the origin of the superconductivity in CsV3Sb5, the spin-fluctuation
mechanism seems a plausible candidate. In the theory of spin-fluctuation mediated superconductivity,
the singlet pair scattering of a Cooper pair at k to k′ is proportional to the RPA spin susceptibilityKreisel et al. (2017); Scalapino (2012), one expects that the gap function on different parts Fermi surface connected by
and other sixfold-symmetric wavevectors has opposite signs, according to the linearized gap equations.









Superconductive Pairing Strengths:
By solving the linearized gap eqaution (10), we obtain the largest singlet and triplet pairing strengths as a function of the Coulomb interaction . The results shown in Fig. 4 indicate the singlet pairing dominates in the parameter range of eV. This suggests that the Cooper pairs in CsV3Sb5 are singlet pairing. It is consistent with the decrease of Knight shift of Sb with decline of temperatureMu et al. (2021). Meanwhile, we find that there exists the distinct difference in the SC gap functions on the two Fermi surfaces, the SC pairing gap function on inner Fermi surface is almost two order smaller in magnitude than that on outer Fermi surface.
The largest singlet pairing gap functions g(k) at eV and 0.8 eV are plotted in Fig. 5. These gap functions show sign-change at the high symmetry k points on the Fermi surface.
Further analysis in Fig. 6 shows when eV, the gap function exhibiting the antisymmetry with respect to the axis and the axis, i.e., dxy-wave-like symmetry, on the outer Fermi sheet and weak g-wave symmetry on the inner Fermi sheet. The gap function on the inner Fermi sheet is about smaller than that on the outer Fermi sheet by two orders in magnitude. When eV, the
gap functions slightly change, while still are dxy-wave-like.
These suggest that the dxy-wave-like paring is dominant in CsV3Sb5. The dxy-wave-like pairing
is in consistent with the results of finite linear term of thermal conductivity at ultra low temperatureZhao et al. (2021b) and the V-shaped gapChen et al. (2021d), which suggest the nodal superconductivity in CsV3Sb5. However, the study of impurity effectsXu et al. (2021) on superconductivity by STM and the appearance of Hebel-Slichter peakMu et al. (2021) in just below TC proposes S-wave pairing in CsV3Sb5. To uncover the structure of the superconducting gap in CsV3Sb5, further experiments on superconducting state, such as angular-resolved photoemission spectroscopy (ARPES), Bogoliubov quasiparticle interference, and phase-sensitive tests, are crucial and highly expected.
In fitting the present effective model (1), we elaborately consider the major bands contributed from the 3d orbits of V ions and ignore the bands contributed from Sb 5p orbits. The latter consists of the central Fermi surface around the point which arises from Sb 5p orbits and a few of Fermi surface fragments arising from the hybridization between dominant Sb 5p orbits and partial V 3d orbit.
One notices an experimental fact that upon applying pressure, the central Fermi surface and Sb-related 5 bands of CsV3Sb5 almost do not vary with the disappearance of the charge-density-wave order Liu et al. (2021), while the superconducting properties change considerably with increasing pressure, suggesting that the present fitted effective minimal model is responsible for the unconventional superconductivity in CsV3Sb5.
Contrast to the present singlet dxy-like superconductive pairing symmetry in our effective minimal model for CsV3Sb5, very recently
Wu et al. fitted another effective 6-orbital model Wu et al. (2021b) based on the electronic structures of KV3Sb5, they found that within the RPA their model favors the triplet f-wave pairing symmetry.
This indicates that the superconductive pairing symmetry is sensitive to the details of the band structures in AV3Sb5. Our present singlet pairing results agree with recent experiments, suggesting the plausible of the present effective minimal model for the superconductivity in AV3Sb5.
In summary, we have obtained an effective low-energy six-band model for CsV3Sb5 by fitting the the first-principles electronic structures. Within the random phase approximation and on the basis of the effective minimal model, we have found that the superconducting pairing strength increases with the lift of Coulomb correlation and decline of temperature, and superconductive pairing symmetry is singlet, most probably with the dxy-wave-like symmetry. These results highlight the essence of the unconventional superconductivity in Kagome compounds AV3Sb5. Also, one may recall that the full effective model should include the central Fermi surface and a few of Fermi surface fragments ignored in the present study, the role of these dominant Sb 5p bands on the nature of the superconductivity in Kagome compounds AV3Sb5 is worthy of further investigations.
Acknowledgements.
The authors thank the supports from the NSFC of China under Grant nos. 11774350 and 51727806, Program of Chinese Academy of Sciences, Science Challenge Project No. TZ2016001. Numerical calculations were partly performed at the Center for Computational Science of CASHIPS, the ScGrid of the Supercomputing Center, the Computer Network Information Center of CAS, the CSRC computing facility, and Hefei Advanced Computing Center.Note added. After we finished the manuscript, we realized that Lin et al. suggested that the Pomerranchuk fluctuations may lead to the superconductivity in the Kagome metals AV3Sb5 Lin and Nandkishore (2021). Whether the van Hove singularity related Pomeranchuk fluctuations could survive in the present intermediate correlated compounds deserves further study.
References
- Lu et al. (2011) Y.-M. Lu, Y. Ran, and P. A. Lee, Phys. Rev. B 83, 224413 (2011).
- Chen et al. (2021a) C. Chen, I. Sodemann, and P. A. Lee, Phys. Rev. B 103, 085128 (2021a).
- Ortiz et al. (2019) B. R. Ortiz, L. C. Gomes, J. R. Morey, M. Winiarski, M. Bordelon, J. S. Mangum, I. W. H. Oswald, J. A. Rodriguez-Rivera, J. R. Neilson, S. D. Wilson, et al., Phys. Rev. Mater. 3, 094407 (2019).
- Ortiz et al. (2020) B. R. Ortiz, S. M. L. Teicher, Y. Hu, J. L. Zuo, P. M. Sarte, E. C. Schueller, A. M. M. Abeykoon, M. J. Krogstad, S. Rosenkranz, R. Osborn, et al., Phys. Rev. Lett. 125, 247002 (2020).
- Yin et al. (2021) Q. Yin, Z. Tu, C. Gong, Y. Fu, S. Yan, and H. Lei, Chin. Phys. Lett. 38, 037403 (2021).
- Ortiz et al. (2021) B. R. Ortiz, P. M. Sarte, E. M. Kenney, M. J. Graf, S. M. L. Teicher, R. Seshadri, and S. D. Wilson, Phys. Rev. Mater. 5, 034801 (2021).
- Chen et al. (2021b) K. Y. Chen, N. N. Wang, Q. W. Yin, Y. H. Gu, K. Jiang, Z. J. Tu, C. S. Gong, Y. Uwatoko, J. P. Sun, H. C. Lei, et al., Phys. Rev. Lett. 126, 247001 (2021b).
- Zhang et al. (2021a) Z. Zhang, Z. Chen, Y. Zhou, Y. Yuan, S. Wang, J. Wang, H. Yang, C. An, L. Zhang, X. Zhu, et al., Phys. Rev. B 103, 224513 (2021a).
- Chen et al. (2021c) X. Chen, X. Zhan, X. Wang, J. Deng, X.-B. Liu, X. Chen, J.-G. Guo, and X. Chen, Chin. Phys. Lett. 38, 057402 (2021c).
- Zhu et al. (2021) C. C. Zhu, X. F. Yang, W. Xia, Q. W. Yin, L. S. Wang, C. C. Zhao, D. Z. Dai, C. P. Tu, B. Q. Song, Z. C. Tao, et al., arXiv:2104.14487 (2021).
- Yu et al. (2021) F. H. Yu, D. H. Ma, W. Z. Zhuo, S. Q. Liu, X. K. Wen, B. Lei, J. J. Ying, and X. H. Chen, Nat. Commun. 12, 3645 (2021).
- Ni et al. (2021) S. Ni, S. Ma, Y. Zhang, J. Yuan, H. Yang, Z. Lu, N. Wang, J. Sun, Z. Zhao, D. Li, et al., Chin. Phys. Lett. 38, 057403 (2021).
- Fu et al. (2021) Y. Fu, N. Zhao, Z. Chen, Q. Yin, Z. Tu, C. Gong, C. Xi, X. Zhu, Y. Sun, K. Liu, et al., Phys. Rev. Lett. 127, 207002 (2021).
- Xu et al. (2021) H.-S. Xu, Y.-J. Yan, R. Yin, W. Xia, S. Fang, Z. Chen, Y. Li, W. Yang, Y. Guo, and D.-L. Feng, Phys. Rev. Lett. 127, 187004 (2021).
- Zhao et al. (2021a) H. Zhao, H. Li, B. R. Ortiz, S. M. L. Teicher, P. Takamori, M. Ye, Z. Wang, B. Leon, S. D. Wilson, and Z. Ilija, Nature (London) 599, 216 (2021a).
- Chen et al. (2021d) H. Chen, H. Yang, B. Hu, Z. Zhao, J. Yuan, Y. Xing, G. Qian, Z. Huang, G. Li, Y. Ye, et al., Nature (London) 599, 222 (2021d).
- Jiang et al. (2021) Y.-X. Jiang, J.-X. Yin, M. M. Denner, N. Shumiya, B. R. Ortiz, G. Xu, Z. Guguchia, J. He, M. S. Hossain, X. Liu, et al., Nat. Mater. 20, 1353 (2021).
- Shumiya et al. (2021) N. Shumiya, M. S. Hossain, J.-X. Yin, Y.-X. Jiang, B. R. Ortiz, H. Liu, Y. Shi, Q. Yin, H. Lei, S. S. Zhang, et al., Phys. Rev. B 104, 035131 (2021).
- Wang et al. (2021) Z. Wang, Y.-X. Jiang, J.-X. Yin, Y. Li, G.-Y. Wang, H.-L. Huang, S. Shao, J. Liu, P. Zhu, N. Shumiya, et al., Phys. Rev. B 104, 075148 (2021).
- Mu et al. (2021) C. Mu, Q. Yin, Z. Tu, C. Gong, H. Lei, Z. Li, and J. Luo, Chin. Phys. Lett. 38, 077402 (2021).
- Zhao et al. (2021b) C. C. Zhao, L. S. Wang, W. Xia, Q. W. Yin, J. M. Ni, Y. Y. Huang, C. P. Tu, Z. C. Tao, Z. J. Tu, C. S. Gong, et al., arXiv:2102.08356 (2021b).
- Tan et al. (2021) H. Tan, Y. Liu, Z. Wang, and B. Yan, Phys. Rev. Lett. 127, 046401 (2021).
- Zhang et al. (2021b) J.-F. Zhang, K. Liu, and Z.-Y. Lu, Phys. Rev. B 104, 195130 (2021b).
- Wu et al. (2021a) W. Wu, X. Wang, and Z. Zeng, arXiv:2112.08559 (2021a).
- LaBollita and Botana (2021) H. LaBollita and A. S. Botana, arXiv:2108.04876 (2021).
- Luo et al. (2021) H. Luo, Q. Gao, H. Liu, Y. Gu, D. Wu, C. Yi, J. Jia, S. Wu, X. Luo, Y. Xu, et al., arXiv:2107.02688 (2021).
- Li et al. (2021) H. Li, H. Zhao, B. R. Ortiz, T. Park, M. Ye, L. Balents, Z. Wang, S. D. Wilson, and I. Zeljkovic, arXiv:2104.08209 (2021).
- Liu et al. (2021) Z. Liu, N. Zhao, Q. Yin, C. Gong, Z. Tu, M. Li, W. Song, Z. Liu, D. Shen, Y. Huang, et al., Phys. Rev. X 11, 041010 (2021).
- Kang et al. (2021) M. Kang, S. Fang, J.-K. Kim, B. R. Ortiz, S. H. Ryu, J. Kim, J. Yoo, G. Sangiovanni, D. D. Sante, B.-G. Park, et al., arXiv:2105.01689 (2021).
- Cho et al. (2021) S. Cho, H. Ma, W. Xia, Y. Yang, Z. Liu, Z. Huang, Z. Jiang, X. Lu, J. Liu, Z. Liu, et al., arXiv:2105.05117 (2021).
- Feng et al. (2021) X. Feng, K. Jiang, Z. Wang, and J. Hu, Sci. Bull. 66, 1384 (2021).
- Denner et al. (2021) M. M. Denner, R. Thomale, and T. Neupert, Phys. Rev. Lett. 127, 217601 (2021).
- Wu et al. (2021b) X. Wu, T. Schwemmer, T. Müller, A. Consiglio, G. Sangiovanni, D. Di Sante, Y. Iqbal, W. Hanke, A. P. Schnyder, M. M. Denner, et al., Phys. Rev. Lett. 127, 177001 (2021b).
- Sun et al. (2012) L. Sun, X.-J. Chen, J. Guo, P. Gao, Q.-Z. Huang, H. Wang, M. Fang, X. Chen, G. Chen, Q. Wu, et al., Nature (London) 483, 67 (2012).
- Shahi et al. (2018) P. Shahi, J. P. Sun, S. H. Wang, Y. Y. Jiao, K. Y. Chen, S. S. Sun, H. C. Lei, Y. Uwatoko, B. S. Wang, and J.-G. Cheng, Phys. Rev. B 97, 020508 (2018).
- Kenney et al. (2021) E. M. Kenney, B. R. Ortiz, C. Wang, S. D. Wilson, and M. J. Graf, J. Phys. Condens. Matter 33, 235801 (2021).
- Yang et al. (2020) S.-Y. Yang, Y. Wang, B. R. Ortiz, D. Liu, J. Gayles, E. Derunova, R. Gonzalez-Hernandez, L. Smejkal, Y. Chen, S. S. P. Parkin, et al., Sci. Adv. 6, eabb6003 (2020).
- Mazin and Johannes (2005) I. I. Mazin and M. D. Johannes, Nat. Phys. 1, 91 (2005).
- Matano et al. (2007) K. Matano, G. q. Zheng, D. Chen, C. Lin, J. Cmaidalka, R. Meng, and C. Chu, J. Magn. Magn. Mater. 310, 687 (2007).
- Takimoto et al. (2002) T. Takimoto, T. Hotta, T. Maehira, and K. Ueda, J. Phys. Condens. Matter 14, L369 (2002).
- Takimoto et al. (2003) T. Takimoto, T. Hotta, and K. Ueda, J. Phys. Condens. Matter 15, S2087 (2003).
- Kubo (2007) K. Kubo, Phys. Rev. B 75, 224509 (2007).
- Graser et al. (2009) S. Graser, T. A. Maier, P. J. Hirschfeld, and D. J. Scalapino, New J. Phys. 11, 025016 (2009).
- Scalapino (2012) D. J. Scalapino, Rev. Mod. Phys. 84, 1383 (2012).
- Maier et al. (2019) T. Maier, T. Berlijn, and D. J. Scalapino, Phys. Rev. B 99, 224515 (2019).
- Kreisel et al. (2017) A. Kreisel, B. M. Andersen, P. O. Sprau, A. Kostin, J. C. S. Davis, and P. J. Hirschfeld, Phys. Rev. B 95, 174504 (2017).
- Lin and Nandkishore (2021) Y.-P. Lin and R. M. Nandkishore, arXiv:2107.09050 (2021).