Effect of relaxation time on the squeezed correlations of bosons for evolving sources in relativistic heavy-ion collisions

In relativistic heavy-ion collisions, the interactions between the particles in sources lead to a modification of boson mass in the sources, and thus give rise to a squeezed correlation of boson-antiboson AsaCso96 ; AsaCsoGyu99 . This squeezed correlation is caused by the Bogoliubov transformation between the creation (annihilation) operators of the quasiparticles in the source and the free observable particles, and impels the boson and antiboson to move in opposite directions. So, it is also known as squeezed back-to-back correlation (SBBC) AsaCso96 ; AsaCsoGyu99 ; Padula06 . The measurements of the SBBC of bosons can provide information on the interaction between the meson and the source medium, and will be helpful to understand the properties of the particle-emitting sources AsaCso96 ; AsaCsoGyu99 ; Padula06 ; Padula10 ; Zhang15 ; Zhang16 .

Hydrodynamics has been widely used in relativistic heavy-ion collisions to describe the evolution of particle-emitting source. In hydrodynamic description it is assumed that the source system is under the local equilibrium, i.e. the evolution is the so-called “quasi-static process”. However, quasi-static process is a rough approximation. Because the SBBC is sensitive to the time distribution of the source, dealing appropriately with the temporal factors is of interest in calculations of the SBBC functions for evolving sources.

${\rm D}$ mesons contain a heavy quark (charm quark) produced during the early stage of relativistic heavy-ion collisions. The SBBC of ${\rm D}$ mesons is stronger than that of light mesons and useful for probing the source properties in the early stage Zhang16 ; Padula10JPG ; AGYang-CPL-18 ; XuZhang2019 ; XuZhang2019a In this paper, we put forth a method to calculate the SBBC function with relaxation-time modification for evolving sources and investigate the effects of relaxation time on the SBBC functions of ${\rm D}^{0}{\rm\bar{D}}^{0}$ in relativistic heavy-ion collisions using hydrodynamic model VISH2$+$1 VISH2+1 . We find that the SBBC functions decrease when relaxation time is taken into consideration. The change increases with increasing relaxation time and becomes serious for the large relative deviations of the chaotic and squeezed amplitudes at the start of evolution from their equilibrium values, respectively.

The rest of this paper is organized as follows. In Sec. II, we present the formulas of the SBBC functions for evolving sources with relaxation-time approximation. In Sec. III, we investigate the influences of relaxation time on the SBBC functions of ${\rm D}^{0}{\rm\bar{D}}^{0}$ in relativistic heavy-ion collisions. Finally, a summary and discussion are given in Sec. IV.

The SBBC function of boson-antiboson with momenta ${\mathbf{p}}_{1}$ and ${\mathbf{p}}_{2}$ is defined as AsaCsoGyu99 ; Padula06

where,

are the so-called chaotic and squeezed amplitudes, respectively AsaCsoGyu99 ; Padula06 , $\omega_{\mathbf{p}}=\sqrt{{\mathbf{p}}^{2}+m^{2}}$ is energy of free boson with mass $m$, $a$ and $a^{\dagger}$ are annihilation and creation operators of the free boson, respectively, and $\langle\cdots\rangle$ indicates the ensemble average.

For a homogeneous thermal-equilibrium source with fixed volume $V$ and existing in temporal interval [0–$\Delta t$] with time distribution $F(t)$, the amplitudes $G_{c}({\mathbf{p}},{\mathbf{p}})$ and $G_{s}({\mathbf{p}},-{\mathbf{p}})$ can be expressed as AsaCsoGyu99 ; Padula06

where

where $\Omega_{\mathbf{p}}=\sqrt{{\mathbf{p}}^{2}+m^{\prime 2}}$ is energy of the quasi-particle with mass $m^{\prime}$ in source medium and $n_{\mathbf{p}}$ is the boson distribution of the quasiparticle, and $\widetilde{F}(\omega_{\mathbf{p}},\Delta t)$ is Fourier transform of time distribution.

For a evolving source, quantities $g_{c}({\mathbf{p}},{\mathbf{p}})$ and $g_{s}({\mathbf{p}},-{\mathbf{p}})$ may be given by

where $g^{0}_{c}({\mathbf{p}},{\mathbf{p}})$ and $g^{0}_{s}({\mathbf{p}},-{\mathbf{p}})$ are the quantities in equilibrium state, given by Eqs. (4) and (5), and $\tau_{c}$ and $\tau_{s}$ are the relaxation-time parameters related to the system ability of recovering equilibrium. Relaxation-time approximation is an usual method for dealing with the quantities in evolution systems. In this approximation, parameters $\tau_{c,s}$ are needed to be smaller than the width of temporal interval, $\tau_{c,s}<\Delta t$, and they tend to zero under the quasi-static condition.

Assuming $\tau_{c}=\tau_{s}={\bar{\tau}}$, Eqs. (7) and (8) give

where $\Delta^{0}_{c,s}$ are differences of $g_{c,s}$ between the start of evolution and equilibrium, and it is assumed that the differences are approximately proportional to $g^{0}_{c,s}$ with proportionality parameters $\delta^{0}_{c,s}$, respectively. Parameter $\delta^{0}_{c}$ ($\delta^{0}_{s}$) denotes the relative deviation of the chaotic (squeezed) amplitude at the start of evolution from its equilibrium value. Then, the SBBC function $C_{\rm SBB}({\mathbf{p}},-{\mathbf{p}})$ for an evolving source is given by,

For a hydrodynamic source, the chaotic and squeezed amplitudes, $G_{c}({{\mathbf{p}}_{1}},{{\mathbf{p}}_{2}})$ and $G_{s}({{\mathbf{p}}_{1}},{{\mathbf{p}}_{2}})$, can be expressed in the relaxation-time approximation, as AsaCsoGyu99 ; Padula06 ; Padula10 ; Zhang15 ; Zhang16 ,

where $d^{4}\sigma_{\mu}(r)=f_{\mu}(r)d^{3}{\mathbf{r}}\,dt$ is the four-dimension element of freeze-out hypersurface, $q^{\mu}_{1,2}=p^{\mu}_{1}-p^{\mu}_{2}$, $K^{\mu}_{1,2}=(p^{\mu}_{1}+p^{\mu}_{2})/2$, $c^{\prime}_{{\mathbf{p}}^{\prime}_{1},{\mathbf{p}}^{\prime}_{2}}$ and $s^{\prime}_{{\mathbf{p}}^{\prime}_{1},{\mathbf{p}}^{\prime}_{2}}$ are the coefficients of Bogoliubov transformation between the creation (annihilation) operators of the quasiparticles and the free particles, $n^{\prime}_{{\mathbf{p}}^{\prime}_{1},{\mathbf{p}}^{\prime}_{2}}$ is the boson distribution associated with the particle pair in local frame, ${\mathbf{p}}_{i}^{\prime}~{}(i=1,2)$ is local-frame momentum AsaCsoGyu99 ; Padula06 ; Padula10 ; Zhang15 ; Zhang16 . In Eqs. (II) and (II), $[1+\delta^{0}_{c,s}e^{-t^{\prime}/{\bar{\tau}}}]$ is the factor for relaxation-time influence, where $t^{\prime}$ is local frame time. Eqs. (II) and (II) will reduce to the usual forms as in AsaCsoGyu99 ; Padula06 ; Padula10 ; Zhang15 ; Zhang16 when $\bar{\tau}=0$.

Dividing the whole time evolution into a series of time steps ($j=1,2,\cdots$) with the same step width, we have

where $\Delta\tau$ is the step width of time in local frame, $t(t^{\prime})=\gamma_{v}t^{\prime}$, $\gamma_{v}=1/\sqrt{1-{\mathbf{v}}^{2}}$, ${\mathbf{v}}$ is the velocity of fluid element, and $D(t^{\prime})$ is local time distribution in each time step. Taking $D(t^{\prime})$ to be an uniform distribution, the relaxation-time factors for $G_{c}({\mathbf{p}}_{i},{\mathbf{p}}_{i})~{}(i=1,2)$ and $G_{s}({\mathbf{p}}_{1},{\mathbf{p}}_{2})$ are,

We show in Figs. 1(a) and 1(b) the SBBC functions $C(\Delta\phi)$ of the ${\rm D}^{0}{\rm\bar{D}}^{0}$ pair in the hydrodynamic model VISH2$+$1 VISH2+1 for Au+Au collisions at RHIC energy $\sqrt{s_{NN}}=200$ GeV with 0–80% centrality, and in momentum intervals 0.55–0.65 GeV$/c$ and 1.15–1.25  GeV$/c$, respectively. Here, $\Delta\phi$ is the azimuthal angle difference between the transverse momenta ${\mathbf{p}}_{1T}$ and ${\mathbf{p}}_{2T}$ of the two D mesons, and the results of dashed, solid, dot-dashed, and two-dot-dashed lines are for the parameters ($\delta^{0}_{c}=\delta^{0}_{s}=\delta^{0}=0.5$, $\bar{\tau}=0$ fm$/c$, without relaxation-time modification), ($\delta^{0}_{c}=\delta^{0}_{s}=\delta^{0}=0.5$, $\bar{\tau}=0.2$ fm$/c$), ($\delta^{0}_{c}=\delta^{0}_{s}=\delta^{0}=0.25$, $\bar{\tau}=0.4$ fm$/c$), and ($\delta^{0}_{c}=\delta^{0}_{s}=\delta^{0}=0.5$, $\bar{\tau}=0.4$ fm$/c$), respectively. In the VISH2$+$1 model VISH2+1 used here, the event-by-event initial conditions of MC-Glb VISHb are employed, the ratio of the shear viscosity to entropy density of the QGP is taken to be 0.08 Shen11-prc ; Qian16-prc , and the freeze-out temperature is taken to be $T_{f}=150$ MeV according to the comparisons of the model transverse momentum spectrum of $\rm D^{0}$ AGYang-CPL-18 with the RHIC-STAR experimental data STAR-PRL113-2014 (see the Fig. 3 in Ref. AGYang-CPL-18 ). In the calculations, the time step width is taken to be 1 fm$/c$, free $\rm D^{0}$ meson mass is taken to be 1.865 GeV$/c^{2}$, and the in-medium average mass and width are taken from the results of FMFK calculations FMFK-PRC06 ; MFFK-PRL04 ; AGYang-CPL-18 .

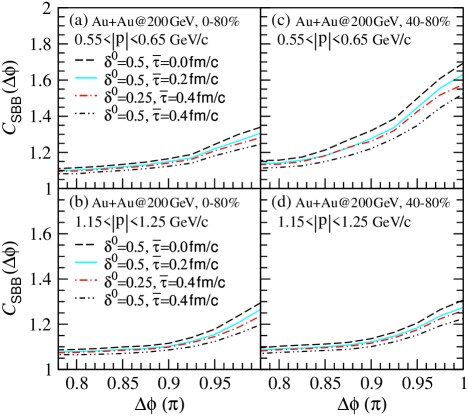
One can see from Figs. 1(a) and 1(b) that relaxation time decreases the SBBC functions. This change increases with increasing relaxation-time parameter $\bar{\tau}$ and the parameter $\delta^{0}$. Relaxation-time parameter reflects the ability of recovering equilibrium of system. In thermodynamics, high temperature and violent collisions may increase the ability. The parameter $\delta^{0}$ is related to expanding velocity of system. The SBBC functions in the lower momentum interval are higher than those in the higher momentum interval because of a more serious in-medium mass modification at low momenta than that at high momenta AGYang-CPL-18 , and the more serious oscillations of single-event SBBC functions at higher momentum Zhang15 may also lead to a lower average SBBC function Zhang16 ; AGYang-CPL-18 .

We show in Figs. 1(c) and 1(d) the SBBC functions $C(\Delta\phi)$ of the ${\rm D}^{0}{\rm\bar{D}}^{0}$ pair in the hydrodynamic model for Au+Au collisions at RHIC energy $\sqrt{s_{NN}}=200$ GeV with 40–80% centrality, and in momentum intervals 0.55–0.65 GeV$/c$ and 1.15–1.25  GeV$/c$, respectively. One can see also that relaxation-time modification decreases the SBBC functions. Similarly, the influence increases with increasing relaxation-time parameter $\bar{\tau}$ and the parameter $\delta^{0}$. Compared to the results for the collisions with 0–80% centrality, the SBBC functions for the collisions with 40–80% centrality are higher. The reason for this is mainly that the source temporal distribution is narrow in peripheral collisions Zhang16 . The contributions to the SBBC functions at lower $\Delta\phi$ are mainly from the more peripheral collisions, which are small both in spatial and temporal sizes AGYang-CPL-18 . The differences between the SBBC functions for the collisions with 0–80% and 40–80% centralities become small in the higher momentum interval.

We have investigated the effects of relaxation time on the SBBC functions of boson-antiboson pairs in relativistic heavy-ion collisions. A method for calculating the SBBC functions for evolving sources with relaxation-time modefication is put forth. Using the method in hydrodynamic model, we investigate the SBBC functions of ${\rm D}^{0}{\rm\bar{D}}^{0}$ in Au+Au collisions at RHIC energy $\sqrt{s_{NN}}=200$ GeV with 0–80% and 40–80% centralities. It is found that the relaxation time lead to a decrease of the SBBC functions. This change increases with increasing relaxation time and becomes serious for the large relative deviations of the chaotic and squeezed amplitudes at the start of evolution from their equilibrium values, respectively.

Relaxation-time approximation is an usual method to calculate quantities in a near-equilibrium evolving system. In viscous hydrodynamic models, relaxation times of shear and bulk viscosities are introduced, which may change the system space-time structure. However, the relaxation times associated with the quantities are also needed to be taken into account in their calculations with the hydrodynamic model, because the quantities undergo a transition from nonequilibrium to equilibrium in each temporal step. It is meaningful to consider appropriately relaxation time in calculating a sensitive time-depend observable.

Using a hydrodynamic model, one can obtain the source temperature as a space-time function. The final observed particles are assumed to be emitted thermally from a four-dimension hypersurface with the fixed freeze-out temperature, which can be determined by comparing the calculated observables, for example particle transverse-momentum spectra, with experimental data. In this paper, we use the viscous hydrodynamic model VISH2$+$1 VISH2+1 to produce the freeze-out hypersurface and calculate the SBBC functions with and without the relaxation-time term $\delta^{0}e^{-t^{\prime}/{\bar{\tau}}}$. The effect of relaxation time reduces the SBBC functions. This effect may retain in an ideal hydrodynamic model although the viscosity leads to a change of the freeze-out hypersurface.

Because the SBBC is caused by the particle mass modification in the source medium, analyzing SBBC may perhaps become a new technique to extract the information of the particle in-medium interactions in the future, although there are not experimental data to compare with now. On the other hand, it is hard to deal with the particle scattering in detail in a bulk evolution model. In our model calculations we assume that the $\rm D$ mesons have a mass shift and width, which are obtained from the FMFK calculations FMFK-PRC06 ; MFFK-PRL04 ; AGYang-CPL-18 , in the sources because of the in-medium interactions. More detailed studies of the influence of particle scattering on the SBBC, based on a cascade model (for instance, a multi-phase transport model Lin_PRC72_2005 ; HWangJHChen_NST32_2021 ) or a hybrid model (for instance, the hydro+UrQMD model SongBassHeinz_PRC83_2011 ; KarHuoPetBle_PRC91_2015 ) will be of interest.