Effect of Coulomb Interaction on Seebeck Coefficient of Organic Dirac Electron System $\alpha$-(BEDT-TTF)₂I₃

As a model that describes a pseudo-two-dimensional electronic system in $\alpha$-(BEDT-TTF)₂I₃, we use the two-dimensional (2D) extended Hubbard model [13], where the effects of the insulating layer of I^3- molecules are ignored  [49], except for their contribution to transfer integrals. The hopping energies up to the next nearest neighbor are obtained by a first-principles calculation [50].

Figure 1 shows a unit cell and a network of the hopping energies between each molecular site in the $a$–$b$ conduction plane. There are four sublattices, conventionally labeled A, A^′, B, and C in the unit cell represented by the broken line. Here, inversion-symmetry points exist in the middle of the A and A^′ sites, and at the B and C sites. As revealed by the analysis of Seo et al. [13], the nearest-neighbor Coulomb interaction along the $a$ axis plays a principal role in driving the phase transition in $\alpha$-(BEDT-TTF)₂I₃ between the massless DE phase and the CO phase. Therefore, in addition to the on-site Coulomb interaction $U$, we only take into account the nearest-neighbor Coulomb interactions $V_{a}$ and $V_{b}$ indicated by the dashed arrow in Fig. 1. In what follows, lattice constants, the Boltzmann constant $k_{B}$, and the Planck constant $\hbar$ are taken as unity. Note that, throughout this paper, eV is used as the unit of energy.

The extended Hubbard model is given by

where $i$ and $j$ are the coordinates of the unit cell, $\alpha$ and $\beta$ represent the four sublattices ($=$ A, A^′, B, and C) in the unit cell, and $\sigma$ is the spin index. Here, an electron number operator is defined by $n_{i,{\alpha},{\sigma}}=a^{{\dagger}}_{i,{\alpha},{\sigma}}a_{i,{\alpha},{\sigma}}$. The first term is the kinetic energy, and the second term is the on-site Coulomb interaction. The third term represents the nearest-neighbor Coulomb interaction, where $V_{a}$ is used for driving the CO transition, and we treat $V_{b}$ as a constant. Further, $<\cdots>$ and $<<\cdots>>$ in the subscripts of summations refer to adding up the terms of the nearest and next-nearest neighbor, respectively. $t_{i,{\alpha};j,\beta}$ shows the hopping between each site in Fig. 1 and is given as $t_{a1}=-0.0267$ ($-0.0101$), $t_{a2}=-0.0511$ ($-0.0476$), $t_{a3}=0.0323$ ($0.0093$), $t_{b1}=0.1241$ ($0.1081$), $t_{b2}=0.1296$ ($0.1109$), $t_{b3}=0.0513$ ($0.0551$), $t_{b4}=0.0152$ ($0.0151$), $t_{a1^{\prime}}=0.0119$ ($0.0088$), $t_{a3^{\prime}}=0.0046$ ($0.0019$), $t_{a4^{\prime}}=0.0060$ ($0.0009$) at ambient pressure and temperature $T=0.0008$ ($0.03$: room temperature). In this study, we treat the temperature dependence of $t_{i,{\alpha};j,\beta}$ by a linear interpolation of the hopping values at $T=0.0008$ and RT in Ref. [50], as follows:

By performing a Fourier inverse transform, $a_{i,\alpha,{\sigma}}={N_{L}}^{-{1}/{2}}\sum_{\bf k}a_{{\bf k}\alpha\sigma}e^{i{\bf k}\cdot{\bf r_{i}}}$ ($N_{L}$ is a system size), and Hartree approximation on Eq. (1), the Hamiltonian $H_{\rm MF}$ and its energy eigenvalue $E_{\nu\sigma}({\bf k})$ in the mean field approximation are obtained as follows:

where $\varepsilon_{\alpha\beta}({\bf k})=\sum_{\bm{\delta}}t_{\alpha\beta}e^{{\rm i}{\bf k}{\bm{\cdot}}{\bm{\delta}}}$ ($\bm{\delta}$ is a vector between unit cells), and $\nu=1,2,3,4$ indicates a band index. Here, $d_{\alpha\nu\sigma}({\bf k})$ is a wave function diagonalizing $H_{\rm MF}$. The average electron number at each site is determined by $\langle n_{\alpha\sigma}\rangle=\sum_{{\bf k},\nu}|d_{\alpha\nu\sigma}({\bf k})|^{2}f(E_{\nu\sigma}({\bf k}))$, where $f(E_{\nu\sigma}({\bf k}))=\left(1+\exp(E_{\nu\sigma}({\bf k})/T)\right)^{-1}$ is a Fermi distribution function, and the chemical potential $\mu$ is determined by the following equation:

Because $\alpha$-(BEDT-TTF)₂I₃ has a $\frac{3}{4}$-filled band, the deviation of filling $\langle\delta n\rangle$ is zero when there is no impurity. We assume $\langle\delta n\rangle=10^{-6}$ ($1$ppm), because a small amount of electron doping has been confirmed in some samples of $\alpha$-(BEDT-TTF)₂I₃ [8, 9].

A single particle green function $G^{0R}_{\alpha\beta}(\omega,{\bf k})$ and the density of state $\mathcal{N}(\omega)$ are given by

The critical value of $V_{a}$ for the CO transition at $T=0$ is $V_{a}^{C}=0.198$. In the following, we compare numerical results in three cases: $(U,V_{a},V_{b})=(0,0,0)$ (non-interacting case); $(U,V_{a},V_{b})=(0.4,0,18,0.05)$ (massless DE phase appearing at any temperatures); and $(U,V_{a},V_{b})=(0.4,0.199,0.05)$ (CO transition occurring at $T_{\rm CO}=0.002$).

The Seebeck coefficient is given by the Nakano–Kubo formula for linear response theory [45, 46, 47, 43, 40]. The Seebeck coefficient at a low temperature limit $S(\mu,T\sim 0)$ is calculated using the Mott formula:

where $e>0$ is the elementary charge.

Moreover, $S(\mu,T)$ at finite temperatures [44, 41] is given by

where $L_{11}$ and $L_{12}$ are coefficients for the electric field $\bf E$, and the temperature gradient $-{\bm{\nabla}}T$ of the current density $\bf j$ and heat flow density ${\bf j}^{Q}$ is defined by

where $L_{11}$ is equal to the DC conductivity. In this study, $L_{12}$ and the direct current conductivity $L_{11}=\sigma_{yy}$ in the direction of the $a(y)$ axis of the conduction plane are calculated using the expression of the transport coefficient ${\mathscr{L}}^{(m)}_{y}$, as follows:

where

$N_{L}$ indicates the system size and the velocity matrix ${\bf v}^{y}_{\nu}({\bf k})$ is a derivative of the energy eigenvalue $\tilde{\epsilon}_{\alpha\beta\sigma}({\bf k})$ regarding the wave number $k_{y}$. This is obtained by converting it to a band representation, ${\bf v}^{y}_{\nu\nu^{\prime}\sigma}({\bf k})=\sum_{\alpha\beta}d^{*}_{\alpha\nu\sigma}({\bf k})v^{y}_{\alpha\beta\sigma}({\bf k})d_{\beta\nu^{\prime}\sigma}({\bf k})$, using the wave function $d_{\alpha\nu\sigma}({\bf k})$.

Regarding the effect of impurity scattering on the Seebeck coefficient [42], the impurity potential term is derived as follows:

and is added as a perturbation to $H_{\rm MF}$. Here $\sum_{i\alpha}^{N_{\rm imp}}$ means the summation over all impurities in the system. ${\bf r_{i}}$ ($i=1,\cdots,N_{\rm imp}$) represents a coordinate about unit cells, and $N_{\rm imp}$ is the total number of impurities. $H_{\rm imp}$ is treated within the $T$-matrix approximation to include the energy dependence with the relaxation time $\tau_{\nu}(\omega)$ [51, 52, 48, 53, 22, 25]. As a result, the retarded self-energy $\Sigma^{R}_{\nu\sigma}(\omega,{\bf k})$ and the damping constant $\gamma_{\nu\sigma}(\omega,{\bf k})$ are obtained as follows:

where the impurity density $c_{\rm imp}=\frac{N_{\rm imp}}{N_{L}}=0.02$ and the strength of the impurity potential $V_{0}=0.1$. We assume that the impurities are distributed uniformly. As the above equation indicates, the relaxation time within the $T$-matrix approximation $\tau_{\nu}(\omega)$ is inversely proportional to $c_{\rm imp}$ and shows the energy dependence that reflects the shape of the density of state $\mathcal{N}(\omega)$. More specifically, $\tau_{\nu}(\omega)$ diverges when $c_{\rm imp}$ or $\mathcal{N}(\omega)$ become zero. In order to avoid the divergence of $\tau_{\nu}(\omega)$, we set the cutoff to $5\times 10^{6}$ $\hbar$(eV)^-1 (1 $\hbar$(eV)${}^{-1}\sim 6.58\times 10^{-16}$ s) caused by the effects of scattering beyond the $T$-matrix approximation.

Figure 2(a) shows the energy bands near the chemical potential at $V_{a}=0.199$ and $T=0.01$. There is a pair of tilted Dirac cones, and the Dirac points are located in the vicinity of the chemical potential. We show the $T$ dependence of the CO gap $2\Delta_{\rm CO}$ in the non-interacting case, $V_{a}=0.180$, and $V_{a}=0.199$ in Fig. 2(b). $2\Delta_{\rm CO}$ is determined as the indirect gap between $E_{1}({\bf k})$ and $E_{2}({\bf k})$, and becomes a finite value below $T_{\rm CO}=0.002$. The inset of Fig. 2(b) shows the $V_{a}$ dependence of $T_{\rm CO}$, where the inversion symmetry is broken in the CO phase. The CO gap shows the non-monotonic temperature dependence at low temperatures, owing to the temperature dependence of the transfer integrals. Figure 2(c) shows the density of states $\mathcal{N}(\omega)$ near the Fermi energy at the massless DE phase at those three $V_{a}$ values. Because the Hartree term induced by $V_{a}$ enhances the electron-hole asymmetry in the energy bands, the density of states in the band $\nu=1(2)$ increases (decreases) near the Fermi energy as $V_{a}$ increases. Such a deformation of the energy band is caused by the relative change to the charge density at each sublattice with the increase of $V_{a}$, as shown in the inset of Fig. 2(c). Figure 2(d) shows the $T$ dependence of $\mu$ measured from the contact point or the center of energy gap at those three $V_{a}$ values. In the non-interacting case, $\mu$ decreases monotonically as $T$ increases, and $\mu$ is negative (hole-like) except at very low temperatures $T<2\times 10^{-4}$, because the Van Hove singularity in the band $\nu=1$ is closer to the Dirac point than that of the band $\nu=2$ [8]. At very low temperatures $T<2\times 10^{-4}$, $\mu$ is positive, owing to the small amount of electron doping $\langle\delta n\rangle=10^{-6}$. In cases where $V_{a}=0.180$ and $V_{a}=0.199$, $\mu$ becomes positive at high temperatures near $T\sim 0.01$, because the electron-hole asymmetry of the density of states in the energy scale of $T$ is enhanced by the Hartree term, as shown in Fig. 2(c). In the case where $V_{a}=0.199$, $\mu$ has a large positive value near $T=0$, because $2\Delta_{\rm CO}$ is finite below $T_{\rm CO}=0.002$, as shown in Fig. 2(b) and the inset of Fig. 2(d). Thus, the $T$ dependence of $\mu$ is strongly influenced by electron-hole asymmetry and the Coulomb interaction.

The chemical potential $\mu$ dependence of the Seebeck coefficient $S$, the DC conductivity $L_{11}=\sigma_{yy}$ in the denominator of $S$, and $L_{12}$ in the numerator of the $S$ are shown in Fig. 3(a), (b), and (c) at several temperatures for $V_{a}=0.199$. As temperature $T$ decreases, $S(\mu)$ forms gentle positive and negative peaks which come from the function shape of $L_{12}(\mu)$ [38, 39]. On the other hand, $S(\mu)$ shows specifically large positive and negative peaks in $\left|\mu\right|<\Delta_{\rm CO}\simeq 0.002$ at $T$ = $0.001$ ($<T_{\rm CO}=0.002$). These large peaks in $|\mu|<\Delta_{\rm CO}$ and discontinuous changes near $\mu\simeq\pm\Delta_{\rm CO}$ arises mainly from the sharp decrease of $\sigma_{yy}(\mu)$ at $|\mu|<\Delta_{\rm CO}$ as $T$ decreases (See Fig. 3(b) and (c)). We note that, overall, $S(\mu=0)>0$ and $S(\mu)$ shift to positive values. Because the Seebeck coefficient is influenced by the carrier doping $\langle\delta n\rangle=10^{-6}$ as well as the electron-hole asymmetry of the band structure, as discussed in Subsection III.D, the sign of $S(\mu)$ does not have a one-to-one correspondence with the sign of $\mu=\mu(\langle\delta n\rangle,T)$. In the following, $\langle\delta n\rangle$ is fixed as $10^{-6}$ unless otherwise noted.

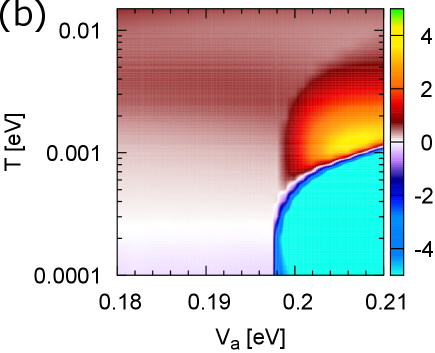
Figure 4(a) shows the temperature dependence of $S$ in the non-interacting case, $V_{a}=0.180$, and $V_{a}=0.199$. Here, $S(T)$ in the non-interacting case decreases monotonously as the temperature decreases, and changes the sign from positive to negative at temperature $T=2\times 10^{-4}$, corresponding to the sign change of $\mu$ from negative (hole-like) to positive (electron-like), as shown in Fig. 2(d). As $V_{a}$ increases, $S(T)$ near $T\sim 0.01$ decreases, because $\mu$ near $T\sim 0.01$ increases and becomes positive, as shown in Fig. 2(d). As a result, a gentle peak is induced by $V_{a}$ around $T=0.005$. This gentle peak is similar to that observed in Ref. [33, 11]. At $V_{a}=0.199$, we find a sharp peak with $S(T)$ just below $T_{\rm CO}$, as a result of a sudden decrease in $L_{11}$ and the energy dependence of the relaxation time with impurity scattering, as discussed in the Subsection III.C. Moreover in $T<T_{\rm CO}$, because $\mu$ suddenly changes its sign from negative to positive owing to the existence of a finite $2\Delta_{\rm CO}$ (see Figs. 2(b) and 2(d)), $S(T)$ rapidly decreases and changes its sign from positive to negative, as shown by the single-dotted line in Fig. 4(a). This behavior qualitatively demonstrates the peak structure observed near $T_{\rm CO}$ in experiments. The inset of Fig. 4(a) shows $S(T)$ at the low temperature region ($0\leq T\leq 0.003$). Here, $S(T)$ has a negative value at low temperatures, owing to the slight electron doping. At the limit of $T\to 0$, $S$ becomes zero according to the Mott formula, but if the temperature is slightly finite, the contribution of $S(T)\to 0$ from $T\sim 0$ competes for the contribution, and $S(T)$ remains finite on account of carrier doping. Thus, $S(T)$ changes its value considerably. Figure 4(b) shows a color plot of the Seebeck coefficient: $S$ versus $V_{a}$ and $T$. The temperature at which point the sign of $S$ inverts at $T<T_{\rm CO}$ shifts to a higher temperature as $V_{a}$ increases (Note that we only calculated a few points to plot Fig. 4(b) and the oscillatory behavior near the phase transition in this figure is an error on the plot caused by the lack of data points).

In this subsection, we focus on the effect of impurity scattering and the contribution of the energy dependence of the relaxation time $\tau(\omega)$ on the $T$ dependence of the Seebeck coefficient $S(T)$. Figure 5(a) shows the $\omega$ dependence of $\tau(\omega)$ at the wave number $|{\bf k}|=k_{F}$ and $V_{a}=0.199$ considering impurity scattering according to the $T$-matrix approximation with $c_{\rm imp}=0.02$ and $V_{0}=0.1$. As shown in the Fig. 5(a), $\tau(\omega)$ is about inversely proportional to the density of state $\mathcal{N}_{\alpha\sigma}(\omega)$ and reflects the shape of $\mathcal{N}_{\alpha\sigma}(\omega)$ at each temperature (e.g., the Van Hove singularity, Dirac point, and energy gap, regarding which see Fig. 2(c)). $T_{\rm Peak}$ is defined as the temperature where the peak structure appears in the massless DE phase, and $T_{\rm Inv}$ is characterized by the sign inversion of $S(T)$ in $T<T_{\rm CO}$ for visualization purposes.

Figures 5(b) and 5(c) show the temperature dependence of DC conductivity $\sigma_{yy}(T)$ and $L_{12}(T)$ corresponding to the denominator and numerator of $S(T)$ shown in Fig. 5(d), respectively, in cases with $\tau(\omega)$ (solid line with point) and a constant $\tau=5\times 10^{6}$. There are drastic differences between these cases. We found that the gentle peak structure at $T_{\rm Peak}$ in the massless DE phase is derived from $L_{12}(T)$ with $\tau(\omega)$. The sudden increase in the absolute value of $S(T)$ at $T<T_{\rm CO}$, however, is caused by the decrease of $\sigma_{yy}(T)$. The sign inversion temperature $T_{\rm Inv}$ of $S(T)$ corresponds to that of $L_{12}(T)$, and it is determined by both the $T$ dependence of $\mu(T)$ (Fig. 2(d)) and the $\mu$ dependence of $S(\mu)$ (Fig. 3) The thorn-like structure between $T_{\rm Inv}$ and $T_{\rm CO}$ appears only when the sample is slightly electron-doped, $\langle\delta n\rangle>0$.

Figure 6 shows $S(T)$ in a non-doping case ($\langle\delta n\rangle=0$ ppm). In this case, because the chemical potential does not reverse its sign from negative to positive at low temperatures ($T<0.001$), $S(T)$ is always positive, as shown in Fig. 6. At $T<T_{\rm CO}$, $S(T)$ increases suddenly and has a large positive value at low temperatures, because $\sigma_{yy}(T)$ reaches zero, although $S(T)$ becomes zero at $T=0$, as shown in the inset of Fig. 6.

Next, we consider the relationship between the electron-hole asymmetry of the energy band and the Seebeck coefficient using a tilted Weyl model [8] to represent the tilted Dirac cone of $\alpha$-(BEDT-TTF)₂I₃. In general, when the Seebeck coefficient is calculated using a symmetrical electron-hole energy band, the sign inversions of the carrier and Seebeck coefficient correspond to each other. However in the previous subsection, the Seebeck coefficient $S(T)$ showed a positive value at high temperatures, even though the chemical potential $\mu$ was positive (Fig. 2(d) and Fig. 4(a)). Moreover, the positive chemical potential at finite temperatures, from the contribution of the Hartree term ($\mu>0$ at $T\sim 0.01$), does not agree with the temperature dependence of the Hall coefficient, as observed in experiments with $\alpha$-(BEDT-TTF)₂I₃ [9]. These results can never be obtained with calculations using a symmetrical electron-hole band, indicating that $S>0$ ($S<0$) when the carrier is hole-like (electron-like). Therefore, in this subsection, we show that the sign of the Seebeck or Hall coefficients calculated with an asymmetrical electron-hole energy band does not always match the sign of the carrier, and the energy where their signs invert shifts from the effects of the electron-hole asymmetry.

We introduce a tilted Weyl Hamiltonian that represents the low-energy band dispersion of $\alpha$-(BEDT-TTF)₂I₃, as follows [8, 54]:

In the first term of Eq. (20), $\sigma_{0}$ means a unit matrix and $\sigma_{x}$, $\sigma_{y}$, $\sigma_{z}$ indicate the Pauli matrices. ${\bf k^{\prime}}_{0}$ is a wave number which indicates infinitesimally different from the Dirac point ${\bf k}_{0}$, and ${\bf\tilde{k}}={\bf k}-{\bf k^{\prime}}_{0}$ is defined as a wave number measured from ${\bf k^{\prime}}_{0}$. Also, ${\bf v}_{\rho}({\bf k_{0}^{\prime}})$ is calculated by the velocity matrix $u_{\nu,\nu^{\prime}}^{\tau}({\bf k})$ defined as follows:

where $\tau=x,y$ and $\tilde{\epsilon}_{\alpha\beta}({\bf k})$ and $d_{\alpha\nu}({\bf k})$ are given by Eqs. (4) and (5). Each component of ${\bf v}_{\rho}({\bf k_{0}^{\prime}})$ are respectively given by ${\bf v}_{x}={\rm Re}[{\bf u}_{12}({\bf k^{\prime}}_{0})]$, ${\bf v}_{y}=-{\rm Im}[{\bf u}_{12}({\bf k^{\prime}}_{0})]$, ${\bf v}_{z}=\frac{1}{2}\left[{\bf u}_{11}({\bf k^{\prime}}_{0})-{\bf u}_{22}({\bf k^{\prime}}_{0})\right]$, and ${\bf v}_{0}=\frac{1}{2}\left[{\bf u}_{11}({\bf k^{\prime}}_{0})+{\bf u}_{22}({\bf k^{\prime}}_{0})\right]$ [8]. The second term of the Hamiltonian $H$ is a chemical potential term which only shifts the origin of energy, and the third term is distorting the Dirac cone and changes the electron-hole asymmetry of the energy dispersion [54]. This curvature term is derived from the second derivative of $\tilde{\epsilon}_{\alpha\beta}({\bf k})$ about the wave number $k_{\tau}$ [18] by assuming the isotropy on the differential of $\tilde{\epsilon}_{\alpha\beta}({\bf k})$ about each $k_{\tau}$. Here, we control the sign and magnitude of the curvature term using mass change ratio $X$ which changes in the range of $-1<X<1$ and a mass parameter $m$ is set as a constant ($m=1$). Eq. (20) leads to the next energy dispersion:

As an example, the density of states at $X=-1$ and $X=1$ are shown in Figure 7(a).

To obtain the Seebeck coefficient and the Hall coefficient, $L_{11}=\sigma_{yy}$ and $L_{12}$ are calculated using the transport coefficient ${\mathscr{L}}^{(m)}_{y}$ (Eq. (15)) with the energy dispersion (Eq. (22)). Here, the Hall conductivity is calculated by the following approximated formula, exclusively considering the intra-band contribution [55, 56, 8]:

where $H$ is a magnetic field and $\Gamma$ is a phenomenologically introduced damping constant for impurity scattering. Here, $\Gamma$ depends on the temperature, such that $\Gamma=\Gamma_{0}+\theta T$. We set $\Gamma_{0}=10^{-5}$ and $\theta=10^{-3}$. The DC conductivity along the $b(x)$ axis $\sigma_{xx}$ is also calculated using the same formula as $\sigma_{yy}$, and the Hall coefficient $R_{H}$ is obtained by

In this study, we assume electronic carriers, and we set the chemical potential to $\mu=0.0001$.

Figure 7(b) shows the Seebeck coefficient with respect to the mass change ratio $X$ in $\mu=0.0001$ and the three temperature cases: $T=0.005$, $0.0025$, and $5\times 10^{-5}$. In the case of $T=5\times 10^{-5}$, which is the lowest temperature among the three cases, the Seebeck coefficient is independent of $X$ and becomes a negative constant, reflecting the positive $\mu$. However, as the temperature increases with $T=0.0025$ and $0.005$, $S(X)$ gradually behaves proportionally to $X$, and a range of $X$ appears such that $S(X)$ is positive. The sign of $S$ is determined by the sign of $L_{12}$, as shown in Eq. (10). A reason for this $T$- and $X$-dependent $S$ behavior is perhaps that the change in the electron-hole asymmetry more easily affects the value of $L_{12}$ as the temperature increases. Because the higher energy part of the density of states more positively contributes to the value of $L_{12}$, the density of states is reflected by change in electron-hole asymmetry.

By contrast, the absolute value of the Hall coefficient $|R_{H}(X)/R_{0}|$ with respect to the mass change ratio $X$ is shown in Figure 7(c) for $\mu=0.0001$ where $T=0.005$, $0.0025$, and $5\times 10^{-5}$. Here, we set $R_{0}={\pi^{2}v_{x}^{2}}/{ec\Gamma_{0}^{2}}$ and $v_{x}=|{\bf v}_{x}|\sim 0.01$. The Hall coefficient $R_{H}$ also reflects the shape of the density of state as it reaches higher temperatures, and a range of $X$ appears such that $R_{H}$ is positive, despite $\mu>0$. (The sharp “V”-shaped structure of $|R_{H}(X)/R_{0}|$ in Fig. 7 refers to the sign inversion of $R_{H}$.)