Dynamics of ultrafast heated radiative plasmas driven by petawatt laser lights
Abstract
A relativistic petawatt laser light can heat heavy metals over keV temperature isochorically and ionize them almost fully. Copious hard X-rays are emitted from the high-Z hot plasma which acts as X-ray sources, while they work as a cooling process of the plasma. The cooling process can affect on the creation of high energy density plasma via the interaction, however, the details are unknown. The X-ray spectrum depends on the plasma temperature, so that it is worthwhile to investigate the radiation cooling effects. We here study the isochoric heating of a solid silver foil irradiated by relativistic laser lights with a help of particle-in-cell simulations including Coulomb collisions, ionizations, and radiation processes. We have conducted a parameter survey varying laser intensity, , to check the cooling effects while keeping the incident laser energy constant. The silver plasma heated mainly by the resistive heating dissipates its energy by keV X-ray emissions in a picosecond time scale. The radiation power from the silver foil is found to be comparable to the incident laser power when the laser intensity is less than under the constant energy situation. The evolution of the plasma energy density inside the target is then suppressed, due to which a highly compressed collisional shock is formed at the target surface and propagates into the plasma. The radiation spectra of the keV silver plasma are also demonstrated.
1 Introduction
The advent of petawatt laser systems enables us to explore the high field science and the high energy density science in a wide parameter range. Kilo-joule (kJ) class petawatt lasers, e.g. LFEX and NIF-ARC, having picoseconds pulse durations heat dense plasmas over peta-pascal pressures [1], and also accelerate particles more efficiently than short pulse laser lights with the similar intensity [2, 3]. The other type of petawatt laser lights has extremely short pulse duration of a few tens femtoseconds and a micron-revel focal spot with an intensity over W/cm2. The laser plasma interaction with such a ultrashort and extreme laser light, e.g. J-KAREN-P and ELI-beamlines, initiates the QED processes accompanying copious gamma-rays and subsequent pair productions. Recently the laser-driven heavy ion acceleration via the target normal sheath acceleration (TNSA) had been demonstrated using a thin silver foil irradiated by J-KAREN-P laser light [4]. The silver ions are ionized over charge states 40 and they are accelerated by the TNSA at the target rear surface. The ionization degree of the heavy ions is an important factor for the efficient acceleration. There are some numerical works to evaluate the ionization degrees of heavy metals in the laser-ion acceleration [4, 5, 6] and in the isochoric heating [7].
Since such intense laser and high- plasma interactions accompany a considerable amount of hard X-rays emissions, it is critically important to understand the characteristics of the radiations and their effect on the plasma heating and the laser-ion acceleration. Understanding the radiation properties of the hot heavy metal is a key to realize high brightness X-ray sources for various applications including a diagnostic of the dense plasma core in the laser fusion. Although Mishra et al. [7] had considered the radiation effects in the isochoric heating, the model considered only the integrated radiation powers in the photon energies. To clarify the radiation effects on the laser-high plasma interaction including the radiation properties is the main motivation of the study.
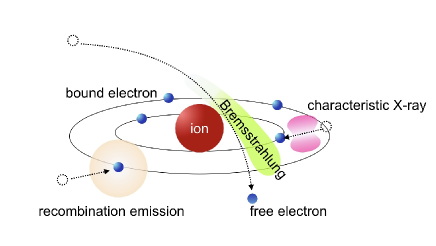
Hard X-rays with photon energies over keV are emitted in heavy metal targets when the petawatt laser light is irradiated on the target surface. Energetic electrons injected into the target drive the bulk plasma heating and also the radiation processes illustrated in Fig. 1. When the electron collides with an atom or partially ionized ion, a bound electron might be kicked out, and the outer bound electron subsequently comes down to the inner electron orbit by emitting a X-ray photon (characteristic X-ray). The characteristic X-ray between K- and L-shells is called as . When the hot electron suffers a large angle scattering by the nucleus, the electron changes the direction and emits photons with continuous spectrum (bremsstrahlung). The photon energies via bremsstrahlung depends on the atomic number , as and the photon energy increases as increases [8]. When the free electron is recombined to the orbit, a X-ray photon is also emitted with energy depending on both the bound orbit and the energy of the free electron before recombination.
The time integrated conversion efficiency to hard X-rays from the input laser energy have been studied experimentally [9, 10], and the temporal scales of the X-ray emissions are observed to be around the laser pulse durations. However, the time evolution of the radiative plasmas cannot be investigated from the observations. The energy loss due to radiation decreases the electron temperature, which will affect the creation of the radiative plasmas.
This paper is organized in the following way. Section II presents the radiation model coupled to the particle-in-cell (PIC) simulations and also the theoretical estimation of the isochoric heating and the radiation cooling effect. In Section III we present one-dimensional (1D) and two-dimensional (2D) PIC simulation results and compare the simulation results to the theoretical estimation. Section IV is dedicated to the discussion and summary.
2 Radiation model in PIC simulations
We use a PIC code, PICLS, which features binary collisions among charged particles, dynamic ionization processes in gas and solid density plasmas, and also radiation processes [7, 11, 12, 13]. In the present work, we included bremsstrahlung, radiative recombination, and radiative de-excitation illustrated in Fig. 1 in a thin silver plasma. The emissivities of these three radiative processes were computed by the Collisional Radiative Equilibrium (CRE) model [14] for various ion densities and electron temperatures. We computed the emissivities for plasmas with ion densities from to cm-3 and electron temperatures from 1 eV to 100 keV. The photon energy range considered in the calculations is from 1 eV to 100 keV. In the simulations, we calculate the radiated energy by linearly interpolating in log10 scale the database with the average electron temperature and ion density in each PIC cell. The emitted energy is subtracted from the bulk electron energy in the cell, so that the plasma is cooled down by the radiation emission.
Figure 2 shows the emissivity spectra from a solid silver plasma at electron temperatures of 0.1, 1, and 10 keV. Most part of the spectra consist of continuous components which correspond to bremsstrahlung and radiative recombination processes. Spikes correspond to the characteristic X-rays. For higher , the high energy continuous component via bremsstrahlung and recombination increases, and consequently, the fraction of the characteristic X-rays decreases.

We have studied a silver plasma heating by a short pulse laser light using the 1D PICLS simulation including the radiation cooling [15]. We here extend the analysis to study the radiation effect on the plasma dynamics including the multidimensional effect by conducting 2D PICLS simulations. In this study, we consider only an optically thin plasma. The temperature of the target reaches above keV via the interaction. In a solid plasma at such high temperature, the length with optical thickness equal to 1 for hard X-rays is a several microns.
Before going to the simulations, here, we estimate the impact of the radiation cooling during the isochoric heating of a thin silver foil using the emissivities from the CRE model. When the thin foil is irradiated by a relativistic petawatt laser light, the hot electrons are generated at the interaction surface and they flow into the target with mega-ampere current. The hot electron current is then neutralized by the bulk return current, and thus the target is heated mainly by the resistive (Joule) heating over keV temperature. The achievable electron temperature via the resistive heating is derived as [16],
| (1) |
as a function of the normalized laser amplitude and the interaction time normalized by the laser oscillation period . Here, is a constant where the elementary charge, the electron rest mass, and the speed of light. is the Coulomb logarithm, is the absorption coefficient, is the ion density normalized by the critical density , and is the laser electric field amplitude.

We can estimate the radiation power density from the CRE database using given by Eq. 1 at the time when the laser irradiates the target over time where is the laser pulse duration normalized by the laser oscillation period. The absorbed energy is stored in the plasma as the electron energy density . We define the cooling time as the time scale the plasma energy is taken away by the radiation as
| (2) |
If the laser pulse duration is less than , the radiation cooling is negligible during the laser heating. While, if is longer than , the radiation cooling affects seriously on the temporal evolution of the bulk electron temperature.
We plotted the ratio as a function of and in Fig. 3. The reddish area indicates the laser heating power exceeds the radiation power, while the blueish area means the radiation power overcomes the laser heating power. The solid line represents the laser condition where the both powers becomes equal, i.e. . In the region above this line, the laser isochoric heating will be degraded by the radiation cooling. Note that the region dominated by the radiation cooling () is seen for the over-picosecond pulse durations ps for the silver target. We also plot a white dashed line which corresponds to the border for a copper (Cu) target. It can be seen that radiations from a Cu foil are negligible for most of the current high intensity laser lights. Heavier metals, e.g. gold, have the radiation cooling effect with a shorter pulse duration.
In the following 1D-PICLS simulations, we chose 6 laser profiles as shown in Fig. 3 by the white circles. For all the cases, we keep the laser energy constant, but change the laser amplitude and pulse duration. These laser parameters are achievable by the modern laser facilities. Figure 4 shows the simulation setup configuration.

The 1D simulations have the system size and a 1 m silver foil target with ion density at the center. The target is composed of pre-plasma () with a scale length of 0.2 , and solid foil (). The initial charge state of the silver target is . The ionization potential of the silver ion is set by the NIST database [17]. The incident laser wavelength is fixed to . We have varied from 20 to 2 and pulse duration from to with the Gaussian pulse profile with maintaining the input laser energy constant. The peak amplitude reaches to the foil surface at . We include the Coulomb collisions, field ionizations, and impact ionizations in all the simulations. While the radiation calculations are on and off to see the impact of the radiation loss. The multi-dimensional effects are checked with the 2D-PICLS code. In the 2D simulations, we used the same laser pulse profile as in 1D calculation with .The simulation box size is , and the laser light is focused on the center of the target with a spot diameter .
3 Simulation Results
3.1 1D: radiation cooling
We conducted 1D simulations to investigate the radiation cooling effect. Figure 5 shows the temporal evolution of the bulk electron temperature for the simulations with the radiation cooling. The temperature was measured in the region where the ion density was over 29 which corresponds to the half of the initial solid density. We see the degradation of the peak bulk temperature for the lower intensity cases. For the case with and ps, saturates around keV even though the laser pulse is still irradiated. It is also seen that the life time of 10 keV silver plasma is a few picoseconds. This infers that the plasma internal energy will be converted to the hard X-rays in a few picosecond time scale. We also show the result for and fs without the radiation loss by the red dashed line. In this case, the temperature decreases only via the adiabatic cooling due to the plasma expansion. We see that the adiabatic cooling is much slower than the radiative cooling. The conversion rate from the laser energy to the hard X-ray emissions, which is discussed later, is about for the current laser configurations. When the electron temperature drops to , the emissivity decreases significantly as shown in Fig. 2. Hence, at the time later than , the temperature stays at about in the cases of .
In the present research, we have included only non-relativistic bremsstrahlung emissions. Therefore, hot electrons with energies over do not suffer from the radiation energy loss. Relativistic electrons emit photons with energies over MeV, so called -rays via bremsstrahlung or the radiation damping. The energy conversion rate for -rays is much less than [12], so that -rays do not affect the plasma heating.

Figures 6 (a) and (b) show electron energy spectra calculated at the moment when the laser irradiation was over for the cases without radiations (a) and with radiations (b). The spectra have two parts, one for the bulk electrons with energies and the other for hot electrons with energies . The peak energy of the bulk electrons is explained by the resistive heating. The Maxwellian distribution with the bulk electron temperature calculated from Eq. (1) for and fs is plotted by the dotted line as a reference. We see that the reference line agrees well with the bulk electron component of . Note here that from Eq. (1), we see the slightly increases with the weaker amplitude and longer pulse duration but it is almost same around 10 keV for the same pulse energy cases. The hot electrons are induced in the laser-plasma interaction at the target surface. Their average energy is given by the ponderomotive scaling as . For example, derives [18]. The hot electron temperature decreases as decreases as seen in the spectra in the energy range .
The radiation cooling effect on the electron spectra is seen in Fig. 6 (b). Compared with Fig. 6 (a), the peak bulk electron energy of 3.0 and 2.0 shift to the lower energy, while other cases do not, as predicted in the discussion of Fig. 3.

3.2 1D: effect of radiation cooling on plasma dynamics
Since the plasma dynamics reflect how the radiations cool down the plasma, it is worthwhile to investigate the dynamics under a situation in which the radiations take the plasma energy significantly. Figure 7 shows the temporal evolution of electron temperature (green solid lines) and electron phase - plot (dots) around the target observed at the moments when the laser peak reached the solid surface () and at fs. The laser is the long pulse with and ps. The plots (a) and (b) represent the results with radiations, and (c) and (d) represent those without radiations. Initially, the silver foil is located in the region .

In the interaction region with the laser light ( m), is similar not depending on whether the radiations are taken into account or not. This is because the hot plasma expanding in front of the dense plasma region has a low density, so that the dominant radiation via bremsstrahlung, whose power is proportional to the square of the ion density, is negligible. In the solid region ( m), in the case with the radiations stays low around 100 eV while without the radiations is hotter exceeding 1 keV. The temperature has a gradient due to the thermal diffusion from the hot region. The electron momentum distribution inside the solid density region shrinks in the vertical direction in (a) and (b) due to the radiation.
Figures 8 (a), (b), (d), and (e) show the temporal evolution of ion densities (green lines) normalized by and electron energy densities (PPa) (purple lines) observed at the same time in the same simulations of Fig. 7. The broken lines indicate the initial foil region. (a)-(c) are the plots for the simulations with radiations, and (d)-(f) are those for the simulations without radiations.
At , the foil surface is pushed forward by the hot electrons’ pressure. The compressed ion density at the foil surface in (a) is about 4 times higher than the initial density. The increase of is significantly higher than the case without radiations. Due to the radiation cooling, the electron pressure inside the solid region decreases. Hence, the bulk plasma can be compressed more easily with the radiation cooling effect. A strong radiation happens in the compressed region, which results a dent in the temperature profile at in Fig. 7 (b).
Figures 8 (c) and (f) display ion phase diagram and ion density distribution at . The ion momentum is normalized by where is the ion mass. It can be seen that the collisional shock is formed because of the pressure gradient. Since the upstream pressures in both with and without radiations are similar, the speed of the compressed surface is similar, with radiations and without radiations as indicated by the dotted lines in (c) and (f). The acoustic speed at 1 keV is with for the case with radiations and with for the case without radiations where is the average ion charge state in each simulation. The shock speed is explained well by [19] where and are uncompressed and compressed ion densities, respectively, through the shock surface. In the case with radiations, which is 3 times slower than the case without radiations. And thus the target with radiation takes 3 times longer time to expand into vacuum than the case without radiation. We also confirmed the momentum and energy conservations through the shock surface [19]. These results show that the radiation cooling affects the plasma dynamics by reducing the shock speed in the dense plasma.

3.3 1D: hard X-ray emissions
A hot metal plasma with keV electron temperature has a potential to be a hard X-ray source. We calculated the conversion efficiency from the laser light to hard X-ray photons with energies of 18-75 . The photons with this energy range could be a backlight source for the high density plasma experiments [10]. Figure 9 (a) shows the conversion efficiency of Ag (circles) and Al (triangles) foils with thickness of 1 m. The emitted X-ray energy was obtained by integrating the X-ray emissivity over photon frequency and solid angle in each PIC cell and summing the energy during the simulations. It is found that the conversion efficiency of Ag is nearly two-orders of magnitude higher than that of Al. The bulk electron temperatures achieved by the laser irradiation are almost same around 10 keV in both materials. At such high temperature, the Al plasma is fully ionized and the Ag plasma is almost fully ionized to the charge state of 45.
Below we explain the high X-ray yields in the Ag target. The bremsstrahlung is the dominant radiation process and its emission power density (W/cm3) depends on the charge state of the plasma as where is electron number density (1/cm3), is electron temperature (eV), and is ion number density (1/cm3) with charge state [20]. If we assume the charge neutral state, . Since the ratio of the atomic number of Ag and Al is , the radiation power of bremsstrahlung from the Ag plasma is times higher than that from the Al plasma. In addition to bremsstrahlung, strong emissions through the radiative recombination process are expected in the Ag plasma. The power of the radiative recombination emission of Ag is close to that of bremsstrahlung, so that the Ag plasma has about two-orders of magnitude higher emission than the Al plasma.

Note here that the dependence of the conversion efficiency on the laser intensity in Fig.,9 (a) is weak in the intensity regime , since the achievable electron temperature via the resistive heating is not much changed when the total laser energy is same. In the case of laser intensity below W/cm2, the efficiency decreases to a half of other cases. This is due to the radiation cooling that occurs in the picosecond time scale during the laser plasma interaction. Namely, the electron temperature cannot reaches keV-level in the dense plasma region with radiations as seen in Figs. 6 and 7, and thus over-keV X-ray emissions are suppressed. Figure 9 (b) shows emission energy spectra in the simulations with the different laser amplitudes. Here, the spectra for photon energy were calculated as
| (3) |
where and denote indices of the photon energy group and the spatial grid, respectively. is emissivity of photon energy of where and are Planck constant and photon frequency, respectively, and . The time integration is taken over the total simulation time . Figure 9 (b) indicates that the photons with energies above from bremsstrahlung and recombination processes mainly contribute to the cooling.
We see that the emission energy over 3 keV decreases significantly in the case of due to the radiation cooling as indicated with an arrow in Fig. 9 (b). This result is consistent with the lower conversion efficiency seen in Fig. 9 (a). The emissivity of bremsstrahlung is proportional to [21], and therefore, the peak of the emission energy appears around the energy comparable to the electron temperature.
3.4 2D simulation

We conducted 2D PIC simulations to see the multi-dimensional aspect of the radiation cooling effect. A solid silver foil was placed at the region of initially. The initial charge state of the silver ion is 1. We use the laser parameter of and ps, which shows the significant radiation cooling during the laser irradiation in the 1D PIC simulation. The laser light is focused with a spot diameter normally at the center (). The laser electric field oscillates in the -direction, namely, the laser is p-polarized.
Figure 10 shows the electron temperature distribution with (a), (b) and without (c), (d) radiations. Figures (a) and (c) show the temperature distribution at the moment when the peak of laser arrived at the foil surface. In front of the target , the pre-plasma is heated to . The electron temperature in (a) and (c) have almost identical distribution in the pre-plasma region. Since the emissivity is proportional to the plasma density, e.g., bremsstrahlung depends on the square of the plasma density as discussed in Sec. 3.3, the radiation cooling effect is small in the low density region.
Electron temperature inside the foil increases along the incident laser axis via the resistive heating, and reaches with radiations and without radiations. The heat propagates from the interaction surface via the thermal diffusion. Overall, as expected from the 1D calculation results, the temperature of the case with radiation is lower than that without radiation. These results are consistent quantitatively with 1D results as shown in Fig. 7. (b) and (d) show the temporal evolution of the electron temperature distribution in the direction. Here, the temperature is averaged inside the foil. In the case with radiation, the peak temperature was reduced to . On the other hand, in the case without radiation, the temperature continued increasing during the laser irradiation. Comparing (a) and (c), we see that the target expansion front slows down with the radiation cooling. This is due to that plasma expansion speed is given approximately by the ion acoustic velocity which is proportional to . Since the expanding plasma density is low, the radiation cooling is not significant, and consequently, the temperature at the rear side was higher than that inside of the solid density foil.
Figure 11 shows spectra of the areal density of the radiation energy during the laser plasma interaction period calculated as
| (4) |
where is the emissivity. The spatial integral is taken over the laser spot region inside the foil , i.e., and . The solid line represents the sum of the emissivity from the plasma in the 2D simulation with the radiation cooling. The dashed line shows the result when the cooling effect is neglected during the interaction. Below the photon energy of which mainly comes from plasma at temperature below 1 keV, the two lines are similar. Above the photon energy of , the emission energy without radiation cooling is about 2 times higher. The difference was due to the difference in the temperature distribution seen in Figs. 10 (b) and (d), namely, the higher temperature in (b) results larger hard X-ray emissions. This means that, without considering the radiation cooling effect, the emission energy will be overestimated especially for higher energy X-rays.

4 Conclusions
We studied the dynamics of the ultrafast heating of a silver thin foil by relativistic petawatt laser lights, which have the constant energy, by using the collisional PIC simulations with the radiation cooling. The silver plasma heated to a keV-level electron temperature dissipates its energy by hard X-ray emissions in the time scale of a few picoseconds. When the laser pulse duration is shorter than the picosecond order and the intensity is over , the radiation cooling effect on the plasma heating is negligible. On the other hand, the radiation cooling affects significantly during the laser irradiation with an over-picosecond pulse and intensity less than W/cm2. The radiation cooling decreased the electron temperature and suppressed hard X-ray emission, and therefore, the hard X-ray emission will be overestimated when the radiation cooling effect is neglected. To consider the radiation cooling is also important in simulating the plasma dynamics. Since the bulk plasma can be compressed more easily with the radiation cooling, a highly compressed collisional shock is formed in the dense plasma. It has been observed that thermal diffusion was suppressed at the compressed region by the strong radiation cooling.
In the current study, the silver plasma is thin enough to be optically thin, so that hard X-ray photons escape without reabsorption. If the target becomes thicker, we need to consider the radiation transport. We leave it as our future work to see how the radiation transport affects the energy transport in dense plasmas.
Acknowledgments
This study was supported by the JSPS KAKENHI grant number JP19KK0072, JP20H00140, JP20K14439, and the Foundation for the Promotion of Ion Engineering.
References
References
- [1] K Matsuo et al 2020 Phys. Rev. Lett. 124 035001
- [2] A Yogo et al 2017 Nat. Comm. 7 42451
- [3] D Mariscal et al 2019 Phys. Plsamas 26 043110
- [4] M Nishiuchi at al 2020 Phys. Rev. Res. 2 033081
- [5] D Kawahito and Y Kishimoto 2020 Phys. Plasmas 27 033108
- [6] J. Domański and J. Badziak 2020 JINST 15 C05037
- [7] R Mishra, P Leblanc, Y Sentoku, M S Wei and F. N. Beg 2013 Phys. Plasmas 20 072704
- [8] B Hou, J Nees, A Mordovankis, M Wilcox, G Mourou, L M Chen, J -C Kieffer, C C Chamberlain and A Krol 2006 Appl. Phys. B 83, 81-85
- [9] H -S Park et al 2006 Phys. Plasmas 13 56309
- [10] B Börm, D Khaghani and P. Neumayer 2019 Phys. Plasmas 26 023109
- [11] Y Sentoku and A J Kemp 2008 Jour. Comp. Phys. 227 6846-6861
- [12] R R Pandit and Y Sentoku 2012 Phys. Plasmas 19 073304
- [13] Y Sentoku, I Paraschiv, R Royle, R C Mancini and T Johzaki 2014 Phys. Rev. E 90 051102(R)
- [14] D Saltzmann 1998 Atomic Physics in Hot Plasmas (USA: Oxford University Press New York Oxford)
- [15] K Sugimoto, N Higashi, N Iwata, A Sunahara, T Sano and Y Sentoku 2020 High Energy Density Phys. 36 100816
- [16] P Leblanc and Y Sentoku 2014 Phys. Rev. E 89 023109
- [17] https://physics.nist.gov/PhysRefData/ASD/ionEnergy.html
- [18] S C Wilks, W L Kruer, M Tabak and A B Langton 1992 Phys. Rev. Lett, 69 1383
- [19] Ya B Zel’dovich and Yu P Raizer 2002 Physics of shock waves and high-temperature hydrodynamic phenomena, p46 (USA: Dover publication)
- [20] J D Huba 2016 NRL PLASMA FORMULARY (USA: Naval Research Laboratory)
- [21] George B Rybicki and Alan P Lightman 1979 Radiative Processes In Astrophysics, p160 (USA: Wiley-VCH)