Dynamics of transposable elements generates
structure and symmetries in genetic sequences

Transposable elements (TEs) are DNA sequences that can relocate themselves in new sites of the genome. They were firstly discovered in maize by B. McClintock in the mid-1940s and initially considered as parasites with no functional roles MC50 . Nowadays TEs are known to be ubiquitous in both prokaryotes and eukaryotes genomes FP07 ; K81 and little doubts are left of their prominent role in genome evolution, shaping structure and function in a multitude of ways BBGGetal18 ; F12 . As TEs constitute more than half of the sequence in many higher eukaryotes, a fingerprint of their presence can be quantitatively extracted from the statistical properties of their host DNA. Indeed, TEs properties were shown to be crucial in explaining structural global features of genome sequences HGBSH ; SRMA16 ; MA13 ; MAL05 ; HJ96 ; BGHPSS93 .

Recently, Albrecht-Buehler B06 suggested that TEs were the main driving force for the emergence of the second Chargaff parity rule. This rule states that, in each strand of the DNA, the frequencies of a short oligonucleotide $\mathbf{w}$ is approximately equal to that of its symmetrically related $\mathbf{\hat{w}}$, obtained from $\mathbf{w}$ by reversing the order of the symbols and substituting each nucleotide with its conjugated $A~{}\leftrightarrow~{}T$ and $C~{}\leftrightarrow~{}G$ (e.g. $\mathbf{w}=ACTGGCT$, $\hat{\mathbf{w}}=AGCCAGT$). It has been first observed by Chargaff in the 1950s RKC68 and since then detected across different organisms leading to different proposals for its origin and function R91 ; MB06 ; NA06 ; QC01 ; FTW92 ; P93 ; BF99 ; PHB02 ; KFCHZZL09 ; ABGRPF13 ; BF99b ; LL99 ; ZH10 ; HMO12 ; CBHDK19 ; FTPM19 . The importance of Albrecht-Buehler explanation is that it shows how this symmetry naturally emerges as an asymptotic outcome of the cumulative action of inversions/transpositions, one of the main mechanism of relocation of TEs. As we will show, while the proposed mechanism nicely induces Chargaff symmetry in the asymptotic DNA, it does it at the cost of trivialisation of the structural properties of the sequence: symmetry is obtained because of the complete randomization of the full double-stranded DNA.

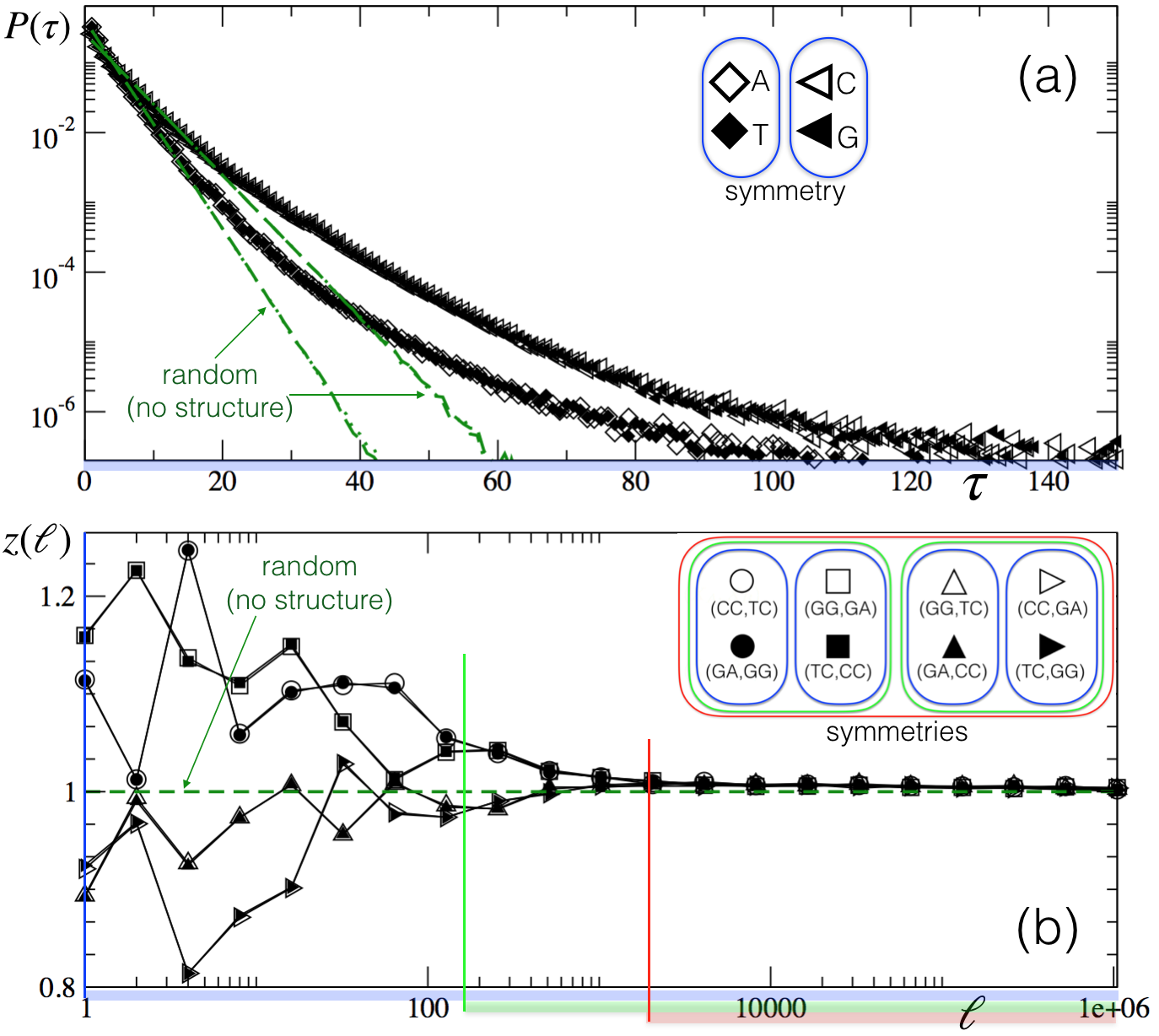
In view of the ubiquity of complex structures in genomes PBGHSSS92 ; LK92 ; V92 ; A92 ; P92 ; LMK94 ; ATVAMA01 ; FS12 ; CPTC15 , this result raises the question whether symmetry can appear without a full randomization of the sequence and in a way that is compatible with the existence of structure. The importance of this question is enhanced by our recent findings CDEA18 that Chargaff symmetry extends beyond the frequencies of short oligonucleotides – remaining valid on scales where non-trivial structure is present – and that an hierarchy of other symmetries exists, nested at different structural scales. This findings are confirmed in Fig. 1, which shows how commonly used indicators of structures, such as recurrence-time distribution (panel a) and correlation functions (panel b), coincide for symmetrically related observables at different scales.

In this work we present a biologically motivated dynamical process that explains the observed relation between symmetry and structure in DNA sequences. In particular, we propose a model that mimics the action (inversion/transpositions) of TEs on DNA and we analytically describe its dynamical behavior. Using indicators to quantify both symmetry and the presence of non-trivial structure in symbolic sequences, we show that the co-occurrence of symmetry and structure is an emergent statistical property in sequences generated by such model, reproducing the same hierarchical relation detected in extant genomes.

We consider symbolic sequences $\mathbf{s}=\{s_{i}\}_{i=1}^{N}$ of length $|\mathbf{s}|=N$ with $s_{i}\in\mathcal{A}=\{A,C,G,T\}$. Given a subsequence $\mathbf{a}$ of $\mathbf{s}$ (a word) we denote its corresponding reverse-complemented word as $\hat{\mathbf{a}}$, obtained from $\mathbf{a}$ by reversing the order of the symbols and substituting each nucleotide $\{A,C,G,T\}$ by its complementary one $A~{}\leftrightarrow~{}T$ and $C~{}\leftrightarrow~{}G$. We call $f_{x}(\mathbf{s})$ the percentage of the nucleotide $x$ in the sequence $\mathbf{s}$. Finally, we denote by $CG(\mathbf{s}):=f_{C}(\mathbf{s})+f_{G}(\mathbf{s})$ (the so called CG-content). In the following, it will be useful to partition the full set $\mathcal{A}^{N}$ into disjoint subsets of fixed CG-content $\mathcal{B}^{N}(k):=\{\mathbf{s}\in\mathcal{A}^{N}|CG(\mathbf{s})=k/N\}$; $\mathcal{A}^{N}=\cup_{k=0}^{N}\mathcal{B}^{N}(k)$.

We introduce the following simple indicators of the presence of Chargaff Symmetry and of non-trivial structure composition of a given sequence $\mathbf{s}$.

To quantify the compliance of $\mathbf{s}$ with Chargaff symmetry, we average the normalized difference of the abundance between a nucleotide and its symmetric one (see PHB02 where a similar measure was firstly introduced)

$I_{sym}=0$ indicates a fully Chargaff-symmetric sequence, $I_{sym}=1$ is obtained for a sequence for which Chargaff is perfectly violated ($f_{A}=f_{C}=0.5,f_{T}=f_{G}=0$), and $I_{sym}=0.08$ is obtained for a $2\%$ variation of equal frequencies (e.g., $f_{A}=f_{C}=0.23,f_{T}=f_{G}=0.27$). For simplicity, we consider $I_{sym}>0.08$ to be a violation of Chargaff symmetry.

To quantify the presence of non-trivial structures in a given symbolic sequence $\mathbf{s}$ we first compute the distribution $P(\tau)$ of distances $\tau$ between two successive occurrence of the same nucleotide $x$. For random sequences, $P(\tau)$ decays exponentially as $P(\tau)={f_{x}}{(1-f_{x})^{\tau-1}}$ and thus has average $1/f_{x}$ and standard deviation $\sqrt{1-f_{x}}/f_{x}$ (which is $\approx 1/f_{x}$ for small $f_{x}$). In contrast, the presence of a fat tail (standard deviation much larger than the mean) is considered a signature of a complex organization. We thus quantify structure as the distance of $\mathbf{s}$ from random sequences by

where $\mu_{\tau}\equiv\langle\tau\rangle$ and $\sigma_{\tau}\equiv\sqrt{\langle\tau^{2}\rangle-\langle\tau\rangle^{2}}$ are the mean and standard deviation of the measured $P(\tau)$, and $\sqrt{1-f_{x}}$ is the expected $\sigma_{\tau}/\mu_{\tau}$ for nucleotide $x$ in a random sequence. For random sequence we thus have $I_{str}(\mathbf{s})=0$, while departure from this value mark the presence of non-trivial structure. For simplicity, we consider $I_{str}>0.01$ to be a signature of structure.

We investigate symmetry and structure of sequences that evolve through the following dynamics, that maps one sequence $\mathbf{s}(t)\in\mathcal{A}^{N}$ into another sequence $\mathbf{s}({t+1})\in\mathcal{A}^{N}$ by mimicking the action of TEs B06 . The dynamics is defined composing two actions:

• (i)

  pick a random position $j$ of $\mathbf{s}$ and a random size $\ell\geq 0$, with $\langle\ell\rangle=L$ ¹¹1More precisely, the pairs $(j,\ell)$ are drawn, independently from previous iterations, from a joint distribution $\rho(j,\ell)$ chosen such that its marginal $\phi(\ell)$ has support contained in $[0,N]$, finite average $L$, and the conditional distribution of positions $\psi(j|\ell)$ is uniform in $[1,N-\ell+1]$. We consider distributions $\phi(\ell)$ that guarantee ergodicity of the Markov Chain. We expect ergodicity to be generically valid; e.g., it suffices to have non-zero probability for the identity transformation (i.e. $\phi(0)\neq 0$) and for single-nucleotide complementing ($\psi(1)\neq 0$).

• (ii)

  replace the subsequence $\mathbf{b}\equiv\{s_{i}\}_{i=j}^{j+\ell-1}$ of size $\ell$ starting at position $j$, by its reverse complement $\hat{\mathbf{b}}$.

The couple $(j,\ell)$ parametrizes the effect of an inversion/transposition, which we denote by $g_{(j,\ell)}:\mathcal{A}^{N}\to\mathcal{A}^{N}$. Its action has interesting properties: $g_{(j,\ell)}$ is an involution for every $(j,\ell)$ and the total number of $C$ and $G$ (or, equivalently, of $A$ and $T$) is invariant under $g$: $CG(\mathbf{s}_{t})=CG(\mathbf{s}_{0})\quad\forall t$. This implies that the dynamics is restricted to the invariant subspace of sequences with constant CG-content $\mathcal{B}^{N}(CG(\mathbf{s}_{0}))$.

The dynamics can be equivalently described as an ergodic Markov chain over the space of sequences $\mathcal{B}^{N}(CG(\mathbf{s}_{0}))$. The fact that $g_{(j,\ell)}$ is an involution forces the transition matrix to be bi-stochastic and thus in the asymptotic equilibrium all sequences are equiprobable. This means that, for $t\to\infty$ and irrespective of the initial ancient DNA sequence, the evolution asymptotically leads to sequences that can be equivalently considered generated by an independent and identically distributed (iid) process with $p(G)=p(C)=CG(\mathbf{s}_{0})/2$ and $p(A)=p(T)=(1-CG(\mathbf{s}_{0}))/2$. Therefore, the expected value of our indicators of symmetry and structure Eqs. (1) and (2) vanish asymptotically

for any initial sequence ${\bf s}(0)$²²2We can intuitively understand this result by noting that each action of the transposon effectively creates two cuts in the sequence and moves them by a distance $L$ on average. Since cuts can happen at any location, this process eventually mixes complementary basis at different positions and breaks any correlations originally present in $\mathbf{s}(0)$.. This shows analytically that the TE dynamics asymptotically leads to Chargaff symmetric sequences, in agreement with previous claims B06 . However, this symmetric equilibrium is a (trivial) consequence of a full randomization. Therefore our results show also that the current explanations of the second Chargaff parity rule B06 is not satisfactory as it is not compatible with any structure, which is known to remain significant at distances of several thousands of nucleotides PBGHSSS92 ; LK92 ; V92 ; A92 ; P92 ; LMK94 ; ATVAMA01 ; FS12 ; CPTC15 (see also Fig.1). Next we show that the same TE dynamics is rich enough by showing that symmetric sequences with non-trivial structure are generated pre-asymptotically as long-lived metastable states of TEs dynamics.

We now investigate symmetry and structure of the sequences $\mathbf{s}(t)$ by computing how our indicators $I_{sym}$ an $I_{str}$ depend on time $t$ (i.e., their values after $t$ applications of $g_{(j,\ell)}$). We show that Chargaff symmetry emerges much before equilibrium, together with a complex domain-like structure.

We first investigate structural properties of sequences after a finite number $t$ of iterations. We define a domain of $\mathbf{s}(t)$ as a subsequence of consecutive sites that have been involved in the same series of reverse/complement events. We then distinguish between domains of type $\Gamma$ and $\hat{\Gamma}$, depending on whether the number of transformations $g$ they were involved is even or odd, respectively. By definition, the starting sequence is composed by a single domain of type $\Gamma$. After one iteration it is split into three domains, two of type $\Gamma$ and one of type $\hat{\Gamma}$ of length $\ell_{1}$, corresponding to the subsequence involved in the first reverse/complement event. We now compute the average sizes $\langle\ell_{\Gamma}\rangle(t)$ and $\langle\ell_{\hat{\Gamma}}\rangle(t)$ of domains after $t$ iterations. Three regimes can be identified:

We now explain how structure $I_{str}(\mathbf{s}(t))$ and symmetry $I_{sym}({\bf s}(t))$ depend on the domain sizes $\langle\ell_{\Gamma}\rangle$ and $\langle\ell_{\hat{\Gamma}}\rangle$ and thus on the different regimes.

• $I_{str}(\mathbf{s})$

  : in order to identify the contribution of the dynamics in generating complex structural features, we consider an initial $\mathbf{s}(0)$ generated by an iid process (no structure, $I_{str}(0)=0$). With this choice, a value $I_{str}\neq 0$ signal the construction, under the action of the dynamics, of different domain-types. In particular, at $t_{metastable}$ and for $L>>1$, the total variance $\sigma_{\tau}^{2}$ can be estimated, using the law of total variance, as the sum of two components: one that measure variability of the mean of returns between domain-types and the other measuring variability of returns within each type. Accordingly $I_{str}(t)$ grows from $0$ to the value $I_{str}(t_{metastable})>0$ at the end of the first regime. In the second regime the domain sizes decay and $I_{str}(t)$ decreases to zero at equilibrium (at $t_{equilibrium}$). In terms of regimes we thus expect: (i) $I_{str}$ grows; (ii) $I_{str}$ decays; (iii) $I_{str}=0$.

• $I_{sym}({\bf s})$

  : each domain of type $\Gamma$ is a subsequence of the ancient sequence $\mathbf{s}(0)$. If average size of such domains at time $t$ is large enough, the frequency of each nucleotide are approximately the same as their frequency in $\mathbf{s}(0)$; similarly for $\hat{\Gamma}$ and $\mathbf{\hat{s}}(0)$. No constraints are imposed to the symmetry of the ancient genome. In particular, if the original sequence is not Chargaff symmetric $I_{sym}(\mathbf{s}(0))>0$ then the symmetry remains broken for all $t\lesssim t_{metastable}$ as quantified by $I_{sym}(\mathbf{s}(t))\simeq\frac{t}{N}\left|\langle\ell_{\Gamma}\rangle(t)-\langle\ell_{\hat{\Gamma}}\rangle(t)\right|I_{sym}(\mathbf{s}(0))$. In terms of regimes we thus expect: (i) $I_{sym}>0$; (ii) $I_{sym}=0$; (iii) $I_{sym}=0$.

Altogether, the estimations and calculations above lead to the following predictions for the presence of symmetry and structure as a function of time $t$ (regimes i-iii):

• (i)

  $0\leq t\leq t_{metastable}=N/L:$
  Structure $I_{str}>0$ but no symmetry $I_{sym}>0$.

• (ii)

  $t_{metastable}=N/L\leq t\leq t_{equilibrium}=N$
  Structure $I_{str}>0$ and symmetry $I_{sym}=0$.

• (iii)

  $t_{equilibrium}=N<t;$
  Symmetry $I_{sym}=0$ but no structure $I_{str}=0$.

In Fig. 2 we confirm these predictions in a numerical simulation.

The crucial feature of the TE dynamics discussed above is that in regime (ii) both non-trivial structure and symmetry co-exists in the generated sequences. The time (measured in number of iterations) for which this regime is valid is orders of magnitude larger than that of the first regime, as the ratio $t_{equilibrium}/t_{metastable}=L$ corresponds to the average size of transposable elements (for example $L\simeq 10^{2}$ in Homo Sapiens CBCHO07 ). We thus denote such long-lived regime as metastable and we expect it to be generically observed, even though it does not correspond to the stable equilibrium of our model.

The DNA sequences in the metastable regime are characterized by a symmetric domain-like structure. Domain models have been already introduced in literature to reproduce the complex structure generically observed in extant DNAs BGHPSS93 ; N92 ; KB93 ; PBHSSG93 ; BGRO96 ; BOFZSCMR85 ; ARLR02 ; CBCHO07 . In particular if the distribution of domain sizes has a fat tail, this will lead to a long-range correlated sequence BGHPSS93 , signalled by a slow decay of $P(\tau)$. The novelty of our approach is twofold: firstly, the domain-like structure in the metastable regime is an emergent property of the TE dynamics (it is not imposed a priori); secondly, such complex structure is intertwined with symmetry, that itself is an output of the dynamics. In particular, we have shown that sequences in the metastable regime are not only Chargaff symmetric ($I_{sym}=0$), they reproduce the hierarchical relation between symmetry and structure that is a distinctive feature of extant genomes (see Fig. 3 ).

In Fig.4 we report $I_{sym}$ and $I_{str}$ computed for genomes of different families, together with the values obtained from our dynamics. It shows that symmetry and structure coexist in most cases. The sequences from Animals shows enhanced structure while the cases of Archaea and Bacteria shows a moderate signatures of structure, in agreement with the temporal behaviour of our model (i.e., associating $t$ with the age of the genomes). Note that symmetry and structure properties are both statistical observations we made on the full DNA sequence. Any evolutionary constraint that pertains a small percentage of an organism genome does not affect these statistical observation in a sensible way. As an example, the protein-coding regions of Homo-Sapiens account for $~{}1.5\%$ of the full sequence. On the other hand, care should be taken when dealing with many different organisms: extensions of the model incorporating additional aspects of DNA evolution will be required for a quantitative comparison with the empirical data.

We have shown how a model that captures the action of transposable elements (TEs) is able to reproduce the intricate relation between symmetry and structure present in DNA sequences. We find that symmetry and structure change differently at different time scales (i.e., for different number of actions of TEs). For a large (pre-asymptotic) time interval, the sequences obtained in our model show the same non-trivial structures and an hierarchy of symmetries (including Chargaff) as in actual DNA sequences (confront panels (b) of Fig.1 and Fig.3). Our mathematical model is extremely simplified and includes the essential elements to explain the onset of symmetry and structure. In particular, it mimics only a simple action of TEs (reverse-complement), ignoring the fact that TEs are classified in different families, have different properties, and act according to different mechanisms JS88 ; munoz ; JBK .

We expect that incorporating more details of the TE dynamics in our model will refine our understanding of their role in shaping statistical properties of DNA sequences, in particular in an evolutionary viewpoint that would lead to refinements in the data-model comparison presented in Fig. 4.