Dynamics of the semigroup of contractive automorphisms of Banach spaces
Abstract.
Motivated by some recent twaddles on Mazur rotations problem, we study the “dynamics” of the semigroup of contractive automorphisms of Banach spaces, mostly in finite-dimensional spaces. We focus on the metric aspects of the “action” of such semigroups, the size of the orbits and semitransitivity properties, and their impact on the geometry of the unit ball of the underlying space.
Key words and phrases:
Mazur rotations problem; contractive automorphism; semitransitivity; Banach space; Hilbert spaceVersion
1. Introduction
This paper studies the “dynamics” of the semigroup of contractive automorphisms of finite dimensional normed spaces. Our interest in this subject, and even the topic itself, stems from Mazur rotations problem: Is every separable Banach space whose group of linear isometries acts transitively on the unit sphere isometric (or isomorphic) to a Hilbert space? (Cf. [1, remarque à la section 5 du chapitre XI].)
We are not going to go into this issue, firstly because there is a very recent survey paper on the subject and secondly because we believe that our study is (moderately) interesting in its own right. In any case, we recommend the reader to have a look at the papers [3, 8, 4, 7].
We consider only real spaces; most of the time we work in finite dimensions, often in the plane. In particular denotes with the norm for , while , and denotes the corresponding unit vector of .
Given a (real) normed space , its (closed unit) ball is the set and is the unit sphere. We write for the space of all (bounded, linear) endomorphisms of with the operator norm . An operator on is an automorphism if there is such that . An operator is contractive, or a contraction, if . This means that .
Clearly, the contractive automorphisms of form a semigroup of that we will denote by . We are interested in the “action” of on the unit sphere of , especially in the size of the “orbits” for . Note that if then there is always such that , so considering only points of is fine. Life without local convexity can be much harder, see [12] for examples of rigid quasi Banach spaces.
The space already provides a quite interesting example (see Figure 1 and the comments following Theorem 2.3):
-
•
for some .
-
•
for any other .
-
•
For each the set is a neighbourhood of relative to .
2. Semitransitivity
A Banach space is said to be semitransitive (ST) if for every there is such that . Hilbert spaces are ST: actually they are even transitive, that is, can be taken to be isometric, that is, . This quickly follows from the 2D case and the existence of orthogonal complements. Any other example in sight? Not yet. To understand what the issue is really about we need to introduce a couple of definitions.

Let be a finite dimensional (FD) space (or even a Banach space isomorphic to a Hilbert space) with unit ball and unit sphere . An ellipsoid in is the closed unit ball (centered at the origin) of an Euclidean norm equivalent to the original norm of . Ellipsoids are invariably assumed to be centered at the origin. If with some norm, then a disc (centered at ) is a set of the form , where and is the usual Euclidean norm.
We say that an ellipsoid is inner at if and . We say that is outer at if and . The following duality argument will be used over and over without further mention: if and are such that , then is inner (respectively, outer) at if and only if the dual ellipsoid is outer (respectively, inner) at .
Those (nonzero) points where the norm is (Gâteaux) differentiable are called smooth. This happens to if and only if there is exactly one functional such that and . Such an is called a support functional, necessarily agrees with , and is often denoted by . If the norm is differentiable off the origin the space itself is called smooth and the mapping sending each point into its unique support functional (and to ) is called the duality map.
It is clear that points that admit inner ellipsoids are smooth, while those that have outer ellipsoids are extreme. The following remark is obvious, yet very useful:
Lemma 2.1.
Let be a finite dimensional space and assume .
-
•
If is a smooth point of then so is .
-
•
If is an extreme point of then so is .
-
•
If admits an inner ellipsoid, then so does.
-
•
If admits an outer ellipsoid, then so does.
The following result is almost obvious, just using compactness:
Lemma 2.2.
In a finite dimensional space, the set of points admitting inner ellipsoids is dense in the unit sphere and the set of points admitting outer ellipsoids is nonempty.
See [6, Lemma 3.4] for an extension to infinite dimensional spaces. The following characterization is in turn a particularization of [6, Proposition 3.5].
Theorem 2.3.
For a finite dimensional space the following are equivalent:
-
(a)
is semitransitive.
-
(b)
Every point of the unit sphere admits inner and outer ellipsoids.
-
(c)
is semitransitive.
Proof.
The implication (a)(b) is clear after Lemma 2.1 and 2.2. The converse (b)(a) follows from the fact that if admits an inner ellipsoid and admits an outer ellipsoid, then . Indeed, let be inner at and outer at . Since all Hilbert spaces of the same dimension are isometric there is which maps onto . Clearly and by transitivity there is an isometry of the norm associated to such that . The composition is a contraction since .
On the other hand, by the remark preceding Lemma 2.1, satisfies (b) if and only if does, hence (b) is equivalent to (c) too. ∎
The above criterion shows that for and the spaces are not ST (if the unit vectors do not have inner ellipsoids; if they do not have outer ellipsoids). The paper [6] contains examples of ST norms on the plane which were constructed with slightly different purposes, using sledgehammers to crack nuts. Example 2.7 below is much simpler; Example 2.8 exhibits a rather unexpected behaviour.
Let us call flat if there exists some homogeneous hyperplane such that is a neighbourhood of relative to —note that . If is flat, then for all . Indeed, let be a norm-one functional such that , put , and let be any linear isomorphism. If is sufficiently small, the automorphism given by , where , is contractive —and sends to , of course.
Call pilgrim if is dense in . It is clear from Lemma 2.2 that every FD normed space has pilgrim points. As for the “size” of the set of pilgrim points it is nearly obvious that is strictly convex and smooth, then the set of pilgrim points is dense in the unit sphere of . See why? On the other hand, we have just seen that the orbit of any flat point consists precisely of the set of flat points of and this means that in any polyhedral space the set of pilgrim points is dense in the sphere. The same is true for spaces whose unit ball is the the intersection of two ellipsoids.

It is also clear that a FD space whose set of pilgrim points is dense in the unit sphere must must have some kind of regularity: if we mix a polyhedral norm with some strictly convex norm, we loose the density of the set of pilgrim points —think of the norm in that agrees with in the first quadrant and with in the second one.
The following example shows that some natural conjectures that one might come up with are false:
Example 2.4.
A uniformly convex and smooth normed space whose sphere is not the orbit of any point. Pick and define a norm on letting
All points on the sphere admit both inner and outer ellipsoids, except which have neither inner ellipsoids ( is too small) nor outer ( is too large). The inexorable conclusion is that if , then neither can be in the orbit of nor in the orbit of .

The notion of curvature (of a plane curve) is very useful both for understanding the geometry of the norm and for checking the ST character of norms in the plane. As far as this paper is concerned, everything we need to know about curves can be found in the lovely book by the Bucks [5, §8.4]. Let be an interval and be a rectifiable curve parameterized by arc length. If , and is twice differentiable at , then the curvature of at is defined as We are aware that there is a small problem here if is a double (or multiple) point of since depends not only on , but also on . We will not insist on this point. Note also that this notion of curvature refers to the usual Euclidean norm, although other approaches are possible (see [9, §4.3]).
If is the graph of a function , in the sense that for , then
| (1) |
where , and we no longer assume parameterized by its arc length (see Bucks’ [5, Exercise 5 on p. 416]). As a consequence:
Lemma 2.5.
Let be convex domains in with (piecewise) smooth boundaries . If and are tangent at (with the same inward-pointing normal) and then there is a neighbourhood of such that .
Proof.
In view of (1) this is a restatement of the fact that if is a real-valued function of a single variable with and , then is non-negative in some neighbourhood of . ∎
Since a circle of radius has curvature at all points the Lemma implies that if has finite curvature at , then belongs to a disc which is contained in . What is more interesting than it may seem:
Lemma 2.6.
Let be the unit ball of a norm on and let . Then admits an inner ellipsoid (ellipse) if and only if there is a disc such that and .
Dually, admits an outer ellipsoid if and only if there is a disc such that and .
Sketch of the proof.
We only prove the first part, being the “only if” part clear: if is an ellipse of semi-axes and , then contains the disc of radius centered at the inner normal and passing through .
To prove the converse it suffices to check the following: Let and . Let and . Then there is an ellipsoid that passes through and is contained in the convex hull of .
Indeed, the equation of any ellipse with center the origin is
If besides the tangent line at is “vertical” we have
since .
On the other hand (see Buck’s [5, Exercise 6 on p. 416]), the curvature of a plane curve satisfying the equation is given by the formula
Let us compute the curvature at . Clearly, we have , so
Hence taking large enough does the trick. ∎
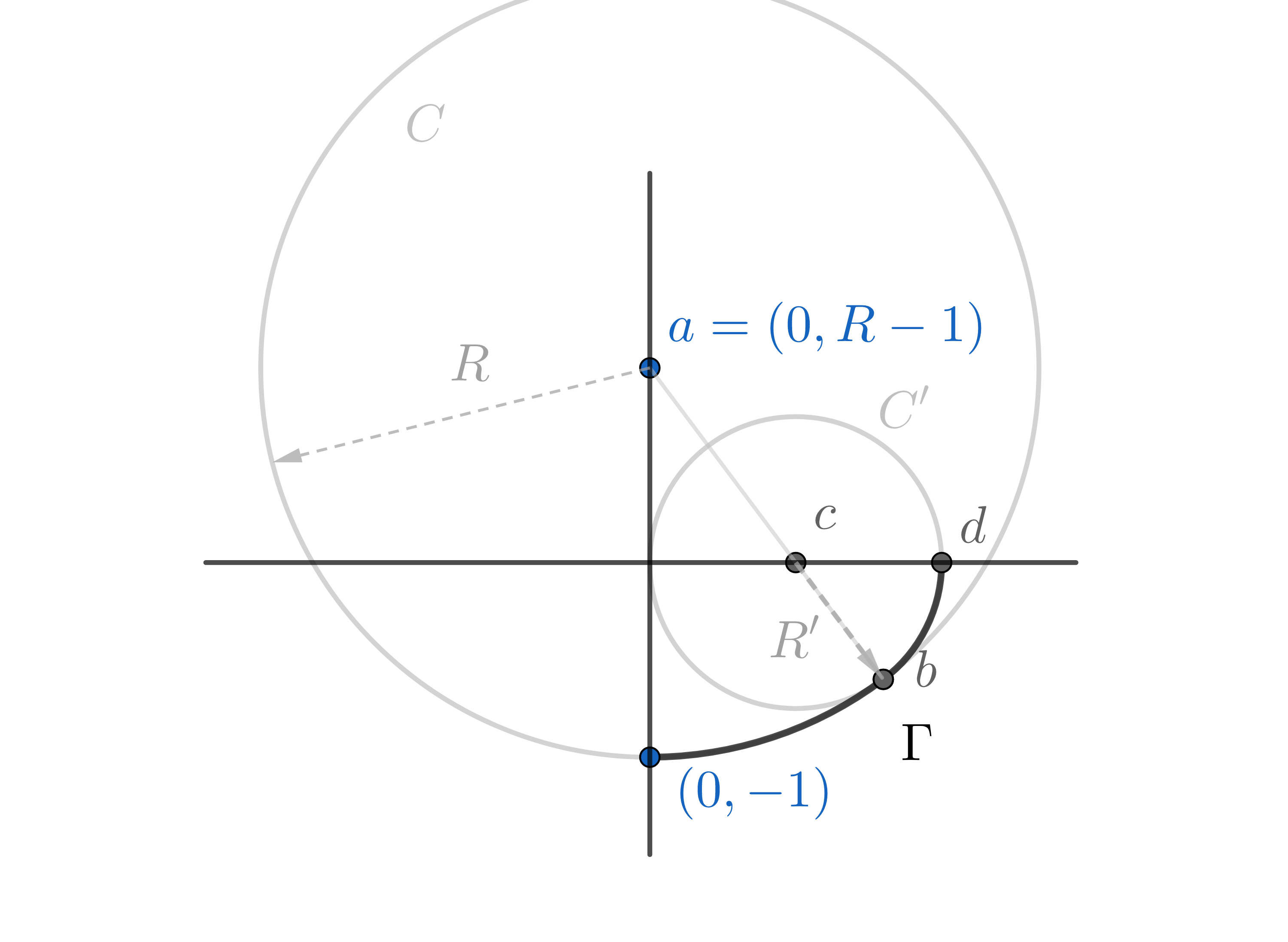
Example 2.7.
Semitransitive spaces splicing arcs of circles.
Here is a simple example of ST norm on . Fix any and let be the circle of center and radius . Let be any point of such that and . Let be the intersection of the horizontal axis and the line joining and . Let be the circle of center and radius . Note that passes through and that . Let be the rightmost point in the insersection of and the horizontal axis. Let be the curve (in the fourth quadrant) that agrees with from to and with from to .
It is clear that there is exactly one norm on the plane such that and also that is ST since every point in the unit sphere satisfies the criteria provided by Lemma 2.6.
Let be a FD space and assume that the orbit of is . Put
Then . An obvious “category” argument and the fact that the sets are compact in show that for every open set there is such that has nonempty interior in .
This fosters the idea that ST spaces could be boundedly semitransitive (BST) in the following sense: there is a constant such that, for every there is such that and .
Unfortunately this is not the case in general:
Example 2.8.
A (2-dimensional) semitransitive space which is not boundedly semitransitive.
Recall that given a locally integrable function , where is an interval containing the origin, the formulæ
define a plane curve such that
-
•
for all .
-
•
If is a Lebesgue point of , then the curvature of at is . See [10, Definition 7.1.19]

Let us first define as follows (see Figure 5):
-
•
For each the value of on is .
-
•
Otherwise .
Then we consider the curve defined as above, with , and call it . Now look at the endpoint of corresponding to : a moment’s reflection suffices to realize that:
-
•
The initial point of is .
-
•
since , both and are strictly positive for and parametrizes naturally.
-
•
The (semi) tangent line to at has strictly positive slope and, moreover, if is the only point of that line that lies on the “horizontal” axis, then .
It follows (see Figure 4) that there exist a pair of circles such that is tangent to at , is tangent to the line at and and are mutually tangent at some other intermediate point, say .
Let be the curve that “agrees” with between and , with between and and with between and . It is clear that there is exactly a norm, say , on whose unit sphere contains .
We want to see that the resulting space is ST. Observe that is a (“smooth”) countable union of arcs of circles: going from right to left we find first the arcs and , then an arc of circle of radius 1 and lenght , then an arc of circle of radius and lenght , then another arc of circle of radius 1 and lenght , then an arc of circle of radius and lenght and so on. These arcs accumulate at the point in the obvious sense. Finally we have an arc of radius 1, centered at the origin, between and .
Now it should be clear that all points of admit inner discs and also that all of them, except , have outer discs. But actually admits an outer disc whose radius is not very large. Indeed for every the (Lebesgue) measure of the set is at least . Therefore, if we put , then for . Since
it is clear that cannot leave the disc of radius centered at for any , which is enough.
The resulting normed plane, whose sphere is , cannot be BST because the inverse of a contractive automorphism sending a point with small curvature to a point of large curvature must have large norm, see why? If you still do not see it clearly, take a look at the upcoming Proposition 3.1.
3. Bounded semitransitivity
We now study BST spaces. It turns out that these admit a quite elegant geometric characterization. Before going any further, recall that the modulus of uniform convexity of a Banach space is the function defined by
| (2) |
Note that represents the distance between the midpoint of and and its closest multiple in the unit sphere (the larger the MUC the more convex the ball is) and that one can replace all inequalities by equalities in (2) without altering the value of . We say that is of power type 2 if for some and all .
Hilbert spaces have “optimal” MUC given by
Condition (d) below is stated also in terms of the modulus of uniform smoothness (MUS, a measure of the “flatness” of the unit ball which we do not even define here). It will suffice to recall here that has MUS of power type 2 if and only if has MUC of power type 2, so that (d) is equivalent to: Both and have MUC of power type . We refer the reader to [11, § 1.e] for the basics on uniform convexity and smoothness.
Proposition 3.1.
For a finite dimensional space the following are equivalent:
-
(a)
is boundedly semitransitive.
-
(b)
is boundedly semitransitive.
-
(c)
There is a constant such that every admits an inner ellipsoid and an outer ellipsoid such that .
-
(d)
has moduli of uniform convexity and smoothness of power type .
The remainder of the section is devoted to proving this result. Let’s get the boring parts out of the way now. The equivalence (a)(b) can be proved as in Theorem 4.2 since taking Banach space adjoints preserves automorphisms, inverses, and the operator norm.
(a)(c). Assume is BST with constant . Fix and let and be inner and outer ellipsoids at , respectively, which exists by ST and Theorem 4.2. Clearly for sufficiently large . Pick and then such that , with . Then is inner at , is outer at , and .
The implication (c)(a) can be proved as the implication (b)(a) of Theorem 4.2, just following the track of the norms.
We now adress (c)(d). The proof uses the so-called modulus of strong extremality, defined for and as:
It is not hard to see that —only the easiest part “” will be used here.
Assume admits an outer ellipsoid with . This implies that if denotes the Euclidean norm corresponding to , then . An easy computation based on the fact that and are tangent at shows that
where, as the reader may guess, stands for the modulus of strong extremality of the Euclidean norms. Thus, (c) implies that where depends only on . The fact that has MUS of power type 2 follows from the fact that a finite dimensional space satisfies (c) if and only if its dual does since a Banach space has MUS of power type 2 if and only if its dual has MUC of power type 2.
It only remains to check that (d)(c), which amounts to see that if has MUC of power type 2, then there is a constant such that every admits an outer ellipsoid such that .
The proof is based on the following, surely well-known, observation:
Lemma 3.2.
Let be a normed space with modulus of uniform convexity . Let and assume that is a supporting hyperplane at . Assume and write , with and . Then and so .
Proof.
One can assume that has dimension 2 and also that . Since we have and so . In particular is correctly defined and since for all we may assume .
We encourage the reader to draw their own monikers. Let be the only negative multiple of such that . We claim that even , which is clear just applying the definition of MUC to which equals the distance between and , taking into account that the midpoint of and lies in the line and that for all . In particular . Nice, isn’t it? ∎
To complete the proof, let be an Euclidean norm on such that for some constant , for instance one could take the norm associated to the ellipsoid of minimal volume containing . We define a two-parameter family of Euclidean norms as follows: Given , let be the (or a fixed) support functional of at and set , so that each can be written as , with and — of course and . Then, for each we set
| (3) |
Note that for fixed and that for each fixed , the norms are all uniformly equivalent and uniformly equivalent to . Hence it suffices to see that there exists such that for all . But if we assume for some it is clear from the Lemma that if and are such that belongs to , then
It follows that for all and since we have that the ellipsoid is outer at , which is enough.
Remark 3.3.
The proof actually shows that a Banach space isomorphic to a Hilbert space has MUC of power type 2 if and only if the points of its unit sphere admit uniformly bounded outer ellipsoids and that it has MUS of power type 2 if and only if the points of the unit sphere admit inner ellipsoids whose intersection contains a neighbourhood of the origin.
4. Uniform micro-semitransitivity
Definition 4.1.
A Banach space (or its norm) is said to be uniformly micro-semitransitive (UMST) if for every there exists such that whenever satisfy there is such that with .
The interest in UMST stems from the facts that all 1-complemented FD subspaces of a separable and transitive Banach space are UMST ([6, Theorem 3.2]) and that the only previously known UMST norms were the Euclidean norms, which made it conceivable that UMST would be a characteristic property of Hilbert spaces.
Unfortunately this is not the case: in this Section we prove that every norm on the plane whose dual is also turns out to be UMST.
The remainder of this section is devoted to proving the following.
Theorem 4.2.
Every norm on the plane whose unit sphere has strictly positive curvature at every point is uniformly micro-semitransitive.
The following “uniform” version of Lemma 2.5 is the key ingredient of the proof of Theorem 4.2. It will be applied in due course to compare the unit sphere of the given norm with its image under a slightly-changing automorphism.
Lemma 4.3.
Let be twice differentiable curves parameterized by arc length, and . Assume that:
-
(a)
and are tangent at and .
-
(b)
If for , then .
Then and meet only at .
Proof.
We may assume that is the origin and . Since for . Applying the Mean Value Theorem to (and then the Implicit Function Theorem) we see that if then there exist and a function such that the set agrees with the graph of . For the same reason, taking (b) into account, we have that agrees with the graph of certain function . We have . We may and do assume that and are strictly positive in their respective domains. Let us check that . Otherwise there is in the common domain of and such that . Put : note that and that since for sufficiently small. Clearly and this implies that there is such that . Put . Then and and for . Hence letting , and applying (1), we obtain
a contradiction. ∎

Let be a (smooth) norm on the plane and let be its unit sphere with the standard (counterclockwise) orientation. If is a regular parametrization of preserving the orientation and , put that is, the only point in such that is positively oriented.
It is almost obvious that if are close in and is close to the identity and maps to , then , with . From now on we denote by the only linear endomorphism of that maps to and to , with the subscript omitted if . This is actually an automorphism unless and, quite clearly,
Lemma 4.4.
Let be a 2-dimensional space with smooth norm.
-
(a)
for all and all .
-
(b)
If is strictly convex and for some , then is proportional to .
-
(c)
for all and all .
-
(d)
If the norm of is , then there exists a constant (depending on ) such that for all and all .
Proof.
(a) and (b) are clear. To prove (c) note that if , then since the coordinate is completely determined by . In particular . However does not agree with unless is a Radon plane (one in which Birkhoff orthogonality is symmetric, do not worry if you have forgotten or never knew what this means; let us just add that while the spheres of Figure 8 are Radon, that of Figure 7 is not). Nevertheless, . In particular,
(d) Clearly, the map is Lipschitz. For we have
which is enough: and . ∎
Note that if is assumed to be merely smooth, the proof yields as .
We now analyze the variation of the curvature under certain linear transformations. The following result applies in particular when the curve is a sphere and .
Lemma 4.5.
Let be linearly independent in and and let be the only linear endomorphism such that . Assume is a regular curve such that and let . Then and
Proof.
After applying a suitable linear transformation (a rotation followed by scaling or viceversa) we may assume and in which case is implemented by the matrix
By the Implicit Function Theorem we can describe near as the graph of a certain funtion defined near and we then have
see (1). Now, using the argument of as a parameter we have
One the other hand (see [5, Equation 8-34 on p. 410]), since we have
| (4) | ||||
| (5) |
The core of the proof of Theorem 4.2 is the following piece:
Lemma 4.6.
Under the hypotheses of Theorem 4.2 for every there exists such that is contractive for all such that .
Proof.
If we assume the contrary then there exists such that for every there exist with and such that .
Passing to subsequences without mercy we may assume that are convergent. Put and and let us show that . One has and so and Lemma 4.4(b) shows that . Now since does not vary if we replace by and by we can even assume that . Hence, it suffices to check the following:
For each there exists (depending on and ) such that if then the only common point of and in the ball of radius and centre is itself.
With an eye in Lemma 4.3 let be the supremum of the set
| (6) |
Since and are tangent at the following statement implies through Lemma 4.3:
For each there exists such that if then , provided and .
We first observe that there is a constant such that for all and this implies that for each there is such that if and , then
In particular, if and , then In a similar vein, Lemma 4.4(d) implies that for each there is such that
In particular, if , then
hence,
| (7) |
Now, we fix and take , where is the infimum of the set in (6).
Let us present some UMST norms on the plane in the light of Theorem 4.2. The first set of examples uses polar coordinates.
Example 4.7.
Let be a and -periodic function satisfying the condition
| (8) |
for all (equivalently, for ). Then the formula , where are the polar coordinates of , defines a norm on the plane that satisfies the hypotheses of Theorem 4.2 and is therefore uniformly-micro-semitransitive.
All norms on the plane satisfying the hypotheses of Theorem 4.2 arise in this way.

Indeed if is a curve with polar representation , with twice differentiable, then the curvature of at the point of polar coordinates is given by
If in addition is -periodic and satisfies (8) then the bounded domain enclosed by is automatically convex ( has no point of inflection) and thus is the unit sphere of a norm on which is actually given by . Of course is off the origin if and only if is . The converse is obviously true.
Note that if (pointwise), then holds. The first functions that satisfy this condition that come to mind are with even and ; see Figure 7.

A different kind of example is the following: assume is off the origin on . Given put This new norm is again and the “new” duality map, which is given by is positive definite since , being the Hessian of a convex function, is positive semi-definite. When this implies that all points of the sphere have strictly positive curvature and so is UMST.
We do not know if the converse of Theorem 4.2 is true, although many of the implications of the proof are clearly reversible. Assume is a UMST plane and let be a parametrization of the unit sphere by the arc-length relative to the usual Euclidean norm. It is relatively easy to see that there is , whose complement has measure zero, where is twice differentiable and is uniformly continuous. In particular the curvature, which is defined on , has a continuous extension to . Thus, the question seems to be whether UMST planes are absolutely smooth in the sense of [2].
On the other hand, the theorem is crying out for a generalisation for arbitrary (finite) dimension. Of course we need a different hypothesis in “the general case”. But for a Banach space (necessarily isomorphic to a Hilbert space) the following statements are equivalent:
-
•
Both and are -smooth off the origin.
-
•
The function given by is -smooth and is positive definite for all .
(See [6, Proof of Proposition 3.7].) These in turn are equivalent to the hypothesis of Theorem 4.2 when has dimension 2 and we conjecture that they are equivalent to UMST in finite dimensions.
References
- [1] S. Banach, Théorie des Operations linéaires (French) [Theory of linear operators], Monografie Matematyczne 1, Inst. Mat. Polskiej Akad. Nauk, Warszawa 1932; freely available at the Polish Digital Mathematical Library on http://pldml.icm.edu.pl. Reprinted by Chelsea Publishing Co., New York, 1955 and Éditions Jacques Gabay, Sceaux, 1993.
- [2] T. Banakh, Any isometry between the spheres of absolutely smooth 2-dimensional Banach spaces is linear, J. Math. Anal. Appl. 500 (2021) paper 125104.
- [3] J. Becerra Guerrero, Á. Rodríguez-Palacios, Transitivity of the norm on Banach spaces, Extracta Math. 17 (2002) 1–58.
- [4] J. Becerra Guerrero, Á. Rodríguez-Palacios, Banach spaces with a large semigroup of contractive automorphisms, J. Math. Anal. Appl. 475 (2019) 642–667.
- [5] R.C. Buck, E.F. Buck, Advanced Calculus. Third Edition. McGraw–Hill, 1978.
- [6] F. Cabello Sánchez, Wheeling around Mazur rotations problem. Preprint 2021, arXiv:2109.01906.
- [7] F. Cabello Sánchez, S. Dantas, V. Kadets, S.K. Kim, H.J. Lee, M. Martín, On Banach spaces whose group of isometries acts micro-transitively on the unit sphere, J. Math. Anal. Appl. 488 (2020) 124046, 14 pp.
- [8] F. Cabello Sánchez, V. Ferenczi, B. Randrianantoanina, On Mazur rotations problem and its multidimensional versions, São Paulo Journal of Mathematical Sciences 16 (2022) 406–458.
- [9] J. Cabello Sánchez, A reflection on Tingley’s problem and some applications, J. Math. Anal. Appl. 476 (2019) 319–336.
- [10] R. Kannan, C.K. Krueger, Advanced Analysis on the Real Line, Universitext, Springer-Verlag, New York, 1996, x+259 pp.
- [11] J. Lindenstrauss, L. Tzafriri, Classical Banach Spaces II. Function Spaces, Ergebnisse der Mathematik und ihrer Grenzgebiete bd. 97, Springer-Verlag, New York, 1979.
- [12] J.W. Roberts, Every locally bounded space with trivial dual is the quotient of a rigid space, Illinois J. Math. 45 (2001) 1119–1144.