Dynamics of the critical point in QCD: critical pions and diffusion in Model G
Abstract
We present a detailed study of the finite momentum dynamics of the critical point of QCD, which lies in the dynamic universality class of “Model G”. The critical scaling of the model is analyzed in multiple dynamical channels. For instance, the finite momentum analysis allows us to precisely extract the pion dispersion curve below the critical point. The pion velocity is in striking agreement with the predictions relation and static universality. The pion damping rate and velocity are both consistent with the dynamical critical exponent of “Model G”. Similarly, although the critical amplitude for the diffusion coefficient of the conserved charges is small, it is clearly visible both in the restored phase and with finite explicit symmetry breaking, and its dynamical scaling is again consistent with . We determine a new set of universal dynamical critical amplitude ratios relating the diffusion coefficient to a suitably defined order parameter relaxation time. We also show that in a finite volume simulation, the chiral condensate diffuses on the coset manifold in a manner consistent with dynamical scaling, and with a diffusion coefficient that is determined by the transport coefficients of hydrodynamic pions. Finally, the amplitude ratios (together with other non-universal amplitudes also reported here) compile all relevant information for further studies of “Model G” both in and out of equilibrium.
I Introduction
High-multiplicity reactions in colliders are a unique tool to explore the phase diagram of QCD. Their ability to probe different phases and phase transitions crucially relies on a precise understanding of its dynamics in a hot and dense state. Arguably one of the most impactful results of the scientific program of the Relativistic Heavy-Ion Collider (RHIC) was the discovery of a very short thermalization time after which the quark-gluon plasma created in the collision exhibits collective behavior, faithfully reproduced by hydrodynamics. This phenomenon is key to the predictive power of heavy-ion collisions.
This work is a direct continuation of [1] and touches on the nature of the appropriate hydrodynamic theory required by heavy-ion collisions. Away from a phase transition, the hydrodynamics of a system is fully characterized by symmetries and conserved charges. At criticality, the dynamics of the order parameter and its coupling to the conserved charges also needs to be considered [2]. This is crucial to the dynamics of two-flavor QCD in the chiral limit, close to its second order phase transition [3]. In the chiral limit, the hydrodynamic theory above is specified by an unbroken symmetry group with corresponding conserved charges. Below the symmetry is broken to and the associated massless Goldstone modes (the pions) must be incorporated into the hydrodynamic effective theory [4, 5, 6]. Finally, in the critical region the appropriate macroscopic description includes an order parameter (), and the effective theory interpolates between the two hydrodynamic limits above and below the critical point.
Beyond the theoretical appeal of the chiral limit, the real-world up and down quark masses are small compared to QCD scales, to the point where it is legitimate to ask whether aspects of real-world QCD close to its phase transition can be recovered by deforming the massless limit. For static quantities this question was asked in [7, 8] and led to further studies of the chiral critical point with explicit symmetry breaking [9, 10, 11, 12, 13, 14, 15, 16, 17]. These studies, when combined with important results from Lattice QCD at various quark masses [18, 19, 20, 21], indicate that the static properties of the chiral crossover in real world QCD can be reasonably understood using universality considerations and the existence of a critical point in the massless two-flavor limit.
It remains to be seen whether the dynamics of the chiral crossover can be similarly understood using the proximity of QCD to the critical point. The relevant hydrodynamics of the phase transition lies in the dynamical universality class of “Model G” in the Halperin-Hohenberg classification scheme [3], which predicts the existence of long-range chiral modes that describe the evolution of soft pions in the crossover region. When the symmetry is explicitly broken, the pions develop a mass, tempering the impact of these modes on the dynamics on the system. Nevertheless, although these modes contribute negligibly to the energy momentum tensor, they survive over time scales much longer than the typical relaxation time and most definitely affect the long-range dynamics of chiral observables in QCD in the crossover region.
For an experimental perspective, although it is challenging to systematically measure soft pions of transverse momenta smaller than , recent analyses uncovered some discrepancies between state-of-the-art hydrodynamic models and available data in this momentum range. The results are indicative that conventional hydrodynamics does not fully describe the long wavelength dynamics of these pseudo-Goldstone modes [22, 23, 24].
Taking these indications into consideration, and further encouraged by the proposed upgrade to the ALICE detector [25] which will be more sensitive to low pions, a natural question, already raised in [3, 6] and subsequently studied further [26, 27], is the following: what is the effect of the critical chiral dynamics on the hydrodynamics of real-world QCD? To answer this question a more precise and detailed understanding of the dynamics of “Model G” itself is required.
Over the years, a series of classical-statistical simulations have been presented in the literature [28, 29, 30, 31, 32, 33, 34], building up towards studies of the dynamics of “Model G” and “Model H”, the critical model of the conjectured second order phase transition at the finite baryon chemical potential [35]. In a similar spirit, functional Renormalization Group (fRG) studies have been carried out in [36, 37, 38, 39, 40, 41, 42]. Although limitted to mean field, holographic models can provide additional analytical insight into the dynamics of the chiral phase transition [43].
This work expands on [1] (where the first successful numerical simulations of “Model G” were presented) by extending the zero momentum analysis to finite momenta. With this extension, we are able to quantify the dispersion curve of critical pions in detail and study the critical diffusion of the conserved charges. We show that in a finite volume simulation the orientation of the chiral condensate diffuses on the three sphere (the coset manifold), with a diffusion coefficient determined by the transport coefficients of hydrodynamic pions in infinite volume. When chiral symmetry is explicitly broken, the diffusive dynamics is coupled to a Hamiltonian structure determined by the pion mass, and the combined evolution dynamically realizes the -regime of QCD at finite temperature111 The regime is when the quark mass is small and the volume is large, but . Here is the chiral condensate as a function of temperature – see [45] for an overview. . We also compute new universal dynamical ratios relating the diffusion coefficient to the (appropriately defined) order parameter relaxation time, which we also determine both above and on the critical line. In total, these measurements corroborate the dynamical scaling of “Model G” with critical exponent across multiple observables, ranging from the pion velocity and damping rate, to the diffusion of the charges222Here is the dimensionality of space.. These results will prove essential to the next step of this series of work, which will quantitatively analyze the non-equilibrium dynamics of the expanding critical system.
II Overview of Model G and its phases
II.1 Model G
The theory we are considering is a generalization of “Model G” of [2] and was first introduced in [3]. It is the relevant hydrodynamic theory constructed around the critical point of “2-flavor chiral QCD”, namely QCD with massless up and down quarks (). It contains a order parameter , a proxy for the quark condensate of real QCD, dynamically coupled to vector and axial charges333 Here and denote indices; , , , etc. denote the three isospin indices, i.e. the components of ; finally, spatial indices are notated , and . The dot product indicates an appropriate contraction of indices when clear from context, e.g. , , and . , and respectively. They correspond to the original iso-vector and iso-axial vector currents, and , respectively. These can be conveniently combined into an antisymmetric tensor of charge densities :
| (1) | ||||
| (2) |
The free energy (or effective Hamiltonian) in the presence of an explicit symmetry breaking can be studied using an Landau-Ginzburg action
| (3) |
where
| (4) |
with negative. In equilibrium, the charges have Gaussian fluctuations set by a susceptibility , which is the same coefficient for both the iso-vector and the iso-axial-vector charges near the critical point. The interactions between the charges and the order parameter enters the dynamics through the equations of motion and are determined by the non-trivial Poisson brackets between these fields – see [3, 27] for explicit expressions and a derivation. This construction leads to the following evolution equations
| (5a) | ||||
| (5b) | ||||
| (5c) | ||||
| (5d) | ||||
Here, for example, denotes the anti-symmetrization, . The coefficients and are the bare kinetic coefficients associated with the order parameter and the charges. The bare diffusion coefficient of the charges is . The constant is a coupling of the field , and has the units of in our conventions. Finally, and are the appropriate noises, which are defined through their two-point correlations [2]
| (6a) | ||||
| (6b) | ||||
The dissipative Model G dynamics relaxes to the equilibrium distribution for the fields and [2]
| (7) |
which reproduces the static critical behavior of the model.
The basic observable that will be analyzed are statistical two-point function between fields as a function of relative momentum and time. In the presence of the explicit breaking the flavor index can always be decomposed in a longitudinal and transverse direction, therefore it is natural to define:
| (8) |
for the scalar channel, and
| (9) |
for the pseudo-scalar channel. The statistical correlators for the charges are defined analogously
| (10) | ||||
| (11) |
Note that all these correlators can be studied in mean field, see [27].
At zero explicit breaking , we will also consider isotropized charge and field correlators
| (12) | ||||
| (13) |
II.2 Simulations
This paper is a continuation of [1] and presents results obtained by numerically solving equations (5a)-(5d), using an algorithm detailed in Appendix A of [1]. The stepper combines a symplectic integrator for the Hamiltonian evolution and Metropolis updates for the dissipative step. Throughout we will present our results in lattice units, setting , and setting the lattice spacing to unity, . This amounts to setting and and choosing the microscopic lattice spacing so that the model reproduces the correlation length of the physical system. The pole frequency of the pion near the critical point is reproduced by this choice of units. The quartic coupling is set to and the model is simulated close to its critical mass, . The reduced temperature and magnetic field are defined as in [12] :
| (14) |
where is chosen so that the magnetization scales as
| (15) |
on the critical line, . For and in the broken phase the magnetization scales as
| (16) |
with amplitude444Note an unfortunate misprint in [1]. Equation (29) in the published version should read . The then quoted parameters and lead to a parametrization , with and . , . The non-universal parameters and completely fix the properties of the magnetic equation of state close to the critical point.
For the static critical exponents quoted here and below we take the values and from [12]. For the correction-to-scaling exponent we take [46] and the for the dynamical critical exponent we take [3], where is the number of spatial dimensions. A summary of all exponents used in this work is given in Table 2 of App. B.
We performed additional analyses along the critical line using the data generated in [1] for different lattice sizes . We also generated an extensive set of data at , both in the broken () and restored () phases. The dynamical parameters were chosen as in our previous work, , and . Our full dataset is summarized in Table 1.
For context, we also display the correlation length (in lattice units) for our different simulations in Fig. 1. The correlation lengths in the restored phase and on the critical line correspond to the fits presented in App. B.1 and B.2. As discussed below, in the broken phase the hydrodynamic theory is characterized by a pion EFT at the longest wavelengths. The pion parameter is a matching coefficient in the EFT, which characterizes the pion’s fluctuations and scales as the inverse correlation length close to the critical point [47, 5]. We will use as an estimate for the correlation length in the broken phase which is determined numerically in App. B.3. Here the factor of is conventional and is motivated by the fact that finite volume corrections to correlation functions (which are computable using the pion EFT [47]) are organized in powers of with order one coefficients, see App. B.3. The black data points correspond to the different temperatures we simulated.
| Phase | ||||||||||||||||||||||||||||||||||
| Restored |
|
|
||||||||||||||||||||||||||||||||
| Critical line | 0 | 80 |
|
|||||||||||||||||||||||||||||||
| Broken |
|
|
|
0 |

Before diving into a quantitative study, we use the rest of this section to present the qualitative behavior of the different channels in the restored and broken phases (with ) and on the critical line ( and ).
II.3 The restored phase with
In the restored phase, the symmetry is unbroken and there is no distinction between the axial and vector channels. The order parameter simply dissipates towards equilibrium on a finite (if long) timescale. But, both the iso-vector and iso-axial vector charges are exactly conserved. As a result, the non-trivial dynamics at the longest wavelengths is fully encoded in the correlators of conserved charges at finite momenta. Indeed, for wavelengths long compared to the (diverging) correlation length , the diffusion equation remains a valid hydrodynamic description of the system:
| (17) |
Thus, the relaxation rate of a diffusive mode of wavenumber is controlled by the diffusion coefficient leading to the correlators (see App. A.1):
| (18) |
The charge correlations in the simulation are illustrated on the left-hand side of Fig.2, where we plot the axial correlator (orange) and the vector correlator (blue), for the first two momenta, for a given temperature. We clearly see that the two channels are degenerate. The dependence is consistent with the expected diffusive behavior.
In writing the diffusion equation in eq. (17) we have integrated out the contributions to the currents from the order parameter, which then leads the scaling behavior of the transport coefficient. As discussed below, the order parameter has a dynamical relaxation time of order with . The diffusive modes have a relaxation time of , which is of order at the boundary of applicability of the diffusion equation, . In the spirit universality, all modes of with wavelengths of order should have a similar relaxation time, dictating the expected scaling of the diffusion coefficient, .
On the right-hand side of Fig. 2, we show the dependence of the vector correlator (we could have equivalently chosen the axial) on . This very weak dependence seems at first to be in contradiction with the expected critical scaling of the diffusion coefficient . As we will see more clearly in the next section, this apparent contradiction originates in the presence of a large regular constant contribution to , and by the smallness of its non-universal critical amplitude. Nevertheless, we will extract the critical contribution to in Sect. III.1.


II.4 The critical line
We next study the critical line, , and study the effect of explicit symmetry breaking, . One of the qualitative outcomes of our previous work [1] was to demonstrate the emergence of damped pion waves already on the critical line. This qualitative observation was obtained from the modes of the axial current and the pions correlators. The same qualitative observation holds for non-zero momentum and is observed in Fig. 3. At the level of the charge correlators, the magnetic field lifts the degeneracy between the axial and vector channels. The axial correlator then displays characteristic oscillations associated with axial charge propagation in the form of damped pion waves. The vector channel on the other hand remains purely diffusive. As in the restored phase, we already observe that the critical behavior of the vector diffusion constant is weak.


II.5 Broken phase with
Below the critical point the longest wavelength modes are characterized by massless Goldstone bosons, which describe phase fluctuations of the chiral condensate555For clarity we will restore the temperature in this section.. Following [5, 6], these fluctuations are parametrized by an angle with . We are assuming that the chiral condensate is nearly aligned with the pole of the three sphere (the coset manifold) and takes the form
| (19) |
where is a unit vector that is approximately parametrized by to first order in the angular deviation. When the wavelength of is long compared to the correlation length , a hydrodynamic description of is valid, and the fluctuations of modes with wavelength order simply determine the critical behavior of the parameters of the hydrodynamic theory.
The free energy associated with the phase and charge fluctuations in the hydrodynamic approximation is
| (20) |
where we have included a mass term, which is relevant only when the magnetic field is non-zero and is determined by the Gell-Mann, Oakes, Renner relation
| (21) |
We will set for the remainder of this section. The resulting hydrodynamic equations of motion for the pions and axial charge take the form666 In [26] the dissipative coefficient was called . In mean field theory the hydrodynamic parameter equals the bare parameter [27]. A notable feature of these equations when the symmetry is explicitly broken is that the same coefficient controls both the damping rate at finite momentum and the mass term, see eq. (65). This is a general result dictated by entropy considerations [3, 26, 48] and related locality arguments [49]. This became widely recognized through a sequence of explicit holographic computations in different contexts with explicitly broken symmetries [50, 51, 52, 53] – for a review see [54]. The pion dynamics in a holographic model of the phase transition is described in [43] and can be profitably compared to mean field theory results of [27].
| (22a) | ||||
| (22b) | ||||
| which reflects from the Poisson bracket between the phase and the charge, . The vector charge remains diffusive | ||||
| (22c) | ||||
The hydrodynamic system is solved in App. A.1 and the resulting pion eigen-waves have dispersion relations
| (23) |
where
| (24) |
The form of the correlation function from the hydrodynamic theory is determined in App. A.1
| (25) |
At large wavelengths the pion effective theory determines the static and dynamic correlation functions. The static correlation function for can be read off from the free energy in (20) and is singular in the massless limit:
| (26) |
By contrast, the static fluctuations of the are bounded (if diverging) and determined by the static susceptibility of the critical point, which scales as
| (27) |
The and are part of an multiplet and their correlators must be the same order of magnitude at the boundary of applicability of the pion EFT, . Since the vev scales as , the pion constant must scale as [47]. We have anticipated this scaling in Fig. 3 where (with in our adopted units) served as a definition of the correlation length in the broken phase.
Because of these scalings, the long-wavelength behavior of the static and dynamic correlation functions of are dominated by the phase fluctuations. Specifically, the static correlation function reads
| (28) |
up to corrections of order . Additional finite volume corrections to this formula are given in App. B.3 and are suppressed by [47]. Phase fluctuations also determine the dynamic correlations
| (29) |
and Fig. 4 (Left) exhibits the correlation function, which shows characteristic pion oscillations of (25) become increasingly damped near the critical point. The critical scaling of and are extracted numerically in the next section and are ultimately summarized in Fig. 7.
In a finite volume simulation the orientation of the chiral condensate is not fixed, but diffuses in time due to thermal noise. Indeed, a stochastic variable with variance
| (30) |
should be added to (22a). Integrating this equation over the volume shows that the angular zero mode has a variance which increases in time
| (31) |
This result (which is presented in detail in App. A.2) relates the vev diffusion coefficient to the pion kinetic coefficients, . The diffusion rate decreases with increasing volume and is suppressed relative to the pion damping rate, , by one power of length, . When the magnetic field is non-zero the Fokker-Planck equation describing the motion of the chiral condensate on the three sphere features a rich interplay between Hamiltonian and diffusive dynamics, which is developed in App. A.2.
Turning to the conserved charges, the correlation function of the vector and axial-vector charges in the broken phase are intrinsically different. The axial charge is coupled through in equations of motion to the pions and its correlation function reflects this coupling (see App. A.1)
| (32) |
The vector charge continues to obey the diffusion equation with corresponding response functions
| (33) |
Separating the vector and axial vector response in the absence of explicit symmetry breaking is challenging, since the condensate forms in an arbitrary direction. Moreover, because of finite volume, this direction is not completely fixed, but slowly wanders along the coset manifold. This can be addressed in future work. For now we have simply computed the combined correlator
| (34) |
which is exhibited in Fig. 4 (Right). The result curves show a mix of exponential decay and oscillating pion waves.
It is striking how the hydrodynamic EFT and the pattern of chiral symmetry break essentially dictates the scaling dynamical response of “Model G” [5, 6]. A summary of the reasoning proves an overview of the next section.
- (i)
-
(ii)
At the boundary of applicability of the pion EFT , the pion frequency is . But, since the pions are part of an multiplet, the order parameter must inherit this dynamical timescale, , setting the dynamical critical exponent of Model G, . will be extracted in the restored phase, Fig. 5 (Left), and on the critical line, Fig. 6 (Left).
-
(iii)
Close to the critical point and for , the real and imaginary parts of should be commensurate if the critical point is characterized by a single time scale. This reasoning dictates the scaling of the pion damping coefficient, . The scaling of is exhibited in Fig. 7 (Left).
- (iv)
Finally, the vev diffusion coefficient is also consistent with these scalings. Taking the scaling of and we see the angular variance given in (31) grows as
| (35) |
At the critical point where , the angular variance increases as
| (36) |
which is again consistent with a universal dynamical critical timescale of with a common critical exponent of .


III Relaxation time and finite momenta dynamics
III.1 , restored phase: scaling of the correlation time
We first determine the order parameter relaxation time from the two-point function . Specifically, we define as the autocorrelation time of at zero momentum
| (37) |
which is motivated by an exponential decay, (in practice, we cutoff the integral at some and make sure the results are independent of this technicality). Qualitatively, the decorrelation of is characterized by a single timescale without significant structure.
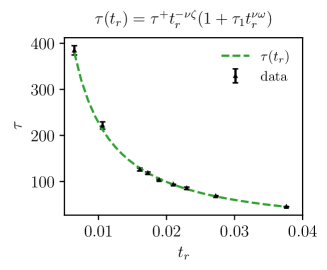

From scaling, we expect the correlation time to behave as
| (38) |
with the critical exponents , , and given in Table 2 in App. B. The resulting fit (with the exponents fixed) is shown in Fig. 5 and we find
| (39) | ||||
| (40) |
The growth of near the is nicely consistent with .
The diffusion coefficient of the charges is also expected to show dynamical critical scaling, but since the charges are conserved, the coefficient has to be extracted from finite momentum correlators. In particular, we expect the vector correlator in the restored phase to behave as
| (41) |
as discussed in the previous section. Similar to the order parameter case, we have the relation
| (42) |
which we use in practice to extract from our data. It is important that the correlator be well described by an exponential, which is clearly seen in Fig. 2.
Again, we introduce a cutoff and make sure the results are independent of this choice. As discussed above, we expect to be comparable at the boundary of applicability of the diffusive description, . This means that the diffusion coefficient should scale with the correlation length as, .
The critical behavior of appears to be weak and its regular part cannot be neglected. To take this into account, we add a constant to our fit
| (43) |
In an abuse of notation, here is the renormalized diffusion coefficient far above , which we determine independently by running our simulations without the coupling to the order parameter, leading to
| (44) |
This parameter is different from the bare lattice parameter (also called ) which controls the Metropolis updates of the charge at the scale of the lattice spacing (see [1] in Appendix A.c for further details). Fixing and fitting and in (43), we get the following determination of the non-universal amplitudes
| (45) | ||||
| (46) |
is small as was anticipated based on a one loop calculation using mean field propagators [27].
Using the non-universal amplitude from the correlation length determined in App. B.1, we can combine these results into a universal dynamical amplitude ratio
| (47) |
which numerically encodes the coupling between the charge diffusion and the order parameter relaxation at criticality. The universal dynamical ratio presented here is new and will prove useful to any future study which realizes the critical dynamics of Model G.
III.2 The critical line


We next study the dynamics on the critical line, and . As in the previous section we define the order parameter relaxation time from the correlation of the field
| (48) |
The results for as a function of the magnetic field are shown in Fig. 6, and are fit with the expected scaling form
| (49) |
with fixed exponents , , and given in Table 2 of App. B, and fitted parameters
| (50) | ||||
| (51) |
As in the restored phase, the subleading term with exponent is necessary to have a reasonable fit compatible with the expected dynamical exponent, .
Similarly, the diffusion coefficient is defined in the same way as in the restored phase
| (52) |
and we adopt an analogous strategy and functional form to fit the dependence of on the correlation length
| (53) |
As in the previous section, is the regular part of the diffusion coefficient and is extracted from our diffusion only runs. The fit results are shown in Fig. 6 and the fit parameters are
| (54) | ||||
| (55) |
The singular part of the diffusion coefficient diverges next to the critical point with the expected exponent and the subleading correction improves the quality of the fit. Including the regular part of the diffusion coefficient is crucial to extracting the scaling of with , since the critical amplitude is small, as anticipated in the one loop computation in [27].
The results for the order parameter and the diffusion coefficient can be concisely recast as a universal amplitude ratio
| (56) |
where is the amplitude associated with the longitudinal correlation length and is determined in App. B.2. Note that within numerical errors the dynamical ratio on the critical line matches the one in the restored phase (47).
III.3 and the broken phase
Our aim in this section is to extract the matching coefficients of the pion hydrodynamic EFT by studying the momentum dependence of the correlators and analyzing the pion dispersion curve. To this end, we study for various and and analyze the two lowest non-zero momentum modes, and . We then perform some fits using the hydro prediction (25) and extract the parameters and . and are subsequently extrapolated to infinite volume using the forms
| (57a) | ||||
| (57b) | ||||
with , , , and as parameters. As discussed in Sect. II.5, finite volume corrections to the dynamics of the Goldstone modes scale inversely with the linear extent of the lattice and are therefore important to control. Including and as fit parameters captures this characteristic volume dependence and proved crucial to reliably extracting and from this analysis. The fitting procedure, together with other systematic checks, are presented in detail in App. C.
In the static case, a finite volume pion EFT was developed many years ago by Hasenfratz and Leutwyler and can be used to determine the first correction to the chiral condensate analytically [47]. We used their expansion in App. B.3 to determine velocity and, as we show below, the result agrees with the dynamic fit using (57). In Sect. II.5 we have taken the first steps in developing a real time finite volume analog of their work by deriving the vev diffusion coefficient in (31) and a corresponding forced Fokker-Planck equation on the coset manifold in App. A.2. But, a more complete analysis is left for future work.


Knowing and , we can proceed further and study their scaling with temperature. We start with a study of the critical behavior of , shown on the left hand side of Fig. 7. We use the following scaling ansatz
| (58) |
and obtain the following fit parameters
| (59) | ||||
| (60) | ||||
| (61) |
with a of , which is mostly driven by the large fluctuation around . The exponents , and the subleading were held fixed. As in all the previous cases, including a subleading correction and a regular part is necessary to obtain a precise fit. We did not find a way to independently fix the regular part for this analysis. This leads to a degeneracy between and , resulting in large errors for both of these parameters. This problem does not affect the extracted value of the leading amplitude, .
The Goldstone velocity is shown on the right hand side of Fig. 7. The data are fitted with the expected scaling form,
| (62) |
with and fixed, yielding
| (63) | ||||
| (64) |
The is with degrees of freedom. The relatively large value of the is due to the very high precision of our data. It is driven by the points farther away from the critical point and probably reflects the fact that our data are sensitive to sub-subleading corrections. We also show the determination of obtained from the static analysis in App. B.3. The analysis makes use of (28) but exploits the known finite volume analysis of Hasenfratz and Leutwyler [47]. The agreement between the static analysis and the fits to the real time correlation functions is remarkable and is a highly non-trivial confirmation of the low-energy EFT.
Ideally, at this point we would complete this study by determining the critical amplitude of the diffusion coefficient in the broken phase. However, because the amplitude is small, and because finite volume corrections are only suppressed by , we were unable to unambiguously extract this amplitude with the current dataset and our current understanding of finite volume corrections. We can clearly see the diffusive behavior, but the coefficient is constant within uncertainty.
IV Discussion
In this work, we performed an extensive study of the finite momentum dynamics of “Model G”, the critical dynamical model corresponding to two-flavor QCD in the chiral limit. Across all different phases of the theory, we exhibited striking agreement between theoretical predictions and our full-fledged numerical simulations. In particular, although the critical amplitude is small, we showed that the critical contribution to the vector diffusion coefficient scales with the correct dynamical critical exponent, both in the restored phase and along the critical line. After additionally extracting the critical relaxation time of the order parameter (which also scales appropriately), we recast these new results as universal dynamical amplitude ratios , , which reflect the coupling between the order parameter and the diffusive dynamics. Next, we took on the challenge of studying the finite momentum dynamics of the broken phase at zero magnetic field. Because the simulation is at finite volume, the chiral condensate is not constant but wanders through the coset manifold at a finite rate. We show that the diffusion coefficient for this process is consistent with dynamical scaling and is determined by the transport coefficients of a pion hydrodynamic EFT, which we review in Sect. II.5. Despite this subtlety, we were able to clearly observe the critical pion dynamics. The culmination of this part is presented in Fig. 7, which compares the pion dispersion relation measured in this work to the scaling predictions for the pion damping rate and velocity close to the critical point. The agreement is striking and further exemplifies the precision of our numerics.
Future directions to be explored are diverse. One avenue is to refine the treatment of finite volume effects in the broken phase by developing a finite volume real time EFT for the dynamics of the chiral condensate in the spirit of [47] and [55]. The first steps in this direction are presented in App. A.2, which worked out a Fokker-Planck description for the dissipative and Hamiltonian dynamics of the condensate on the coset manifold. This provides a real time description of QCD in the -regime, suggesting connections with Random Matrix Theory [45].
A more physically motivated direction is the study of the Kibble-Zurek dynamics of this model. Physical systems are typically not tuned at their physical point, but traverse the phase transition, with their relevant coupling varying at a finite rate. This finite rate competes with the critical relaxation rate of the system and prevents the correlation length from diverging. When transiting from the restored to the broken phase, this competition results in the formation of finite-length domains with different values of the condensate. A careful examination of this phenomenon, both in the presence and absence of explicit symmetry breaking, will be crucial to any future phenomenological predictions. We plan to utilize the precision measurements presented here and in our prior work [1] to study this phenomenon in detail.
Acknowledgements
The authors are grateful to J. Pawlowski, F. Rennecke, S. Schlichting and L. von Smekal for interesting discussions and A. Soloviev and J. Bhambure for their collaboration on this work. This work was supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, Grants Nos. DE-SC0012704 (AF) and DE-FG88ER41450 (DT).
Appendix A Hydrodynamics
This appendix extends the discussion of the hydrodynamics of the broken phase given in Sect. II.5. We will keep the temperature explicit in this section, following the practice of II.5.
A.1 Correlation functions from the pion EFT
Here we will review the temporal correlation functions which arise the from pion hydro equations of motion, (22), but include the explicit symmetry breaking term and noise. Although these correlators are limits of the mean field results derived in [27], they transcend mean field and follow directly from the hydrodynamic equations of motion.
The hydrodynamic equations (see Sect. II.5) for the phase and axial charge read
| (65a) | ||||
| (65b) | ||||
| which follows from the Poisson bracket between the phase and the charge, . The vector charge remains diffusive | ||||
| (65c) | ||||
The noise added to the right-hand-side of Eq. (65) has variances given by the Fluctuation-Dissipation Theorem (FDT)
| (66a) | ||||
| (66b) | ||||
| (66c) | ||||
where .
The equations are easily solved. For instance, we can Fourier transform in space and write the solution to the vector equation by integrating from up to (with )
| (67) |
The variance in the initial condition is determined from the free energy functional in (20) and reads
| (68) |
Alternatively one can integrate from past infinity to determine the initial condition:
| (69) |
Computing the variance of using the variance of the noise in (66c) reproduces (68), which demonstrates how the noise and dissipation work together in establishing the equilibrium state. By either method
| (70) |
An identical strategy can be used in the axial channel by finding the eigen functions of the system. As in the vector case, we Fourier transform in space and calculate response function. It is convenient to work with the vector of variables777For simplicity, will denote a single isospin component of these fields. where and . The static susceptibility is diagonal in these variables, and can be read off from the free energy written in (20)
| (71) |
As in the diffusion example, the static susceptibility sets the initial conditions for the subsequent evolution. The equations of motion take the form and eigen-values of are
| (72) |
The homogeneous solutions are . The full matrix of correlation functions
| (73) |
reads
| (74) |
with . In the body of the text this result is used in the massless limit in (25) and (32).
A.2 Diffusion of the chiral condensate on the coset manifold
A.2.1 Free diffusion on the three sphere
In a finite volume simulation the chiral condensate is not fixed but diffuses on the coset manifold. Let us examine this diffusion by analyzing the zero mode of the hydrodynamic equations of motion given in (65), but limiting the discussion to . In finite volume the fields take the form
| (75) | ||||
| (76) |
The axial charge is exactly conserved and there is no net charge in the box, and consequently the mode is zero for . Then, integrating (22a) over volume, the zero mode of satisfies a random walk
| (77) |
Solving for and computing its variance leads to (31), which is reproduced here for convenience
| (78) |
i.e. . The noise satisfies
| (79) |
The probability density satisfies the diffusion equation
| (80) |
The direction of the chiral condensate is labeled by a unit vector on the three sphere . We have parametrized this direction by three angles, , assuming they are small. The coordinates provide a local Cartesian coordinate patch for the three sphere close to the pole. In a general coordinate system the diffusion equation reads
| (81) |
where is the Laplacian on the sphere. More explicitly, a set of coordinates covering the three sphere is
| (82) |
where is approximately close to the north pole.
A.2.2 Explicit symmetry breaking, forced diffusion, and the -regime of QCD
When the symmetry is explicitly broken by a magnetic field, the axial charge must be reconsidered. In this case the zero modes satisfy the equations of motion
| (83) | ||||
| (84) |
where the statistics of are given in (79). The variables and are canonical conjugates . To illustrate the structure of these equations we introduce a traditional notation
| (85) |
and the equations of motion are written
| (86) | ||||
| (87) |
Here and are the inverse temperature and volume respectively, and is the diffusion coefficient introduce earlier. Finally the Hamiltonian for the zero modes is
| (88) |
The Fokker-Planck equation for the phase space probability density follows from the Langevin dynamics and reads [56, 57, 58]
| (89) |
We emphasize that the canonical measure for the probability density is invariant under canonical change of coordinates.
We have worked with a set of spatial coordinates, which parametrize a region close to the pole of the three sphere by Cartesian coordinates. We then make a canonical change of variables to the polar coordinates given in (82). The Hamiltonian is generalized to include larger angles and reads
| (90) |
where is the metric of the sphere in (82). Here we used the original free energy in (3) and the Gell-Mann, Oakes, Renner relation to deduce the potential for the zero mode
| (91) |
The change of coordinates leads to the Fokker-Planck equation in its final form
| (92) |
where is the covariant derivative on the three sphere.
It is straightforward to see that the steady state solution to this equation is the equilibrium probability distribution
| (93) |
If the momenta are of no interest they can be integrated over yielding
| (94) |
which is consistent with the partition functions discussed in [47].
It is satisfying that the dissipative dynamics of the finite volume chiral condensate on the three sphere is controlled by the (infinite volume) pion pole mass and damping coefficient. Indeed, the Fokker-Planck equation provides a detailed real time picture of the so called “epsilon” regime of QCD. In this regime the quark mass is very small, but is of order unity. The thermodynamics of this regime has been extensively studied using Random Matrix Theory and chiral perturbation theory (see [45] for an overview). It would be interesting to pursue this connection further.
Appendix B Static measurements in the model
In this appendix we determine the correlation length and the magnetic susceptibility in the restored phase and along the critical line. In particular, their non-universal critical amplitudes serve to define universal ratios, including the novel dynamical ones introduced in the main text. We also determine the pion constant using static measurements. For convenience we collect the critical exponents used in this work in Table 2.
| exponent | definition | value | Ref. |
| 0.380(2) | [12] | ||
| 0.7377(41) | [12] | ||
| 1.4531(104) | [12] | ||
| 4.824(9) | [12] | ||
| 0.4024(2) | [12] | ||
| 0.7927(4) | [12] | ||
| 0.755(5) | [46] | ||
| [3] |
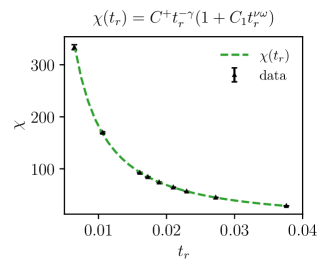
B.1 Restored phase
The magnetic susceptibility in the restored phase is defined as
| (95) |
and the zero momentum limit is notated with
| (96) |
A standard estimator of the correlation length is the so-called “second-moment correlation length” [46], computed as
| (97) |
with the susceptibility of the first Fourier mode
| (98) |
We fit their dependence on the reduced temperature to
| (99) | ||||
| (100) |
The exponent is the first subleading scaling exponent. To perform the fit, we fix , and to the values presented in Tab. 2 and fit , , and . The fits are presented in Fig. 8. We obtain
| (101) |
The chi-square for the fit of the correlation length is and the one for the susceptibility is . These values, together with the value the non-universal value for the magnetization in the restored phase
| (102) |
that was extracted in Ref. [1]888Note an unfortunate misprint. Equation (29) in the published version should read . The then quoted parameters and lead to and .
| (103) |
allow us to compute the universal ratio [59]
| (104) |
This value is indeed compatible with the of [59].

B.2 Critical line
At a non-zero magnetic field the magnetization will be parallel to the magnetic field. Then it is natural to define and measure the longitudinal and transverse susceptibilities:
| (105) | ||||
| (106) |
The static susceptibilities are shown in Fig. 9. As a fitting function, we chose the scaling prediction with the first subleading correction
| (107) |


To extract the correlation length in the longitudinal and the transverse directions we measure the second-moment correlation length as in (97) with
| (108) | ||||
| (109) |
The scaling prediction fixes the fitting function as
| (110) | ||||
| (111) |
and the result of the fit is shown in Fig. 10.


The universal ratio is consistent with the more precise estimate done in [59].
B.3 Broken phase and the pion velocity
Our goal in this appendix is to extract the infinite volume chiral condensate and pion velocity by analyzing static correlators below the critical point at . The resulting parameterization of the velocity is shown in Fig. 7 (Right). We will use the magnetization
| (112) |
the static correlation function , and their their dependence on volume to extract and in the infinite volume limit.
In infinite volume the magnetization remains constant in time and determines the chiral condensate
| (113) |
Here is an arbitrary unit vector on the three-sphere characterizing the orientation of the condensate. However, in any finite volume
| (114) |
since the condensate orientation vector stochastically explores the in time – see App. A.2.
One way to extract is to look at the fluctuations of , evaluating , which is approximately at large volumes. The leading deviation of from at finite volume comes from the fluctuations of long wavelength Goldstone modes and can be neatly analyzed with a Euclidean pion effective theory [47, 60] In the chiral limit the only parameter of the EFT is the pion constant . When a finite magnetic field is included the chiral condensate is also a parameter.
Apart from a slightly different fitting procedure, the current determination of simply repeats the analysis done in our earlier work for the larger lattices and datasets used here [1]. The expansion relating and takes the form [47, 1]
| (115) |
and is valid for . The numerical coefficients are known analytically in terms of “shape coefficients” and , but are of no interest here.
To determine the chiral condensate, we plotted versus at fixed temperature, and made various fits with (115) to determine and . We estimated the systematic uncertainty in the extracted values of by adding a term to the fit form and comparing to a fit based on (115). Except for the point closest to the systematic uncertainty is smaller than our statistical uncertainty, which would not have been the case if only the first term in the expansion had been used.
Our results for are shown in the right panel of Fig. 11, This is fit with the functional form
| (116) |
with fit parameters , . The results for the vev amplitude and subleading corrections are compatible with our previous results. For comparison, we also show the fit results for the first term . Clearly, for precision work, the subleading corrections are important in the temperature range we are considering.
The decay constant of the pion EFT can be extracted using similar methods The correlation function of the scalar field at small wavenumbers
| (117) |
is dominated by the massless Goldstone mode. Recalling eq. (28) with , the correlation function takes the form
| (118) |
to leading order in the pion EFT. However, there are important corrections to this result stemming from the finite system size, which are of order and are captured by the leading order pion EFT. Short distance correlations of order and smaller lead to higher derivative terms in the pion EFT, which are not included. Naturally, these terms become increasingly important near the critical point. Following the perturbative expansion of Hasenfratz and Leutwyler the correction takes the form
| (119) |
where is a “shape coefficient” reflecting the fluctuations of pions in a cubic box. Numerically for and :
| (120) |
To extract we plotted for the first Fourier mode as a function of system size and fitted the result for and using (120). The subleading correction in (120) was treated as a free parameter, although it is broadly consistent with the extracted above and the determined here.
The data on are shown in Fig. 11. Asymptotically, should behave as
| (121) |
where is a critical exponent. We are unable to extract from our measurements. Instead, we have simply fit a form
| (122) |
with and , which gives a heuristic parametrization of the results shown in the figure. There is a hint in the data that is non-zero.


Given the fit results for in (116) and (122) for we can extract the velocity
| (123) |
The uncertainty is dominated by the contribution from as (which is nearly unity) in total provides a ten percent correction. In Fig. 11 we have varied the fit parameters in the range allowed by the fits to deduce the static velocity and its uncertainty.
Appendix C Axial channel systematics in the broken phase
We record in this appendix our systematic analysis leading to the extraction of and in the broken phase.
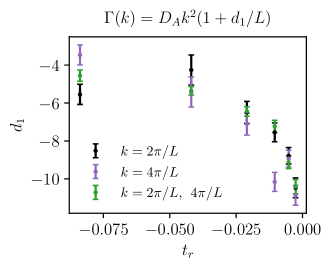
To validate the fitting form (57)
| (124) | ||||
| (125) |
and the specific dependence on the size of the axial diffusion coefficient , we fit the damping coefficient as function of the reduce temperature using three different datasets: , and the combined sample. Figure 12 shows the results obtained for and the leading volume correction across the three different datasets. The consistency of the fit among the different datasets and the values of exemplify the importance of the size-dependent term in (57) in the axial diffusion coefficient. Conversely, the remaining systematic dispersion between the different datasets can be considered as an evaluation of the remaining systematic errors.
The same strategy is adopted for the extraction of the parameter for the dispersion curves, that is fitted as
| (126) |
where the quadratic term was needed to improve the quality of the fit. In Figure 13 we show the results for the coefficient and . We see that in this case, the systematic errors are smaller and that the fit agrees very well across all different datasets.
Let us conclude this appendix by commenting on our assessment of statistical errors for this analysis. We subdivided each simulation in the time direction into blocks and fit each block independently. We then used the mean and the standard error of this set of block fits as an estimator for the best fit parameters and their statistical error.



References
- Florio et al. [2022] A. Florio, E. Grossi, A. Soloviev, and D. Teaney, Dynamics of the critical point in QCD, Phys. Rev. D 105, 054512 (2022), arXiv:2111.03640 [hep-lat] .
- Hohenberg and Halperin [1977] P. C. Hohenberg and B. I. Halperin, Theory of Dynamic Critical Phenomena, Rev. Mod. Phys. 49, 435 (1977).
- Rajagopal and Wilczek [1993] K. Rajagopal and F. Wilczek, Static and dynamic critical phenomena at a second order QCD phase transition, Nucl. Phys. B399, 395 (1993), arXiv:hep-ph/9210253 [hep-ph] .
- Son [2000] D. T. Son, Hydrodynamics of nuclear matter in the chiral limit, Phys. Rev. Lett. 84, 3771 (2000), arXiv:hep-ph/9912267 [hep-ph] .
- Son and Stephanov [2002a] D. T. Son and M. A. Stephanov, Real time pion propagation in finite temperature QCD, Phys. Rev. D66, 076011 (2002a), arXiv:hep-ph/0204226 [hep-ph] .
- Son and Stephanov [2002b] D. T. Son and M. A. Stephanov, Pion propagation near the QCD chiral phase transition, Phys. Rev. Lett. 88, 202302 (2002b), arXiv:hep-ph/0111100 [hep-ph] .
- Pisarski and Wilczek [1984] R. D. Pisarski and F. Wilczek, Remarks on the Chiral Phase Transition in Chromodynamics, Phys. Rev. D 29, 338 (1984).
- Wilczek [1992] F. Wilczek, Application of the renormalization group to a second order QCD phase transition, Int. J. Mod. Phys. A 7, 3911 (1992), [Erratum: Int.J.Mod.Phys.A 7, 6951 (1992)].
- Toussaint [1997] D. Toussaint, Scaling functions for O(4) in three-dimensions, Phys. Rev. D 55, 362 (1997), arXiv:hep-lat/9607084 .
- Engels and Vogt [2010] J. Engels and O. Vogt, Longitudinal and transverse spectral functions in the three-dimensional O(4) model, Nucl. Phys. B 832, 538 (2010), arXiv:0911.1939 [hep-lat] .
- Engels and Karsch [2012] J. Engels and F. Karsch, The scaling functions of the free energy density and its derivatives for the 3d O(4) model, Phys. Rev. D 85, 094506 (2012), arXiv:1105.0584 [hep-lat] .
- Engels and Karsch [2014] J. Engels and F. Karsch, Finite size dependence of scaling functions of the three-dimensional O(4) model in an external field, Phys. Rev. D 90, 014501 (2014), arXiv:1402.5302 [hep-lat] .
- Butti et al. [2003] A. Butti, A. Pelissetto, and E. Vicari, On the nature of the finite temperature transition in QCD, JHEP 08, 029, arXiv:hep-ph/0307036 .
- Braun and Klein [2009] J. Braun and B. Klein, Finite-Size Scaling behavior in the O(4)-Model, Eur. Phys. J. C 63, 443 (2009), arXiv:0810.0857 [hep-ph] .
- Braun et al. [2011] J. Braun, B. Klein, and P. Piasecki, On the scaling behavior of the chiral phase transition in QCD in finite and infinite volume, Eur. Phys. J. C 71, 1576 (2011), arXiv:1008.2155 [hep-ph] .
- Braun et al. [2012] J. Braun, B. Klein, and B.-J. Schaefer, On the Phase Structure of QCD in a Finite Volume, Phys. Lett. B 713, 216 (2012), arXiv:1110.0849 [hep-ph] .
- Braun et al. [2020] J. Braun, W.-j. Fu, J. M. Pawlowski, F. Rennecke, D. Rosenblüh, and S. Yin, Chiral Susceptibility in (2+1)-flavour QCD, (2020), arXiv:2003.13112 [hep-ph] .
- Ding et al. [2019] H. T. Ding et al. (HotQCD), Chiral Phase Transition Temperature in ( 2+1 )-Flavor QCD, Phys. Rev. Lett. 123, 062002 (2019), arXiv:1903.04801 [hep-lat] .
- Kotov et al. [2021] A. Y. Kotov, M. P. Lombardo, and A. Trunin, QCD transition at the physical point, and its scaling window from twisted mass Wilson fermions, Phys. Lett. B 823, 136749 (2021), arXiv:2105.09842 [hep-lat] .
- Cuteri et al. [2021] F. Cuteri, O. Philipsen, and A. Sciarra, On the order of the QCD chiral phase transition for different numbers of quark flavours, JHEP 11, 141, arXiv:2107.12739 [hep-lat] .
- Kaczmarek et al. [2020] O. Kaczmarek, F. Karsch, A. Lahiri, L. Mazur, and C. Schmidt, QCD phase transition in the chiral limit (2020) arXiv:2003.07920 [hep-lat] .
- Nijs et al. [2021] G. Nijs, W. van der Schee, U. Gürsoy, and R. Snellings, Transverse Momentum Differential Global Analysis of Heavy-Ion Collisions, Phys. Rev. Lett. 126, 202301 (2021), arXiv:2010.15130 [nucl-th] .
- Mazeliauskas and Vislavicius [2020] A. Mazeliauskas and V. Vislavicius, Temperature and fluid velocity on the freeze-out surface from , , spectra in pp, p-Pb and Pb-Pb collisions, Phys. Rev. C 101, 014910 (2020), arXiv:1907.11059 [hep-ph] .
- Devetak et al. [2020] D. Devetak, A. Dubla, S. Floerchinger, E. Grossi, S. Masciocchi, A. Mazeliauskas, and I. Selyuzhenkov, Global fluid fits to identified particle transverse momentum spectra from heavy-ion collisions at the Large Hadron Collider, JHEP 06, 044, arXiv:1909.10485 [hep-ph] .
- ALI [2018] Expression of Interest for an ALICE ITS Upgrade in LS3 (2018).
- Grossi et al. [2020] E. Grossi, A. Soloviev, D. Teaney, and F. Yan, Transport and hydrodynamics in the chiral limit, Phys. Rev. D 102, 014042 (2020), arXiv:2005.02885 [hep-th] .
- Grossi et al. [2021] E. Grossi, A. Soloviev, D. Teaney, and F. Yan, Soft pions and transport near the chiral critical point, Phys. Rev. D 104, 034025 (2021), arXiv:2101.10847 [nucl-th] .
- Berges et al. [2010] J. Berges, S. Schlichting, and D. Sexty, Dynamic critical phenomena from spectral functions on the lattice, Nucl. Phys. B 832, 228 (2010), arXiv:0912.3135 [hep-lat] .
- Täuber [2017] U. C. Täuber, Phase Transitions and Scaling in Systems Far from Equilibrium, Ann. Rev. Condensed Matter Phys. 8, 185 (2017), arXiv:1604.04487 [cond-mat.stat-mech] .
- Schlichting et al. [2020] S. Schlichting, D. Smith, and L. von Smekal, Spectral functions and critical dynamics of the model from classical-statistical lattice simulations, Nucl. Phys. B 950, 114868 (2020), arXiv:1908.00912 [hep-lat] .
- Schweitzer et al. [2020] D. Schweitzer, S. Schlichting, and L. von Smekal, Spectral functions and dynamic critical behavior of relativistic theories, Nucl. Phys. B 960, 115165 (2020), arXiv:2007.03374 [hep-lat] .
- Schweitzer et al. [2021] D. Schweitzer, S. Schlichting, and L. von Smekal, Critical dynamics of relativistic diffusion, (2021), arXiv:2110.01696 [hep-lat] .
- Schaefer and Skokov [2022] T. Schaefer and V. Skokov, Dynamics of non-Gaussian fluctuations in model A, Phys. Rev. D 106, 014006 (2022), arXiv:2204.02433 [nucl-th] .
- Chattopadhyay et al. [2023] C. Chattopadhyay, J. Ott, T. Schaefer, and V. Skokov, Dynamic scaling of order parameter fluctuations in model B, (2023), arXiv:2304.07279 [nucl-th] .
- Son and Stephanov [2004] D. T. Son and M. A. Stephanov, Dynamic universality class of the QCD critical point, Phys. Rev. D70, 056001 (2004), arXiv:hep-ph/0401052 [hep-ph] .
- Canet et al. [2003] L. Canet, B. Delamotte, D. Mouhanna, and J. Vidal, Nonperturbative renormalization group approach to the Ising model: A Derivative expansion at order partial**4, Phys. Rev. B 68, 064421 (2003), arXiv:hep-th/0302227 .
- Benitez et al. [2009] F. Benitez, J. P. Blaizot, H. Chate, B. Delamotte, R. Mendez-Galain, and N. Wschebor, Solutions of renormalization group flow equations with full momentum dependence, Phys. Rev. E 80, 030103 (2009), arXiv:0901.0128 [cond-mat.stat-mech] .
- De Polsi et al. [2021] G. De Polsi, G. Hernández-Chifflet, and N. Wschebor, Precision calculation of universal amplitude ratios in O(N) universality classes: Derivative expansion results at order O(4), Phys. Rev. E 104, 064101 (2021), arXiv:2109.14731 [cond-mat.stat-mech] .
- Roth and von Smekal [2023] J. V. Roth and L. von Smekal, Critical dynamics in a real-time formulation of the functional renormalization group, (2023), arXiv:2303.11817 [hep-ph] .
- Floerchinger [2012] S. Floerchinger, Analytic Continuation of Functional Renormalization Group Equations, JHEP 05, 021, arXiv:1112.4374 [hep-th] .
- Floerchinger [2016] S. Floerchinger, Variational principle for theories with dissipation from analytic continuation, JHEP 09, 099, arXiv:1603.07148 [hep-th] .
- Dupuis et al. [2021] N. Dupuis, L. Canet, A. Eichhorn, W. Metzner, J. M. Pawlowski, M. Tissier, and N. Wschebor, The nonperturbative functional renormalization group and its applications, Phys. Rept. 910, 1 (2021), arXiv:2006.04853 [cond-mat.stat-mech] .
- Cao et al. [2022] X. Cao, M. Baggioli, H. Liu, and D. Li, Pion dynamics in a soft-wall AdS-QCD model, JHEP 12, 113, arXiv:2210.09088 [hep-ph] .
- Flory et al. [2022] M. Flory, S. Grieninger, and S. Morales-Tejera, Critical and near-critical relaxation of holographic superfluids, (2022), arXiv:2209.09251 [hep-th] .
- Damgaard [2011] P. H. Damgaard, Chiral Random Matrix Theory and Chiral Perturbation Theory, J. Phys. Conf. Ser. 287, 012004 (2011), arXiv:1102.1295 [hep-ph] .
- Hasenbusch [2022] M. Hasenbusch, Three-dimensional -invariant models at criticality for , Phys. Rev. B 105, 054428 (2022), arXiv:2112.03783 [hep-lat] .
- Hasenfratz and Leutwyler [1990] P. Hasenfratz and H. Leutwyler, Goldstone Boson Related Finite Size Effects in Field Theory and Critical Phenomena With O() Symmetry, Nucl. Phys. B 343, 241 (1990).
- Armas et al. [2021] J. Armas, A. Jain, and R. Lier, Approximate symmetries, pseudo-Goldstones, and the second law of thermodynamics, (2021), arXiv:2112.14373 [hep-th] .
- Delacrétaz et al. [2022] L. V. Delacrétaz, B. Goutéraux, and V. Ziogas, Damping of Pseudo-Goldstone Fields, Phys. Rev. Lett. 128, 141601 (2022), arXiv:2111.13459 [hep-th] .
- Ammon et al. [2019] M. Ammon, M. Baggioli, and A. Jiménez-Alba, A Unified Description of Translational Symmetry Breaking in Holography, JHEP 09, 124, arXiv:1904.05785 [hep-th] .
- Amoretti et al. [2019] A. Amoretti, D. Areán, B. Goutéraux, and D. Musso, Universal relaxation in a holographic metallic density wave phase, Phys. Rev. Lett. 123, 211602 (2019), arXiv:1812.08118 [hep-th] .
- Donos et al. [2021] A. Donos, P. Kailidis, and C. Pantelidou, Dissipation in holographic superfluids, JHEP 09, 134, arXiv:2107.03680 [hep-th] .
- Ammon et al. [2022] M. Ammon, D. Arean, M. Baggioli, S. Gray, and S. Grieninger, Pseudo-spontaneous symmetry breaking in hydrodynamics and holography, JHEP 03, 015, arXiv:2111.10305 [hep-th] .
- Baggioli and Goutéraux [2023] M. Baggioli and B. Goutéraux, Colloquium: Hydrodynamics and holography of charge density wave phases, Rev. Mod. Phys. 95, 011001 (2023), arXiv:2203.03298 [hep-th] .
- Yao and Täuber [2022] L. H. Yao and U. C. Täuber, Critical dynamics of the antiferromagnetic O(3) nonlinear sigma model with conserved magnetization, Phys. Rev. E 105, 064128 (2022), arXiv:2204.11145 [cond-mat.stat-mech] .
- Kittel [1961] C. Kittel, Elementary Statistical Physics (Wiley, 1961).
- Arnold [2000a] P. B. Arnold, Symmetric path integrals for stochastic equations with multiplicative noise, Phys. Rev. E 61, 6099 (2000a), arXiv:hep-ph/9912209 .
- Arnold [2000b] P. B. Arnold, Langevin equations with multiplicative noise: Resolution of time discretization ambiguities for equilibrium systems, Phys. Rev. E 61, 6091 (2000b), arXiv:hep-ph/9912208 .
- Engels et al. [2003] J. Engels, L. Fromme, and M. Seniuch, Correlation lengths and scaling functions in the three-dimensional O(4) model, Nucl. Phys. B 675, 533 (2003), arXiv:hep-lat/0307032 .
- Dimitrovic et al. [1991] I. Dimitrovic, P. Hasenfratz, J. Nager, and F. Niedermayer, Finite size effects, Goldstone bosons and critical exponents in the d = 3 Heisenberg model, Nucl. Phys. B 350, 893 (1991).