Dynamics of Symmetry-Protected Topological Matter on a Quantum Computer

Miguel Mercado [email protected] Department of Physics and Astronomy, University of Southern California, Los Angeles, CA 90089-0484 Kyle Chen Pritzker School of Molecular Engineering, The University of Chicago, Chicago, IL 60637 Parth Hemant Darekar Department of Electrical and Computer Engineering, University of Southern California, Los Angeles, CA 90089-0484 Department of Electrical and Computer Engineering, University of Maryland, College Park, Maryland 20742 Aiichiro Nakano Collaboratory for Advanced Computing and Simulations, University of Southern California, Los Angeles, CA 90089-0484 Rosa Di Felice Department of Physics and Astronomy, University of Southern California, Los Angeles, CA 90089-0484 CNR Institute of Nanoscience, Modena, Italy Stephan Haas Department of Physics and Astronomy, University of Southern California, Los Angeles, CA 90089-0484

Abstract

Control of topological edge modes is desirable for encoding quantum information resiliently against external noise. Their implementation on quantum hardware, however, remains a long-standing problem due to current limitations of circuit depth and noise, which grows with the number of time steps. By utilizing recently developed constant-depth quantum circuits in which the circuit depth is independent of time, we demonstrate successful long-time dynamics simulation of bulk and surface modes in topological insulators on noisy intermediate-scale quantum (NISQ) processors, which exhibits robust signatures of localized topological modes. We further identify a class of one-dimensional topological Hamiltonians that can be readily simulated with NISQ hardware. Our results provide a pathway towards stable long-time implementation of topological quantum spin systems on present day quantum processors.

^†^†preprint: APS/123-QED

Introduction.—Understanding topological properties of matter is a current frontier of physics [1, 2, 3, 4, 5, 6, 7]. Chiral phenomena, in particular, have been ubiquitously sought after in recent years for their novel emergent behaviors which have been observed, for example, in acoustic and mechanical systems [8, 9, 10, 11, 12, 13, 14], photonics [15, 16, 17, 18, 19], and magnetic materials [20, 21, 22, 23, 24, 25]. Symmetry-protected topological (SPT) phases, the paradigmatic models for realizing such chiral states, are characterized by their protection via global symmetries which have become well-studied in the space-domain [26, 27, 28, 29, 30]. A consequence of topological symmetry protection is the predicted robustness of SPT phases against local noise and perturbations, opening avenues for foundational research and numerous device applications in quantum science [31, 32, 33, 34, 35], such as novel high-performance transistors [36, 37, 38], quantum sensors [39, 40], and protected room-temperature transport devices [41, 42, 43, 44].

Despite this enticing context, thorough investigation of chiral topological modes within the time-domain curiously remains ambiguous, especially within the context of open system time evolution [45, 46]. Understanding the role of topology in the dynamics of quantum systems therefore, is a timely endeavor, which - however - has been exceptionally challenging to realize and control due to the inherent difficulty of accessing sensitive many-body quantum states [47, 48, 49].

As intrinsically quantum platforms, a pioneering application of quantum computers is the physical simulation of many-body systems [50, 51, 52, 53, 54], where in special-use cases practical quantum advantage has recently been shown to be achievable [55]. Such is the potential of quantum simulation that topological physics is currently being explored using photonic simulators [56, 57, 58, 59, 60], ultracold atoms [61, 62, 63, 9, 64, 65], hybrid-quantum simulation [66], and periodically driven quantum simulators [67, 68, 69].

While these provide a promising route to investigate condensed matter systems, many-body interactions that would otherwise be intractable for analog quantum simulators are well suited for digital quantum simulation, which provides universal capability to realize any finite-dimensional local Hamiltonian using sequences of quantum circuits [54, 70, 71]. Although topological states have been prepared and observed using digital quantum simulation [72, 73, 74, 75, 76, 77, 78], the analysis of transient behavior of topological modes in the time-domain presents a particular set of challenges. A primary reason is the effect of read-out noise and gate-error rates, which have sharply limited reliable quantum simulation of interacting many-body systems [79].

The computational power and effectiveness of current noisy intermediate-scale quantum (NISQ) computers is restricted by the number and quality of qubits. In fact, NISQ-era qubits have short coherence times and high gate-error rates [80], which demand the requirement for noise mitigation and error correction schemes. Moreover, quantum simulations for generic Hamiltonians require that the circuit depth scales linearly at minimum with the number of simulation time steps, according to the No-Fast-Forwarding Theorem [81, 82, 83]. These restraints make prolonged time evolution of many-body systems exceedingly challenging for conventional approaches.

To date, a reliable method to realize the long-time dynamics of topological phases of matter using digital quantum simulation is not available due to the aforementioned limitations. Prior simulations are largely restricted in the number and width of time-step intervals, making the analysis of transient dynamics, which is non-negligible when interaction with the environment is present, unreachable.

We introduce a method to realize the long-time quantum dynamics of topological matter using contemporary quantum hardware, positioning NISQ computation as a favorable environment to probe novel phases of matter. In comparison to previous methods [75, 76, 72, 73, 74, 77, 78], which have been limited in the total time duration or restricted entirely to the space-domain, our protocol enables the quantum simulation of topological states in one spatial dimension nominally up to arbitrarily long times. We call to attention a subset of Hamiltonians with novel topological properties that are now tractable with this result. Its ability to predict physical results does not rely on employing readout error mitigation or post-processing techniques, though the output precision can be complemented by such techniques. By engineering interactions between qubits, we implement and analyze three different topologically non-trivial states. Specifically, we construct the desired topological phases via staggered coupling, using a topological mirror, and introducing a topological defect. We utilize the time-step compression of recently developed constant-depth quantum circuits [84, 85], which possess the key property that the depth required to execute a quantum simulation is constant with respect to the number of time steps compared to linear or exponential. This inherent feature of matchgates enables the construction of topological Hamiltonians as quantum circuits to be simulated for arbitrary time. This is achieved because the constituents of constant-depth circuits, matchgates, have the symmetric property that the product of two matchgates is itself a matchgate, allowing for the decomposition into native gates with only two CNOT gates, while conventionally three CNOT gates are needed. This reduction enables the Trotter error to be made negligible by breaking the simulation down into small time steps. We point out that while fixed-depth circuits were recently designed to map spin and fermionic models onto quantum hardware [85, 86], their physical implementation towards topological models and rigorous investigation of their experimental result has not yet been carried out. Subsequently, we provide an analysis of the long-time dynamics of bulk and edge modes, and observe that the topological modes are coherently stabilized in each case using our method, where transient data is clearly visible.

Dynamics of topological insulators as constant-depth circuits.—We simulate the time evolution of coupled SPT insulator systems using quantum circuits. In this approach, the non-trivial topology is introduced via locally varying nearest-neighbor couplings between lattice sites that host magnetic dipoles.

We implement the topological states using a 1D Quantum Spin Hamiltonian, given by

\mathcal{H}=-\sum_{i=1}^{N-1}J_{z,i}Z_{i}Z_{i+1}-h_{x}\sum_{i=1}^{N}X_{i},

(1)

where $Z_{i}$ , $X_{i}$ denote the spin-1/2 Pauli $z$ and $x$ matrices acting on qubit $i$ , $J_{z,i}$ denotes the $z$ -direction coupling between qubits $i$ and $i+1$ , and $h_{x}$ is an external magnetic field in the $x$ direction. By particular choices of $J_{z,i}$ , the signature bulk and edge modes of topological insulator systems emerge and are tunable; we extensively examine multiple cases. We note that while Eq. (1) presents a quantum Hamiltonian with couplings between qubits along the $z$ direction and external field in the $x$ direction, the model generalizes to couplings and fields along any direction, where nearest neighbor interactions are confined to two or less directions, and the external field acts along one perpendicular direction.

A schematic of the topological configurations is given in Fig. 1. In general, when the coupling $J^{\prime}$ is greater than $J$ , the system enters a topologically nontrivial regime, and exhibits protected topological modes that exist on the weakly-coupled edges of the system [87, 88, 89, 90, 91, 27, 92, 93, 94]. Fig. 1(a) shows a topological edge mode, which can be created and protected via alternating weak couplings $J$ and strong couplings $J^{\prime}$ in a chain. Fig. 1(b) shows a mirror configuration, which can be created by using weak couplings $J$ connecting the qubits on the edge, and strong couplings $J^{\prime}$ connecting the “bulk” qubits, thus creating edge modes at the two ends of the chain. Fig. 1(c) illustrates a topological defect, which can be created in the center of the chain by choosing strong couplings $J^{\prime}$ at the edges and weak couplings $J$ connecting the bulk qubits.

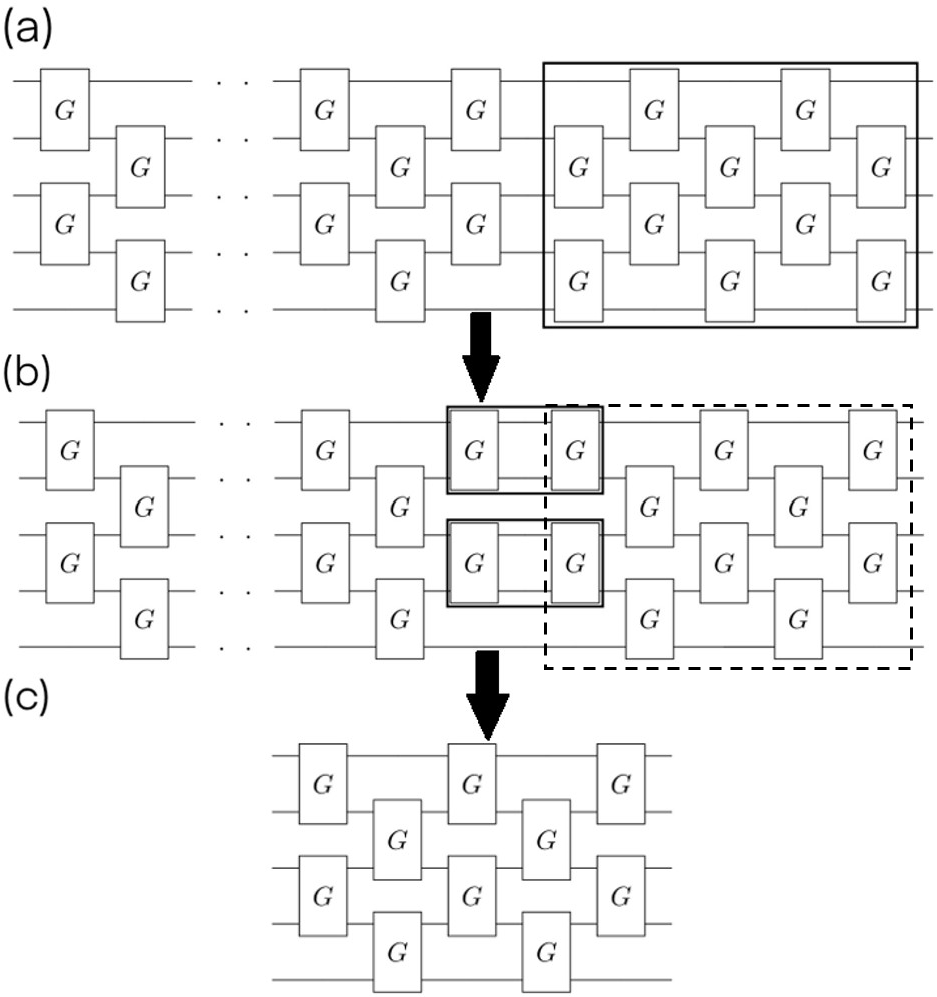
As a special class of quantum circuits, constant-depth circuits have a constant scaling rate in circuit depth with time step, as compared to conventional circuits or low-depth circuits which scale linearly or exponentially. This class of Hamiltonians thus embodies a nontrivial exception to the No-Fast-Forwarding Theorem [83, 96]. The time-step compression of constant-depth circuits follows directly from their intrinsic matchgate property, which utilizes symmetry to downfold the total amount of circuits needed to construct quantum algorithims on native gates.

According to this property, the product of two matchgates is also a matchgate, constituting an SU(2) Lie Algebra [84]. This allows the decomposition of a matchgate into native gates, which conventionally requires three CNOT gates, to be executed with only two CNOT gates with constant-depth circuits. Therefore, $N(N-1)$ CNOT gates are required to simulate a system with $N$ spins. This compression in resource requirement allows the Trotter error, which is proportional to the size of the time step, to be negligible, by breaking down the simulation into miniature time steps which can be repeated many times. We elaborate on this method in Sec. II of the Supplementary Material [95].

In Fig. 2, we illustrate the construction of constant-depth circuits for 5-qubit spin systems. We map SPT insulators into constant-depth circuits, splitting the total evolution into discretized time steps $\Delta t=0.1$ in units of the inverse applied magnetic field $\hbar/h_{x}$ following the convention $\hbar=1$ . In principle, one can continually reduce the Trotter error by breaking down the total simulation time into increasingly smaller time-step intervals.

In order to generate the circuits for these systems, we employ numerical optimization to identify optimal circuit parameters. This is accomplished by first computing the time evolution operator associated with each topological spin system, which defines a target matrix. After constructing the constant-depth circuit structure, which contains $N$ matchgate columns for a system with $N$ qubits, we compute its corresponding circuit matrix. Then, we generate optimized constant-depth circuits by minimizing the distance between the target and circuit matrix. This procedure is detailed in Sec. III of Supplementary Material [95]. We point out that generation of constant-depth circuits can be achieved independently of the optimization method used.

Realization on quantum hardware.—We implement the time-evolution of SPT insulator models using an IBM transmon-based quantum computer [97], demonstrating that topological physics can be coherently observed with ibmq_manila, a quantum processor with five qubits. Our experiments using five-qubit chains illustrate that the strength of topological effects in the many-body dynamics are predominantly dictated by the contrast between J and J’. Because of their intrinsic gap, the equilibration time of each topological model is only weakly dependent on system size [98]. Moreover, we expect exponentially fast convergence in system length of gapped states [99]; these two observations have been checked empirically using additional hardware calculations. As realized on NISQ processors, each model is subjected to environmental noise that is intrinsic to the quantum device itself [100], which exists independently from the noise of Trotter error-type which is mitigated by constant-depth circuits. We compare our results with classical simulations, using Exact Diagonalization to numerically solve the closed-system dynamics as ground truth (Sec. IV of the Supplementary Material [95]).

The IBM hardware results for the topological mirror case in Fig. 1(b) are shown in Fig. 3, where the $z$ -direction magnetization is reported for each qubit as a function of time, over the total open system evolution. Presented in the left panel of Fig. 3 is the real-space data obtained from the quantum hardware solid blue lines), while the right panel of Fig. 3 shows the corresponding power spectrum in frequency space generated by performing a Fourier Transform solid red lines. The experimental result is plotted against its respective closed system Fourier spectrum in dotted red lines for reference.

For this configuration, we expect strongly localized topological surface modes on both open ends of the quantum spin chain. Furthermore, since there is spatial mirror symmetry in the system parameters, qubits 1 and 5 should be equivalent, as well as qubits 2 and 4.

Indeed, the result obtained from the quantum hardware accurately corroborates these expectations. A clear signature of topological surface modes is evidenced by the strong temporal oscillations of the magnetization in qubits 1 and 5, translating into sharp low energy modes in the power spectrum, indicated by arrows in Fig. 3. Their frequency depends on the choice of Hamiltonian parameters $J,J^{\prime},h_{x}$ , whereas their lifetime is characterized by the damping rate $\gamma$ as in a fitting formula, $m(t)\propto\exp(-\gamma t)$ . We remark that in the complementary closed system calculation, this frequency is equivalent to the energy difference between pairs of eigenstates. These topological mode signatures are the salient feature preserved amidst noise in the hardware results. Constant-depth circuits have stabilized the SPT modes, producing longer-lived states at the edge of the system, which has not been observable with conventional quantum circuits (see Supplementary Fig. S13 [95]).

In contrast, the“bulk” qubits 2, 3, and 4 do not display any oscillations, in analogy with the equivalent closed quantum system dynamics [47] discussed in Sec. IV of the Supplementary Material [95]. Furthermore, we observe site dependent transient dynamics in the time window $t\in[0,4]$ , with the odd site qubits settling into their steady state markedly earlier than the even sites, as indicated by the black dots in the left panel of Fig. 3, which were obtained using the criteria for equilibration times of noisy finite systems outlined in Ref. [98], namely, when the expectation value of an observable approaches its average $\overline{\mathcal{A}}$ and begins fluctuating about it with fluctuations $\delta\mathcal{A}=\sqrt{\overline{\mathcal{A}^{2}}-\overline{\mathcal{A}}^{2}}$ . Here we choose a definition based on the physical reasoning that finite sized, gapped quantum states produce quasi-periodic dynamics, which is visible in the local magnetization. The orange lines are obtained by fitting the exponential damping function to the short-time data, indicating with the black star where this transient functional dependence does not apply anymore. The corresponding value of the local average magnetization $\overline{\langle\sigma^{z}_{i}\rangle}=\frac{1}{T}\int_{0}^{T}\langle\sigma^{z}_{i}(t)\rangle dt$ is plotted as the dotted green line. We conclude that the topological surface modes equilibrate rapidly and fluctuate robustly upon reaching their steady state, in contrast to the bulk qubits which undergo gradual temporal decay and require going out to much longer times to observe their full equilibration—underscoring the stabilizing effect of topology in the open quantum system dynamics. Finally, the observed large DC (zero energy) feature in the power spectrum is due to the polarization of the qubit spins along the $z$ -direction.

Moving to the other topological configurations shown in Figs. 1(a) and 1(c), we also find agreement between real-time evolution on NISQ hardware and the equivalent closed system quantum dynamics. Specifically, in the staggered coupling model of Fig. 1(a), a sharp amplitude in Fourier space is detected on the first qubit, which is weakly coupled with the bulk, indicating a long lived topological surface mode. In the topological defect case of Fig. 1(c), a strongly localized state with temporal low-frequency oscillation is observed on the center qubit, (Supplementary Material Sec. IIIB [95]). We add that the corresponding shot noise reported is a minor effect compared to the overall trend in the local magnetization, which is clear by isolating the small fluctuations from the local moving average of the magnetization of all qubits (see Supplementary Material Sec. IIID [95]).

We emphasize that the presented results are measured data on NISQ devices, without any noise mitigation or error correction techniques. Despite this, the constant-depth method measurably outperforms conventional Trotterization, in which each qubit undergoes rapid decay where noise due to large Trotter error scrambles discernable signatures in the data (see Supplementary Fig. S13 [95]). Using this method to isolate the Trotter error, our results show that topological phases exhibit robust dynamics when subjected to the intrinsic noise of quantum devices, which is unavoidable due to pervasive hardware defects or ambient interactions. Our study demonstrates that circuit compression techniques can be effectively used with available NISQ devices to study dynamics of novel phases of matter despite the known NISQ challenges of noise and limited system size.

Fast-forwardable topological models.—The results reported here are general and can be utilized to realize the long-time dynamics for a host of topological systems. We illustrate how to apply our method to probe topological phenomena in open systems where the environmental interaction is driven by the intrinsic noise of the gate-based quantum device and highlight a notable subset of models, pointing out experimentally accessible procedures to control non-trivial states. First, one can straightforwardly realize protected modes by manufacturing corresponding symmetries of a desired Hamiltonian $H$ through artificial design of couplings $J$ , demonstrated by models depicted in Fig 1. Particularly, the presence or absence of chiral symmetry $\mathcal{C}$ determines the existence of topological modes in SPT phases [27, 94, 101, 102, 103], which can be further categorized into chiral-symmetric Hamiltonians that maintain or break combinations of time-reversal $\mathcal{T}$ symmetry and particle-hole (charge-conjugation) $\mathcal{P}$ symmetry. It has been proven that quadratic Hamiltonians can be fast-forwarded [83], meaning that a system with $N$ spins requires only $N(N-1)$ CNOT gates to simulate. This follows from the fact that matchgates for quadratic Hamiltonians can be decomposed into native circuits requiring two CNOT gates. For further technical details, see Supplementary Material Sec. II [95].

Therefore, one can completely tune the presence and character of topological modes through our method by modulating interactions $J$ on two or less axes to realize discrete symmetries in $\mathcal{H}$ of particular interest, such as chiral symmetry $\mathcal{C}$ , which is then decomposed into matchgates. This can be written generally as $\mathcal{H}=c^{{\dagger}}Hc$ , where

H=\begin{pmatrix}A&B&\\ -B^{*}&-A^{*}&\end{pmatrix},

(2)

with arbitrary matrices $A$ , $B$ satisfying $A=A^{{\dagger}}$ and $B^{T}=-B$ , and $c^{\dagger}_{j}$ and $c_{j}$ denoting the fermionic creation and annihilation operators which define the column vector operator $c=(c_{1}\ldots c_{n}c^{{\dagger}}_{1}\ldots c^{{\dagger}}_{n})^{T}$ . obeying $U_{\mathcal{C}}^{-1}\mathcal{H}U_{\mathcal{C}}=-\mathcal{H}$ , where $U_{\mathcal{C}}$ is defined as the chiral symmetry operator, $\mathcal{C}=\mathcal{P}\cdot\mathcal{T}$ .

We argue that this opens many interesting directions in one dimension, particularly in studying open system dynamics of models in the AIII, BDI, CI, and DIII universality classes [102]. In higher dimensions, it has been shown that $n$ -band topological insulator Hamiltonians can be mapped to 1D hardcore boson chains by representing their single-particle hopping as an $n$ -particle hopping living on distinct sublattices of a 1D chain as shown in Ref. [76], which can be applied to generalize our method through application of matchgate symmetries. We point out that it has recently been shown that certain number-conserving bosonic Hamiltonians can also be fast-forwarded [96]. Another procedure to probe topological modes is to induce spatial localization within the lattice by modulating $J$ . This is exemplified by the model in Fig. 1(c), which realizes a topological defect which can be interpreted as a domain wall in the center of the system between two configurations [104, 105], we further elaborate on this process in Sec. IC of the Supplementary Material [95].

Discussion.—We introduced a method that greatly improves dynamical simulations of quantum systems using contemporary quantum processors. By utilizing the time-step compression of constant-depth circuits, the transient dynamics of novel many-body systems is achievable up to arbitrary long times, which to date has remained one of the major challenges of the NISQ era.

Using this approach, we showed how open system quantum dynamics where the environmental interaction is driven by the intrinsic noise of the quantum hardware itself can be stabilized by exploiting topological properties of matter. While conventional qubits suffer from rapid decoherence, one can create much longer lived qubits through utilizing the topologically stabilized surface states as shown in our study. These long lived states present a host of potential applications. For example, one may use such topologically stabilized states to create robust and highly local quantum sensing devices through tuning the magnetic field $h_{x}$ and couplings $J$ and $J^{\prime}$ closer relative to each other to induce a critical state [106]. In this state, the qubits have higher sensitivity, which combined with the advantage of being longer-lived can potentially be applied as a quantum sensor. Alternatively, one can tune $h_{x}$ farther than $J$ and $J^{\prime}$ to maximize the contrast between $J$ and $J^{\prime}$ . In principle, tuning the system as such will increase the effectiveness of using topological modes as qubits with longer-lived coherence times.

The constant-depth quantum circuits method provides a clear pathway towards executing long-time dynamical simulations of topological quantum spin systems. Our one-dimensional protocol can be extended to higher dimensions by complementing it with larger system implementations and mathematical developments to the regime of validity of the matchgate algebra [107]. While in this study we demonstrate the versatility of this approach by executing dynamics of simple paradigmatic topological models with relatively small resource requirements, one can also apply the method to study long-time dynamics of more complex cases, such as in Aubry-André-Harper models [108, 109, 110, 111, 112, 113], generalized Su-Schrieffer-Heeger models [114, 115, 116], and Kitaev chains [31, 117]. We also identify the circuit implementation of integrable interacting and open systems as a possible future direction. We point out that generally while simulating systems with dissipation necessitates at minimum linear scaling, if the system is integrable, then compression techniques can be used to generate circuits with constant depth scaling for this special class of interacting systems. Another promising future direction is dynamical studies of Higher Order Topological Insulators (HOTI)s [118, 119, 120], which can be made tractable with ongoing improvements in circuit compression methods.

Acknowledgements We thank Lindsay Bassman Oftelie of CNR-NANO, Pisa, Italy for valuable discussion and insight. AN was supported by an NSF grant OAC-2118061. RDF was partially supported by the Defense Advanced Research Projects Agency (DARPA), Contract No. HR001122C0063, by PNRR-Italy HPC Spoke 10 and by PRIN 2022W9W423. We acknowledge the use of IBM Quantum services for this work, including devices available through Oak Ridge National Laboratory (QCUP CPH150). The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team.

References

Chiu et al. [2016] C.-K. Chiu, J. C. Y. Teo, A. P. Schnyder, and S. Ryu, Classification of topological quantum matter with symmetries, Rev. Mod. Phys. 88, 035005 (2016).
Ozawa et al. [2019] T. Ozawa, H. M. Price, A. Amo, N. Goldman, M. Hafezi, L. Lu, M. C. Rechtsman, D. Schuster, J. Simon, O. Zilberberg, and I. Carusotto, Topological photonics, Rev. Mod. Phys. 91, 015006 (2019).
Huber [2016] S. Huber, Topological mechanics, Nature Physics 12, 621 (2016).
Yang et al. [2015] Z. Yang, F. Gao, X. Shi, X. Lin, Z. Gao, Y. Chong, and B. Zhang, Topological acoustics, Phys. Rev. Lett. 114, 114301 (2015).
Łepkowski [2022] S. P. Łepkowski, Advances in topological materials: Fundamentals, challenges and outlook, Nanomaterials 12, 10.3390/nano12193522 (2022).
Sharma et al. [2022] M. M. Sharma, P. Sharma, N. K. Karn, and V. P. S. Awana, Comprehensive review on topological superconducting materials and interfaces, Superconductor Science and Technology 35, 083003 (2022).
Kumar et al. [2020] N. Kumar, S. N. Guin, K. Manna, C. Shekhar, and C. Felser, Topological quantum materials from the viewpoint of chemistry, Chemical Reviews 121, 2780–2815 (2020).
Xue et al. [2022] H. Xue, Y. Yang, and B. Zhang, Topological acoustics, Nature Reviews Materials 7, 974–990 (2022).
Zhang et al. [2018a] X. Zhang, M. Xiao, Y. Cheng, M.-H. Lu, and J. Christensen, Topological sound, Communications Physics 1, 10.1038/s42005-018-0094-4 (2018a).
Serra-Garcia et al. [2018] M. Serra-Garcia, V. Peri, R. Süsstrunk, O. R. Bilal, T. Larsen, L. G. Villanueva, and S. D. Huber, Observation of a phononic quadrupole topological insulator, Nature 555, 342–345 (2018).
Ni et al. [2019] X. Ni, M. Weiner, A. Alù, and A. B. Khanikaev, Observation of higher-order topological acoustic states protected by generalized chiral symmetry, Nature materials 18, 113—120 (2019).
Fan et al. [2019] H. Fan, B. Xia, L. Tong, S. Zheng, and D. Yu, Elastic higher-order topological insulator with topologically protected corner states, Phys. Rev. Lett. 122, 204301 (2019).
Wakao et al. [2020] H. Wakao, T. Yoshida, H. Araki, T. Mizoguchi, and Y. Hatsugai, Higher-order topological phases in a spring-mass model on a breathing kagome lattice, Phys. Rev. B 101, 094107 (2020).
Wu et al. [2020] Q. Wu, H. Chen, X. Li, and G. Huang, In-plane second-order topologically protected states in elastic kagome lattices, Phys. Rev. Appl. 14, 014084 (2020).
Price et al. [2022] H. Price, Y. Chong, A. Khanikaev, H. Schomerus, L. J. Maczewsky, M. Kremer, M. Heinrich, A. Szameit, O. Zilberberg, Y. Yang, B. Zhang, A. Alù, R. Thomale, I. Carusotto, P. St-Jean, A. Amo, A. Dutt, L. Yuan, S. Fan, X. Yin, C. Peng, T. Ozawa, and A. Blanco-Redondo, Roadmap on topological photonics, Journal of Physics: Photonics 4, 032501 (2022).
El Hassan et al. [2019] A. El Hassan, F. K. Kunst, A. Moritz, G. Andler, E. J. Bergholtz, and M. Bourennane, Corner states of light in photonic waveguides, Nature Photonics 13, 697–700 (2019).
Xie et al. [2018] B.-Y. Xie, H.-F. Wang, H.-X. Wang, X.-Y. Zhu, J.-H. Jiang, M.-H. Lu, and Y.-F. Chen, Second-order photonic topological insulator with corner states, Phys. Rev. B 98, 205147 (2018).
Chen et al. [2019] X.-D. Chen, W.-M. Deng, F.-L. Shi, F.-L. Zhao, M. Chen, and J.-W. Dong, Direct observation of corner states in second-order topological photonic crystal slabs, Phys. Rev. Lett. 122, 233902 (2019).
Li et al. [2020a] X.-X. Li, B. Li, and P.-B. Li, Simulation of topological phases with color center arrays in phononic crystals, Phys. Rev. Res. 2, 013121 (2020a).
Bernevig et al. [2022] B. A. Bernevig, C. Felser, and H. Beidenkopf, Progress and prospects in magnetic topological materials, Nature 603, 41–51 (2022).
Li et al. [2019] Z. Li, Y. Cao, P. Yan, and X. Wang, Higher-order topological solitonic insulators, npj Computational Materials 5, 10.1038/s41524-019-0246-4 (2019).
Li et al. [2020b] Z.-X. Li, Y. Cao, X. R. Wang, and P. Yan, Symmetry-protected zero modes in metamaterials based on topological spin texture, Phys. Rev. Appl. 13, 064058 (2020b).
Li et al. [2020c] Z.-X. Li, Y. Cao, X. R. Wang, and P. Yan, Second-order topological solitonic insulator in a breathing square lattice of magnetic vortices, Phys. Rev. B 101, 184404 (2020c).
Wang and Wang [2021] X. S. Wang and X. R. Wang, Topological magnonics, Journal of Applied Physics 129, 151101 (2021).
Zhuo et al. [2023] F. Zhuo, J. Kang, A. Manchon, and Z. Cheng, Topological phases in magnonics, Advanced Physics Research 10.1002/apxr.202300054 (2023).
Wen [1990] X. G. Wen, Topological Order in Rigid States, Int. J. Mod. Phys. B 4, 239 (1990).
Ryu et al. [2010] S. Ryu, A. P. Schnyder, A. Furusaki, and A. W. W. Ludwig, Topological insulators and superconductors: tenfold way and dimensional hierarchy, New Journal of Physics 12, 065010 (2010).
Qi and Zhang [2011] X.-L. Qi and S.-C. Zhang, Topological insulators and superconductors, Reviews of Modern Physics 83, 1057–1110 (2011).
Li et al. [2021] L. Li, S. Mu, C. H. Lee, and J. Gong, Quantized classical response from spectral winding topology, Nature Communications 12, 10.1038/s41467-021-25626-z (2021).
Senthil [2015] T. Senthil, Symmetry-protected topological phases of quantum matter, Annual Review of Condensed Matter Physics 6, 299–324 (2015).
Kitaev [2001] A. Y. Kitaev, Unpaired majorana fermions in quantum wires, Physics-Uspekhi 44, 131 (2001).
Pollmann et al. [2012] F. Pollmann, E. Berg, A. M. Turner, and M. Oshikawa, Symmetry protection of topological phases in one-dimensional quantum spin systems, Phys. Rev. B 85, 075125 (2012).
McClarty [2022] P. A. McClarty, Topological magnons: A review, Annual Review of Condensed Matter Physics 13, 171–190 (2022).
He et al. [2022] Q. L. He, T. L. Hughes, N. P. Armitage, Y. Tokura, and K. L. Wang, Topological spintronics and magnetoelectronics, Nature Materials 21, 15 (2022).
Jin et al. [2023] K.-H. Jin, W. Jiang, G. Sethi, and F. Liu, Topological quantum devices: a review, Nanoscale 15, 10.1039/D3NR01288C (2023).
Hu et al. [2017] G. Hu, Y. Zhang, L. Li, and Z. Wang, Piezotronic transistor based on topological insulators, ACS Nano 12 (2017).
Chen et al. [2021] J. Chen, T. Zhang, J. Wang, N. Zhang, W. Ji, S. Zhou, and Y. Chai, Field‐effect chiral anomaly devices with dirac semimetal, Advanced Functional Materials 31, 2104192 (2021).
Vandenberghe and Fischetti [2017] W. Vandenberghe and M. Fischetti, Imperfect two-dimensional topological insulator field-effect transistors, Nature Communications 8, 14184 (2017).
Budich and Bergholtz [2020] J. Budich and E. Bergholtz, Non-hermitian topological sensors, Physical Review Letters 125 (2020).
Viti et al. [2016] L. Viti, D. Coquillat, A. Politano, K. Kokh, Z. Aliev, M. Babanly, O. Tereshchenko, W. Knap, E. Chulkov, and M. Vitiello, Plasma-wave terahertz detection mediated by topological insulators surface states, Nano Letters 16, 80 (2016).
Ohnishi et al. [2022] K. Ohnishi, M. Aoki, R. Ohshima, E. Shigematsu, Y. Ando, T. Takenobu, and M. Shiraishi, All‐electric spin device operation using the weyl semimetal, wte2, at room temperature, Advanced Electronic Materials 9, 10.1002/aelm.202200647 (2022).
Shumiya et al. [2022] N. Shumiya, M. S. Hossain, J.-X. Yin, Z. Wang, M. Litskevich, C. Yoon, Y. Li, Y. Yang, Y.-X. Jiang, G. Cheng, Y.-C. Lin, Q. Zhang, Z.-J. Cheng, T. A. Cochran, D. Multer, X. P. Yang, B. Casas, T.-R. Chang, T. Neupert, Z. Yuan, S. Jia, H. Lin, N. Yao, L. Balicas, F. Zhang, Y. Yao, and M. Z. Hasan, Evidence of a room-temperature quantum spin hall edge state in a higher-order topological insulator, Nature Materials 21, 1111–1115 (2022).
Olbrich et al. [2014] P. Olbrich, L. E. Golub, T. Herrmann, S. N. Danilov, H. Plank, V. V. Bel’kov, G. Mussler, C. Weyrich, C. M. Schneider, J. Kampmeier, D. Grützmacher, L. Plucinski, M. Eschbach, and S. D. Ganichev, Room-temperature high-frequency transport of dirac fermions in epitaxially grown ${\mathrm{sb}}_{2}{\mathrm{te}}_{3}$ - and ${\mathrm{bi}}_{2}{\mathrm{te}}_{3}$ -based topological insulators, Phys. Rev. Lett. 113, 096601 (2014).
Luo et al. [2023a] L. Luo, D. Cheng, C. Huang, X. Yang, C. Vaswani, M. Mootz, Y. Yao, X. Liu, M. Dobrowolska, J. K. Furdyna, I. E. Perakis, and J. Wang, Room temperature persisting surface charge carriers driven by intense terahertz electric fields in a topological insulator Bi2Se3, APL Materials 11, 121119 (2023a), https://pubs.aip.org/aip/apm/article-pdf/doi/10.1063/5.0181223/18281958/121119_1_5.0181223.pdf .
de Groot et al. [2022] C. de Groot, A. Turzillo, and N. Schuch, Symmetry protected topological order in open quantum systems, Quantum 6, 856 (2022).
Veríssimo et al. [2023] L. M. Veríssimo, M. L. Lyra, and R. Orús, Dissipative symmetry-protected topological order, Phys. Rev. B 107, L241104 (2023).
Bjerlin et al. [2022a] J. Bjerlin, A. S. Sørensen, and S. Haas, Probing majorana modes via local spin dynamics, Phys. Rev. B 106, 035414 (2022a).
Xu et al. [2015] J.-P. Xu, M.-X. Wang, Z. L. Liu, J.-F. Ge, X. Yang, C. Liu, Z. A. Xu, D. Guan, C. L. Gao, D. Qian, Y. Liu, Q.-H. Wang, F.-C. Zhang, Q.-K. Xue, and J.-F. Jia, Experimental detection of a majorana mode in the core of a magnetic vortex inside a topological insulator-superconductor ${\mathrm{bi}}_{2}{\mathrm{te}}_{3}/{\mathrm{nbse}}_{2}$ heterostructure, Phys. Rev. Lett. 114, 017001 (2015).
Zhou et al. [2020] Y. Zhou, E. M. Stoudenmire, and X. Waintal, What limits the simulation of quantum computers?, Phys. Rev. X 10, 041038 (2020).
Feynman [1982] R. P. Feynman, Simulating physics with computers, International Journal of Theoretical Physics 21, 467 (1982).
Cirac and Zoller [2012] J. I. Cirac and P. Zoller, Goals and opportunities in quantum simulation, Nature Physics 8, 264 (2012).
Georgescu et al. [2014] I. M. Georgescu, S. Ashhab, and F. Nori, Quantum simulation, Rev. Mod. Phys. 86, 153 (2014).
Bassman et al. [2021] L. Bassman, M. Urbanek, M. Metcalf, J. Carter, A. F. Kemper, and W. A. de Jong, Simulating quantum materials with digital quantum computers, Quantum Science and Technology 6, 043002 (2021).
Smith et al. [2019] A. Smith, M. S. Kim, F. Pollmann, and J. Knolle, Simulating quantum many-body dynamics on a current digital quantum computer, npj Quantum Information 5, 10.1038/s41534-019-0217-0 (2019).
Daley et al. [2022] A. J. Daley, I. Bloch, C. Kokail, S. Flannigan, N. Pearson, M. Troyer, and P. Zoller, Practical quantum advantage in quantum simulation, Nature 607, 667 (2022).
Kitagawa et al. [2012] T. Kitagawa, M. A. Broome, A. Fedrizzi, M. S. Rudner, E. Berg, I. Kassal, A. Aspuru-Guzik, E. Demler, and A. G. White, Observation of topologically protected bound states in photonic quantum walks, Nature Communications 3, 10.1038/ncomms1872 (2012).
Cheng et al. [2019] Q. Cheng, Y. Pan, H. Wang, C. Zhang, D. Yu, A. Gover, H. Zhang, T. Li, L. Zhou, and S. Zhu, Observation of anomalous $\pi$ modes in photonic floquet engineering, Phys. Rev. Lett. 122, 173901 (2019).
Haldane and Raghu [2008] F. D. M. Haldane and S. Raghu, Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry, Phys. Rev. Lett. 100, 013904 (2008).
Li et al. [2015] Z. Li, R. xin Wu, Q.-B. Li, Z. fang Lin, Y. Poo, R.-J. Liu, and Z.-Y. Li, Observation of broadband unidirectional transmission by fusing the one-way edge states of gyromagnetic photonic crystals, Opt. Express 23, 9658 (2015).
Khanikaev and Shvets [2017] A. B. Khanikaev and G. Shvets, Two-dimensional topological photonics, Nature Photonics 11, 763 (2017).
de Léséleuc et al. [2019] S. de Léséleuc, V. Lienhard, P. Scholl, D. Barredo, S. Weber, N. Lang, H. P. Büchler, T. Lahaye, and A. Browaeys, Observation of a symmetry-protected topological phase of interacting bosons with rydberg atoms, Science 365, 775–780 (2019).
Ebadi et al. [2021] S. Ebadi, T. T. Wang, H. Levine, A. Keesling, G. Semeghini, A. Omran, D. Bluvstein, R. Samajdar, H. Pichler, W. W. Ho, S. Choi, S. Sachdev, M. Greiner, V. Vuletić, and M. D. Lukin, Quantum phases of matter on a 256-atom programmable quantum simulator, Nature 595, 227–232 (2021).
Cardarelli et al. [2022] L. Cardarelli, S. Julià-Farré, M. Lewenstein, A. Dauphin, and M. Müller, Accessing the topological mott insulator in cold atom quantum simulators with realistic rydberg dressing (2022), arXiv:2203.14818 [cond-mat.quant-gas] .
Zhao et al. [2022] E. Zhao, C. He, and G.-B. Jo, ”designing synthetic topological matter with atoms and lights”, Light, science & applications 11, 46 (2022).
Potirniche et al. [2017] I.-D. Potirniche, A. C. Potter, M. Schleier-Smith, A. Vishwanath, and N. Y. Yao, Floquet symmetry-protected topological phases in cold-atom systems, Phys. Rev. Lett. 119, 123601 (2017).
Shi et al. [2023] Y.-H. Shi, Y. Liu, Y.-R. Zhang, Z. Xiang, K. Huang, T. Liu, Y.-Y. Wang, J.-C. Zhang, C.-L. Deng, G.-H. Liang, Z.-Y. Mei, H. Li, T.-M. Li, W.-G. Ma, H.-T. Liu, C.-T. Chen, T. Liu, Y. Tian, X. Song, S. Zhao, K. Xu, D. Zheng, F. Nori, and H. Fan, Quantum simulation of topological zero modes on a 41-qubit superconducting processor, Physical Review Letters 131, 10.1103/physrevlett.131.080401 (2023).
Dumitrescu et al. [2022] P. T. Dumitrescu, J. G. Bohnet, J. P. Gaebler, A. Hankin, D. Hayes, A. Kumar, B. Neyenhuis, R. Vasseur, and A. C. Potter, Dynamical topological phase realized in a trapped-ion quantum simulator, Nature 607, 463–467 (2022).
Chen et al. [2020] B. Chen, S. Li, X. Hou, F. Zhou, P. Qian, F. Mei, S. Jia, N. Xu, and H. Shen, Digital quantum simulation of floquet topological phases with a solid-state quantum simulator (2020), arXiv:2012.05495 [quant-ph] .
Harle et al. [2023] N. Harle, O. Shtanko, and R. Movassagh, Observing and braiding topological majorana modes on programmable quantum simulators, Nature Communications 14, 10.1038/s41467-023-37725-0 (2023).
Lloyd [1996] S. Lloyd, Universal quantum simulators, Science 273, 1073 (1996).
Satzinger et al. [2021] K. J. Satzinger, Y.-J. Liu, A. Smith, C. Knapp, M. Newman, C. Jones, Z. Chen, C. Quintana, X. Mi, A. Dunsworth, C. Gidney, I. Aleiner, F. Arute, K. Arya, J. Atalaya, R. Babbush, J. C. Bardin, R. Barends, J. Basso, A. Bengtsson, A. Bilmes, M. Broughton, B. B. Buckley, D. A. Buell, B. Burkett, N. Bushnell, B. Chiaro, R. Collins, W. Courtney, S. Demura, A. R. Derk, D. Eppens, C. Erickson, L. Faoro, E. Farhi, A. G. Fowler, B. Foxen, M. Giustina, A. Greene, J. A. Gross, M. P. Harrigan, S. D. Harrington, J. Hilton, S. Hong, T. Huang, W. J. Huggins, L. B. Ioffe, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, T. Khattar, S. Kim, P. V. Klimov, A. N. Korotkov, F. Kostritsa, D. Landhuis, P. Laptev, A. Locharla, E. Lucero, O. Martin, J. R. McClean, M. McEwen, K. C. Miao, M. Mohseni, S. Montazeri, W. Mruczkiewicz, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Y. Niu, T. E. O’Brien, A. Opremcak, B. Pató, A. Petukhov, N. C. Rubin, D. Sank, V. Shvarts, D. Strain, M. Szalay, B. Villalonga, T. C. White, Z. Yao, P. Yeh, J. Yoo, A. Zalcman, H. Neven, S. Boixo, A. Megrant, Y. Chen, J. Kelly, V. Smelyanskiy, A. Kitaev, M. Knap, F. Pollmann, and P. Roushan, Realizing topologically ordered states on a quantum processor, Science 374, 1237–1241 (2021).
Mei et al. [2020] F. Mei, Q. Guo, Y.-F. Yu, L. Xiao, S.-L. Zhu, and S. Jia, Digital simulation of topological matter on programmable quantum processors, Phys. Rev. Lett. 125, 160503 (2020).
Azses et al. [2020] D. Azses, R. Haenel, Y. Naveh, R. Raussendorf, E. Sela, and E. G. D. Torre, Identification of symmetry-protected topological states on noisy quantum computers, Physical Review Letters 125, 10.1103/physrevlett.125.120502 (2020).
Choo et al. [2018] K. Choo, C. W. von Keyserlingk, N. Regnault, and T. Neupert, Measurement of the entanglement spectrum of a symmetry-protected topological state using the IBM quantum computer, Physical Review Letters 121, 10.1103/physrevlett.121.086808 (2018).
Koh et al. [2022a] J. M. Koh, T. Tai, Y. H. Phee, W. E. Ng, and C. H. Lee, Stabilizing multiple topological fermions on a quantum computer, npj Quantum Information 8, 10.1038/s41534-022-00527-1 (2022a).
Koh et al. [2022b] J. M. Koh, T. Tai, and C. H. Lee, Simulation of interaction-induced chiral topological dynamics on a digital quantum computer, Physical Review Letters 129, 10.1103/physrevlett.129.140502 (2022b).
Tan et al. [2021] A. T. K. Tan, S.-N. Sun, R. N. Tazhigulov, G. K.-L. Chan, and A. J. Minnich, Realizing symmetry-protected topological phases in a spin-1/2 chain with next-nearest neighbor hopping on superconducting qubits (2021), arXiv:2112.10333 [quant-ph] .
Smith et al. [2022] A. Smith, B. Jobst, A. G. Green, and F. Pollmann, Crossing a topological phase transition with a quantum computer, Physical Review Research 4, 10.1103/physrevresearch.4.l022020 (2022).
Bassman Oftelie et al. [2020] L. Bassman Oftelie, K. Liu, A. Krishnamoorthy, T. Linker, Y. Geng, D. Shebib, S. Fukushima, F. Shimojo, R. K. Kalia, A. Nakano, and P. Vashishta, Towards simulation of the dynamics of materials on quantum computers, Phys. Rev. B 101, 184305 (2020).
Preskill [2018] J. Preskill, Quantum computing in the NISQ era and beyond, Quantum 2, 79 (2018).
Childs and Kothari [2010] A. M. Childs and R. Kothari, Limitations on the simulation of non-sparse hamiltonians, Quantum Info. Comput. 10, 669–684 (2010).
Berry et al. [2006] D. W. Berry, G. Ahokas, R. Cleve, and B. C. Sanders, Efficient quantum algorithms for simulating sparse hamiltonians, Communications in Mathematical Physics 270, 359 (2006).
Atia and Aharonov [2017] Y. Atia and D. Aharonov, Fast-forwarding of hamiltonians and exponentially precise measurements, Nature Communications 8, 10.1038/s41467-017-01637-7 (2017).
Oftelie et al. [2022] L. B. Oftelie, R. V. Beeumen, E. Younis, E. Smith, C. Iancu, and W. A. de Jong, Constant-depth circuits for dynamic simulations of materials on quantum computers, Materials Theory 6, 10.1186/s41313-022-00043-x (2022).
Kökcü et al. [2022a] E. Kökcü, D. Camps, L. Bassman Oftelie, J. K. Freericks, W. A. de Jong, R. Van Beeumen, and A. F. Kemper, Algebraic compression of quantum circuits for hamiltonian evolution, Phys. Rev. A 105, 032420 (2022a).
Kökcü et al. [2022b] E. Kökcü, T. Steckmann, Y. Wang, J. K. Freericks, E. F. Dumitrescu, and A. F. Kemper, Fixed depth hamiltonian simulation via cartan decomposition, Phys. Rev. Lett. 129, 070501 (2022b).
Chen et al. [2011] X. Chen, Z.-C. Gu, and X.-G. Wen, Complete classification of one-dimensional gapped quantum phases in interacting spin systems, Physical Review B 84, 10.1103/physrevb.84.235128 (2011).
Pollmann et al. [2010] F. Pollmann, A. M. Turner, E. Berg, and M. Oshikawa, Entanglement spectrum of a topological phase in one dimension, Physical Review B 81, 10.1103/physrevb.81.064439 (2010).
Su et al. [1979] W. P. Su, J. R. Schrieffer, and A. J. Heeger, Solitons in polyacetylene, Phys. Rev. Lett. 42, 1698 (1979).
Jackiw and Rebbi [1976] R. Jackiw and C. Rebbi, Solitons with fermion number ½, Phys. Rev. D 13, 3398 (1976).
Meier et al. [2016] E. J. Meier, F. A. An, and B. Gadway, Observation of the topological soliton state in the su–schrieffer–heeger model, Nature Communications 7, 10.1038/ncomms13986 (2016).
Tang and Wen [2012] E. Tang and X.-G. Wen, Interacting one-dimensional fermionic symmetry-protected topological phases, Phys. Rev. Lett. 109, 096403 (2012).
Fukusumi and Iino [2021] Y. Fukusumi and S. Iino, Open spin chain realization of a topological defect in a one-dimensional ising model: Boundary and bulk symmetry, Phys. Rev. B 104, 125418 (2021).
Han et al. [2020] S.-H. Han, S.-G. Jeong, S.-W. Kim, T.-H. Kim, and S. Cheon, Topological features of ground states and topological solitons in generalized su-schrieffer-heeger models using generalized time-reversal, particle-hole, and chiral symmetries, Phys. Rev. B 102, 235411 (2020).
[95] See Supplemental Material at [URL will be inserted by publisher], which includes Refs. [28], [30], [134-139] for Supplement Secs. I-IV and additional technical details on implementation and analysis.
Gu et al. [2021] S. Gu, R. D. Somma, and B. Şahinoğlu, Fast-forwarding quantum evolution, Quantum 5, 577 (2021).
Aleksandrowicz et al. [2019] G. Aleksandrowicz, T. Alexander, P. Barkoutsos, L. Bello, Y. Ben-Haim, D. Bucher, F. J. Cabrera-Hernández, J. Carballo-Franquis, A. Chen, C.-F. Chen, J. M. Chow, A. D. Córcoles-Gonzales, A. J. Cross, A. Cross, J. Cruz-Benito, C. Culver, S. D. L. P. González, E. D. L. Torre, D. Ding, E. Dumitrescu, I. Duran, P. Eendebak, M. Everitt, I. F. Sertage, A. Frisch, A. Fuhrer, J. Gambetta, B. G. Gago, J. Gomez-Mosquera, D. Greenberg, I. Hamamura, V. Havlicek, J. Hellmers, Łukasz Herok, H. Horii, S. Hu, T. Imamichi, T. Itoko, A. Javadi-Abhari, N. Kanazawa, A. Karazeev, K. Krsulich, P. Liu, Y. Luh, Y. Maeng, M. Marques, F. J. Martín-Fernández, D. T. McClure, D. McKay, S. Meesala, A. Mezzacapo, N. Moll, D. M. Rodríguez, G. Nannicini, P. Nation, P. Ollitrault, L. J. O’Riordan, H. Paik, J. Pérez, A. Phan, M. Pistoia, V. Prutyanov, M. Reuter, J. Rice, A. R. Davila, R. H. P. Rudy, M. Ryu, N. Sathaye, C. Schnabel, E. Schoute, K. Setia, Y. Shi, A. Silva, Y. Siraichi, S. Sivarajah, J. A. Smolin, M. Soeken, H. Takahashi, I. Tavernelli, C. Taylor, P. Taylour, K. Trabing, M. Treinish, W. Turner, D. Vogt-Lee, C. Vuillot, J. A. Wildstrom, J. Wilson, E. Winston, C. Wood, S. Wood, S. Wörner, I. Y. Akhalwaya, and C. Zoufal, Qiskit: An Open-source Framework for Quantum Computing (2019).
Campos Venuti et al. [2013] L. Campos Venuti, S. Yeshwanth, and S. Haas, Equilibration times in clean and noisy systems, Phys. Rev. A 87, 032108 (2013).
Golinelli et al. [1992] O. Golinelli, T. Jolicoeur, and R. Lacaze, Haldane gaps in a spin-1 heisenberg chain with easy-plane single-ion anisotropy, Phys. Rev. B 45, 9798 (1992).
Guimarães et al. [2023] J. D. Guimarães, J. Lim, M. I. Vasilevskiy, S. F. Huelga, and M. B. Plenio, Noise-assisted digital quantum simulation of open systems using partial probabilistic error cancellation, PRX Quantum 4, 040329 (2023).
Liu et al. [2023] D. Liu, P. Matveeva, D. Gutman, and S. T. Carr, Elementary models of three-dimensional topological insulators with chiral symmetry, Physical Review B 108, 10.1103/physrevb.108.035418 (2023).
Kitaev et al. [2009] A. Kitaev, V. Lebedev, and M. Feigel’man, Periodic table for topological insulators and superconductors, in AIP Conference Proceedings (AIP, 2009).
Altland and Zirnbauer [1997] A. Altland and M. R. Zirnbauer, Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures, Phys. Rev. B 55, 1142 (1997).
Estarellas et al. [2017] M. P. Estarellas, I. D’Amico, and T. P. Spiller, Topologically protected localised states in spin chains, Scientific Reports 7, 10.1038/srep42904 (2017).
Teo and Hughes [2017] J. C. Teo and T. L. Hughes, Topological defects in symmetry-protected topological phases, Annual Review of Condensed Matter Physics 8, 211 (2017), https://doi.org/10.1146/annurev-conmatphys-031016-025154 .
Sarkar et al. [2022] S. Sarkar, C. Mukhopadhyay, A. Alase, and A. Bayat, Free-fermionic topological quantum sensors, Phys. Rev. Lett. 129, 090503 (2022).
Kökcü et al. [2023] E. Kökcü, D. Camps, L. B. Oftelie, W. A. de Jong, R. V. Beeumen, and A. F. Kemper, Algebraic compression of free fermionic quantum circuits: Particle creation, arbitrary lattices and controlled evolution (2023), arXiv:2303.09538 [quant-ph] .
Aubry and André [1980] S. Aubry and G. André, Analyticity breaking and anderson localization in incommensurate lattices, Proceedings, VIII International Colloquium on Group-Theoretical Methods in Physics 3 (1980).
Harper [1955] P. G. Harper, Single Band Motion of Conduction Electrons in a Uniform Magnetic Field, Proceedings of the Physical Society A 68, 874 (1955).
Hofstadter [1976] D. R. Hofstadter, Energy levels and wave functions of bloch electrons in rational and irrational magnetic fields, Phys. Rev. B 14, 2239 (1976).
Das Sarma et al. [1988] S. Das Sarma, S. He, and X. C. Xie, Mobility edge in a model one-dimensional potential, Phys. Rev. Lett. 61, 2144 (1988).
Biddle et al. [2009] J. Biddle, B. Wang, D. J. Priour, and S. Das Sarma, Localization in one-dimensional incommensurate lattices beyond the aubry-andré model, Physical Review A 80, 10.1103/physreva.80.021603 (2009).
Das Sarma et al. [1990] S. Das Sarma, S. He, and X. C. Xie, Localization, mobility edges, and metal-insulator transition in a class of one-dimensional slowly varying deterministic potentials, Phys. Rev. B 41, 5544 (1990).
Xie et al. [2019] D. Xie, W. Gou, T. Xiao, B. Gadway, and B. Yan, Topological characterizations of an extended su–schrieffer–heeger model, npj Quantum Information 5, 10.1038/s41534-019-0159-6 (2019).
Ahmadi et al. [2020] N. Ahmadi, J. Abouie, and D. Baeriswyl, Topological and nontopological features of generalized su-schrieffer-heeger models, Phys. Rev. B 101, 195117 (2020).
Väyrynen and Ojanen [2011] J. I. Väyrynen and T. Ojanen, Chiral topological phases and fractional domain wall excitations in one-dimensional chains and wires, Phys. Rev. Lett. 107, 166804 (2011).
Fu and Kane [2008] L. Fu and C. L. Kane, Superconducting proximity effect and majorana fermions at the surface of a topological insulator, Phys. Rev. Lett. 100, 096407 (2008).
Schindler et al. [2018] F. Schindler, A. M. Cook, M. G. Vergniory, Z. Wang, S. S. P. Parkin, B. A. Bernevig, and T. Neupert, Higher-order topological insulators, Science Advances 4, 10.1126/sciadv.aat0346 (2018).
Luo et al. [2023b] X.-J. Luo, X.-H. Pan, C.-X. Liu, and X. Liu, Higher-order topological phases emerging from su-schrieffer-heeger stacking, Phys. Rev. B 107, 045118 (2023b).
Benalcazar and Cerjan [2022] W. A. Benalcazar and A. Cerjan, Chiral-symmetric higher-order topological phases of matter, Phys. Rev. Lett. 128, 127601 (2022).
Gooth et al. [2023] J. Gooth, S. Galeski, and T. Meng, Quantum-hall physics and three dimensions, Reports on Progress in Physics 86, 044501 (2023).
Wu et al. [2019] H. Wu, P. Zhang, P. Deng, Q. Lan, Q. Pan, S. A. Razavi, X. Che, L. Huang, B. Dai, K. Wong, X. Han, and K. L. Wang, Room-temperature spin-orbit torque from topological surface states, Phys. Rev. Lett. 123, 207205 (2019).
Zhang et al. [2018b] D.-W. Zhang, Y.-Q. Zhu, Y. X. Zhao, H. Yan, and S.-L. Zhu, Topological quantum matter with cold atoms, Advances in Physics 67, 253–402 (2018b).
Bjerlin et al. [2022b] J. Bjerlin, A. S. Sørensen, and S. Haas, Probing majorana modes via local spin dynamics, Physical Review B 106, 10.1103/physrevb.106.035414 (2022b).
You et al. [2014] J. Q. You, Z. D. Wang, W. Zhang, and F. Nori, Encoding a qubit with majorana modes in superconducting circuits (2014), arXiv:1108.3712 [cond-mat.supr-con] .
Zhong et al. [2016] Y. P. Zhong, D. Xu, P. Wang, C. Song, Q. J. Guo, W. X. Liu, K. Xu, B. X. Xia, C.-Y. Lu, S. Han, J.-W. Pan, and H. Wang, Emulating anyonic fractional statistical behavior in a superconducting quantum circuit, Phys. Rev. Lett. 117, 110501 (2016).
Song et al. [2018] C. Song, D. Xu, P. Zhang, J. Wang, Q. Guo, W. Liu, K. Xu, H. Deng, K. Huang, D. Zheng, S.-B. Zheng, H. Wang, X. Zhu, C.-Y. Lu, and J.-W. Pan, Demonstration of topological robustness of anyonic braiding statistics with a superconducting quantum circuit, Phys. Rev. Lett. 121, 030502 (2018).
Roushan et al. [2014] P. Roushan, C. Neill, Y. Chen, M. Kolodrubetz, C. Quintana, N. Leung, M. Fang, R. Barends, B. Campbell, Z. Chen, B. Chiaro, A. Dunsworth, E. Jeffrey, J. Kelly, A. Megrant, J. Mutus, P. J. J. O’Malley, D. Sank, A. Vainsencher, J. Wenner, T. White, A. Polkovnikov, A. N. Cleland, and J. M. Martinis, Observation of topological transitions in interacting quantum circuits, Nature 515, 241 (2014).
Aasen et al. [2016] D. Aasen, M. Hell, R. V. Mishmash, A. Higginbotham, J. Danon, M. Leijnse, T. S. Jespersen, J. A. Folk, C. M. Marcus, K. Flensberg, and J. Alicea, Milestones toward majorana-based quantum computing, Phys. Rev. X 6, 031016 (2016).
Mao and Wang [2015] T. Mao and Z. D. Wang, Quantum simulation of topological majorana bound states and their universal quantum operations using charge-qubit arrays, Phys. Rev. A 91, 012336 (2015).
Yao et al. [2012] X.-C. Yao, T.-X. Wang, H.-Z. Chen, W.-B. Gao, A. G. Fowler, R. Raussendorf, Z.-B. Chen, N.-L. Liu, C.-Y. Lu, Y.-J. Deng, Y.-A. Chen, and J.-W. Pan, Experimental demonstration of topological error correction, Nature 482, 489 (2012).
Kitaev [2003] A. Kitaev, Fault-tolerant quantum computation by anyons, Annals of Physics 303, 2 (2003).
Nigg et al. [2014] D. Nigg, M. Müller, E. A. Martinez, P. Schindler, M. Hennrich, T. Monz, M. A. Martin-Delgado, and R. Blatt, Quantum computations on a topologically encoded qubit, Science 345, 302 (2014).
Pfeuty [1970] P. Pfeuty, The one-dimensional ising model with a transverse field, Annals of Physics 57, 79 (1970).
Valiant [2002] L. G. Valiant, Quantum circuits that can be simulated classically in polynomial time, SIAM Journal on Computing 31, 1229 (2002), https://doi.org/10.1137/S0097539700377025 .
Bogolyubov et al. [1958] N. N. Bogolyubov, V. V. Tolmachev, and D. V. Shirkov, A New method in the theory of superconductivity, Fortsch. Phys. 6, 605 (1958).
Jackiw and Schrieffer [1981] R. Jackiw and J. Schrieffer, Solitons with fermion number 12 in condensed matter and relativistic field theories, Nuclear Physics B 190, 253 (1981).
Valatin [1958] J. G. Valatin, Comments on the theory of superconductivity, Nuovo Cim. 7, 843 (1958).
Delplace et al. [2011] P. Delplace, D. Ullmo, and G. Montambaux, Zak phase and the existence of edge states in graphene, Phys. Rev. B 84, 195452 (2011).