Dynamical Symmetries and Symmetry-Protected Selection Rules in Periodically Driven Quantum Systems
Abstract
In recent experiments, the light-matter interaction has reached the ultrastrong coupling limit, which can give rise to dynamical generalizations of spatial symmetries in periodically driven systems. Here, we present a unified framework of dynamical-symmetry-protected selection rules based on Floquet response theory. Within this framework, we study rotational, parity, particle-hole, chiral, and time-reversal symmetries and the resulting selection rules in spectroscopy, including symmetry-protected dark states (spDSs), symmetry-protected dark bands (spDBs), and symmetry-induced transparency (siT). Specifically, dynamical rotational and parity symmetries establish spDS and spDB conditions. Particle-hole symmetry introduces spDSs for symmetry-related Floquet states and also a siT at quasienergy crossings. Chiral symmetry and time-reversal symmetry alone do not imply spDS conditions but can be combined to define a particle-hole symmetry. These symmetry conditions arise from destructive interference due to the synchronization of symmetric quantum systems with the periodic driving. Our predictions reveal new physical phenomena when a quantum system reaches the strong light-matter coupling regime, which is important for superconducting qubits, atoms and molecules in optical fields or plasmonic cavities, and optomechanical systems.
pacs:
Introduction. Over the last few decades, the light-matter interaction strength has been pushed to the ultrastrong coupling regime in optomechanical systems [1], quantum dots, atoms and molecules in optical or plasmonic cavities [2, 3, 4, 5, 6], and superconducting quantum circuits [7, 8, 9]. As standard nonlinear perturbation theory [10] becomes unfeasible under these conditions, Floquet response theory has been developed recently, describing systems that are subject to a strong but time-periodic driving field (of frequency ), and a weak but arbitrary probe field [11, 12, 13, 14]. For a monochromatic probe of frequency , system observables generate response frequencies termed Floquet bands [15].
Spatial symmetries give rise to appealing physical properties. Inversion symmetry results in selection rules for dipole transitions; particle-hole, chiral, and time-reversal symmetries establish the so-called periodic table, a classification scheme for topological insulators [16, 17, 18], and symmetries have an essential impact on transport properties [19, 20, 21, 22, 23, 24, 25]. For periodically driven systems, these spatial symmetries can be generalized to dynamical symmetries that can give rise to a generalized periodic table for topological insulators [26, 27] and new control mechanisms [28, 29, 30, 31, 32, 33, 34, 35]. Dynamical symmetries have been used to control the coherent destruction of tunneling effect [36] and induce selection rules for high harmonic generation [37, 38, 39, 40].
| Symmetry | Effect | Example |
|---|---|---|
| RS | spDS | benzene ring (Fig. 1) |
| spDB | ||
| PS | spDS | two-level system (Fig. 3) |
| spDB | ||
| PHS | spDS | dimer (Fig. 2) |
| 2 PHS | siT | two-level system (Fig. 3) |
| TRS | none | |
| CS | none | |
| none | aDS | all (Figs. 1,2 ,3) |
In this Letter, we introduce a unified conceptual framework of selection rules based on general dynamical symmetries of periodically driven quantum systems as described by Floquet response theory [41]. Physically, the synchronization of symmetric quantum systems with the periodic driving gives rise to destructive interference effects in Floquet space and thus to forbidden transitions between Floquet states. This set of forbidden transitions defines the symmetry-protected selection rules that are robust against symmetry-preserving parameter variations. Specifically, there are four types of forbidden transitions ordered in increasing degree of complexity: (i) accidental dark states (aDSs), appearing for a specific combination of system parameters; (ii) symmetry-protected dark states (spDSs), which refer to the symmetry-protected absence of a complete transition line similar to symmetry-protected excitations of topological band structures; (iii) symmetry-protected dark bands (spDBs), which refer to the absence of a complete Floquet band due to a combination of spDSs; (iv) symmetry-induced transparency (siT), which refers to the vanishing transition intensity at the degeneracy of quasienergies. Except for the aDS, which is not symmetry related, we establish symmetry-protected selection rules for important dynamical symmetries, which are classified in Table 1.
Floquet response theory. We apply a semiclassical approach based on the general Hamiltonian
| (1) |
where describes a system driven by a periodic classical electromagnetic field of frequency . The probe field is given by a continuum of photonic operators with frequencies , which are coupled via the dipole transition operator with strength to the driven system. The physical properties of are determined by the Floquet equation
| (2) |
where and are the corresponding Floquet states and quasienergies that generalize the concept of eigenstates and eigenenergies of time-independent systems. It is implicitly assumed that the driven system is weakly dissipative such that, for long times, it approaches the stationary state
| (3) |
which is diagonal in the Floquet basis and thus synchronizes with the driving . Equation (3) is consistent with the Floquet-Redfield equation [42, 43, 44, 45] describing periodically driven open quantum systems. In the model calculations, we assume the special distribution , i.e., a Floquet-Gibbs distribution, but all our predictions hold even if the Floquet-Gibbs distribution breaks down [45]. Strongly dissipative systems could be addressed by generalizing our approach to non-Hermitian Hamiltonians [18] or via the polaron transformation [46].
The interaction of with the probe field is treated using the input-output formalism and a perturbation expansion for small . The input field consists of a bichromatic probe field (of frequencies and , integer ). As shown separately [14], the intensity change of the output field at frequency proportional to the coherence is given by , where the susceptibility can be evaluated using Floquet response theory and reads
| (4) |
The index denotes the Floquet band, which describes nonelastic scattering of the probe field, and the dynamical dipole matrix elements read
| (5) |
The parameters have been added phenomenologically and denote dephasing rates.
Unified conceptual framework of dynamical-symmetry-protected selection rules. We consider the following class of symmetry operations [26]:
| (6) |
where is a time-independent spatial operator. By specifying , , and , one can define a set of dynamical symmetries. Applying Eq. (6) to the Floquet equation Eq. (2), one can identify relations between Floquet states and :
| (7) |
These relations can be used to evaluate the dynamical dipole elements in Eq. (5). Imposing an invariance condition for the transition dipole operator and using Eq. (7), we investigate symmetry-protected selection rules for rotational, parity, particle-hole, chiral and time-reversal symmetries.
Within the unified framework, we can establish symmetry-protected selection rules that are robust against symmetry-conserved variations and unique for strong light-matter interactions. Among others, we investigate dark states, which are defined by the condition , such that the corresponding resonances in Eq. (4) vanish. This condition not only generalizes the dark state condition in the standard response theory to the strong-coupling regime for but also introduces distinct dark states effects for . All selection rules are a consequence of destructive interference due to the synchronization of the system state with the periodic driving: (i) The dark state condition can be fulfilled by special combinations of parameters, which we denote as an aDS, or (ii) as a consequence of a symmetry, which we denote as a spDS. (iii) An entire Floquet band can vanish because for specific , which we denote as a spDB. (iv) By analyzing the susceptibility in terms of Eq. (7), we establish the condition for the siT, which is due to a destructive interference of two transitions with .
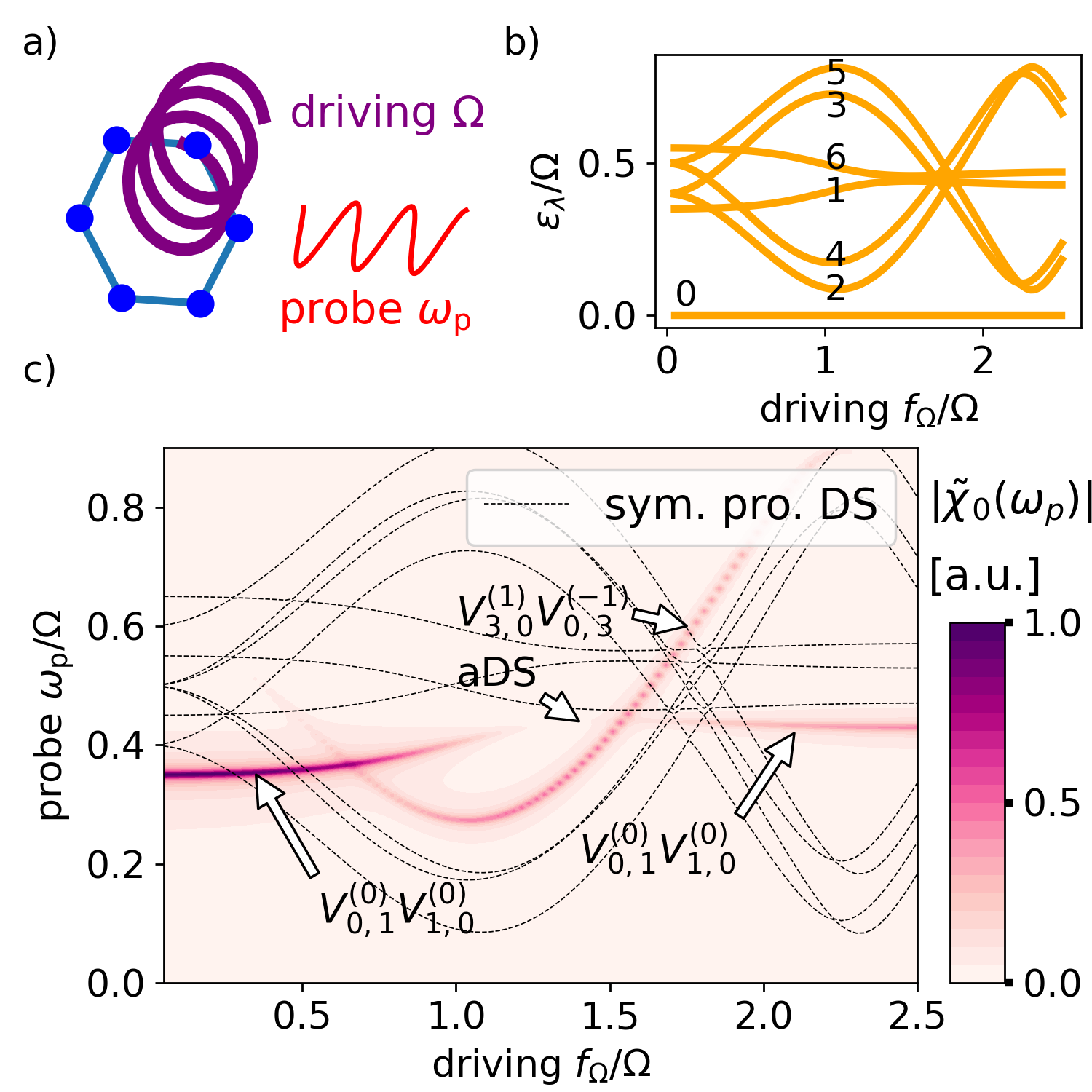
Rotational symmetry. With , a unitary , and with a positive integer , Eq. (6) defines a dynamical rotational symmetry [47] that gives rise to the eigenvalue equation with eigenvalues and integer . As shown in detail in the Supplemental Material [48], for a dipole transition operator with and , the dynamical rotational symmetry establishes a sufficient condition for spDSs:
| (8) |
Applying Eq. (8) to evaluate the susceptibility in Eq. (4), we find
| (9) |
which is the condition for the complete disappearance of Floquet band , i.e., a spDB. Physically, this effect appears as the stationary state Eq. (3) synchronizes with the driving field such that the density matrix adopts the dynamical rotational symmetry, i.e., .
As an example, we consider a benzene ring driven by circularly polarized light sketched in Fig. 1(a), which is described by a tight-binding Hamiltonian:
where denotes the excitation on site (defined modulo ), is the on-site energy, is the tunneling constant, and is the time-dependent tunneling strength with the driving amplitude . The driving terms are motivated by the Peierls substitution describing a vectorial current-gauge-field coupling [49] with a circularly rotating vector potential . The dipole transition operator excites the ground state to the single-excitation manifold, whose quasienergies are depicted in Fig. 1(b). The stationary state is in agreement with Eq. (3), i.e., a Floquet-Gibbs state for low temperatures. A rotational symmetry is fulfilled for and .
In Fig. 1(c), we depict the susceptibility of the benzene model. The resonances of the dark states defined by Eq. (8) are marked by dashed lines (optically invisible), and only two transitions, and , are visible. An aDS can be found for at . As a consequence of the spDB in Eq. (9), only Floquet bands with appear.
Parity symmetry. A dynamical parity symmetry is a specification of the dynamical rotational symmetry with and a Hermitian operator such that the spDS condition Eq. (8) and the spDB condition Eq. (9) are equally valid. The spDSs will be illustrated for the two-level system (TLS) in Eq. (13) along with the siT discussed below.
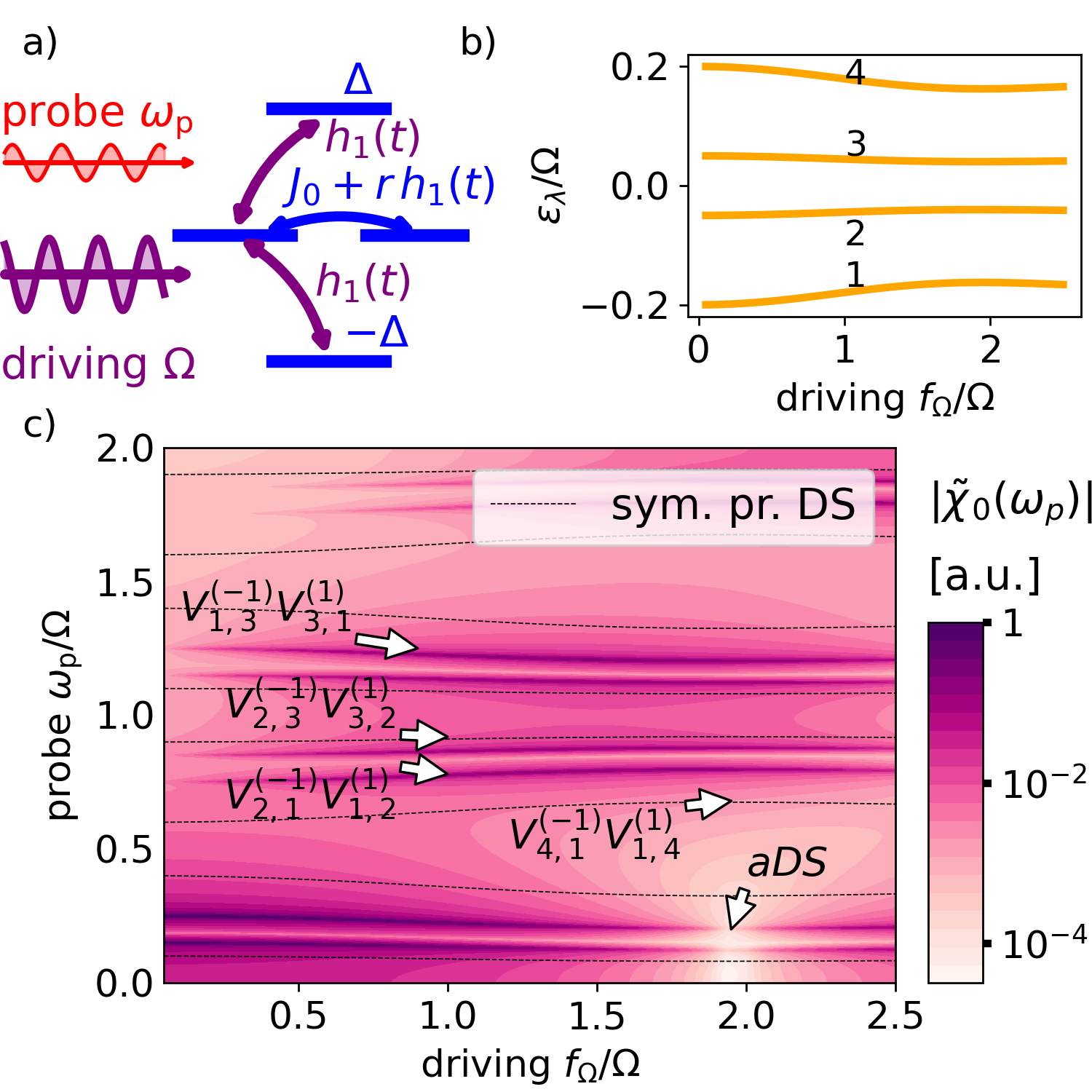
Particle-hole symmetry. A particle-hole symmetry is defined for , with integers , , and with a unitary operator and the complex conjugation operator , such that The particle-hole symmetry establishes a symmetry between the excitation and deexcitation processes and has its origin in fermionic systems, where adding and removing quasiparticles results in physically equivalent behaviors. Here we use the particle-hole symmetry in a general context. Using the particle-hole symmetry in Eq. (2), we find that each Floquet state with quasienergy has its symmetry related partner with energy and a gauge-dependent . For , the particle-hole symmetry gives rise to a rotational symmetry defined by and such that the dark state selection rules of the rotational symmetry apply. The particle-hole symmetry can give rise to a distinct dark state condition. For a dipole transition operator with , , , and , the particle-hole symmetry results in for the symmetry-related states , so that
| (10) |
as shown in detail in the Supplementary Material [48]. In contrast to Eq. (8), where each transition can vanish for an appropriate , only transitions between symmetry-related states are affected by Eq. (10).
To illustrate Eq. (10), we use the dimer model sketched in Fig. 2(a), with the Hamiltonian given by
| (11) | |||||
where , and and label the ground state, two single-excitation states, and the double-excitation state, respectively. is the excitation gap, is the tunneling constant, and is the driving field. The term enhances higher-order dipole elements . The particle-hole symmetry is defined by and . The quasienergy spectrum in Fig. 2(b) is symmetric with respect to . The dipole transition operator is , such that . In Fig. 2(c), we depict the susceptibility in Eq. (4). According to the above considerations, the transitions between the particle-hole symmetry-related pairs vanish, i.e., for all . These resonances are marked by dashed lines. The other transitions not affected by the symmetry constrain remain visible in Fig. 2(c).
Symmetry-induced transparency. The particle-hole symmetry can also give rise to a siT at the quasienergy crossing of the symmetry-related Floquet states . While a spDS is generated by a vanishing dipole element, , the siT is generated by a destructive interference of two transitions with . As shown in the Supplementary Material [48] in detail, for two distinct particle-hole symmetries , and , the siT condition reads
| (12) |
where denote the reference times related to .
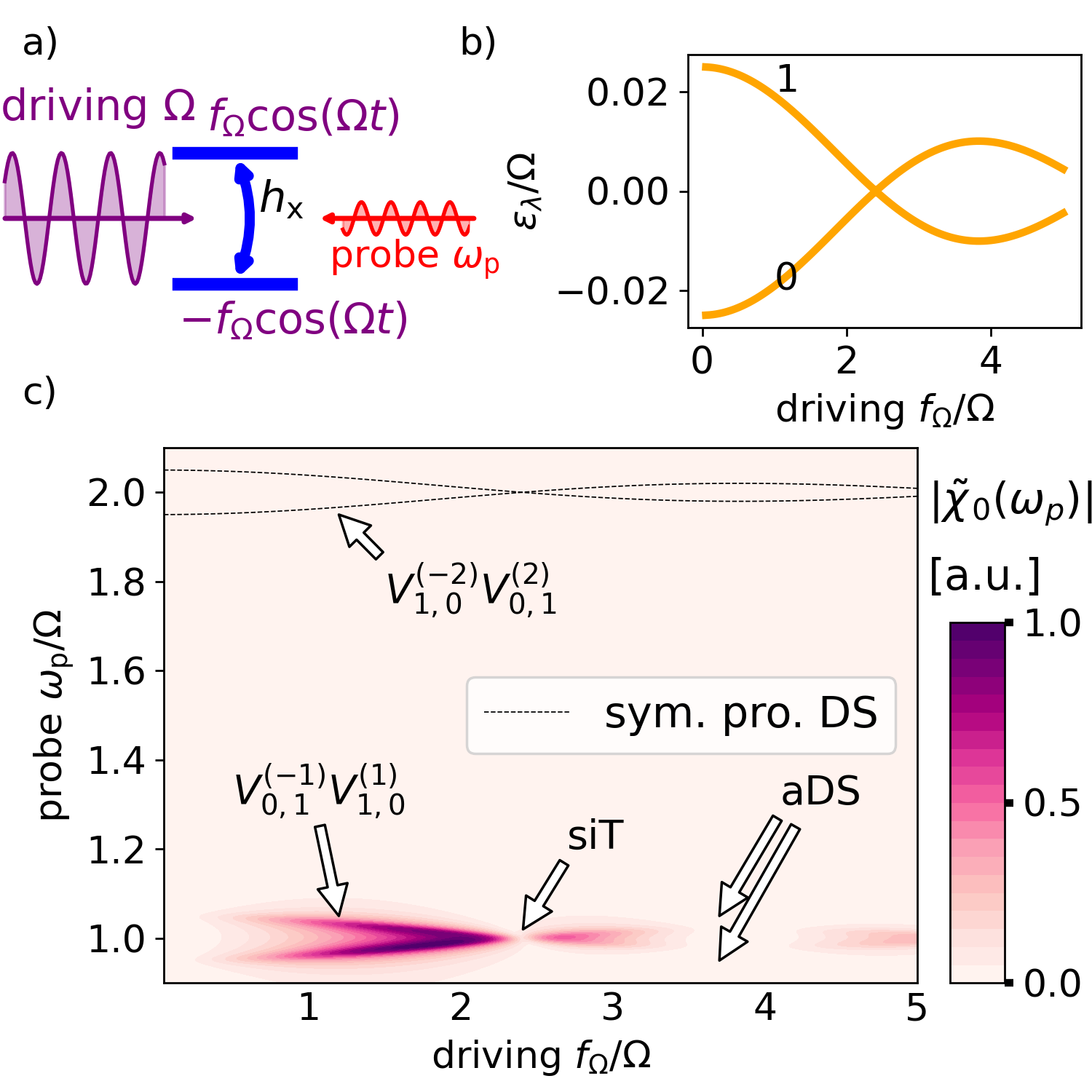
For illustration, we consider an ac-driven TLS sketched in Fig. 3(a) and described by the Hamiltonian
| (13) |
where are the Pauli matrices, is the tunneling amplitude, and the driving strength. The TLS is weakly dissipative, as in the spin-boson model, such that it reaches the stationary state in Eq. (3). The dipole transition operator in Eq. (1) is . For and , the TLS exhibits a dynamical parity symmetry defined above, which gives rise to the coherent destruction of tunneling effect at an exact quasienergy crossing, depicted in Fig. 3(b) at [36, 50], and enables the siT in the current context. Additionally, the TLS exhibits spDSs and spDBs according to Eq. (8) and Eq. (9) as for even because of the dynamical parity symmetry.
For the TLS, a particle-hole symmetry is defined for and . For , a second particle-hole symmetry is given for and . As in this case and , siT with appears according to Eq. (12), and the response is complete suppressed for all . In Fig. 3(c), we consider for a finite but small such that the quasienergy degeneracy is lifted except of the crossing, and the particle-hole symmetry is slightly broken. As a consequence, the siT is not complete but scales as at the crossing.
Time-reversal and chiral symmetries. A time-reversal symmetry (chiral symmetry) is defined by Eq. (6) for (), arbitrary , and , (), where () is a unitary operator. As shown in the Supplementary Material [48], neither time-reversal symmetry nor chiral symmetry alone implies spDSs. However, the combination of time-reversal symmetry and chiral symmetry defines a particle-hole symmetry with , and . When they further fulfill , , , and , such that , spDSs appear because of the particle-hole symmetry. In general, the presence of any two symmetries out of particle-hole symmetry, chiral symmetry, and time-reversal symmetry implies the existence of the third one.
Conclusions. Using a unified conceptional framework based on Floquet response theory, we have predicted selection rules in periodically driven quantum systems, namely accidental dark states, symmetry-protected dark states, symmetry-protected dark bands, and symmetry-induced transparency. The latter three effects are protected by symmetries such that variations of symmetry preserving parameters do not destroy them. These symmetry-induced selection rules result from the destructive interference of a driven system synchronized to the periodic driving. The different effects have been illustrated in three example systems fulfilling different symmetries, demonstrating the flexibility and generality of our unified framework. The predicted selection rules are valid even for more complicated and realistic systems as long as the corresponding dynamical symmetries are fulfilled.
Our theoretical results are experimentally observable in systems that can reach the strong light-matter coupling regime such as cold-atom experiments [2] and superconducting circuits [51, 52, 53, 54]. For experiments with molecules, strong driving fields are necessary to generate high-order Floquet bands, but in cavity QED or plasmonic fields, the strong driving interaction condition can be relaxed for molecule ensembles interacting collectively with the light field [55, 56].
Acknowledgements. G. E. gratefully acknowledges financial support from the China Postdoc Science Foundation (Grant No. 2018M640054 ) and the Natural Science Foundation of China (Grant Nos. 11950410510 and U1930402), J. C. acknowledges support from the NSF (Grant Nos. CHE 1800301 and CHE1836913). The authors thank Tao Wang for helpful discussions.
References
- Fang et al. [2017] K. Fang, J. Luo, A. Metelmann, M. H. Matheny, F. Marquardt, A. A. Clerk, and O. Painter, Generalized nonreciprocity in an optomechanical circuit via synthetic magnetism and reservoir engineering, Nat. Phys. 13, 465 (2017).
- Yin et al. [2020] M.-J. Yin, T. Wang, X.-T. Lu, T. Li, Y.-B. Wang, X.-F. Zhang, W.-D. Li, A. Smerzi, and H. Chang, Rabi spectroscopy and sensitivity of a Floquet engineered optical lattice clock, arXiv:2007.00851 (2020).
- Li et al. [2020a] X. Li, D. Dreon, P. Zupancic, A. Baumgärtner, A. Morales, W. Zheng, N. R. Cooper, T. Donner, and T. Esslinger, Measuring the dynamics of a first order structural phase transition between two configurations of a superradiant crystal (2020a), arXiv:2004.08398 [cond-mat.quant-gas] .
- Pino et al. [2015] J. D. Pino, J. Feist, and F. J. Garciavidal, Signatures of Vibrational Strong Coupling in Raman Scattering, J. Phys. Chem. C 119, 29132 (2015).
- Shalabney et al. [2015] A. Shalabney, J. George, J. A. Hutchison, G. Pupillo, C. Genet, and T. W. Ebbesen, Coherent coupling of molecular resonators with a microcavity mode, Nat. Commun. 6, 5981 (2015).
- Sukharev and Nitzan [2017] M. Sukharev and A. Nitzan, Optics of exciton-plasmon nanomaterials, J. Phys. Condens. Matter 29, 443003 (2017).
- Pietikäinen et al. [2017] I. Pietikäinen, S. Danilin, K. S. Kumar, A. Vepsäläinen, D. S. Golubev, J. Tuorila, and G. S. Paraoanu, Observation of the Bloch-Siegert shift in a driven quantum-to-classical transition, Phys. Rev. B 96, 020501 (2017).
- Forn-Díaz et al. [2019] P. Forn-Díaz, L. Lamata, E. Rico, J. Kono, and E. Solano, Ultrastrong coupling regimes of light-matter interaction, Rev. Mod. Phys. 91, 025005 (2019).
- Kockum et al. [2019] A. F. Kockum, A. Miranowicz, S. De Liberato, S. Savasta, and F. Nori, Ultrastrong coupling between light and matter, Nat. Rev. Phys. 1, 19 (2019).
- Mukamel [1995] S. Mukamel, Principles of nonlinear optical spectroscopy (Oxford University Press, New York, 1995).
- Kohler [2018] S. Kohler, Dispersive readout: Universal theory beyond the rotating-wave approximation, Phys. Rev. A 98, 023849 (2018).
- Gu and Franco [2018] B. Gu and I. Franco, Optical absorption properties of laser-driven matter, Phys. Rev. A 98, 063412 (2018).
- Cabra et al. [2020] G. Cabra, I. Franco, and M. Y. Galperin, Optical properties of periodically driven open nonequilibrium quantum systems, J. Chem. Phys. 152, 094101 (2020).
- Engelhardt and Cao [tion] G. Engelhardt and J. Cao, Signatures of dynamical symmetries in Floquet response theory and spontaneous emission processes (in preparation).
- Kumar et al. [2020] A. Kumar, M. Rodriguez-Vega, T. Pereg-Barnea, and B. Seradjeh, Linear response theory and optical conductivity of Floquet topological insulators, Phys. Rev. B 101, 174314 (2020).
- Altland and Zirnbauer [1997] A. Altland and M. R. Zirnbauer, Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures, Phys. Rev. B 55, 1142 (1997).
- Langbehn et al. [2017] J. Langbehn, Y. Peng, L. Trifunovic, F. von Oppen, and P. W. Brouwer, Reflection-symmetric second-order topological insulators and superconductors, Phys. Rev. Lett. 119, 246401 (2017).
- Kawabata et al. [2019] K. Kawabata, T. Bessho, and M. Sato, Classification of exceptional points and non-Hermitian topological semimetals, Phys. Rev. Lett. 123, 066405 (2019).
- Duan et al. [2020] C. Duan, C.-Y. Hsieh, J. Liu, J. Wu, and J. Cao, Unusual transport properties with noncommutative system–bath coupling operators, J. Phys. Chem. Lett. 11, 4080 (2020).
- Thingna et al. [2020] J. Thingna, D. Manzano, and J. Cao, Magnetic field induced symmetry breaking in nonequilibrium quantum networks, New J. Phys. 22, 083026 (2020).
- Wu et al. [2013] J. Wu, R. J. Silbey, and J. Cao, Generic Mechanism of Optimal Energy Transfer Efficiency: A Scaling Theory of the Mean First-Passage Time in Exciton Systems, Phys. Rev. Lett. 110, 200402 (2013).
- Chuang et al. [2016] C. Chuang, C. K. Lee, J. M. Moix, J. Knoester, and J. Cao, Quantum diffusion on molecular tubes: Universal scaling of the 1D to 2D transition, Phys. Rev. Lett. 116, 196803 (2016).
- Thingna et al. [2016] J. Thingna, D. Manzano, and J. Cao, Dynamical signatures of molecular symmetries in nonequilibrium quantum transport, Sci. Rep. 6, 28027 (2016).
- Engelhardt and Cao [2019] G. Engelhardt and J. Cao, Tuning the Aharonov-Bohm effect with dephasing in nonequilibrium transport, Phys. Rev. B 99, 075436 (2019).
- Fleming [2009] I. Fleming, Molecular orbitals and organic chemical reactions. Student edition (Wiley-VCH, Weinheim, Germany, 2009).
- Roy and Harper [2017] R. Roy and F. Harper, Periodic table for Floquet topological insulators, Phys. Rev. B 96, 155118 (2017).
- Peng and Refael [2019] Y. Peng and G. Refael, Floquet second-order topological insulators from nonsymmorphic space-time symmetries, Phys. Rev. Lett. 123, 016806 (2019).
- Engelhardt et al. [2016] G. Engelhardt, M. Benito, G. Platero, and T. Brandes, Topological instabilities in ac-driven bosonic systems, Phys. Rev. Lett. 117, 045302 (2016).
- Engelhardt et al. [2017] G. Engelhardt, M. Benito, G. Platero, and T. Brandes, Topologically enforced bifurcations in superconducting circuits, Phys. Rev. Lett. 118, 197702 (2017).
- Gómez-León and Platero [2012] A. Gómez-León and G. Platero, Transport blocking and topological phases using ac magnetic fields, Phys. Rev. B 85, 245319 (2012).
- Yuen-Zhou et al. [2016] J. Yuen-Zhou, S. K. Saikin, T. Zhu, M. C. Onbasli, C. A. Ross, V. Bulovic, and M. A. Baldo, Plexciton Dirac points and topological modes, Nat. Commun. 7, 11783 (2016).
- Yan et al. [2019] Y. Yan, Z. Lü, J. Y. Luo, and H. Zheng, Role of generalized parity in the symmetry of the fluorescence spectrum from two-level systems under periodic frequency modulation, Phys. Rev. A 100, 013823 (2019).
- Yan et al. [2018] Y. Yan, Z. Lü, J. Y. Luo, and H. Zheng, Multiphoton-resonance-induced fluorescence of a strongly driven two-level system under frequency modulation, Phys. Rev. A 97, 033817 (2018).
- Chinzei and Ikeda [2020] K. Chinzei and T. N. Ikeda, Time crystals protected by Floquet dynamical symmetry in Hubbard models, Phys. Rev. Lett. 125, 060601 (2020).
- Buča et al. [2019] B. Buča, J. Tindall, and D. Jaksch, Non-stationary coherent quantum many-body dynamics through dissipation, Nat. Commun. 10, 1730 (2019).
- Grossmann et al. [1991] F. Grossmann, T. Dittrich, P. Jung, and P. Hänggi, Coherent destruction of tunneling, Phys. Rev. Lett. 67, 516 (1991).
- Bavli and Metiu [1993] R. Bavli and H. Metiu, Properties of an electron in a quantum double well driven by a strong laser: Localization, low-frequency, and even-harmonic generation, Phys. Rev. A 47, 3299 (1993).
- Alon et al. [1998] O. E. Alon, V. Averbukh, and N. Moiseyev, Selection rules for the high harmonic generation spectra, Phys. Rev. Lett. 80, 3743 (1998).
- Alon et al. [2000] O. E. Alon, V. Averbukh, and N. Moiseyev, High harmonic generation of soft x-rays by carbon nanotubes, Phys. Rev. Lett. 85, 5218 (2000).
- Alon [2002] O. E. Alon, Dynamical symmetries of time-periodic hamiltonians, Phys. Rev. A 66, 013414 (2002).
- [41] G. Engelhardt and J. Cao, Signatures of dynamical symmetries in floquet response theory and spontaneous emission processes, (in preparation) .
- Kohler et al. [1998] S. Kohler, R. Utermann, P. Hänggi, and T. Dittrich, Coherent and incoherent chaotic tunneling near singlet-doublet crossings, Phys. Rev. E 58, 7219 (1998).
- Blattmann et al. [2015] R. Blattmann, P. Hänggi, and S. Kohler, Qubit interference at avoided crossings: The role of driving shape and bath coupling, Phys. Rev. A 91, 042109 (2015).
- Shirai et al. [2015] T. Shirai, T. Mori, and S. Miyashita, Condition for emergence of the Floquet-Gibbs state in periodically driven open systems, Phys. Rev. E 91, 030101 (2015).
- Engelhardt et al. [2019] G. Engelhardt, G. Platero, and J. Cao, Discontinuities in Driven Spin-Boson Systems due to Coherent Destruction of Tunneling: Breakdown of the Floquet-Gibbs Distribution, Phys. Rev. Lett. 123, 120602 (2019).
- Xu and Cao [2016] D. Xu and J. Cao, Non-canonical distribution and non-equilibrium transport beyond weak system-bath coupling regime: A polaron transformation approach, Front. Phys. 11, 110308 (2016).
- [47] One can construct a Hamiltonian fulfilling a time-rotational symmetry defined by where for arbitrary Hermitian operators , and the arbitrary functions shall be periodic.
- [48] See Supplemental Materials for a detailed derivation of the symmetry-protected selection rules.
- Bernevig and Taylor [2013] B. A. Bernevig and L. H. Taylor, Topological Insulators and Topological Superconductors (Princeton University Press, 2013).
- Gong et al. [2009] J. Gong, L. Morales-Molina, and P. Hänggi, Many-body coherent destruction of tunneling, Phys. Rev. Lett. 103, 133002 (2009).
- Wang et al. [2019] T. Wang, Z. Zhang, L. Xiang, Z. Jia, P. Duan, Z. Zong, Z. Sun, Z. Dong, J. Wu, Y. Yin, and G. Guo, Experimental Realization of a Fast Controlled-Z Gate via a Shortcut to Adiabaticity, Phys. Rev. Applied 11, 034030 (2019).
- Zha et al. [2020] C. Zha, V. M. Bastidas, M. Gong, Y. Wu, H. Rong, R. Yang, Y. Ye, S. Li, Q. Zhu, S. Wang, Y. Zhao, F. Liang, J. Lin, Y. Xu, C.-Z. Peng, J. Schmiedmayer, K. Nemoto, H. Deng, W. J. Munro, X. Zhu, and J.-W. Pan, Ergodic-localized junctions in a periodically-driven spin chain, arXiv:2001.09169 (2020).
- Magazzù et al. [2018] L. Magazzù, P. Forndiaz, R. Belyansky, J. L. Orgiazzi, M. A. Yurtalan, M. Otto, A. Lupascu, C. Wilson, and M. Grifoni, Probing the strongly driven spin-boson model in a superconducting quantum circuit, Nat. Commun. 9, 1403 (2018).
- Chen et al. [2020] M.-B. Chen, B.-C. Wang, S. Kohler, Y. Kang, T. Lin, S.-S. Gu, H.-O. Li, G.-C. Guo, X. Hu, H.-W. Jiang, G. Cao, and G.-P. Guo, Double resonance landau-zener-stückelburg-majorana interference in circuit qed (2020), arXiv:2011.03697.
- Herrera and Spano [2016] F. Herrera and F. C. Spano, Cavity-controlled chemistry in molecular ensembles, Phys. Rev. Lett. 116, 238301 (2016).
- Li et al. [2020b] T. E. Li, A. Nitzan, and J. E. Subotnik, On the origin of ground-state vacuum-field catalysis: Equilibrium consideration, J. Chem. Phys. 152, 234107 (2020b).
Supplementary Material
I Floquet equation and dynamical symmetries
In this supplemental information, we provide details to establish the symmetry-protected dark state conditions, which are sketched in the main text. The starting point is the Floquet equation
| (14) |
and the time-spatial symmetry relation for a Hamiltonian in the Floquet space
| (15) |
where the symmetry is specified by the spatial operator , the time-shift , and .
II Dynamical Dipole elements
The susceptibility, introduced in the main text,
| (16) |
is expressed in terms of the dynamical dipole elements
| (17) |
which fulfill
| (18) | |||||
This relation will be used to prove the symmetry-protected dark state condition based on a dynamical particle-hole symmetry in Sec. IV.
III Rotational symmetry
Here we present the derivation of the dark state condition imposed by a dynamical rotational symmetry. For a unitary operator , with a positive integer , and , the general dynamical symmetry condition Eq. (15) specifies to a rotational symmetry
| (19) |
Applying Eq. (19) to Eq. (14), we find
| (20) |
This implies that every Floquet state is also an eigenstate of the rotational symmetry operator, such that
| (21) |
with eigenvalues and integers . We require that the transition dipole operator obeys with . Combining with Eq. (14), the dynamical dipole element fulfills
Recalling that , the last line establishes the dark state condition for a dynamical rotational symmetry
| (22) |
which is presented in the main text.
IV Pariticle-hole symmetry
Here, we provide details to establish the dark state condition induced by a dynamical particle-hole symmetry
| (23) |
where assumes the values for integers and and depends on the specific system. We obtain Eq. (23) from the general definition of the dynamical symmetries Eq. (15) for , with the complex conjugation operator and the unitary operator , and . Applying the definition in Eq. (23) to the Floquet equation Eq. (14), we find
| (24) |
which indicates that for every Floquet state with quasienergy , there is a symmetry-related partner
| (25) |
with quasienergy , and a gauge-dependent phase factor . The phase factor cannot be removed by a simple gauge transformation as the two Floquet states and are coupled. However, we can apply Eq. (25) twice and obtain
| (26) |
In general, , and we cannot find a gauge transformation such that . Only if and , we have , which will be used in the evaluation of the dynamical dipole elements. Furthermore, we require with . Using Eq. (25) and Eq. (26), we find that the dynamical dipole element obeys
| (27) | |||||
where we have used Eq. (18) in the last line. From line two to line three we have used the -periodicity of the integrand. This proves the particle-hole symmetry induced condition for dark states
| (28) |
which is presented in the main text.
V Chiral symmetry
Here we derive a constrain for the dynamical dipole elements under a dynamical chiral symmetry, and explain why the chiral symmetry on its own does not imply a symmetry-protected dark state condition. For a unitary , and an arbitrary , the general dynamical symmetry relation Eq. (15) defines a chiral symmetry
| (29) |
Applying this definition to the Floquet equation Eq. (14), we find
| (30) |
Similar to the particle-hole symmetry, Eq. (30) implies that for every Floquet state with quasienergy , there is a symmetry-related partner
| (31) |
with quasienergy and a gauge-dependent phase factor . The can not be arbitrarily changed by a gauge transformation. Chiral symmetry is not sufficient to determine a constrain for the dynamical dipole elements. To see this we conjugate Eq. (31) and insert it into itself, and obtain
| (32) |
When requiring , we can find a gauge transformation, for which . Using this and with to evaluate the dynamical dipole elements, we find
| (33) | |||||
where we have used Eq. (18) in the last line, and the periodicity of the integrand in line three. This relation alone does not imply a dark-state condition for the dynamical dipole elements. If was real (e.g., because of another symmetry relation), Eq. (33) would indeed imply a dark state condition, but chiral symmetry alone is not sufficient to guarantee this.
VI Time-reversal symmetry
Similar to the chiral symmetry, the time-reversal symmetry alone does not impose a dark state condition. A time-reversal symmetry in Eq. (15) is defined for , with a unitary operator , the complex conjugation operator , , and an arbitrary , so that
| (34) |
Applying this definition to the Floquet equation, we find
| (35) |
Thus, all Floquet states fulfill
| (36) |
with a phase factor , which can be transformed away by a gauge transformation. Using this to evaluate the dipole elements, we find
Similar to the chiral symmetry, this does not establish a dark state condition.
VII Combined chiral symmetry and time reversal symmetry
Importantly, the chiral-symmetry relation Eq. (33) and the time-reversal symmetry relation Eq. (LABEL:eq:dynamicalDipolElementsTRSymmetrySI) together do provide a sufficient condition for a symmetry-protected dark state. In the derivations in Sec. V, and Sec. VI we could choose the gauge fields independently, such that and . Yet, these gauges conditions can not be simultaneous fulfilled in general. However, the combination of a time-reversal symmetry and a chiral symmetry defines a particle-hole symmetry with and . When we additionally require that , , , such that , and , all requirements for symmetry-protected dark states in Sec. IV are fulfilled.
VIII Symmetry-induced transparency
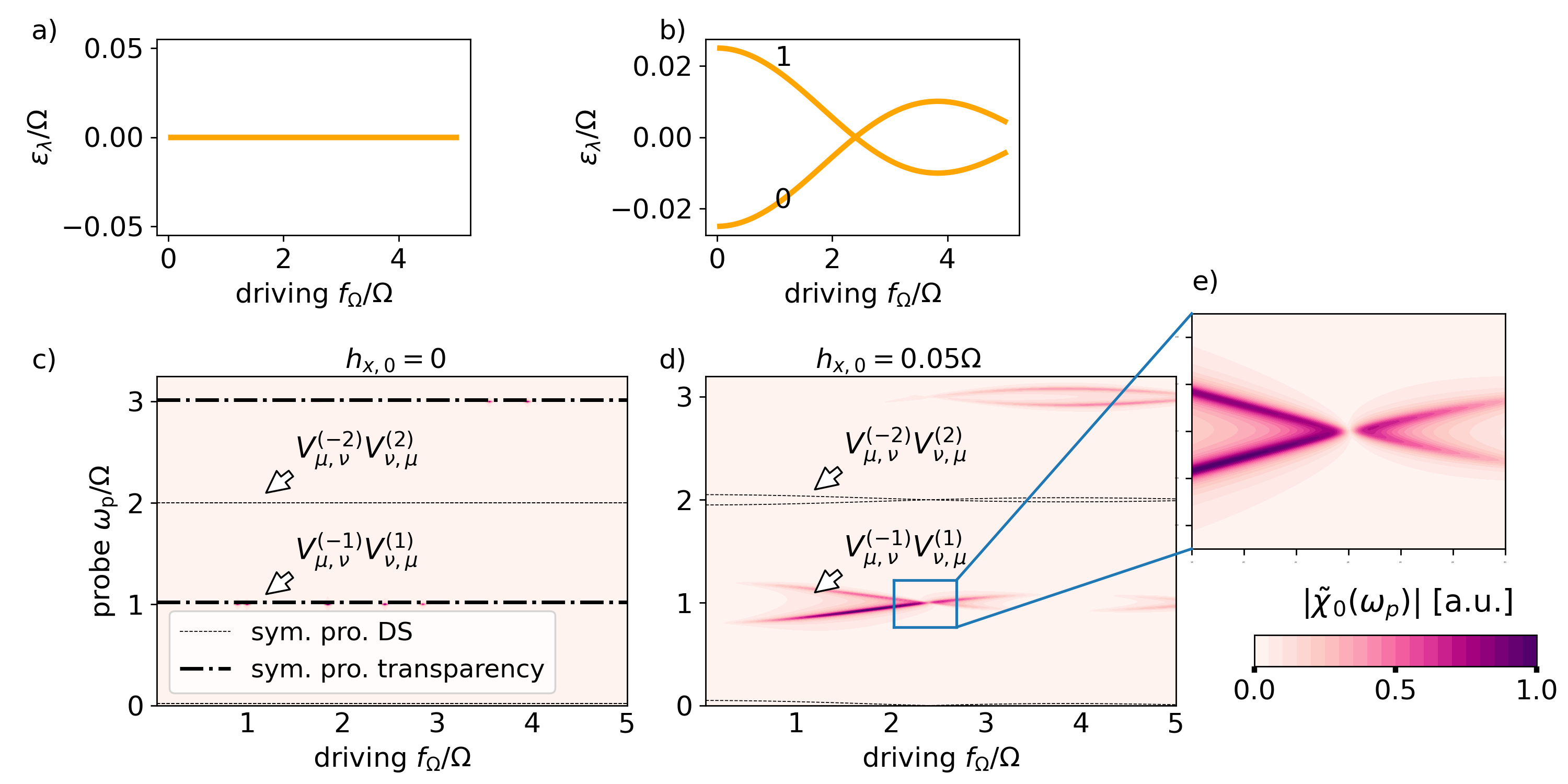
The symmetry-protected dark states and symmetry-protected dark bands introduced before are defined by vanishing dynamical dipole elements in Eq. (17). Here we want to introduce a distinct transparency effect, which is also protected by dynamical symmetries. In order to distinguish it from the symmetry-protected dark states and symmetry-protected dark bands, we coin it symmetry-protected transparency. We also explain a weaker form of it, i.e., symmetry-induced transparency.
While a symmetry-protected dark state is generated by a vanishing dipole element, i.e., , the symmetry-protected transparency is generated by a destructive interference of two transitions with non-vanishing dipole elements. More precisely, the transparency effect appears when for a given resonance the corresponding two terms in the susceptibility in Eq. (16) cancel each other, which requires
| (38) |
which will be investigated in the following.
The transparency effect appears as a consequence of two distinct particle-hole symmetries, if two symmetry-related resonances corresponding to the quasienergies become degenerate, i.e., . We denote the two particle-hole symmetries with , with corresponding time shifts , and require as well as (i.e., they are distinct). The Floquet states with form a subspace of dimension two. As and commute, and , there is a basis of this subspace such that
| (39) |
In this basis, there are no pairs of symmetry-related partners as introduced in Sec. IV. From Eq. (39) we obtain a basis with a symmetry-related pair by
| (40) |
which are related by the symmetry operations as
| (41) |
Thus, we have established symmetry-related pairs with respect to . Please note that the gauges phases are fixed by the procedure, such that we do not consider them in the following calculations. Using the symmetry to evaluate the dynamical dipole elements, we find
Using to evaluate the dipole elements based on Eq. (27), we find . Combining both results, we obtain
| (43) |
Inserting Eq. (43) into Eq. (38), we find the transparency condition
| (44) |
which is the condition presented in the main text. Noteworthy, for the two resonances can also add up constructively.
For illustration, we consider the ac-driven two-level system (TLS) which is introduced in the main text in Eq. (12). Its Hamiltonian reads
| (45) |
where are the Pauli matrices, is the tunneling amplitude, and the driving strength. The dipole transition operator is .
For , a particle-hole symmetry is defined for and , and a second particle-hole symmetry is given for and . The quasienergy spectrum is flat, i.e., , as depicted in Fig. 4(a). As , a symmetry-protected transparency with appears for all according to the condition Eq. (44). We note that the transitions for even , e.g. , are additionally suppressed because of a dark state selection rule imposed by the dynamical parity symmetry introduced in the letter.
For a finite but small , the symmetry is slightly broken. The quasienergy spectrum is not flat anymore as can be seen in Fig. 4(b). There is still a quasienergy crossing close to , giving rise to a coherent destruction of tunneling. In Fig. 4(d) we depict . Because of the lifted quasienergy degeneracy, the transitions are now visible. However, the system is still transparent at the quasienergy crossing. This is a consequence of the symmetry-protected transparency, which remains approximately valid as the symmetry is only slightly broken. In order to emphasize the relation to the symmetry-protected transparency, we coin this weaker effect symmetry-induced transparency. The symmetry-induced transparency scales as at the crossing. It is related to a small asymmetry of the response peaks of . Instead of the Floquet-Gibbs distribution, we choose and as the stationary state distribution in Fig. 4(c) to highlight the symmetry-induced transparency.