Dynamical Influence of a Central Massive Object on Double-Barred Galaxies: Self-Destruction Mechanism of Secondary Bars

The galaxy model adopted in this study is based on Model 2 used in Maciejewski & Sparke (2000). The components were a spheroid (i.e., stellar bulge + dark matter halo), a stellar disc, and two stellar bars; their respective density distributions are described below. For the bulge and halo components, we adopted the following density distribution of the modified Hubble profile:

$$\rho(r)=\rho_{\mathrm{b}}\left(1+\frac{r^{2}}{r_{\mathrm{b}}^{2}}\right)^{-1.5},$$

(1)

where $r^{2}=x^{2}+y^{2}+z^{2}$, $r_{\mathrm{b}}$ is the scale length of the bulge, and $\rho_{\mathrm{b}}$ is the central density. The disc component adopted the surface density distribution of the Kuzmin–Toomre model.

$$\Sigma(R)=\Sigma_{\rm d,0}\left(1+\frac{R^{2}}{R_{\rm d}^{2}}\right)^{-1.5},$$

(2)

where $R^{2}=x^{2}+y^{2}$, $\Sigma_{\rm d,0}$ is the central surface density and $R_{\rm d}$ is the scale length of the disc. The potentials of both the density distributions can be calculated analytically (Binney & Tremaine, 2008).

For the two-bar components, the density distribution of the prolate Ferrers ellipsoid is assumed to be

$$\rho(x,y,z)=\left\{\begin{array}[]{ll}\rho_{0}\left(1-m^{2}\right)^{n}&{\rm if}~{}~{}m<1,\\ 0&{\rm otherwise},\end{array}\right.$$

(3)

where $m^{2}=x^{2}/a^{2}+y^{2}/b^{2}+z^{2}/c^{2}$ and $\rho_{0}$ represents the central density with $n=2$. The gravitational potential and acceleration of the Ferrers ellipsoid cannot be determined analytically from the above density distribution. This study employed the polynomial expansion approximation of Pfenniger (1984) to calculate the gravitational potential and accelerations of $n=2$ Ferrers ellipsoids¹¹1The original equations in Pfenniger (1984) include certain typos. We fixed these by following Olle & Pfenniger (1998).. The numerical values for each parameter are summarised in Table 1. The circular velocity curve ($V_{\rm cir}$) is shown in Figure 1.

Figure 2 shows the angular velocity curves ($\Omega$; dashed line) and $\Omega-\kappa/2$ (dotted line) of the M0 model. Here, $\Omega\equiv V_{\rm circ}/R$ and $\kappa$ are the angular and radial epicyclic frequencies, respectively, which are evaluated from the axisymmetric gravitational potential of the galaxy (Binney & Tremaine, 2008). Further, $\Omega_{\rm p}$ and $\Omega_{\rm s}$ denote the pattern speeds of the primary and secondary bars, respectively. As evident, the primary bar has two inner Lindblad resonances (ILRs) at approximately 0.15 and 2.3 kpc, and a co-rotation (CR) resonance at approximately 2.2 kpc. Further, the secondary bar has no ILR but a CR at approximately 2.2 kpc. These resonance radii changed in the presence of CMC (see Section 2.2).

To investigate the dynamic effects of CMOs in orbits with double bars, we introduced a fixed CMO in a double-barred potential. For simplicity, following previous studies (Shen & Sellwood, 2004; Du et al., 2017), we modeled the gravitational potential of the CMO as a Plummer sphere:

$$\Phi_{\mathrm{CMO}}(r)=-\frac{GM_{\mathrm{CMO}}}{\sqrt{r^{2}+\epsilon_{\mathrm{CMO}}^{2}}},$$

(4)

where $M_{\rm CMO}$ and $\epsilon_{\rm CMO}$ are the mass and scale lengths of CMO, respectively.

The mass of the CMO is an interesting parameter in the interaction between CMO and the secondary bar from $N$-body simulations studied by Du et al. (2017) and Guo et al. (2020). In this study, we introduced the $M_{\rm CMO}=0$, $10^{6}M_{\odot}$, $10^{7}M_{\odot}$, and $10^{8}M_{\odot}$ cases as models, because we considered that CMO increased its mass because of the action of the secondary bar and other factors. Expressed as a ratio of the galaxy mass, the ratios are $M_{\rm CMO}$/$M_{\rm galaxy}\approx 0$, $10^{-5}$, $10^{-4}$, and $10^{-3}$. Because $\epsilon_{\rm CMO}$ controls the compactness of the CMO, we used $\epsilon_{\rm CMO}=10$ pc to mimic a compact CMO such as SMBH and NSC. The parameters of the CMOs used in this study are summarised in Table 2.

Figure 3 shows $\Omega-\kappa/2$ as a function of $R$ for each model, with the horizontal lines representing $\Omega_{\rm p}$ and $\Omega_{\rm s}$. The intersection of these lines and curves indicated the radius of the ILR. Open circles and triangles denote the locations of the inner ILR of the primary bar, iILR(p), and inner inner ILR of the primary bar, iiILR(p), respectively, whereas open squares indicate the location of the ILR of the secondary bar, ILR(s). As evident, the increase in the mass of the CMO significantly affected the axisymmetric gravitational field of the galaxy, resulting in changes in $\Omega-\kappa/2$. Consequently, the location of the iILR(p) and the appearance of new resonances are shifted. The location of iILR(p) shifted inward and was situated at approximately $R=0.1$ kpc in the M7 model, whereas it was located at approximately $R=0.14$ kpc in the M0 and M6 models. The M8 model lacked the iILR(p) but identified two new resonances, the ILR(s) of the secondary bar and the iiILR(p) of the primary bar, in the M6 and M7 models. In the M7 model, the locations of iILR(p) and iiILR(p) were nearly identical, situated at approximately $R=0.1$ kpc, and the location of iiILR(p) shifts outwards compared with the M6 model. Finally, in the M8 model, the ILR(s) moved further to approximately $R=0.13$ kpc, and both iiILR(p) and iILR(p) disappeared.

This study focused on multiperiodic orbits to support the time-dependent gravitational potential of a two-dimensional (2D) double-barred galaxy, as invoked by Maciejewski & Sparke (1997, 2000). Before explaining these supporting orbits, we review orbital families in a rigidly rotating single bar. A rigidly rotating single-bar potential comprises two main families of stable periodic orbits: $x_{1}$ and $x_{2}$ (Contopoulos & Papayannopoulos, 1980; Athanassoula et al., 1983). In general, periodic orbits always move along the same curve (i.e., closed orbits). If they are stable, they form backbones of a steady potential; the nearby orbits are trapped around them (Binney & Tremaine, 2008). Stable periodic orbitals are referred to as parent orbits. The stable periodic orbits in a single-bar potential, that is, the $x_{1}$ orbital family, comprise orbits elongated in the direction of the bar major axis, whereas the $x_{2}$ orbital family comprises orbits elongated perpendicular to the major axis. In the self-consistent single bar, most stars are in orbits trapped around the $x_{1}$ family (Sparke & Sellwood, 1987; Pfenniger & Friedli, 1991). Hence, the $x_{1}$ family constitutes the primary backbone of the orbital structure of a rigidly rotating single bar.

However, if a gravitational potential has a double bar, it pulsates with a $\omega_{\mathrm{p}}=2\left(\Omega_{\rm s}-\Omega_{\rm p}\right)$ frequency in a system where one bar is fixed (the factor of two is because of bisymmetry). Hence, in general, orbits in a double-barred potential lack a conserved integral of motion and are not closed in any rotating frame of reference. Instead, stars are often assumed to be chaotic, exploring large regions of the phase space. However, Maciejewski & Sparke (1997, 2000) alluded that these potentials admit families of regular multiperiodic orbits. They postulated that these are closed curves, which, when populated with stars moving in a double-bar potential, return to their original positions every time the bars return to the same relative orientation. They referred to these curves as “loops”. These are the double-frequency orbits driven by two bars (Maciejewski & Athanassoula, 2007). Stars trapped around these stable loops could form the building blocks for a long-lived, double-barred galaxy (Maciejewski & Athanassoula, 2008), similar to the manner in which stars are trapped near the $x_{1}$ family in a single-barred galaxy. Hence, the loops are generalizations of the parent orbits in a single bar.

Figure 4 shows an example of a loop in the M0 model (i.e., no CMO) drawn by outputting stars when the relative direction of the bar becomes a specific angle. Based on the relative direction of the bar, the flatness of the closed orbit and alignment of the axis with the secondary bar are slightly different. However, the closed orbit rotates along the gravitational potential of the secondary bar. Thus, the loops shown in Figure 4 can be considered the building block orbits of a self-consistent double-barred galaxy.

However, the self-consistency of loops is not always guaranteed. In fact, Maciejewski & Sparke (2000) suggested that a long-lived secondary bar may exist only when a corotation resonance (CR) of the secondary bar, $R_{\rm CR(s)}$ is located near the ILR of the primary bar, $R_{\rm ILR(p)}$. This condition was satisfied in our galaxy models (Figure 2).

The ring width diagram method aims to determine the initial conditions required for a particle to form a ‘loop’ orbit in a double-barred gravitational potential. Ring width ($w$) is the radial width of the ring drawn by the orbit when the orbit of a particle is calculated for a sufficiently long time in a galaxy. Here, $w$ of the loop orbit is very small, whereas that of an orbit with large free oscillation to the loop orbit is large.

To create the ring width map, we assumed that the major axes of the two bars coincided at $t=0$ and the initial conditions for the particle were $(x,y,z,v_{x},v_{y},v_{z})=(0,y_{\rm init},0,v_{x,\rm init},0,0)$, where $y_{\rm init}$ and $v_{x,\rm init}$ are the initial values of $y$ and $v_{x}$, respectively. The equations of motion were integrated for 30 Gyr, and the positions and velocities of the particles were recorded only when the major axes of the primary and secondary bars were aligned using the loop property.

To obtain $w$, we divided the ring into 40 parts, wherein for each region, we considered the difference between the far and near points, denoted as $w_{i}~{}(i=1,2,...,40)$. Subsequently, the average value of $w_{i}$ was obtained as follows:

$$w^{\prime}=\sum_{i=1}^{40}\frac{w_{i}}{40}.$$

(5)

Furthermore, $w^{\prime}$ can be normalized by the total time average $r_{\rm ave}$ of the particle $r(t)=x^{2}+y^{2}$. Consequently, the ring width $w$ can be obtained as

$$w=\frac{w^{\prime}}{r_{\rm{ave}}}.$$

(6)

By following this procedure, the initial conditions required for a particle to form a loop orbit with a double-barred gravitational potential can be determined.

Figure 5 shows an examination of the ring-width diagrams for each model, where the ring width ($w$) is represented by gray colors derived from the initial conditions determined by the horizontal and vertical axes. In the absence of a CMO, our M0 model replicated the analysis in Maciejewski & Sparke (2000). The model exhibited a prominent outer arch and two inner islands, with the outer arch corresponding to the $x_{1}$ orbits of the primary bar and the two inner islands corresponding to the $x_{2}$ orbits of the primary bar. However, for a double-bar system, the inner arch exhibits a gap, which divides it into left and right islands (Maciejewski & Sparke, 2000), similar to our calculations. In this case, they showed that the right- and left-side islands comprised the $x_{\rm 2p}$ and $x_{\rm 2s}$ orbits, respectively. Therefore, the loops supporting the primary bar were the $x_{\rm 1p}$ and $x_{\rm 2p}$ orbits, and those supporting the secondary bar are the $x_{\rm 1s}$ and $x_{\rm 2s}$ orbits. This is because the major axes of $x_{\rm 1p}$ and $x_{\rm 2p}$ orbits and the major axis of the gravitational potential indicate that the primary bars are consistently nearly coincident. Similarly, the major axes of $x_{\rm 1s}$ and $x_{\rm 2s}$ orbits and the major axis of the gravitational potential indicate that the secondary bar is always almost coincident.

The introduction of a CMO into the model significantly altered the structure of the ring-width diagrams. The ring-width diagram of the M6 model is shown in the upper right panel of Figure 5. Two additional “gaps” were observed in the ring width distribution related to the $x_{\rm 1s}$ orbits owing to the presence of the CMO, with these new distributions tentatively named $x_{\rm 1s}^{\prime}$ and $x_{\rm 1s}^{\prime\prime}$. With the increase in the CMO mass in the M7 and M8 models (lower left panels of Figure 5), these gaps shifted positions. Further, the $x_{\rm 1s}^{\prime\prime}$ orbital region expanded, whereas the gaps between the $x_{\rm 1s}$ and $x_{\rm 1s}^{\prime}$ orbits and the $x_{\rm 1s}^{\prime}$ orbits disappeared.

Through comparisons of the locations of the gaps with the resonance radii, the presence and growth of the CMO were found to substantially influence the orbital structures, particularly in the inner regions. In the M0 model, iILR(p) (open circle in Figure 3) corresponds to the break between the $x_{\rm 1s}$ and $x_{\rm 2s}$ orbits in the ring-width diagram (approximately $y_{\rm init}=0.1$–0.2, $v_{x,\rm init}=100$–300). In the M6 model, ILR(s) and iiILR(p) (open squares and triangles in Figure 3, respectively) correspond to the two lower-left breaks in the ring-width diagram (approximately $y_{\rm init}=0.01$–0.1, $v_{x,\rm init}=30$–60 and approximately $y_{\rm init}=0.01$–0.04, $v_{x,\rm init}=10$–30, respectively). In M7 model, the outward shifts of ILR(s) and iiILR(p) (squares and triangles in Figure 3, respectively) correspond to the movement of the two gaps to the upper right of the ring-width diagram (approximately $y_{\rm init}=0.01$–0.2, $v_{x,\rm init}=80$–200, and approximately $y_{\rm init}=0.01$–0.2, $v_{x,\rm init}=30$–90, respectively). The changes in the M8 model were more intricate: the ILR(s) (open squares in Figure 3) corresponds to the break between the $x_{\rm 2s}$ and $x_{\rm 1s}^{\prime\prime}$ orbits in the ring-width diagram (approximately $y_{\rm init}=0.01$–0.4, $v_{x,\rm init}=100$–300). Further, the disappearance of iiILR(p) corresponds to the disappearance of the break in the ring-width diagram, and the $x_{\rm 2s}$ orbital in the ring-width diagram is deformed because iILR(p) vanishes as well. Thus, the support on the left side (approximately $y_{\rm init}=0.05$–0.1, $v_{x,\rm init}=200$–400) is lost. Hence, we conclude that the presence of a CMO and its growth significantly influence the orbital structures, particularly in the inner regions, owing to the alteration of the resonances and contribution to the emergence of gaps in the ring-width diagrams.

As described in Section 3.1, we established the emergence of new orbital resonances in double-barred galaxies with a CMO, which resulted in significant dynamic shifts. To further investigate the effect of these resonances on the orbits, we analyze their properties, such as regularity or chaos, using the surface of section (SOS).

The SOS, a powerful tool for orbit analysis, is constructed at any accessible Jacobi energy (Binney & Tremaine, 2008; Shen & Sellwood, 2004). Using Cartesian coordinates in the rotating frame of the secondary bar and aligning the major axis of the secondary bar with the $x$-axis, we recorded the values of $(y,v_{y})$ for multiple orbits, each having the same $E_{\rm J,s}$ and crossing the minor axis ($y$-axis) as $v_{x}>0$. In this frame, the Jacobi energy of a particle is expressed as $E_{\rm J,s}\equiv E-\Omega_{\rm s}L_{z}$, where $E$ and $L_{z}$ represent the energy and angular momentum around the $z$-axis, respectively. The resulting $(y,v_{y})$ SOS depicts the particles moving within a limited 2D space, where the maximum possible excursion ($y_{\rm max}$) on the minor axis of the secondary bar is determined by the given $E_{\rm J,s}$.

Regular orbits that conserve another integral of motion in addition to $E_{\rm J,s}$, produce an invariant curve–a series of points lying on a closed curve in the SOS. By contrast, irregular chaotic orbits conserve only one integral of motion (i.e., $E_{\rm J,s}$) and occupy a region in the SOS. Because the double-frequency orbits, which serve as parent orbits in double-barred galaxies, possess another conserved quantity (Section 2.3), they are distributed in a one-dimensional manner within the SOS. Our analysis enabled us to determine whether these orbit types are dominant at a given Jacobi energy.

Figs. 6 and 7 show the SOSs with different $E_{\rm J,s}$, corresponding to $y_{\rm max}=0.05$ and 0.1 kpc, respectively. According to our definition, the right- and left-sides of the SOS are for forward and reverse rotation relative to the bar rotation, respectively. Hereafter, we focus only on the right-hand sides of the SOSs because it is known that the $x_{1}$ and $x_{2}$ orbits (i.e., $x_{\rm 2p}$ and $x_{\rm 2s}$), which are important parent orbits of the bar, are in forward rotation with the bar.

Our SOS analyses revealed a distinct “torus” structure, representing one-dimensional invariant curves, in our M0, M7, and M8 models at a $y_{\rm max}$ of 0.05 kpc (Figure 6). This structure is less evident in the M6 model, primarily because the iso-Jacobi energy curve (dotted green lines in Figure 5) intersects with gaps in the M6 model, as opposed to intersecting with the dark regions in the M0, M7, and M8 models. Similarly, a distinct “torus” structure can be observed in the M0, M6, and M8 models at $y_{\rm max}=0.05$ kpc but not in the M7 model (Figure 7). This indicates that the orbits within the loop were regular, whereas the gaps or resonances in the ring width diagram contained chaotic orbits.

In summary, these findings suggest that, with an increase in the CMO mass, the regular orbits are gradually disrupted from the center to the outer region owing to the shifting resonance location. Once the resonance passed, the CMO’s spherically symmetric potential resulted in the formation of regular circular orbits that could not support the bar structure in a double-barred galaxy.

In this section, we analyze the multiperiodic regular orbits or loops of each model. Figure 8 shows the loops that uphold the secondary bars in each model. Figure 8 focuses on the sub-kpc region at the center, where the major axis of the secondary bar is the $x$-axis. The resonance radii of the primary and secondary bars are marked with various line patterns. In all cases, a lack of an orbital family at these resonance locations and a transition to a different orbital family on either side were observed.

In the M0 model, the $x_{\rm 1s}$-orbital family is located inside the inner ILR of the primary bar iILR(p), whereas the $x_{\rm 2s}$-orbital family is located in the outer part. The size of the secondary bar is correlated with the area occupied by $x_{\rm 2s}$, where $x_{\rm 1s}$ occupies a significantly smaller area. Therefore, the $x_{\rm 2s}$-orbital family plays a significant role in maintaining a secondary bar.

As discussed in Section 3.1, new orbital families $x_{\rm 1s}^{\prime}$ and $x_{\rm 1s}^{\prime\prime}$ emerged within the $x_{\rm 2s}$ orbital family in the models with a CMO. The $x_{\rm 1s}$ and $x_{\rm 2s}$ orbital families are presented in the second row of Figure 8, $x_{\rm 1s}^{\prime}$ orbital family in the third row, and $x_{\rm 1s}^{\prime\prime}$ orbital family in the bottom row. In the M6 and M7 models, variations in the orbital families related to the CMO occurred within the iILR(p), whereas the $x_{\rm 2s}$ orbital family remained relatively unaffected by the CMC. However, in the M8 model, the $x_{\rm 1s}^{\prime\prime}$ orbital family is sufficiently developed to overlap with the region occupied by the $x_{\rm 2s}$ orbital family.

We examined the inability of the secondary bar to gain support from the newly formed $x_{\rm 1s}^{\prime\prime}$-orbital family, which contributes to its destruction. The $x_{\rm 1s}^{\prime\prime}$ orbital family with its major axis perpendicular to that of the secondary bar does not align with the structure of the secondary bar. This is similar to the notion that the $x_{2}$ orbital family cannot provide consistent support for the bar in a single bar model (Binney & Tremaine, 2008). Therefore, we expect that the $x_{\rm 1s}^{\prime\prime}$ orbital family will not be able to uphold a secondary bar as it becomes dominant. Briefly, the M8 model fails to maintain the secondary bar.

In this section, the conditions that lead to secondary bar destruction are explored. As discussed in the previous sections, it is postulated that the secondary bar disintegrates when the $x_{\rm 1s}^{\prime\prime}$ region, owing to its intrusion into the $x_{\rm 2s}$ region, loses self-consistency. Based on the results presented in Figure 8, in the M6–M7 models, where $x_{\rm 1s}^{\prime\prime}$ does not extend into the $x_{\rm 2s}$ region, the progression from the innermost region is $x_{\rm 1s}^{\prime\prime}$, ILR(s), iiILR(p), iILR(p), and $x_{\rm 2s}$. With the expansion of the CMO, the $x_{\rm 1s}^{\prime\prime}$, ILR(s), and iiILR(p) regions increase gradually. However, in the M7 model, the $x_{\rm 1s}^{\prime\prime}$ region remained small because of the minimal size of ILR(s). By contrast, in the M8 model, the disappearance of iiILR(p) and iILR(p) facilitated the expansion of ILR(s), resulting in $x_{\rm 1s}^{\prime\prime}$ orbits extending their region.

Conversely, a condition signifying that the secondary bar has already broken is the relocation of ILR(s) into the region previously occupied by $x_{\rm 2s}$ orbits. The radial expansion of ILR(s) prompts an enlargement of the $x_{\rm 1s}^{\prime\prime}$-orbit region, which already lost its self-consistency by the time it entered the $x_{\rm 2s}$ region. Consequently, the encroachment of ILR(s) into the $x_{\rm 2s}$ region is a strong indicator of secondary bar disintegration.

This scenario is illustrated in Figure 9. We label the first event (I) as the disappearance of the intersection and the second event (II) as the intrusion of the ILR into the $x_{\rm 2s}$ orbit region. Event (I) corresponds to the disappearance of iiILR(p) and iILR(p) when the minimum value of the rotation rate minus half the radial frequency ($\Omega-\kappa/2$) exceeded the pattern speed of the primary bar ($\Omega_{\rm p}$). Event (II) refers to the encroachment of ILR(s) and $x_{\rm 1s}^{\prime\prime}$ orbit into the $x_{\rm 2s}$ orbit region as ILR(s) moved beyond the gray zone in this figure. The conditions of the secondary bar disruption can be inferred from these two events, which occurred in conjunction with an increase in CMO mass, occurring between events (I) and (II).

We estimated the $M_{\rm CMO}/M_{\rm galaxy}$ ratio under the secondary bar destruction conditions. Given that Event (I) aligned closely with the M7 model and Event (II) approximated the M8 model, it is plausible to assume $M_{\rm CMO}$ at the time (I) is $10^{7}~{}{M_{\rm\odot}}$ and $M_{\rm CMO}$ at the time (II) is $10^{8}~{}{M_{\rm\odot}}$. In this scenario, the timing of the secondary bar disruption in our model aligns with a $M_{\rm CMO}/M_{\rm galaxy}$ ratio of approximately $10^{-3}$. This result is consistent with the findings of $N$-body simulations in previous studies (Du et al., 2017).

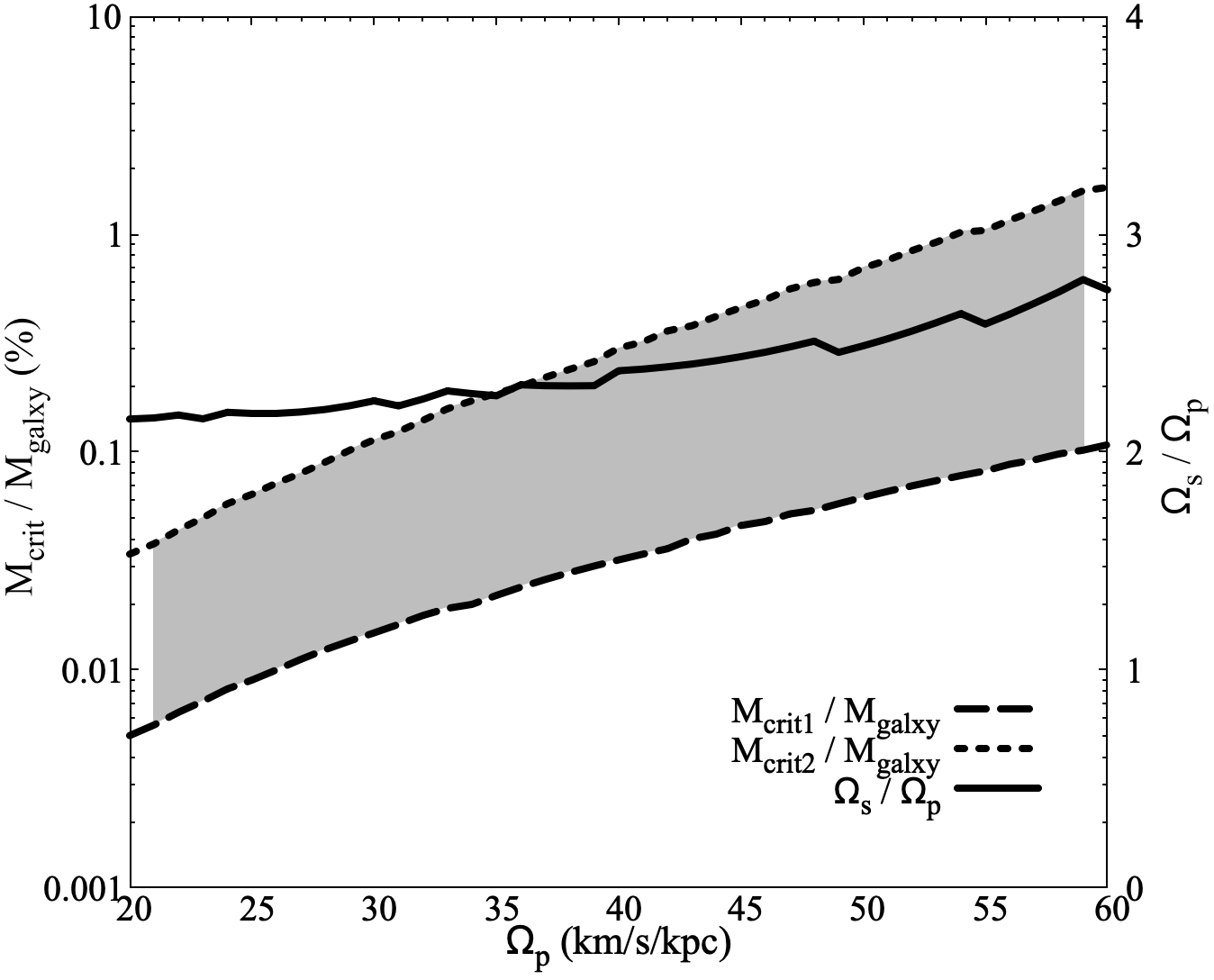
We now focus on the more general conditions. The preceding discussion relies on the results derived under the assumption of the pattern speeds applied in this study. However, as suggested by the discussion thus far, the effect of the CMO is pivotal in determining the position of the resonance radius, which is crucial for secondary bar disruptions. Consequently, we explored the dependence of the disruption conditions of the secondary bar on the bar pattern speed. Henceforth, we discuss the relationship between $M_{\rm CMO}/M_{\rm galaxy}$ and bar pattern speeds.

Given that the secondary bar forms within the radius of the outer ILR of the primary bar ($R_{\rm oILR(p)}$), the double bar can coexist stably if the co-rotation radius of the secondary bar ($R_{\rm CR(s)}$), which is approximately equivalent to the long radius of the secondary bar, and is within $R_{\rm oILR(p)}$. In this scenario, $R_{\rm CR(s)}\leq R_{\rm oILR(p)}$ holds true (Maciejewski & Athanassoula, 2008; Maciejewski & Small, 2010). From the intersection of $\Omega-\kappa/2$ and $\Omega_{\rm p}$, $R_{\rm oILR(p)}$ is determined, and $\Omega_{\rm s}$ is set such that $R_{\rm CR(s)}$ is equal (see Figure 10). If we denote this process by $f(x)$, the relationship is obtained as

$$\Omega_{\rm s}=f(\Omega_{\rm p}).$$

(7)

The derived ratio $\Omega_{\rm s}/\Omega_{\rm p}=f(\Omega_{\rm p})/\Omega_{\rm p}$ is plotted in Figure 11, yields a value in the range of 2.1–2.6, given that 20  km s^-1 kps^-1$\lesssim\Omega_{\rm p}\lesssim$60  km s^-1 kps^-1 (Aguerri, Debattista & Corsini, 2003; Rautiainen, Salo & Laurikainen, 2008).

For double-bar galaxies satisfying eq.(7), we calculated the CMO masses at which Events (I) and (II) occurred. The CMO masses where Events (I) and (II) occurred are denoted as $M_{\rm crit,I}$ and $M_{\rm crit,II}$, respectively. Figure 11 shows $M_{\rm crit,I}/M_{\rm galaxy}$ and $M_{\rm crit,II}/M_{\rm galaxy}$ for a given $\Omega_{\rm p}$. A notable feature is that with increase in $\Omega_{\rm p}$, $M_{\rm crit,I}/M_{\rm galaxy}$ and $M_{\rm crit,II}/M_{\rm galaxy}$ increased slowly/blue. As shown in Fig. 3, this is because the farther the line $\Omega_{\rm p}$ moves upward, the larger the CMO mass must be to eliminate the intersection of $\Omega-\kappa/2$ and $\Omega_{\rm p}$. Similarly, the more we move the line of $\Omega_{\rm p}$, the more the intersection point of $\Omega-\kappa/2$ and $\Omega_{\rm p}$ shifts to the left in the figure. Therefore, the mass of the CMO must be increased to slide the intersection point into the region of iILR(p).

As shown in Figure 11, Event (I) occurred at $M_{\rm CMO}/M_{\rm galaxy}\approx 10^{-4}$–$10^{-3}$ and Event (II) occurred at $M_{\rm CMO}/M_{\rm galaxy}\approx 10^{-3}$–$10^{-2}$. As the secondary bar is projected to collapse between events (I) and (II), we can infer that a realistic double bar collapses when $M_{\rm CMO}/M_{\rm galaxy}$ ranges As $10^{-4}$–$10^{-2}$. This aligns with the results of Du et al. (2017) and Guo et al. (2020), who postulated that the secondary bar collapses when the CMO mass reaches approximately $10^{-3}$ of the total stellar mass. Thus, we can argue that this elucidates the mechanism of secondary bar destruction through an increase in CMO mass.