Dynamical descalarization in Einstein-Maxwell-scalar theory
Abstract
For an asymptotically flat hairy black hole in the Einstein-Maxwell-scalar (EMS) theory, we study the possibility of shedding off its scalar hair via nonlinear scalar perturbation fully interacting with the background spacetime. We examine the effect of the perturbation strength on the descalarization. The results show that the effective charge to mass ratio of the black hole plays the key role in the dynamical descalarization. The descalarization at the threshold is continuous. This indicates a second order phase transition.
I Introduction
In the framework of general relativity (GR), we have the black hole no hair theorem which states that a black hole can be described by only three macroscopic degrees of freedom (mass , electric charge and angular momentum ). In order to overcome problems in GR, such as the non-renormalization and the inevitable singularities etc., modified theories have been introduced to study the gravity. In the modified gravity, it was found that hairy black holes with more degrees of freedom can exist Herdeiro2015 ; Volkov2015 , for example in the Einstein-dilaton-Gauss-Bonnet theory Torii1997 ; Kanti1997 ; Kleihaus2011 ; Kleihaus2015 ; Pani2011 ; Herdeiro2014 ; Ayzenberg2014 , or with other matter fields HHVolkov1989 ; HHBizon1990 ; HHGreene1993 ; HHMaeda1994 ; HHLuckock1986 ; HHDroz1991 . In this paper, we focus on the black hole solutions with non-trivial scalar hair. They can be generated by the self-interaction potential of the scalar field Herdeiro2015 ; Zou:2014sja ; Mai:2020sac ; Hong:2020miv ; Mayo:1996mv ; Collodel:2022jly . For a Kerr black hole, the mass term of the scalar field induces superradiant instability and creates a stationary scalar hair around the black hole Cardoso:2005vk ; Dolan:2007mj ; Hod:2012px ; Herdeiro:2014goa . The dilatonic coupling between the scalar field and other source terms (curvature term or electromagnetic field) can also permit the hairy black hole solutions Torii1997 ; Kanti1997 ; Kleihaus2011 ; Kleihaus2015 ; Pani2011 ; Herdeiro2014 ; Ayzenberg2014 ; Zhang2021j ; Zhang2021a ; Richarte2022 ; Zhang:2015jda .
There exists a dynamical process, called spontaneous scalarizationDamour1993 ; Damour1996 ; Harada1997 ; Cardoso2013 ; Cardoso2013b ; Zhang2014 , to address scalar hair onto bald black holes and transform them into hairy black holes Doneva1711 ; Herdeiro2018 ; Fernandes2019 ; Silva1711 ; Antoniou1711 ; Cunha1904 ; Dima:2020yac ; Herdeiro2009 ; Berti2009 ; Brihaye2018 ; Guo2021 ; Ripley2020 ; Ripley2021 ; Ripley2020b ; Kuan2021 , branching from the Reissner-Nordström (RN) or Schwarzschild black holes. In this paper we focus on the Einstein-Maxwell-scalar (EMS) theory which induces the spontaneous scalarization through a non-minimal coupling between the scalar field and the electromagnetic field Herdeiro2018 ; Fernandes2019 ; Guo2021 . This model allows the electro-vacuum solution (the RN black hole), in different from the Einstein-Maxwell-dilaton theory Zhang2021j ; Zhang2021a ; Richarte2022 . Under an arbitrary small perturbation, the RN solution in this model spontaneously evolves to the hairy solution and the corresponding dynamic evolution was investigated in Xiong:2022ozw ; Zhang2021b ; Luo:2022roz for different asymptotic behaviors of spacetimes. In Xiong:2022ozw we confirmed that the growth rate of scalar hair for spontaneous scalarization is consistent with the fundamental instability mode calculated in the linear perturbation theory.
In addition to the scalarization, scalar hair on hairy black holes can also be removed through descalarization processes. The dynamic process of black hole descalarization was studied in Silva2020 ; Doneva:2022byd ; Elley:2022ept for the scalar-Gauss-Bonnet (sGB) theory where the removal of scalar hair is realized by the head-on collision of binary black holes. However, in these articles, the backreaction of scalar to the spacetime is not taken into account, where the nonlinear scalar equation of motion was only examined on the background. Another descalarization mechanism induced by accretion was also studied in generalized scalar-tensor theory Kuan2022 ; Liu:2022eri ; Liu:2022fxy . In EMS theory, the dynamical descalarization was studied in asymptotically anti-de Sitter (AdS) spacetime Zhang:2022cmu . It was found that the descalarization can be either continuous in models allowing spontaneous scalarization or discontinuous in models allowing nonlinear scalarization at the threshold. The descalarization has attracted more and more attention recently due to its potential observational signature in the gravitational wave signal Silva2020 ; Kuan2022 ; Doneva:2022byd ; Zhang:2022cmu ; Liu:2022eri ; Elley:2022ept ; Liu:2022fxy .
To simulate the astrophysical environment, we concentrate our attention in an asymptotically flat spacetime and consider the fully nonlinear dynamical descalarization process of shedding off scalar hair from a spherically symmetric scalarized black hole in the EMS theory. In EMS theory, hairy black holes exist only when charge to mass ratio is high and the scalar field is strongly coupling to the Maxwell field. If the final black hole mass increases so that the charge to mass ratio drops, the scalar hair can be deprived. In this work we will exhibit that such descalarization process can happen for a single black hole absorbing enough energy.
The organization of the paper is as follows. In section II we will introduce the EMS model, write out the equations of motion and discuss the initial conditions. Then in III we will present numerical result on the descalarization and disclose the relation between the energy dissipation and descalarization. Finally in the last section, we will summarize the obtained results.
II The EMS model
The action of the Einstein-Maxwell-scalar theory
| (1) |
where is the Ricci scalar, is the scalar field, and is the Maxwell gauge field. In this work, we take an exponential coupling
| (2) |
which remains a symmetry in the action (1). The equations of motion for the gravity, scalar and Maxwell field are respectively
| (3) | ||||
| (4) | ||||
| (5) |
The non-minimal coupling between the scalar field and the Maxwell field provides the scalar field a negative effective mass, which triggers the tachyonic instability of the scalar field perturbation in the RN black hole background in some parameter region.
II.1 The nonlinear equations
To simulate the nonlinear descalarization of shedding of scalar hair from a spherically symmetric hairy black hole in the EMS model, we use the Painlevé-Gullstrand (PG)-like coordinate ansatz
| (6) |
This coordinate is regular on the horizon and allows one of the radial boundaries of the numerical evolution to be within the black hole horizon. We take the gauge field as
| (7) |
then the Maxwell equation (5) gives , in which is interpreted as the electric charge. For numerical simulation we introduce auxiliary variables
| (8) |
The equations of motion become
| (9) | ||||
| (10) | ||||
| (11) | ||||
| (12) | ||||
| (13) |
and can be solved directly by a given from equation (8, 9) and (10). We use them to obtain the initial profile and the detailed process will be explained in subsection II.3.
The boundary conditions for the nonlinear evolution are given by
| (14) |
Here is the Arnowitt-Deser-Misner (ADM) mass, which includes the energy of the gravity, Maxwell and scalar fields in the system Hayward:1994bu . The first condition implies that we take the time coordinate as the proper time of the observer at spacial infinity. We will use the Misner-Sharp mass defined as
| (15) |
which tends to the total mass when . We also define the mass density
| (16) |
to exhibit the mass distribution of spacetime to better reveal the differences between the scalarized black hole and the scalar-free black hole. The reduced horizon area is given by
| (17) |
where the is the area of the apparent horizon.
II.2 Spontaneous scalarization
We first solve the equations of motion and display the space of parameters for the existence of scalarized black holes in the EMS theory in Fig.1. The results are consistent with Herdeiro2018 . In the gray region, the tachyonic instability of the scalar field in the bald RN black hole background is triggered. At the nonlinear level, while the RN black hole is perturbed by an arbitrarily small scalar perturbation, the scalar field exponentially grows and converges to a certain value, as shown in the left panel of Fig.2. In the final state, the black hole is covered by static scalar hair.

The right panel of Fig.2 shows that the reduced horizon area of the scalarized black hole branches off the RN black hole, and stays bigger. From the perspective of black hole thermodynamics, this tells us that a hairy black hole contains larger entropy than a bald black hole. At a threshold value of the charge to mass ratio, the thermodynamic instability can destroy the scalar-free black hole and transform it to a hairy black hole through a phase transition. For the hairy black hole, its charge to mass ratio can exceed the maximum value of the RN hole.


II.3 Initial conditions for descalarization
In this subsection, we discuss the initial condition for studying the dynamical descalarization. We add a wave packet of scalar field perturbation to the initial scalarized black hole, as shown in the left panel of Fig.3. Specifically, the initial scalar pulse is given by
| (18) | ||||
| (19) |
in which are the solutions of the scalar field, metric function and the horizon radius of the background scalarized black hole, respectively. is the strength of the initial perturbation and . The sign in (19) implies an ingoing/outgoing initial pulse respectively.
Given an initial perturbation, one can work out the initial metric functions by solving constraint equations (9,10) with an appropriate boundary condition at the spatial infinity. According to the relation between and the Misner-Sharp mass (15), we can describe this operation from the perspective of the Misner-Sharp mass. From (14) the parameter , which is the asymptotic value of Misner-Sharp mass at infinity, can be divided into two part
| (20) |
The is the mass of the original scalarized black hole system which we fixed as . The is the additional mass from the wave packet. The energy is positively related to the strength of the wave packet.


The right panel of Fig.3 sketches the behavior of the Misner-Sharp mass for appropriate parameters . Although initially the blue line completely coincides with the yellow line for the original of the scalarized black hole, at the position of the wave packet we observe a rapid jump in the blue line because of the addition of energy from the scalar perturbation.
The evolution is examined by using the fourth order difference method in the radial direction and the fourth order Runge-Kutta method in the time direction. We work out in the radial region from to , where always lies in the apparent horizon during the evolution. The radial space is compatified in a region by a coordinate transformation . More details were discussed in Xiong:2022ozw .
III Numerical results
III.1 Descalarization
In this subsection, we discuss the process of the descalarization. We first confirm the validity of our program. As shown in Fig.4, a scalarized black hole without scalar perturbation keeps unchanged. The orange line describes a scalarized black hole with an outgoing scalar perturbation and the blue line is for a scalarized black hole with an infalling of scalar wave packet respectively.




The blue line in the upper right panel manifests that the scalar hair is deprived by the ingoing wave packet after a certain period of time. Most energy of the wave packet is absorbed by the scalarized black hole and then decreases below the critical value as indicated in Fig.1. This leads the hairy black hole finally evolves into a bald RN black hole.
The situation for the outgoing wave packet is the opposite. Only very small amount of energy is absorbed by the black hole. Almost all energy of the wave packet escapes to the infinity and thus a cliff-like elevation appears in the orange line for the Misner-Sharp mass at the far region (). The escaping energy has little impact on the black hole system, which is clear by comparing the black and orange lines. As a result, the scalar hair is only a little smaller than the original scalarized black hole.
The results of choosing different coupling strength are shown by the red line in Fig.4. is still above when , so that the hairy black hole survives but with less scalar hair. The critical value decreases with the increase of as shown in Fig.1.
The diverse evolution results with three initial conditions shown in blue, orange, red lines have the same total mass . The asymptotic expression for the Misner-Sharp mass and at far region is given by and , respectively. We use interpolation to fit the first of the data of the Misner-Sharp mass to obtain the effective mass of each black hole system. All systems we simulated here has the same total mass . But the values of are 1.000 (black), 1.025 (orange), 1.488 (blue), 1.486 (red) respectively. The remaining energy are carried by the scalar field escaping to the infinity.




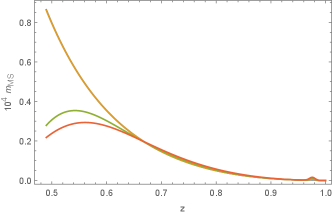
Then we investigate the dynamical descalarization under the same set of model parameters (, ), but with varying strength . In the upper left panel of Fig. 5, the scalar field decreases with the increase of until the scalar hair is removed. This relation is more explicit in the left panel of Fig. 6. Note that the descalarization at the threshold is continuous. This implies that the descalarization is a second order phase transition. The scalar field distributions of the final state are also displayed in Fig. 5. The red circle in the left bottom panel is enlarged at the upper right corner. The Misner-Sharp mass and its density at late times are also shown. The mass density of the scalarized black hole in the near horizon region is smaller than the descalarized one (the RN black hole).


In the right plot of Fig.6 we confirm the conclusions above, the effective parameter , where is the effective mass of the black hole system, determines whether the final state of evolution is scalarized or descalarized. The gray horizontal dashed line in the right panel denotes the threshold value for the shedding of scalar hair at .
In this subsection, we fix the mass of initial black hole . The total energy of the system increases with the perturbation, as shown in (20). Descalarization is essentially a dynamic process in which the charge to mass ratio decreases from scalarized region to the scalar-free region, as marked in the Fig.1 by two arrows. The crucial point is that the scalarized black hole must absorb extra energy. It is noteworthy that we select the effective mass instead of the ADM mass to calculate the charge to mass ratio. The ADM mass, which serves as the total energy of this system at the spatial infinity, can no longer accurately describe the energy of the black hole system in the dynamical evolution. Scalar perturbations going outwards to the spatial infinity occupies considerable amount of and they should be removed from the total mass .
III.2 Energy dissipation and scalarization
The charge to mass ratio plays a crucial role in the scalarization/descalarization. In this subsection, we fix the total mass and discuss the effect of energy dissipation to the infinity on the descalarization. The total mass consists of the contribution from the initial RN black hole and the scalar perturbation. We fix such that a static black hole system with lives in the region where no scalarized solution exists, as shown in Fig.1. However, for a dynamical system, some of the energy inevitably escapes to the infinity such that the effective charge to mass ratio becomes larger than and the final solution is scalarized. This is shown in Fig.7. Here we specify the initial configuration as a scalar-free RN black hole plus a finite outgoing scalar perturbation (18, 19) with . Fig.7 shows that part of the energy of the scalar field transmitted outward to infinity in time evolution. This results in a larger so that the final black hole becomes scalarized.

Fig.8 shows that the scalar hair forms only when , the strength of the initial perturbation, is large enough. The difference in the Misner-Sharp mass density between the scalarized black hole and the RN black hole is similar to the previous subsection. We can observe the outward dissipation of energy of the perturbation in the region near the infinity (). It looks small but actually accounts for a considerable proportion of the total energy because of the compactification and the long spacing of grid points near the infinity. For smaller , the initial RN black hole occupies more energy such that the effective charge to mass ratio is smaller. The final solution can not be scalarized. However, for larger , the initial RN black hole occupies less energy such that the effective charge to mass ratio is larger. The final solution can be scalarized. In other words, the initial perturbation divides part of the total energy . This results in the reduction of the initial energy of the RN black hole, i.e., the effective mass of the black hole is less than . With the increase of , the decreases until exceeds the critical value which eventually leads to the scalarization of black hole.

IV Summary and discussion
In this paper, we have investigated the physical process of shedding of scalar hair from scalarized black holes in the EMS theory in asymptotically flat spacetime. We concentrated on the coupling function , which permits the spontaneous scalarization. We started with a scalarized black hole obtained directly from solving the equations of motion. Then we injected scalar perturbations to the spacetime and considered various situations of the injections. We observed a new physical process in addition to binary black hole merge, which allows a single scalarized black hole to remove its scalar hair after absorbing enough energy. We find that the effective charge to mass ratio plays the key role in the descalarization. Fixing the coupling parameter , the transformation from hairy to bald black holes can only happen when becomes small enough.
In Fig. 6, we found that the descalarization process is continuous at the threshold so that the phase transition is of the second order. This is consistent with situation in the AdS spacetime Zhang:2022cmu . On the other hand, it was observed that in the EMS theory with higher order coupling function, such as , the descalarization can be discontinuous resembling the first order phase transition in the AdS spacetime Zhang:2022cmu . It will be of great interest to study the dynamical descalarization with higher order couplings in asymptotically flat spacetime and examine the critical behaviors disclosed in Zhang2021 .
Acknowledgments
This work is supported by the Natural Science Foundation of China under Grant No. 11805083, 11905083, 12005077, 12075202 and Guangdong Basic and Applied Basic Research Foundation (2021A1515012374).
References
- (1) C. A. R. Herdeiro and E. Radu, “Asymptotically flat black holes with scalar hair: a review,” Int. J. Mod. Phys. D 24, no.09, 1542014 (2015) [arXiv:1504.08209 [gr-qc]].
- (2) M. S. Volkov, “Hairy black holes in the XX-th and XXI-st centuries,” The Fourteenth Marcel Grossmann Meeting On Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories: Proceedings of the MG14 Meeting on General Relativity, University of Rome “La Sapienza”, Italy, 12–18 July 2015. 2018. [arXiv:1601.08230 [gr-qc]].
- (3) T. Torii, H. Yajima and K. i. Maeda, Dilatonic black holes with Gauss-Bonnet term, Phys. Rev. D 55,739 (1997) [gr-qc/9606034].
- (4) P. Kanti and K. Tamvakis, “Colored black holes in higher curvature string gravity,” Phys. Lett. B 392, 30-38 (1997) [arXiv:hep-th/9609003 [hep-th]].
- (5) B. Kleihaus, J. Kunz and E. Radu, Rotating Black Holes in Dilatonic Einstein-Gauss-Bonnet Theory, Phys. Rev. Lett. 106, 151104 (2011) [arXiv:1101.2868 [gr-qc]].
- (6) B. Kleihaus, J. Kunz, S. Mojica and E. Radu, Spinning black holes in Einstei-Gauss-Bonnet-dilaton theory: Nonperturbative solutions, Phys. Rev. D 93, no. 4, 044047 (2016) [arXiv:1511.05513 [gr-qc]].
- (7) P. Pani, C. F. B. Macedo, L. C. B. Crispino and V. Cardoso, Slowly rotating black holes in alternative theories of gravity, Phys. Rev. D 84, 087501 (2011) [arXiv:1109.3996 [gr-qc]].
- (8) C. A. R. Herdeiro and E. Radu, Kerr black holes with scalar hair, Phys. Rev. Lett. 112,221101 (2014) [arXiv:1403.2757].
- (9) D. Ayzenberg and N. Yunes, Slowly-Rotating Black Holes in Einstein-Dilaton-GaussBonnet Gravity: Quadratic Order in Spin Solutions, Phys. Rev. D 90, 044066 (2014) Erratum: [Phys. Rev. D 91, no. 6, 069905 (2015)] [arXiv:1405.2133 [gr-qc]].
- (10) M. S. Volkov and D. V. Galtsov, Non-Abelian Einstein Yang-Mills black holes, JETP Lett. 50 (1989) 346;
- (11) P. Bizon, Colored black holes, Phys. Rev. Lett. 64 (1990) 2844;
- (12) B. R. Greene, S. D. Mathur and C. M. O’Neill, Eluding the no hair conjecture: Black holes in spontaneously broken gauge theories, Phys. Rev. D 47 (1993) 2242;
- (13) K. I. Maeda, T. Tachizawa, T. Torii and T. Maki, Stability of nonAbelian black holes and catastrophe theory, Phys. Rev. Lett. 72, 450 (1994) [gr-qc/9310015].
- (14) H. Luckock and I. Moss, BLACK HOLES HAVE SKYRMION HAIR, Phys. Lett. B 176 (1986) 341;
- (15) S. Droz, M. Heusler and N. Straumann, New black hole solutions with hair, Phys. Lett. B 268 (1991) 371. [arXiv:2005.06677 [gr-qc]].
- (16) D. C. Zou, Y. Liu, C. Y. Zhang and B. Wang, “Dynamical probe of thermodynamical properties in three-dimensional hairy AdS black holes,” EPL 116, no.4, 40005 (2016) [arXiv:1411.6740 [hep-th]].
- (17) Z. F. Mai and R. Q. Yang, “Stability analysis of a charged black hole with a nonlinear complex scalar field,” Phys. Rev. D 104, no.4, 044008 (2021) [arXiv:2101.00026 [gr-qc]].
- (18) J. P. Hong, M. Suzuki and M. Yamada, “Spherically Symmetric Scalar Hair for Charged Black Holes,” Phys. Rev. Lett. 125, no.11, 111104 (2020) [arXiv:2004.03148 [gr-qc]].
- (19) A. E. Mayo and J. D. Bekenstein, “No hair for spherical black holes: Charged and nonminimally coupled scalar field with selfinteraction,” Phys. Rev. D 54, 5059-5069 (1996) [arXiv:gr-qc/9602057 [gr-qc]].
- (20) L. G. Collodel and D. D. Doneva, “Solitonic Boson Stars: Numerical solutions beyond the thin-wall approximation,” [arXiv:2203.08203 [gr-qc]].
- (21) V. Cardoso and S. Yoshida, “Superradiant instabilities of rotating black branes and strings,” JHEP 07, 009 (2005) [arXiv:hep-th/0502206 [hep-th]].
- (22) S. R. Dolan, “Instability of the massive Klein-Gordon field on the Kerr spacetime,” Phys. Rev. D 76, 084001 (2007) [arXiv:0705.2880 [gr-qc]].
- (23) S. Hod, “Stationary Scalar Clouds Around Rotating Black Holes,” Phys. Rev. D 86, 104026 (2012) [erratum: Phys. Rev. D 86, 129902 (2012)] [arXiv:1211.3202 [gr-qc]].
- (24) C. A. R. Herdeiro and E. Radu, “Kerr black holes with scalar hair,” Phys. Rev. Lett. 112, 221101 (2014) [arXiv:1403.2757 [gr-qc]].
- (25) C. Y. Zhang, S. J. Zhang and B. Wang, “Charged scalar perturbations around Garfinkle–Horowitz–Strominger black holes,” Nucl. Phys. B 899, 37-54 (2015) [arXiv:1501.03260 [hep-th]].
- (26) C. Y. Zhang, P. Liu, Y. Liu, C. Niu and B. Wang, Dynamical scalarization in Einstein-Maxwell-dilaton theory, Phys. Rev. D 105, no.2, 024073 (2022) [arXiv:2111.10744 [gr-qc]].
- (27) C. Y. Zhang, P. Liu, Y. Liu, C. Niu and B. Wang, “Evolution of anti–de Sitter black holes in Einstein-Maxwell-dilaton theory,” Phys. Rev. D 105, no.2, 024010 (2022) [arXiv:2104.07281 [gr-qc]].
- (28) M. G. Richarte, É. L. Martins and J. C. Fabris, “Scattering and absorption of a scalar field impinging on a charged black hole in the Einstein-Maxwell-dilaton theory,” Phys. Rev. D 105, no.6, 064043 (2022) [arXiv:2111.01595 [gr-qc]].
- (29) Damour, Thibault, and Gilles Esposito-Farese. ”Nonperturbative strong-field effects in tensor-scalar theories of gravitation.” Physical Review Letters 70.15 (1993): 2220.
- (30) T. Damour and G. Esposito-Farese, “Tensor-scalar gravity and binary pulsar experiments,” Phys. Rev. D 54 (1996), 1474-1491 [arXiv:gr-qc/9602056 [gr-qc]].
- (31) T. Harada, “Stability analysis of spherically symmetric star in scalar-tensor theories of gravity,” Prog. Theor. Phys. 98 (1997), 359-379 [arXiv:gr-qc/9706014 [gr-qc]].
- (32) V. Cardoso, I. P. Carucci, P. Pani and T. P. Sotiriou, Black holes with surrounding matter in scalar-tensor theories, Phys. Rev. Lett. 111 (2013), 111101 [arXiv:1308.6587 [gr-qc]].
- (33) V. Cardoso, I. P. Carucci, P. Pani, and T. P. Sotiriou, Matter around Kerr black holes in scalar-tensor theories: Scalarization and superradiant instability, Phys. Rev. D 88, 044056 (2013).
- (34) C. Y. Zhang, S. J. Zhang and B. Wang, Superradiant instability of Kerr-de Sitter black holes in scalar-tensor theory, JHEP 08 (2014), 011 [arXiv:1405.3811 [hep-th]].
- (35) D. D. Doneva and S. S. Yazadjiev, New Gauss-Bonnet Black Holes with Curvature-Induced Scalarization in Extended Scalar-Tensor Theories, Phys. Rev. Lett. 120, no.13, 131103 (2018) [arXiv:1711.01187 [gr-qc]].
- (36) H. O. Silva, J. Sakstein, L. Gualtieri, T. P. Sotiriou and E. Berti, Spontaneous scalarization of black holes and compact stars from a Gauss-Bonnet coupling, Phys. Rev. Lett. 120, no.13, 131104 (2018) [arXiv:1711.02080 [gr-qc]].
- (37) G. Antoniou, A. Bakopoulos and P. Kanti, Evasion of No-Hair Theorems and Novel Black-Hole Solutions in Gauss-Bonnet Theories, Phys. Rev. Lett. 120, no.13, 131102 (2018) [arXiv:1711.03390 [hep-th]].
- (38) P. V. Cunha, C. A. Herdeiro and E. Radu, Spontaneously Scalarized Kerr Black Holes in Extended Scalar-Tensor-Gauss-Bonnet Gravity, Phys. Rev. Lett. 123, no.1, 011101 (2019) [arXiv:1904.09997 [gr-qc]].
- (39) A. Dima, E. Barausse, N. Franchini and T. P. Sotiriou, “Spin-induced black hole spontaneous scalarization,” Phys. Rev. Lett. 125 (2020) no.23, 231101. [arXiv:2006.03095 [gr-qc]].
- (40) C. A. R. Herdeiro, E. Radu, H. O. Silva, T. P. Sotiriou and N. Yunes, Spin-induced scalarized black holes, Phys.Rev.Lett. 126 (2021) 1, 011103. [arXiv:2009.03904 [gr-qc]].
- (41) E. Berti, L. G. Collodel, B. Kleihaus and J. Kunz, Spin-induced black-hole scalarization in Einsteinscalar-Gauss-Bonnet theory, Phys.Rev.Lett. 126 (2021) 1, 011104. [arXiv:2009.03905 [gr-qc]].
- (42) C. A. R. Herdeiro, E. Radu, N. Sanchis-Gual and J. A. Font, “Spontaneous Scalarization of Charged Black Holes,” Phys. Rev. Lett. 121, no.10, 101102 (2018) [arXiv:1806.05190 [gr-qc]].
- (43) P. G. S. Fernandes, C. A. R. Herdeiro, A. M. Pombo, E. Radu and N. Sanchis-Gual, “Spontaneous Scalarisation of Charged Black Holes: Coupling Dependence and Dynamical Features,” Class. Quant. Grav. 36, no.13, 134002 (2019) [erratum: Class. Quant. Grav. 37, no.4, 049501 (2020)] [arXiv:1902.05079 [gr-qc]].
- (44) G. Guo, P. Wang, H. Wu and H. Yang, “Scalarized Einstein-Maxwell-scalar Black Holes in Anti-de Sitter Spacetime,” [arXiv:2102.04015 [gr-qc]].
- (45) Y. Brihaye, C. Herdeiro and E. Radu, “The scalarised Schwarzschild-NUT spacetime,” Phys. Lett. B 788, 295-301 (2019) [arXiv:1810.09560 [gr-qc]].
- (46) J. L. Ripley and F. Pretorius, Dynamics of a Z2 symmetric EdGB gravity in spherical symmetry, Class. Quant. Grav. 37 (2020) no.15, 155003. [arXiv:2005.05417 [gr-qc]].
- (47) W. E. East and J. L. Ripley, “Evolution of Einstein-scalar-Gauss-Bonnet gravity using a modified harmonic formulation,” Phys. Rev. D 103 (2021) no.4, 044040 [arXiv:2011.03547 [gr-qc]].
- (48) W. E. East and J. L. Ripley, “Dynamics of Spontaneous Black Hole Scalarization and Mergers in Einstein-Scalar-Gauss-Bonnet Gravity,” Phys. Rev. Lett. 127 (2021) no.10, 101102 [arXiv:2105.08571 [gr-qc]].
- (49) H. J. Kuan, D. D. Doneva and S. S. Yazadjiev, “Dynamical Formation of Scalarized Black Holes and Neutron Stars through Stellar Core Collapse,” Phys. Rev. Lett. 127 (2021) no.16, 161103 [arXiv:2103.11999 [gr-qc]]
- (50) W. Xiong, P. Liu, C. Niu, C. Y. Zhang and B. Wang, “Dynamical spontaneous scalarization in Einstein-Maxwell-scalar theory,” Chin. Phys. C 46, no.9, 095103 (2022) [arXiv:2205.07538 [gr-qc]].
- (51) C. Y. Zhang, P. Liu, Y. Liu, C. Niu and B. Wang, “Dynamical charged black hole spontaneous scalarization in anti–de Sitter spacetimes,” Phys. Rev. D 104, no.8, 084089 (2021) [arXiv:2103.13599 [gr-qc]].
- (52) W. K. Luo, C. Y. Zhang, P. Liu, C. Niu and B. Wang, “Dynamical spontaneous scalarization in Einstein-Maxwell-scalar models in anti–de Sitter spacetime,” Phys. Rev. D 106, no.6, 064036 (2022) [arXiv:2206.05690 [gr-qc]].
- (53) H. O. Silva, H. Witek, M. Elley and N. Yunes, “Dynamical Descalarization in Binary Black Hole Mergers,” Phys. Rev. Lett. 127 (2021) no.3, 031101 [arXiv:2012.10436 [gr-qc]].
- (54) D. D. Doneva, A. Vañó-Viñuales and S. S. Yazadjiev, “Dynamical descalarization with a jump during black hole merger,” [arXiv:2204.05333 [gr-qc]].
- (55) M. Elley, H. O. Silva, H. Witek and N. Yunes, “Spin-induced dynamical scalarization, de-scalarization and stealthness in scalar-Gauss-Bonnet gravity during black hole coalescence,” [arXiv:2205.06240 [gr-qc]].
- (56) H. J. Kuan, A. G. Suvorov, D. D. Doneva and S. S. Yazadjiev, “Gravitational waves from accretion-induced descalarization in massive scalar-tensor theory,” [arXiv:2203.03672 [gr-qc]].
- (57) Y. Liu, C. Y. Zhang, W. L. Qian, K. Lin and B. Wang, “Dynamic generation or removal of a scalar hair,” [arXiv:2206.05012 [gr-qc]].
- (58) Y. Liu, C. Y. Zhang, Q. Chen, Z. Cao, Y. Tian and B. Wang, “The critical scalarization and descalarization of black holes in a generalized scalar-tensor theory,” [arXiv:2208.07548 [gr-qc]].
- (59) C. Y. Zhang, Q. Chen, Y. Liu, W. K. Luo, Y. Tian and B. Wang, “Dynamical transitions in scalarization and descalarization through black hole accretion,” Phys. Rev. D 106, no.6, L061501 (2022) [arXiv:2204.09260 [gr-qc]].
- (60) S. A. Hayward, “Gravitational energy in spherical symmetry,” Phys. Rev. D 53, 1938-1949 (1996) [arXiv:gr-qc/9408002 [gr-qc]].
- (61) C. Y. Zhang, Q. Chen, Y. Liu, W. K. Luo, Y. Tian and B. Wang, “Critical Phenomena in Dynamical Scalarization of Charged Black Holes,” Phys. Rev. Lett. 128, no.16, 161105 (2022) [arXiv:2112.07455 [gr-qc]].