Dynamical behavior of Pielou’s difference system with exponential term ¹¹1 Corresponding author. E-mail address:mouyang@xmut.edu.cn

Ouyang Miao^1,2,∗, Qianhong Zhang³
¹School of Mathematics, Southwest Jiaotong University,
Chengdu, Sichuan 610000,China
²School of Mathematics and Statistics, Xiamen University of Technology,
Xiamen, Fujian 361000, China
³School of Mathematics and Statistics, Guizhou University of Finance and Economics,
Guiyang, Guizhou 550025, China

Abstract

In this paper, we investigate a type of Pielou’s difference system with exponential term

y_{n+1}=\frac{az_{n}}{p+z_{n}}e^{-y_{n}},\;\;\;\;\;\;\\ z_{n+1}=\frac{by_{n}}{q+y_{n}}e^{-z_{n}}.

where the parameters $a,b,p,q,$ are positive real numbers and the initial values $y_{0},z_{0}$ are arbitrary nonnegative real numbers. Using the mean value theorem and Lyapunov functional skills, we obtained some sufficient conditions which guarantee the boundedness and persistence of solution, and global asymptotic stability of the equilibriums. Moreover, two numerical examples are given to elaborate on the results.

MSC: 39A10 CLC: O159.7

Keywords: difference equation, equilibrium point; stability, boundedness, persistence, stability

1. Motivation

Discrete time single-species model is the most appropriate mathematical description of life histories of organism whose reproduction occurs only once a year during a very short season. These models are widely used in fisheries and many organisms [1-5].

In 1965, Pielou’s equation, as a discrete analogue of the delay logistic equation, was proposed by Pielou [6-7].

x_{n+1}=\frac{\alpha x_{n}}{1+x_{n-1}},n=0,1,2,...,

(1.1)

where $p$ is a positive real number.

In fact, there are many conclusions on Pielou’s equation that can be accounted briefly: If $\alpha\leq 1$ , then zero is a globally asymptotically stable equilibrium of Eq.(1.1) , if $\alpha>1$ , and $x_{0}\in(0,\infty)$ , then $\bar{y}=\alpha-1$ is a positive globally asymptotically stable equilibrium of Eq(1.1) . Other properties, such as periodicity, oscillation of Pielou’s equation, one can refer to [8-12].

In 2001, Metwally, Grove and Ladas [13] investigated the global stability of a difference model in mathematical biology

x_{n+1}=\alpha+\beta x_{n-1}\mathrm{e}^{-x_{n}},\quad n=0,1,2,\ldots,

(1.2)

where $\alpha$ is the immigration rate and $\beta$ the population growth rate.

In 2006, Ozturk [14] researched the convergence, the boundedness and periodic character of the positive solutions of the following difference equation

x_{n+1}=\frac{\alpha+\beta e^{-x_{n}}}{\gamma+x_{n-1}},\quad n=0,1,2,\ldots,

(1.3)

where the constants $\alpha,\beta,\gamma$ , and the initial values $x_{-1},x_{0},$ are positive real numbers.

Based on the previous works, Papaschinopoulos et al. [15] studied the asymptotic behavior of the solutions of two difference equations systems with exponential form, respectively.

\begin{array}[]{cc}x_{n+1}=a+by_{n-1}e^{-x_{n}},&y_{n+1}=c+dx_{n-1}e^{-y_{n}}.\\ \\ x_{n+1}=a+by_{n-1}e^{-y_{n}},&y_{n+1}=c+dx_{n-1}e^{-x_{n}}.\end{array}

(1.4)

where the constants $a,b,c,d$ , and the initial values $x_{-1},x_{0},y_{-1},y_{0}$ are positive real numbers.

Also, Papaschinopoulos et al.[16] studied the asymptotic behavior of the solutions of difference systems of exponential form, respectively,

\begin{array}[]{ll}x_{n+1}=\frac{\alpha+\beta e^{-y_{n}}}{\gamma+y_{n-1}},&y_{n+1}=\frac{\delta+\epsilon e^{-x_{n}}}{\zeta+x_{n-1}}.\\ \\ x_{n+1}=\frac{\alpha+\beta e^{-y_{n}}}{\gamma+x_{n-1}},&y_{n+1}=\frac{\delta+\epsilon e^{-x_{n}}}{\zeta+y_{n-1}}.\\ \\ x_{n+1}=\frac{\alpha+\beta e^{-x_{n}}}{\gamma+y_{n-1}},&y_{n+1}=\frac{\delta+\epsilon e^{-y_{n}}}{\zeta+x_{n-1}}.\end{array}

(1.5)

where $\alpha,\beta,\gamma,\delta,\epsilon,\zeta$ , and the initial values $x_{-1},x_{0},y_{-1},y_{0}$ are positive constants.

Hereafter, many researchers have worked out colorful homologous-series results. Readers can refer to [17-30].

In this paper, by incorporating Pielou’s equation to extend exponential type difference system, we study the dynamical behavior of the solutions to the following system

y_{n+1}=\frac{az_{n}}{p+z_{n}}e^{-y_{n}},\;\;\;\;\;\;\\ z_{n+1}=\frac{by_{n}}{q+y_{n}}e^{-z_{n}}.

(1.6)

where the parameters $a,\;b,\;p,\;q\;$ are positive numbers, and the initial values $x_{0},y_{0}$ are arbitrary nonnegative real numbers.

The main aim of our work is to study the boundedness and persistence of positive solutions of system (1.6), and its asymptotic behavior. Furthermore, using the iteration method of nonlinear difference equations and Lyapunov function skills, we derive some conditions so that system (1.6) has a unique positive equilibrium, and global asymptotically stability of the equilibrium.

2. Persistence and boundedness

In order to establish the persistence and boundedness of system (1.6), we introduce the following definitions and notations.

Definition 2.1 Let $(y_{n},z_{n})$ be an solution of system (1.6), the boundedness and persistence of $(y_{n},z_{n})$ is defined as follows:

(i) The sequences $\{y_{n}\},\{z_{n}\}$ of positive solution are said to be bounded, if there exist positive real numbers $N_{1},N_{2},$ such that $\mbox{supp}y_{n}\subset\left(0,N_{1}\right],\mbox{supp}z_{n}\subset\left(0,N_{2}\right],n=1,2,\cdots.$

(ii) The sequences $\{y_{n}\},\{z_{n}\}$ of positive solution are said to be persistence, if there exist positive real numbers $M_{1},M_{2},$ such that $\mbox{supp}y_{n}\subset\left[M_{1},\infty\right),\mbox{supp}z_{n}\subset\left[M_{2},\infty\right),n=1,2,\cdots.$

(iii) The sequences $\{y_{n}\},\{z_{n}\}$ of positive numbers are said to be bounded and persistence if there exist positive real numbers $M_{1},N_{1},M_{2},N_{2}$ such that $\mbox{supp}y_{n}\subset[M_{1},N_{1}],\mbox{supp}z_{n}\subset[M_{2},N_{2}],$ $n=1,2,\cdots$ .

Theorem 2.1 Consider system (1.6), if $p,q\in(0,+\infty),a,b\in(0,1),y_{0},z_{0}\in(0,+\infty)$ , then the following statements are true.

(i) the positive solution ${y_{n}},{z_{n}}$ of system (1.6) is bounded.

(ii) the positive solution ${y_{n}},{z_{n}}$ of system (1.6) is persistence.

Proof. (i) Let $\{y_{n}\},\{z_{n}\}$ be the solution sequence of system (1.6), for any positive initial values, obviously, ${y_{n}}>0,{z_{n}}>0.$ Therefore

e^{-y_{n}}\leq 1,\ \ e^{-z_{n}}\leq 1.

(2.1)

From (1.6) and (2.1), we have

\left\{\begin{array}[]{l}y_{n+1}\leq\frac{az_{n}}{p+z_{n}},\\ \\ z_{n+1}\leq\frac{by_{n}}{q+y_{n}}.\end{array}\right.

(2.2)

Consider the system of difference equations

\left\{\begin{array}[]{l}x_{n+1}=\frac{aw_{n}}{p+w_{n}},\\ \\ w_{n+1}=\frac{bx_{n}}{q+x_{n}}.\end{array}\right.

(2.3)

Let $(x_{n},w_{n})$ be a solution of (2.3) such that

x_{0}=y_{0},\ \ w_{0}=z_{0}.

(2.4)

Simplify (2.3), we get

\left\{\begin{array}[]{l}x_{n+1}=\frac{abx_{n-1}}{pq+(p+b)x_{n-1}},\\ \\ w_{n+1}=\frac{abw_{n-1}}{pq+(q+a)w_{n-1}}.\end{array}\right.

(2.5)

Set

X_{n}=\frac{1}{x_{n}},\ W_{n}=\frac{1}{w_{n}}.

(2.4) turns to

X_{0}=\frac{1}{y_{0}},\ \ W_{0}=\frac{1}{z_{0}}.

(2.6)

Then (2.5) turns into

\left\{\begin{array}[]{l}X_{n+1}=\frac{p+b}{ab}+\frac{pq}{ab}X_{n-1},\\ \\ W_{n+1}=\frac{q+a}{ab}+\frac{pq}{ab}W_{n-1}.\end{array}\right.

(2.7)

From (2.6) and (2.7), we obtain

\left\{\begin{array}[]{l}X_{n}=\lambda_{1}\left(\sqrt{\frac{pq}{ab}}\right)^{n}+\lambda_{2}\left(-\sqrt{\frac{pq}{ab}}\right)^{n}+\frac{p+b}{ab-pq},\\ \\ W_{n}=\mu_{1}\left(\sqrt{\frac{pq}{ab}}\right)^{n}+\mu_{2}\left(-\sqrt{\frac{pq}{ab}}\right)^{n}+\frac{q+a}{ab-pq}.\end{array}\right.

(2.8)

Where $\lambda_{1},\lambda_{2},\mu_{1},\mu_{2}$ are expressions of $X_{0},W_{0}$ .

From the relations between (2.2) and (2.7), we know

\left\{\begin{array}[]{l}y_{n+1}\leq\frac{1}{\lambda_{1}\left(\sqrt{\frac{pq}{ab}}\right)^{n}+\lambda_{2}\left(-\sqrt{\frac{pq}{ab}}\right)^{n}+\frac{p+b}{ab-pq}},\\ \\ z_{n+1}\leq\frac{1}{\mu_{1}\left(\sqrt{\frac{pq}{ab}}\right)^{n}+\mu_{2}\left(-\sqrt{\frac{pq}{ab}}\right)^{n}+\frac{q+a}{ab-pq}}.\par\end{array}\right.

(2.9)

From Eq.(1.6), without lose of correctness, we can get some loose upper bound to simplfy the expression,

\left\{\begin{array}[]{l}y_{n+1}\leq a,\\ \\ z_{n+1}\leq b.\end{array}\right.

(2.10)

Therefore, we have the boundedness of the solution of Eq.(1.6) .

(ii) Consider the function

f(x)=\frac{ax}{p+x},\ \ \ (\mbox{resp. }g(x)=\frac{bx}{q+x}).

where $x\in(0,+\infty).$ Since $f^{\prime}(x)=\frac{ap}{(p+x)^{2}}>0,(\mbox{resp.}g^{\prime}(x)=\frac{bq}{(q+x)^{2}}>0,$ it’s easy to know $f(x),g(x)$ are increasing functions. So, for $\forall(y_{0},z_{0})\in(0,+\infty)$

\left\{\begin{array}[]{l}y_{n+1}\geq\frac{az_{0}}{p+z_{0}}e^{-b},\\ \\ z_{n+1}\geq\frac{by_{0}}{q+y_{0}}e^{-a}.\end{array}\right.

(2.11)

It shows the solutions of Eq.(1.6) is permanent.

Theorem 2.2. The positive solution ${y_{n}},{z_{n}}$ of system (1.6) are boundedness and persistence.

3. Stability

In order to obtain the existence and the attractivity of the unique positive equilibrium of system (1.6), we give the following definitions, notations and Lemmas.

Definition 3.1 [14] Let $I\subset R$ and let $f,g:I\times I\rightarrow I$ be continuous differential functions. Consider the systems of difference equations

y_{n+1}=f\left(y_{n},z_{n}\right),z_{n+1}=g\left(y_{n},z_{n}\right),\quad n=0,1,2,\cdots,

(3.1)

where the initial conditions $y_{0},z_{0}\in I$ . $(\bar{y},\bar{z})$ is said to be an equilibrium of Eq. (3.1) if

\bar{y}=f(\bar{y},\bar{z}),\bar{z}=g(\bar{y},\bar{z}).

Definition 3.2 [14] (i) The equilibrium $(\bar{y},\bar{z})$ of Eq. (3.1) is called locally stable if for every $\varepsilon>0$ , there exists $\delta>0$ such that $y_{0},z_{0}\in I$ with $\left|y_{0}-\bar{y}\right|+\left|z_{0}-\bar{z}\right|<\delta$ , then $\left|y_{n}-\bar{y}\right|+\left|z_{n}-\bar{z}\right|<\varepsilon$ for all $n\geq 0.$
(ii) The equilibrium $(\bar{y},\bar{z})$ of Eq. (3.1) is called locally asymptotically stable if it is locally stable, and if there exists $\gamma>0$ such that $y_{0},z_{0}\in I$ with $\left|y_{0}-\bar{y}\right|+\left|z_{0}-\bar{z}\right|<\gamma$ , then $\lim_{n\rightarrow\infty}y_{n}=\bar{y},\lim_{n\rightarrow\infty}z_{n}=\bar{z}.$
(iii) The equilibrium $(\bar{y},\bar{z})$ of Eq. (3.1) is called a global attractor if for every $y_{0},z_{0}\in I$ we have $\lim_{n\rightarrow\infty}y_{n}=\bar{y},\lim_{n\rightarrow\infty}z_{n}=\bar{z}$ .
(iv) The equilibrium $(\bar{y},\bar{z})$ of Eq. (3.1) is called globally asymptotically stable if it is locally stable and a global attractor.
(v) The equilibrium $(\bar{y},\bar{z})$ of Eq. (3.1) is unstable if it is not stable.

Theorem 3.1. (i) System (1.6) always has a zero equilibrium.
(ii) If

\frac{ab}{pq}>1,

(3.2)

then system (1.6) has a unique positive equilibrium.

Proof (i) It’s obvious. So we omit.
(ii) Let $(\bar{y},\bar{z})$ be the positive equilibrium of system (1.6), i.e.

\bar{y}=\frac{a\bar{z}}{p+\bar{z}}e^{-\bar{y}},\quad\bar{z}=\frac{b\bar{y}}{q+\bar{y}}e^{-\bar{z}}.

(3.3)

From (2.11), we know

0\leq y_{0}e^{-b}<\bar{y}<a,\ \ 0\leq z_{0}e^{-a}<\bar{z}<b.

(3.4)

We consider the homologous algebraic system of system (1.6),

y=\frac{az}{p+z}e^{-y},\quad z=\frac{by}{q+y}e^{-z}.

(3.5)

From (3.5), one has that

z=\frac{pye^{y}}{a-ye^{y}},\ \ y=\frac{qze^{z}}{b-ze^{z}}.

(3.6)

Substituting (3.6) into system (3.5), we get

e^{\frac{pye^{y}}{a-ye^{y}}}=\frac{by}{q+y}\frac{a-ye^{y}}{pye^{y}},\ \ e^{\frac{qze^{z}}{b-ze^{z}}}=\frac{az}{p+z}\frac{b-ze^{z}}{qze^{z}}.

(3.7)

Set

G(y)=e^{\frac{pye^{y}}{a-ye^{y}}}+\frac{b}{q+y}\frac{ye^{y}-a}{pe^{y}},

(3.8)

Let $\epsilon_{1}\rightarrow 0^{+}$ ,

G(\epsilon_{1})=1-\frac{ab}{pq},

(3.9)

Since condition (3.2) is satisfied, we have

G(\epsilon_{1})<0.

(3.10)

On the other hand, from (3.8),

G(a)=e^{\frac{pae^{y}}{a-ae^{a}}}+\frac{b}{q+a}\frac{ae^{a}-a}{pe^{a}}>0.

(3.11)

and

G^{\prime}(y)=e^{\frac{pye^{y}}{a-y}}\cdot\frac{ap(y+1)e^{y}}{\left(a-ye^{y}\right)^{2}}+\frac{e^{y}+a}{pe^{y}}\cdot\frac{b}{q+y}+\frac{a-ye^{y}}{pe^{y}}\frac{b}{(q+y)^{2}}>0.

(3.12)

(3.12) implies $G(y)$ is an increasing function for $y\in(\epsilon_{1},a)$ .
Similarly, set

H(z)=e^{\frac{qze^{z}}{b-ze^{z}}}+\frac{a}{p+z}\frac{ze^{z}-b}{qe^{z}},

(3.13)

Let $\epsilon_{2}\rightarrow 0^{+}$ ,

H(\epsilon_{2})=1-\frac{ab}{pq},

(3.14)

Noting condition (3.2), we have

H(\epsilon_{2})<0.

(3.15)

From (3.13), we have

H(b)=e^{\frac{qbe^{z}}{b-be^{b}}}+\frac{a}{p+b}\frac{be^{b}-b}{qe^{b}}>0,

(3.16)

and

H^{\prime}(z)=e^{\frac{qze^{z}}{b-z}}\cdot\frac{bq(z+1)e^{z}}{\left(b-ze^{z}\right)^{2}}+\frac{e^{z}+b}{qe^{z}}\cdot\frac{a}{p+z}+\frac{b-ze^{z}}{qe^{z}}\frac{a}{(p+z)^{2}}>0.

(3.17)

(3.17) shows $H(z)$ is increasing function for $z\in(\epsilon_{2},b)$ .

Therefore, we have that $(\bar{y},\bar{z})\in(\epsilon_{1},a)\times(\epsilon_{2},b)$ is the unique positive equilibrium of (1.6).

To have a more accurate estimation of $(\bar{y},\bar{z})$ , we give a more narrow range by (2.9). Here, noting the lower upper bounds as $y^{*},z^{*}$ ,

y_{n+1}<\frac{ab-pq}{p+b}=y^{*},\ \ z_{n+1}<\frac{ab-pq}{q+a}=z^{*}.

(3.18)

Set $(y_{*},z_{*})$ be higher bound of $(\bar{y},\bar{z})$ , i. e.,

y_{*}=\frac{qz_{*}e^{z_{*}}}{b-z_{*}e^{z_{*}}}<y_{n+1},\ \ z_{*}=\frac{py_{*}e^{y_{*}}}{a-y_{*}e^{y_{*}}}<z_{n+1}.

(3.19)

In fact, considering function $g(x)=\frac{cxe^{x}}{d-xe^{x}}$ , since $g^{\prime}(x)=\frac{cd(x+1)e^{x}}{(d-xe^{x})^{2}}>0$ for $x\in(0,\infty)$ . That means $y$ (resp. $z$ ) in (3.6) will attain its minimums when $z$ (resp. $y$ ) come to the minimum.

Now, let’s find the expressions of $y_{*},z_{*}$ .
Noting (1.6), since $y_{n+1}$ increases responding $z_{n}$ , decrease responding $y_{n}$ , we have

y_{n}\geq\frac{az_{*}}{p+z_{*}}e^{-y^{*}},\ \ z_{n}\geq\frac{by_{*}}{q+y_{*}}e^{-z^{*}}.

(3.20)

By the definition of equilibrium, noting (3.18), there exists $N>0,$ for $n>N,$ $y_{n}=y_{*},z_{n}=z_{*}$ , i.e.,

y_{*}=\frac{az_{*}}{p+z_{*}}e^{-y^{*}},\ \ z_{*}=\frac{by_{*}}{q+y_{*}}e^{-z^{*}}.

(3.21)

Manipulating (3.21), we have

y_{*}=\frac{abe^{-\left(y^{*}+z^{*}\right)}-pq}{be^{-z^{*}}+p},\ \ z_{*}=\frac{abe^{-\left(y^{*}+z^{*}\right)}-pq}{ae^{-y^{*}}+q}.

(3.22)

The unique positive equilibrium $(\bar{y},\bar{z})$ of system (1.6)

y_{*}<\bar{y}<y^{*},\ \ z_{*}<\bar{z}<z^{*}.

(3.23)

The proof is completed.

Theorem 3.2. (i) If

\frac{a}{p}<1,\ \ \frac{b}{q}<1.

(3.24)

$(0,0)$ is locally asymptotically stable.

(ii) If

e^{y_{*}}>a,\ \ e^{z_{*}}>b.

(3.25)

$(\bar{y},\bar{z})$ is locally asymptotically stable.

Proof. (i) From system (1.6), the linearized equation of system (1.6) at $(0,0)$ is

\phi_{n+1}=T~{}\phi_{n}.

(3.26)

where

\begin{array}[]{ll}\phi_{n}=\left[\begin{array}[]{c}y_{n}\\ z_{n}\end{array}\right],&T=\left[\begin{array}[]{cc}0&\frac{a}{p}\\ \frac{b}{q}&0\end{array}\right].\end{array}

(3.27)

Under condition (3.24), by Theorem 1.3.7 [25], the equilibrium point (0,0) of system (1.6) is locally asymptotically stable.

(ii) The linearized system of system (1.6) at $(\bar{y},\bar{z})$ is

\phi_{n+1}=T_{(\bar{y},\bar{z})}\phi_{n}=\left[\begin{array}[]{cc}-\frac{a\bar{z}e^{-\bar{y}}}{p+\bar{z}}&\frac{ape^{-\bar{y}}}{\left(p+\bar{z}\right)^{2}}\\ \\ \frac{bqe^{-\bar{z}}}{\left(q+\bar{y}\right)^{2}}&-\frac{b\bar{y}e^{-\bar{z}}}{q+\bar{y}}\end{array}\right]~{}\phi_{n}.

(3.28)

where

T_{(\bar{y},\bar{z})}=\left[\begin{array}[]{cc}A&B\\ C&D\end{array}\right].

In fact,

\begin{array}[]{c}|A|+|B|=\left|-\frac{a\bar{z}e^{-\bar{y}}}{p+\bar{z}}\right|+\left|\frac{ape^{-\bar{y}}}{(p+\bar{z})^{2}}\right|=\frac{a\bar{z}e^{-\bar{y}}(p+\bar{z})+ape^{-\bar{y}}}{(p+\bar{z})^{2}}<ae^{-\bar{y}}<ae^{-y_{*}},\\ \\ |C|+|D|=\left|\frac{bqe^{-\bar{z}}}{(q+\bar{y})^{2}}\right|+\left|-\frac{b\bar{y}e^{-\bar{z}}}{q+\bar{y}}\right|=\frac{b\bar{y}e^{-\bar{z}}(q+\bar{y})+bqe^{-\bar{z}}}{(q+\bar{y})^{2}}<be^{-\bar{z}}<be^{-z_{*}}.\end{array}

(3.29)

Noting condition (3.25), the inequations (3.29) implies

|A|+|B|<1,\ \ |C|+|D|<1.

(3.30)

The eigenvalue equation of (3.28) is

\lambda^{2}+\left(A+D\right)\lambda+\left(AD-BC\right)=0.

(3.31)

From (3.30), one has

|A+D|<1+(AD-BC)<2.

(3.32)

by Theorem 1.1.1 [26], the eigenvalues of Eq.(3.31) lie inside the unit disk. So the positive equilibrium $(\bar{y},\bar{z})$ of system (1.6) is locally asymptotically stable.

The proof is completed.

Theorem 3.3. (i) If

ab<\min(p,q),

(3.33)

the zero equilibrium is a global attractor.
(ii) If

az^{*}\leq\bar{y}\left(p+z^{*}\right)e^{y_{*}},\ \ ~{}~{}~{}~{}~{}~{}by^{*}\leq\bar{z}\left(q+y^{*}\right)e^{z_{*}}.

(3.34)

the equilibrium $(\bar{y},\bar{z})$ is a global attractor.
Proof. Consider the following discrete time analog of the Lyapunov function, mentioned in [31].

V_{n}(\bar{y},\bar{z})=\left[\left(y_{n}-\bar{y}\right)-1-\ln\left(y_{n}-\bar{y}\right)\right]+\left[\left(z_{n}-\bar{z}\right)-1-\ln\left(z_{n}-\bar{z}\right)\right].

The nonnegativity of $V_{n}$ follows from:

x-1-\ln x\geq 0,\quad\forall x>0.

Herefore, we have

-\ln\left(\frac{y_{n+1}-\bar{y}}{y_{n}-\bar{y}}\right)\leq-\frac{y_{n+1}-y_{n}}{y_{n+1}-\bar{y}},\ \ -\ln\left(\frac{z_{n+1}-\bar{z}}{z_{n}-\bar{z}}\right)\leq-\frac{z_{n+1}-z_{n}}{z_{n+1}-\bar{z}}.

Assume

\begin{array}[]{ll}V_{n+1}(\bar{y},\bar{z})-V_{n}(\bar{y},\bar{z})=&\left[\left(y_{n+1}-\bar{y}\right)-1-\ln\left(y_{n+1}-\bar{y}\right)\right]-\left[\left(z_{n+1}-\bar{z}\right)-1-\ln\left(z_{n+1}-\bar{z}\right)\right]\\ \\ &-\left[\left(y_{n}-\bar{y}\right)-1-\ln\left(y_{n}-\bar{y}\right)\right]+\left[\left(z_{n}-\bar{z}\right)-1-\ln\left(z_{n}-\bar{z}\right)\right]\\ \\ &\leq\left(y_{n+1}-y_{n}\right)\left(1-\frac{1}{y_{n+1}-\bar{y}}\right)+\left(z_{n+1}-z_{n}\right)\left(1-\frac{1}{z_{n+1}-\bar{z}}\right)\\ \\ &\leq(a-\epsilon_{1})(\frac{y_{n+1}-\bar{y}-1}{y_{n+1}-\bar{y}})+(b-\epsilon_{2})(\frac{z_{n+1}-\bar{z}-1}{z_{n+1}-\bar{z}}).\end{array}

(3.35)

Consider the zero equilibrium (0,0),

\begin{array}[]{ll}V_{n+1}(0,0)-V_{n}(0,0)&\leq(a-\epsilon_{1})(\frac{y_{n+1}-1}{y_{n+1}})+(b-\epsilon_{2})(\frac{z_{n+1}-1}{z_{n+1}})\\ \\ &=(a-\epsilon_{1})(\frac{az_{n}-(p+z_{n})e^{y_{n}}}{az_{n}})+(b-\epsilon_{2})(\frac{by_{n}-(q+y_{n})e^{z_{n}}}{by_{n}})\\ \\ &\leq(a-\epsilon_{1})(\frac{ab-(p+\epsilon_{2})e^{\epsilon_{1}}}{a\epsilon_{2}})+(b-\epsilon_{2})(\frac{ba-(q+\epsilon_{1})e^{\epsilon_{2}}}{b\epsilon_{1}}).\end{array}

(3.36)

Set $\epsilon=\min(\epsilon_{1},\epsilon_{2}),$ (3.36) becomes

V_{n+1}(0,0)-V_{n}(0,0)\leq(a-\epsilon)(\frac{ab-(p+\epsilon)e^{\epsilon}}{a\epsilon})+(b-\epsilon)(\frac{ab-(q+\epsilon)e^{\epsilon}}{b\epsilon}).

(3.37)

Let $\epsilon\rightarrow 0^{+}$ , since (3.33) holds true, we have

V_{n+1}(0,0)-V_{n}(0,0)\leq 0,

(3.38)

for all $n\geq 0$ .

For the fact $V_{n}$ is non-increasing and non-negative, we know that $\lim_{n\rightarrow\infty}V_{n}\geq 0.$ Hence,

\lim_{n\rightarrow\infty}(V_{n+1}-V_{n})=0.

It follows that $\lim_{n\rightarrow\infty}y_{n}=0,\lim_{n\rightarrow\infty}z_{n}=0$ . Furthermore, $V_{n}\leq V_{0}$ , for all $n\geq 0$ , which shows that $(0,0)\in[\epsilon_{1},a]\times[\epsilon_{2},b]$ is a global attractor.

(ii ) Next, we will prove the globally asymptotically stability of the unique positive equilibrium $(\bar{y},\bar{z})$ .
We consider the following discrete time analog of the Lyapunov function

W_{n}(\bar{y},\bar{z})=\bar{y}\left(\frac{y_{n}}{\bar{y}}-1-\ln\frac{y_{n}}{\bar{y}}\right)+\bar{z}\left(\frac{z_{n}}{\bar{z}}-1-\ln\frac{z_{n}}{\bar{z}}\right).

The nonnegativity of $W_{n}$ follows from the following inequality:

x-1-\ln x\geq 0,\quad\forall x>0.

Furthermore,

-\ln\left(\frac{y_{n+1}}{y_{n}}\right)\leq-\frac{y_{n+1}-y_{n}}{y_{n+1}},\ \ -\ln\left(\frac{z_{n+1}}{z_{n}}\right)\leq-\frac{z_{n+1}-z_{n}}{z_{n+1}}.

Since (3.34) holds true, it follows that

\ \begin{array}[]{ll}W_{n+1}-W_{n}=&\bar{y}\left(\frac{y_{n+1}}{\bar{y}}-1-\ln\frac{y_{n+1}}{\bar{y}}\right)+\bar{z}\left(\frac{z_{n+1}}{\bar{z}}-1-\ln\frac{z_{n+1}}{\bar{z}}\right)\\ \\ &-\bar{y}\left(\frac{y_{n}}{\bar{y}}-1-\ln\frac{y_{n}}{\bar{y}}\right)-\bar{z}\left(\frac{z_{n}}{\bar{z}}-1-\ln\frac{z_{n}}{\bar{z}}\right)\\ \\ &\leq\left(y_{n+1}-y_{n}\right)\left(1-\frac{\bar{y}}{y_{n+1}}\right)+\left(z_{n+1}-z_{n}\right)\left(1-\frac{\bar{z}}{z_{n+1}}\right)\\ \\ &=\left(y_{n+1}-y_{n}\right)\frac{az_{n}-\bar{y}\left(p+z_{n}\right)e^{y_{n}}}{az_{n}}+\left(z_{n+1}-z_{n}\right)\frac{by_{n}-\bar{z}\left(q+y_{n}\right)e^{z_{n}}}{by_{n}}\\ \\ &\leq\left(y^{*}-y_{*}\right)\frac{az^{*}-\bar{y}\left(p+z^{*}\right)e^{y_{*}}}{az^{*}}+\left(z^{*}-z_{*}\right)\frac{by^{*}-\bar{z}\left(q+y^{*}\right)e^{z_{*}}}{by^{*}}\\ \\ &\leq 0.\end{array}

(3.39)

In fact, $f(x)=\frac{p+x}{ax}$ is a non-increase function , $-\frac{p+x}{ax}\leq-\frac{p+x^{*}}{ax^{*}},$ for $\forall x\in(x_{*},x^{*})$ .
As $W_{n}$ being non-increasing and non-negative, it follows that $\lim_{n\rightarrow\infty}W_{n}\geq 0.$ Hence,

\lim_{n\rightarrow\infty}W_{n+1}-W_{n}=0.

It follows that

\lim_{n\rightarrow\infty}y_{n}=\bar{y},\lim_{n\rightarrow\infty}z_{n}=\bar{z}.

Furthermore, $W_{n}\leq W_{0}$ for all $n\geq 0$ , which shows that $(\bar{y},\bar{z})\in[y_{*},y^{*}]\times[z_{*},z^{*}]$ is a global attractor.

Theorem 3.4. (i) If (3.33), the zero equilibrium is global asympotically stable.
(ii) If (3.34), the positive equilibrium $(\bar{y},\bar{z})$ is global asympotically stable.

Proof. By Theorem 3.2, Theorem 3.3, the equilibrium $(0,0)$ and $(\bar{y},\bar{z})$ of system (1.6) is globally asymptotically stable.

4. Numerical examples

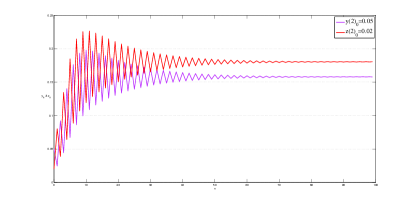
Example 4.1 Consider the parameters $a=0.8,b=0.9,p=0.6,q=0.5,$ and initial values $y(1)_{0}=0.35,z(1)_{0}=0.26,$ the Pielou’s system with exponential terms (1.6) is as follows,

y_{n+1}=\frac{0.8z_{n}}{0.6+z_{n}}e^{-y_{n}},\;\;\;\;\;\;\\ z_{n+1}=\frac{0.9y_{n}}{0.5+y_{n}}e^{-z_{n}}.

(4.1)

The solution of Eq.(4.1) $(y_{n},z_{n})\in[\frac{az_{0}}{p+z_{0}}e^{-a},a]\times[\frac{by_{0}}{q+y_{0}}e^{-b},b]=[0.1087,0.8]\times[0.1507,0.9]$ .
For the initial value $y(2)_{0}=0.05,z(2)_{0}=0.02$ , the solution $(y_{n},z_{n})\in[0.0116,0.8]\times[0.0333,0.9]$ .

Refer to caption — Figure 1: The positive equilibrium dynamics of system (4.1).

It is obvious that conditions (3.2),(3.25) and (3.34) are satisfied. For the positive initial value wherever, Eq.(4.1) has the unique positive equilibrium $(\bar{y},\bar{z})\in[y_{*},y^{*}]\times[z_{*},z^{*}]$ ,(see Fig.1-Fig.2).
where

y_{*}=\frac{abe^{-\left(y^{*}+z^{*}\right)}-pq}{be^{-z^{*}}+p}=0.0751,\ \ y^{*}=\frac{p+b}{ab-p^{2}}=0.2800.\\

z_{*}=\frac{abe^{-\left(y^{*}+z^{*}\right)}-pq}{ae^{-y^{*}}+q}=0.0850,\ \ z^{*}=\frac{q+a}{ab-q^{2}}=0.3231.

Example 4.2 Consider the parameters $a=0.6,b=0.5,p=0.8,q=0.9,$ the Pielou’s system with exponential terms (1.6) is as follows,

y_{n+1}=\frac{0.6z_{n}}{0.8+z_{n}}e^{-y_{n}},\;\;\;\;\;\;\\ z_{n+1}=\frac{0.5y_{n}}{0.9+y_{n}}e^{-z_{n}}.

(4.2)

For the positive initial value wherever, the solution of Eq.(4.2) $(y_{n},z_{n})\in[0,0.6]\times[0,0.5]$ .

The parameters meet that conditions (3.24) and (3.33) . It is obvious that $(0,0)$ is the globally asymptotic stable. (see Fig.3-Fig.4.).

5. Conclusions

(i) System(1.6) is always persistent and bounded for $p,q\in(0,\infty),a,b\in(0,1)$ .

(ii) System(1.6) always has a zero equilibrium; If $a<p,~{}~{}b<q$ , and $ab<\min(p,q),$ then (0,0) is global asymptotic stable.

(iii) If $ab>pq$ , System(1.6) has a unique positive equilibrium $\bar{y},\bar{z}\in(y_{*},y^{*})\times(z_{*},z^{*})$ ; Moreover, if $e^{y_{*}}>a,~{}~{}e^{z_{*}}>b$ and $az^{*}\leq\bar{y}\left(p+z^{*}\right)e^{y_{*}},\ ~{}by^{*}\leq\bar{z}\left(q+y^{*}\right)e^{z_{*}}$ ,then $(\bar{y},\bar{z})$ is global asymptotic stable.

Conflict of interest

The authors declare that they have no competing interests.

Acknowledgment

This work was financially supported by Guizhou Scientific and Technological Platform Talents ([2022]020-1), Scientific Research Foundation of Guizhou Provincial Department of Science and Technology([2020]1Y008, [2022]021, [2022]026), and Scientific Climbing Programme of Xiamen University of Technology (XPDKQ20021).

Reference

[1] M. Kot, Elements of Mathematical Ecology , Cambridge University Press, New York, 2001.
[2] R. Beverton and S. Holt, On the dynamics of exploited fish populations, Fisheries Investigations, Ser 2, , 19 (1957), 1–533.
[3] MDL. Sen, The generalized Beverton-Holt equation and the control of populations, Applied Mathematical Modelling , 32 (2008), 2312-2328.
[4] X. Ding, W. Li , Stability and bifurcation of numerical discretization Nicholson blowflies equation with delay , Discrete Dyn. Nat. Soc , 2006 (2006), 1-12. Article ID 19413.
[5] A.J. Nicholson , An outline of the dynamics of animal populations , Aust. J. Zool , 2 (1954), 9-65 .
[6] E. C. Pielou, An Introduction to Mathematical Ecology , John Wiley $\&$ Sons, New York, 1965.
[7] E. C. Pielou, Population and Community Ecology, Gordon and Breach , New York, 1974.
[8] Camouzis, E. , Ladas, G. Periodically forced Pielou’s equation, J. Math. Anal. Appl, 333(1) (2007), 117-127.
[9] Kulenovi $\acute{c}$ , M.R.S. , Merino, Stability analysis of Pielou’s equation with period-two coefficient, J. Difference Equ. Appl, 13(5) (2007), 383-406.
[10] Ishihara, Keigo; Nakata, Yukihiko, On a generalization of the global attractivity for a periodically forced Pielou’s equation , J. Difference Equ. Appl. 18(3) (2012),375-396.
[11] Zhao, Houyu Analytic invariant curves for an iterative equation related to Pielou’s equation , J. Difference Equ. Appl. 19 (2013), no. 7, 1082-1092.
[12] Nyerges, Gabor, A note on a generalization of Pielou’s equation , J. Difference Equ. Appl. 14(5) (2008), 563-565.
[13] E. El-Metwally, E.A. Grove, G. Ladas, R. Levins, M. Radin, On the difference equation $x_{n}+1=\alpha+\beta x_{n}-1e^{-}x_{n}$ , Nonlinear Anal, 47 (2001), 4623-4634.
[14] I. Ozturk, F. Bozkurt, S. Ozen, On the difference equation $y_{n}+1=\frac{\alpha}{+}\beta e^{-}y_{n}\gamma+y_{n}-1$ , Appl. Math. Comput, 181 (2006), 1387-1393.
[15] Papaschinopoulos, G.; Ellina, G.; Papadopoulos, K. B. , Asymptotic behavior of the positive solutions of an exponential type system of difference equations , Appl. Math. Comput, 245 (2014), 181-190.
[16] Papaschinopoulos, G.; Radin, M. ; Schinas, C. J. , Study of the asymptotic behavior of the solutions of three systems of difference equations of exponential form , Appl. Math. Comput, 218 (2012), 5310-5318.
[17] A. Matsumoto, F. Szidarovszky, Asymptotic behavior of a delay differential neoclassical growth model , Sustainability, 5 (2013), 440-455.
[18] X. Ding, R. Zhang , On the difference equation $x_{n}+1=(\alpha x_{n}+\beta x_{n}-1)e^{-}x_{n}$ , Adv. Difference Equ , 2008 (2008), http://dx.doi.org/10.1155/2008/876936. 7pages.
[19] L. Shaikhet, Stability of equilibrium states for a stochastically perturbed Mosquito population equation , Dyn. Contin. Discrete Impuls. Syst. Ser. B Appl.Algorithms , 21 (2) (2014), . 185-196.
[20] T. Awerbuch, E. Camouzis, G. Ladas, R. Levins, E.A. Grove, M. Predescu , A nonlinear system of difference equations , linking mosquitoes, habitats and community interventions , Commun. Appl. Nonlinear Anal , 15 (2) (2008) 77-88.
[21] B. Iricanin, S. Stevic, On two systems of difference equations , Discrete Dyn. Nat. Soc , 4 (2010) . (Article ID 405121).
[22] G. Papaschinopoulos, N. Fotiades, C.J. Schinas, On a system of difference equations including exponential terms , J. Difference Equ. Appl , 20 (5-6) (2014), 717-732.
[23] MDL Sen, S. Alonso-Quesada, Control issues for the Beverton-Holt equation in ecology by locally monitoring the environment carrying capacity: Nonadaptive and adaptive cases, Applied Mathematics and Computation , 215 (2009), 2616-2633.
[24] M. Bohner, S. Streipert, Optimal harvesting policy for the Beverton-Holt model, Mathematical Biosciences and Engineering , 13 (2016), 673-695.
[25] V. L. Kocic, G. Ladas, Global behavior of nonlinear difference equations of higher order with application , Kluwer Academic Publishers, Dordrecht, 1993.
[26] M. R. S. Kulenonvic, G. Ladas, Dynamics of second order rational difference equations with open problems and conjectures , Chapaman $\&$ Hall/CRC,Boca Raton, 2002.
[27] Khan, A. Q.; Qureshi, M. N., Behavior of an exponential system of difference equations , Discrete Dyn. Nat. Soc, Art. ID 607281, 9 pp (2014).
[28] Papaschinopoulos, G.; Fotiades, N. ; Schinas, C. J., On a system of difference equations including negative exponential terms , J. Difference Equ. Appl., 20 (2014), 717-732.
[29] W. Chen, W. Wang, Global exponential stability for a delay differential neoclassical growth model , Adv. Difference Equ., 2014 (2014), 325.
[30] L. Shaikhet , Lyapunov Functionals and Stability of Stochastic Functional Differential Equations , Springer , Dordrecht, Heidelberg, New York, London,
[31] Enatsu, Y, Nakata, Y, Muroya, Y, Global stability for a class of discrete SIR epidemic models , Math. Biosci. Eng., 7 (2) (2010), 347-361.

Dynamical behavior of Pielou’s difference system with exponential term 111 Corresponding author. E-mail address:mouyang@xmut.edu.cn