Dynamical and static spin structure factors of Heisenberg antiferromagnet on honeycomb lattice in the presence of Dzyaloshinskii-Moriya interaction
Abstract
We have theoretically studied the spin structure factors of Heisenberg model on honeycomb lattice in the presence of longitudinal magnetic field, i.e. magnetic field perpendicular to the honeycomb plane, and Dzyaloshinskii-Moriya interaction. The possible effects of next nearest neighbor exchange constant are investigated in terms of anisotropy in the Heisenberg interactions. This spatial anisotropy is due to the difference between nearest neighbor exchange coupling constant and next nearest neighbor exchange coupling constant. The original spin model hamiltonian is mapped to a bosonic model via a hard core bosonic transformation where an infinite hard core repulsion is imposed to constrain one boson occupation per site. Using Green’s function approach, the energy spectrum of quasiparticle excitation has been obtained. The spectrum of the bosonic gas has been implemented in order to obtain two particle propagator which corresponds to spin structure factor of original Heisenberg chain model Hamiltonian. The results show the position of peak in the dynamical transverse spin structure factor at fixed value for Dzyaloshinskii Moriya interaction moves to higher frequency with magnetic field. Also the intensity of dynamical transverse spin structure factor is not affected by magnetic field. However the Dzyaloshinskii Moriya interaction strength causes to decrease the intensity of dynamical transverse spin structure factor. The increase of magnetic field does not varied the frequency position of peaks in dynamical longitudinal spin susceptibility however the intensity reduces with magnetic field. Our results show static transverse structure factor is found to be monotonically decreasing with magnetic field and temperature for different vlaues of next nearest neighbor coupling exchange constant.
pacs:
codes 75.10.Pq,75.40.Gb, 66.70.-f, 44. 10.+iKeywords: A. structure factor; D. honeycomb; D. hard core.
I Introduction
Quantum magnetism on geometrically two-dimensional (D) frustrated spin systems with have lately received massive attetions, due to their potential for realizing the quantum spin liquid, a magnetically disordered state which respects all the symmetries of the systems, even at absolute zero temperatureokuma ; zvygain ; fihlo ; ito ; balent . The spin model, recently attracted many interests, is the Heisenberg model with first and second antiferromagnetic exchange interaction in honeycomb lattice. In sufficiently low dimensional spin systems, the quantum mechanical zero point motion can forbid long range magnetic order and produce a quantum spin liquid state, a correlated state that breaks no symmetry and possesses topological properties, possibly sustaining fractionalized excitationsanderson1 ; fazekas ; liang ; sachdev1 ; sandvik . Although the triangular lattice was first theoretically proposed by Andersonanderson1 as an ideal benchmark to search for the quantum spin liquid, it was soon found that the antiferromagnetic Heisenberg model on a triangular lattice is magnetically ordered with a 120 arrangement of the spins. Despite the intense activity, only a small number of triangular materials have been identified as possible candidates for quantum spin liquid behavior such as th layered organic materials. Hence, there is a need to find evidence for quantum spin liquid behavior in more compounds. Honeycomb lattice materials have attracted lots of attetion in recent years due to their interesting and poorly understood magnetic properties. Inorganic materials such as Na2 Co2TeO6lefan , BaCo2(AsO2)2 martin , are examples of honeycomb lattice spin half antiferromagnets. It is important then to understand theoretically the magnetic properties of interacting localized moments on the frustrated honeycomb lattice as has been previously done on triangular lattices. Althogh the numerical evidence for a quantum spin liquid in the half-filled Hubbard model on the honeycomb lattice has been questionedsorella , exact diagonalization studies on the Heisenberg model with have found evidence for short range spin gapped phases for suggesting the presence of a Resonance Valence Bond (RVB) state. Slow neutrons scatter from solids via magnetic dipole interaction in which the magnetic moment of the neutron interacts with the spin magnetic moment of electrons in the solid. The inelastic cross-section for magnetic neutron scattering from a magnetic system can be expressed in terms of spin density correlation functions. Specially, field induced effects on the dynamical spin correlation function in low dimensional quantum spin models have been attracting much interest from theoretical and experimental point of view in recent years affleck ; uimin ; dimitriev . AF Heisenberg chain in the presence of axial anisotropy at finite non zero values for magnetic field is a solvable model. Its ground state properties have been investigated within Bethe-Ansatzbethe ; faddeev . Static thermodynamic quantities, eg. the specific heat, the magnetic susceptibility and magnetization have been investigated by several methods including thermodynamic Bethe Ansatz, Quantum Monte Carlo and Density Matrix Renormalization Groupklumper ; johnston ; klumper1 .
Spin-orbit coupling induces both symmetric and antisymmetric anisotropic properties or Dzyaloshinskii-Moriya spin anisotropymoriya in the exchange coupling between nearest neighbour spins. A Dzyaloshiskii-Moriya (DM) interaction with a DM vector perpendicular to the layer produces an easy-plane spin anisotropic Hamiltonian for honeycomb lattice. DM interaction breaks symmetry of the model and reduces it to symmetry around the axis perpendicular to the honeycomb plane. This DM interaction is believed to orient the spins in the 2D layer. For applied large magnetic fields () along perpendicular to the plane, the Zeeman term overcomes the antiferromagnetic spin coupling and the ground state is a field induced ferromagnetic state with gapped magnon excitations. Decreasing the magnetic field at the zero temperature, the magnon gap vanishes at the critical field () and a spiral transverse magnetic ordering develops. At finite temperature () and in the absence of exchange anisotropy, the frustration leads to an incommensurate spiral structure for transverse spin component below the critical line in the plane.
Hard core bosonic representation has been introduced to transform a spin Hamiltonian to bosonic one whereby the excitation spectrum is obtainedauerbach ; mahan . This mapping between the bosonic gas and original spin model is valid provided to add the hard core repulsion between particles in the bosonic Hamiltonianmahan . An anisotropic exchange interaction due to DM interaction adds a hopping term for bosonic particles to the main part of bosonic model Hamiltonian. Such term leads to different universal behavior in addition to change of critical points and thermodynamic properties.
In this paper, we intend to find the effects of antisymmetric exchange interaction (DM interaction) and magnetic field on dynamical spin structure factor of localized electrons on honeycomb lattice at finite temperature in the field induced gapped spin-polarized phase. Specially, we study the effects of Dzyaloshinskii-Moriya interaction strength and next nearest neighbor exchange constant on the spin structure factors of Heisenberg model on honeycomb structure for magnetic fields above critical field . We have addressed the frequency behaviors of transverse and longitudinal structure factors of anisotropic antiferromagnetic Heisenberg model on honeycomb lattice for different values of magnetic field above threshold field. We have implemented the hard core boson transformation for spin operators which gives the excitation spectrum in terms of many body calculations for bosonic gasgorkov . We have used Brueckner approach gorkov to find the bosonic self-energy to get the spinon dispersion relation. In order to calculate structure factors of the spin model Hamiltonian including antisymmetric anisotropic Dzyaloshinskii-Moriya term, we have used one particle excitation spectrum of hard core bosonic model Hamiltonian. We obtain both transverse and longitudinal spin structure factors from one and two particle bosonic Green’s function. Also the effects of next nearest neighbor exchange constant and DM interaction strength on temperature dependence of transverse static spin susceptibility have been investigated in details.
II Theoretical formalism
The general form of anisotropic spin Hamiltonian on the monolayer honeycomb lattice which contains antisymmetric exchange interaction between spins in the presence of a magnetic field is written in the following form
| (1) |
The lattice structure of honeycomb lattice has been shown in Fig.(1). The symbol and in Eq.(1) implies the nearest neighbor and next nearest neighbor sites in a honeycomb lattice, respectively. is the nearest neighbor coupling constant between spins, while denotes the next nearest neighbor coupling constant between spins. is thae axis perpendicular to the honeycomb plane. The antisymmetric spin exchange originating from the relativistic spin-orbit interaction is also known as Dzyaloshinskii-Moriya (DM) interaction. The third term in Eq.(1) with describes the DM interaction between nearest neighbor sites. Also is the gyromagnetic constant and denotes the Bohr magneton. The gyromagnetic constant value is independent of the type of lattice and gets the same value for honeycomb lattices such as graphene. This constant is related to the structure of localized electron in the lattice. is the magnetic field strength. The magnetic field is applied as perpendicular to honeycomb plane. Anisotropy due to DM interaction and Zeeman term violate SU(2) symmetry of the isotropic Heisenberg model Hamiltonian.
In order to obtain the bosonic representation of the model hamiltonian two different bosonic operators are required. Therefore spin operators are transformed to bosonic ones as
| (2) |
denotes the unit cell index and label two sublattices. creates a boson in unit cell with index on sublattice . Exploiting above transformation, we have the following one particle bosonic hamiltonian
| (3) | |||||
Based on Fig.(1), the symbol implies the characters of neighbor unit cells including nearest neighbor atomic sites. The translational vectors connecting neighbor unit cells are given by
| (4) |
Also index implies the characters of neighbor unit cells including next nearest neighbor atomic sites. The translational vector are given by
| (5) |
where the length of until cell vectors is considered to be one. In terms of Fourier space transformation of Bosonic operators, the bilinear part of model Hamiltonian is given by
| (6) |
The coefficients in the above equation are
| (7) |
The wave vectors are considered in the first Brillouin zone of the honeycomb lattice. Also the quartic part of the model Hamiltonian is obtained as follows
| (8) |
In order to reproduce the SU(2) spin algebra, bosonic particles must also obey the local hard-core constraint , i.e only one boson can occupy a single site of lattice. In terms of Fourier transformation of bosonic operators, we can write this part of the Hamiltonian as
| (9) |
where implies the strength of the hard core repulsion. In fact is the local intrasite integration between hard core bosons. The effect of hard core repulsion part () of the interacting Hamiltonian in Eq.(4) is dominant compared with the quartic term in Eq.(8). Under taking limit the excitation spectrum of bosonic gas describe the excitation spectrum of original spin model Hamiltonian.
Using a unitary transformation as
| (10) |
the bilinear part of the Hamiltonian is diagonalized as
| (11) |
The Bogoliubov coefficients are given by
| (12) |
According to bilinear part of bosonic model Hamiltonian in Eq.(6), Fourier transformation of the noninteracting Green’s function matrix elements are written in the following form
| (13) |
where denotes the bosonic Matsubara’s frequency. Also denotes the temperature of the system. In Eq.(13), symbol means time-ordering operator. Since the hard core bosonic repulsion is on-site interaction between bosons, Wick’s theoremmahan concludes that only the diagonal elements of bosonic self-energy matrix gets non zero value. Thus we can write down a Dyson’s equation for the interacting Green’s function matrix () as
| (16) | |||||
| (19) |
where is normal retarded self-energies diagonal element due to hard core repulsion between bosons. After using Dyson’s series mahan for the interacting Matsubara Green’s function matrix in Eq.(19) , the low energy limit of single particle retarded Green’s function matrix elements are
| (20) |
The renormalized excitation spectrum and renormalized single particle weight are given by
| (21) |
Since the Hamiltonian in Eq.(4) is short ranged and is large, the Brueckner’s approach (ladder diagram summation) rezania2008 ; fetter ; gorkov can be employed for calculating bosonic self-energies in the low density limit of bosonic gas and for low temperature. Firstly, the scattering amplitude (t-matrix) of hard core bosons is introduced where . is momentum vector and implies the Matsubara’s frequency of the th bosonic particle. The basic approximation made in the derivation of is that we have considered the diagonal elements of bosonic Green’s function for making . It is due to the strongly intrasite interaction between bosons. According to the Feynman’s rules in momentum space at finite temperature () and after taking limit , the scattering amplitude can be written as the following form
| (22) |
where is the number of unit cells and wave vector belongs to the first Brillouin zone of honeycomb lattice. is the Boltzmann constant. We can perform the summation over Matsubara frequencies in the Eq.(22) according to Feynman rulesmahan and the final result for scattering amplitude is obtained by
| (23) |
where describes the Bose-Einstien distribution function. The hard core self-energy is obtained by using the scattering amplitude obtained in Eq.(22).
| (24) |
The hard core self-energy is obtained by integration over internal Matsubara’s frequency ()
| (25) |
It should be noted that index is the integer number. We can simply obtain the retarded self-energy by analytic continuation () of Eq.(25). The contribution of on the final results is very small beecause it is composed of quartic terms in the bosonic operators. It is therefore treated in mean-field approximation. This is equivalent to take only one-loop diagrams in to account (first order in ). On the mean field level we have where each and is a pair of boson operators. We can write for each pair of operators,
| (26) |
Thus, the effect of is to renormalize the coefficients of bilinear part of the Hamiltonian according to the following relations
| (27) |
The renormalized coefficients (Eq.(27)) will be considered to calculate the self-energy which are independent of energy (nonretarded in time representation).
III Dynamical and static spin structure factors
The correlation function between spin components of localized electrons at different times can be expressed in terms of one and two particle bosonic Green’s functions. The frequency Fourier transformation of this correlation function produces the dynamical spin susceptibility. The frequency position of peaks in dynamical spin susceptibility are associated with collective excitation localized electrons described by Heisenberg model Hamiltonian. These excitations are related to the spin excitation spectrum of localized electrons on Honeycomb structure. In the view point of experimental interpretation, the dynamical spin susceptibility of the localized electrons of the system is proportional to inelastic cross-section for magnetic neutron scattering from a magnetic system that can be expressed in terms of spin density correlation functions of the system. In other words the differential inelastic cross section is proportional to imaginary part of spin susceptibilities. denotes the energy loss of neutron beam which is defined as the difference between incident and scattered neutron energies. The solid angle implies the orientation of wave vector of scattered neutrons from the localized electrons of the sample. We can assume the wave vector of incident neutrons is along direction. The solid angle depends on the polar angle between wave vector of scattered neutrons and the wave vector of the incident neutrons. A note is in order here. The solid angle is different from the excitation spectrum of hard core bosonic particles , i.e. , , in Eq.(21). The frequency position of peaks in determines the spin excitation spectrum of the magnetic systemdoniach . In order to study the general spin excitation spectrum of the localized electron of the systems, both transverse and longitudial dynamical spin-spin correlation functions have been calculated.
According to the linear-response theory, the components of spin susceptibility tensor are written by
| (28) | |||||
that impliy the spatial directions and is the bosonic frequency. is the wave vector belonging to the first Brillouin one of honeycomb lattice. Since each unit cell in honeycomb lattice includes two different sublattices, the Fourier transformation of spin operators in Eq.(28) is exprssed in terms of both bosonic operators and as
| (29) |
Here, we define transverse dynamical spin suceptibility, i.e. , in terms of components of spin susceptibility tensor, ,
| (30) |
so that spin ladder operators are given as and . Using the definitions of Fourier transformation of spin operators in Eq.(29), we can calculate the Matsubara representation of transverse dynamical spin suceptibility in terms of one particle bosonic Green’s function as
| (31) | |||||
where the matrix elements of interacting Green’s function () have been expressed in Eq.(20). Also the Matsubara’ form of longitudinal dynamical spin susceptibility is written based on two particle Green’s function
| (32) | |||||
After using Wick’s theoremmahan and performing Matsubara frequency summation rules, the following expression has been obtained for longitudinal dynamical spin susceptibility
| (33) | |||||
The dynamical spin structure factor for both longitudinal and transverse spin directions are obtained based on retarded presentation of susceptibilities as
| (34) |
so that and are retarded dynamical spin structure factors for longitudinal and transverse components of spins, respectively. It is proportional to the contribution of localized spins in the neutron differential cross-section. For each the dynamical structure factor has peaks at certain energies which represent collective excitations for bosonic gas which correspond to the spin excitation spectrum of the original model.
Static transverse spin structure factor () which is a measure of magnetic long range ordering for spin components along the plane, i.e. transverse direction, can be related to imaginary part of retarded dynamical spin susceptibility using following relation.
| (35) | |||||
Substituting Eq.(20) into Eq.(31) and using Matsubara frequency summation rules Eq.(35), the final result for transverse static structure factor is given by
| (36) |
In the next section, the numerical results of dynamical spin structure and static spin structure have been presented for various magnetic field and DM interaction strength.
IV Results and discussions
The numerical reuslts of spin structure factors of the spin 1/2 Heisenberg model on honeycomb lattice in the field induced spin-polarized phase have been presented in this section. The frequency behaviors of dynamical spin susceptibilities and temperature dependence of static spin structure factors are studied. The effects of both magnetic field and Dzyaloshinskii-Moriya term strength on the behaviors of structure factors are investigated. In the limit of , the ground state of the original spin model Hamiltonian is a field induced spin-polarized state and a finite energy gap exists to the lowest excited state. The decrease in magnetic field lowers the energy gap which eventually vanishes at the critical magnetic field (). The effects of hard core interaction on the excitation spectrum have been obtained by the Green’s function approach in the context of Brueckner’s formalism above threshold field where the density of bosonic gas is small.
The single particle excitation should be found from a self-consistent solution of Eqs.(21,23,25,27) with the substitutions , , in the corresponding equations. The process is started with an initial guess for and by using Eq.(21) we find corrected excitation energy. This is repeated until convergence is reached. Using the final values for excitation spectrum we can calculate the dynamical and static spin structure factors by Eqs.(31,33,34,36). We discuss the numerical results for thermodynamic properties in the field induced spin polarized regime where energy spectrum of spin model hamiltonian includes a finite energy gap between ground state and first excited state. Therefore as long as excitation spectrum has non zero values, the system preserves its gapped spin polarized phase. In the following numerical results for both static and dynamical spin susceptibilities the wave vector has been fixed at generic wave vector .
The effect of DM interaction strength, , on critical magnetic field has been studied in Fig.(2). In this figure, energy gap () versus magnetic field for different values of Dzyaloshinskii-Moriya interaction strength for by setting has been plotted. Fig.(2) shows that the energy gap vanishes as the magnetic field approaches the critical value for . For all values of , the gap vanishes at the critical point where the transition from gapped spin liquid phase to the gapless one occurs. Moreover the critical field tends to higher value with increase of according to Fig.(2).
In Fig.(3), the dynamical transverse spin structure factor, i.e. , has been plotted as a function of frequency for different next nearest neighbor coupling exchange constants, namely , at fixed magnetic field for . For each value for , there are two sharp peaks in imaginary part of transverse dynamical spin susceptibility at low and high frequencies. These frequency positions of sharp peaks describe the transverse magnetic excitation spectrum of the localized electrons on honeycomb structure. As shown in Fig.(3), the lower frequency peak have lower height in comparison with the higher frequency peak for each value of . The height of each peak corresponds to the intensity of scattered neutrons from the sample which describes the inelastic scattering cross section of neutron beam. Moreover the frequency of each peak is equal to the difference between scattered neutron beam energy and incident neutron energy beam. This energy difference is absorbed by the localized electrons which causes to magnetic excitation of transvesre components of spins. According to Fig.(3), it is clearly observed that frequency position of peaks in the imaginary part of transverse spin susceptibility, , goes to lower values with increase of next nearest neighbor exchange constant . It can be understood from this fact that the energy gap between ground state and first excited state decreases with and consequently the magnetic excitation appears at lower frequency. Moreover the Fig.(3) implies the intensity of scattered neutron beam from the sample is independent of and the heights of peaks in transverse spin structure factor are the same. The emergence of peaks in the dynamical spin susceptibilities of Heisenberg chain have been shown for magnetic fields below threshold one using quantum Monte Carlo method based on the stochastic series expansion and maximum entropy methodbrenig . At threshold magnetic field, the energy gap closes so that long range magnetic ordering develops for magnetic field below threshold one. Based on Fig.(2), the normalized threshold magnetic field is about . The estiamtion value for exchange coupling constant is around . Thus one can obtain the threshold magnetic field Tesla. However the magnetic field for theoretical studies of Heisenberg model Hamiltonian on lattice structures has been considered as normalized value langer ; zotos . In theoretical studies the qualitative behavior of physical parameters in terms of magnetic field is more important. Also the normalized magnetic field value reported in the theoretical works is in the region . Also dynamical structure factor of two dimensional antiferromagnet in high fields has been investigated within spin-wave theory using self-consistent approach beyond the approximationfuhrman . The emergence of sharp peak in the frequency behavior of spin structure factor has been predicted in this work in analogy to our work.
The effect of Dzyaloshinskii-Moriya interaction strength, , as anisotropy parameter on the frequency behavior of imaginary part of dynamical transverse spin susceptibility has been shown in Fig.(4) for at fixed temperature . Based on experimental works on inorganic Heisenberg magnetic materialslefan ; martin the real value for is expected. This normalized temperature corresponds to . Also longitudinal magnetic field has been fixed at . This figure includes the sharp peaks at finite frequencies for each value of . In the absence of there is no the low frequency excitation mode and we see a collective magnetic excitation mode at . In the presence of finite , an excitation mode appears at low frequencies so that the position of peaks tends to lower values with increase of . This is a signature of the decrease of energy gap with increase of Dzyaloshinskii Moriya interaction strength. Moreover it is cearly observed the high frequency of excitation mode goes to higher values with Dzyaloshinskii-Moriya interaction strength. Another novel feature in Fig.(4) is the reduction of intensity of scattered neutrons at frequencies above 4.0 with increase of .
We have also studied the effect of longitudinal magnetic field on frequency behavior of imaginary part of dynamical transverse spin susceptibility. In Fig.(5), has been plotted versus normalized frequency for different values of magnetic field above critical field for for at fixed temperature . As shown in Fig.(5), the frequency position of sharp peaks that describe the magnetic excitation mode of the localized electrons moves to higher values upon increasing magnetic field. It can be understood from this fact that energy gap between ground state and first excited state in bosonic gas spectrum enhances with . Also the height of peaks that is proportional to the intensity of scattered neutrons from the electrons of the sample is independent of magnetic field.
In Fig.(6), the longitudinal dynamic structure factor has been shown as a function of frequency for different amounts of for and . This figure shows that there is not sharp peaks in imaginary part of longitudinal dynamical spin susceptibility in contrast of transverse susceptibility case. In fact there is no well defined magnetic collective excitation spectrum for transverse components of spins. has two peak at low and high frequencies for each value of . High frequency peaks appear at frequency however the intensity of these peaks increase with according to Fig.(6). Low frequency peaks moves to lower values upon increase of next nearest neighbor exchange constant. Moreover the intensity of these peaks enhances with similar to the case of high frequency peaks. Also it is clearly observed that disappears in frequency region above 3.5 for all values of . There are the clear differences between numerical results in Figs.(5,6). Fig.(5) shows very sharp peaks for transverse spin susceptibility while the broaden peaks is clearly observed for longitudinal dynamical spin susceptibility in Fig.(6). Also the magnitude of peaks in transverse and longitudinal susceptibilities are clearly different. These differences arises from this point that magnetic excitation spectrum for different spin components of localized electrons are different. In the presence of magnetic field along direction, the magnetic excitation for longitudinal components of spins is not well performed. This fact can be understood form this point the applying magnetic field causes to allignment of spin direction along direction. In other words the applied magnetic field suppresses to excite the spin components along direction. Thus there is no well defined excitation spectrum for components of localized spins. In other words the dynamical spin susceptibility includes only broaden peaks according to Fig.(6). This is not the case for magnetic excitation spectrum of transverse components od localized spins. These components are perpendicular to the magnetic field direction so that the excitation of transverse components of spins is well performed. This point demonstrates the frequency behavior of transverse dynamical susceptibility has sharp well defined peaks. The difference between the magnitudes of peaks for transverse and longitudinal spin susceptibilities is related to intensity of scattered neutrons from the sample. The applying the magnetic field leads to different intensity of scattered neutron beam for transverse and longitudinal components of localized spins.
The effect of Dzyaloshinskii-Moriya interaction strength, , on frequency behavior of for magnetic field at has been shown in Fig.(7). For each value of , there is two separate peaks in the imaginary part of longitudinal dynamical spin susceptibility versus frequency. The first peak appears at frequency for all values of while the position of the second peak moves to higher frequency with increase of based on Fig.(7). Another feature in this figure is the enahncement of the amount of with at fixed value of frequency.
In Fig.(8), we present the imaginary part of longitudinal dynamical spin susceptibility of localized electrons on honeycomb lattice versus normalized frequency for different magnetic fields, namely for fixed values of and . All plots in Fig.(8) show the position of peaks is almost the same for various values of magnetic field however the intensity of peaks reduces with magnetic field strength. This reduction of intensity can be justified based on the increase of energy gap with .
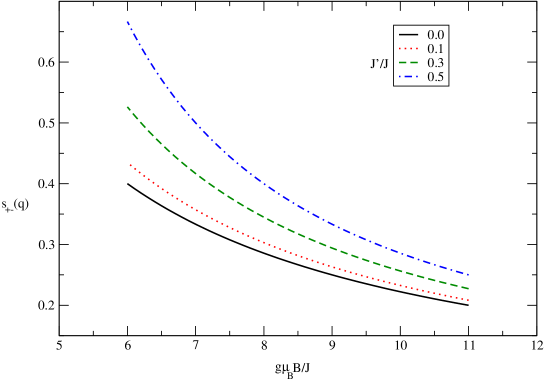
The behavior of transverse static spin structure factor versus normalized magnetic field for different values of has been presented in Fig.(9). Temperature and DM interaction strength have been fixed at and , respectively. This figure implies static spin structure for spin components parallel to the honeycomb plane shows a monotonic deceasing behavior in terms of magnetic field for all values of . This behavior can be understood from this fact that magnetic field causes to reduce the magnetic ordering for transverse components of spins which decreases transverse static structure factor. In addition, at fixed vales of magnetic field, lower next nearest neighbor exchange constant causes lower energy gap and consequently higher values in transverse structure factor.
The effect of Dzyaloshinskii-Moriya interaction strength on magnetic field dependence of transverse static spin structure factor has been shown in Fig.(10). Here transverse structure factor decreases with magnetic field as shown in Fig.(10). A monotonic decreasing behavior for transverse static structure factor has been observed for each DM interaction strength. Moreover transverse structure factor enhances with increasing .
We have also studied the dependence of transverse static spin structure factor on normalized temperature. In Fig.(11), we have plotted the static structure factor of localized electrons on honeycomb lattice as a function of normalized temperature for different values of for . The magnetic field is set to . However the real value of this magnetic field is higher than 60 Tesla, the qualitative behavior of static structure factor in the presence of finite magnetic field is the main aim of this study. Thus a finite non zero normalized magnetic field, for example , has been considered so that the spin liquid phase is valid in this situation. According to this figure, structure factor is less temperature dependent for because the thermal fluctuations has no effect on magnetic ordering. Upon more increase of temperature the transverse static structure factor decreases for each value of . Another novel feature in Fig.(11) is the reduction of structure factor with decrease of at fixed temperature. This arises from this fact that energy gap increases with decreasing .
Finally, static transverse spin structure factor as a function of temperature for various DM interaction parameter has been studied in Fig.(12) for . Transverse static structure factor has a constant value for temperatures below 1.0. Upon increasing temperature above 1.0, thermal fluctuations becomes considerable and consequently the structure factor decreases. For structure factor is approximately independent of DM interaction strength where all plots fall on each other in this temperature region. Moreover at fixed temperature below 3.0 the static structure factor rises with DM interaction strength due to decrease of energy gap with .
We would like to add few comments on the possibility of quantum spin liquid on a Heisenberg honeycomb antiferromagnet. Quantum spin liquid phase originates from the finite band gap in excitation spectrum of Heisenberg model hamiltonian on the lattice. Such finite band gap leads to the exponential behavir for spatial correlation function between localized spins on the lattice. The investigation of quantum spin liquid phase on honeycomb lattice in the absence of external magnetic field has been performed using theoretical and numerical methodssorella ; assaad ; wang ; clark ; cabra . However there is finite energy gap in excitation spectrum of Heisenberg model on honeycomb lattice for magnetic field above critical one. As in Fig.(2) shown, the energy gap gets non zero value fpr magnetic fields higher than critical one. Based on Fig.(2), our results show the threshold magnetic field, where energy gap closes, is in the . This energy gap in excitation spectrum arises from Zeeman splitting effect duen spin degrees of freedom. This gapped spin liquid phase due to applying magnetic field is named field induced ferromagnetic phase. At any temperature, a non zero threshold magnetic field is found so that the energy gap in the spectrum appears and quantum spin liquid phase develops for magnetic fields above threshold one. The inelastic scattering cross section of neutrons from the localized spins for each magnetic phase is applied to study the collective magnetic excitation modes of the system. In fact dynamical spin susceptibility corresponding to the inelastic scattering cross section has no infromation regarding the magnetic phase of the system. Of course the divergence behavior of static spin structure factor can be an evidence for phase transition in the system.
V Conclusions
In conclusion, we have the effects of both nexnearest neighbor coupling exchange constant and spin-orbit coupling on the magnetic structure factors and collective magnetic modes of Heisenberg model Hamiltonian on honeycomb lattice. Using hard core bosonic transformation, the excitation spectrum of the model hamiltonian has been found. The dynamical transverse and longitudinal spin susceptibilities have been calculated using Wick’s theorem and excitation spectrum of the model. The results show the transverse spin susceptibility includes the sharp well defined peaks while the longitudinal spin susceptibility has sharp peaks in its frequency dependence. Also the behavior of static spin susceptibilities in terms of magnetic field and temperature has been investigated for different spin-orbit coupling strengths. Based on our results, the transverse static spin structure factor decreases with increae of magnetic field for different next nearest neighbor exchange constants and spin-orbit coupling interactions.











References
References
- (1) R. Okuma, etal, Nature Communications 10, 1229 (2019)
- (2) S. A. Zvygain, D. Graf, T. Sakurai, S. Kimura, H. Nojiri, J. Wosnitza, H. Ohta, T. Ono, H. Tanaka, Nature Communications 10, 1064 (2019)
- (3) A. M. do nascimento-Junior, R. R. Montenegro-Fihlo, Phys. Rev. B 99, 064404 (2019)
- (4) T. Ito, C. Iino, N. Shibata, Phys. Rev . B 97, 184409 (2018)
- (5) L. Balent, Nature (London) 464, 199 (2010)
- (6) P. W. Anderson, Mat. Res. Bull 8, 153 (1973)
- (7) P. Fazekas and P. W. Anderson, Phil. Mag 30, 423 (1974)
- (8) S. Liang, B. Doucot and P. W. Anderson, Phys. Rev. Lett 61, 365 (1988)
- (9) S. Sachdev, Phys. Rev. B 45, 12377 (1992)
- (10) A. W. Sandvik, Phys. Rev. Lett 95, 207203 (2005)
- (11) E. Lefancoise, etal. Phys. Rev. B 94, 214416 (2016)
- (12) N. Martin, L. -P Regnault, and S. Klimko, J. Phys. Conf. Ser 340, 012012 (2012)
- (13) S. Sorella, Y. Otsuka, S. Yunoki, Scientific Reports 2, 992 (2012)
- (14) I. Affleck and M. Oshikawa, field induced gap in Cu benzoate and other spin half antiferromagnetic chains, Phys. Rev. B 60, 1038 (1999)
- (15) G. Uimim, Y. Kudasov, P. Fulde and A. Ovchinikov, Low energy excitations of Yb4As3 in a magnetic field, Euro, Phys. J. B 16, 241 (2000)
- (16) D. Dimitriev and V. Krivnov, gap genertaion in the XXZ model in transverse field, Phys. Rev. B 70, 144414 (2004)
- (17) H. Bethe, Z. Phys. B 91, 507 (1931)
- (18) L. D. Faddeev and L. A. Takhtajan, Phys. Lett. A 85, 375 (1981)
- (19) A. Klümper, Z. Phys. B 91, 507(1993)
- (20) D. C. Johnston, R. K. Kremer, M. Troyer, X. Wang, A. Klümper, S. L. Buďko, A. F. Panchula, and P. C. Canfield, Phys. Rev. B 61, 9558 (2000)
- (21) A. Klümper, D. C. Johnston, Phys . Rev. Lett 84, 4701 (2000)
- (22) T. Moriya, Phys. Rev 120, 91 (1960)
- (23) Auerbach A 1994 Interacting electrons and Quantum Magnetism (New York: springer-Verlag Inc.)
- (24) G. D. Mahan, Many-partilce physics (Kluwer Academic/Plenum Publishers, 2000).
- (25) A. Abrikosov, L.Gorkov, and T. Dzyloshinskii, Methods of Quantum Field Theory in Statistical Physics (Dover, New York, 1975)
- (26) H. Rezania, A. Langari and P. Thalmeier, Phys.Rev. B 77, 094438 (2008)
- (27) A. L. Fetter and J. D. Walecka, Quantum Theory of Many Particle Systems (Mc Graw-Hill, 1971)
- (28) S. Doniach and E. H. Sondheimer, Green’s functions for solid state physicists (Imperial College Press, London, 1999)
- (29) S. Grossjohann and W. Brenig, Phys. Rev. B 79, 094409 (2009)
- (30) S. Langer, R. Darradi, F. Heidrich-Meisner and W. Brenig, Phys. Rev. B 82, 104424 (2010)
- (31) C. Psaroudaki and X. Zotos, J. Stat. Mech 2016, 063103 (2016)
- (32) W. T. Fuhrman, M. Mourigal, M. E. Zhitomirsky and A. L. Chernyshev Phys. Rev. B 85, 184405 (2012)
- (33) F. F. Assaad, and L. F. Herbut, Phys. Rev. X 3, 031010 (2013)
- (34) F. Wang, Phys. Rev. B 82, 024419 (2019)
- (35) B. K. Clark, D. A. Abanin, and S. L. Sondhi, Phys. Rev. lett 107, 087204 (2011)
- (36) D. C. Cabra, C. A. Lamas, and H. D. Rosales Phys. Rev. B 83, 094506 (2011)