Dynamic Response of Wigner Crystals

Interacting two-dimensional electron system (2DES) subjected to high perpendicular magnetic fields ($B$) and cooled to low temperatures exhibits a plethora of exotic states Jain (2007). The Wigner crystal (WC) Wigner (1934) terminates the sequence of fractional quantum Hall states at very small landau level filling factor Jiang et al. (1990); Goldman et al. (1990); Li et al. (1991); Santos et al. (1992); Sajoto et al. (1993); Pan et al. (2002); Maryenko et al. (2018); Hossain et al. (2020); Chung et al. (2022); Lozovik and Yudson (1975); Lam and Girvin (1984); Levesque et al. (1984); Andrei et al. (1988); Williams et al. (1991); Li et al. (1997); Ye et al. (2002); Chen et al. (2004); Li et al. (1995); Deng et al. (2019); Chen et al. (2006); Drichko et al. (2016); Tiemann et al. (2014). This electron solid is pinned by the ubiquitous residual disorder, manifests as an insulating phase in DC transport Jiang et al. (1990); Goldman et al. (1990); Li et al. (1991); Santos et al. (1992); Sajoto et al. (1993); Pan et al. (2002); Maryenko et al. (2018); Hossain et al. (2020); Chung et al. (2022), and the electrons’ collective motion is evidenced by a resonance in AC transport Lozovik and Yudson (1975); Lam and Girvin (1984); Levesque et al. (1984); Andrei et al. (1988); Williams et al. (1991); Li et al. (1997); Ye et al. (2002); Chen et al. (2004). A series of experiments have been applied to investigate this correlated solid, such as the nonlinear $I-V$ response Goldman et al. (1990); Williams et al. (1991), the noise spectrum Li et al. (1991), the huge dielectric constant Li et al. (1995), the weak screening efficiency Deng et al. (2019), the melting process Chen et al. (2006); Drichko et al. (2016); Deng et al. (2019), the nuclear magnetic resonance Tiemann et al. (2014) and the optics Zhou et al. (2021); Smoleński et al. (2021).

Capacitance measurements have revealed a series of quantum phenomena Mosser et al. (1986); Ashoori et al. (1992); Smith et al. (1986); Yang et al. (1997); Eisenstein et al. (1994); Zibrov et al. (2017); Irie et al. (2019); Eisenstein et al. (1992); Jo et al. (1993); Li et al. (2011); Zibrov et al. (2018); Tomarken et al. (2019); Deng et al. (2019). In this work, we examine the WC formed in an ultra-high mobility 2DES at $\nu\lesssim$ 1/5 using high-precision capacitance measurement Zhao et al. (2022a, b). We find an exceedingly large capacitance at low measurement frequency $f$ while the conductance is almost zero. This phenomenon is inconsistent with transporting electrons, but rather an evidence that the synchronous vibration of electrons induces a polarization current. When we increase $f$, our high-precision measurement captures the fine structure of the resonance response with a puzzling ”half-dome” structure. Our systematic, quantitative results provide an in-depth insight of this murky quantum phase.

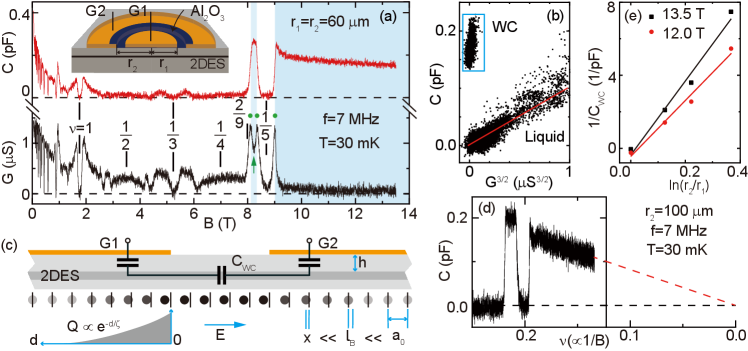
Our sample consists an ultra-clean low-density 2DES confined in a 70-nm-wide GaAs quantum well with electron density $n\simeq 4.4\times 10^{10}$ cm^-2 and mobility $\mu\simeq$ 17 $\times 10^{6}$ cm²/(V$\cdot$s). Each device has a pair of front concentric gates G1 and G2, whose outer and inner radius are $r_{1}$ and $r_{2}$, respectively; see the inset of Fig. 1(a) ¹¹1See Supplemental Material for detailed description of our sample information and measurement techniques.. We study four devices with $r_{1}=$60 $\mu$m and $r_{2}=$ 60, 80, 100 and 140 $\mu$m, respectively. We measure the capacitance $C$ and conductance $G$ between the two gates using a cryogenic bridge and analyze its output with a custom-made radio-frequency lock-in amplifier Zhao et al. (2022a, b); Note (1).

Fig. 1(a) shows the $C$ and $G$ measured from the $r_{1}=r_{2}=$ 60 $\mu$m sample. Both $C$ and $G$ decrease as we increase the magnetic field $B$, owing to the magnetic localization where the 2DES conductance $\sigma\propto(ne^{2}\tau)/m^{\star}(1+\omega_{c}^{2}\tau^{2})$, $m^{\star}$, $\omega_{c}$ and $\tau$ are the effective mass, cyclotron frequency and transport scattering time of the electrons, respectively Zhao et al. (2022b). The $C$ and $G$ are finite at $\nu=1/2$ and 1/4 where the 2DES forms compressible composite Fermion Fermi sea. When $\nu$ is an integer or a certain fraction such as 1/3 and 1/5, the 2DES forms incompressible quantum Hall liquids so that both $C$ and $G$ vanish ²²2The zero of $C$ and $G$ can be defined either by extrapolating their field dependence to $B=\infty$, or by their values at strong quantum hall states such as $\nu=1$. These two approaches are consistent with each other and the dash lines in Fig. 1(a) represent the deduced zero..

In all the above cases, the current is carried by transporting electrons, so that $C$ has a positive dependence on $G$, i.e. $C\propto G^{3/2}$, as shown in Fig. 1(b) Zhao et al. (2022b). Such a correlation discontinues when the WC forms at very low filling factors $\nu\lesssim 1/5$, see the blue shaded regions of Fig. 1(a). The vanishing conductance $G$ suggests that the electrons are immovable, however, the surprisingly large capacitance $C$ evidences that the WC hosts a current even surpassing the conducting Fermi sea at $\nu=1/2$ and 1/4 at much lower magnetic field! The phase transition between the WC and the liquid states are clearly evidenced by spikes in $G$ (marked by solid circles in Fig. 1(a)) and sharp raises in $C$. A developing minimum is seen in $G$ at $1/5<\nu<2/9$ (marked by the up-arrow) when $C$ has a peak. This $G$ minimum develops towards zero and the $C$ peak saturates when the solid phase is stronger (see black traces in Fig. 3(a)). This is consistent with the reentrant insulating phase Jiang et al. (1990); Goldman et al. (1990); Williams et al. (1991); Li et al. (1991); Chen et al. (2004); Shayegan (2006, 1998).

It is important to mention that the 2DES in our devices is effectively “isolated” and we are merely transferring charges between different regions within one quantum phase. Similar to the dielectric materials which also have no transporting electrons, the collective motion of all electrons, i.e. the $k\to 0$ phonon mode of WC, can generate polarization charges and corresponding polarization current in response to the in-plane component of applied electric field. An infinitesimally small but ubiquitous disorder pins the WC so that electrons can only be driven out of their equilibrium lattice site by a small displacement $\mathbf{x}$, as shown in Fig. 1(c). During the experiments, we use excitation $V_{\text{in}}\simeq$ 0.1 mV${}_{\text{rms}}$ and the measured WC capacitance is $\sim$ 0.15 pF at 13.5 T. The polarization charge accumulated under the inner gate is $Q=CV_{\text{in}}\sim$ 100 $e$. The corresponding electron displacement at the boundary of the inner gate, $|\mathbf{x}(r_{1})|\simeq Q/(2\pi r_{1}ne)\sim 0.6$ nm, is much smaller than the magnetic length $l_{B}=\sqrt{\hbar/eB}\sim 8$ nm, substantiating our assumption that the electrons vibrate diminutively around their equilibrium lattice sites.

An ideal, disorder-free WC is effectively a perfect dielectric with infinite permittivity, so that the device capacitance should be close to its zero-field value $C_{0}\sim$ 1 pF when 2DES is an excellent conductor. We note that $C_{0}$ is consistent with the device geometry, $\epsilon_{0}\epsilon_{\text{GaAs}}\pi r_{1}^{2}/h\simeq$ 1.3 pF, where $\epsilon_{\text{GaAs}}=12.8$ is the relative dielectric constant of GaAs and $h\simeq$ 960 nm is the depth of 2DES. However, the measured $C\sim 0.15$ pF in the WC regime is much smaller than $C_{0}$. This discrepancy is likely caused by the friction-like disorder which poses a pinning force $\simeq-\beta\mathbf{x}$ on the electrons. When the crystal’s inversion symmetry is broken, i.e. $\mathbf{x}$ is non-uniform and $\mathcal{J}(\mathbf{x})$ is finite, the electron-electron interaction generates a restoring force $\simeq-a_{0}\mu_{ij}\mathcal{J}(\mathbf{x})$, where $\mu_{ij}$, $a_{0}$ and $\mathcal{J}(\mathbf{x})$ are the elastic tensor, WC lattice constant and the Jacobi matrix of $\mathbf{x}$, respectively. At the low frequency limit, the WC is always at equilibrium and all forces are balanced, $e\mathbf{E}-a_{0}\mu_{ij}\mathcal{J}(\mathbf{x})-\beta\mathbf{x}=0$, $\mathbf{E}$ is the total parallel electric field on the WC.

$\mathbf{E}$ is approximately zero under the metal gates, since the gate-to-2DES distance $h$ is small. Therefore, $\mathbf{x}$ decreases exponentially when the distance from the gate boundary $d$ increases, $\mathbf{x}\propto\exp(-d/\zeta)$, where $\zeta=\mu a_{0}/\beta$ is the decay length. Deeply inside the gates, electrons feel neither parallel electric field nor net pressure from nearby electrons, so that their displacement $\mathbf{x}$ remains approximately zero. This region does not contribute to the capacitive response, and the effective gate area reduces to about $2\pi r_{1}\zeta$ and $2\pi r_{2}\zeta$ at the inner and outer gate, respectively. Because $r_{1}=r_{2}=$ 60 $\mu$m in Fig. 1(a), the experimentally measured $C\approx\epsilon_{0}\epsilon_{\text{GaAs}}/h\cdot 2\pi r_{1}\zeta/2\simeq$ 0.15 pF at 13.5 T corresponds to a decay length $\zeta\simeq$ 6.7 $\mu$m. Interestingly, our result shows a linear dependence $C\propto 1/B$ in Fig. 1(d), suggesting that $\beta\propto l_{B}^{-2}$ if we assume $\mu_{ij}$ is independent on $B$. Especially, the pinning becomes infinitely strong, i.e. $\beta\to\infty$, at the extreme quantum limit $l_{B}\to 0$.

The permittivity of a disorder-pinned WC is no longer infinitely large, since a non-zero electric field $\mathbf{E}$ is necessary to sustain a finite $\mathbf{x}$. If we assume $\mathbf{x}$ is a constant in the ring area between the two gates, so that $e\mathbf{E}=\beta\mathbf{x}$. The residual $\mathbf{E}$ can be modeled as a serial capacitance $C_{\text{WC}}\approx 2\pi ne^{2}/\beta\cdot[\ln(r_{2}/r_{1})]^{-1}$ in our device. We then measure different devices with $r_{1}$= 60 $\mu$m and $r_{2}=60$, 80, 100 and 140 $\mu$m, and calculate the corresponding $C_{\text{WC}}$ through $C_{\text{WC}}^{-1}=C^{-1}-(r_{1}+r_{2})/r_{2}\cdot C_{r_{1}=r_{2}}^{-1}$, see Fig. 1(e). By fitting the linear dependence $C_{\text{WC}}^{-1}\propto\ln(r_{2}/r_{1})$, we estimate the pinning strength $\beta$ to be about 1.3 $\times 10^{-9}$ and 1.1 $\times 10^{-9}$ N/m at $B=13.5$ and 12 T, respectively ³³3Alternatively, $C_{\text{WC}}$ can be modeled as a cylinder capacitor whose height equals the effective thickness of the 2DES, $Z_{0}\approx 45$ nm. The WC dielectric constant is $\epsilon_{\text{WC}}=(2\pi\epsilon_{0}Z_{0}\partial(C_{\text{WC}}^{-1})/\partial\ln(r_{2}/r_{1}))^{-1}\approx 2\times 10^{4}$ at 13.5 T, consistent with previous reported value in ref. Li et al. (1995).. Finally, assuming $\mu_{ij}\approx\mu\cdot\delta_{ij}$, we can estimate the WC elastic modulus $\mu\approx\beta\cdot\zeta/a_{0}$. For example, $\mu$ is about $1.6\times 10^{-7}$ N/m at 13.5 T.

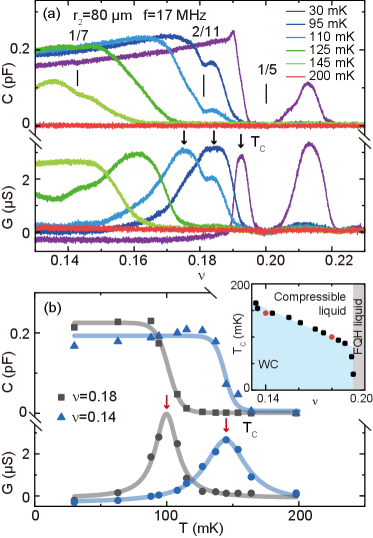
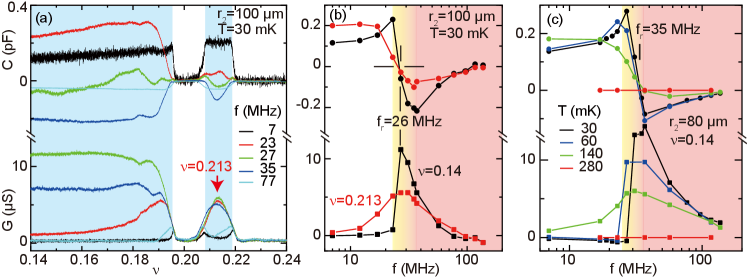
Fig. 2 reveals an intriguing temperature-induced solid-liquid phase transition when the WC melts. Fig. 2(a) shows $C$ and $G$ taken from the $r_{2}=80$ $\mu$m sample at various temperatures. At a certain temperature, e.g. at $T\approx 110$ mK, $C\sim 0.2$ pF when the 2DES forms WC at $\nu\lesssim 0.16$ and vanishes when it is a liquid phase at $\nu\gtrsim 0.18$. $G$ has a peak at $\nu\simeq 0.175$ when $C$ vs. $\nu$ has the maximal negative slope, and it is small when the 2DES is either a WC at $\nu<0.17$ or a liquid at $\nu>0.19$ ⁴⁴4We observe developing minimum at $\nu=1/7,2/11$ during the solid-liquid phase transition, signaling that the fractional quantum Hall state emerges Pan et al. (2002); Chung et al. (2022).. At very high temperature $T\gtrsim$ 200 mK, both $C$ and $G$ are close to zero. In Fig. 2(b), we summarized $C$ and $G$ as a function of $T$ at two different filling factors to better illustrate this solid-liquid transition. At $\nu\simeq 0.14$, for example, $C$ is large and $G$ is small at $T\lesssim 100$ mK when the WC is stable ⁵⁵5$C$ vs. $T$ has a slightly positive slope in the WC region, possibly due to the softening of disorder pinning., while both of them become small at $T\gtrsim 200$ mK when the 2DES is a liquid. The $G$ has a peak at a critical temperature $T_{C}$, marked by the red arrows, around which the precipitous decrease of $C$ happens. Alternatively, $T_{C}$ at a certain filling factor $\nu$ can be defined as the temperature when the $G$ has a peak (black arrow in Fig. 2(a)) at $\nu$. We summarize $T_{C}$ obtained using these two equivalent procedures in the Fig. 2(b) inset with corresponding red and black symbols. $T_{C}$ has a linear dependence on $\nu$ whose two intercepts are $T_{C}\simeq 340$ mK at the extreme quantum limit $\nu=0$, and $\nu\simeq$ 1/4 at $T_{C}=0$ mK.

The Fig. 2(b) evolution can be qualitatively understood by the coexistence of transport and polarization currents at the solid-liquid transition. The large $C$ reduces to almost zero when the transport current dominates over the polarization current. $G$ is a measure of the 2DES’s capacity to absorb and dissipate power. It is negligible if either of these two currents dominates, since the polarization current is dissipation-less and the dissipating transport current is difficult to excite. $G$ becomes large when these two currents coexist nip and tuck at intermediate $T$ when the excited polarization charge can be just dissipated by the transport current.

The WC exhibits a resonance when we increase the excitation frequency. In Fig. 3(a), the $C$ and $G$ measured from the $r_{2}=100$ $\mu$m sample using different excitation frequencies change enormously when the WC presents (blue shaded region). $G$ is almost zero and $C$ is large at $f\simeq 7$ MHz, and $G$ becomes finite and $C$ becomes even larger at $f\simeq 23$ MHz. At slightly higher frequency 27 MHz, $G$ reaches its maximum and $C$ drops to about zero. Further increasing $f$, $G$ gradually declines while $C$ first becomes negative at 35 MHz and then gradually approaches zero. The summarized $C$ and $G$ vs. $f$ at two certain fillings in Fig. 3(b), resembles qualitatively a resonant behavior with resonance frequency $f_{r}\simeq 26$ MHz (when $C=0$). Fig. 3(c) studies this resonance at different temperatures. The data is taken from the $r_{2}\simeq$ 80 $\mu$m sample whose resonance frequency is about 35 MHz ⁶⁶6$f_{r}$ has no obvious dependence with sample geometry, which is about 35, 35, 26 and 29 MHz for samples with $r_{2}$ = 60, 80, 100, 140 $\mu$m, respectively.. The abrupt change of $C$ near $f_{r}$ becomes gradual and the $G$ peak flattens at higher temperatures. Both $C$ and $G$ become flat zero at $T\gtrsim 280$ mK. It is noteworthy that, as long as a resonance is seen, $f_{r}$ is nearly independent on the filling factor (Fig. 3(b)) and temperatures (Fig. 3(c)). This is consistent with another experimental study using surface acoustic wave Drichko et al. (2016).

The resonance of WC is usually explained by the pinning mode Fogler and Huse (2000); Ye et al. (2002). The resonance frequency is related to the mean free path $L_{T}$ of the transverse phonon through $L_{T}=(2\pi\mu_{t,cl}/neBf_{r})^{1/2}$, where $\mu_{t,cl}=0.245e^{2}n^{3/2}/4\pi\epsilon_{0}\epsilon_{\text{GaAs}}$ is the classical shear modulus of WC. $f_{r}=26$ MHz corresponds to $L_{T}\simeq$ 3.2 $\mu$m, very similar to $\zeta\simeq 6.7$ $\mu$m in our Fig. 1(c) discussion. This is justifiable because both $L_{T}$ and $\zeta$ describe the length-scale within which the collective motion of WC is damped/scattered by the random pinning potential.

Before ending the discussion, we would like to highlight the puzzling ”half-dome” structure of the resonance. $G$ has a regular-shaped resonance peak, i.e. $G$ decreases gradually on both sides of $f_{r}$, when either the WC is weak ( $\nu\simeq 0.213$ in Fig. 3(b)) or the temperature is high ($T\simeq 140$ mK in Fig. 3(c)). Surprisingly, the resonance peak becomes quite peculiar when the WC is strong at $\nu\simeq 0.14$ and $T\simeq 30$ mK. $G$ gradually decreases from its peak at $f_{r}$ on the high frequency side $f>f_{r}$, while it vanishes instantly when the frequency is lower than $f_{r}$, resulting in a ”half-dome” $G$ vs. $f$ trace. Meanwhile, the $C$ increases by $\sim 2$ times and then abruptly changes to negative at $f_{r}$. This anomalous ”half-dome” feature is seen in all of our devices as long as the WC is strong and temperature is sufficiently low, suggesting a threshold frequency for the power dissipation.

In conclusion, using the extraordinarily high-precision capacitance measurement technique, we investigate the dynamic response of WC systematically. From the quantitative results and using a simple model, we can study several physical properties of the WC such as elastic modulus, dielectric constant, pinning strength, etc., and discover a puzzling ”half-dome” feature in the resonance peak. Our results certainly shine light on the study of WC and provides new insight on its dynamics.