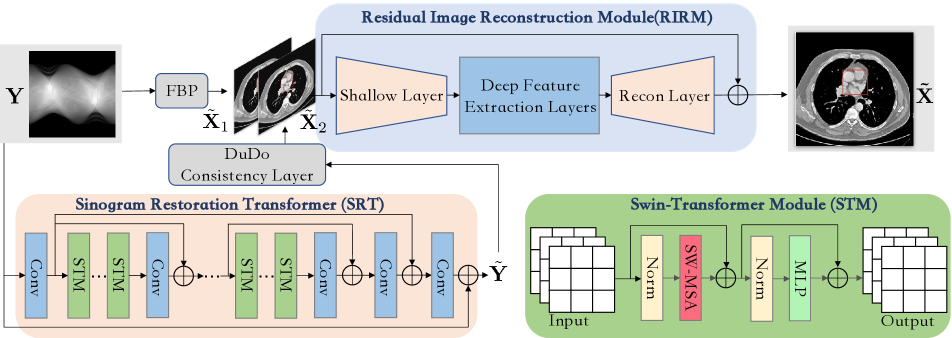
DuDoTrans: Dual-Domain Transformer Provides More
Attention for Sinogram Restoration in Sparse-View CT Reconstruction
Abstract
While Computed Tomography (CT) reconstruction from X-ray sinograms is necessary for clinical diagnosis, iodine radiation in the imaging process induces irreversible injury, thereby driving researchers to study sparse-view CT reconstruction, that is, recovering a high-quality CT image from a sparse set of sinogram views. Iterative models are proposed to alleviate the appeared artifacts in sparse-view CT images, but the computation cost is too expensive. Then deep-learning-based methods have gained prevalence due to the excellent performances and lower computation. However, these methods ignore the mismatch between the CNN’s local feature extraction capability and the sinogram’s global characteristics. To overcome the problem, we propose Dual-Domain Transformer (DuDoTrans) to simultaneously restore informative sinograms via the long-range dependency modeling capability of Transformer and reconstruct CT image with both the enhanced and raw sinograms. With such a novel design, reconstruction performance on the NIH-AAPM dataset and COVID-19 dataset experimentally confirms the effectiveness and generalizability of DuDoTrans with fewer involved parameters. Extensive experiments also demonstrate its robustness with different noise-level scenarios for sparse-view CT reconstruction. The code and models are publicly available at https://github.com/DuDoTrans/CODE.
1 Introduction and Motivation
Computed Tomography (CT) is a widely used clinically diagnostic imaging procedure aiming to reconstruct a clean CT image from observed sinograms , but its accompanying radiation heavily limits its practical usage. To decrease the induced radiation dose and reduce the scanning time, Sparse-View (SV) CT is commonly applied. However, the deficiency of projection views brings severe artifacts in the reconstructed images, especially when common reconstruction methods such as analytical Filtered Backprojection (FBP) and algebraic reconstruction technique (ART) [25] are used, which poses a significant challenge to image reconstruction.

To tackle the artifacts, some iterative methods are proposed to impose the well-designed prior knowledge (ideal image properties) via additional regularization terms , such as Total Variation (TV) based methods [27, 23], Nonlocal-based methods [38], and sparsity-based methods [2, 16]. Although these models have achieved better qualitative and quantitative performances, they suffer from over-smoothness. Besides, the iterative optimization procedure is often computationally expensive and requires careful case-by-case hyperparameter tuning, which is practically less applicable.
With the success of CNNs in various vision tasks [13, 34, 14, 45, 46], CNN-based models are carefully designed and exhibit potential to a fast and efficient CT image reconstruction [7, 15, 35, 1, 8, 11]. These methods render the potential to learn a better mapping between low-quality images, such as reconstructed results of FBP, and ground-truth images. Recently, Vision Transformer [5, 6, 9, 18] has gained attention with its long-range dependency modeling capability, and numerous models have been proposed in medical image analysis [6, 44, 3, 39, 37]. For example, TransCT [40] is proposed as an efficient method for low-dose CT reconstruction, while it suffers from memory limitation with involved patch-based operations. Besides, these deep learning-based methods ignore the informative sinograms, which makes their reconstruction inconsistent with the observed sinograms.
To alleviate the problem, a series of dual-domain (DuDo) reconstruction models [21, 30, 43, 42] are proposed to simultaneously enhance raw sinograms and reconstruct CT images with both enhanced and raw sinograms, experimentally showing that enhanced sinograms contribute to the latter reconstruction. Although these DuDo methods have shown satisfactory performances, they neglect the global nature of the sinogram’s sampling process, which is inherently hard to be captured via CNNs, as CNNs are known for extracting local spatial features. This motivates us to go a step further and design a more applicable architecture for sinogram restoration.
Inspired by the long-range dependency modeling capability & shifted window self-attention mechanism of Swin Transformer [22], we specifically design the Sinogram Restoration Transformer (SRT) by considering the time-dependent characteristics of sinograms, which restore informative sinograms and overcome the mismatch between the global characteristics of sinograms and local feature modeling of CNNs. Based on the SRT module, we finally propose Dual-Domain Transformer (DuDoTrans) to reconstruct CT image. Compared with previous image reconstruction methods, we summarize several benefits of DuDoTrans as follows:
-
•
Considering the global sampling process of sinograms, we introduce SRT module, which has the advantages of both Swin-Transformer and CNNs. It has the desired long-range dependency modeling ability, which helps better restore the sinograms and has been experimentally verified in CNN-based, Transformer-based, and deep-unrolling-based reconstruction framework.
-
•
With the powerful SRT module for sinogram restoration, we further propose Residual Image Reconstruction Module (RIRM) for image-domain reconstruction. To compensate for the drift error between the dual-domain optimization directions, we finally utilize the proposed differentiable DuDo Consistency Layer to keep the restored sinograms consistent with reconstructed CT images, which induces the final DuDoTrans. Hence, DuDoTrans not only has the desired long-range dependency and local modeling ability, but also has the benefit of dual-domain reconstruction.
-
•
Reconstruction performance on the NIH-AAPM dataset and COVID-19 dataset experimentally confirms the effectiveness, robustness, and generalizability of the proposed method. Besides, by adaptively employing Swin-Transformer and CNNs, our DuDoTrans has achieved better performance with fewer parameters as shown in Figure 1 and similar FLOPs (shown in later experiments), which makes the model practical in various applications.
2 Backgrounds and Related Works
2.1 Tomographic Image Reconstruction
Human body tissues, such as bones and organs, have different X-ray attenuation coefficients . When considering a 2D CT image, the distribution of the attenuation coefficients , where indicate positions, represents the underlying anatomical structure. The principle of CT imaging is based on the fundamental Fourier Slice Theorem, which guarantees that the 2D image function can be reconstructed from the obtained dense projections (called sinograms). When imaging, projections of the anatomical structure are indeed inferred by the emitted and received X-ray intensities according to the Lambert-Beer Law. Further, when under a polychromatic X-ray source with an energy distribution , the CT imaging process is given as:
| (1) |
where represents the sinogram generation process, i.e., Radon transformation (commonly defined with a fan-beam imaging geometry). With the above forward process, CT imaging aims to reconstruct from the obtained projections (abbreviation for simplicity) with the estimated/learned function . In practical SVCT, the projection data is incomplete, where the total projection views are sampled uniformly in a circle around the patient. This reduced sinogram information heavily limits the performance of previous methods and results in artifacts. In order to alleviate the phenomena, many works have been recently proposed, which can be categorized into the following two groups: Iterative-based reconstruction methods [27, 23, 38, 2, 16] and Deep-learning-based reconstruction methods[13, 34, 14, 45, 46]. Different from these prevalent works, our method DuDoTrans is based on deep-learning, but is the only dual-domain method based on Transformer.
2.2 Transformer in Medical Imaging
Based on the powerful attention mechanism [29, 4, 10, 36, 26, 41] and patch-based operations, Transformer is applied to many vision tasks [9, 28, 12, 22]. Especially, Swin Transformer [22] incorporates such an advantage with the local feature extraction ability of CNNs. With such an intuitive manner, Swin-Transformer-based models [19] have relieved the limitation of memory in previous Vision Transformer-based models. Based on these successes and for better modeling the global features of medical images, Transformer has been applied to medical image segmentation [6, 44, 3, 20], registration [39], classification [37, 31], and achieved surprising improvements. Nevertheless, few works explore Transformer structures in SVCT reconstruction. Although TransCT [40] attempts to suppress the noise artifacts in low-dose CT with Transformer, they neglect the consideration of global sinogram characteristics in their design, which is taken into account in DuDoTrans.
3 Method
As shown in Fig. 2, we build DuDoTrans with three modules: (a) Sinogram Restoration Transformer (SRT), (b) DuDo Consistency Layer, and (c) Residual Image Reconstruction Module (RIRM). Assume that a sparse-view sinogram is given, we first use FBP [25] to reconstruct a low-quality CT image . Simultaneously, the SRT module is introduced to output an enhanced sinogram , followed by the DuDo Consistency Layer to yield another estimation . At last, these low-quality images and are concatenated and fed into RIRM to predict the CT image , which will be supervised with the corresponding clean CT image . We next introduce the above-involved modules in detail.
3.1 Sinogram Restoration Transformer
Sinogram restoration is extremely challenging since the intrinsic information not only contains spatial structures of human bodies, but follows the global sampling process. Specifically, each line of a sinogram are sequentially sampled with overlapping information of surrounding sinograms. In other words, 1-D components of sinograms heavily correlate with each other. The global characteristic makes it difficult to be captured with traditional CNNs, which are powerful in local feature extraction. For this reason, we equip this module with the Swin-Transformer structure, which enables it with long-range dependency modeling ability. As shown in Fig. 2, SRT consists of successive residual blocks, and each block contains normal Swin-Transformer Module (STM) and a spatial convolutional layer, which have the capacity of both global and local feature extraction. Given the degraded sinograms, we first use a convolutional layer to extract the spatial structure . Considering it as , then STM components of each residual block output with the following formulation:
| (2) |
where denotes a convolutional layer, denotes Swin-Transformer layers, and represents the successive operation of Swin-Transformer Layers. Finally, the enhanced sinograms are estimated with:
| (3) |
As a restoration block, is used to supervise the output of the SRT:
| (4) |
where is the ground truth sinogram, and it should be given when training.
3.2 DuDo Consistency Layer
Although input sinograms have been enhanced via the SRT module, directly learning from the concatenation of and leaves a drift between the optimization directions of SRT and RIRM. To compensate for the drift, we make use of a differentiable DuDo Consistency Layer to back-propagate the gradients of RIRM. In this way, the optimization direction imposes the preferred sinogram characteristics to , and vice versa. To be specific, given the input fan-beam sinogram , the DuDo Consistency Layer first converts it into parallel-beam geometry, followed with Filtered Backprojection:
| (5) |
To additionally keep the restored sinograms consistent with the ground-truth CT image , is proposed as follows:
| (6) |
3.3 Residual Image Reconstruction Module
As a long-standing clinical problem, the final goal of CT image reconstruction is to recover a high-quality CT image for diagnosis. With the initially estimated low-quality images that help rectify the geometric deviation between the sinogram and image domains, we next employ Shallow Layer to obtain shallow features of input low-quality image :
| (7) |
Then a series of Deep Feature Extraction Layers are introduced to extract deep features:
| (8) |
where . Finally, we utilize a Recon Layer to predict the clean CT image with residual learning:
| (9) |
To supervise our network optimization, the below loss is used for this module:
| (10) |
The full objective of our model is:
| (11) |
where and are blending coefficients, which are both empirically set as 1 in experiments.
Note that the intermediate convolutional layers are used to communicate between image space and patch-based feature space . Further, by dynamically tuning the depth and width , SRT modules are flexible in practice depending on the balance between memory and performance. We will explore this balancing issue in later experiments.
4 Experimental Results
4.1 Experimental Setup
Datasets. We first train and test our model with the “2016 NIH-AAPM-Mayo Clinic Low Dose CT Grand Challenge” [24] dataset. Specifically, we choose a total of 1746 slices (resolution 512512) from five patients to train our models, and use 314 slices of another patient for testing. We employ a scanning geometry of Fan-Beam X-Ray source with 800 detector elements. There are four SV scenarios in our experiment, corresponding to = [24, 72, 96, 144] views. Note that these views are uniformly distributed around the patient. The original dose data are collected from the chest to the abdomen under a protocol of 120 kVp and 235 effective mAs (500mA/0.47s). To simulate the photon noise in numerical experiments, we add to sinograms mixed noise that is by default composed of 5% Gaussian noise and Poisson noise with an intensity of 5.
Implementation details and training settings. Our models are implemented using the PyTorch framework. We use the Adam optimizer [17] with = (0.9, 0.999) to train these models. The learning rate starts from 0.0001. Models are all trained on a Nvidia 3090 GPU card for 100 epochs with a batch size of 1.
Evaluation metrics. Reconstructed CT images are quantitatively measured by the multi-scale Structural Similarity Index Metric (SSIM) (with level = 5, Gaussian kernel size = 11, and standard deviation = 1.5) [32, 33] and Peak Signal-to-Noise Ratio (PSNR).
| Method | PSNR | SSIM | RMSE |
|---|---|---|---|
| FBPConvNet | 31.47 | 0.8878 | 0.0268 |
| DuDoNet | 31.57 | 0.8920 | 0.0266 |
| FBPConvNet+SRT | 32.13 | 0.8989 | 0.0248 |
| ImgTrans | 32.50 | 0.9010 | 0.0238 |
| DuDoTrans | 32.68 | 0.9047 | 0.0233 |
(a)
 (d)
(d)
(b)
 (e)
(e)
(c)
 (f)
(f)
4.2 Ablation Study and Analysis
We next prove the effectiveness of our proposed SRT module and exhaust the best structure for DuDoTrans. Firstly, we conduct the experiments with the five models: (a) FBPConvNet [15], (b) DuDoNet [21], (c) FBPConvNet+SRT, which combines (a) with our proposed SRT, (d) ImgTrans, which replaces the image-domain model in (a) with Swin-Transformer [22], and (e) our DuDoTrans. The experimental settings are by default with = 96, and the results are shown in Table 1.
The Effectiveness of SRT. Comparing models (a) and (c) in Table 1, the performance is improved 0.66 dB, which confirms that the SRT module output indeed provides useful information for the image-domain reconstruction.
The exploration of RIRM. Inspired by the success of Swin-Transformer in low-level vision tasks, we simply replace the post-precessing module of FBPConvNet with Swin-Transformer, named ImgTrans. Comparing it with the baseline model (a), the achieved 1 dB improvement confirms that Transformer is skilled at characterizing deep features of images, and a thorough exploration is worthy.
The effectiveness of DuDoTrans. When comparing (d) and (e), the boosted 0.18 dB proves SRT effectiveness again. Further, comparing (b) and (e), both dual-domain architectures with corresponding CNNs and Transformer, the improvement demonstrates that Transformer is very suitable in CT reconstruction.
We then investigate the impact of each sub-module on the performance of DuDoTrans:
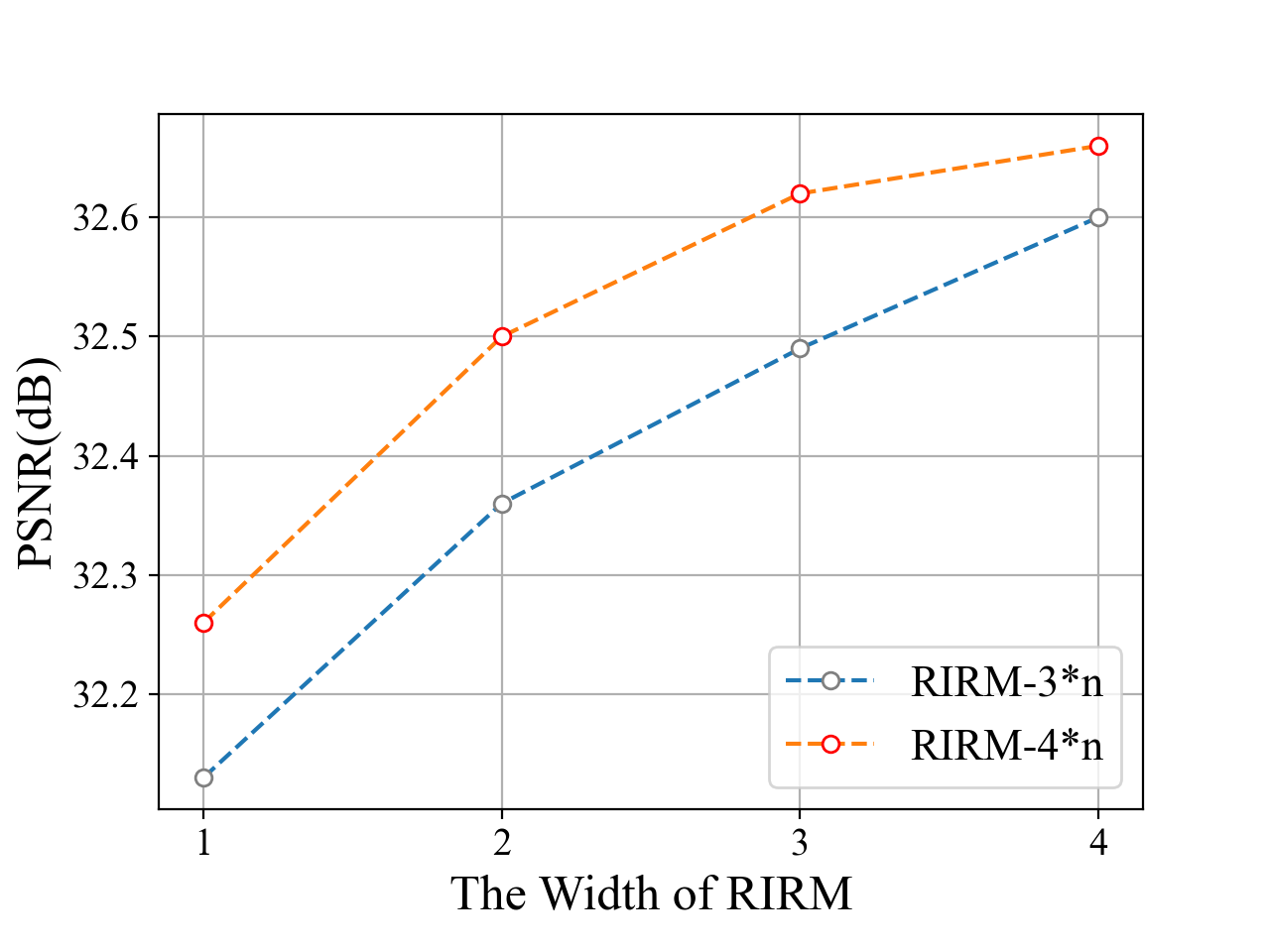
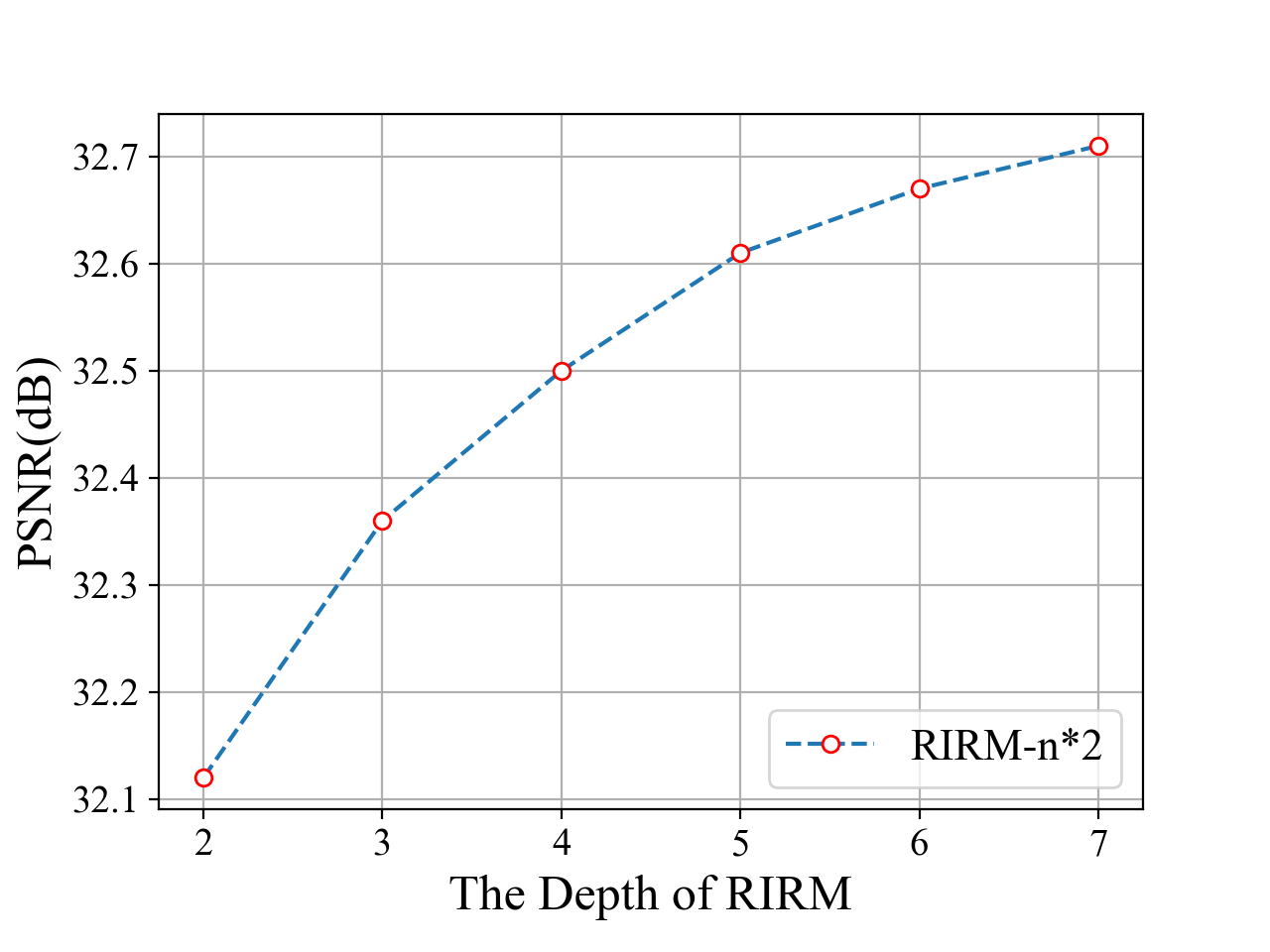
RIRM depth and width. Similar to the SRT structure, the RIRM depth represents the number of sub-modules of RIRM, and the RIRM width describes the number of successive Swin-Transformers in each sub-module. Results in Fig 3 (a) and (b) show the corresponding effect of the RIRM width and RIRM depth on the reconstruction performance. When increasing the RIRM depth (with fixed RIRM width 2), the performance is improved quickly when RIRM depth is smaller than 4. Then the PSNR improvement slows down, while the introduced computational cost is increased. Then we fix RIRM depth equal to 3 (blue) and 4 (yellow) and increase RIRM width, and find that the performance is improved fast till RIRM width = 3. After balancing the computation cost and performance improvement, we set RIRM width and depth to 4 and 2, respectively, which is a small model with similar FLOPs to FBPConvNet.
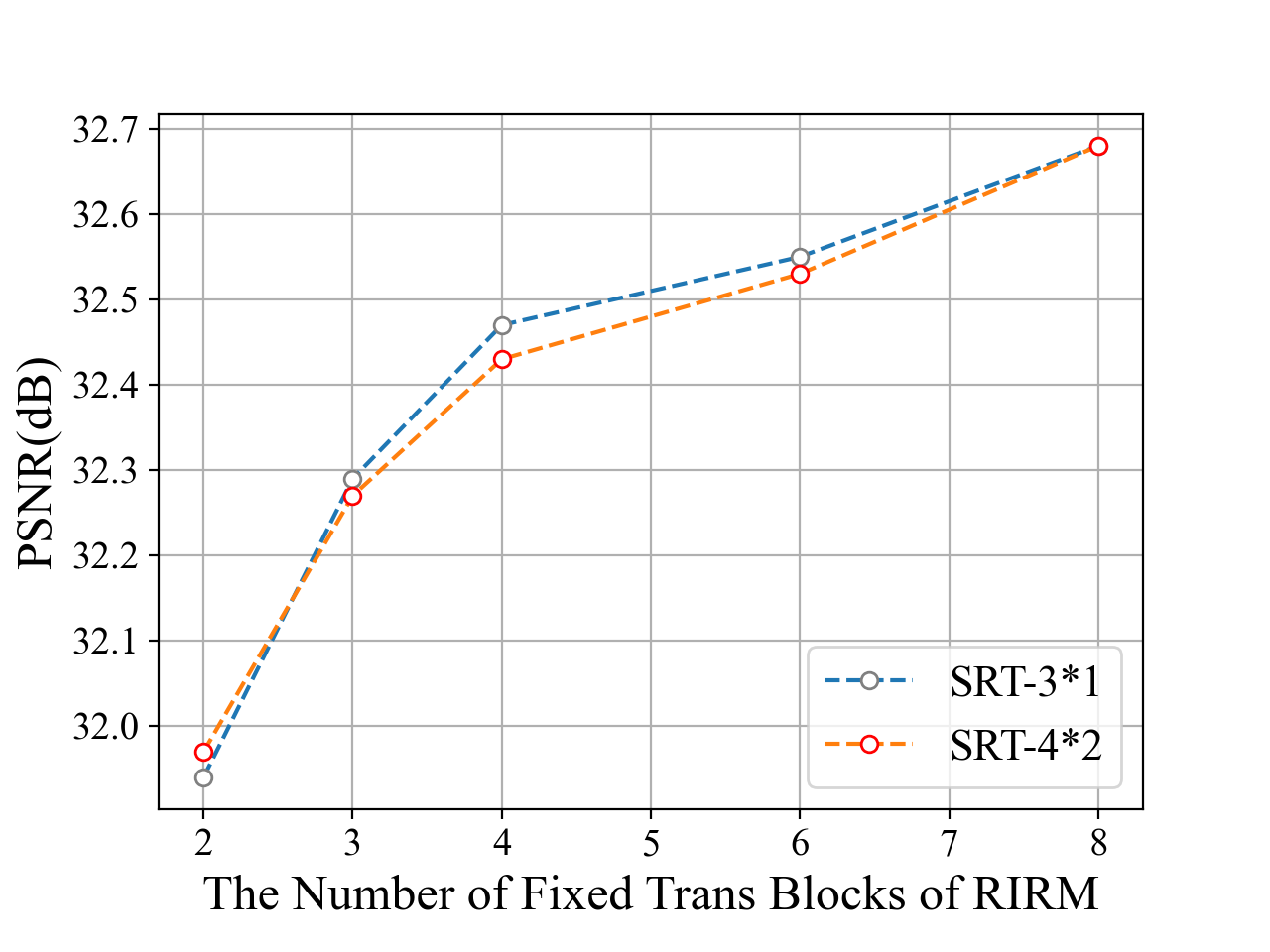
The SRT size. With a similar procedure, we explore the most suitable architecture for the SRT module. As Fig 3 (c) shows, with fixed RIRM depth and width. the performance is not influenced when we enlarge the SRT size (depth and width as introduced in Section 3.1). Specifically, we test five paired models whose RIRM depth and width are set to {(2, 1), ( 3, 1), (3, 2), (4, 2), (5, 2)}, respectively. Then we increase (,) from (3, 1) to (4, 2), but the PSNR is even reduced sometimes. Therefore, we set SRT depth and with to (3, 1) as default in later experiments.
| NIH-AAPM | Param(M) | = 24 | = 72 | = 96 | = 144 | Time(ms) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |||
| FBP [25] | – | 14.58 | 0.2965 | 17.61 | 0.5085 | 18.13 | 0.5731 | 18.70 | 0.6668 | – |
| FBPCovNet [15] | 13.39 | 27.10 | 0.8158 | 30.80 | 0.8671 | 31.47 | 0.8878 | 32.74 | 0.9084 | 155.53 |
| DuDoNet [21] | 25.80 | 26.47 | 0.7977 | 30.94 | 0.8816 | 31.57 | 0.8920 | 32.96 | 0.9106 | 145.65 |
| ImgTrans | 0.22 | 27.46 | 0.8405 | 31.76 | 0.8899 | 32.50 | 0.9010 | 33.50 | 0.9157 | 225.56 |
| DuDoTrans | 0.44 | 27.55 | 0.8431 | 31.91 | 0.8936 | 32.68 | 0.9047 | 33.70 | 0.9191 | 243.81 |
| Noise-H1 | = 24 | = 72 | = 96 | = 144 | Time(ms) | ||||
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | ||
| FBP [25] | 14.45 | 0.2815 | 17.52 | 0.4898 | 18.04 | 0.5541 | 18.63 | 0.6483 | – |
| FBPCovNet [15] | 27.12 | 0.8171 | 30.74 | 0.8798 | 31.44 | 0.8874 | 32.65 | 0.9070 | 148.58 |
| DuDoNet [21] | 26.40 | 0.7932 | 30.84 | 0.8792 | 31.47 | 0.8900 | 32.87 | 0.9090 | 146.36 |
| ImgTrans | 27.35 | 0.8395 | 31.65 | 0.8882 | 32.42 | 0.8993 | 33.36 | 0.9133 | 244.64 |
| DuDoTrans | 27.45 | 0.8411 | 31.80 | 0.8911 | 32.55 | 0.9021 | 33.48 | 0.9156 | 242.38 |
| Noise-H2 | |||||||||
| FBP [25] | 14.29 | 0.2652 | 17.40 | 0.4688 | 17.94 | 0.5325 | 18.55 | 0.6267 | – |
| FBPCovNet [15] | 27.11 | 0.8168 | 30.61 | 0.8764 | 31.40 | 0.8865 | 32.52 | 0.9047 | 151.39 |
| DuDoNet [21] | 26.28 | 0.7857 | 30.68 | 0.8755 | 31.34 | 0.8871 | 32.73 | 0.9066 | 152.11 |
| ImgTrans | 27.18 | 0.8361 | 31.49 | 0.8855 | 32.26 | 0.8963 | 33.15 | 0.9096 | 244.16 |
| DuDoTrans | 27.29 | 0.8377 | 31.64 | 0.8881 | 32.36 | 0.8986 | 33.24 | 0.9113 | 261.45 |
| Noise-H3 | |||||||||
| FBP [25] | 13.24 | 0.1855 | 16.56 | 0.3543 | 17.20 | 0.4121 | 17.96 | 0.5018 | – |
| FBPCovNet [15] | 26.08 | 0.7512 | 29.16 | 0.8294 | 30.37 | 0.8592 | 31.02 | 0.8706 | 152.04 |
| DuDoNet [21] | 24.77 | 0.6820 | 29.01 | 0.8216 | 29.86 | 0.8456 | 31.25 | 0.8736 | 151.50 |
| ImgTrans | 25.39 | 0.7933 | 30.20 | 0.8624 | 31.13 | 0.8707 | 31.52 | 0.8691 | 220.78 |
| DuDoTrans | 24.77 | 0.7844 | 30.26 | 0.8632 | 30.86 | 0.8753 | 31.58 | 0.8747 | 241.71 |
Further, we analyze the convergence, robustness, and effect of the training dataset scale.
Convergence. In Fig. 3 (d), we plot the convergence curve of FBPConvNet, ImgTrans, and DuDoTrans. Evidently, the introduction of Transformer Structure not only improves the final results, but also stabilizes the training process. Besides, our Dual-Domain design achieves consistently better results, compared with ImgTrans.
Robustness. In practice, the photon noise in the imaging process influences the reconstructed images, therefore the robustness to such noise is important for application usage. Here, we simulate such noise with mixed noise (Gaussian & Poisson noise). Specifically, we train models with default noise level and test them with varied Poisson noise levels (with fixed Gaussian noise), whose intensity correspond to [1, 5, 1, 5], and show the results in Fig. 3 (e). Evidently, our models achieve better performances except when the intensity is 1, which noise is extremely hard to be suppressed, while DuDoTrans is still better than CNN-based methods, which confirms its robustness.
Training dataset scale. Vision Transformers need large-scale data to exhibit performance, and thus limits its development in medical imaging. To investigate it, we train FBPConvNet, ImgTrans, and DuDoTrans with [20%, 40%, 60%, 80%, 100%] of our original training dataset, and show the performance in Fig. 3 (f). Obviously, reconstruction performance of DuDoTrans is very stable till the training dataset decreases to 20%, in which case training data is too less for all models to perform well and DuDoTrans still achieves the best performance.
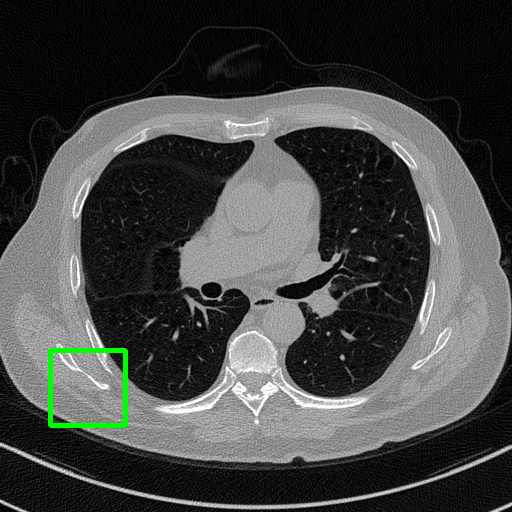
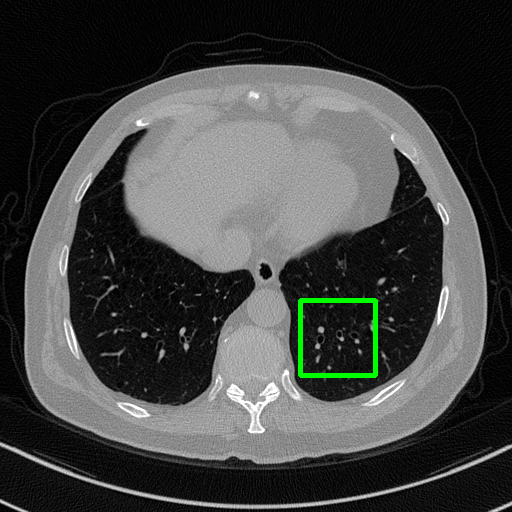
Ground Truth
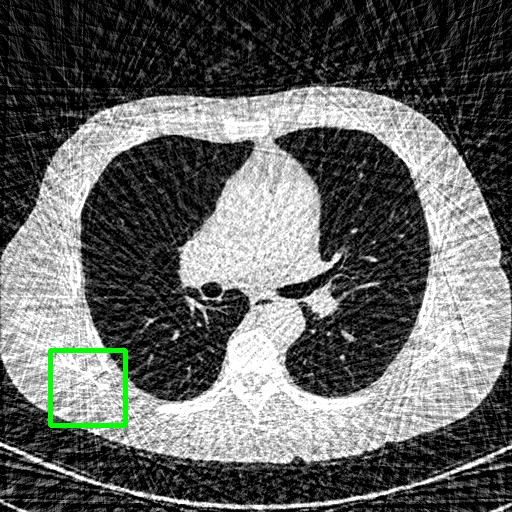
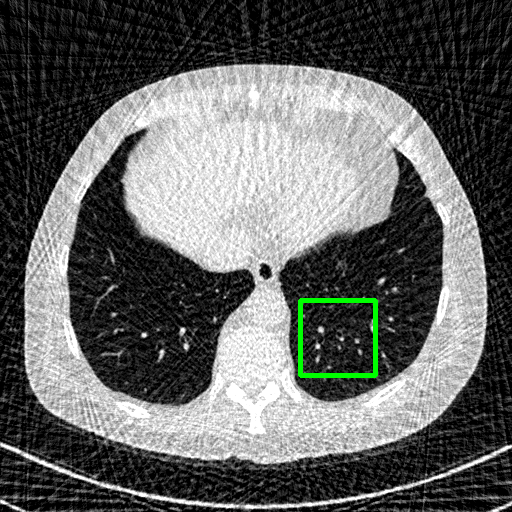
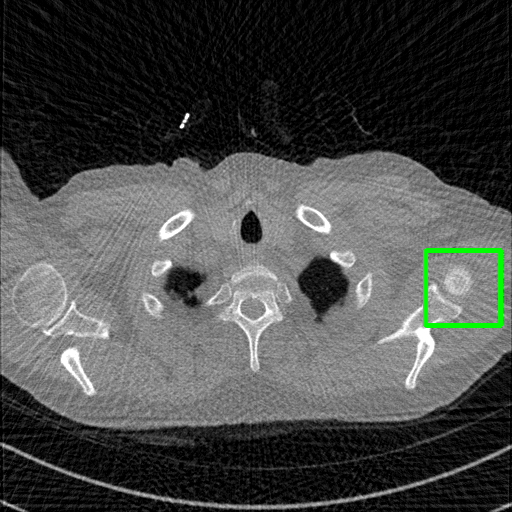
FBP
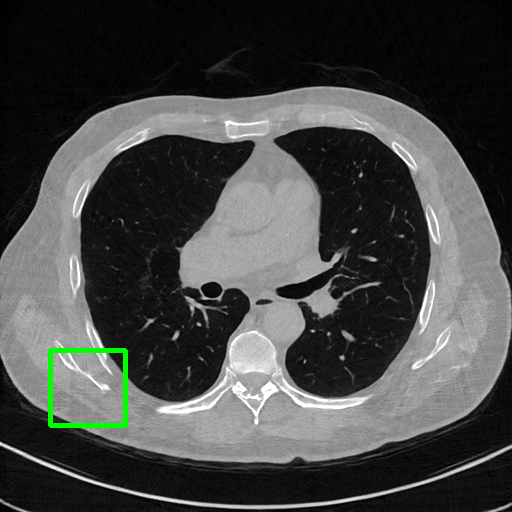
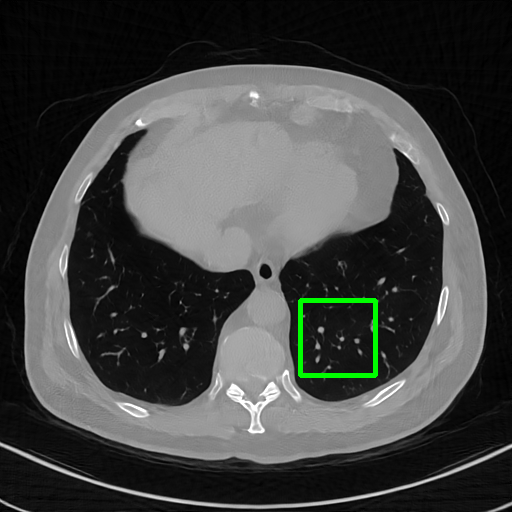
FBPConvNet
DuDoNet
ImgTrans
DuDoTrans
| COVID-19 | = 24 | = 72 | = 96 | = 144 | Time(ms) | ||||
|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | ||
| FBP [25] | 14.82 | 0.3757 | 18.16 | 0.5635 | 18.81 | 0.6248 | 19.36 | 0.7070 | – |
| FBPCovNet [15] | 26.43 | 0.8015 | 32.84 | 0.9407 | 33.72 | 0.9409 | 34.62 | 0.9651 | 149.48 |
| DuDoNet [21] | 26.97 | 0.8558 | 33.10 | 0.9429 | 32.57 | 0.9380 | 36.13 | 0.9722 | 153.25 |
| ImgTrans | 27.24 | 0.8797 | 35.58 | 0.9580 | 37.31 | 0.9699 | 39.90 | 0.9801 | 222.14 |
| DuDoTrans | 27.74 | 0.8897 | 35.62 | 0.9596 | 37.83 | 0.9727 | 40.20 | 0.9794 | 244.46 |
4.3 Sparse-View CT Reconstruction Analysis
We next conduct thorough experiments to test the performance of DuDoTrans on various sparse-view scenarios. Specifically, we first train models when is 24, 72, 96, 144, respectively. The results are shown in Table 3, and DuDoTrans have achieved consistently better results. Besides, we observe that ImgTrans and DuDoTrans are more stable in training, and the learned parameters are both extremely small, compared with CNN-based models. Furthermore, the improvement of DuDoTrans over ImgTrans becomes larger when the increases, which confirms the usefulness of restored sinograms in reconstruction.
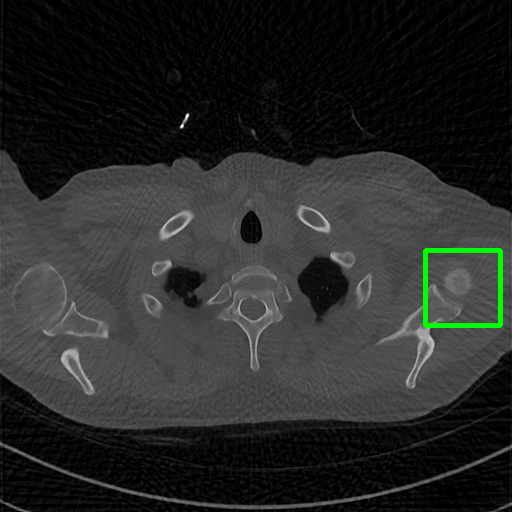
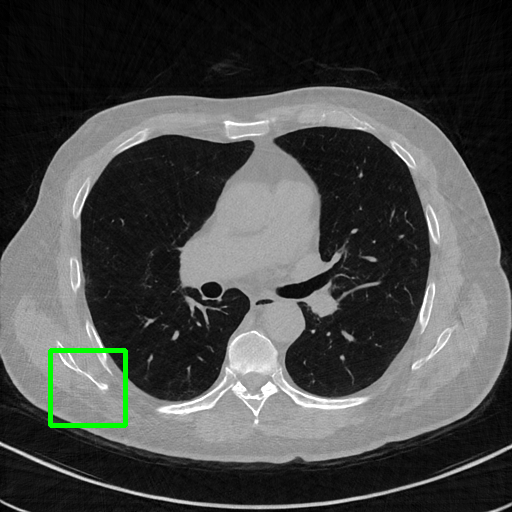
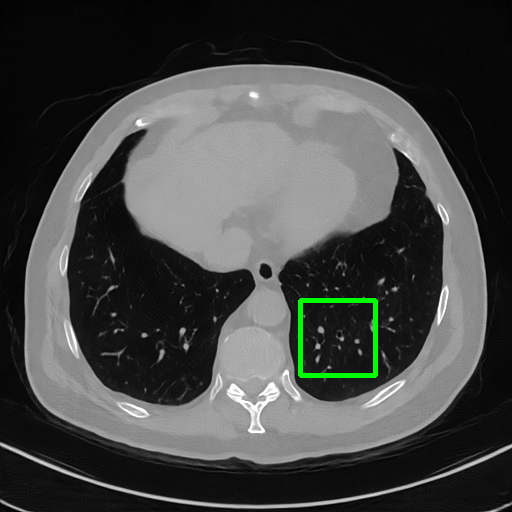
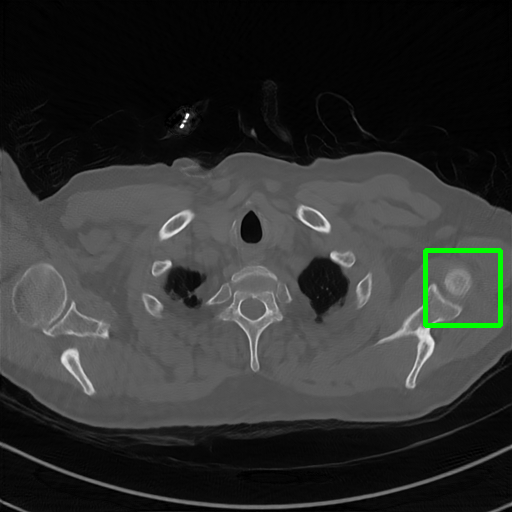
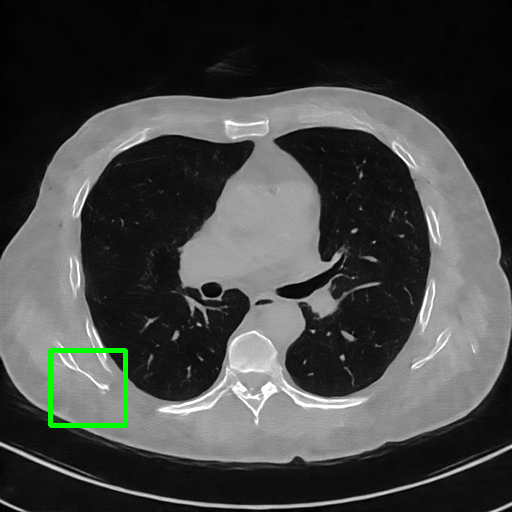
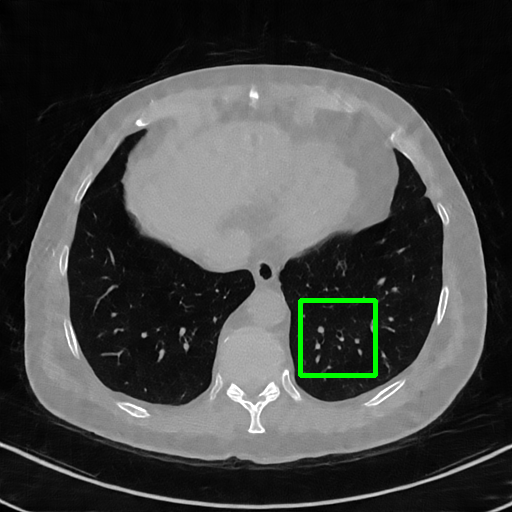
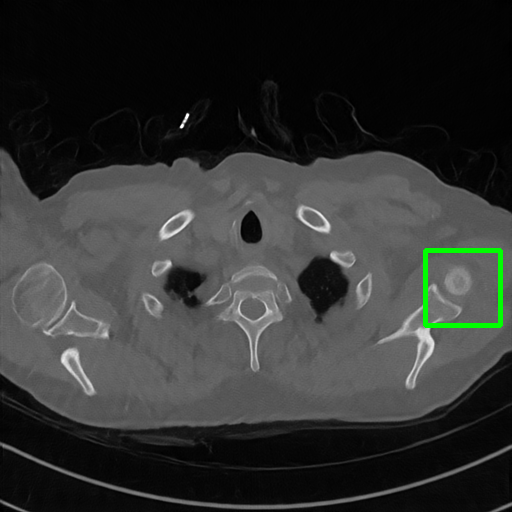
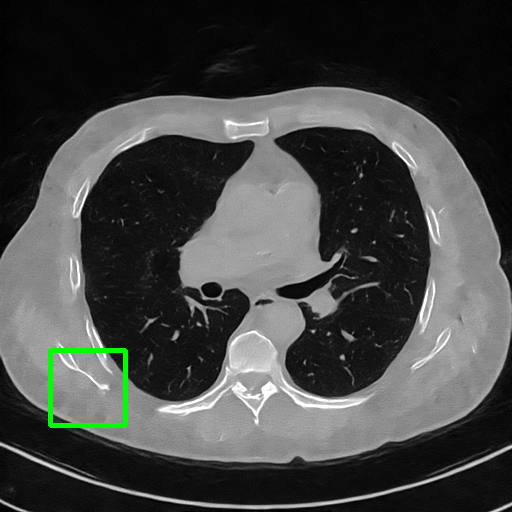
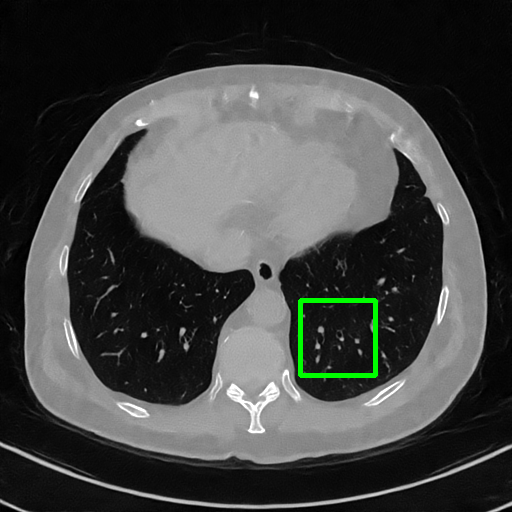
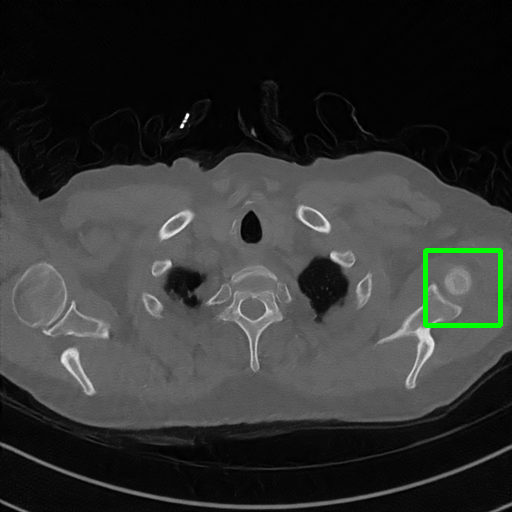
Qualitative comparison. We also visualize the reconstructed images of these methods in Fig. 4 with = [72, 96 ,144] (See more visualizations in Appendix). In all three rows, our DuDoTrans shows better detail recovery, and sparse-view artifacts are suppressed. Further, when decreasing , where raw sinograms are too messy to be restored and low-quality images from FBP are too hard to capture global features, Transformer-based models exhibit reduced performance. The phenomena suggests that we should design suitable structures with the Transformer and CNNs, facing with different cases.
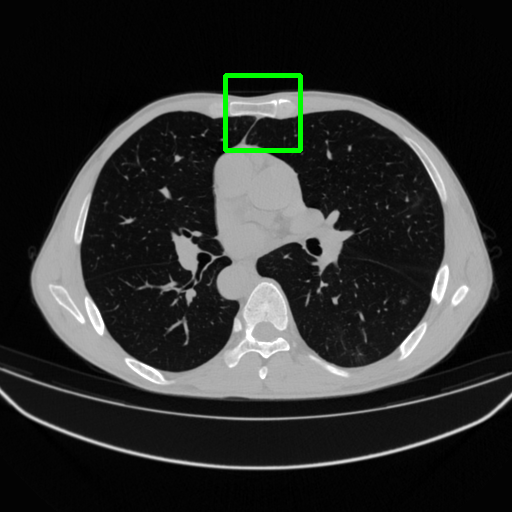
Ground Truth
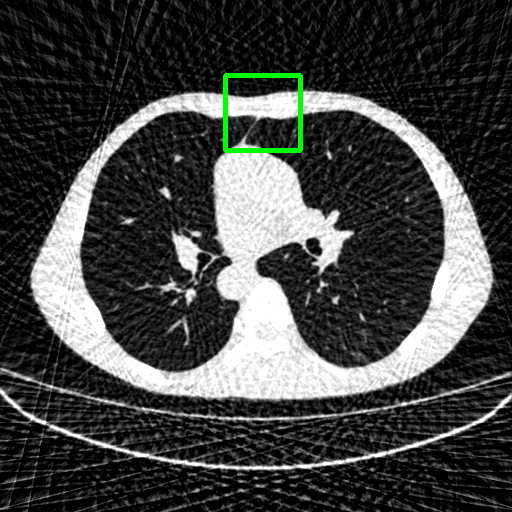
FBP
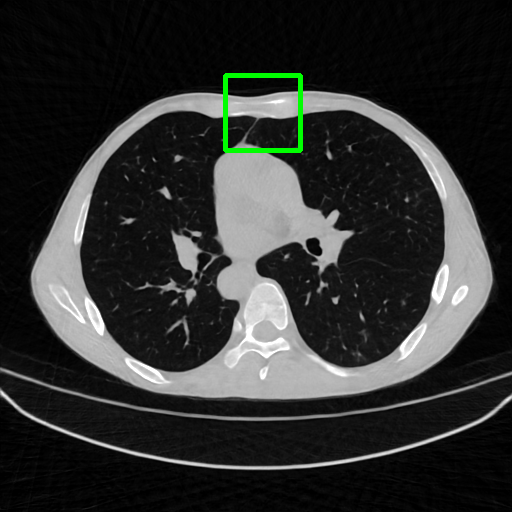
FBPConvNet
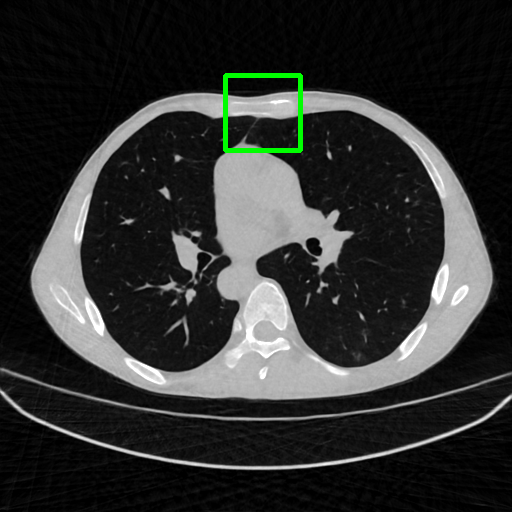
DuDoNet
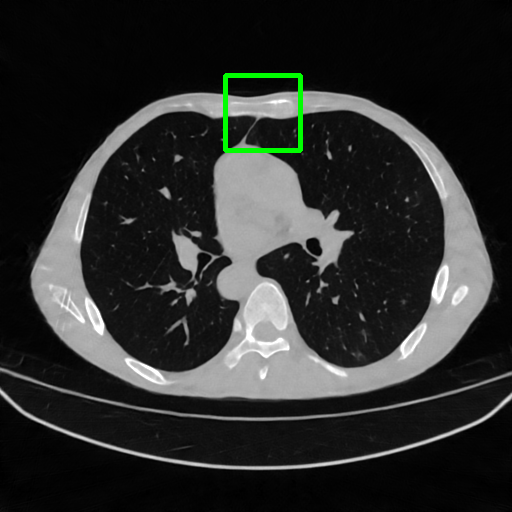
ImgTrans
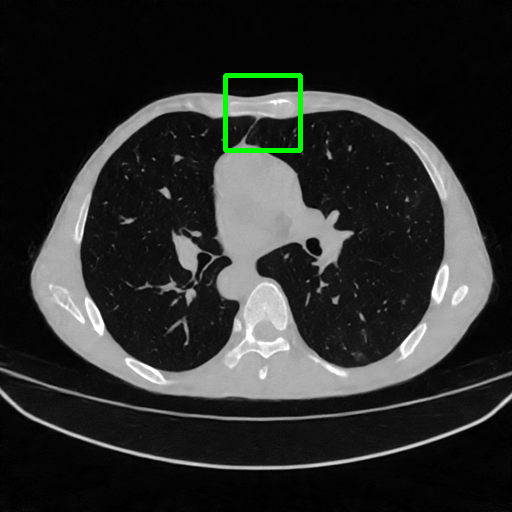
DuDoTrans
Robustness with noise in SVCT. With the decrease of view number , input sinograms would be messier, which makes SVCT more difficult. Therefore, we test the robustness of all trained models with aforementioned Poisson noise levels when = [24, 72, 96, 144], and report performances in Table. 3. The included notation Noise-H1, Noise-H2, and Noise-H3 correspond to Poisson intensity [1, 5, 1]. Compared with CNN-based methods, ImgTrans and DuDoTrans show better robustness. Across involved cases, DuDoTrans shows the best performance. Nevertheless, when Poisson intensity is 1, DuDoTrans fails to exceed ImgTrans and FBPConvNet, which is caused by the extremely messy sinograms. In this case, restoring sinograms is too difficult and DuDoNet also fails.
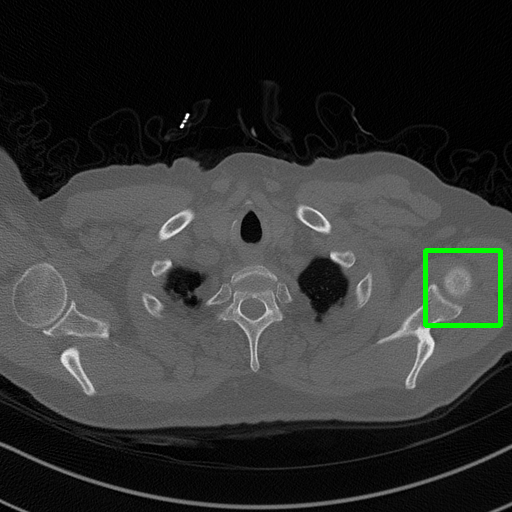
Generalizablity on COVID-19 dataset. Finally, we use slices of another patient in the COVID-19 dataset to test the generalizability of trained models, and quantitative performances are compared in Table 4. ImgTrans and DuDoTrans have achieved a larger improvement about 4-5 dB over CNN-based methods, which shows that the long-range dependency modeling ability helps capture the intrinsic global property of general CT images. Further, our DuDoTrans exceeds ImgTrans about 0.4 dB in all cases, even larger than the original NIH-AAPM dataset. The improvement ensures that DuDoTrans generalizes well to out-of-distribution CT images. Besides, we also show the visualization images in Fig. 5 when = 96. Coinciding with the quantitative comparison, our DuDoTrans show better reconstruction on both global patterns and local details.
4.4 Computation comparison
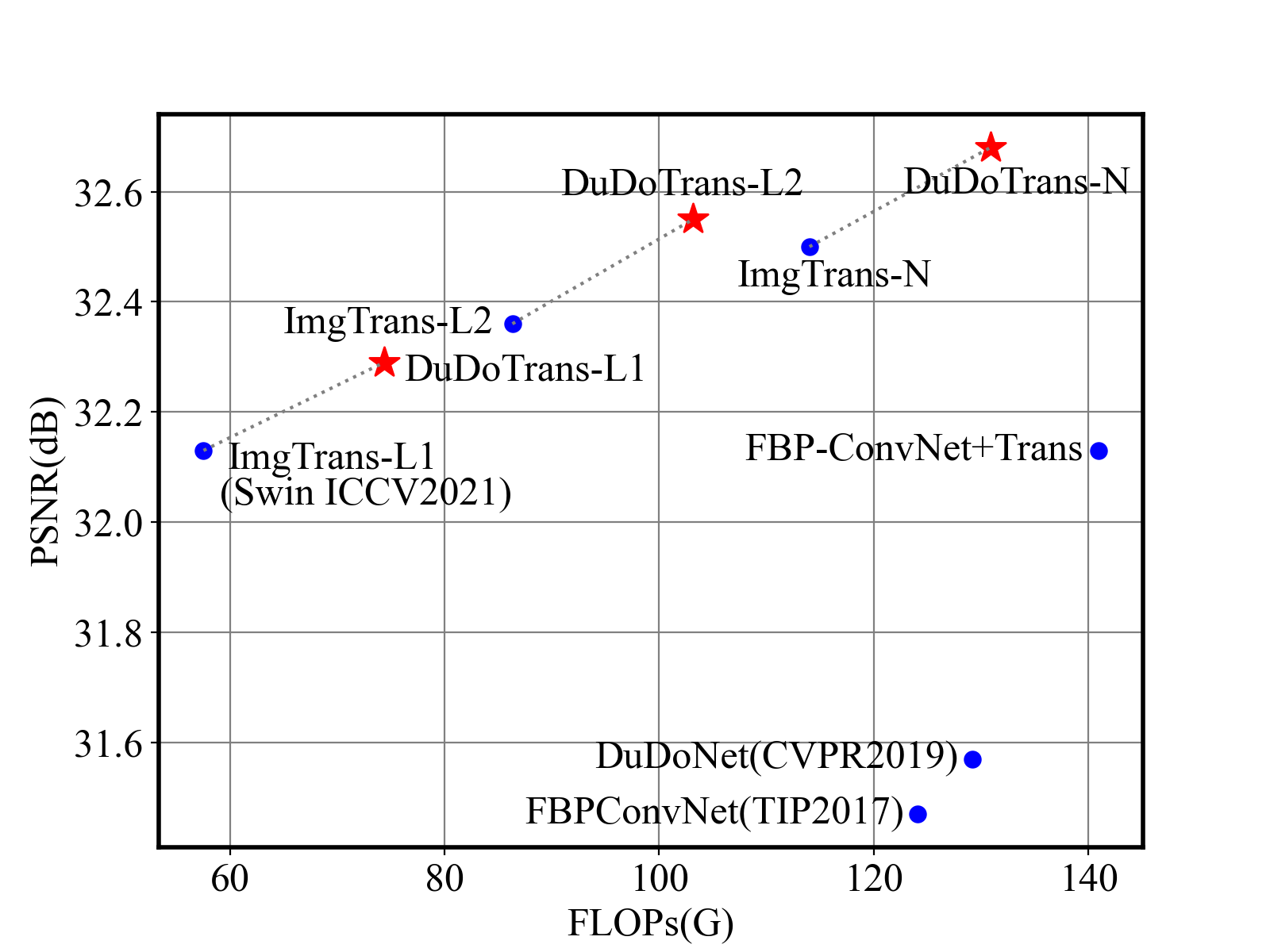
As a practical problem, reconstruction speed is necessary when deployed in modern CT machines. Therefore, we compare the parameters and FLOPs versus performances in Fig 1 and Fig. 6, respectively. We find that Transformer-based methods have achieved better performances with fewer parameters, and our DuDoTrans exceeds ImgTrans with only a few additional parameters. As known, the patch-based operations and the attention mechanism are computationally expensive, which limits their application usage. Therefore, we further compare the FLOPs of these methods. As shown, light versions (DuDoTrans-L1, DuDoTrans-L2) have achieved 0.8-1 dB improvement with fewer FLOPs, and DuDoTrans-N with default size has enlarged the improvement to 1.2 dB. Besides, we report the inferring time in each Table 2 3 4, and computation time is very similar to CNN-based methods, whose additional consumption is because of the patch-based operations.
| Method | PSNR | SSIM | |
|---|---|---|---|
| FBPConvNet [15] | 31.47 | 0.8878 | |
| w/o SRT | PDNet [1] | 31.62 | 0.8894 |
| ImgTrans | 32.50 | 0.9010 | |
| FBPConvNet+SRT | 32.13 | 0.8989 | |
| w/ SRT | PDNet+SRT | 32.38 | 0.9045 |
| DuDoTrans | 32.68 | 0.9047 |
4.5 Discussion
As in Table 1, we have shown the effectiveness of SRT with FBPConvNet [15] and ImgTrans [22], which are two post-processing methods. Recently deep-unrolling methods have attracted much attention in reconstruction. To concretely verify the SRT module’s effectiveness, we further combine it with PDNet [1], which is a deep-unrolling method. Results of involved three paired models (w/ v.s. w/o SRT) are shown in Table 5 with default experimental settings when = 96 (See other cases when = [24, 72, 144] in Appendix). All these three reconstruction methods have been improved by the use of the SRT module. Furthermore, our DuDoTrans still performs the best without any unrolling design. Thus, our SRT is flexible and powerful probably in any existing reconstruction framework.
5 Conclusion
We propose a transformer-based SRT module with long-range dependency modeling capability to exploit the global characteristics of sinograms, and verify it in CNN-based, Transformer-based, and Deep-unrolling reconstruction framework. Further, via combining SRT and similarly-designed RIRM, we yield DuDoTrans for SVCT reconstruction. Experimental results on the NIH-AAPM dataset and COVID-19 dataset show that DuDoTrans achieves state-of-the-art reconstruction. To further benefit DuDoTrans with the accordingly designing advantage of deep-unrolling methods, we will explore “DuDoTrans + unrolling” in the future.
Acknowledge. This work was supported by the National Natural Science Foundation of China under Grant No. 12001180 and 12101061.
References
- [1] Jonas Adler and Ozan Öktem. Learned primal-dual reconstruction. IEEE transactions on medical imaging, 37(6):1322–1332, 2018.
- [2] Peng Bao, Wenjun Xia, Kang Yang, Weiyan Chen, Mianyi Chen, Yan Xi, Shanzhou Niu, Jiliu Zhou, He Zhang, Huaiqiang Sun, et al. Convolutional sparse coding for compressed sensing ct reconstruction. IEEE transactions on medical imaging, 38(11):2607–2619, 2019.
- [3] Hu Cao, Yueyue Wang, Joy Chen, Dongsheng Jiang, Xiaopeng Zhang, Qi Tian, and Manning Wang. Swin-unet: Unet-like pure transformer for medical image segmentation. arXiv preprint arXiv:2105.05537, 2021.
- [4] Yue Cao, Jiarui Xu, Stephen Lin, Fangyun Wei, and Han Hu. Gcnet: Non-local networks meet squeeze-excitation networks and beyond. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, pages 0–0, 2019.
- [5] Nicolas Carion, Francisco Massa, Gabriel Synnaeve, Nicolas Usunier, Alexander Kirillov, and Sergey Zagoruyko. End-to-end object detection with transformers. In European Conference on Computer Vision, pages 213–229. Springer, 2020.
- [6] Hanting Chen, Yunhe Wang, Tianyu Guo, Chang Xu, Yiping Deng, Zhenhua Liu, Siwei Ma, Chunjing Xu, Chao Xu, and Wen Gao. Pre-trained image processing transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 12299–12310, 2021.
- [7] Hu Chen, Yi Zhang, Mannudeep K Kalra, Feng Lin, Yang Chen, Peixi Liao, Jiliu Zhou, and Ge Wang. Low-dose ct with a residual encoder-decoder convolutional neural network. IEEE transactions on medical imaging, 36(12):2524–2535, 2017.
- [8] Weilin Cheng, Yu Wang, Hongwei Li, and Yuping Duan. Learned full-sampling reconstruction from incomplete data. IEEE Transactions on Computational Imaging, 6:945–957, 2020.
- [9] Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929, 2020.
- [10] Jun Fu, Jing Liu, Haijie Tian, Yong Li, Yongjun Bao, Zhiwei Fang, and Hanqing Lu. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 3146–3154, 2019.
- [11] Harshit Gupta, Kyong Hwan Jin, Ha Q Nguyen, Michael T McCann, and Michael Unser. Cnn-based projected gradient descent for consistent ct image reconstruction. IEEE transactions on medical imaging, 37(6):1440–1453, 2018.
- [12] Kai Han, An Xiao, Enhua Wu, Jianyuan Guo, Chunjing Xu, and Yunhe Wang. Transformer in transformer. arXiv preprint arXiv:2103.00112, 2021.
- [13] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
- [14] Gao Huang, Zhuang Liu, Laurens Van Der Maaten, and Kilian Q Weinberger. Densely connected convolutional networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 4700–4708, 2017.
- [15] Kyong Hwan Jin, Michael T McCann, Emmanuel Froustey, and Michael Unser. Deep convolutional neural network for inverse problems in imaging. IEEE Transactions on Image Processing, 26(9):4509–4522, 2017.
- [16] Kyungsang Kim, Jong Chul Ye, William Worstell, Jinsong Ouyang, Yothin Rakvongthai, Georges El Fakhri, and Quanzheng Li. Sparse-view spectral ct reconstruction using spectral patch-based low-rank penalty. IEEE transactions on medical imaging, 34(3):748–760, 2014.
- [17] Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
- [18] Yawei Li, Kai Zhang, Jiezhang Cao, Radu Timofte, and Luc Van Gool. Localvit: Bringing locality to vision transformers. arXiv preprint arXiv:2104.05707, 2021.
- [19] Jingyun Liang, Jiezhang Cao, Guolei Sun, Kai Zhang, Luc Van Gool, and Radu Timofte. Swinir: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 1833–1844, 2021.
- [20] Ailiang Lin, Bingzhi Chen, Jiayu Xu, Zheng Zhang, and Guangming Lu. Ds-transunet: Dual swin transformer u-net for medical image segmentation. arXiv preprint arXiv:2106.06716, 2021.
- [21] Wei-An Lin, Haofu Liao, Cheng Peng, Xiaohang Sun, Jingdan Zhang, Jiebo Luo, Rama Chellappa, and Shaohua Kevin Zhou. Dudonet: Dual domain network for ct metal artifact reduction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 10512–10521, 2019.
- [22] Ze Liu, Yutong Lin, Yue Cao, Han Hu, Yixuan Wei, Zheng Zhang, Stephen Lin, and Baining Guo. Swin transformer: Hierarchical vision transformer using shifted windows. arXiv preprint arXiv:2103.14030, 2021.
- [23] Faisal Mahmood, Nauman Shahid, Ulf Skoglund, and Pierre Vandergheynst. Adaptive graph-based total variation for tomographic reconstructions. IEEE Signal Processing Letters, 25(5):700–704, 2018.
- [24] C McCollough. Tu-fg-207a-04: Overview of the low dose ct grand challenge. Medical physics, 43(6Part35):3759–3760, 2016.
- [25] Frank Natterer. The mathematics of computerized tomography. SIAM, 2001.
- [26] Prajit Ramachandran, Niki Parmar, Ashish Vaswani, Irwan Bello, Anselm Levskaya, and Jonathon Shlens. Stand-alone self-attention in vision models. arXiv preprint arXiv:1906.05909, 2019.
- [27] Emil Y. Sidky and Xiaochuan Pan. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Physics in Medicine & Biology, 53(17):4777, 2008.
- [28] Hugo Touvron, Matthieu Cord, Matthijs Douze, Francisco Massa, Alexandre Sablayrolles, and Hervé Jégou. Training data-efficient image transformers & distillation through attention. In International Conference on Machine Learning, pages 10347–10357. PMLR, 2021.
- [29] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In Advances in neural information processing systems, pages 5998–6008, 2017.
- [30] Ce Wang, Haimiao Zhang, Qian Li, Kun Shang, Yuanyuan Lyu, Bin Dong, and S Kevin Zhou. Improving generalizability in limited-angle ct reconstruction with sinogram extrapolation. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 86–96. Springer, 2021.
- [31] Xiyue Wang, Sen Yang, Jun Zhang, Minghui Wang, Jing Zhang, Junzhou Huang, Wei Yang, and Xiao Han. Transpath: Transformer-based self-supervised learning for histopathological image classification. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 186–195. Springer, 2021.
- [32] Zhou Wang, Alan C Bovik, Hamid R Sheikh, and Eero P Simoncelli. Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing, 13(4):600–612, 2004.
- [33] Zhou Wang, Eero P Simoncelli, and Alan C Bovik. Multiscale structural similarity for image quality assessment. In The Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, 2003, volume 2, pages 1398–1402. Ieee, 2003.
- [34] Zidi Xiu, Junya Chen, Ricardo Henao, Benjamin Goldstein, Lawrence Carin, and Chenyang Tao. Supercharging imbalanced data learning with energy-based contrastive representation transfer. In Advances in Neural Information Processing Systems. Curran Associates, Inc., 2021.
- [35] Qingsong Yang, Pingkun Yan, Yanbo Zhang, Hengyong Yu, Yongyi Shi, Xuanqin Mou, Mannudeep K Kalra, Yi Zhang, Ling Sun, and Ge Wang. Low-dose ct image denoising using a generative adversarial network with wasserstein distance and perceptual loss. IEEE transactions on medical imaging, 37(6):1348–1357, 2018.
- [36] Minghao Yin, Zhuliang Yao, Yue Cao, Xiu Li, Zheng Zhang, Stephen Lin, and Han Hu. Disentangled non-local neural networks. In European Conference on Computer Vision, pages 191–207. Springer, 2020.
- [37] Shuang Yu, Kai Ma, Qi Bi, Cheng Bian, Munan Ning, Nanjun He, Yuexiang Li, Hanruo Liu, and Yefeng Zheng. Mil-vt: Multiple instance learning enhanced vision transformer for fundus image classification. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 45–54. Springer, 2021.
- [38] Dong Zeng, Jing Huang, Hua Zhang, Zhaoying Bian, Shanzhou Niu, Zhang Zhang, Qianjin Feng, Wufan Chen, and Jianhua Ma. Spectral ct image restoration via an average image-induced nonlocal means filter. IEEE Transactions on Biomedical Engineering, 63(5):1044–1057, 2015.
- [39] Yungeng Zhang, Yuru Pei, and Hongbin Zha. Learning dual transformer network for diffeomorphic registration. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 129–138. Springer, 2021.
- [40] Zhicheng Zhang, Lequan Yu, Xiaokun Liang, Wei Zhao, and Lei Xing. Transct: Dual-path transformer for low dose computed tomography. arXiv preprint arXiv:2103.00634, 2021.
- [41] Hengshuang Zhao, Jiaya Jia, and Vladlen Koltun. Exploring self-attention for image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 10076–10085, 2020.
- [42] Bo Zhou, Xiongchao Chen, S Kevin Zhou, James S Duncan, and Chi Liu. Dudodr-net: Dual-domain data consistent recurrent network for simultaneous sparse view and metal artifact reduction in computed tomography. Medical Image Analysis, page 102289, 2021.
- [43] Bo Zhou and S Kevin Zhou. Dudornet: Learning a dual-domain recurrent network for fast mri reconstruction with deep t1 prior. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 4273–4282, 2020.
- [44] Hong-Yu Zhou, Jiansen Guo, Yinghao Zhang, Lequan Yu, Liansheng Wang, and Yizhou Yu. nnformer: Interleaved transformer for volumetric segmentation. arXiv preprint arXiv:2109.03201, 2021.
- [45] S Kevin Zhou, Hayit Greenspan, Christos Davatzikos, James S Duncan, Bram Van Ginneken, Anant Madabhushi, Jerry L Prince, Daniel Rueckert, and Ronald M Summers. A review of deep learning in medical imaging: Imaging traits, technology trends, case studies with progress highlights, and future promises. Proceedings of the IEEE, 2021.
- [46] S Kevin Zhou, Hoang Ngan Le, Khoa Luu, Hien V Nguyen, and Nicholas Ayache. Deep reinforcement learning in medical imaging: A literature review. Medical Image Analysis, 2021.