Driven Hubbard model on a triangular lattice: tunable Heisenberg antiferromagnet with chiral three-spin term

Periodically driven quantum systems have been studied extensively over the last several years, both theoretically dunlap ; gross ; kaya ; das ; russo ; nag ; laza ; sharma ; dutta ; sengupta ; agarwala1 ; agarwala2 ; lubini ; frank ; udupa ; mukherjee1 ; mukherjee2 ; haldar ; eckardt1 ; rapp ; zheng ; greschner ; laza1 ; alessio ; ponte1 ; laza2 ; ponte2 ; eckardt2 ; bukov ; khemani ; keyser ; else ; itin ; mikami ; su ; raciunas ; ghosh ; mentink and experimentally bloch ; kita ; tarr ; recht ; mahesh ; langen ; jotzu ; eckardt3 ; mciver ; meinert ; bordia ; mukh (see Refs. rev1, ; rev2, ; rev3, ; rev4, ; rev5, ; rev6, ; rev7, for reviews). Such systems can exhibit a wide variety interesting phenomena such as dynamical freezing dunlap ; das ; nag ; sengupta ; agarwala1 ; agarwala2 ; lubini ; mukherjee2 ; haldar , the generation of non-trivial band structures and states localized at the boundaries of the system oka ; kitagawa10 ; lindner11 ; jiang11 ; gu ; trif12 ; gomez12 ; dora12 ; liu13 ; tong13 ; rudner13 ; katan13 ; lindner13 ; kundu13 ; schmidt13 ; reynoso13 ; wu13 ; manisha13 ; perez ; reichl14 ; carp ; xiong ; dutreix1 ; manisha17 ; zhou ; deb ; sur , and time crystals khemani ; else ; zhang . While periodic driving of systems of non-interacting electrons has been studied very extensively, the effects of interactions along with periodic driving have also been studied by several groups eckardt1 ; rapp ; zheng ; greschner ; laza1 ; alessio ; ponte1 ; laza2 ; ponte2 ; eckardt2 ; bukov ; khemani ; keyser ; else ; agarwala2 ; itin ; mikami ; su ; raciunas ; sur ; ghosh ; meinert ; bordia ; mukh ; mentink .

For undriven (time-independent) systems, it is often of interest to consider a subset of states such as the ground state and low-lying excitations which dominate the low-temperature properties of the system. For this purpose it is convenient to find an effective low-energy Hamiltonian $H_{eff}$ which describes such states; the derivation of $H_{eff}$ usually involves taking into account all the other states in a perturbative way. For a system in which the Hamiltonian changes with time, we cannot define energy eigenstates and there is no concept of low-energy states. However, as we will see, we can define an effective time-independent Hamiltonian which describes a particular sector of the system, such as the spin sector in which each site is occupied by only one electron whose spin can point up or down.

In this paper, we will consider the Hubbard model of spin-1/2 electrons on a triangular lattice with a nearest-neighbor hopping amplitude $g$ and an on-site interaction $U$. In the absence of periodic driving, it is known that when the system is at half-filling and $U\gg g$, then up to order $g^{2}$, the low-energy Hamiltonian takes the form of a Heisenberg antiferromagnet with nearest-neighbor interactions of the form $J{\vec{S}}_{i}\cdot{\vec{S}}_{j}$ where $J=4g^{2}/U$. We will consider what happens when this model is subjected to a periodically varying electric field which points in some direction in the plane of the lattice. The effect of the electric field will be incorporated in the model using the Peierls prescription peierls . We will show that up to order $g^{3}$, the Floquet Hamiltonian which describes Floquet eigenstates in the spin sector (i.e., with large weights for states in which every site is singly occupied) has the following form. At order $g^{2}$ and $g^{3}$ there is a Heisenberg antiferromagnetic term $J_{a}{\vec{S}}_{i}\cdot{\vec{S}}_{j}$ which couples nearest neighbors but the coupling $J_{a}$ has three different values depending on the orientation of the bond joining the two sites. In addition, if the periodically varying electric field is not time-reversal symmetric, a chiral three-spin interaction of the form $C{\vec{S}}_{i}\cdot{\vec{S}}_{j}\times{\vec{S}}_{k}$ can appear at order $g^{3}$ on each triangle, with $C$ having opposite values $\pm C$ on up- and down-pointing triangles. The values of the four couplings, $J_{a}$ and $C$, can be tuned by varying the time-dependence and direction of the periodically varying electric field and the driving frequency $\omega$. A spin model with four such couplings has not been studied earlier to the best of our knowledge although Refs. weng, ; yunoki, ; hauke, ; gonzalez, have studied models with different values of $J_{a}$ and $C=0$, and models with all $J_{a}$’s equal and $C$ having the same sign on up- and down-pointing triangles have been studied in Refs. wietek, and gong, . We will then study the ground state phase diagram of our four-parameter spin model using exact diagonalization (ED) of systems with 36 sites. We find a rich phase diagram consisting of three collinear ordered phases, one coplanar ordered phase, and three disordered (spin-liquid) phases. These phases can be distinguished from each other in several ways including the locations of the peaks of the static spin structure function $S({\vec{q}})$ in the Brillouin zone of $\vec{q}$, the minimum value of the correlation function $C({\vec{r}})$ in real space, the fidelity susceptibility of the ground state rams , and crossings of the energies of the ground state and first excited state.

The plan of the paper is as follows. In Sec. II we introduce the Hubbard model on a triangular lattice in the presence of a periodically varying electric field. In Sec. III we derive the effective spin Hamiltonian using a Floquet perturbation theory which works in the limit that the nearest-neighbor hopping is much smaller than the Hubbard interaction $U$ and the driving frequency $\omega$. We will find that there are nearest-neighbor Heisenberg antiferromagnetic terms with three different couplings $J_{\alpha},~{}J_{\beta},~{}J_{\gamma}$ and a chiral three-spin term with coefficient $\pm C$ on up- and down-pointing triangles. In Sec. IV, we study the ground state phase diagram of the effective Floquet Hamiltonian in the classical limit and then use spin-wave theory to look at the excitations in the collinear phases. This is followed by Sec. V in which we study the spin model in detail using ED for various values of $J_{\alpha},~{}J_{\beta},~{}J_{\gamma}$ and $C$. We look at several quantities derived from the ground state wave function such as the static structure function in both real and momentum space and the fidelity susceptibility to obtain the ground state phase diagram. A rich phase diagram is found with four ordered phases and three spin-liquid phases. We conclude in Sec. VI by summarizing our main results and pointing out possible directions for future studies.

We consider the one-band Hubbard model of spin-1/2 electrons on a triangular lattice at half-filling. The Hamiltonian is given by

$$H~{}=~{}-~{}g~{}\sum_{<i,j>,\sigma}(c_{i,\sigma}^{\dagger}c_{j,\sigma}~{}+~{}{\rm H.c.})~{}+~{}U~{}\sum_{i}~{}n_{i,\uparrow}n_{i,\downarrow},$$

(1)

where $g$ is the hopping amplitude between neighboring sites, and $U>0$ is the on-site repulsive interaction. In the absence of driving and in the limit of large interaction, $U\gg g$, the lowest energy sector of the Hamiltonian is described by an antiferromagnetic Heisenberg spin model at half-filling and by the t-J model away from half-filling. Additionally, we drive the Hamiltonian periodically with a time varying in-plane electric field ${\vec{E}}({\vec{r}},t)={\vec{E}}({\vec{r}},t+T)$. To consider the most general cases, we will assume that the electric field is not time-reversal symmetric, i.e., that there is no $t_{0}$ such that ${\vec{E}}({\vec{r}},t)={\vec{E}}({\vec{r}},t_{0}-t)$. This property of the electric field will turn out to be important for our study since, as we will see, it gives rise to an additional term in the effective spin Hamiltonian. (Such an electric field can be realized by, say, superposing two sinusoidal electric fields with different frequencies and a phase difference as we will see in Sec. V). We will take the form of the electric field to be ${\vec{E}}(t)={\hat{n}}{\cal E}(t)$, where ${\hat{n}}$ denotes a unit vector in the plane of the triangular lattice, and we will parametrize the direction of $\hat{n}$ by an angle $\theta$ with respect to the $\hat{x}$ axis.

The time-dependent electric field is incorporated in our model through a vector potential in the phase of the nearest-neighbor hopping following the Peierls prescription. Since ${\vec{E}}=-(1/c)\partial{\vec{A}}/\partial t$, the vector potential is ${\vec{A}}(t)={\hat{n}}{\cal A}(t)$ where ${\cal A}(t)=-c\int_{0}^{t}dt^{\prime}{\cal E}(t^{\prime})$. [We will assume that the electric field does not have a dc component, i.e., $\int_{0}^{T}dt{\cal E}(t)=0$. Then ${\cal A}(t)$ will also be a periodic function of $t$.] The phase of the hopping from a site at ${\vec{r}}_{j}$ to a site at ${\vec{r}}_{i}$ is given by $(q/\hbar c){\vec{A}}\cdot({\vec{r}}_{i}-{\vec{r}}_{j})$ where $q$ is the charge of the electron. Hence the periodic driving modifies the term $-gc_{i,\sigma}^{\dagger}c_{j,\sigma}$ in the Hamiltonian to $-g~{}e^{i(q/\hbar c){\cal A}(t)\hat{n}\cdot({\vec{r}}_{i}-{\vec{r}}_{j})}~{}c_{i,\sigma}^{\dagger}c_{j,\sigma}$.

Figure 1 illustrates how the different quantities look for a single triangle with sides of unit length whose sites are labeled as $1$, $2$ and $3$. (We have chosen the triangle to be up-pointing along the $\hat{y}$ axis.) If $t_{ij}$ is the hopping amplitude from site-$j$ to site-$i$, we have

	$\displaystyle t_{12}$	$\displaystyle=$	$\displaystyle g~{}e^{~{}i(q/\hbar c){\cal A}(t)\cos(\pi/3-\theta)},$
	$\displaystyle t_{23}$	$\displaystyle=$	$\displaystyle g~{}e^{~{}i(q/\hbar c){\cal A}(t)\cos(\pi-\theta)},$
	$\displaystyle t_{31}$	$\displaystyle=$	$\displaystyle g~{}e^{~{}i(q/\hbar c){\cal A}(t)\cos(\pi/3+\theta)},$		(2)

and $t_{ji}~{}=~{}t^{*}_{ij}$. Then the periodically driven Hamiltonian for this triangle is

	$\displaystyle H_{\bigtriangleup}(t)$	$\displaystyle=$	$\displaystyle-\sum_{\sigma}(t_{12}~{}c_{1,\sigma}^{\dagger}c_{2,\sigma}+t_{23}~{}c_{2,\sigma}^{\dagger}c_{3,\sigma}+t_{31}~{}c_{3,\sigma}^{\dagger}c_{1,\sigma}$		(3)
			$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}+~{}{\rm H.c.})~{}+~{}U~{}\sum_{i=1}^{3}~{}n_{i,\uparrow}n_{i,\downarrow}.$

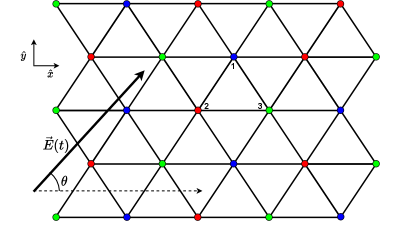
To obtain the Hamiltonian for the entire triangular lattice, we sum up the Hamiltonians for all triangles, both up-pointing and down-pointing, with Hamiltonians $H_{\bigtriangleup}(t)$ and $H_{\bigtriangledown}(t)$. In the next section we will use Floquet perturbation theory to derive the effective model in the large $U$ (Mott insulator) limit of this driven model. We shall see that the states in the spin sector (in which all sites are occupied by only one electron) are governed by a Heisenberg Hamiltonian with different exchange couplings on different bonds and an additional chiral three-spin term whose sign is opposite for up-pointing ($\bigtriangleup$) and down-pointing triangles ($\bigtriangledown$).

To obtain the effective Hamiltonian in the large $U$ limit using Floquet perturbation theory, we start with the Hubbard model on a single triangle. We write the Hamiltonian in Eq.  (3) as $H_{\bigtriangleup}~{}=~{}H_{0}+V$ where

	$\displaystyle H_{0}$	$\displaystyle=$	$\displaystyle~{}U~{}\sum_{i=1}^{3}~{}n_{i,\uparrow}n_{i,\downarrow},$
	$\displaystyle V(t)$	$\displaystyle=$	$\displaystyle~{}-\sum_{\sigma}(t_{12}~{}c_{1,\sigma}^{\dagger}c_{2,\sigma}~{}+~{}t_{23}~{}c_{2,\sigma}^{\dagger}c_{3,\sigma}~{}+~{}t_{31}~{}c_{3,\sigma}^{\dagger}c_{1,\sigma}$
			$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}+~{}{\rm H.c.})$

We now consider the eigenstates of the static part of the Hamiltonian, $H_{0}$, which will serve as the basis for subsequent calculations. For a half-filled system we can have three electrons on the triangle. Then the total number of basis states is $20$. They can be classified according to the number of up and down spins (in $S_{z}$ basis) which are listed below:

• (a)

  One state with all three spins pointing up.

• (b)

  Nine states with two up spins and a down spin. Six of these states have a double occupancy.

• (c)

  Nine states with one up and two down spins. Here also six states have a double occupancy.

• (d)

  One state with all the three spins pointing down.

The reason for this classification is that these four sectors do not mix with each other since they have different values of the $z$-component of the total spin, $S^{z}$, which commutes with both $H_{0}$ and $V(t)$.

Sectors (a) and (d) are identical in terms of the eigenvalues of $H_{0}$ as are the sectors (b) and (c). Since the states in sector (a) and (d) are exact eigenstates of $V(t)$, the non-trivial eigenstates of $H_{0}$ are governed by states in sectors (b) and (c) which are related by the spin rotation operator which takes $S^{z}\rightarrow-S^{z}$. Hence we will derive the effective Hamiltonian for only sector (b). The nine basis states $\ket{\psi_{n}}$ in sector (b) are labeled as shown in Fig. 2. A general state $\ket{\psi(t)}$ with two up spins and one down spin can be written as a linear combination of these basis states as $\ket{\psi(t)}=\sum_{n=1}^{9}~{}c_{n}(t)\ket{\psi_{n}}~{}e^{-iE_{n}t}$, where $E_{n}$’s are the eigenvalues of $H_{0}$. (We will set $\hbar$ equal to 1 in the rest of this paper). According to our notation $E_{1}~{}=~{}E_{2}~{}=~{}E_{3}~{}=~{}0$ and $E_{n}~{}=~{}U$ for $n=4,5,\cdots,9$. We will follow the convention of defining the basis states in terms of the creation operators as follows. In Fig. 2, the state $\ket{\psi_{1}}~{}=~{}c_{1\downarrow}^{\dagger}c_{2\uparrow}^{\dagger}c_{3\uparrow}^{\dagger}\ket{0}$, whereas $\ket{\psi_{4}}~{}=~{}c_{1\uparrow}^{\dagger}c_{1\downarrow}^{\dagger}c_{3\uparrow}^{\dagger}\ket{0}$, namely, the three site labels are non-decreasing as we go from left to right, and at the same site, $\uparrow$ appears to the left of $\downarrow$.

Next, $\ket{\psi(t)}$ satisfies the time-dependent Schrödinger equation $i\partial\ket{\psi(t)}/\partial t=(H_{0}+V(t))\ket{\psi(t)}$. Using the expansion of $\ket{\psi(t)}$, we obtain a set of linear differential equations for the coefficients $c_{n}$,

$\displaystyle i\frac{dc_{n}}{dt}=~{}\sum_{m=1}^{9}~{}\bra{\psi_{n}}V(t)\ket{\psi_{m}}~{}e^{i(E_{n}-E_{m})t}~{}c_{m}(t),$

(4)

where $n=1,2,\cdots,9$.

In our chosen basis, the matrix $\bra{\psi_{n}}V(t)\ket{\psi_{m}}$ matrix looks like

$\displaystyle\begin{pmatrix}0&0&0&t_{21}&-t_{31}&0&t_{12}&-t_{13}&0\\ 0&0&0&-t_{21}&0&t_{32}&-t_{12}&0&t_{32}\\ 0&0&0&0&t_{31}&-t_{32}&0&t_{13}&-t_{23}\\ t_{12}&-t_{12}&0&0&-t_{32}&0&0&0&t_{13}\\ -t_{13}&0&t_{13}&-t_{23}&0&t_{12}&0&0&0\\ 0&t_{23}&-t_{23}&0&t_{21}&0&-t_{13}&0&0\\ t_{21}&-t_{21}&0&0&0&-t_{31}&0&t_{23}&0\\ -t_{31}&0&t_{31}&0&0&0&t_{32}&0&-t_{21}\\ 0&t_{32}&-t_{32}&t_{31}&0&0&0&-t_{12}&0\\ \end{pmatrix}.$

Since the $t_{ij}$’s are periodic functions of time, they can be expanded as a Fourier series. The expressions for the time-dependent hoppings are therefore

	$\displaystyle t_{12}$	$\displaystyle=$	$\displaystyle~{}g~{}\sum_{m=-\infty}^{\infty}\gamma_{m}~{}e^{im\omega t},$
	$\displaystyle t_{23}$	$\displaystyle=$	$\displaystyle~{}g~{}\sum_{m=-\infty}^{\infty}\alpha_{m}~{}e^{im\omega t},$
	$\displaystyle t_{31}$	$\displaystyle=$	$\displaystyle~{}g~{}\sum_{m=-\infty}^{\infty}\beta_{m}~{}e^{im\omega t},$		(6)

where $\alpha_{m}$, $\beta_{m}$ and $\gamma_{m}$ are generally complex.

In Floquet theory, we define a Floquet operator which unitarily evolves the system through one time period $T$ as

$$U_{T}~{}=~{}{\cal T}e^{-(i/\hbar)\int_{0}^{T}dt~{}H(t)},$$

(7)

where $\cal T$ denotes time-ordering. If $\ket{\psi(t)}$ is an eigenstate of $U_{T}$, we have

$$\ket{\psi(T)}=U_{T}\ket{\psi(0)}=e^{~{}-i\epsilon T}\ket{\psi(0)},$$

(8)

where $\epsilon$ is the quasienergy for the state $\ket{\psi(t)}$. Then in terms of the basis states $\ket{\psi_{n}}$ and coefficients $c_{n}(t)$, we have

$\displaystyle c_{n}(T)~{}e^{~{}-iE_{n}T}$

$\displaystyle=$

$\displaystyle\sum_{m=1}^{9}\bra{\psi_{n}}U_{T}\ket{\psi_{m}}~{}c_{m}(0)$

(9)

for $n=1,2,\cdots,9$. In the following subsections, we will solve Eq. (4) perturbatively in powers of $g$ to obtain an effective Hamiltonian $H_{eff}$ such that $e^{~{}-iH_{eff}T}=U_{T}$ up to the desired power of $g$.

In this section we will consider the spin-$1/2$ Hamiltonian on the triangular lattice and study its classical limit where the value of the spin $S$ at each site is taken to infinity. Having found the classical ground state we will then use spin-wave theory to study the excitations above the classical ground state.

In the large-$S$ limit, we have to put a factor of $1/S$ in front of the three-spin term so that it scales in the same way (i.e., as $S^{2}$) as the two-spin terms. We therefore consider the Hamiltonian

	$\displaystyle H_{S}$	$\displaystyle=$	$\displaystyle\sum_{{\vec{n}}}~{}[J_{\alpha}{\vec{S}}_{\vec{n}}\cdot{\vec{S}}_{\vec{n}+\vec{u}}+J_{\beta}{\vec{S}}_{\vec{n}}\cdot{\vec{S}}_{\vec{n}+\vec{v}}+J_{\gamma}{\vec{S}}_{\vec{n}}\cdot{\vec{S}}_{\vec{n}+\vec{w}}]$		(23)
			$\displaystyle+~{}\frac{C}{S}~{}[\sum_{\vec{n},\bigtriangleup}~{}{\vec{S}}_{\vec{n}}\cdot{\vec{S}}_{\vec{n}+\vec{u}}\times{\vec{S}}_{\vec{n}+\vec{w}}$
			$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}-\sum_{\vec{n},\bigtriangledown}~{}{\vec{S}}_{\vec{n}}\cdot{\vec{S}}_{\vec{n}+\vec{w}}\times{\vec{S}}_{\vec{n}+\vec{v}}].$

Since we are looking at the classical limit, we can take the components of spin to be commuting objects. We will now look at some classical spin configurations and find the ranges of parameters $(J_{\alpha},J_{\beta},J_{\gamma},C)$ where each of these is stable. Before proceeding further, we note that $\vec{w}=\vec{u}+\vec{v}$, and the coordinates $\vec{n}$ of any site can be uniquely written as

$$\vec{n}=m_{1}\vec{u}+m_{2}\vec{v},$$

(24)

where $m_{1},~{}m_{2}$ are integers.

We first consider a collinear spin configuration in which all the spins point along the $\pm\hat{z}$ direction in the spin space, and they also satisfy

	$\displaystyle{\vec{S}}_{\vec{n}}\cdot{\vec{S}}_{\vec{n}+\vec{u}}$	$\displaystyle=$	$\displaystyle-S^{2},$
	$\displaystyle{\vec{S}}_{\vec{n}}\cdot{\vec{S}}_{\vec{n}+\vec{v}}$	$\displaystyle=$	$\displaystyle S^{2},$
	$\displaystyle{\vec{S}}_{\vec{n}}\cdot{\vec{S}}_{\vec{n}+\vec{w}}$	$\displaystyle=$	$\displaystyle-S^{2},$		(25)

for all values of $\vec{n}$. Following Fig. 3 and Eq. (24), we see that a spin configuration which satisfies Eqs. (25) is given by

$${\vec{S}}_{\vec{n}}~{}=~{}S(0,0,(-1)^{m_{1}}).$$

(26)

For a large system with $N$ sites and periodic boundary conditions, we find that the classical energy of this configuration is given by

$$E_{cl}~{}=~{}NS^{2}~{}(-~{}J_{\alpha}~{}+~{}J_{\beta}~{}-~{}J_{\gamma}).$$

(27)

[Note that the three-spin term in Eq. (23) does not contribute to the energy in any collinear spin configuration. We will therefore set $C=0$ in the rest of this analysis.] We will now use spin-wave theory anderson ; kubo to find the energy-momentum dispersion of the excitations around the classical ground state in Eq. (26). We use the Holstein-Primakoff transformation holstein to write the spin operators in terms of bosonic operators as

	$\displaystyle S_{\vec{n}}^{z}$	$\displaystyle=$	$\displaystyle S~{}-~{}{a_{\vec{n}}}^{\dagger}a_{\vec{n}},$
	$\displaystyle S_{\vec{n}}^{+}$	$\displaystyle=$	$\displaystyle\sqrt{2S~{}-~{}a_{\vec{n}}^{\dagger}a_{\vec{n}}}~{}a_{\vec{n}}$
	$\displaystyle S_{\vec{n}}^{-}$	$\displaystyle=$	$\displaystyle a_{\vec{n}}^{\dagger}~{}\sqrt{2S~{}-~{}a_{\vec{n}}^{\dagger}a_{\vec{n}}},$		(28)

at the sites where ${\vec{S}}_{\vec{n}}=S(0,0,1)$, and

	$\displaystyle S_{\vec{n}}^{z}$	$\displaystyle=$	$\displaystyle-~{}S~{}+~{}a_{\vec{n}}^{\dagger}a_{\vec{n}},$
	$\displaystyle S_{\vec{n}}^{+}$	$\displaystyle=$	$\displaystyle a_{\vec{n}}^{\dagger}\sqrt{2S~{}-~{}a_{\vec{n}}^{\dagger}a_{\vec{n}}},$
	$\displaystyle S_{\vec{n}}^{-}$	$\displaystyle=$	$\displaystyle\sqrt{2S~{}-~{}a_{\vec{n}}^{\dagger}a_{\vec{n}}}~{}a_{\vec{n}},$		(29)

at the sites where ${\vec{S}}_{\vec{n}}=S(0,0,-1)$. Making the standard large-$S$ approximation of replacing $\sqrt{2S~{}-~{}a_{\vec{n}}^{\dagger}a_{\vec{n}}}\to\sqrt{2S}$, we find that Eq. (23) takes the form

	$\displaystyle H_{S}$	$\displaystyle=$	$\displaystyle NS^{2}~{}(-~{}J_{\alpha}~{}+~{}J_{\beta}~{}-~{}J_{\gamma})$		(30)
			$\displaystyle+~{}S~{}\sum_{\vec{n}}~{}[(2J_{\alpha}~{}-~{}2J_{\beta}~{}+~{}2J_{\gamma})~{}a_{\vec{n}}^{\dagger}a_{\vec{n}}$
			$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}+~{}J_{\alpha}~{}(a_{\vec{n}}^{\dagger}a_{{\vec{n}}+{\vec{u}}}^{\dagger}~{}+~{}{\rm H.c.})$
			$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}+~{}J_{\beta}~{}(a_{\vec{n}}^{\dagger}a_{{\vec{n}}+{\vec{v}}}~{}+~{}{\rm H.c.})$
			$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}+~{}J_{\gamma}~{}(a_{\vec{n}}^{\dagger}a_{{\vec{n}}+{\vec{w}}}^{\dagger}~{}+~{}{\rm H.c.})].$

Fourier transforming to momentum space, we obtain

	$\displaystyle H_{S}$	$\displaystyle=$	$\displaystyle NS^{2}~{}(-~{}J_{\alpha}~{}+~{}J_{\beta}~{}-~{}J_{\gamma})$
			$\displaystyle+~{}S~{}\sum_{\vec{k}}~{}[(2J_{\alpha}~{}-~{}2J_{\beta}~{}+~{}2J_{\gamma})~{}a_{\vec{k}}^{\dagger}a_{\vec{k}}$
			$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}+~{}J_{\alpha}~{}\cos({\vec{k}}\cdot{\vec{u}})~{}(a_{\vec{k}}^{\dagger}a_{-{\vec{k}}}^{\dagger}~{}+~{}a_{\vec{k}}a_{-{\vec{k}}})$
			$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}+~{}2J_{\beta}~{}\cos({\vec{k}}\cdot{\vec{v}})~{}a_{\vec{k}}^{\dagger}a_{\vec{k}}$
			$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}+~{}J_{\gamma}~{}\cos({\vec{k}}\cdot{\vec{w}})~{}(a_{\vec{k}}^{\dagger}a_{-{\vec{k}}}^{\dagger}~{}+~{}a_{\vec{k}}a_{-{\vec{k}}})],$

where the sum over ${\vec{k}}$ runs over the complete Brillouin zone. The above Hamiltonian couples modes at ${\vec{k}}$ and $-{\vec{k}}$. Using the Bogoliubov transformation to diagonalize the Hamiltonian, we find that the spin-wave spectrum is given by

	$\displaystyle E_{\vec{k}}$	$\displaystyle=$	$\displaystyle S~{}\sqrt{(C_{\vec{k}}~{}+~{}D_{\vec{k}})~{}(C_{\vec{k}}~{}-~{}D_{\vec{k}})},$
	$\displaystyle C_{\vec{k}}$	$\displaystyle=$	$\displaystyle J_{\alpha}+J_{\gamma}-J_{\beta}+J_{\beta}~{}\cos({\vec{k}}\cdot{\vec{v}}),$
	$\displaystyle D_{\vec{k}}$	$\displaystyle=$	$\displaystyle J_{\alpha}~{}\cos({\vec{k}}\cdot{\vec{u}})~{}+~{}J_{\gamma}~{}\cos({\vec{k}}\cdot{\vec{w}}).$		(32)

We see that the spin-wave energy vanishes at ${\vec{k}}=(0,0)$ and ${\vec{k}}=\pi(1,1/\sqrt{3})$ which correspond to Goldstone modes. We therefore expect that in this phase the static structure function $S({\vec{q}})$ should have a peak at ${\vec{q}}=\pi(1,1/\sqrt{3})$. We can also see this directly from the form of the classical spin configuration in Eq. (26). Since the two-spin correlation between sites ${\vec{0}}=(0,0)$ and ${\vec{n}}$ is equal to ${\vec{S}}_{\vec{0}}\cdot{\vec{S}}_{{\vec{n}}}=S^{2}(-1)^{m_{1}}$, we see from Eqs. (22) and (24) that the Fourier transform,

$$S({\vec{q}})~{}=~{}\sum_{\vec{n}}~{}e^{-i{\vec{q}}\cdot{\vec{n}}}~{}{\vec{S}}_{\vec{0}}\cdot{\vec{S}}_{{\vec{n}}},$$

(33)

will have a peak at ${\vec{q}}=\pi(1,1/\sqrt{3})$. We will see later that this agrees with our numerical results based on ED.