DRIP: Domain Refinement Iteration with Polytopes for Backward Reachability Analysis of Neural Feedback Loops

As in [7], we assume linear time-invariant (LTI) dynamics,

where $\mathbf{x}_{t}\in\mathds{R}^{n_{x}}$ is the state at discrete timestep $t$, $\mathbf{u}_{t}\in\mathds{R}^{n_{u}}$ is the input, $\mathbf{A}\in\mathds{R}^{n_{x}\times n_{x}}$ and $\mathbf{B}\in\mathds{R}^{n_{x}\times n_{u}}$ are known system matrices, and $\mathbf{c}\in\mathds{R}^{n_{x}}$ is a known exogenous input. We assume $\mathbf{x}_{t}\in\mathcal{X}\subseteq\mathds{R}^{n_{x}}$ and $\mathbf{u}_{t}\in\mathcal{U}\subseteq\mathds{R}^{n_{u}}$, where $\mathcal{X}$ and $\mathcal{U}$ are convex sets defining the operating region of the state space and control limits, respectively. The closed-loop dynamics are

where $\pi(\cdot)$ is a state-feedback control policy, discussed next.

The control policy, $\pi:\mathcal{X}\to\mathcal{U}$, can be an arbitrary computation graph, composed of primitives that can be linearly relaxed [11, 12, 13]. For example, given an $m$-layer NN with $n_{i}$ neurons in layer $i$ and nonlinear activation $\sigma_{i}:\mathds{R}^{n}\to\mathds{R}^{n}$ such that post-activation $\mathbf{z}_{i}=\sigma_{i}(\mathbf{z}_{i-1})$ (e.g., ReLU, sigmoid), we need to be able to define $\bm{\alpha}_{l,i},\bm{\beta}_{l,i},\bm{\alpha}_{u,i},\bm{\beta}_{u,i}$ such that

For each primitive, values of $\bm{\alpha}_{l,i},\bm{\beta}_{l,i},\bm{\alpha}_{u,i},\bm{\beta}_{u,i}$ depend on the algorithm employed and are derived from intermediate bounds over the activation of the network, which can be obtained by applying the bound computation procedure (described next) to subsets of the network.

CROWN [14] and LIRPA algorithms in general [11] enable backward propagation of bounds (from function output to input, not to be confused with backward in time). For example, consider evaluating a lower bound on $\mathbf{c}\cdot\mathbf{z}_{i}+b$, using the relaxations defined in Eq. 3 to replace $\mathbf{z}_{i}$:

where $[\mathbf{c}]^{+}=\max(\mathbf{c},0)$ and $[\mathbf{c}]^{-}=\min(\mathbf{c},0)$. Through backsubstitution, we transformed a lower bound defined as a linear function over $\mathbf{z}_{i}$ into a lower bound defined as a linear function over $\mathbf{z}_{i-1}$. By repeated application of this procedure to all operations in the network, we can obtain bounds that are affine in the input. That is, for a computation graph $p$ from Eq. 2, with input $\mathbf{x}_{t}$ and output $\mathbf{x}_{t+1}$, given an objective matrix $\mathbf{C}\in\mathds{R}^{n_{\text{facets}}\times n_{x}}$, we compute $\mathbf{M}\in\mathds{R}^{n_{\text{facets}}\times n_{x}}$ and $\mathbf{n}\in\mathds{R}^{n_{\text{facets}}}$ such that

If $\mathbf{x}_{t}$ is within some known set $\mathcal{X}_{t}$, these bounds can be concretized by solving $\min_{\mathbf{x}_{t}\in\mathcal{X}_{t}}\mathbf{M}\mathbf{x}_{t}+\mathbf{n}$. Closed-form solutions exist for some forms of $\mathcal{X}_{t}$.

Prior CROWN-based backward reachability works [5, 7, 6] relaxed the control policy $\pi$, whereas this work directly relaxes the closed-loop dynamics, $p$, drawing inspiration from [3], which focused on forward reachability.

For target set $\mathcal{X}_{T}\subseteq\mathcal{X}$, define $t$-step BP and BR sets as

where $t>0$ and $p^{t+1}\triangleq p\circ p^{t}$. We will typically drop the arguments and simply write $\mathcal{R}_{t},\mathcal{P}_{t}$. Clearly, $\mathcal{P}_{t}\subseteq\mathcal{R}_{t}$. Since exactly computing BP sets is computationally difficult, this work aims to compute BP over-approximations (BPOAs), which provide a (guaranteed) conservative description of all states that will lead to the target set. For sets, upper bar notation conveys an outer bound, e.g., $\bar{\mathcal{A}}\supseteq\mathcal{A}$; for vectors, bar notation conveys upper/lower bounds, e.g., $\underaccent{\bar}{\mathbf{a}}\leq\mathbf{a}\leq\bar{\mathbf{a}}$.

One efficient way to outer bound $\mathcal{R}_{-1}$ with hyper-rectangle ${[\underaccent{\bar}{\mathbf{x}}_{-1},\bar{\mathbf{x}}_{-1}]}$ is to solve the following optimization problems for each state $k\in[n_{x}]$, with the $i$-th standard basis vector, $\mathbf{e}_{i}$ [1]:

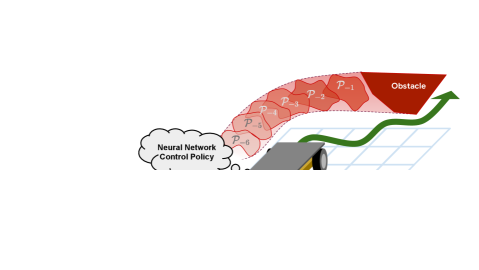
Whereas prior work (e.g., [7]) represents BPOAs as hyper-rectangles, this work introduces a formulation based on halfspace-representation (H-Rep) polytopes.

While $\bar{\mathcal{R}}_{-1}$ provides a domain for relaxing the NN, this domain is often excessively conservative and leads to large BPOAs. To address this issue, this work leverages the following to tighten the domain used for relaxation.

This iterative refinement can be performed, for example, for a specified number of steps or until the reduction in BPOA volume between refinement steps reaches some threshold.

Existing algorithms [1, 5, 7, 6] simplified the bound computation by assuming the domain over which to relax the network was a hyper-rectangle $\mathcal{X}=[\mathbf{l},\mathbf{u}]^{d}$, which enables

Assuming that the input domain is a convex polytope $\mathcal{C}$, the strategy consists in first solving $2d$ LPs, $l_{i}=\min_{x\in\mathcal{C}}x_{i}$ and $u_{i}=\max_{x\in\mathcal{C}}x_{i}$, to obtain the hyperrectangular bounds on $\mathcal{C}$, which may introduce conservativeness.

Instead, the simplex is another domain that enables efficient concretization of linear bounds, but also enables natural representation of a convex polytope. For $\mathcal{X}=\Delta_{d}=\left\{\mathbf{x}\in\mathcal{R}^{d}|\ \mathbf{x}\geq 0,\sum_{i}^{d}x_{i}=1\right\}$,

where $\mathbf{M}_{\text{argmin[M]}}$ is a vector of the minimum of each row of $\mathbf{M}$. We can represent a convex polytope $\mathcal{C}$, with a simplex and a transformation based on its vertices $\left\{\mathbf{v}_{0},\mathbf{v}_{1},\dotsc,\mathbf{v}_{n}\right\}$:

where $\mathbf{V}=[\mathbf{v}_{0}^{T};\mathbf{v}_{1}^{T};\dotsc;\mathbf{v}_{n-1}^{T}]\in\mathds{R}^{n_{v}\times n_{x}}$. Fig. 1 shows how this is integrated in the bound propagation: the multiplication by the matrix of vertices is simply prepended to the NN controller as an initial linear layer (an exact representation of polytope $\mathcal{C}$).

To summarize an implementation of the proposed approach, we first describe the method for relaxing $p$ (Algorithm 1) over a simplex domain, then show how to calculate the BPOA for a single timestep (Algorithm 2), then describe how to compute BPOAs over multiple timesteps (Algorithm 3).

Given an objective matrix $\mathbf{C}\in\mathds{R}^{h\times n_{x}}$, Algorithm 1 aims to compute $\mathbf{M},\mathbf{n}$ such that $\mathbf{C}\mathbf{x}_{t}\leq\mathbf{M}\mathbf{x}_{t-1}+\mathbf{n}$ $\forall\mathbf{x}_{t-1}\in\texttt{conv\_hull}(\mathbf{V})$. Add a linear transformation to the front of the closed-loop dynamics to obtain a new function, $f_{\text{simplex}}:\Delta_{n_{v}}\to\mathcal{X}$ (3). Then, define the parameters of each relaxation $\bm{\alpha}_{l,i},\bm{\beta}_{l,i},\bm{\alpha}_{u,i},\bm{\beta}_{u,i}$, from Eq. 3, specifying the standard $n_{v}$-simplex as the bounds on the function’s input (4). Finally, compute backward bounds from the objective, $\mathbf{C}$, to the current state, $\mathbf{x}_{t}$, stopping before reaching the added linear transformation (5).

Algorithm 2 describes the proposed method for computing a BPOA, $\bar{\mathcal{P}}_{-1}$. First, extract $\mathbf{A}_{T},\mathbf{b}_{T}$ as the H-rep of the target set polytope. Then, hyper-rectangle $\bar{\mathcal{R}}_{-1}$ is computed by solving $2n_{x}$ LPs (2), and the BPOA, $\bar{\mathcal{P}}_{-1}$, is initialized as $\bar{\mathcal{R}}_{-1}$. To refine that estimate, loop for $n_{\text{iters}}$ (3). If using DRIP, at each iteration, compute the vertex representation (V-rep) of the current BPOA (5, we used [15]) and run Algorithm 1 with $\mathbf{C}=\mathbf{A}_{T}$ on this simplex domain (6). If using DRIP-HPoly, find hyperrectangle bounds on $\bar{\mathcal{P}}_{-1}$ and run CROWN [14] with $\mathbf{C}=\mathbf{A}_{T}$ on this hyperrectangular domain. Note that DRIP-HPoly completely avoids the conversion between H-Rep and V-Rep, which may be desirable for higher dimensional systems. Either way, then set the parameters of the H-rep of the refined BPOA using the CROWN relaxation and target set along with the prior iteration’s BPOA. Update $\bar{\mathcal{P}}_{-1}$ and the loop continues. After $n_{\text{iters}}$, $\bar{\mathcal{P}}_{-1}$ is returned. To calculate BPOAs for a time horizon $\tau$, Algorithm 3 calls Algorithm 2 $\tau$ times, using the next step’s BPOA as the target set.

First, we analyze the growth of $n_{\text{facets}}$ from domain refinement iteration. At $t{=}-1$, the BPOA starts with $n_{\text{facets}}=2n_{x}$ (hyperrectangle, $\bar{\mathcal{R}}_{-1}$). At each iteration, the BPOA gains at most $2n_{x}$ facets, meaning $n_{\text{facets}}{=}2n_{x}+2n_{\text{iters}}n_{x}$ at the end of the first timestep’s domain iteration. At $t{=}-2$, the BPOA again starts with $n_{\text{facets}}{=}2n_{x}$, but at each iteration we add $2n_{x}+2n_{\text{iters}}n_{x}$ facets, as the target set is the BPOA at $t{=}-1$. After $T$ steps of $n_{\text{iters}}$ iterations, the BPOA has at most $O(n_{\text{iters}}^{T}n_{x})$ facets.

DRIP-HPoly: Assume solving 1 LP has complexity $O((n+d)^{1.5}nL)$ [16], with $n$ variables, $d$ constraints, and $L$ encoding bits. BR bounds require $2n_{x}$ LPs, where each has $n_{\text{facets}}+2n_{u}$ constraints and $n_{x}+n_{u}$ decision variables. Assuming $n_{\text{facets}}{>}2n_{u}$ and $n_{x}{>}n_{u}$, this gives $O((n_{x}+n_{\text{iters}}^{T}n_{x})^{1.5}n_{x}L)=O(n_{\text{iters}}^{1.5T}n_{x}^{2.5}L)$ runtime across all $T$ timesteps. At each refinement iteration, we find rectangular bounds and run CROWN. Finding rectangular bounds is similar to getting BR bounds except it is done $n_{\text{iters}}$ times, giving $O(n_{\text{iters}}^{1.5T+1}n_{x}^{2.5}L)$. CROWN time complexity is $O(m^{2}n^{3})$ for an $m$-layer network with $n$ neurons per layer and $n$ outputs [14]; since we have $O(n_{\text{iters}}^{T-1}n_{x})$ rows in the objective, we get $O(m^{2}n^{3}n_{\text{iters}}^{T}n_{x})$ (assuming $n{>}n_{x}$ and $n{>}n_{u}$). Relaxing the closed-loop dynamics would be the same ($p$ contains the control NN with a constant number of additional layers). Thus, to compute BPOAs for $T$ timesteps, DRIP-HPoly’s complexity is $O(n_{\text{iters}}^{1.5T+1}n_{x}^{2.5}L+m^{2}n^{3}n_{\text{iters}}^{T}n_{x})$.

DRIP: Polytope domain relaxation affects the analysis in 3 places: vertex enumeration (converting from H-rep to V-rep), CROWN relaxation (network width), and LP (number of constraints). Since each BPOA starts as a hyperrectangle, the polytopes are always bounded. Assume that vertex enumeration time complexity for a bounded polytope is $O(n^{2}dv)$ with $v$ vertices from $n$ hyperplanes in $d$ dimensions [17]. Here, $d=n_{x}$ and we assume $\Theta(n_{\text{facets}}^{\lfloor\frac{n_{x}}{2}\rfloor})$ (worst-case caused by cyclic polytopes [18]) vertices, which corresponds to $O(n_{\text{facets}}^{2+\lfloor\frac{n_{x}}{2}\rfloor}n_{x})$. Recall that after $T$ timesteps of $n_{\text{iters}}$ iterations, the BPOA would have $O(n_{\text{iters}}^{T}n_{x})$ facets; it could thus have $O(n_{\text{iters}}^{T\lfloor\frac{n_{x}}{2}\rfloor}n_{x}^{\lfloor\frac{n_{x}}{2}\rfloor})$ vertices. Therefore, the time complexity of vertex enumeration is $O(n_{\text{iters}}^{T(2+\lfloor\frac{n_{x}}{2}\rfloor)}n_{x}^{3+\lfloor\frac{n_{x}}{2}\rfloor})$. Analagously, the CROWN runtime is $O(n_{\text{iters}}m^{2}(n_{\text{iters}}^{\lfloor\frac{n_{x}}{2}\rfloor}n_{x}^{\lfloor\frac{n_{x}}{2}\rfloor})^{3}n_{\text{iters}}^{T}n_{x})=O(m^{2}n_{\text{iters}}^{1+T+3T\lfloor\frac{n_{x}}{2}\rfloor}n_{x}^{3\lfloor\frac{n_{x}}{2}\rfloor+1})$, since we add a single layer to the NN with one neuron per polytope vertex. For the LP runtime, there are $O(n_{\text{iters}}^{T-1}n_{x})$ constraints, leading to $O(n_{\text{iters}}^{1.5(T-1)}n_{x}^{3.5}L)$ time complexity. The full DRIP algorithm has time complexity of $O(n_{\text{iters}}^{T(2+\lfloor\frac{n_{x}}{2}\rfloor)}n_{x}^{3+\lfloor\frac{n_{x}}{2}\rfloor}+m^{2}n_{\text{iters}}^{1+T+3T\lfloor\frac{n_{x}}{2}\rfloor}n_{x}^{3\lfloor\frac{n_{x}}{2}\rfloor+1}+n_{\text{iters}}^{1.5(T-1)}n_{x}^{3.5}L)$.

In practice, the runtime may be much better. For example, $T=1$ for Fig. 4, which eliminates a source of exponential growth. Alternatively, rather than allowing the number of facets to grow exponentially, one could simply solve an LP at each iteration/timestep to obtain an constant-size outer bound on the latest BPOA. While this would certainly reduce the exponential growth in $n_{\text{facets}}$, our numerical experiments suggest that such a step is not necessary in practice for the systems considered.

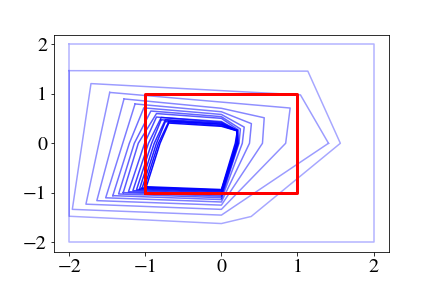
Using the double integrator system and learned policy from [1] (2 hidden layers each with 5 neurons), Fig. 2 demonstrates the substantial improvement in reachable set tightness enabled by our proposed method. For a target set (red) $\mathcal{X}_{T}=[4.5,5.0]\times[-0.25,0.25]$, the true BP sets are shown in solid colors for each timestep, and the BPOAs are shown in the same colors with dashed lines. For example, Fig. 3(a) implements the prior work [5], in which BPOAs become very conservative after a few timesteps. By adding the refinement loop (Section 3.2), Fig. 3(d) shows substantial improvement with $n_{\text{iters}}=5$.

However, increasing $n_{\text{iters}}>5$ does not improve the results with the prior LP and hyper-rectangular BPOA formulation. Instead, the middle column shows the impact of the proposed formulation from Section 3.1, in which the closed-loop dynamics are relaxed to directly provide BPOAs as polytopes. A key reason behind this improvement is the use of the target set’s facets as the objective matrix during the backward pass of the CROWN algorithm. When increasing $n_{\text{iters}}$ to 5, we see nearly perfect bounds on the first three BP sets, with tighter yet still somewhat loose bounds on the final two timesteps.

The impact of the polytope domain used in the relaxation (Section 3.3) is shown in the rightmost column. Because the first iteration always uses the hyper-rectangular $\mathcal{R}_{-t}$, we expect to see no difference between Fig. 3(b) and Fig. 3(c). However, Fig. 3(f) shows much tighter BPOAs in the last two timesteps when compared to Fig. 3(e).

Overall, the massive improvement in BPOA tightness between the prior work [5] (Fig. 3(a)) and the proposed approach (Fig. 3(f)) would enable a practitioner to certify safety when starting from a larger portion of the state space.

Fig. 3 provides quantitative analysis of the tradeoff between tightness and computational runtime for the various methods. Final step error is the ratio $\frac{A_{\text{BPOA}}-A_{\text{BP}}}{A_{\text{BP}}}$, where $A_{\mathcal{A}}$ denotes the area of set $\mathcal{A}$. Runtime is plotted as the mean and shaded standard deviation over 20 trials (with the worst one discarded). For the 3 variants of the proposed algorithms, by increasing $n_{\text{iters}}$, we observe an improvement in error at the cost of additional runtime.

The red triangle corresponds to Fig. 3(a) [5]. The pink curve corresponds the leftmost column of Fig. 2, which adds a refinement loop on the relaxation domain (Section 3.2). The blue curve corresponds to the middle column of Fig. 2, which uses polytope BPOAs (Section 3.1). The green curve corresponds to the rightmost column of Fig. 2, which uses polytope relaxation domains (Section 3.3).

A key cause of the computation time reduction between red/pink and green/blue is that the new formulation replaces many of the LPs with closed-form polytope descriptions. Overall, we observe a $371\times$ improvement in the error. Moreover, this experiment did not require any set partitioning and was still able to provide very tight BPOAs.

Next, we use DRIP to certify that a robot will not collide with an obstacle for any initial condition in the state space (outside of the obstacle itself). We use the 2D ground robot dynamics, policy, and obstacle from [5, 7] (2 hidden layers each with 10 neurons). The target set is partitioned into 4 cells (2 per dimension), which we note is $4\times$ fewer cells than in [5, 7]. For each cell, the 1-step BPOA is calculated for $n_{\text{iters}}$, and the returned BPOA is the convex hull of the union of vertices for each cell’s BPOA.

Fig. 4(a) shows the target set (red) and BPOAs for $n_{\text{iters}}=\{0,1,\ldots,15\}$ (blue, darker corresponds to larger $n_{\text{iters}}$). When $n_{\text{iters}}=15$, $\bar{\mathcal{P}}_{-1}\subseteq\mathcal{X}_{T}$. By Corollary A.2 of [7], this certifies that the system can only reach the obstacle if it starts from within the obstacle; there is no need to compute BPOAs for further timesteps. Fig. 4(b) shows BPOAs with rollouts of the closed-loop dynamics from 400 random initial states, although sampling trajectories is not necessary given the certificate.