Draft & Verify: Lossless Large Language Model Acceleration via Self-Speculative Decoding
Abstract
We present a novel inference scheme, self-speculative decoding, for accelerating Large Language Models (LLMs) without the need for an auxiliary model. This approach is characterized by a two-stage process: drafting and verification. The drafting stage generates draft tokens at a slightly lower quality but more quickly, which is achieved by selectively skipping certain intermediate layers during drafting. Subsequently, the verification stage employs the original LLM to validate those draft output tokens in one forward pass. This process ensures the final output remains identical to that produced by the unaltered LLM. Moreover, the proposed method requires no additional neural network training and no extra memory footprint, making it a plug-and-play and cost-effective solution for inference acceleration. Benchmarks with LLaMA-2 and its variants demonstrated a speedup up to 1.99.111Code is available at https://openreview.net/attachment?id=ACC2nQYzPYS&name=software, and will be released with the Apache-2.0 License.
1 Introduction
Transformer-based Large Language Models (LLMs), such as GPT-3/4, PaLM, and LLaMA, have been widely adopted in various real-world applications Bommasani et al. (2021); Liang et al. (2022); Brown et al. (2020); Min et al. (2022); Chan et al. (2022); Touvron et al. (2023). However, their inference costs have raised significant concerns, especially for latency-sensitive scenarios Pope et al. (2022). The main efficiency bottleneck is the autoregressive decoding process. This process decodes each output token sequentially, leading to a high number of Transformer calls; furthermore, each Transformer call is typically memory bandwidth-bound, resulting in low computation utility and thus longer wall-clock time Shazeer (2019). For instance, decoding 128 tokens autoregressively using LLaMA-2-13B on an A100 GPU can take up to 100 longer than a sequence-level forward pass on the same number of tokens, highlighting the substantial inefficiency inherent in the current decoding process.
Established model compression techniques such as quantization Han et al. (2015), pruning Molchanov et al. (2016), and distillation Hinton et al. (2015) have been employed to alleviate these costs. While these solutions have proven extremely effective, they usually require changing the model architecture, changing the training procedure, re-training or fine-tuning the models, and do not maintain identical outputs.
In parallel to model compression, speculative execution is being explored to accelerate the autoregressive decoding process Leviathan et al. (2023); Chen et al. (2023). These methods train an auxiliary draft model that can quickly generate some draft output tokens. Subsequently, the original LLM, referred to as the verify model, then checks the acceptability of these draft tokens with one single forward pass. This verification step ensures that the outputs are derived from the original LLM’s probability distribution.
However, an essential issue of existing speculative execution methods is the need to identify or train a suitable draft model that can generate outputs consistent with the verify model. It becomes more tricky when the LLM is already a fine-tuned model, e.g. LLaMA-2-Chat Touvron et al. (2023), CodeLLaMA Rozière et al. (2023). How to find or train a draft model that can effectively mimic the outputs of such a tailored model is a formidable task, with no straightforward or guaranteed solutions. Furthermore, the introduction of an additional draft model escalates the GPU memory overhead, increasing deployment challenges particularly on devices with restricted memory capacity.

In this paper, we present self-speculative decoding, a novel approach to accelerate the inference of LLMs. This method builds on the principles of speculative execution, but with a unique twist: it utilizes one LLM for both drafting and verification stages. The key insight driving our approach is the observation that skipping certain layers in LLMs does not significantly compromise the generation quality Liu et al. (2023). As such, by selectively bypassing some intermediate layers, we can use the LLM itself to generate draft tokens. These tokens are then verified by the original LLM in a single forward pass. Figure 1 illustrates this two-stage decoding process. The blue arrow indicates the inference path of the original model, while the green arrow depicts the inference path during the drafting stage. Notably, both inference paths share the same model so we do not need a standalone draft model with extra memory overhead.

Implementing self-speculative decoding poses two main challenges: (a) determining which layers and the number of layers to skip during drafting, and (b) deciding the timing to stop generating draft tokens. To tackle the first challenge, we formulate it as an optimization problem, which accepts the combinations of layers to bypass as input and aims to minimize the average inference time per token. We employ Bayesian optimization Jones et al. (1998) to solve this problem. The optimization is performed offline at the model level, and the searched layer combinations are fixed. The second challenge pertains to determining the optimal number of draft tokens () to generate. As shown in Figure 2, the choice of significantly influences the end-to-end speedup: for an acceptance rate below 80%, is optimal, and for rates above 80%, a larger is necessary. This observation underscores that a static is not universally applicable. To tackle this variability, we introduce an adaptive draft-exiting mechanism, which stops generating draft tokens once its confidence level drops below a threshold. This intervention prevents unnecessary computation and potential discard of additional draft tokens, thereby enhancing efficiency.
To summarize, our main contributions are: (1) Inference scheme: we propose self-speculative decoding, a practical, plug-and-play solution for inference acceleration that does not require further neural network training and avoids additional memory overhead; (2) Optimization strategies: we adopt Bayesian optimization to select which layers to skip during drafting and propose a simple yet effective method to adaptively determine the number of draft tokens; (3) Evaluation: we evaluate our method on text summarization and code generation tasks, and the experimental results indicate that our method can achieve up to 1.99 in end-to-end speedup.
2 Related Work
Transformer-based LLM inference.
As LLMs continue to evolve rapidly, we are seeing a surge of systems specifically engineered for LLM inference, including Faster Transformer NVIDIA , Orca Yu et al. (2022), LightSeq Wang et al. (2021), PaLM inference Pope et al. (2022), TurboTransformers Fang et al. (2021), Deepspeed Inference Aminabadi et al. (2022), FlexGen Sheng et al. (2023), Text Generation Inference HuggingFace (2023), etc. The token generation phase typically takes up the majority of the end-to-end inference time compared to the prompting encoding phase. Despite the introduction of system optimizations by those state-of-the-art systems to improve the inference speed, there is still a gap in the careful co-design of algorithms and systems. This is necessary to fully harness the potential of hardware efficiency during LLM inference computation.
Model Compression.
Various model compression methods have been studied for model inference. For example, quantization Han et al. (2015); Jacob et al. (2018); Nagel et al. (2019); Zhao et al. (2019); Yao et al. (2022); Park et al. (2022); Dettmers et al. (2022); Xiao et al. (2022); Frantar et al. (2022), pruning or sparsification Molchanov et al. (2016); Liu et al. (2018); He et al. (2019); Hoefler et al. (2021); Frantar and Alistarh (2023); Liu et al. (2023); Bansal et al. (2022), and distillation Hinton et al. (2015); Cho and Hariharan (2019); Tang et al. (2019); Touvron et al. (2021) have been applied to speed up the inference of the machine learning model, particularly LLMs. While these solutions are extremely effective, they often necessitate modifications to the model architecture and the training procedure. This usually involves re-training or fine-tuning the models. And it is important to note that these methods do not result in identical outputs.
Speculative Execution.
Speculative execution Burton (1985); Hennessy and Patterson (2011) is employed in computer architecture where a system performs some task in advance if that task is known to be required after the previous task. Speculative decoding Chen et al. (2023); Leviathan et al. (2023) has been proposed as an effective strategy to boost the inference speed of LLMs. Previously, Stern et al. (2018) proposed to use block-wise parallel decoding to accelerate greedy decoding of attention models. However, these methods need to train or select a high-quality draft model, and also result in increased memory overhead. Yang et al. (2023) proposed to copy the reference text tokens and validate them in a forward pass. However, this method relies on the repetitiveness assumption, and thus does not apply to general scenario generation. In contrast, our approach does not incur additional memory overhead and does not hinge on explicit assumptions about data distribution.
Early Exit.
Early exit allows the model to choose different calculation paths based on the input during the inference process to achieve acceleration. Various early exit techniques for encoder-only Transformers Devlin et al. (2019) have been proposed Xin et al. (2020b); Schwartz et al. (2020); Liu et al. (2020); Xin et al. (2020a); Hou et al. (2020); Zhou et al. (2020); Liao et al. (2021); Zhu (2021); Li et al. (2021); Sun et al. (2022). Recently, Schuster et al. (2022) further verified the effectiveness of early exit on the encoder-decoder LLM Raffel et al. (2020). Inspired by these works, we opt to skip certain intermediate layers during drafting.
3 Method
In this section, we first go through the standard autoregressive decoding. Subsequently, we provide a detailed depiction of our proposed method, including selectively skipping layers during drafting, and adaptively determining the number of draft tokens.
3.1 Standard Autoregressive Decoding
Existing LLMs typically follow an autoregressive decoding process. Given a prompt sequence , the model calculates the probability distribution of the next token . We present a greedy decoding process in Algorithm 1. In practice, instead of choosing the token with the highest probability (as in greedy decoding), we can sample tokens based on their probability distribution, which introduces some randomness and generates more diverse outputs.
Ideally, the computational cost of autoregressive decoding is comparable to that of sequence-level forward processing for an equivalent number of tokens.222 In fact, due to the causal nature of language modeling, autoregressive decoding could potentially save some attention computation. However, this decoding process is significantly bounded by the memory bandwidth of the device. When decoding each token, all the model parameters need to pass through the accelerator chip. So the model size divided by the memory bandwidth gives a hard ceiling on the decoding speed, resulting in a much longer inference time.
3.2 Self-Speculative Decoding
To mitigate the inherent inefficiency of autoregressive decoding, speculative decoding can be employed to enhance the inference speed of LLMs. This strategy involves two models: an LLM that we want to optimize, and a draft model that runs faster, albeit potentially at a lower quality. Speculative decoding can be explained as a two-stage process: (1) drafting: the draft model first generates draft tokens from a given prompt sequence , denoted as . (2) verification: following the drafting stage, the original LLM is then employed to validate these draft tokens. This validation is accomplished in a single forward pass, where the LLM predicts the probability distributions for each draft token and assesses whether they align with the draft tokens. Once a draft token is not validated, we use the original LLM’s prediction to override , and start the next round of drafting beginning from token .
The above process is based on the observation that computing the forward pass of a short continuation of tokens in parallel is not much slower than that of a single token. Consequently, the verification stage could be significantly more efficient than decoding tokens using the original LLM in standard autoregressive decoding.
In contrast to existing methods that use a standalone draft model to obtain draft tokens, our paper proposes a novel ‘self-speculative’ approach. We employ the original LLM itself for both the drafting and verification stages. During the drafting stage, the LLM selectively skips some of its intermediate layers so as to generate draft tokens quicker. Subsequently, these draft tokens are verified by the original LLM. Algorithm 2 presents a detailed description of the greedy decoding process. A complete sampling-based decoding process is elaborated in Appendix K.
Despite the simplicity of the main idea of self-speculative decoding, it poses several challenges:
Challenge 1: First, it is non-trivial to determine which layers and the number of layers to skip during drafting. If an excessive number of layers are skipped, the quality of the draft could be significantly compromised. This could result in a low acceptance rate in the verification stage, consequently increasing the overall inference time. On the other hand, if fewer layers are skipped, it ensures a higher acceptance, but also caps the maximum speedup that could be achieved.
Challenge 2: It is hard to decide when to stop the generation of draft tokens. As shown in Figure 2, the choice of the number of draft tokens to generate significantly influences the end-to-end speedup. In speculative decoding, if a draft token is rejected, all subsequent draft tokens will be discarded. Therefore, generating an excessive number of draft tokens could lead to unnecessary computation, thereby increasing the inference time.
In Sections 3.3 and 3.4, we will detail our approach to address these two challenges respectively.
3.3 Selection of Skipped Layers
The selection of skipped layers is essential in our method, shaping the configuration of the draft model and, consequently, the speedup achieved via self-speculative decoding. This selection process must carefully balance two key factors: the draft model’s ‘effectiveness’ and ‘efficiency.’ Both are intrinsically linked to the selection of skipped layers and significantly influence the overall performance of our method. Specifically:
(1) The ‘effectiveness’ of the draft model is quantified by the acceptance rate, which measures the agreement between the draft and verify models. However, we note that an exclusive focus on optimizing the acceptance rate could lead to no layers being skipped, i.e. the draft model identical to the verify model, resulting in an acceptance rate of 100%, but without any speedup.
(2) On the other hand, the ‘efficiency’ of the draft model can be quantified by the number of layers in the draft model. Indeed, minimizing the number of layers can reduce the inference latency of the draft model, but an extreme setup where all layers are skipped would result in the draft model generating low-quality tokens. This would drastically lower the acceptance rate, negating any potential speedup.
In this section, we frame the layer selection process as an optimization problem, our primary objective is to optimize the average inference time per verified token. This metric provides a comprehensive measure of the end-to-end inference time, including both drafting and verifying stages, normalized by the number of verified tokens.
Objective Function. This metric is a function of the selection of layers to be skipped in the draft model. The function, represented as , takes the selection of layers () as input and returns the average inference time per verified token on a development set. Here, is a vector that represents the layers to be skipped.
Optimization Problem. The optimization problem’s goal is to find the input that minimizes the objective function . This problem can be formally expressed as:
| (1) |
While a brute force search could find the globally optimal solution for smaller models with a manageable solving space, it becomes prohibitively expensive for larger language models with many layers (e.g., for LLaMA-2-70B).

To tackle this, we employ Bayesian optimization Jones et al. (1998). As shown in Figure 3, it iteratively selects new inputs for evaluation, based on a surrogate model of the objective function, i.e. Gaussian process Rasmussen et al. (2006), and an acquisition function. The latter balances exploration (testing inputs where the model’s prediction is uncertain) and exploitation (testing inputs where the model anticipates a favorable result). This procedure continues until a predetermined number of iterations is reached. We use the obtained to accelerate text generation, and is fixed for each model (i.e., generating draft model at model-level) without further updating. When the draft model’s target tasks vary significantly, task-level optimization is more appropriate to achieve good performance. Specifically, building the development set of optimization process from a single data source to mitigate inter-task interference.
In addition, while we here adopt skipping intermediate layers as a simple yet effective strategy to expedite the drafting stage, our scheme can be integrated with quantization Dettmers et al. (2022) and sparsification Sun et al. (2023) to further reduce resource consumption, as detailed in Appendix H.
3.4 Adaptive Draft-Exiting Mechanism
Our self-speculative decoding approach incorporates an adaptive draft-exiting mechanism to enhance computational efficiency during the drafting stage. In speculative decoding, if a draft token is rejected, all subsequent draft tokens will be discarded accordingly. The draft-exiting mechanism prevents the wasteful allocation of computational resources toward draft tokens that are less likely to be accepted in the verification stage.
Specifically, it compares the predicted probability of each draft token against a threshold . If the predicted probability falls below such that , indicating low confidence, it immediately stops drafting. This approach ensures a better use of computing by focusing on the generation and verification of high-quality tokens, thereby improving the overall efficiency.
Moreover, it is worth noting that a static threshold may not accurately reflect the actual acceptance rate between the drafting and verification stages. For example, more challenging examples with a lower acceptance rate would be better served by a higher . To avoid the need for case-by-case threshold determination, we use an adaptive threshold that adjusts dynamically according to an updating rule, thereby allowing for an accurate reflection of the acceptance rate and better handling of examples in different difficulties. We denote the acceptance rate () at -th drafting stage as . Consequently, the update rule is defined as follows:
| (2) | ||||
| (3) | ||||
| (4) |
where represents a target acceptance rate, is the update step-size, and and are factors designed to mitigate fluctuations of and respectively. Notably, when is 1, . We update after each verification stage. This updating rule ensures that the acceptance rate remains in close proximity to a target acceptance rate .
4 Evaluation
4.1 Setup
We evaluate a diverse range of models including LLaMA-2-13B, LLaMA-2-13B-Chat, CodeLLaMA-13B, and LLaMA-2-70B. Detailed setup can be found in Appendix B. We perform Bayesian optimization333https://github.com/bayesian-optimization/BayesianOptimization (MIT License) is used. (BO) for 1000 iterations to select the skipped layers in the drafting stage444Appendix B reports the offline BO time at model-level.. Results of tuning the number of BO iterations are reported in Appendix E. The datasets include CNN/Daily Mail (CNN/DM), Extreme Summarization (XSum), and HumanEval. These tasks cover the evaluation of text and code generation capabilities. Appendix I shows effectiveness on more diverse tasks such as solving math problems and open-domain chitchat. We perform 1-shot evaluation for CNN/DM and XSum, and compare the ROUGE-2 Lin (2004). We compare pass@1 and pass@10 Kulal et al. (2019) for HumanEval. We randomly sample 1000 instances from the testset for CNN/DM and XSum.
4.2 Main Results
| Model | Method | Temp. | CNN/DM | XSum | ||
|---|---|---|---|---|---|---|
| ROUGE-2 | Speedup | ROUGE-2 | Speedup | |||
| LLaMA-2-13B | Autoregressive | 0.0 | 0.106 | 1.000 | 0.124 | 1.000 |
| LLaMA-2-13B | Self-Speculative | 0.0 | 0.108 | 1.572 | 0.125 | 1.429 |
| LLaMA-2-13B | Autoregressive | 0.2 | 0.111 | 1.000 | 0.117 | 1.000 |
| LLaMA-2-13B | Self-Speculative | 0.2 | 0.111 | 1.529 | 0.117 | 1.377 |
| LLaMA-2-13B-Chat | Autoregressive | 0.0 | 0.144 | 1.000 | 0.109 | 1.000 |
| LLaMA-2-13B-Chat | Self-Speculative | 0.0 | 0.143 | 1.409 | 0.109 | 1.224 |
| LLaMA-2-13B-Chat | Autoregressive | 0.2 | 0.143 | 1.000 | 0.106 | 1.000 |
| LLaMA-2-13B-Chat | Self-Speculative | 0.2 | 0.145 | 1.383 | 0.108 | 1.210 |
| LLaMA-2-70B | Autoregressive | 0.0 | 0.130 | 1.000 | 0.118 | 1.000 |
| LLaMA-2-70B | Self-Speculative | 0.0 | 0.130 | 1.992 | 0.118 | 1.598 |
| LLaMA-2-70B | Autoregressive | 0.2 | 0.131 | 1.000 | 0.108 | 1.000 |
| LLaMA-2-70B | Self-Speculative | 0.2 | 0.131 | 1.964 | 0.110 | 1.560 |
| Model | Method | HumanEval | Speedup | |
|---|---|---|---|---|
| CodeLLaMA-13B | Autoreg. | pass@1 | 0.311 | 1.000 |
| CodeLLaMA-13B | Self-Spec. | pass@1 | 0.317 | 1.456 |
| CodeLLaMA-13B | Autoreg. | pass@10 | 0.659 | 1.000 |
| CodeLLaMA-13B | Self-Spec. | pass@10 | 0.659 | 1.345 |
We evaluate the performance of our decoding scheme, denoted as ‘Self-Speculative’, with both greedy decoding (temperature = 0.0) and random sampling (temperature = 0.2/0.6), across text and code generation. The baseline is ‘Autoregressive’, which uses the original model to perform standard autoregressive decoding. The experiments involve various scales of LLaMA-2 and its fine-tuned models. The results can be found in Tables 1 and 2. We visualize the layer skipping distribution for different models in Appendix C.
For text generation tasks, Table 1 shows that our method, when applied with temperature settings of 0.0 and 0.2 achieves considerable speedups ranging from 1.210 to 1.992. Another important observation from these results is the minimal to nonexistent loss in ROUGE-2555 We attribute any slight differences observed in the case of greedy decoding to numerical rounding errors. , which verifies a core advantage of our decoding scheme, namely consistent output quality. In Section J.1, we compare the ROUGE-2 with other mainstream LLMs and evaluate the various metrics (ROUGE-1 and ROUGE-L) to quantitatively show our output quality. Moreover, the case study in Section J.2 qualitatively presents consistent output examples. In particular, our approach can be effectively applied on LLaMA-2-13B-Chat, a fine-tuned LLaMA-2-13B for conversation scenarios, indicating the compatibility of our method with fine-tuned models. This effectively addresses the dependency of the original speculative decoding method on high-quality draft models, which can be challenging to train and obtain, especially for fine-tuned models. Furthermore, the higher speedup achieved on LLaMA-2-70B suggests that larger models introduce more redundancy. This allows the drafting stage to skip a larger percentage of intermediate layers, thereby enhancing the overall speedup.
We also tested CodeLLaMA-13B, another fine-tuned LLaMA-2-13B for code generation. We used the HumanEval benchmark. Table 2 shows that we achieve speedups of 1.345 and 1.456, respectively, while maintaining similar task scores in terms of pass@1 and pass@10. This further validates the compatibility of our scheme for coding.
4.3 Impact of Skipped Layer Selection
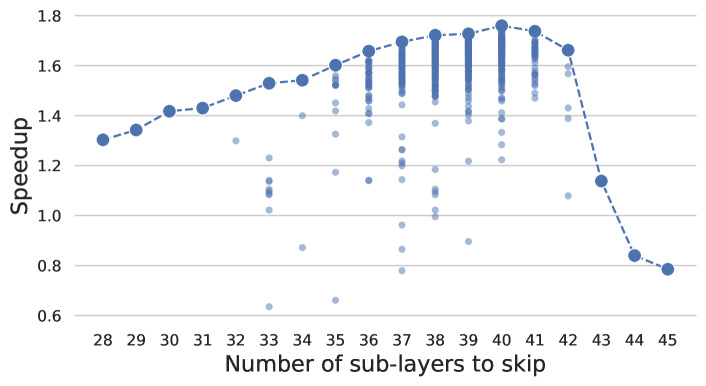
To investigate the impact of skipped layer selection, we conduct experiments on LLaMA-2-13B, which comprises 80 layers. Throughout the BO process, we track the number of layers skipped, denoted as , and the speedup relative to the autoregressive baseline. Figure 4 shows the results, where the dashed line indicates the maximum speedup for runs that skip the same number of layers.
These results reveal that: (1) The peak end-to-end speedup is observed when about half of the layers are skipped during the drafting stage; (2) The specific combination of layers skipped also plays a significant role. In particular, an inappropriate combination of skipped layers can actually result in a decrease in the end-to-end inference speed. (3) There is a noticeable drop in speedup when more than 42 layers are skipped. This suggests that the quality of drafting significantly deteriorates when an excessive number of layers are omitted.
These findings indicate the importance of layer selection in the implementation of self-speculative decoding. However, alternative layer skipping strategies do not achieve satisfactory speedup compared to BO, as detailed in Appendix D.
Performance degradation in drafting may be compensated by adopting aggressive skipping strategy and further training the draft model on a small amount of data, as described in Appendix F. This finding aligns with the Sheared-LLaMA Xia et al. (2023), which shows the effectiveness of pruning followed by fine-tuning on a small corpus.
4.4 Effectiveness of Draft-Exiting
Here we explore the effectiveness of the adaptive draft exit mechanism, specifically whether a threshold is needed and whether a static threshold is sufficient. Our settings are LLaMA-2-13B, CNN/DM, and greedy decoding.
Fixed Number of Draft Tokens. We evaluated a self-speculative decoding variant where the draft model generates a constant number of tokens. As Table 3 shows, speedup initially increases with , then decreases. This pattern arises as a large (e.g., ) produces many tokens likely to fail verification, wasting computation in drafting.
While an appropriate , e.g. , can partially alleviate this issue, a static setting limits the draft model’s potential and achieves only a modest speedup (1.44). This is because a static does not adapt to the complexity of different instances. Ideally, we should use a larger for simpler instances and a smaller for challenging ones.
Moreover, Table 3 reveals that the acceptance rate and speedup do not have a direct proportionality. For instance, when , the acceptance rate peaks at 0.924, yet the speedup is only 1.37. This discrepancy is due to the overly conservative , which underutilizes the draft model’s capacity. By generating fewer draft tokens, we miss opportunities to produce more valid draft tokens, thus limiting the overall speedup.
Draft-Exiting with Static Threshold. Another variant is to stop generating draft tokens if the confidence score falls below a predefined static threshold. Table 4 shows that different static thresholds have large differences in acceleration (1.38~1.58). This highlights the importance of adaptively determining the appropriate threshold to optimize the speedup. Specifically, we observe that high thresholds (=0.8) tend to underestimate the capabilities of the drafting model. Despite a high acceptance rate (=0.935), this does not necessarily result in the best speedup due to a reduced number of drafting tokens (1.55). Conversely, a lower threshold (=0.2) tends to overestimate the drafting model’s capabilities, leading to a significantly lower acceptance rate (=0.749), wasting computational resources during the drafting stage, and thereby leading to slower inference speed (1.38).
| 2 | 4 | 6 | 8 | Adaptive | |
|---|---|---|---|---|---|
| ROUGE-2 | 0.107 | 0.107 | 0.107 | 0.107 | 0.108 |
| 0.924 | 0.865 | 0.807 | 0.748 | 0.919 | |
| Speedup | 1.37 | 1.44 | 1.42 | 1.36 | 1.57 |
| 0.2 | 0.4 | 0.6 | 0.8 | Adaptive | |
|---|---|---|---|---|---|
| ROUGE-2 | 0.107 | 0.107 | 0.107 | 0.107 | 0.108 |
| 0.749 | 0.852 | 0.909 | 0.935 | 0.919 | |
| Speedup | 1.38 | 1.52 | 1.58 | 1.55 | 1.57 |
Draft-Exiting with Adaptive Threshold. To address the issue of optimal threshold determination, we propose an adaptive draft-exiting mechanism. Specifically, we evaluate the acceptance rate and compare it to a target acceptance rate. The threshold is updated with an updating rule depicted in Section 3.3. Table 4 shows that the speedup achieved by our adaptive threshold update method (1.57) is comparable to, if not superior to, the speedup achieved with careful tuning of static thresholds. This indicates that dynamic threshold updating yields efficient and stable inference acceleration. This is mainly because the acceptance rate gets closer to the target by adjusting the value in a timely manner for instances of varying difficulties. Also, Appendix G reveals the adaptive draft-exiting is insensitive to changes in .

4.5 Evolution of Draft-Exiting Threshold
Figure 5 captures the evolution of the draft-exiting threshold across different models and datasets over approximately 5,000 drafting and verification iterations. We can observe that our strategy adeptly adjusts the threshold, facilitating effective acceleration. However, the substantial variability across different models and datasets confirms the limitation of static threshold settings and the necessity for adaptive updates.
4.6 Breakdown of Computation
| Operation | Autoregressive | Self-Speculative |
|---|---|---|
| Drafting | - | 25.51.14 ms |
| - Attention | - | 14.60.65 ms |
| - MLP | - | 9.460.42 ms |
| Verification | - | 10.72.81 ms |
| - Attention | - | 7.551.91 ms |
| - MLP | - | 2.730.80 ms |
| update | - | 0.610.14 µs |
| Latency * | 56.31.23 ms | 36.83.23 ms |
| - Attention | 39.70.91 ms | 22.22.33 ms |
| - MLP | 14.30.29 ms | 12.21.22 ms |
Table 5 presents a computation breakdown comparing the baseline with our ‘Self-Speculative’ decoding method. Our approach exhibits a significant speedup in average inference time per token compared to ‘Autoregressive’. This speedup is primarily attributed to two key techniques: the selection of skipped layers and the adaptive draft-exiting. Notably, the drafting stage consumes the majority of inference latency, highlighting the need for draft model optimizations to improve overall inference speedup. Importantly, our adaptive exit mechanism ( update) incurs negligible computational cost as it does not involve neural network calculations.
5 Conclusion
In this paper, we introduced self-speculative decoding, a novel and efficient inference scheme that accelerates Transformer-based LLMs. Our method does not depend on additional neural network training and incurs no extra device memory, making it a highly practical and cost-effective solution for inference acceleration. Moreover, we used Bayesian optimization to search for layers to skip in drafting and proposed an adaptive draft-exiting mechanism to improve the end-to-end inference speed. Benchmark tests with LLaMA-2 and its fine-tuned models demonstrated a speedup of up to 1.99. For future work, we aim to explore more sophisticated model compression strategies to further accelerate the drafting stage for low-resource scenarios.
6 Ethical Considerations
In compliance with ethical considerations, we emphasize that the entirety of our research revolves around open-source datasets, models, and tools. Notably, we exclusively focus on improving model inference efficiency and do not engage in any commercial usage or ethical implications.
7 Limitations
While our self-speculative decoding scheme presents benefits for accelerating LLMs, there are a few limitations to consider. Firstly, the utilization of Bayesian optimization to determine the layers to be skipped during the drafting stage may require several hours. Nonetheless, this limitation is not critical, as this process is a one-time, offline execution at the model level. Secondly, our method does not involve any neural network training, which imposes a constraint on the number of layers that can be skipped. An excessive reduction in layers could result in a significant drop in the acceptance rate, thereby diminishing the achieved speedup. Although fine-tuning the draft model–a sub-graph of the original model–could potentially mitigate this issue and yield a better speedup, as shown in Appendix F, it incurs additional memory overhead since the draft model no longer shares the same parameters with the original model. In addition, we can refer to FlashAttention Dao (2023) and vLLM Kwon et al. (2023) and similar works to further adapt our technique for batched decoding.
References
- Aminabadi et al. (2022) Reza Yazdani Aminabadi, Samyam Rajbhandari, Ammar Ahmad Awan, Cheng Li, Du Li, Elton Zheng, Olatunji Ruwase, Shaden Smith, Minjia Zhang, Jeff Rasley, et al. 2022. Deepspeed-inference: Enabling efficient inference of transformer models at unprecedented scale. In 2022 SC22: International Conference for High Performance Computing, Networking, Storage and Analysis (SC), pages 646–660. IEEE Computer Society.
- Bansal et al. (2022) Hritik Bansal, Karthik Gopalakrishnan, Saket Dingliwal, Sravan Bodapati, Katrin Kirchhoff, and Dan Roth. 2022. Rethinking the role of scale for in-context learning: An interpretability-based case study at 66 billion scale. arXiv preprint arXiv:2212.09095.
- Bommasani et al. (2021) Rishi Bommasani, Drew A Hudson, Ehsan Adeli, Russ Altman, Simran Arora, Sydney von Arx, Michael S Bernstein, Jeannette Bohg, Antoine Bosselut, Emma Brunskill, et al. 2021. On the opportunities and risks of foundation models. arXiv preprint arXiv:2108.07258.
- Brown et al. (2020) Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. 2020. Language models are few-shot learners. Advances in neural information processing systems, 33:1877–1901.
- Burton (1985) F Warren Burton. 1985. Speculative computation, parallelism, and functional programming. IEEE Transactions on Computers, 100(12):1190–1193.
- Chan et al. (2022) Stephanie CY Chan, Adam Santoro, Andrew Kyle Lampinen, Jane X Wang, Aaditya K Singh, Pierre Harvey Richemond, James McClelland, and Felix Hill. 2022. Data distributional properties drive emergent in-context learning in transformers. In Advances in Neural Information Processing Systems.
- Chen et al. (2023) Charlie Chen, Sebastian Borgeaud, Geoffrey Irving, Jean-Baptiste Lespiau, Laurent Sifre, and John Jumper. 2023. Accelerating large language model decoding with speculative sampling. arXiv preprint arXiv:2302.01318.
- Cho and Hariharan (2019) Jang Hyun Cho and Bharath Hariharan. 2019. On the efficacy of knowledge distillation. In Proceedings of the IEEE/CVF international conference on computer vision, pages 4794–4802.
- Cobbe et al. (2021) Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, Christopher Hesse, and John Schulman. 2021. Training verifiers to solve math word problems. arXiv preprint arXiv:2110.14168.
- Dao (2023) Tri Dao. 2023. FlashAttention-2: Faster attention with better parallelism and work partitioning.
- Dettmers et al. (2022) Tim Dettmers, Mike Lewis, Younes Belkada, and Luke Zettlemoyer. 2022. Llm. int8 (): 8-bit matrix multiplication for transformers at scale. arXiv preprint arXiv:2208.07339.
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies.
- Fang et al. (2021) Jiarui Fang, Yang Yu, Chengduo Zhao, and Jie Zhou. 2021. Turbotransformers: an efficient gpu serving system for transformer models. In Proceedings of the 26th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, pages 389–402.
- Frantar and Alistarh (2023) Elias Frantar and Dan Alistarh. 2023. Massive language models can be accurately pruned in one-shot. arXiv preprint arXiv:2301.00774.
- Frantar et al. (2022) Elias Frantar, Saleh Ashkboos, Torsten Hoefler, and Dan Alistarh. 2022. Gptq: Accurate post-training quantization for generative pre-trained transformers. arXiv preprint arXiv:2210.17323.
- Gao et al. (2020) Leo Gao, Stella Biderman, Sid Black, Laurence Golding, Travis Hoppe, Charles Foster, Jason Phang, Horace He, Anish Thite, Noa Nabeshima, Shawn Presser, and Connor Leahy. 2020. The pile: An 800gb dataset of diverse text for language modeling. arXiv preprint arXiv:2101.00027.
- Han et al. (2015) Song Han, Huizi Mao, and William J Dally. 2015. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv preprint arXiv:1510.00149.
- He et al. (2019) Yang He, Ping Liu, Ziwei Wang, Zhilan Hu, and Yi Yang. 2019. Filter pruning via geometric median for deep convolutional neural networks acceleration. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 4340–4349.
- Hennessy and Patterson (2011) John L Hennessy and David A Patterson. 2011. Computer architecture: a quantitative approach. Elsevier.
- Hinton et al. (2015) Geoffrey Hinton, Oriol Vinyals, Jeff Dean, et al. 2015. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531, 2(7).
- Hoefler et al. (2021) Torsten Hoefler, Dan Alistarh, Tal Ben-Nun, Nikoli Dryden, and Alexandra Peste. 2021. Sparsity in deep learning: Pruning and growth for efficient inference and training in neural networks. J. Mach. Learn. Res., 22(241):1–124.
- Hou et al. (2020) Lu Hou, Zhiqi Huang, Lifeng Shang, Xin Jiang, Xiao Chen, and Qun Liu. 2020. Dynabert: Dynamic bert with adaptive width and depth. Advances in Neural Information Processing Systems, 33.
- HuggingFace (2023) HuggingFace. 2023. Text generation inference: Fast optimized inference for LLMs. https://github.com/huggingface/text-generation-inference.
- Jacob et al. (2018) Benoit Jacob, Skirmantas Kligys, Bo Chen, Menglong Zhu, Matthew Tang, Andrew Howard, Hartwig Adam, and Dmitry Kalenichenko. 2018. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 2704–2713.
- Jones et al. (1998) Donald R Jones, Matthias Schonlau, and William J Welch. 1998. Efficient global optimization of expensive black-box functions. Journal of Global optimization, 13:455–492.
- Kulal et al. (2019) Sumith Kulal, Panupong Pasupat, Kartik Chandra, Mina Lee, Oded Padon, Alex Aiken, and Percy S Liang. 2019. Spoc: Search-based pseudocode to code. Advances in Neural Information Processing Systems, 32.
- Kwon et al. (2023) Woosuk Kwon, Zhuohan Li, Siyuan Zhuang, Ying Sheng, Lianmin Zheng, Cody Hao Yu, Joseph E. Gonzalez, Hao Zhang, and Ion Stoica. 2023. Efficient memory management for large language model serving with pagedattention. In Proceedings of the ACM SIGOPS 29th Symposium on Operating Systems Principles.
- Leviathan et al. (2023) Yaniv Leviathan, Matan Kalman, and Yossi Matias. 2023. Fast inference from transformers via speculative decoding. In International Conference on Machine Learning, pages 19274–19286. PMLR.
- Li et al. (2021) Xiaonan Li, Yunfan Shao, Tianxiang Sun, Hang Yan, Xipeng Qiu, and Xuanjing Huang. 2021. Accelerating BERT inference for sequence labeling via early-exit. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics.
- Liang et al. (2022) Percy Liang, Rishi Bommasani, Tony Lee, Dimitris Tsipras, Dilara Soylu, Michihiro Yasunaga, Yian Zhang, Deepak Narayanan, Yuhuai Wu, Ananya Kumar, et al. 2022. Holistic evaluation of language models. arXiv preprint arXiv:2211.09110.
- Liao et al. (2021) Kaiyuan Liao, Yi Zhang, Xuancheng Ren, Qi Su, Xu Sun, and Bin He. 2021. A global past-future early exit method for accelerating inference of pre-trained language models. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pages 2013–2023.
- Lin (2004) Chin-Yew Lin. 2004. Rouge: A package for automatic evaluation of summaries. In Text summarization branches out, pages 74–81.
- Liu et al. (2020) Weijie Liu, Peng Zhou, Zhiruo Wang, Zhe Zhao, Haotang Deng, and Qi Ju. 2020. Fastbert: a self-distilling BERT with adaptive inference time. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics.
- Liu et al. (2018) Zhuang Liu, Mingjie Sun, Tinghui Zhou, Gao Huang, and Trevor Darrell. 2018. Rethinking the value of network pruning. arXiv preprint arXiv:1810.05270.
- Liu et al. (2023) Zichang Liu, Jue Wang, Tri Dao, Tianyi Zhou, Binhang Yuan, Zhao Song, Anshumali Shrivastava, Ce Zhang, Yuandong Tian, Christopher Re, et al. 2023. Deja vu: Contextual sparsity for efficient llms at inference time. In International Conference on Machine Learning, pages 22137–22176. PMLR.
- Min et al. (2022) Sewon Min, Xinxi Lyu, Ari Holtzman, Mikel Artetxe, Mike Lewis, Hannaneh Hajishirzi, and Luke Zettlemoyer. 2022. Rethinking the role of demonstrations: What makes in-context learning work? arXiv preprint arXiv:2202.12837.
- Molchanov et al. (2016) Pavlo Molchanov, Stephen Tyree, Tero Karras, Timo Aila, and Jan Kautz. 2016. Pruning convolutional neural networks for resource efficient inference. arXiv preprint arXiv:1611.06440.
- Nagel et al. (2019) Markus Nagel, Mart van Baalen, Tijmen Blankevoort, and Max Welling. 2019. Data-free quantization through weight equalization and bias correction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 1325–1334.
- (39) NVIDIA. Fastertransformer. https://github.com/NVIDIA/FasterTransformer.
- Park et al. (2022) Gunho Park, Baeseong Park, Se Jung Kwon, Byeongwook Kim, Youngjoo Lee, and Dongsoo Lee. 2022. nuqmm: Quantized matmul for efficient inference of large-scale generative language models. arXiv preprint arXiv:2206.09557.
- Pope et al. (2022) Reiner Pope, Sholto Douglas, Aakanksha Chowdhery, Jacob Devlin, James Bradbury, Anselm Levskaya, Jonathan Heek, Kefan Xiao, Shivani Agrawal, and Jeff Dean. 2022. Efficiently scaling transformer inference. arXiv preprint arXiv:2211.05102.
- Raffel et al. (2020) Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J. Liu. 2020. Exploring the limits of transfer learning with a unified text-to-text transformer. Journal of Machine Learning Research, 21.
- Rasmussen et al. (2006) Carl Edward Rasmussen, Christopher K Williams, et al. 2006. Gaussian processes for machine learning, vol. 1.
- Rozière et al. (2023) Baptiste Rozière, Jonas Gehring, Fabian Gloeckle, Sten Sootla, Itai Gat, Xiaoqing Ellen Tan, Yossi Adi, Jingyu Liu, Tal Remez, Jérémy Rapin, Artyom Kozhevnikov, I. Evtimov, Joanna Bitton, Manish P Bhatt, Cristian Canton Ferrer, Aaron Grattafiori, Wenhan Xiong, Alexandre D’efossez, Jade Copet, Faisal Azhar, Hugo Touvron, Louis Martin, Nicolas Usunier, Thomas Scialom, and Gabriel Synnaeve. 2023. Code llama: Open foundation models for code. arXiv preprint arXiv:2308.12950.
- Schuster et al. (2022) Tal Schuster, Adam Fisch, Jai Gupta, Mostafa Dehghani, Dara Bahri, Vinh Tran, Yi Tay, and Donald Metzler. 2022. Confident adaptive language modeling. Advances in Neural Information Processing Systems, 35.
- Schwartz et al. (2020) Roy Schwartz, Gabriel Stanovsky, Swabha Swayamdipta, Jesse Dodge, and Noah A. Smith. 2020. The right tool for the job: Matching model and instance complexities. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics.
- Shazeer (2019) Noam Shazeer. 2019. Fast transformer decoding: One write-head is all you need. arXiv preprint arXiv:1911.02150.
- Sheng et al. (2023) Ying Sheng, Lianmin Zheng, Binhang Yuan, Zhuohan Li, Max Ryabinin, Daniel Y Fu, Zhiqiang Xie, Beidi Chen, Clark Barrett, Joseph E Gonzalez, et al. 2023. High-throughput generative inference of large language models with a single gpu. arXiv preprint arXiv:2303.06865.
- Stern et al. (2018) Mitchell Stern, Noam Shazeer, and Jakob Uszkoreit. 2018. Blockwise parallel decoding for deep autoregressive models. Advances in Neural Information Processing Systems, 31.
- Sun et al. (2023) Mingjie Sun, Zhuang Liu, Anna Bair, and J. Zico Kolter. 2023. A simple and effective pruning approach for large language models. arXiv preprint arXiv:2306.11695.
- Sun et al. (2022) Tianxiang Sun, Xiangyang Liu, Wei Zhu, Zhichao Geng, Lingling Wu, Yilong He, Yuan Ni, Guotong Xie, Xuanjing Huang, and Xipeng Qiu. 2022. A simple hash-based early exiting approach for language understanding and generation. In Findings of the Association for Computational Linguistics: ACL 2022.
- Tang et al. (2019) Raphael Tang, Yao Lu, Linqing Liu, Lili Mou, Olga Vechtomova, and Jimmy Lin. 2019. Distilling task-specific knowledge from bert into simple neural networks. arXiv preprint arXiv:1903.12136.
- Touvron et al. (2021) Hugo Touvron, Matthieu Cord, Matthijs Douze, Francisco Massa, Alexandre Sablayrolles, and Hervé Jégou. 2021. Training data-efficient image transformers & distillation through attention. In International Conference on Machine Learning, pages 10347–10357. PMLR.
- Touvron et al. (2023) Hugo Touvron, Louis Martin, Kevin Stone, Peter Albert, Amjad Almahairi, Yasmine Babaei, Nikolay Bashlykov, Soumya Batra, Prajjwal Bhargava, Shruti Bhosale, et al. 2023. Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288.
- Wang et al. (2021) Xiaohui Wang, Ying Xiong, Yang Wei, Mingxuan Wang, and Lei Li. 2021. Lightseq: A high performance inference library for transformers. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies: Industry Papers, pages 113–120.
- Xia et al. (2023) Mengzhou Xia, Tianyu Gao, Zhiyuan Zeng, and Danqi Chen. 2023. Sheared LLaMA: Accelerating language model pre-training via structured pruning.
- Xiao et al. (2022) Guangxuan Xiao, Ji Lin, Mickael Seznec, Julien Demouth, and Song Han. 2022. Smoothquant: Accurate and efficient post-training quantization for large language models. arXiv preprint arXiv:2211.10438.
- Xin et al. (2020a) Ji Xin, Rodrigo Nogueira, Yaoliang Yu, and Jimmy Lin. 2020a. Early exiting BERT for efficient document ranking. In Proceedings of SustaiNLP: Workshop on Simple and Efficient Natural Language Processing.
- Xin et al. (2020b) Ji Xin, Raphael Tang, Jaejun Lee, Yaoliang Yu, and Jimmy Lin. 2020b. DeeBERT: Dynamic early exiting for accelerating BERT inference. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics.
- Yang et al. (2023) Nan Yang, Tao Ge, Liang Wang, Binxing Jiao, Daxin Jiang, Linjun Yang, Rangan Majumder, and Furu Wei. 2023. Inference with reference: Lossless acceleration of large language models. arXiv preprint arXiv:2304.04487.
- Yao et al. (2022) Zhewei Yao, Reza Yazdani Aminabadi, Minjia Zhang, Xiaoxia Wu, Conglong Li, and Yuxiong He. 2022. Zeroquant: Efficient and affordable post-training quantization for large-scale transformers. arXiv preprint arXiv:2206.01861.
- Yu et al. (2022) Gyeong-In Yu, Joo Seong Jeong, Geon-Woo Kim, Soojeong Kim, and Byung-Gon Chun. 2022. Orca: A distributed serving system for Transformer-Based generative models. In 16th USENIX Symposium on Operating Systems Design and Implementation (OSDI 22), pages 521–538.
- Zhao et al. (2019) Ritchie Zhao, Yuwei Hu, Jordan Dotzel, Chris De Sa, and Zhiru Zhang. 2019. Improving neural network quantization without retraining using outlier channel splitting. In International conference on machine learning, pages 7543–7552. PMLR.
- Zheng et al. (2023) Lianmin Zheng, Wei-Lin Chiang, Ying Sheng, Siyuan Zhuang, Zhanghao Wu, Yonghao Zhuang, Zi Lin, Zhuohan Li, Dacheng Li, Eric. P Xing, Hao Zhang, Joseph E. Gonzalez, and Ion Stoica. 2023. Judging llm-as-a-judge with mt-bench and chatbot arena.
- Zhou et al. (2020) Wangchunshu Zhou, Canwen Xu, Tao Ge, Julian McAuley, Ke Xu, and Furu Wei. 2020. Bert loses patience: Fast and robust inference with early exit. Advances in Neural Information Processing Systems, 33.
- Zhu (2021) Wei Zhu. 2021. Leebert: Learned early exit for bert with cross-level optimization. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics.
Appendix A Data
The datasets that we have selected for evaluation are CNN/Daily Mail (CNN/DM), Extreme Summarization (XSum), and HumanEval. These tasks cover a broad spectrum of language processing capabilities, including text and code generation capabilities. We perform 1-shot evaluation for CNN/DM and XSum, and compare the ROUGE-2. We compare pass@10 for HumanEval. For the results of efficiency, we randomly sample 1000 instances from the testset for CNN/DM and XSum.
CNN/Daily Mail (CNN/DM):
This task involves summarizing news articles from the CNN and Daily Mail websites. The models are required to generate a concise summary of each article, testing their ability to understand and condense complex information.
Extreme Summarization (XSum):
In the XSum task, models are asked to produce a single-sentence summary of a news article. This task tests the models’ capability to extract the most salient information from a text and express it in a single, coherent sentence.
HumanEval:
The HumanEval task is a benchmark for Python programming. This task challenges the models with a variety of coding problems that require a wide range of skills, from basic programming to complex problem-solving abilities. It serves to evaluate the models’ understanding of Python syntax, their ability to implement algorithms, and their proficiency in problem-solving using code. This benchmark provides a unique perspective on the models’ capabilities in the realm of programming, complementing the language-focused tasks.
Appendix B Setup
We present the hyperparameter settings of the experiments in Table 6, including the parameters involved in the decoding process, the adaptive draft-exiting mechanism, and the random sampling. For the adaptive draft-exiting mechanism, we set the initial threshold , , , , and is slightly tuned for the data and model, as detailed in Table 6. For sampling-based inference, we by default use for text summarization tasks, and for code generation tasks.
In addition, the key experimental environments on the A100-40GB are CUDA 11.6, PyTorch 1.13.1, and Transformer 4.33.1; For the A100-80GB, the environment is CUDA 11.8, PyTorch 2.0.1, and Transformer 4.33.1. We use an A100-40GB to conduct experiments for LLaMA-2-13B, LLaMA-2-13B-Chat, and CodeLLaMA-13B. We use two A100-80GB with HuggingFace’s accelerate666 https://github.com/huggingface/accelerate (Apache-2.0 License) to conduct experiments for LLaMA-2-70B.
We randomly select 8 instances from the train set and use them to evaluate the inference time per token for Bayesian optimization. This randomness not only ensures the generalizability of our approach but also mitigates any potential bias that could be introduced by the data selection process. The offline Bayesian optimization time for 1000 iterations is about 2.5 hours for LLaMA-2-13B, LLaMA-2-13B-Chat, and CodeLLaMA-13B, and about 6 hours for LLaMA-2-70B.
| Data | Model | Decoding | Adaptive Draft-Exiting | Random Sampling | ||||||
| temperature | ||||||||||
| CNN/DM | LLaMA-2-13B | 512 | 12 | 0.90 | 0.01 | 0.50 | 0.90 | 0.60 | 0.85 | 0.20 |
| CNN/DM | LLaMA-2-13B-Chat | 512 | 12 | 0.85 | 0.01 | 0.50 | 0.90 | 0.60 | 0.85 | 0.20 |
| CNN/DM | LLaMA-2-70B | 512 | 12 | 0.85 | 0.01 | 0.50 | 0.90 | 0.60 | 0.85 | 0.20 |
| XSum | LLaMA-2-13B | 512 | 12 | 0.85 | 0.01 | 0.50 | 0.90 | 0.60 | 0.85 | 0.20 |
| XSum | LLaMA-2-13B-Chat | 512 | 12 | 0.70 | 0.01 | 0.50 | 0.90 | 0.60 | 0.85 | 0.20 |
| XSum | LLaMA-2-70B | 512 | 12 | 0.85 | 0.01 | 0.50 | 0.90 | 0.60 | 0.85 | 0.20 |
| HumanEval | CodeLLaMA-13B | 512 | 12 | 0.90 | 0.01 | 0.50 | 0.90 | 0.60 | 0.95 | 0.60 |
| GSM8K | CodeLLaMA-13B | 512 | 12 | 0.90 | 0.01 | 0.50 | 0.90 | 0.60 | 0.95 | 0.60 |
| GSM8K | CodeLLaMA-13B-Instruct | 512 | 12 | 0.80 | 0.01 | 0.50 | 0.90 | 0.60 | 0.95 | 0.60 |
| MT-bench | LLaMA-2-13B-Chat | 512 | 12 | 0.85 | 0.01 | 0.50 | 0.90 | 0.60 | 0.85 | 0.20 |





| Strategy | First | Mid. | Last | Rand. | BO |
|---|---|---|---|---|---|
| ROUGE-2 | 0.108 | 0.108 | 0.107 | 0.107 | 0.108 |
| 0.091 | 0.393 | 0.508 | 0.592 | 0.919 | |
| Speedup | 0.696 | 0.887 | 0.951 | 1.01 | 1.57 |
| #Iteration | 200 | 400 | 600 | 800 | 1000 |
|---|---|---|---|---|---|
| ROUGE-2 | 0.108 | 0.107 | 0.108 | 0.108 | 0.108 |
| 0.903 | 0.938 | 0.920 | 0.919 | 0.919 | |
| Speedup | 1.35 | 1.52 | 1.58 | 1.57 | 1.57 |
| #Token | 0 | 20M | 40M | 60M | 75M |
|---|---|---|---|---|---|
| ROUGE-2 | 0.106 | 0.106 | 0.106 | 0.106 | 0.106 |
| 0.695 | 0.902 | 0.901 | 0.900 | 0.893 | |
| Speedup | 1.15 | 1.91 | 1.94 | 1.96 | 1.85 |
| 10 | 12 | 14 | 16 | 18 | |
|---|---|---|---|---|---|
| ROUGE-2 | 0.107 | 0.108 | 0.108 | 0.108 | 0.107 |
| 0.924 | 0.919 | 0.916 | 0.913 | 0.911 | |
| Speedup | 1.57 | 1.57 | 1.58 | 1.58 | 1.58 |
Appendix C Which layers are skipped?
Figure 6 visualizes the distinct base models corresponding to layer skip distributions within the draft model. Two key observations are made as follows:
First, we observe that there are more skips in the attention layer compared to the MLP layer, suggesting the attention layer is more effective for reducing inference time. This is reinforced by the results in Table 5, where the time spent in the attention layer significantly contributes to the average inference latency per token.
Second, regardless of whether it is the MLP layer or the attention layer, the skipped layers tend to cluster in the latter half of the model. This pattern suggests that most tokens can be accurately predicted in the first half of the model, leaving the second half of the model relatively redundant.
Appendix D Effect of Skip Strategy
Here, we explore the effect of various skip strategies on the performance of generated draft models. We evaluate the CNN/DM on LLaMA-2-13B. Initially, we determine the number of skipped layers using Bayesian optimization, as illustrated in Figure 6(a). We find that the attention layer skips 24 layers, while the MLP layer skips 12 layers. We proceed to apply four strategies, each involving an equal number of layer skips: skipping the initial layers ("First"), middle layers ("Mid."), final layers ("Last"), and randomly sampling layers ("Rand."). The layer skip distribution is visualized in Figure 7.
Table 7 reveals that the fixed strategies of layer skip (first, middle, last) or random skip yield minimal acceleration compared to Bayesian optimization (BO) results. These suboptimal strategies, not optimized for average inference time, result in a draft model with subpar performance (manifested as very low ), inefficient resource utilization in the drafting phase, and ultimately, a lack of speedup. Furthermore, a slightly enhanced speedup is observed when skipping the last layers, likely due to the more severe redundancy in the model’s final portion.
Appendix E Number of Iterations of BO
Subsequently, we explore the influence of the iteration number of Bayesian optimization on the performance of our decoding scheme and report the results in Table 8. The layer skip distribution corresponding to different iteration numbers is depicted in Figure 8.
When applied to the LLaMA-2-13B for the CNN/DM task, we observe that while a higher number of iterations can yield increased acceleration, even a relatively modest number of iterations (e.g., 200) effectively reduces inference time, achieving a speedup of 1.35. Notably, the performance metrics for the 800 and 1000 iterations exhibit consistency due to the same layers being skipped, as shown in Figure 8.
Appendix F Aggressive Skip
In pursuit of higher inference acceleration for users with ample resources, we explore a more aggressive skip strategy to obtain the draft model. To mitigate the performance degradation associated with the aggressive skip, we further train the draft model using 50,000 instances from the Pile dataset Gao et al. (2020), truncating the length of each to 512 tokens, which total up to 25 million tokens. We repeat this training for 3 epochs, resulting in a cumulative utilization of 75 million tokens.
The implementation of the aggressive skip involves skipping the top-K layers based on Bayesian optimization probabilities. For instance, in the case of LLaMA-2-13B, as illustrated in Figure 9, we opt to skip 75% of the attention layers (30 layers) and 32.5% of the MLP layers (13 layers).
Table 9 reveals that when we employ a more aggressive skip without further training (#token is 0), there is a noticeable decrease in the draft model’s quality, with an average acceptance rate of only 0.695. This leads to a significantly reduced speedup of merely 1.15. Nevertheless, by dedicating a portion of the corpus to training, we notably enhance the draft model’s quality, increasing the to 0.900, in line with the target acceptance rate of 0.90. This enhancement enables a further improvement in speedup from 1.57 (shown in Table 1) to 1.96 (trained for 60M tokens), as more layers are skipped777 This finding aligns with the recent Sheared-LLaMA Xia et al. (2023), which shows the effectiveness of pruning followed by further training on a small amount of data.. After training on 75 million tokens, the reason for the reduced acceleration is that we believe the model has a certain degree of overfitting. It is essential to highlight that the aggressive skip strategy necessitates both an extended training process and the additional storage of trained draft models. However, this trade-off is deemed acceptable for users with rich resources.
Appendix G Effect of Max # of Draft Tokens
Ideally, increasing the maximum number of draft tokens while maintaining a high acceptance rate should lead to further improvements in inference acceleration. To explore this, we test the CNN/DM task using LLaMA-2-13B, varying the max draft token , and present the results in Table 10. It is noteworthy that as increases, the speedup remains relatively stable. This observation is primarily attributed to the fact that most tokens do not benefit from excessively large and tend to exit early. In summary, our inference approach shows insensitivity to thanks to the adaptive draft-exiting mechanism. Moreover, setting a relatively large value for (our default is 12) allows this mechanism to perform optimally.
| Quantization | bf16 | fp8 | fp4 | nf4 |
|---|---|---|---|---|
| ROUGE-2 | 0.107 | 0.105 | 0.101 | 0.114 |
| 0.910 | 0.911 | 0.913 | 0.910 | |
| VRAM (GB) | 37.2 | 27.5 | 19.6 | 19.7 |
| Latency (ms) | 32.4 | 113 | 152 | 126 |
| Speedup | 1.53 | 1.61 | 1.36 | 1.35 |
Appendix H Adaptation
We here adopt skipping intermediate layers as a simple yet effective strategy to expedite the drafting stage. While other acceleration techniques such as quantization and structured pruning exist, they fail to offer speed-up proportional to their compression ratio. Meanwhile, they require a separate copy of the altered model parameters, thereby increasing memory overhead. This contradicts the key requirement of no extra memory. Consequently, we adopt layer skipping in our approach. However, our scheme can be integrated with quantization Dettmers et al. (2022) and sparsification Sun et al. (2023) to further reduce resource consumption. In this section, we explore the combination of self-speculative decoding with quantization and sparsification techniques to adapt to users with limited computing resources. We conduct experiments on the CNN/DM task using LLaMA-2-13B, and the layer skip distribution corresponding to the draft model is shown in Figure 10.
H.1 Quantization
First, we integrate our inference approach with the quantization technique, LLM.int8()888https://github.com/TimDettmers/bitsandbytes (MIT License) Dettmers et al. (2022). We evaluate the performance of three quantization schemes: fp8 (8-bit floating-point), fp4 (4-bit floating-point), and nf4 (4-bit normalized float), in comparison to the default bf16 (16-bit brain float point). The results are presented in Table 11. In all quantization settings, we skip the ‘lm head’ layer of the model and do not employ double quantization to save an additional 0.4 bits.
Table 11 illustrates that all three quantization schemes effectively reduce the video memory demand during inference. Notably, the fp4 quantization results in up to a nearly two-fold reduction in memory demand to just 19.6 GB. While there may be an increase in the average inference latency per token due to the dequantization process, this approach makes LLM suitable for scenarios with limited device memory.
| Sparsification | dense | unstructured | 4:8 | 2:4 |
|---|---|---|---|---|
| ROUGE-2 | 0.107 | 0.114 | 0.115 | 0.110 |
| 0.910 | 0.918 | 0.912 | 0.911 | |
| VRAM (GB) | 37.2 | 35.9 | 35.9 | 35.9 |
| Latency (ms) | 32.4 | 30.4 | 29.2 | 30.9 |
| Speedup | 1.57 | 1.50 | 1.47 | 1.48 |
H.2 Sparsification
Subsequently, we assess the performance of self-speculative decoding combined with sparsification techniques, specifically wanda999https://github.com/locuslab/wanda (MIT License) Sun et al. (2023), which includes unstructured sparsity and structured N:M sparsity (4:8 and 2:4) with the sparsity ratio of 0.5. The N:M sparsity constraint specifies that no more than N out of every M contiguous weights can be non-zero.
Table 12 shows that while sparsification may not dramatically reduce VRAM requirements, it does result in a reduction in the average inference latency per token to varying degrees. However, the speedup is slightly down because the base model is also accelerated.
| Data | Model | Method | Perfor. | Speedup |
|---|---|---|---|---|
| GSM8K | CodeLLaMA-13B | Autoreg. | 0.104 | 1.000 |
| GSM8K | CodeLLaMA-13B | Self-Spec. | 0.101 | 1.351 |
| GSM8K | CodeLLaMA-13B-Ins. | Autoreg. | 0.223 | 1.000 |
| GSM8K | CodeLLaMA-13B-Ins. | Self-Spec. | 0.213 | 1.263 |
| MT-bench | LLaMA-2-13B-Chat | Autoreg. | 6.940 | 1.000 |
| MT-bench | LLaMA-2-13B-Chat | Self-Spec. | 6.930 | 1.269 |
Appendix I Exploration of Diverse Tasks
We want to mention that our approach does not require model fine-tuning and its lossless characteristic is task-agnostic. However, we are open to evaluating the effectiveness of our approach on more diverse tasks. Here, we further explore the performance of our decoding scheme on solving math problems (Grade School Math 8K Cobbe et al. (2021)) and open-domain chitchat (MT-bench Zheng et al. (2023)). For GSM8K, we evaluate on base model CodeLLaMA-13B and CodeLLaMA-13B-Instruct and report the problem-solving accuracy of 1318 questions in the test set. For MT-bench, our base model is LLaMA-2-13B-Chat, and we use its program script to ask GPT-4 to give a score of 10 points for each round using their prompt templates and report the average score for a total of 160 answers for two turns of 80 questions.
Grade School Math 8K (GSM8K):
A dataset of 8.5K high-quality linguistically diverse grade school math word problems. The dataset was created to support the task of question answering on basic mathematical problems that require multi-step reasoning. Solutions primarily involve performing a sequence of elementary calculations using basic arithmetic operations (+-×÷) to reach the final answer. This task is generally used to test logic and math in language modeling.
MT-bench:
A benchmark consisting of 80 high-quality multi-turn questions. MT-bench is designed to test multi-turn conversation and instruction-following ability, covering common use cases and focusing on challenging questions to differentiate models. The tasks identify 8 common categories of user prompts to guide its construction: writing, roleplay, extraction, reasoning, math, coding, knowledge I (STEM), and knowledge II (humanities/social science). For each category, The task manually designed 10 multi-turn questions.
Regarding using Bayesian optimization 1,000 iterations to generate a draft model, for GSM8K, we randomly sampled 4 samples from the training set as a development set; for MT-bench, we let GPT-3.5 generate 8 examples according to 8 topics to form an optimized use development set. Other relevant hyperparameters are shown in Table 6.
For GSM8K, we achieve a 1.35 acceleration without compromising task performance. Regarding MT-bench, spanning writing, roleplay, reasoning, math, coding, extraction, stem, and humanities, presents substantial task diversity, posing challenges for generating high-quality and diverse output from draft models. Nevertheless, we still achieve a speedup of about 1.27 with lossless task performance. These findings demonstrate the robustness and commendable performance of our approach across diverse tasks.
Appendix J Exploration of Output Quality
J.1 Quantitative Analysis
LLMs Comparison. Considering this non-fine-tuned, one-shot setting, our score is indeed quite competitive. We attach in Table 14 the performance of other mainstream large language models on CNN/DM and XSum as a reference (data from HELM leaderboard Liang et al. (2022)).
| Model | CNN/DM | XSum |
|---|---|---|
| LLaMA-2-13B (ours) | 0.106 | 0.124 |
| LLaMA-2-13B-Chat (ours) | 0.144 | 0.109 |
| LLaMA-2-70B (ours) | 0.130 | 0.118 |
| OPT (66B) | 0.136 | 0.126 |
| Davinci (175B) | 0.127 | 0.126 |
| Palmyra X (43B) | 0.049 | 0.149 |
| GPT-NeoX (20B) | 0.123 | 0.102 |
| Luminous Base (13B) | 0.110 | 0.105 |
| BLOOM (176B) | 0.080 | 0.030 |
| YaLM (100B) | 0.017 | 0.021 |
| Model | Method | ROUGE | Speedup | ||
|---|---|---|---|---|---|
| 1 | 2 | L | |||
| CNN/DM | Autoreg. | 0.263 | 0.106 | 0.181 | 1.000 |
| CNN/DM | Self-Spec. | 0.266 | 0.108 | 0.183 | 1.429 |
| XSum | Autoreg. | 0.327 | 0.124 | 0.260 | 1.000 |
| XSum | Self-Spec. | 0.328 | 0.125 | 0.261 | 1.377 |
Diverse Metrics. Our experimental setup mainly follows the work of DeepMind Chen et al. (2023). For summarization tasks, ROUGE-2 is a widely recognized evaluation metric, as adopted by Chen et al. (2023); Liang et al. (2022), in addition to ROUGE-1 and ROUGE-L. However, we want to emphasize that we have not disregarded the importance of other metrics such as ROUGE-1 and ROUGE-L. Indeed, we have maintained records of these results as part of our comprehensive analysis, and we will attach them in the appendix in the revision. The results are presented below. And we can see that our conclusions remain consistent – we have been successful in achieving a significant acceleration in task performance without compromising the quality of the outputs. We believe this reaffirms the robustness and efficacy of our approach.
J.2 Qualitative Analysis
We present more qualitative evidence to supplement the quantitative ROUGE-2 score. Please note, however, that our approach is inherently lossless and the performance evaluation is conducted on the original model without any fine-tuning. The task performance of our self-speculative decoding is therefore reliant on the inherent capabilities of the base model utilizing autoregressive decoding. Specifically, using the same base model, in the greedy setting, generation results from self-speculative decoding are identical to those of autoregressive decoding; In the sampling setting, the results generated are from the same distribution as those for autoregressive decoding. These properties of speculative decoding have been mathematically proven in previous work Leviathan et al. (2023). Finally, to address concerns, we present a case study on LLaMA-2-13B, detailed in the Table 16.
Appendix K Algorithm with Sampling
| Data | Temp. | Article/Document | Summary/Highlight | ||
|---|---|---|---|---|---|
| Reference | Autoregressive | Self-Speculative | |||
| CNN/DM | 0.0 | An Arkansas woman became a little richer this week after finding a large diamond at Crater of Diamonds State Park. Susie Clark, of Evening Shade, found the 3.69-carat white diamond in a 37.5-acre search field on Thursday, her last day of a trip to the park with her husband. Clark, | Susie Clark, of Evening Shade, Arkansas, found the diamond on Thursday at Crater of Diamonds State Park . The 3.69-carat gem is teardrop-shaped about the size of a pinto bean . Park interpreter said it’s the largest of the 122 diamonds found this year . | woman who found a 3.69-carat white diamond at Crater of Diamonds State Park in Arkansas has named the gem a ’hallelujah diamond’ because she spotted the gem shortly after praying that she would find something . | woman who found a 3.69-carat white diamond at Crater of Diamonds State Park in Arkansas has named the gem a ’hallelujah diamond’ because she spotted the gem shortly after praying that she would find something . |
| CNN/DM | 0.2 | who first visited the park 33 years ago with her mother and grandmother, prayed to God, asking, ’Are you doing to bless me and let me find a diamond today?’ as she searched the field. Susie Clark, of Evening Shade, Arkansas, found a 3.69-carat white … | Susie Clark, of Evening Shade, Arkansas, found the diamond on Thursday at Crater of Diamonds State Park . The 3.69-carat gem is teardrop-shaped about the size of a pinto bean . Park interpreter said it’s the largest of the 122 diamonds found this year . | woman who found a 3.69-carat diamond at Crater of Diamonds State Park in Arkansas has named the gem a ’hallelujah diamond’ because she spotted the gem shortly after praying that she would find something . | woman who found a 3.69-carat white diamond at Crater of Diamonds State Park in Arkansas has named the gem a ’hallelujah diamond’ because she spotted the gem shortly after praying that she would find something . |
| XSum | 0.0 | The flight provider operates a "bug bounty" scheme that rewards hackers for privately disclosing security flaws rather than sharing them | US airline United has rewarded two hackers who spotted security holes in its website with a million free flight miles each. | Airlines has given out its first rewards to hackers who reported security flaws in its website. | Airlines has given out its first rewards to hackers who reported security flaws in its website. |
| XSum | 0.2 | online. It has given the maximum reward of a million flight miles, worth dozens of trips, to two people. One security expert said the … | US airline United has rewarded two hackers who spotted security holes in its website with a million free flight miles each. | airline has given out two million flight miles to hackers who found security flaws in its website. | airline has given the maximum reward of a million flight miles, worth dozens of trips, to two people. |
We first demonstrate self-speculative sampling with greedy sampling by integrating the adaptive draft-exiting mechanism in Algorithm 3.
In addition to the greedy version of self-speculative decoding that we have presented in the main paper, we also explore a variant that incorporates random sampling, that also incorporated a complete adaptive draft-exiting mechanism, as shown in Algorithm 4. This approach introduces an element of randomness into the selection of tokens for speculative decoding, as opposed to the deterministic nature of the greedy version. In our setup, random sampling is affected by two parameters: temperature and . Higher values of temperature or lead to greater token diversity, while lower values make token selection more deterministic. This variant could potentially lead to diverse decoding paths and outcomes, which may be beneficial in certain scenarios, such as code generation.











