Double universality of the transition in the supercritical state
Abstract
Universality aids consistent understanding of physical properties. This includes understanding the states of matter where a theory predicts how a property of a phase (solid, liquid, gas) changes with temperature or pressure. Here, we show that the matter above the critical point has a remarkable double universality not limited by pressure and temperature. The first universality is the transition between the liquidlike and gaslike states seen in the crossover of the specific heat on the dynamical length scale in deeply supercritical state and characterised by a fixed inversion point. The second universality is the operation of this effect in many supercritical fluids, including N2, CO2, Pb, H20 and Ar. Despite the differences in structure and chemical bonding in these fluids, the transition has the same fixed inversion point deep in the supercritical state. This provides new understanding of the supercritical state previously considered to be a featureless area on the phase diagram and a theoretical guide for improved and more efficient deployment of supercritical fluids in green and environmental applications.
I Introduction
Our view of the phase diagram of ordinary matter is dominated by the three states of solid, liquid, and gas, and the first order phase transition lines between them which branch out from the triple point. Of these phase transitions, two possess coexistence lines which are finite in length, including the solid-gas sublimation line and the liquid-gas boiling line terminating at the critical point. The matter above the critical point, the supercritical matter, was not thought of as a distinct state of matter, instead seen as a homogeneous state intermediate to liquids and gases and lacking transitions. In particular, distinction between liquidlike and gaslike states within this region was thought to be impossible Landau and Lifshitz (1970); Kiran et al. (2000). Critical anomalies such as the heat capacity maxima do not persist far beyond the critical point and furthermore depend on the path taken on the phase diagram Xu et al. (2005); Proctor and Maynard-Casely (2020). Understanding both the supercritical and liquid states involves several fundamental problems related to dynamical disorder and strong inter-molecular interactions Landau and Lifshitz (1970); Proctor and Maynard-Casely (2020); Proctor (2020); Wallace (1998); Chen (2022); Trachenko and Brazhkin (2016). Yet such understanding is believed to enhance the deployment of supercritical fluids in important green and environmental applications Eckert et al. (1996); Sarbu et al. (2000); Akiya and Savage (2002); Savage (1999); Huelsman and Savage (2013); Kiran et al. (2000).
The Frenkel line separates two qualitatively dynamical regimes of particle motion: combined oscillatory and diffusive motion below the line and purely diffusive above the line Cockrell et al. (2021a). Practically, the line is calculated from either the dynamical criterion based on the minima of velocity autocorrelation function or the thermodynamic criterion based on the disappearance of transverse modes. This separation of the supercritical state into two different states involves a physical model. It is interesting to ask whether this separation can also be done in a way which is model-free? A related question is whether the separation involves universality across all supercritical systems in terms of suitably identified physical parameters?
Here, we show that deeply supercritical state has a clearly identifiable transition between liquidlike and gaslike states seen in the dependence of the specific heat on the dynamical length which is doubly-universal. The first universality is a fixed path-independent inversion point of the crossover, seen as the change of the sign of the derivative of with respect to . The second universality is that the location of the inversion point is similar in all simulated fluids, including supercritical N2, CO2, Pb, Ar and to some extent in H2O. Supercritical water has an anomaly, displaying similarities but also differences to the other systems in which the universal transition is identified. The inversion point therefore constitutes a system-independent, path-independent, and an unambiguous separation between two physically distinct supercritical states.
II Results and Discussion
II.1 Specific heat and dynamical length
Using molecular dynamics simulations (see the “Methods” section for detail), we have simulated several fluids with different structure and chemical bonding in order to ascertain the effect in a wide range of systems. We simulate molecular (N2, CO2), metallic (Pb), hydrogen-bonded network fluid (H2O) and noble Ar. Supercritical CO2 and H2O are particularly important from the industrial point of view due to their deployment in extracting, cleaning, dissolving, environmental and green energy applications Akiya and Savage (2002); Savage (1999); Huelsman and Savage (2013); Kiran et al. (2000). We simulate these fluids along several isobars, isotherms, and isochores in the deep supercritical state.
We zero in on the dependence of the specific heat on the dynamical length , where is liquid relaxation time J. Frenkel (1955) (for details of calculation and interpretation of , see the Methods section) and is the transverse speed of sound. The specific heat, (heat capacity per atom), is an obvious important choice of a thermodynamic quantity because it reflects the degrees of freedom in the system. The role of the dynamical length is that it sets the upper range of wavelengths of transverse phonons in the liquidlike regime of supercritical dynamics below the Frenkel line (FL) Cockrell et al. (2021a). Details of this mechanism are given in the Methods section. In the gaslike dynamics above the FL, corresponds to the particle mean free path and sets the wavelength of the remaining longitudinal mode. This way, governs the phase space available to phonons in the system. Since the energy of these phonons contributes to liquid Proctor and Maynard-Casely (2020); Proctor (2020); Wallace (1998); Chen (2022); Trachenko and Brazhkin (2016), we predict a unique universal relationship between and in the supercritical state.
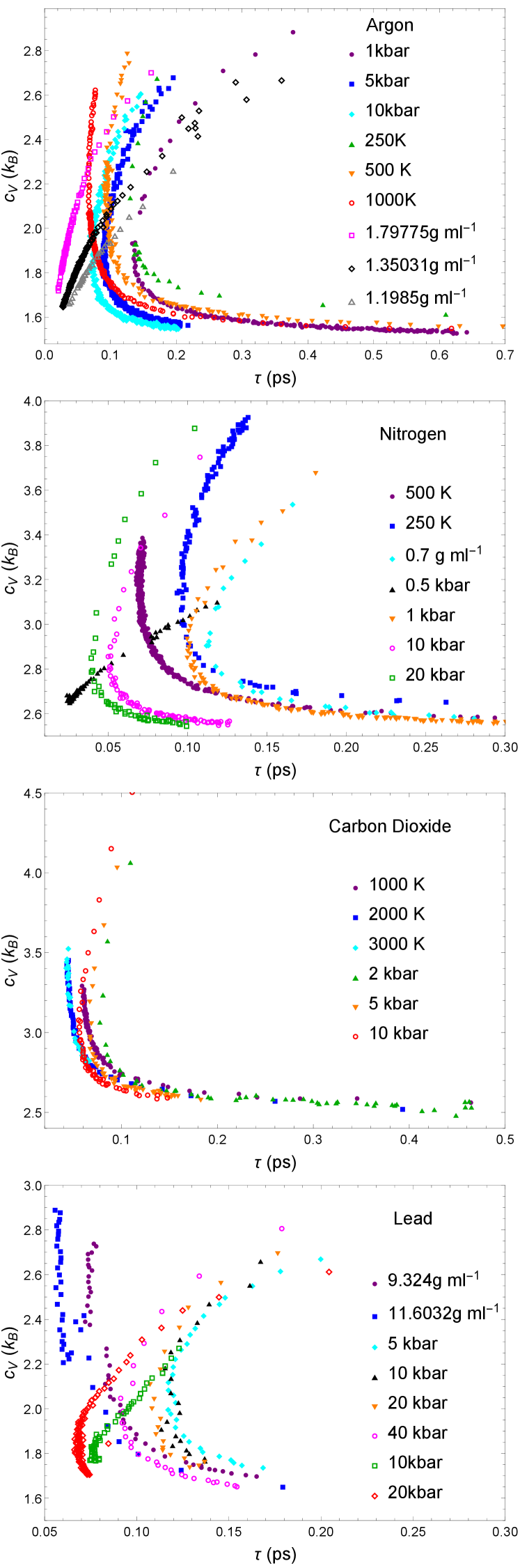
We show the calculated plots of on in nitrogen, carbon dioxide, lead and water in Figs. 1-4. We set everywhere in the paper. The variation of and shown in these Figures corresponds to a very wide range of pressure and temperature. To illustrate this, we also plot several representative paths simulated on the pressure and temperature phase diagram using the argon data Cockrell et al. (2021b) in Fig. 5 and the corresponding plot vs in Fig. 6.






The dependence of on across all simulated paths nearly collapses onto a group of “c”-shaped curves, which we refer to as the main sequence. The main sequence is “c”-shaped and has an inversion point corresponding to the change of the sign of the derivative of with respect to .
The origin of the inversion point is as follows. The dynamical length always has a minimum as a function of temperature when crossing from liquidlike to gaslike regimes of particle dynamics. Recall that this crossover is related to the dynamical crossover at the Frenkel line (FL) Cockrell et al. (2021a). In the liquidlike regime below the FL, particle dynamics combines oscillatory motion around quasi-equilibrium positions and flow-enabling diffusive jumps between these positions J. Frenkel (1955). In this regime, and decrease with temperature. In the gaslike regime above the FL, the oscillatory component of particle motion is lost, leaving the diffusive jumps only Cockrell et al. (2021a). In this regime, becomes the particle mean free path which increases with temperature (see the Methods section for more details). The inversion point is therefore related to the transition between liquidlike and gaslike particle dynamics.
The values of and at the inversion point are physically significant. The value of Å corresponds to the ultraviolet cutoff, approximately equal to the shortest length scale in the condensed matter system: the interatomic separation set by the length of the chemical bond. When matches this lengthscale, the fluid stops supporting all transverse phonons simply because the modes with shorter wavelength are non-existent. Concomitantly, particle dynamics can be viewed as the motion with the particle mean free path approximately equal to the interatomic separation.
The value of of about 2 in monatomic argon and lead is important too. corresponds to the loss of the contributions from the two transverse phonon branches, with only the kinetic part and the potential part of the longitudinal mode remaining. Since this loss corresponds to the disappearance of the oscillatory component of particle motion, is taken as a thermodynamic criterion of the FL Trachenko and Brazhkin (2016); Cockrell et al. (2021a). Phonon anharmonicity can change this result by a relatively small amount Trachenko and Brazhkin (2016), and the disappearance of transverse modes corresponds to approximately. The inversion point in nitrogen and carbon dioxide corresponds to (in molecular systems, is heat capacity per molecule) due to the additional rotational term contributing to . Subtracting from calculated , we arrive at as in monatomic fluids.
We note that the c-plot is not limited in pressure and temperature as long as the system remains chemically unaltered (the same proviso as for the melting line), extending to the entire supercritical state of matter.
All phase diagram paths of different types in argon, nitrogen and carbon dioxide collapse onto the main sequence curve. As discussed in the next section in more detail, along different phase diagram paths follows the same “c”-shape of the main sequence in lead but moderate path dependence remains far from the inversion point. This could be related to the electronic contribution (not accounted for in the theory based on phonons) represented by the many-body empirical potential in classical MD simulations.
Water, however, shows a different behavior in Figure 4. This is not unexpected, given that water possesses many anomalies which continue to inspire enquiry and research Poole et al. (1992); Gallo et al. (2016). Water’s supercritical state is little understood despite extensive exploitation in industrial and environmental applications Akiya and Savage (2002); Savage (1999); Huelsman and Savage (2013); Kiran et al. (2000). The specific heat of liquid water at the melting point at atmospheric pressure is almost twice as high as that of ice and is related to large “configurational” contribution to the liquid heat capacity. This contribution is related to water-specific hydrogen-bonded network undergoing the coordination change from 4 to 6, with the associated contribution to entropy and specific heat Eisenberg and Kauzmann (2005). This effect precludes the description of water’s heat capacity using phonons only as discussed earlier. Although different paths still result in the c-shaped curves, we see significant path dependence in Fig. 4. at the inversion point varies in the range of about 5-6 per molecule. This higher can be understood as a result of the additional configurational term in water mentioned earlier as well as the rotational term. Nevertheless, the inversion points corresponds to close to 1 Å as in previous fluids.
II.2 Path dependence
The universality of the inversion point and “c”-shaped main sequence curves observed in the previous section is best taken in the context of the path dependence of as a function of parameters other than the dynamical length . In this study we performed simulations along isobars, isotherms, and isochores. The dynamical parameter , the relaxation time introduced in the main article, provides a way to compare vs along different paths. In Fig. 7 we observe substantial path dependence of which manifests in several different ways. The first is that different paths, particularly isochores, have different shapes from one another. The second is that these curves do not coincide at the values of or . Third, there is no fixed inversion point. This is to be contrasted to the main sequence curves seen in Figures 1-4 and 6, wherein all phase diagram paths share a cross-system universal fixed inversion point at the minimal value of about = 1 Å and ( in monatomic fluids or appropriately modified in molecular fluids).
In summary, we see very different plots depending on which path on the phase diagram is chosen: there is no fixed inversion point, and all curves are far away from each other. This variation is removed once we plot vs as seen in Figures 1-4 and 6.
Similarly to , is a dynamical parameter. However the stark path dependence of emphasises that the c-transition is not a consequence of simply reducing to dynamics, but that the introduction of the special new dynamical parameter is necessary to achieve a fixed inversion point, data collapse and observe double universality discussed in the next section.
II.3 Double universality
We now come to the main finding of this work related to double universality of the c-transition. The first universality is that for each system, the c-transition plot has an inversion point which is fixed and corresponds to about Å and ( for monatomic systems or appropriately modified in molecular systems) for all paths on the phase diagram, including isobars, isochores and isotherms, spanning orders of magnitude of temperature and pressure. This inversion point provides an unambiguous, theory-independent and path-independent, transition between liquidlike and gaslike states in the sense discussed earlier. The second universality is that this behavior is generic on the supercritical phase diagram and is the same for all fluids simulated.
We now analyse our four systems (which excludes water) on the same set of axes. In order to compare, we must remove the rotational degrees of freedom from the heat capacity of nitrogen and carbon dioxide, which amounts to subtracting 1 from as mentioned earlier. This inter-system plot is presented in Fig. 8a.
The four fluids exhibit qualitatively similar main sequence curves: the “c”-shape is present in all curves, and the divergent liquidlike branches converge into almost the same gaslike branch. This plot exhibits what we are calling “double universality”: the function across not only different phase diagram paths but also across different fluids converges at the universal inversion point of , Å. This inversion point therefore constitutes a system independent, path independent, and unambiguous model-free separation between liquidlike and gaslike states in the supercritical state.
To draw the analogy with ordinary phase transitions, we recall the behaviour of liquid and gas densities on the coexistence line as the critical point is approached, depicted in Fig. 8b. The experimental relationship between reduced density and reduced temperature of the coexisting liquids and gases is system-independent for several small noble and molecular elements near the critical point Guggenheim (1945). In this plot, the specific microscopic details of different systems are often irrelevant to the qualitative behaviour near a phase transition, and the transition falls into a universality class determined by system symmetries and dimensionality Sethna (2006).
The plots in Fig. 8a depict the relationship between a thermodynamic quantity, , and a dynamical quantity, . It is in this sense that we consider the c-transition to represent a dynamical-thermodynamic transition. The system independence of the main sequence for simple fluids is further suggestive of a universal transition operating in the supercritical state. The fixed point of this dynamical-thermodynamic transition approximately corresponds to ( Å, ).

We also note that the “c”-transition is not observed in proximity to the critical point. The critical anomalies, caused by diverging correlation lengths, present in this region disrupt the relationship between the dynamical length and the heat capacity in all systems studied here. As mentioned earlier, the inversion point is far above the critical.
Finally, the universal inversion point and the related dynamical transition at the FL corresponds to the solubility maxima (known as “ridges”) and optimal extracting and dissolving abilities of supercritical fluids Cockrell et al. (2021a). This importantly addresses the widely-held belief that improved and more efficient deployment of supercritical fluids will benefit from better theoretical understanding of the supercritical state Eckert et al. (1996); Sarbu et al. (2000); Kiran et al. (2000). Our current results therefore give a universal way to locate the inversion point where the performance of a supercritical fluid is optimised, improving the supercritical technologies.
III Conclusions
We have shown that the supercritical state has a remarkable double universality. First, the transition between the liquidlike and gaslike states is characterised by fixed inversion point and near path-independence. Second, this effect universally applies to many supercritical fluids. This provides new understanding of the supercritical state of matter and a theoretical guide for improved deployment of supercritical fluids in green and environmental applications.
IV Methods
IV.1 Simulation details
We use DL_POLY molecular dynamics simulations package Todorov et al. (2006). For argon and nitrogen, we use the Lennard-Jones potential fitted to their properties. For nitrogen, we use a rigid two-site Lennard-Jones potential Powles and Gubbins (1976). The potential for carbon dioxide is a rigid-body non-polarisable potential based on a quantum chemistry calculation, with the partial charges derived using the distributed multipole analysis method Gao et al. (2017). The potential was derived and tuned using a large suite of energies from ab initio density functional theory calculations of different molecular clusters and validated against various sets of experimental data including phonon dispersion curves and data. These data included solid, liquid and gas states, gas-liquid coexistence lines and extended to high-pressure and high-temperature conditions Gao et al. (2017). The potential used for water was TIP4P/2005 potential, which is optimised for high pressure and temperature conditions Abascal and Vega (2005). A careful analysis Vega et al. (2009); Vega and Abascal (2011) assigned this potential the highest score in terms of the extent to which the results agree with different experimental properties, including the equation of state, high pressure and temperature behaviour, and structure. The electrostatic interactions were evaluated using the smooth particle mesh Ewald method in the MD simulations of carbon dioxide and water. The potentials for water and carbon dioxide are rigid body potentials. Simulations of lead were performed using an embedded atom model (EAM) potential Belashchenko (2017), which has been used to calculate the properties of molten lead at temperatures up to 25000 K and 280 GPa, which include the range discussed here.
Systems are simulated along several isobars, isotherms, and isochores in the deep supercritical state, with all paths but named exceptions being far from the critical point and Widom line Xu et al. (2005) of their respective phase diagrams. Equilibration was performed in the NPT ensemble with the Langevin thermostat in order to generate the mean densities along the isobars and isotherms. For argon, system sizes between 500 and 108000 atoms were used with no discrepancy in calculated quantities, consistent with the earlier ascertained insensitivity of viscosity to system size Yeh and Gerhard (2004). System sizes of 512 molecules were used for water, nitrogen and carbon dioxide simulations, and 5120 atoms for lead. The timestep used was 1 fs for water and carbon dioxide and 0.5 fs for lead, which conserved total energy under the Velocity-Verlet integrator in the NVE ensemble to one part in . Configurations at the target densities on all paths were then generated, which were then equilibrated with the NVT ensemble for 50 ps. Following this equilibration, we generated 20 independent initial conditions for each state point using seeded velocities, and each of these initial conditions were run for 1 ns in the NVE ensemble during which all properties were calculated. We calculated in the NVE ensemble as Allen and Tildesley (1991):
| (1) |
with the kinetic energy, and the number of translational and rotational degrees of freedom available to the molecule in question.
The shear modulus at high frequency and shear viscosity were calculated using the molecular stress autocorrelation function, from Green-Kubo theory Zwanzig and Mountain (1965); Balucani and Zoppi (1994):
| (2) |
| (3) |
with an off-diagonal component of the microscopic stress tensor. The integration of the long-time tails of autocorrelation functions was implemented using the Green-Kubo formulae Zhang et al. (2015). The 20 independent initial conditions were used to average the autocorrelation function over these initial conditions. The end result for viscosity was insensitive to adding more initial conditions.
The dynamical length was calculated as , where , and is density.
IV.2 Theory: specific heat and dynamical length
In this section, we explain the physical origin of the inter-relationship between the specific heat and the dynamical length in the supercritical state. The specific heat, , is an obvious important choice of a thermodynamic quantity because it reflects the degrees of freedom in the system. The dynamical length and its role are discussed below.
The choice of the dynamical parameter is informed by the Maxwell-Frenkel viscoelastic theory Maxwell (1867); J. Frenkel (1955). A liquid has a combined response to shear stress:
| (4) |
where is the shear strain, is the shear stress, is the shear viscosity and is the high-frequency shear modulus. When the external perturbation stops, the internal stress relaxes according to:
| (5) |
having introduced the Maxwell relaxation time :
| (6) |
Frenkel related this time to the average time between molecular rearrangements. This relationship is backed up by experiments and modelling Jakobsen et al. (2012); Iwashita et al. (2013) and has become an accepted view Dyre (2006).
Using Eq. (4), the Navier-Stokes equation can be generalised to include the elastic response of the liquid, yielding Trachenko and Brazhkin (2016):
| (7) |
where is the transverse velocity field, is the transverse speed of sound and the density.
Seeking the solution of Eq. (7) in the form gives
| (8) |
For , has no real solutions. For larger , the plane waves decay according to the decay time . We therefore define as
| (9) |
which sets the shortest wavevector for propagating transverse phonons and corresponds to the gap in the phonon momentum space Baggioli et al. (2020).
Here, we work in terms of the “dynamical length” featuring in Eq. (9), :
| (10) |
sets the propagation range, or mean free path of transverse phonons, in the liquidlike regime below the FL Cockrell et al. (2021a). This is seen from Eq. (8) which gives the decay factor . Since sets the time over which the shear stress decays in the liquid as discussed earlier or, in other words, the lifetime of transverse phonons, is a measure of their mean free path. This implies no phonons with wavelengths longer than the propagation range and is consistent with Eq. (9).
In the gaslike regime of particle dynamics above the FL Cockrell et al. (2021a), corresponds to the mean free path of particle motion, J. Frenkel (1955). Indeed, the shear modulus in a fluid with no interactions is Zwanzig and Mountain (1965), where is the concentration. Meanwhile, the gaslike viscosity is Blundell and Blundell (2010) , where is the thermal velocity and is the particle mean free path. Noting that , we find . The dynamical length in the gaslike state is (since the speed of sound in the liquidlike state below the FL, , approximately becomes thermal velocity of particles in the gaslike state above the FL, ), and .
We can now see the role played by the dynamical length in the liquidlike and gaslike regimes of the supercritical state. in Eq. (9) increases with temperature because decreases, and the dynamical length in (10) becomes shorter. This reduces the phase space available for transverse phonons Trachenko and Brazhkin (2016). When approaches its shortest value comparable to the Debye vibration period , approaches the Brillouin zone boundary because , where is the interatomic separation. At this point, all transverse modes disappear, corresponding to (this value is equal to the kinetic term and the potential energy of the remaining longitudinal mode Trachenko and Brazhkin (2016)). On further temperature increase, the system crosses over to the gaslike regime where the phonon phase space continues to reduce, albeit now for longitudinal phonons. In particular, the longitudinal phonons with wavelengths shorter than disappear because sets the shortest wavelength in the system. The associated potential energy of the longitudinal phonons reduces, eventually resulting in as in the ideal gas Trachenko and Brazhkin (2016). Since the phonon energy contributes to liquid Proctor and Maynard-Casely (2020); Proctor (2020); Wallace (1998); Chen (2022); Trachenko and Brazhkin (2016), we see that directly affects because it governs the phonon states in the system.
We are grateful to V. V. Brazhkin and J. Proctor for discussions.
References
- Landau and Lifshitz (1970) L. D. Landau and E. M. Lifshitz, Course of Theoretical Physics, vol. 5. Statistical Physics, part 1. (Pergamon Press, 1970).
- Kiran et al. (2000) E. Kiran, P. G. Debenedetti, and C. J. Peters, Supercritical Fluids: Fundamentals and Applications (Kluwer, 2000).
- Xu et al. (2005) L. Xu, P. Kumar, S. V. Buldyrev, S. H. Chen, P. H. Poole, F. Sciortino, and H. E. Stanley, PNAS 102, 16558 (2005).
- Proctor and Maynard-Casely (2020) J. E. Proctor and H. E. Maynard-Casely, The Liquid and Supercritical Fluid States of Matter (CRC Press, 2020).
- Proctor (2020) J. Proctor, Phys. Fluids 32, 107105 (2020).
- Wallace (1998) D. C. Wallace, Phys. Rev. E 57, 1717 (1998).
- Chen (2022) G. Chen, Journal of Heat Transfer 144, 010801 (2022).
- Trachenko and Brazhkin (2016) K. Trachenko and V. V. Brazhkin, Reports on Progress in Physics 79, 016502 (2016).
- Eckert et al. (1996) C. A. Eckert, B. L. Knutson, and P. G. Debenedetti, Nature 383, 313 (1996).
- Sarbu et al. (2000) T. Sarbu, T. Styranec, and E. J. Beckman, Nature 405, 165 (2000).
- Akiya and Savage (2002) N. Akiya and P. E. Savage, Chemical Reviews 102, 2725 (2002).
- Savage (1999) P. E. Savage, Chemical Reviews 99, 603 (1999).
- Huelsman and Savage (2013) C. M. Huelsman and P. E. Savage, The Journal of Supercritical Fluids 81, 200 (2013).
- Cockrell et al. (2021a) C. Cockrell, V. V. Brazhkin, and K. Trachenko, Physics Reports 941, 1 (2021a).
- J. Frenkel (1955) J. Frenkel, Kinetic Theory of Liquids (Oxford University Press, New York, 1955).
- Cockrell et al. (2021b) C. Cockrell, V. V. Brazhkin, and K. Trachenko, Physical Review E 104, 034108 (2021b).
- Poole et al. (1992) P. H. Poole, F. Sciortino, U. Essmann, and H. E. Stanley, Nature 360, 324 (1992).
- Gallo et al. (2016) P. Gallo et al., Chemical Reviews 116, 7463 (2016).
- Eisenberg and Kauzmann (2005) D. S. Eisenberg and W. Kauzmann, The structure and properties of water (Clarendon Press, 2005).
- Guggenheim (1945) E. A. Guggenheim, The Journal of Chemical Physics 13, 253 (1945).
- Sethna (2006) J. Sethna, Entropy, Order Parameters, and Complexity (Oxford University Press, 2006).
- Todorov et al. (2006) I. T. Todorov, W. Smith, K. Trachenko, and M. T. Dove, Journal of Materials Chemistry 16, 1911 (2006).
- Powles and Gubbins (1976) J. G. Powles and K. E. Gubbins, Chemical Physics Letters 38, 405 (1976).
- Gao et al. (2017) M. Gao, A. J. Misquitta, C. Yang, I. T. Todorov, A. Mutter, and M. T. Dove, Molecular Systems Design & Engineering 2, 457 (2017).
- Abascal and Vega (2005) J. L. F. Abascal and C. Vega, The Journal of Chemical Physics 123, 234505 (2005).
- Vega et al. (2009) C. Vega, J. L. F. Abascal, M. M. Conde, and J. L. Aragones, Faraday Discuss. 141, 251 (2009).
- Vega and Abascal (2011) C. Vega and J. L. F. Abascal, Physical Chemistry Chemical Physics 13, 19663 (2011).
- Belashchenko (2017) D. K. Belashchenko, High Temperature 55, 370 (2017).
- Yeh and Gerhard (2004) I.-C. Yeh and H. Gerhard, Journal of Physical Chemistry B 108, 15873 (2004).
- Allen and Tildesley (1991) M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids., Vol. 57 (Clarendon Press, 1991).
- Zwanzig and Mountain (1965) R. Zwanzig and R. D. Mountain, The Journal of Chemical Physics 43, 4464 (1965).
- Balucani and Zoppi (1994) U. U. Balucani and M. Zoppi, Dynamics of the liquid state (Clarendon Press, 1994) p. 336.
- Zhang et al. (2015) Y. Zhang, A. Otani, and E. J. Maginn, Journal of Chemical Theory and Computation 11, 3537 (2015).
- Maxwell (1867) J. C. Maxwell, Philosophical Transactions of the Royal Society of London 157, 49 (1867).
- Jakobsen et al. (2012) B. Jakobsen, T. Hecksher, T. Christensen, N. B. Olsen, J. C. Dyre, and K. Niss, Journal of Chemical Physics 136, 081102 (2012).
- Iwashita et al. (2013) T. Iwashita, D. M. Nicholson, and T. Egami, Physical Review Letters 110, 205504 (2013).
- Dyre (2006) J. C. Dyre, Reviews of Modern Physics 78, 953 (2006).
- Baggioli et al. (2020) M. Baggioli, M. Vasin, V. Brazhkin, and K. Trachenko, Physics Reports 865, 1 (2020).
- Blundell and Blundell (2010) S. Blundell and K. M. Blundell, Concepts in thermal physics (Oxford University Press, 2010).