Double $\phi$ Production in $\bar{p}p$ Reactions Near Threshold

In the simple constituent quark model, the proton (antiproton) wave function contains only up and down quarks (antiquarks). Meanwhile, the $\phi$ meson is nearly a pure $\bar{s}{s}$ state. Consequently, the reaction $\bar{p}p\to\phi\phi$ may occur through two gluon emissions from the $\bar{q}q$ annihilation. All three valence quarks in the proton annihilate with the corresponding three antiquarks in the antiproton to create a purely gluonic state, from which $\phi\phi$ is formed. According to the Okubo-Zweig-Iizuka (OZI) rule, this process, with its disconnected quark lines, should be strongly suppressed.

On the other hand, the reaction $\bar{p}p\to\phi\phi$ may occur through a two-step process involving meson pairs, such as $\omega\omega$. The $\omega\omega$ could be directly formed from the initial $\bar{p}p$ state, and the mixing of $\omega$ and $\phi$ mesons could lead to the creation of the $\phi\phi$ state. We can establish an upper limit for the total cross-section of the $\bar{p}p\to\phi\phi$ by comparing it to the total cross-section of the $\bar{p}p\to\omega\omega$, which is approximately $10$ nb and is expressed as $\sigma(\bar{p}p\to\phi\phi)=\tan^{4}\delta\cdot\sigma(\bar{p}p\to\omega\omega)\approx 10{\rm~{}nb}.$ This approximation is valid if both $\phi$ mesons were created by independent OZI-violating couplings. Here, the angle $\delta(=\Theta_{i}-\Theta)$ represents the difference between the ideal mixing angle $\Theta_{i}=35.3^{\circ}(\sin\Theta_{i}=1/\sqrt{3})$ and the mixing angle $\Theta$ between $(\phi,\omega)$ mesons and the SU(3) states $(\omega_{0},\omega_{8})$.

However, data from the JETSET experiment showed a significant violation of the OZI rule in the $\bar{p}p\to\phi\phi$ reaction JETSET:1994evm ; JETSET:1994fjp ; JETSET:1998akg . The measured cross section of this reaction is $(2-4)\,\mu$b for incoming antiproton momenta ranging from 1.1 to 2.0 GeV$/c$. This value is two orders higher than the expected 10 nb, attributed to the $\phi$-$\omega$ mixing effect.

A substantial OZI rule violation could indicate the presence of intriguing new physics. This violation can occur if a resonant gluonic state like a glueball or a four-quark state containing a significant $\bar{s}s$ admixture Ke:2018evd ; Lu:2019ira contributes to the $\bar{p}p\to\phi\phi$ reaction. According to lattice QCD results, the masses of the $2^{++}$ and $0^{-+}$ glueballs are predicted to be well above 2 GeV, around $(2.39\pm 0.12)$ and $(2.56\pm 0.12)$ GeV Chen:2005mg . However, some phenomenological model calculations point to the mass region near 2.0 GeV, which can be accessed by near-threshold $\phi\phi$ production experiments. A theoretical study using QCD sum rules estimates the masses of the $2^{++}$ and $0^{-+}$ glueballs to be $(2.0\pm 0.1)$ and $(2.05\pm 0.19)$ GeV, respectively Narison:1996fm . In contrast, a recent QCD sum rule calculation predicts the masses of the $2^{++}$ and $0^{-+}$ glueballs to be $(1.86\pm 0.17)$ and $(2.17\pm 0.11)$ GeV Chen:2021bck .

It is suggested that strange quarks could be knocked off directly from the $\bar{q}q$ sea of the proton and the antiproton to create a pair of $\phi$ mesons: $\phi\phi$. The strangeness content (${}^{1}S_{0}~{}\bar{s}s$) of the proton and antiproton might result in the production of $\phi\phi$ through a shake-out or rearrangement process Ellis:1994ww . Importantly, this process does not violate the OZI rule because it involves connected quark diagrams with higher Fock-space components in the nucleon wave function: $|p\rangle=x\sum^{\infty}_{X=0}|uudX\rangle+z\sum^{\infty}_{X=0}|uud\bar{s}sX\rangle,~{}|x|^{2}+|z|^{2}=1,$ where $X$ stands for any number of glueons and light $\bar{q}q$ pairs. The upper limit for the total cross-section of the $\bar{p}p\to\phi\phi$ reaction is given by $\sigma(\bar{p}p\to\phi\phi)=(|z|/|x|)^{4}\cdot\sigma(\bar{p}p\to\omega\omega)\geq 250{\rm~{}nb},$ which is larger than the value from the $\phi$-$\omega$ mixing effect, but still much smaller compared to the experimental data.

The interaction between quarks, induced by instantons, could weaken the OZI suppression. A theoretical study Kochelev:1995kc demonstrates that the violation of the OZI rule in the $\bar{p}p$ annihilation is a nontrivial consequence of the complex structure of the QCD vacuum, which is associated with the existence of the instantons. On the other hand, the large cross-section for the $\bar{p}p\to\phi\phi$ reaction may be explained by considering the hadronic rescattering mechanism. Each transition in the rescattering diagram is OZI-allowed. Lu et al. studied the role of a $\bar{K}K$ intermediate state in a triangle diagram in the $\bar{p}p\to\phi\phi$ reaction Lu:1992xd . The intermediate $\eta\eta$ can also contribute to the $\phi\phi$ production, as the $\eta$ contains $\bar{s}s$ content. In addition, the $\pi\pi\to\bar{K}K$ amplitude could make a sizable contribution. It is worth noting that the kernel $\bar{B}B\to\bar{m}m$ involving a baryon and antibaryon pair is possible. A full calculation involving all possible hadronic rescattering diagrams would be necessary to predict the detailed shape and magnitude of the observed spectrum.

In the context of hadronic degrees of freedom, the $\bar{p}p\to\phi\phi$ reaction can be described using the meson and baryon exchange diagrams. Recent theoretical calculations suggest that the $N^{\ast}(1535)$ exchange in the $t$-channel could play a significant role and provide an essential source for bypassing the OZI rule Shi:2010un . Additionally, a more recent theoretical calculation, using an effective Lagrangian approach, indicates that the inclusion of either $f_{0}$ or $f_{2}$ in the $s$-channel can effectively describe the bump structure near $W\approx 2.2$ GeV Xie:2014tra ; Xie:2007qt . These two previous work included only the $N^{\ast}(1535)$ exchange.

This paper details a theoretical study of the near-threshold $\bar{p}p\to\phi\phi$ reactions using an effective Lagrangian approach. We examine the exchange of a ground state $N$ and three $N^{\ast}$ resonances with $J^{P}=1/2^{-}$ in the $t$- and $u$-channels ($N^{\ast}(1650)$, $N^{\ast}(1895)$, and $N^{\ast}(1535)$ in order of coupling strength) as well as all $f_{0}$ and $f_{2}$ mesons in the $s$-channel. Additionally, we include a pseudoscalar meson, $\eta(2225)$, in the $s$-channel. Our work in a coupled-channel formalism reveals that the $N^{\ast}(1650)$ contributes significantly to the $\phi N$ channel, indicating that the previous work considering only the $N^{\ast}(1535)$ exchange may be insufficient. We determine polarization observables by the $\phi\phi$ production amplitudes of different helicities for the final $\phi\phi$ states. The squared absolute values of the production amplitudes determine unpolarized cross-sections. Therefore, the polarization data provides new information relevant to evaluating the resonance couplings. These observables extend our capabilities to validate the mechanisms of the reaction models used in data analyses through a combined fit of unpolarized cross-sections and polarization measurements. If further experiments confirm a significant violation of the OZI rule, an amplitude analysis of spin-dependent observables will be necessary, for which this paper lays the groundwork.

The paper is organized as follows: In Sec. II, we describe the reaction model for double $\phi$ production in $\bar{p}p$ reactions near the threshold. In Sec. III, we present the numerical calculation results for the total and differential cross sections. Section IV focuses on spin density matrix elements and spin correlations between two $\phi$ mesons. Finally, Sec. V summarizes our conclusions.

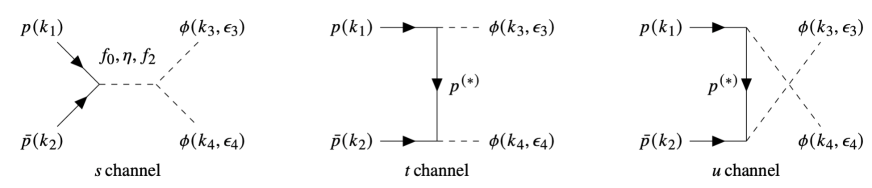
This section briefly introduces the theoretical framework for studying the reaction process $\bar{p}p\to\phi\phi$. The relevant Feynman diagrams are provided in Fig. 1, along with the definition of the four momenta and polarization of the vector meson. The effective Lagrangians for the interaction of Yukawa vertices are defined as follows:

where $S$, $P$, $V$, $T$, and $(N,N^{\prime})$ denote the scalar, pseudoscalar, vector, tensor, and nucleon fields for $J^{P}=(1/2^{\pm},\,3/2^{\pm})$, respectively, while the vector meson is given in the form of the field strength tensor $F_{\mu\nu}=\partial_{\mu}V_{\nu}-\partial_{\nu}V_{\mu}$. Note that we employ the self gauge-invariant Lagrangians for the $SVV$ and $TVV$ interaction vertices, given in Refs. Nam:2005jz ; Katz:2005ir in terms of the hidden-local symmetry (HLS) for the massive vector meson $\phi$. $\Gamma_{5}$ denotes $({\bf 1}_{4\times 4},\gamma_{5})$ for the parity-$(+,-)$ nucleon states. For the $N^{\prime}$, we employed the Rarita-Schwinger formalism Rarita:1941mf . By straightforwardly computing the invariant amplitudes using the interaction Lagrangians, we obtained the total amplitude, which is the sum of the following contributions illustrated in Fig. 2:

Here, $q_{i\pm j}\equiv(k_{i}\pm k_{j})$ and the Mandelstam variables are defined by $(s,t,u)=q^{2}_{s,t,u}$. We also define the rank-4 tensor for the tensor-meson propagator as follows:

To incorporate the spatial extension of the hadrons, which is inversely proportional to a cutoff mass $\Lambda$, and to ensure the unitarity of the scattering process, it becomes necessary to introduce phenomenological strong form factors to the amplitudes. In the present work, we use the following parameterization of the form factors, which satisfy Lorentz invariance as well as the crossing symmetry Davidson:2001rk :

Here, $x$ represents the Mandelstam variables $(s,t,u)$, and $h$ denotes the hadron species. Fitting available experimental data will determine the cutoff mass $\Lambda$ later in Section III.

As previously discussed, when considering the hidden-local symmetry for the $\phi$ meson, it is essential to uphold the (extended) Ward-Takahashi (WT) identity for the total amplitude, as shown below:

In Eq. (13), if we replace $\epsilon_{3,4}$ with $k_{3,4}$, we can see that the scalar-meson pole amplitude in the $s$ channel, as indicated by Eq. (13), satisfies the WT identity due to the self-gauge-invariant nature of the interaction Lagrangian governing the $SVV$ vertex. Similarly, the $s$ channel amplitude for the tensor meson, also represented in Eq. (13), automatically upholds the WT identity. Notably, we use a common form factor $F^{N}_{c}(t,u)$ for both the $t$- and $u$-channel amplitudes in Eq. (13) to maintain the WT identity, resulting in $i\mathcal{M}^{u}_{N,N^{*},N^{\prime*}}+i\mathcal{M}^{t}_{N,N^{*},N^{\prime*}}=0$ for $\epsilon_{3,4}\to k_{3,4}$. We use the following parameterization for the common form factor, explicitly satisfying the on-shell condition:

Thus, we verified that the WT identity is upheld for the total amplitude as follows:

and $i\mathcal{M}^{\mathrm{total}}_{\mu\nu}k^{\nu}_{4}=0$ as well.

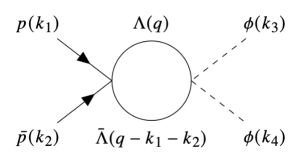
In $\bar{p}p$ scattering, other $\bar{B}B$ channels can open an off-mass shell and decay into two $\phi$ mesons. Hence, in the energy region from $W=E_{\mathrm{threshold}}$ to $2.5$ GeV, a cusp corresponding to the $\bar{\Lambda}\Lambda$ channel opening can appear at $W=2M_{\Lambda}$. To describe the cusp effectively, we consider the one-loop diagram as depicted in Fig. 2. For those Yukawa interaction vertices shown in Fig. 2., we define the following point-interaction Lagrangians to simplify the problem:

The unknown couplings $g_{4B}$ and $g_{VBVB}$ will be taken as free parameters here. Straightforwardly, the amplitude for the loop diagram can be computed as follows:

where the reduced coupling reads $g_{\bar{\Lambda}\Lambda}\equiv g_{4B}g_{VBVB}/M^{5}_{N}$. The amplitude above satisfies the Ward-Takahashi (WT) identity by construction. The integral representing the $\bar{\Lambda}\Lambda$ loop, with cutoff regularization, is given by:

where $x$ indicates the Feynman-parameterization variable and

Here, $\Delta=-x(1-x)s+M^{2}_{\Lambda}$ and $\Delta_{\mu}=-x(1-x)s+\mu^{2}$, in which $\mu$ stands for a cutoff mass, corresponding to the size of two baryon masses $\mu\approx 2M_{\Lambda}$. To prevent the unphysical increase of $i\mathcal{M}_{\bar{\Lambda}\Lambda}$ caused by the terms involving $k_{3,4}$, we multiply by $F_{\mathrm{loop}}=F(s,M_{N},\Lambda_{\mathrm{loop}})$.

In interpreting the reaction mechanism of the reaction process, the spin-density matrix element (SDME) is one of the useful observables. For the current reaction process, there are nine independent SDMEs, considering the two $\phi$-meson helicities, defined similarly in the previous study Kim:2020wrd . The $0$-th element of the SDME for the $\phi$-meson with $k_{3}$ ($\phi_{3}$) is as follows:

In this context, $\lambda_{h}$ represents the helicity of particle $h$ in a specific kinematic frame. We can obtain the SDMEs for the $\phi$-meson with $k_{4}$ ($\phi_{4}$) by simply swapping the subscript indices as $3\leftrightarrow 4$ in Eq. (23). To compare the SDMEs with experimental data, we need to boost the kinematic frame used for the theoretical computation to the $\phi$-meson rest frame. This involves using different spin-quantization axes, such as the helicity, Adair, and Gottfried-Jackson (GJ) frames, as defined in Ref. Kim:2020wrd , by a Wick rotation of the reaction from $(\gamma,\phi)$ to $(\phi_{i},\phi_{j})$.

In this section, we present the numerical results along with their corresponding discussions. We examine the relevant mesons contributing to the $s$-channel in the current reaction process. For the scalar and tensor mesons near the threshold, we select $f_{0}(2020,2100,2200)$ and $f_{2}(1950,2010,2150)$, respectively. Based on experimental data from the Particle Data Group (2022) ParticleDataGroup:2022pth , the pseudoscalar meson $\eta(2225)$ is known to be strongly coupled to $\phi\phi$, so we include this meson in our calculations.

All the relevant numerical inputs for the mesons are listed in Table 1. Here, we show the minimized number of combined coupling constants $g_{\Phi}=g_{\Phi\phi\phi}g_{\Phi NN}$ for $\Phi=(S,P,T)$. This approach considers the limited experimental and theoretical information available for determining each coupling, allowing us to fit the data effectively. In contrast, Ref. ParticleDataGroup:2022pth provides the couplings for the $\eta$ meson as $g_{\eta(\phi\phi,NN)}=(-4.062,0.5)$.

Now, we are in a position to discuss the contributions of nucleon resonances in the $t$ and $u$ channels of our numerical calculations. Xie $et\ al.$ Xie:2014tra highlighted the importance of the strangeness content within nucleons for reproducing data, such as the $N^{*}(1535,1/2^{-})$. Another study by Khemchandani $et\ al.$ Khemchandani:2013nma used the coupled-channel method within the framework of chiral dynamics, specifically the chiral unitary model (ChUM), to demonstrate strong coupling of three s-wave nucleon resonances to the $\phi$-$N$ channel: $N^{*}(1535,1/2^{-})$, $N^{*}(1650,1/2^{-})$, and $N^{*}(1895,1/2^{-})$. The resulting couplings, denoted as $g_{\phi NN^{*}}$, are listed in Table 2.

Furthermore, as discussed in our previous work Nam:2021ayk , a possible pentaquark baryon, $P_{s}(2071,3/2^{-})$, is considered as a $K^{*}\Sigma$ bound state that decays into $\phi N$. Its coupling has been calculated using ChUM Khemchandani:2011et and is presented in the table. Note that we set the values of the tensor-interaction strength $\kappa_{N^{*}}$ to zero due to limited information, except for $\kappa_{\phi NN}$, which is fixed at $-1.65$ Kim:2021adl . For simplicity in the computations, we use a single cutoff $\Lambda_{h}=550$ MeV for all hadronic form factors and $\Lambda_{\rm loop}=300$ MeV with $g_{\Lambda\bar{\Lambda}}=2$ to reproduce the data.

In panel (a) of Fig. 3, we present the full calculations for the total cross-sections $\sigma\equiv\sigma_{p\bar{p}\to\phi\phi}$ as functions of the center-of-mass energy $W$, showing each contribution separately. The experimental data are taken from Ref. JETSET:1994evm ; JETSET:1994fjp ; JETSET:1998akg . The ground-state nucleon ($N$) contribution is significant near the threshold, exhibiting a shoulder-like structure, while the nucleon-resonance ($N^{*}$) contribution becomes stronger as W increases. As expected, the scalar and tensor mesons $f_{0,2}$ are responsible for the bump structure around $W\approx 2.2$ GeV. Additionally, there is a small but finite contribution from the $\eta$ in the $s$ channel. Interestingly, the nontrivial structure around $W=2.25$ GeV is well reproduced by the interference between the cusp effect from the $\Lambda\bar{\Lambda}$-loop contribution and other components. To clarify this observation, in panel (b), we show the total cross-section with and without the cusp effect. We also test the impact of the $\eta$ contribution at $W\approx 2.25$ GeV, which fails to explain the nontrivial structure.

Following a similar approach to Refs. Shi:2010un ; Xie:2014tra ; Xie:2007qt , in panel (c), we attempt to reproduce the data without the ground-state nucleon contribution by modifying the cutoff masses for the form factors, resulting in a fit-compatible with the full calculation shown in panel (a). As expected, the absence of the $N$ contribution causes the shoulder-like structure near the threshold to disappear in panel (c). Additionally, the curve shows better behavior in the higher-energy region beyond $W=2.4$ GeV compared to panel (a). We will further explore these two scenarios, $N+N^{*}$ (full) and $N^{*}$ only, in detail later. In panel (d), we present the numerical results for the angular-dependent differential cross-section $d\sigma/d\cos\theta$ as a function of $W$ and $\cos\theta$, where $\theta$ denotes the scattering angle of the $\phi_{3}$ in the center-of-mass system for the full calculation. As shown, the angular dependence is symmetric about $\theta=\pi/2$ since identical mesons are scattered in the final state. The cross-section decreases as $\theta$ approaches $\pi/2$ from $\theta=0$.

To better understand the angular dependence of the present reaction process, in panels (a-c) of Fig. 4, we show the full results for $d\sigma/d\cos\theta$ as a function of $\cos\theta$ at different energies $W=(2.1-2.3)$ GeV. We also display the separate contributions in the panels. Near the threshold at $W=2.1$ GeV, all contributions are nearly flat, with the ground-state nucleon contributing the most to the cross-section. As the energy increases, the $N$ and $N^{*}$ contributions become more significant, leading to non-trivial angular dependences, such as convex and concave shapes. We also observe that the meson contributions are maximized around $W\approx 2.2$ GeV. Note that the $N$ contribution primarily determines the total curves and their angular dependences. In panels (c – d), we present the full calculation results for $d\sigma/d\cos\theta$ as functions of $W$ for different angles $\theta=(0-\pi/2)$. As already noted in panel (d) of Fig. 3, the magnitude of the cross-sections decreases mainly due to the diminishing $\eta$ and $N$ contributions as the angle increases.

In panel (a) of Fig. 5, we present the full results for the forward differential cross-sections, $d\sigma/dt$, as functions of $-t$ for different values of $W$. As expected from Fig. 4, the curve shapes become more concave with increasing $W$ due to the $N$ contribution. To make the current numerical results more accessible, we separately fit the curves using single-exponential $(d\sigma/dt=ae^{-b|t|})$ and a double-exponential $(d\sigma/dt=a^{\prime}e^{-b^{\prime}|t|}+c^{\prime}e^{-d^{\prime}|t|})$ functions in the region below $|t|<0.2\rm GeV^{2}$. The corresponding fit parameters are listed in Table 3. To better understand the overall $t$-dependence of the cross-section, we plot it as a function of both $-t$ and $W$. A bump structure appears around $W\approx 2.2$ GeV, indicating the contribution from the $f_{0,2}$ mesons.

Now, we turn to the discussion of the spin-density matrix elements (SDMEs) as defined in Eq. (23). The numerical results for $\rho^{\lambda}_{00,10,1-1}$ are plotted in Fig. 6 as functions of $\cos\theta$ for the full calculation, shown across different kinematic frames, namely, the Adair, helicity, and Gottfried-Jackson (GJ) frames, where $\lambda=(0,4)$ represents the $\phi_{4}$ helicity at $W=2.2$ GeV. According to Eq. (23), each SDME approximately follows specific helicity-flip patterns:

where the amplitude is defined as $\mathcal{M}_{\lambda_{3}\lambda_{4}}$. Here, we define the notation $\Delta\lambda_{34}=|\lambda_{3}-\lambda_{4}|$. From the numerical results shown in Fig. 6 and being understood by Eq. (25), we clearly observe that the single $(\Delta\lambda_{34}=1)$ and double $(\Delta\lambda_{34}=2)$ helicity-flip SDMEs become zero at $\cos\theta=\pm 1$, indicating helicity conservation. In contrast, the $\Delta\lambda_{34}=0$ component remains finite Kim:2019kef . We also find that $\rho^{4}_{00}$ is not exactly unity at $\cos\theta=\pm 1$ due to finite helicity non-conserving effects from the $f_{2}$ and $N^{*}$ contributions. As expected, the $\Delta\lambda_{34}=2$ contribution is very small, as seen from $\rho^{0}_{1-1}$. Notably, the shape of the SDMEs is primarily driven by the $N$ contribution, which plays a dominant role in the total cross-section.

In Fig. 7, we plot $\rho^{0,4}_{00}$ as functions of $W$ and $\cos\theta$ for the Adair, helicity, and Gottfried-Jackson (GJ) frames. The energy dependence of the SDMEs is shown to be quite mild. At the same time, meson contributions, such as from the $f_{0}$, introduce a small but non-trivial structure around $W=2.2$ GeV for helicity-conserving cases, i.e., $\lambda=4$ ($\Delta\lambda_{34}=0$). As expected, the $\Delta\lambda_{34}=0$ contributions are significantly larger than those with $\Delta\lambda_{34}=1$.

Finally, we turn to the discussion of polarization observables, which can provide valuable insight into reaction mechanisms by examining various combinations of $\phi$-meson polarizations. In panel (a) of Fig. 8, we present the numerical results for polarized total cross-sections as functions of $W$ for different combinations of $\phi_{3}$ and $\phi_{4}$ polarizations, denoted as $(\epsilon_{\phi_{3}},\epsilon_{\phi_{4}})$. The symbols $\perp$ and $\parallel$ indicate that the polarizations are, respectively, transverse and parallel to the reaction plane, while $\odot$ denotes the longitudinal polarization. It is evident from the Lorentz structure of the invariant amplitudes in Eq. (13), it is clear that the amplitudes are sensitive to polarization and are reduced by certain combinations.

The polarized total cross-sections show significant contributions from $N$ and $N^{*}$ for identical polarization combinations, but these contributions decrease for different combinations. As described by Eq. (13), the $f_{0}$ amplitude becomes zero for the combinations $(\parallel,\perp)$ and $(\parallel,\odot)$, whereas the $\eta$ amplitude remains non-zero only for $(\parallel,\odot)$. In contrast, the $f_{2}$ amplitude remains finite for both combinations. This pattern is illustrated in panel (a) of Fig. 8, showing the bumps corresponding to $f_{0,2}$ and $\eta$, which suggests that meson signals can be enhanced by appropriately adding or subtracting the contributions from different polarization combinations. This approach is tested in panel (b) of Fig. 8, where the $f_{0}$ and $f_{2}$ contributions are more pronounced and better separated due to improved signal-to-background ratios. In panel (c), we present the angular-dependent differential cross-sections in the same manner as in panel (b) for $W=(2.1-2.3)$ GeV. The $f_{2}$ and $\eta$ contributions exhibit qualitatively flat curves near zero degrees, while the $f_{0}$ component shows distinctive angular dependence. Analyzing these polarized angular dependencies allows one to isolate and study specific meson properties more effectively.

As mentioned previously, Ref. Shi:2010un ; Xie:2014tra ; Xie:2007qt considered that the $N^{*}(1530)$ dominates the background of the present reaction process, whereas we include more $N^{*}$ and $N$ contributions. To test these two different scenarios, we suggest measuring an asymmetry characterized by the various combinations of the $\phi$-meson polarizations as follows:

where the $\phi$-meson polarizations are given by $\epsilon_{3,4}=(\parallel,\perp,\odot)$ and $d\sigma\equiv d\sigma/d\cos\theta$. In panel (d) of Fig. 8, we show the polarization asymmetries in Eq. (28) as functions of $\cos\theta$ for the full calculation with $N+N^{*}$ and that with $N^{*}$ only, respectively. As seen in panel (a) of Fig. 8, these two polarization combinations contain much information on the baryon exchanges. It turns out that the angular dependences are distinctively different for the two cases, especially at $\cos\theta=\pm 1$ and $\cos\theta\approx 0$, and these differences can be tested in experiments to pin down a reaction mechanism.

The $\phi$-meson polarizations are given by $\epsilon_{3,4}=(\parallel,\perp,\odot)$, and the differential cross-section is defined as $d\sigma\equiv d\sigma/d\cos\theta$. In panel (d) of Fig. 8, we show the polarization asymmetries from Eq. (28) as functions of $\cos\theta$ for the full calculation with $N+N^{*}$ contributions and the case with $N^{*}$ only. As seen in panel (a) of Fig. 8, these polarization combinations carry significant information about the baryon exchanges. The angular dependences are distinctly different between the two cases, particularly at $\cos\theta=\pm 1$ and $\cos\theta\approx 0$. These differences can be tested experimentally to identify the reaction mechanism.