Double-peaked inflation model: Scalar induced gravitational waves and primordial-black-hole suppression from primordial non-Gaussianity
Abstract
A significant abundance of primordial black hole (PBH) dark matter can be produced by curvature perturbations with power spectrum at small scales, associated with the generation of observable scalar induced gravitational waves (SIGWs). However, the primordial non-Gaussianity may play a non-negligible role, which is not usually considered. We propose two inflation models that predict double peaks of order in the power spectrum and study the effects of primordial non-Gaussianity on PBHs and SIGWs. This model is driven by a power-law potential, and has a noncanonical kinetic term whose coupling function admits two peaks. By field-redefinition, it can be recast into a canonical inflation model with two quasi-inflection points in the potential. We find that the PBH abundance will be altered saliently if non-Gaussianity parameter satisfies . Whether the PBH abundance is suppressed or enhanced depends on the being positive or negative, respectively. In our model, non-Gaussianity parameter takes positive sign, thus PBH abundance is suppressed dramatically. On the contrary, SIGWs are insensitive to primordial non-Gaussianity and hardly affected, so they are still within the sensitivities of space-based GWs observatories and Square Kilometer Array.
I introduction
Ever since the detection of gravitational waves (GWs) by the Laser Interferometer Gravitational-Wave Observatory (LIGO) scientific collaboration and Virgo collaboration Abbott et al. (2016a, b, 2017a, 2017b, 2017c, 2017d, 2019, 2020a, 2020b, 2020c), primordial black holes (PBHs) Carr and Hawking (1974); Hawking (1971) have been drawing much attention as PBHs might be the source of GW events Bird et al. (2016); Sasaki et al. (2016); Takhistov et al. (2021); De Luca et al. (2021a); Abbott et al. (2021). Recently, North American Nanohertz Observatory for Gravitational Waves (NANOGrav) also hints the existence of PBHs De Luca et al. (2021b); Vaskonen and Veermäe (2021); Kohri and Terada (2021); Domènech and Pi (2020); Atal et al. (2021); Yi and Zhu (2021). In addition, it is attractive that PBHs could be the candidate of dark matter (DM).
PBHs are formed by gravitational collapse during a radiation-dominated era when large perturbations reenter the horizon. This mechanism requires the amplitude of the power spectrum of primordial Gaussian curvature perturbation at small scales Sato-Polito et al. (2019). The constraints on power spectrum from the cosmic microwave background (CMB) is at the pivot scale Akrami et al. (2020), so the power spectrum has to be enhanced at least seven orders at small scales during inflation to produce significant abundance of PBH DM Di and Gong (2018); Garcia-Bellido and Ruiz Morales (2017); Germani and Prokopec (2017); Lu et al. (2019); Motohashi and Hu (2017); Espinosa et al. (2018a); Belotsky et al. (2019); Dalianis et al. (2020); Passaglia et al. (2020); Fu et al. (2019); Xu et al. (2020); Lin et al. (2020); Yi et al. (2021a, b); Gao et al. (2021); Fumagalli et al. (2020a); Gundhi et al. (2021); Ballesteros et al. (2020); Ragavendra et al. (2021); Palma et al. (2020); Braglia et al. (2020). Besides PBHs, large curvature perturbations also induce the scalar induced gravitational waves (SIGWs) that contribute to stochastic gravitational-wave background (SGWB) Baumann et al. (2007); Saito and Yokoyama (2009); Orlofsky et al. (2017); Nakama et al. (2017); Inomata et al. (2017); Cai et al. (2019a); Bartolo et al. (2019); Kohri and Terada (2018); Espinosa et al. (2018b); Kuroyanagi et al. (2018); Cai et al. (2019b); Drees and Xu (2021); Inomata et al. (2019a, b); Fumagalli et al. (2020b); Domènech et al. (2020); Braglia et al. (2021); Fumagalli et al. (2021).
Generally, the power spectrum predicted by the slow-roll inflation is nearly scale-invariant and agrees with the observational constraints on large scales with . To amplify the power spectrum on small scales, it is necessary to consider the violation of slow-roll Motohashi and Hu (2017). The canonical inflation model with a flat plateau, namely the so-called quasi-inflection point in potential is usually used to violate the slow-roll conditions and amplify the power spectrum Germani and Prokopec (2017); Di and Gong (2018); Garcia-Bellido and Ruiz Morales (2017); Xu et al. (2020). However, it is difficult to find such a suitable potential with quasi-inflection points during inflation while keeping -folds . We will show that a canonical inflation model with a quasi-inflection point in the potential is equivalent to a noncanonical inflation model where the coupling function of the kinetic term has a peak, up to a field-redefinition. We can have as many peaks in as we want. This amounts to produce corresponding peaks in the power spectrum.
Usually, the power spectrum with a large peak only produces PBHs in a single mass range. We expect that the inflation models with multipeaked power spectrum produce PBHs at different mass ranges. This can explain more DMs and different observational phenomena simultaneously. For example, the canonical model proposed in Ref. Gao and Yang (2021) predicts double peaks in the power spectrum which leads to a double-peaked PBH abundance and also the energy density of SIGWs. In Ref. Zheng et al. (2021), the power spectrum with triple peaks is produced by a triple-bumpy potential. However, the effect of primordial non-Gaussianity is not considered. Based on this motivation, in this paper, with generalized G-inflation models Lin et al. (2020); Yi et al. (2021b, a), we use a noncanonical kinetic term with double-peaked coupling function to produce a power spectrum with two culminations with magnitude at small scales while satisfying CMB constraints at large scales. Moreover, the -folds are reasonably . With different choices of , both potential and Higgs potential can produce such power spectrum. In the period that the inflaton departs from the slow-roll, the non-Gaussianity may differ from that in slow-roll inflations, which predict negligible non-Gaussianity Maldacena (2003). We compute the primordial non-Gaussianity numerically in the squeezed and equilateral limits, and both have their maxima of order .
Intuitively, it seems there are plenty of PBHs formed in two different mass ranges because of the double peaks in the power spectrum. However, this is just an illusion owing to our ignorance of primordial non-Gaussianity. We show that the PBH abundance is sensitive to primordial non-Gaussianity of curvature perturbation and will be strongly altered if the non-Gaussianity parameter satisfies , whether the PBH abundance is suppressed or enhanced depends on non-Gaussianity parameter being positive or negative, respectively. Nevertheless, the magnitude of the fractional energy density of SIGWs is hardly affected by the primordial non-Gaussianity. Although this model predicts double-peaked SIGWs that can be detected by the space-based GW observatories such as Laser Interferometer Space Antenna (LISA) Amaro-Seoane et al. (2017); Danzmann (1997), TianQin Luo et al. (2016), TaijiHu and Wu (2017) and etc, and the Square Kilometer Array (SKA) Moore et al. (2015), there is no significant abundance of PBHs produced with that is positive in the two models.
This paper is organized as follows. In Sec. II, we first explain the equivalence between a noncanonical inflation model with a peak coupling function of noncanonical kinetic term and a canonical model with a flat plateau in the potential and then give the power spectrum produced by noncanonical inflation models. In Sec. III, we present the primordial non-Gaussianities. In Sec. IV, we discuss the PBH abundance from the present models, where we also take consideration of non-Gaussianity. In Sec. V, we compute the SIGWs during radiation dominant. Our conclusions are drew in Sec. VI.
II Inflation models
Considering a kind of generalized G-inflation with a noncanonical kinetic term Lin et al. (2020); Yi et al. (2021a, b)
| (1) |
where , is the inflaton potential, and is a function of . Here we choose . Performing a field-redefinition,
| (2) |
we get ,
| (3) |
where is the potential of canonical field .
The power spectrum of curvature perturbations produced by canonical model Eq. (3) under slow roll is
| (4) |
with
| (5) |
where . From the expression of power spectrum Eq. (4), qualitatively, a flat potential, , will result in an enhancement of power spectrum. For a canonical inflation model, a flat plateau in potential is often required to amplify the power spectrum. In the following, we will see that a peak in results in a quasi-inflection point in of canonical field. Recalling the field-redefinition Eq. (2), we have
| (6) |
| (7) |
where , , and . From Eqs.(6) and (7), we see that if . That is, a large peak in leads to a quasi-inflection point in . We can amplify the power spectrum by choosing a peaked . We demonstrate this with two concrete examples. We generalize the choice of in Ref. Lin et al. (2020) and Refs. Yi et al. (2021b, a); Gao et al. (2021) to produce multiple peaks in power spectrum of curvature perturbation,
| (8) | |||
| (9) |
with . The choice of the function is inspired by Brans-Dicke theory with a noncanonical kinetic term performing a shift of . In order to avoid singularity, we add a small parameter . These parameters , and control the height, the width and the shape of the peak in function , separately.
We denote the models with potential and by M1 and M2, respectively. and both contain two peaks and will lead to two flat plateaus in . With the parameters listed in table 1, the potentials and of canonical field are shown in Fig. 1. Here we choose and for models M1 and M2, where is the value of inflaton when modes leave the horizon. Note that we can always shift by a constant because of Eq. (2). From Fig. 1, we can see that the potentials and of the canonical field both have two flat plateaus, which could result in two large peaks in the power spectrum.
Since the analytic expressions of and are hard to obtain, it is more convenient to work in the noncanonical models, as we will do in the followings.
| Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| M1 | |||||||||
| M2 |


Working in the spatially flat Friedmann-Robertson-Walker (FRW) metric, we obtain the background equations from action (1)
| (10) | |||
| (11) | |||
| (12) |
where the Hubble parameter , and the dot denotes the derivative with respect to the cosmological time . To the second order of comoving curvature perturbation , the action reads
| (13) |
where , and the prime stands for the derivative with respect to the conformal time , where . The slow-roll parameters and are defined as
| (14) |
The leading order action Eq. (13) predicts a Gaussian spectrum, while non-Gaussian features, which we will discuss in Sec. III, arise from cubic action. Varying the quadratic action with respect to , we obtain the Mukhanov-Sasaki equation Mukhanov (1985); Sasaki (1986)
| (15) |
with
| (16) |
The two-point correlation function and the power spectrum are given as follows
| (17) |
where the mode function is the solution to Eq. (15), and is the quantum field of the curvature perturbation that starts evolution from Bunch-Davies vacuum. The dimensionless scalar power spectrum and its spectral index are defined by
| (18) |
| (19) |
With the parameter sets in Table 1, we solve the Eqs. (10)-(12) and (15) numerically. We show in Fig. 2 the evolution of the inflaton and the slow-roll parameter against -folds , and in Fig. 3 the power spectrum. In Tables. 2 and 3, we list the power index, tensor to scalar ratio, the -folds , the peak scales, and the amplitude of the power spectra in models M1 and M2.
| Model | |||
|---|---|---|---|
| M1 | |||
| M2 |
| Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| M1 | ||||||||
| M2 | ||||||||



.
From the upper panels of Fig. 2, there are two successive plateaus for , where the velocity of inflaton dramatically decreases. In other words, there are two transitory phases where the inflaton behaves like in ultra slow-roll (USR) inflation Kinney (2005); Dimopoulos (2017) which correspond to the two valleys of in the lower panels and lead to the double peaks in the power spectrum, as shown in Fig. 3. The second USR phase takes over before the end of the first one, which keeps -folds within a reasonable range. From Fig. 3, both the power spectra produced by M1 and M2 are the order of at large scales, satisfying the constraints from CMB. At small scales, the power spectra are enhanced to the order of , which serves to produce PBHs after the horizon reentry. The power spectra also satisfy the constraints from CMB -distortion, big bang nucleosynthesis (BBN) and pulsar timing array (PTA) observations Inomata and Nakama (2019); Inomata et al. (2016); Fixsen et al. (1996).
III primordial non-Gaussianity
The inflaton in both models experiences a departure from slow roll during several -folds, and the primordial non-Gaussianity may be very different from slow-roll inflation models which predict negligible non-Gaussianity. In this section, we compute the non-Gaussianity of the two models.
The bispectrum is related to the three-point function as Byrnes et al. (2010); Ade et al. (2016)
| (20) |
and the explicit lengthy expression of bispectrum can be found in Refs. Hazra et al. (2013); Arroja and Tanaka (2011); Zhang et al. (2021). The non-Gaussianity parameter is defined as Creminelli et al. (2007); Byrnes et al. (2010)
| (21) |
We numerically compute the non-Gaussianity parameter in the squeezed limit and the equilateral limit. The results are shown in Figs. 4 and 5 for models M1 and M2, respectively. In squeezed limit, the non-Gaussianity parameter is related to the power index by the consistency relation
| (22) |
The consistency relation was derived originally in the canonical single-field inflation with slow-roll conditions Maldacena (2003). Then it was proved to be true for any inflationary model as long as the inflaton is the only dynamical field in addition to the gravitational field during inflation Creminelli and Zaldarriaga (2004). From the upper panels in Figs. 4 and 5, we can see that the consistency relation (22) holds for the two models. Besides, the non-Gaussianity parameter can reach as large as order at certain scales. Specifically, in the squeezed limit and in the equilateral limit for model M1. For model M2, in the squeezed limit and in the equilateral limit. For both models M1 and M2, has a pretty large value due to the steep growth and decrease of the power spectrum. Moreover, the oscillation nature of in both squeezed and equilateral limits originates from the small waggles in the power spectrum, as can be seen from the insets of Figs. 4 and 5.

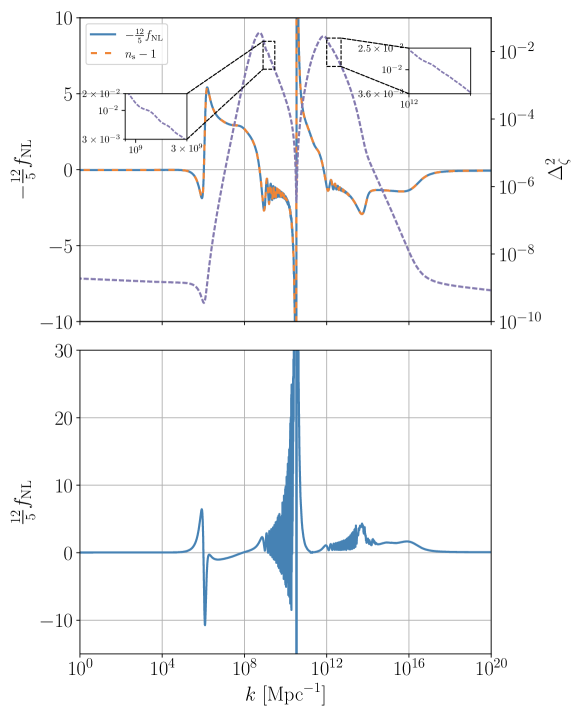
IV PBHs
When the primordial curvature perturbation reenters the horizon during radiation dominated era, if the density contrast exceeds the threshold, it may cause gravitational collapse to form PBHs. The mass of PBH is , where is the horizon mass and we choose the factor Carr (1975). The current fractional energy density of PBHs with mass in DM is Carr et al. (2016); Di and Gong (2018)
| (23) |
where is the solar mass, is the effective degrees of freedom at the formation time, is the current energy density parameter of DM, and is the fractional energy density of PBHs at the formation.
For Gaussian statistic comoving curvature perturbation Özsoy et al. (2018); Tada and Yokoyama (2019)
| (24) |
where is the critical density contrast for the PBHs formation, and is the variance of , the density contrast smoothed on the horizon scales
| (25) |
where W is a window function. During radiation domination, the comoving curvature perturbation is related to density contrast as Musco (2019); De Luca et al. (2019),
| (26) |
Then
| (27) |
is the Fourier transform of window function. We will use a Gaussian window function . The effective degrees of freedom for GeV and for . We take the observational value Aghanim et al. (2020) and Harada et al. (2013); Tada and Yokoyama (2019); Escrivà et al. (2020) in the calculation of PBH abundance 111For the dependence of on the shape of the power spectrum, please refer to Musco (2019); Musco et al. (2021) . The relation between the PBH mass and the scale is Di and Gong (2018)
| (28) |
With Eqs. (23), (24), (28) and the power spectrum obtained in section II, we compute the PBH DM abundance with Gaussian perturbation, , the results are shown in Table 3 and Fig. 6. As excepted, there are two mass ranges of PBHs. From Fig. 6, for the mass range , the PBHs can be the dominance of DM in model M1. The PBH abundance at the peak is about , then almost all DM is PBHs. For M2, is about one percent. In the mass range , the peak of is about and for M1 and M2, respectively. In this mass range, PBHs can be used to explain the origin of Planet 9.

As shown in Sec. III, large non-Gaussianities are produced in M1 and M2, so it is necessary to consider the effect of non-Gaussianity on PBH abundance. The non-Gaussianity-corrected is related to from Gaussian spectrum by Franciolini et al. (2018); Kehagias et al. (2019); Atal and Germani (2019); Riccardi et al. (2021)
| (29) |
where is called the 3rd cumulant,
| (30) |
and
| (31) |
With Gaussian window function, after some calculation, we get
| (32) |
Since the mass of PBHs is almost monochromatic, we can consider only the correction on peak scales. This triple integral is too complicated to perform analytically. We approximately replace by at peaks. This will be justified by numerical computation in our models.
Around the peak, the integral is approximately
| (33) |
Considering that scaling as , then
| (34) |
Substituting Eqs. (27) and (34) into (30), we get
| (35) |
where we used the approximation . Note that the expression of (35) is underestimated because is actually smaller than . The effect of non-Gaussianity of curvature perturbation on PBH abundance is significant unless , namely . The numerical result and approximate result given by Eq. (35) are shown in Table 3. We see that the analytic and numerical results are of the same order. The factor can be extremely small as , and thus is rather infinitesimal. It seems that even though the power spectrum of is amplified to order , the production of PBHs may be violently suppressed by the effect from non-Gaussianities. But honestly, enhancement is also possible as long as , that is, for some models.
The above discussion implies that the abundance of PBH DM could be highly overestimated (or underestimated) without considering non-Gaussianity of . In our model, , which leads to a suppression of PBH formation.
V SIGWs
In Sec. II, we got the power spectrum enhanced at small scales, and we expect that the SIGWs are also amplified. In this section, we compute the energy density fraction of SIGWs.
In Newtonian gauge222For a discussion on the gauge issue of SIGWs, see Lu et al. (2020); Ali et al. (2021); Chang et al. (2020a, b, c); Domènech and Sasaki (2021); Inomata and Terada (2020); Tomikawa and Kobayashi (2020); Yuan et al. (2020); De Luca et al. (2020), the perturbed metric is
| (36) |
where is the Bardeen potential, and the second-order tensor perturbation is transverse and traceless, . In Fourier space, the tensor perturbation is
| (37) |
where the polarization tensors and are
| (38) |
with and are two orthonormal basis vectors which are orthogonal to the wave vector . Neglecting the anisotropic stress, the equation of motion for the tensor perturbation of either polarization is
| (39) |
where and is
| (40) |
in which
| (41) |
The transfer function for the Bardeen potential is defined with its primordial value as
| (42) |
The primordial value is related to the comoving curvature perturbation as
| (43) |
here is defined by
| (44) |
It is worth mentioning that we do not assume anything about the statistical nature of the primordial curvature perturbation, so is affected by the self-interactions of , in which the leading is the primordial non-Gaussianity, and there will be the difference between and obtained in Sec. II.
The solution to Eq. (39) is given by the Green function
| (45) |
where the Green’s function satisfies the equation
| (46) |
During radiation domination, , the Green’s function is
| (47) |
and the transfer function is
| (48) |
where . The power spectrum of tensor perturbation is defined in a similar way to as
| (49) |
Combing the Eqs. (40), (45) and (49), we get the semianalytic expression for Kohri and Terada (2018); Espinosa et al. (2018b)
| (50) |
where . At late time, , the time average of is
| (51) |
The energy density parameter of SIGWs per logarithmic interval of is
| (52) |
Notice that at late time, is a constant since GWs behave like free radiation. With this featrue, we can also express the fractional energy density of SIGWs today as Espinosa et al. (2018b)
| (53) |
where we choose because we are considering the radiation domination.
As mentioned above, the perturbations that induce SIGWs can be non-Gaussian, in order to estimate the contribution of non-Gaussianity to SIGWs, using the nonlinear coupling constant defined as Verde et al. (2000); Komatsu and Spergel (2001)
| (54) |
where is the linear Gaussian part of the curvature perturbation. Then the power spectrum of taking into account of the non-Gaussianity can be expressed as
| (55) |
where , and
| (56) |
It was shown that the non-Gaussian contribution to SIGWs exceeds the Gaussian part if Cai et al. (2019a). Taking as the estimator to parameterize the magnitude of non-Gaussianity Chen et al. (2007), we find the contribution from the non-Gaussian curvature perturbations to SIGWs is negligible, because is not very large at the peak where power spectrum culminates, as shown in Figs. 4 and 5. In the following, we safely use we get in Sec. II instead of to compute SIGWs.
We compute the and the results are shown in Table 3 and Fig. 7. As expected, there are also double peaks in SIGWs at the corresponding scales, and both the peaks are observable in the future. The milli-Hertz SIGWs can be tested by TianQin, Taiji, and LISA. The Hz SIGWs leave a blue-tilted spectrum on the SKA region.

VI conclusion
For PBHs to be all (or most of) the DM, the violation of slow-roll conditions in single-field inflation is necessary as the slow-roll inflation predicts nearly scale-invariant power spectrum of order which hardly generates a significant abundance of PBHs and observable SIGWs. On the other hand, the violation of slow-roll conditions may lead to considerable primordial non-Gaussianity of curvature perturbation. We find that the abundance of PBHs is sensitive to the primordial non-Gaussianity of curvature perturbation and will be altered significantly if the non-Gaussianity parameter . Whether the PBH abundance is suppressed or enhanced depends on being positive or negative, respectively.
We propose a noncanonical inflation model with a double-peak coupling function in the noncanonical kinetic term, which is equivalent to a canonical model with double quasi-inflection points in the potential by field-redefinition. The model driven by both potential and Higgs potential can amplify the power spectrum to at two different small scales while satisfying the constraints from CMB at large scales and keeping -folds . We also numerically calculate the primordial non-Gaussianity in squeezed and equilateral limits. We find that the consistency relation is valid even when the slow-roll conditions are violated. Regrettably, our model predicts large non-Gaussianity with that is positive and the PBH abundance is suppressed saliently, even though the power spectrum is about . However, the energy density of SIGWs is insensitive to primordial non-Gaussianity and thus observable. In this regard, SIGWs are better at characterizing the small-scale power spectrum. In our models, SIGWs will leave a blue-tilted spectrum in SKA sensitivity, and a peak in the sensitivities of LISA, Taiji and TianQin. In addition, it is possible that we observe SIGWs in SGWB, but PBHs hardly exist in the corresponding mass ranges, taking into account the primordial non-Gaussianity.
Acknowledgements.
The author F.Z. would like to thank Prof. Yungui Gong for useful discussion. This research was supported in part by the National Natural Science Foundation of China under Grant No. 11875136; and the Major Program of the National Natural Science Foundation of China under Grant No. 11690021.References
- Abbott et al. (2016a) B. P. Abbott et al. (LIGO Scientific, Virgo), GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence, Phys. Rev. Lett. 116, 241103 (2016a), arXiv:1606.04855 .
- Abbott et al. (2016b) B. P. Abbott et al. (LIGO Scientific, Virgo), Observation of Gravitational Waves from a Binary Black Hole Merger, Phys. Rev. Lett. 116, 061102 (2016b), arXiv:1602.03837 .
- Abbott et al. (2017a) B. . P. . Abbott et al. (LIGO Scientific, Virgo), GW170608: Observation of a 19-solar-mass Binary Black Hole Coalescence, Astrophys. J. Lett. 851, L35 (2017a), arXiv:1711.05578 .
- Abbott et al. (2017b) B. P. Abbott et al. (LIGO Scientific, Virgo), GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral, Phys. Rev. Lett. 119, 161101 (2017b), arXiv:1710.05832 .
- Abbott et al. (2017c) B. P. Abbott et al. (LIGO Scientific, Virgo), GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence, Phys. Rev. Lett. 119, 141101 (2017c), arXiv:1709.09660 .
- Abbott et al. (2017d) B. P. Abbott et al. (LIGO Scientific, VIRGO), GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2, Phys. Rev. Lett. 118, 221101 (2017d), [Erratum: Phys.Rev.Lett. 121, 129901 (2018)], arXiv:1706.01812 .
- Abbott et al. (2019) B. P. Abbott et al. (LIGO Scientific, Virgo), GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs, Phys. Rev. X 9, 031040 (2019), arXiv:1811.12907 .
- Abbott et al. (2020a) R. Abbott et al. (LIGO Scientific, Virgo), GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object, Astrophys. J. Lett. 896, L44 (2020a), arXiv:2006.12611 .
- Abbott et al. (2020b) B. P. Abbott et al. (LIGO Scientific, Virgo), GW190425: Observation of a Compact Binary Coalescence with Total Mass , Astrophys. J. Lett. 892, L3 (2020b), arXiv:2001.01761 .
- Abbott et al. (2020c) R. Abbott et al. (LIGO Scientific, Virgo), GW190412: Observation of a Binary-Black-Hole Coalescence with Asymmetric Masses, Phys. Rev. D 102, 043015 (2020c), arXiv:2004.08342 .
- Carr and Hawking (1974) B. J. Carr and S. W. Hawking, Black holes in the early Universe, Mon. Not. Roy. Astron. Soc. 168, 399 (1974).
- Hawking (1971) S. Hawking, Gravitationally collapsed objects of very low mass, Mon. Not. Roy. Astron. Soc. 152, 75 (1971).
- Bird et al. (2016) S. Bird, I. Cholis, J. B. Muñoz, Y. Ali-Haïmoud, M. Kamionkowski, E. D. Kovetz, A. Raccanelli, and A. G. Riess, Did LIGO detect dark matter?, Phys. Rev. Lett. 116, 201301 (2016), arXiv:1603.00464 .
- Sasaki et al. (2016) M. Sasaki, T. Suyama, T. Tanaka, and S. Yokoyama, Primordial Black Hole Scenario for the Gravitational-Wave Event GW150914, Phys. Rev. Lett. 117, 061101 (2016), [Erratum: Phys.Rev.Lett. 121, 059901 (2018)], arXiv:1603.08338 .
- Takhistov et al. (2021) V. Takhistov, G. M. Fuller, and A. Kusenko, Test for the Origin of Solar Mass Black Holes, Phys. Rev. Lett. 126, 071101 (2021), arXiv:2008.12780 .
- De Luca et al. (2021a) V. De Luca, V. Desjacques, G. Franciolini, P. Pani, and A. Riotto, GW190521 Mass Gap Event and the Primordial Black Hole Scenario, Phys. Rev. Lett. 126, 051101 (2021a), arXiv:2009.01728 .
- Abbott et al. (2021) R. Abbott et al. (LIGO Scientific, Virgo), GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo During the First Half of the Third Observing Run, Phys. Rev. X 11, 021053 (2021), arXiv:2010.14527 .
- De Luca et al. (2021b) V. De Luca, G. Franciolini, and A. Riotto, NANOGrav Data Hints at Primordial Black Holes as Dark Matter, Phys. Rev. Lett. 126, 041303 (2021b), arXiv:2009.08268 .
- Vaskonen and Veermäe (2021) V. Vaskonen and H. Veermäe, Did NANOGrav see a signal from primordial black hole formation?, Phys. Rev. Lett. 126, 051303 (2021), arXiv:2009.07832 .
- Kohri and Terada (2021) K. Kohri and T. Terada, Solar-Mass Primordial Black Holes Explain NANOGrav Hint of Gravitational Waves, Phys. Lett. B 813, 136040 (2021), arXiv:2009.11853 .
- Domènech and Pi (2020) G. Domènech and S. Pi, NANOGrav Hints on Planet-Mass Primordial Black Holes, (2020), arXiv:2010.03976 .
- Atal et al. (2021) V. Atal, A. Sanglas, and N. Triantafyllou, NANOGrav signal as mergers of Stupendously Large Primordial Black Holes, J. Cosmol. Astropart. Phys. 06 (2021) 022, arXiv:2012.14721 .
- Yi and Zhu (2021) Z. Yi and Z.-H. Zhu, NANOGrav signal and LIGO-Virgo Primordial Black Holes from Higgs inflation, (2021), arXiv:2105.01943 .
- Sato-Polito et al. (2019) G. Sato-Polito, E. D. Kovetz, and M. Kamionkowski, Constraints on the primordial curvature power spectrum from primordial black holes, Phys. Rev. D 100, 063521 (2019), arXiv:1904.10971 .
- Akrami et al. (2020) Y. Akrami et al. (Planck), Planck 2018 results. X. Constraints on inflation, Astron. Astrophys. 641, A10 (2020), arXiv:1807.06211 .
- Di and Gong (2018) H. Di and Y. Gong, Primordial black holes and second order gravitational waves from ultra-slow-roll inflation, J. Cosmol. Astropart. Phys. 07 (2018) 007, arXiv:1707.09578 .
- Garcia-Bellido and Ruiz Morales (2017) J. Garcia-Bellido and E. Ruiz Morales, Primordial black holes from single field models of inflation, Phys. Dark Univ. 18, 47 (2017), arXiv:1702.03901 .
- Germani and Prokopec (2017) C. Germani and T. Prokopec, On primordial black holes from an inflection point, Phys. Dark Univ. 18, 6 (2017), arXiv:1706.04226 .
- Lu et al. (2019) Y. Lu, Y. Gong, Z. Yi, and F. Zhang, Constraints on primordial curvature perturbations from primordial black hole dark matter and secondary gravitational waves, J. Cosmol. Astropart. Phys. 12 (2019) 031, arXiv:1907.11896 .
- Motohashi and Hu (2017) H. Motohashi and W. Hu, Primordial Black Holes and Slow-Roll Violation, Phys. Rev. D 96, 063503 (2017), arXiv:1706.06784 .
- Espinosa et al. (2018a) J. R. Espinosa, D. Racco, and A. Riotto, Cosmological Signature of the Standard Model Higgs Vacuum Instability: Primordial Black Holes as Dark Matter, Phys. Rev. Lett. 120, 121301 (2018a), arXiv:1710.11196 .
- Belotsky et al. (2019) K. M. Belotsky, V. I. Dokuchaev, Y. N. Eroshenko, E. A. Esipova, M. Y. Khlopov, L. A. Khromykh, A. A. Kirillov, V. V. Nikulin, S. G. Rubin, and I. V. Svadkovsky, Clusters of primordial black holes, Eur. Phys. J. C 79, 246 (2019), arXiv:1807.06590 .
- Dalianis et al. (2020) I. Dalianis, S. Karydas, and E. Papantonopoulos, Generalized Non-Minimal Derivative Coupling: Application to Inflation and Primordial Black Hole Production, J. Cosmol. Astropart. Phys. 06 (2020) 040, arXiv:1910.00622 .
- Passaglia et al. (2020) S. Passaglia, W. Hu, and H. Motohashi, Primordial black holes as dark matter through Higgs field criticality, Phys. Rev. D 101, 123523 (2020), arXiv:1912.02682 .
- Fu et al. (2019) C. Fu, P. Wu, and H. Yu, Primordial Black Holes from Inflation with Nonminimal Derivative Coupling, Phys. Rev. D 100, 063532 (2019), arXiv:1907.05042 .
- Xu et al. (2020) W.-T. Xu, J. Liu, T.-J. Gao, and Z.-K. Guo, Gravitational waves from double-inflection-point inflation, Phys. Rev. D 101, 023505 (2020), arXiv:1907.05213 .
- Lin et al. (2020) J. Lin, Q. Gao, Y. Gong, Y. Lu, C. Zhang, and F. Zhang, Primordial black holes and secondary gravitational waves from and inflation, Phys. Rev. D 101, 103515 (2020), arXiv:2001.05909 .
- Yi et al. (2021a) Z. Yi, Y. Gong, B. Wang, and Z.-h. Zhu, Primordial black holes and secondary gravitational waves from the Higgs field, Phys. Rev. D 103, 063535 (2021a), arXiv:2007.09957 .
- Yi et al. (2021b) Z. Yi, Q. Gao, Y. Gong, and Z.-h. Zhu, Primordial black holes and scalar-induced secondary gravitational waves from inflationary models with a noncanonical kinetic term, Phys. Rev. D 103, 063534 (2021b), arXiv:2011.10606 .
- Gao et al. (2021) Q. Gao, Y. Gong, and Z. Yi, Primordial black holes and secondary gravitational waves from natural inflation, Nucl. Phys. B 969, 115480 (2021), arXiv:2012.03856 .
- Fumagalli et al. (2020a) J. Fumagalli, S. Renaux-Petel, J. W. Ronayne, and L. T. Witkowski, Turning in the landscape: a new mechanism for generating Primordial Black Holes, (2020a), arXiv:2004.08369 .
- Gundhi et al. (2021) A. Gundhi, S. V. Ketov, and C. F. Steinwachs, Primordial black hole dark matter in dilaton-extended two-field Starobinsky inflation, Phys. Rev. D 103, 083518 (2021), arXiv:2011.05999 .
- Ballesteros et al. (2020) G. Ballesteros, J. Rey, M. Taoso, and A. Urbano, Primordial black holes as dark matter and gravitational waves from single-field polynomial inflation, J. Cosmol. Astropart. Phys. 07 (2020) 025, arXiv:2001.08220 .
- Ragavendra et al. (2021) H. V. Ragavendra, P. Saha, L. Sriramkumar, and J. Silk, Primordial black holes and secondary gravitational waves from ultraslow roll and punctuated inflation, Phys. Rev. D 103, 083510 (2021), arXiv:2008.12202 .
- Palma et al. (2020) G. A. Palma, S. Sypsas, and C. Zenteno, Seeding primordial black holes in multifield inflation, Phys. Rev. Lett. 125, 121301 (2020), arXiv:2004.06106 .
- Braglia et al. (2020) M. Braglia, D. K. Hazra, F. Finelli, G. F. Smoot, L. Sriramkumar, and A. A. Starobinsky, Generating PBHs and small-scale GWs in two-field models of inflation, J. Cosmol. Astropart. Phys. 08 (2020) 001, arXiv:2005.02895 .
- Baumann et al. (2007) D. Baumann, P. J. Steinhardt, K. Takahashi, and K. Ichiki, Gravitational Wave Spectrum Induced by Primordial Scalar Perturbations, Phys. Rev. D 76, 084019 (2007), arXiv:hep-th/0703290 .
- Saito and Yokoyama (2009) R. Saito and J. Yokoyama, Gravitational wave background as a probe of the primordial black hole abundance, Phys. Rev. Lett. 102, 161101 (2009), [Erratum: Phys.Rev.Lett. 107, 069901 (2011)], arXiv:0812.4339 .
- Orlofsky et al. (2017) N. Orlofsky, A. Pierce, and J. D. Wells, Inflationary theory and pulsar timing investigations of primordial black holes and gravitational waves, Phys. Rev. D 95, 063518 (2017), arXiv:1612.05279 .
- Nakama et al. (2017) T. Nakama, J. Silk, and M. Kamionkowski, Stochastic gravitational waves associated with the formation of primordial black holes, Phys. Rev. D 95, 043511 (2017), arXiv:1612.06264 .
- Inomata et al. (2017) K. Inomata, M. Kawasaki, K. Mukaida, Y. Tada, and T. T. Yanagida, Inflationary primordial black holes for the LIGO gravitational wave events and pulsar timing array experiments, Phys. Rev. D 95, 123510 (2017), arXiv:1611.06130 .
- Cai et al. (2019a) R.-g. Cai, S. Pi, and M. Sasaki, Gravitational Waves Induced by non-Gaussian Scalar Perturbations, Phys. Rev. Lett. 122, 201101 (2019a), arXiv:1810.11000 .
- Bartolo et al. (2019) N. Bartolo, V. De Luca, G. Franciolini, A. Lewis, M. Peloso, and A. Riotto, Primordial Black Hole Dark Matter: LISA Serendipity, Phys. Rev. Lett. 122, 211301 (2019), arXiv:1810.12218 .
- Kohri and Terada (2018) K. Kohri and T. Terada, Semianalytic calculation of gravitational wave spectrum nonlinearly induced from primordial curvature perturbations, Phys. Rev. D 97, 123532 (2018), arXiv:1804.08577 .
- Espinosa et al. (2018b) J. R. Espinosa, D. Racco, and A. Riotto, A Cosmological Signature of the SM Higgs Instability: Gravitational Waves, J. Cosmol. Astropart. Phys. 09 (2018) 012, arXiv:1804.07732 .
- Kuroyanagi et al. (2018) S. Kuroyanagi, T. Chiba, and T. Takahashi, Probing the Universe through the Stochastic Gravitational Wave Background, J. Cosmol. Astropart. Phys. 11 (2018) 038, arXiv:1807.00786 .
- Cai et al. (2019b) R.-G. Cai, S. Pi, S.-J. Wang, and X.-Y. Yang, Pulsar Timing Array Constraints on the Induced Gravitational Waves, J. Cosmol. Astropart. Phys. 10 (2019) 059, arXiv:1907.06372 .
- Drees and Xu (2021) M. Drees and Y. Xu, Overshooting, Critical Higgs Inflation and Second Order Gravitational Wave Signatures, Eur. Phys. J. C 81, 182 (2021), arXiv:1905.13581 .
- Inomata et al. (2019a) K. Inomata, K. Kohri, T. Nakama, and T. Terada, Enhancement of Gravitational Waves Induced by Scalar Perturbations due to a Sudden Transition from an Early Matter Era to the Radiation Era, Phys. Rev. D 100, 043532 (2019a), arXiv:1904.12879 .
- Inomata et al. (2019b) K. Inomata, K. Kohri, T. Nakama, and T. Terada, Gravitational Waves Induced by Scalar Perturbations during a Gradual Transition from an Early Matter Era to the Radiation Era, J. Cosmol. Astropart. Phys. 10 (2019) 071, arXiv:1904.12878 .
- Fumagalli et al. (2020b) J. Fumagalli, S. Renaux-Petel, and L. T. Witkowski, Oscillations in the stochastic gravitational wave background from sharp features and particle production during inflation, (2020b), arXiv:2012.02761 .
- Domènech et al. (2020) G. Domènech, S. Pi, and M. Sasaki, Induced gravitational waves as a probe of thermal history of the universe, J. Cosmol. Astropart. Phys. 08 (2020) 017, arXiv:2005.12314 .
- Braglia et al. (2021) M. Braglia, X. Chen, and D. K. Hazra, Probing Primordial Features with the Stochastic Gravitational Wave Background, J. Cosmol. Astropart. Phys. 03 (2021) 005, arXiv:2012.05821 .
- Fumagalli et al. (2021) J. Fumagalli, S. Renaux-Petel, and L. T. Witkowski, Resonant features in the stochastic gravitational wave background, (2021), arXiv:2105.06481 .
- Gao and Yang (2021) T.-J. Gao and X.-Y. Yang, Double peaks of gravitational wave spectrum induced from inflection point inflation, Eur. Phys. J. C 81, 494 (2021), arXiv:2101.07616 .
- Zheng et al. (2021) R. Zheng, J. Shi, and T. Qiu, On Primordial Black Holes generated from inflation with solo/multi-bumpy potential, (2021), arXiv:2106.04303 .
- Maldacena (2003) J. M. Maldacena, Non-Gaussian features of primordial fluctuations in single field inflationary models, J. High Energ. Phys. 05 (2003) 013, arXiv:astro-ph/0210603 .
- Amaro-Seoane et al. (2017) P. Amaro-Seoane et al. (LISA), Laser Interferometer Space Antenna, (2017), arXiv:1702.00786 .
- Danzmann (1997) K. Danzmann, LISA: An ESA cornerstone mission for a gravitational wave observatory, Class. Quant. Grav. 14, 1399 (1997).
- Luo et al. (2016) J. Luo et al. (TianQin), TianQin: a space-borne gravitational wave detector, Class. Quant. Grav. 33, 035010 (2016), arXiv:1512.02076 .
- Hu and Wu (2017) W.-R. Hu and Y.-L. Wu, The Taiji Program in Space for gravitational wave physics and the nature of gravity, Natl. Sci. Rev. 4, 685 (2017).
- Moore et al. (2015) C. J. Moore, R. H. Cole, and C. P. L. Berry, Gravitational-wave sensitivity curves, Class. Quant. Grav. 32, 015014 (2015), arXiv:1408.0740 .
- Mukhanov (1985) V. F. Mukhanov, Gravitational Instability of the Universe Filled with a Scalar Field, JETP Lett. 41, 493 (1985).
- Sasaki (1986) M. Sasaki, Large Scale Quantum Fluctuations in the Inflationary Universe, Prog. Theor. Phys. 76, 1036 (1986).
- Inomata and Nakama (2019) K. Inomata and T. Nakama, Gravitational waves induced by scalar perturbations as probes of the small-scale primordial spectrum, href https://doi.org/10.1103/PhysRevD.99.043511 Phys. Rev. D 99, 043511 (2019), arXiv:1812.00674 .
- Inomata et al. (2016) K. Inomata, M. Kawasaki, and Y. Tada, Revisiting constraints on small scale perturbations from big-bang nucleosynthesis, Phys. Rev. D 94, 043527 (2016), arXiv:1605.04646 .
- Fixsen et al. (1996) D. J. Fixsen, E. S. Cheng, J. M. Gales, J. C. Mather, R. A. Shafer, and E. L. Wright, The Cosmic Microwave Background spectrum from the full COBE FIRAS data set, Astrophys. J. 473, 576 (1996), arXiv:astro-ph/9605054 .
- Kinney (2005) W. H. Kinney, Horizon crossing and inflation with large eta, Phys. Rev. D 72, 023515 (2005), arXiv:gr-qc/0503017 .
- Dimopoulos (2017) K. Dimopoulos, Ultra slow-roll inflation demystified, Phys. Lett. B 775, 262 (2017), arXiv:1707.05644 .
- Byrnes et al. (2010) C. T. Byrnes, M. Gerstenlauer, S. Nurmi, G. Tasinato, and D. Wands, Scale-dependent non-Gaussianity probes inflationary physics, J. Cosmol. Astropart. Phys. 10 (2010) 004, arXiv:1007.4277 .
- Ade et al. (2016) P. A. R. Ade et al. (Planck), Planck 2015 results. XVII. Constraints on primordial non-Gaussianity, Astron. Astrophys. 594, A17 (2016), arXiv:1502.01592 .
- Hazra et al. (2013) D. K. Hazra, L. Sriramkumar, and J. Martin, BINGO: A code for the efficient computation of the scalar bi-spectrum, J. Cosmol. Astropart. Phys. 05 (2013) 026, arXiv:1201.0926 .
- Arroja and Tanaka (2011) F. Arroja and T. Tanaka, A note on the role of the boundary terms for the non-Gaussianity in general k-inflation, J. Cosmol. Astropart. Phys. 05 (2011) 005, arXiv:1103.1102 .
- Zhang et al. (2021) F. Zhang, Y. Gong, J. Lin, Y. Lu, and Z. Yi, Primordial non-Gaussianity from G-inflation, J. Cosmol. Astropart. Phys. 04 (2021) 045, arXiv:2012.06960 .
- Creminelli et al. (2007) P. Creminelli, L. Senatore, M. Zaldarriaga, and M. Tegmark, Limits on f_NL parameters from WMAP 3yr data, J. Cosmol. Astropart. Phys. 03 (2007) 005, arXiv:astro-ph/0610600 .
- Creminelli and Zaldarriaga (2004) P. Creminelli and M. Zaldarriaga, Single field consistency relation for the 3-point function, J. Cosmol. Astropart. Phys. 10 (2004) 006, arXiv:astro-ph/0407059 .
- Carr (1975) B. J. Carr, The Primordial black hole mass spectrum, Astrophys. J. 201, 1 (1975).
- Carr et al. (2016) B. Carr, F. Kuhnel, and M. Sandstad, Primordial Black Holes as Dark Matter, Phys. Rev. D 94, 083504 (2016), arXiv:1607.06077 .
- Özsoy et al. (2018) O. Özsoy, S. Parameswaran, G. Tasinato, and I. Zavala, Mechanisms for Primordial Black Hole Production in String Theory, J. Cosmol. Astropart. Phys. 07 (2018) 005, arXiv:1803.07626 .
- Tada and Yokoyama (2019) Y. Tada and S. Yokoyama, Primordial black hole tower: Dark matter, earth-mass, and LIGO black holes, Phys. Rev. D 100, 023537 (2019), arXiv:1904.10298 .
- Musco (2019) I. Musco, Threshold for primordial black holes: Dependence on the shape of the cosmological perturbations, Phys. Rev. D 100, 123524 (2019), arXiv:1809.02127 .
- De Luca et al. (2019) V. De Luca, G. Franciolini, A. Kehagias, M. Peloso, A. Riotto, and C. Ünal, The Ineludible non-Gaussianity of the Primordial Black Hole Abundance, J. Cosmol. Astropart. Phys. 07 (2019) 048, arXiv:1904.00970 .
- Aghanim et al. (2020) N. Aghanim et al. (Planck), Planck 2018 results. VI. Cosmological parameters, Astron. Astrophys. 641, A6 (2020), arXiv:1807.06209 .
- Harada et al. (2013) T. Harada, C.-M. Yoo, and K. Kohri, Threshold of primordial black hole formation, Phys. Rev. D 88, 084051 (2013), [Erratum: Phys.Rev.D 89, 029903 (2014)], arXiv:1309.4201 .
- Escrivà et al. (2020) A. Escrivà, C. Germani, and R. K. Sheth, Universal threshold for primordial black hole formation, Phys. Rev. D 101, 044022 (2020), arXiv:1907.13311 .
- Musco et al. (2021) I. Musco, V. De Luca, G. Franciolini, and A. Riotto, Threshold for primordial black holes. II. A simple analytic prescription, Phys. Rev. D 103, 063538 (2021), arXiv:2011.03014 .
- Carr et al. (2010) B. J. Carr, K. Kohri, Y. Sendouda, and J. Yokoyama, New cosmological constraints on primordial black holes, Phys. Rev. D 81, 104019 (2010), arXiv:0912.5297 .
- Laha (2019) R. Laha, Primordial Black Holes as a Dark Matter Candidate Are Severely Constrained by the Galactic Center 511 keV -Ray Line, Phys. Rev. Lett. 123, 251101 (2019), arXiv:1906.09994 .
- Dasgupta et al. (2020) B. Dasgupta, R. Laha, and A. Ray, Neutrino and positron constraints on spinning primordial black hole dark matter, Phys. Rev. Lett. 125, 101101 (2020), arXiv:1912.01014 .
- Niikura et al. (2019) H. Niikura et al., Microlensing constraints on primordial black holes with Subaru/HSC Andromeda observations, Nature Astron. 3, 524 (2019), arXiv:1701.02151 .
- Griest et al. (2013) K. Griest, A. M. Cieplak, and M. J. Lehner, New Limits on Primordial Black Hole Dark Matter from an Analysis of Kepler Source Microlensing Data, Phys. Rev. Lett. 111, 181302 (2013).
- Tisserand et al. (2007) P. Tisserand et al. (EROS-2), Limits on the Macho Content of the Galactic Halo from the EROS-2 Survey of the Magellanic Clouds, Astron. Astrophys. 469, 387 (2007), arXiv:astro-ph/0607207 .
- Ali-Haïmoud et al. (2017) Y. Ali-Haïmoud, E. D. Kovetz, and M. Kamionkowski, Merger rate of primordial black-hole binaries, Phys. Rev. D 96, 123523 (2017), arXiv:1709.06576 .
- Raidal et al. (2017) M. Raidal, V. Vaskonen, and H. Veermäe, Gravitational Waves from Primordial Black Hole Mergers, J. Cosmol. Astropart. Phys. 09 (2017) 037, arXiv:1707.01480 .
- Ali-Haïmoud and Kamionkowski (2017) Y. Ali-Haïmoud and M. Kamionkowski, Cosmic microwave background limits on accreting primordial black holes, Phys. Rev. D 95, 043534 (2017), arXiv:1612.05644 .
- Poulin et al. (2017) V. Poulin, P. D. Serpico, F. Calore, S. Clesse, and K. Kohri, CMB bounds on disk-accreting massive primordial black holes, Phys. Rev. D 96, 083524 (2017), arXiv:1707.04206 .
- Wang et al. (2019) S. Wang, T. Terada, and K. Kohri, Prospective constraints on the primordial black hole abundance from the stochastic gravitational-wave backgrounds produced by coalescing events and curvature perturbations, Phys. Rev. D 99, 103531 (2019), [Erratum: Phys.Rev.D 101, 069901 (2020)], arXiv:1903.05924 .
- Franciolini et al. (2018) G. Franciolini, A. Kehagias, S. Matarrese, and A. Riotto, Primordial Black Holes from Inflation and non-Gaussianity, J. Cosmol. Astropart. Phys. 03 (2018) 016, arXiv:1801.09415 .
- Kehagias et al. (2019) A. Kehagias, I. Musco, and A. Riotto, Non-Gaussian Formation of Primordial Black Holes: Effects on the Threshold, J. Cosmol. Astropart. Phys. 12 (2019) 029, arXiv:1906.07135 .
- Atal and Germani (2019) V. Atal and C. Germani, The role of non-gaussianities in Primordial Black Hole formation, Phys. Dark Univ. 24, 100275 (2019), arXiv:1811.07857 .
- Riccardi et al. (2021) F. Riccardi, M. Taoso, and A. Urbano, Solving peak theory in the presence of local non-gaussianities, (2021), arXiv:2102.04084 .
- Lu et al. (2020) Y. Lu, A. Ali, Y. Gong, J. Lin, and F. Zhang, Gauge transformation of scalar induced gravitational waves, Phys. Rev. D 102, 083503 (2020), arXiv:2006.03450 .
- Ali et al. (2021) A. Ali, Y. Gong, and Y. Lu, Gauge transformation of scalar induced tensor perturbation during matter domination, Phys. Rev. D 103, 043516 (2021), arXiv:2009.11081 .
- Chang et al. (2020a) Z. Chang, S. Wang, and Q.-H. Zhu, Note on gauge invariance of second order cosmological perturbations 10.1088/1674-1137/ac0c74 (2020a), arXiv:2009.11025 .
- Chang et al. (2020b) Z. Chang, S. Wang, and Q.-H. Zhu, Gauge Invariant Second Order Gravitational Waves, (2020b), arXiv:2009.11994 .
- Chang et al. (2020c) Z. Chang, S. Wang, and Q.-H. Zhu, On the Gauge Invariance of Scalar Induced Gravitational Waves: Gauge Fixings Considered, (2020c), arXiv:2010.01487 .
- Domènech and Sasaki (2021) G. Domènech and M. Sasaki, Approximate gauge independence of the induced gravitational wave spectrum, Phys. Rev. D 103, 063531 (2021), arXiv:2012.14016 .
- Inomata and Terada (2020) K. Inomata and T. Terada, Gauge Independence of Induced Gravitational Waves, Phys. Rev. D 101, 023523 (2020), arXiv:1912.00785 .
- Tomikawa and Kobayashi (2020) K. Tomikawa and T. Kobayashi, Gauge dependence of gravitational waves generated at second order from scalar perturbations, Phys. Rev. D 101, 083529 (2020), arXiv:1910.01880 .
- Yuan et al. (2020) C. Yuan, Z.-C. Chen, and Q.-G. Huang, Scalar induced gravitational waves in different gauges, Phys. Rev. D 101, 063018 (2020), arXiv:1912.00885 .
- De Luca et al. (2020) V. De Luca, G. Franciolini, A. Kehagias, and A. Riotto, On the Gauge Invariance of Cosmological Gravitational Waves, J. Cosmol. Astropart. Phys. 03 (2020) 014, arXiv:1911.09689 .
- Verde et al. (2000) L. Verde, L.-M. Wang, A. Heavens, and M. Kamionkowski, Large scale structure, the cosmic microwave background, and primordial non-gaussianity, Mon. Not. Roy. Astron. Soc. 313, L141 (2000), arXiv:astro-ph/9906301 .
- Komatsu and Spergel (2001) E. Komatsu and D. N. Spergel, Acoustic signatures in the primary microwave background bispectrum, Phys. Rev. D 63, 063002 (2001), arXiv:astro-ph/0005036 .
- Chen et al. (2007) X. Chen, M.-x. Huang, S. Kachru, and G. Shiu, Observational signatures and non-Gaussianities of general single field inflation, J. Cosmol. Astropart. Phys. 01 (2007) 002, arXiv:hep-th/0605045 .
- Ferdman et al. (2010) R. D. Ferdman et al., The European Pulsar Timing Array: current efforts and a LEAP toward the future, Class. Quant. Grav. 27, 084014 (2010), arXiv:1003.3405 .
- Hobbs et al. (2010) G. Hobbs et al., The international pulsar timing array project: using pulsars as a gravitational wave detector, Class. Quant. Grav. 27, 084013 (2010), arXiv:0911.5206 .
- McLaughlin (2013) M. A. McLaughlin, The North American Nanohertz Observatory for Gravitational Waves, Class. Quant. Grav. 30, 224008 (2013), arXiv:1310.0758 .
- Hobbs (2013) G. Hobbs, The Parkes Pulsar Timing Array, Class. Quant. Grav. 30, 224007 (2013), arXiv:1307.2629 .
- Harry (2010) G. M. Harry (LIGO Scientific), Advanced LIGO: The next generation of gravitational wave detectors, Class. Quant. Grav. 27, 084006 (2010).
- Aasi et al. (2015) J. Aasi et al. (LIGO Scientific), Advanced LIGO, Class. Quant. Grav. 32, 074001 (2015), arXiv:1411.4547 .