Do Selective Prediction Approaches Consistently Outperform the Simplest Baseline ‘MaxProb’?
Selective Prediction Approaches Fail to Consistently Outperform the Simplest Baseline Despite Using Additional Resources
Investigating Selective Prediction Approaches Across Several Tasks in IID, OOD, and Adversarial Settings
Abstract
In order to equip NLP systems with selective prediction capability, several task-specific approaches have been proposed. However, which approaches work best across tasks or even if they consistently outperform the simplest baseline ‘MaxProb’ remains to be explored. To this end, we systematically study ‘selective prediction’ in a large-scale setup of datasets across several NLP tasks. Through comprehensive experiments under in-domain (IID), out-of-domain (OOD), and adversarial (ADV) settings, we show that despite leveraging additional resources (held-out data/computation), none of the existing approaches consistently and considerably outperforms MaxProb in all three settings. Furthermore, their performance does not translate well across tasks. For instance, Monte-Carlo Dropout outperforms all other approaches on Duplicate Detection datasets but does not fare well on NLI datasets, especially in the OOD setting. Thus, we recommend that future selective prediction approaches should be evaluated across tasks and settings for reliable estimation of their capabilities.
1 Introduction
Despite impressive progress made in Natural Language Processing (NLP), it is unreasonable to expect models to be perfect in their predictions. They often make incorrect predictions, especially when inputs tend to diverge from their training data distribution Elsahar and Gallé (2019); Miller et al. (2020); Koh et al. (2021). While this is acceptable for tolerant applications like movie recommendations, high risk associated with incorrect predictions hinders the adoption of these systems in real-world safety-critical domains like biomedical and autonomous robots. In such scenarios, selective prediction becomes crucial as it allows maintaining high accuracy by abstaining on instances where error is likely.
Selective Prediction (SP) has been studied in machine learning Chow (1957); El-Yaniv et al. (2010) and computer vision Geifman and El-Yaniv (2017, 2019), but has only recently gained attention in NLP. Kamath et al. (2020) proposed a post-hoc calibration-based SP technique for Question-Answering (QA) datasets. Garg and Moschitti (2021) distill the QA model to filter out error-prone questions. Unfortunately, despite the shared goal of making NLP systems robust and reliable for real-world applications, SP has remained underexplored; the community does not know which techniques work best across tasks/settings or even if they consistently outperform the simplest baseline ‘MaxProb’ Hendrycks and Gimpel (2017) (that uses the maximum softmax probability as the confidence estimator for selective prediction).
In this work, we address the above point and study selective prediction in a large-scale setup of datasets across NLI, Duplicate Detection, and QA tasks. We conduct comprehensive experiments under In-Domain (IID), Out-Of-Domain (OOD), and Adversarial (ADV) settings that result in the following findings:
-
1.
None of the existing SP approaches consistently and considerably outperforms MaxProb.
Slight improvement in IID: Most of the approaches outperform MaxProb in the IID setting; however, the magnitude of improvement is very small (Figure 1). For instance, MCD achieves an average improvement of just on AUC value across all NLI datasets.
Negligible improvement in OOD: The magnitude of improvement is even lesser () than that observed in the IID setting (Figure 2(a)). In a few cases, we also observe performance degradation (higher AUC than MaxProb).
Performance degradation in ADV: All the approaches fail to even match the MaxProb performance in ADV setting (Figure 2(b)). For instance, MCD degrades the AUC value by on duplicate detection datasets and calibration degrades by on NLI datasets in ADV setting.
-
2.
Approaches do not translate well across tasks: We find that a single approach does not achieve the best performance across all tasks. For instance, MCD outperforms all other approaches on Duplicate Detection datasets but does not fare well on the NLI datasets.
-
3.
Existing approaches require additional resources: MCD requires additional computation and calibration-based approaches require a held-out dataset. In contrast, MaxProb does not require any such resources and still outperforms them, especially in the ADV setting.
Overall, our results highlight that there is a need to develop stronger selective prediction approaches that perform well across tasks while being computationally efficient. To foster development in this field, we release our code and experimental setup.
2 Selective Prediction
2.1 Formulation
A selective prediction system comprises of a predictor () that gives the model’s prediction on an input (), and a selector () that determines if the system should output the prediction made by i.e.
Usually, comprises of a confidence estimator that indicates prediction confidence and a threshold that controls the abstention level:
An SP system makes trade-offs between and . For a dataset , coverage at a threshold is defined as the fraction of total instances answered by the system (where ) and risk is the error on the answered instances:
where, is the error on instance .
With decrease in , coverage will increase, but the risk will usually also increase. The overall SP performance is measured by the area under Risk-Coverage curve El-Yaniv et al. (2010) which plots risk against coverage for all threshold values. Lower the AUC, the better the SP system as it represents lower average risk across all thresholds. We note that confidence calibration and OOD detection are related tasks but are non-trivially different from selective prediction as detailed in section A.
2.2 Approaches
Usually, the last layer of models has a softmax activation function that gives the probability distribution over all possible answer candidates . is the set of labels for classification tasks, answer options for multiple-choice QA, all input tokens (for start and end logits) for extractive QA, and all vocabulary tokens for generative tasks. Thus, predictor is defined as:
Maximum Softmax Probability
(MaxProb): Hendrycks and Gimpel (2017) introduced a simple method that uses the maximum softmax probability as the confidence estimator i.e.
Monte-Carlo Dropout
(MCD): Gal and Ghahramani (2016) proposed to make multiple predictions on the test input using different dropout masks and ensemble them to get the confidence estimate.
Label Smoothing
(LS): Szegedy et al. (2016) proposed to compute cross-entropy loss with a weighted mixture of target labels during training instead of ‘hard’ labels. This prevents the network from becoming over-confident in its predictions.
Calibration
(Calib): In calibration, a held-out dataset is annotated based on the correctness of the model’s predictions (correct as positive and incorrect as negative) and another model (calibrator) is trained on this annotated binary classification dataset. The softmax probability assigned to the positive class is used as the confidence estimator for SP. Kamath et al. (2020) study a calibration-based SP technique for Question Answering datasets. They train a random forest model as calibrator over features such as input length and probabilities of top 5 predictions. We refer to this approach as Calib C. Inspired by calibration technique presented in Jiang et al. (2021), we also train calibrator as a regression model (Calib R) by annotating the heldout dataset on a continuous scale instead of categorical labels (positive and negative as done in Calib C). We compute these annotations using MaxProb as:
Furthermore, we train a transformer-based model for calibration (Calib T) that leverages the entire input text instead of features derived from it Garg and Moschitti (2021).
3 Experimental Setup
3.1 Tasks and Settings:
We conduct experiments with datasets across Natural Language Inference (NLI), Duplicate Detection, and Question-Answering (QA)s tasks and evaluate the efficacy of various SP techniques in IID, OOD, and adversarial (ADV) settings.
NLI: We train our models with SNLI Bowman et al. (2015) / MNLI Williams et al. (2018) / DNLI Welleck et al. (2019) and use HANS McCoy et al. (2019) , Breaking NLI Glockner et al. (2018), NLI-Diagnostics Wang et al. (2018) , Stress Test Naik et al. (2018) as adversarial datasets. While training with SNLI, we consider SNLI evaluation dataset as IID and MNLI, DNLI datasets as OOD. Similarly, while training with MNLI, we consider SNLI and DNLI datasets as OOD.
3.2 Approaches:
Training: We run all our experiments using bert-base model Devlin et al. (2019) with batch size of and learning rate ranging in . All experiments are done with Nvidia V100 16GB GPUs.
Calibration: For calibrating QA models, we use input length, predicted answer length, and softmax probabilities of top predictions as the features (similar to Kamath et al. (2020)). For calibrating NLI and duplicate detection models, we use input lengths (of premise/sentence1 and hypothesis/sentence2), softmax probabilities assigned to the labels, and the predicted label as the features. We train calibrators using random forest implementations of Scikit-learn Pedregosa et al. (2011) for Calib C and Calib R approaches, and train a bert-base model for Calib T. In all calibration approaches, we calibrate using the IID held-out dataset and use softmax probability assigned to the positive class as the confidence estimate for SP.
Label Smoothing: For LS, we use MaxProb of the model trained with label smoothing as the confidence estimator for SP. To the best of our knowledge, LS is designed for classification tasks only. Hence, we do not evaluate it for QA tasks.




4 Results and Analysis
4.1 Slight Improvement in IID
We compare SP performance of various approaches under IID setting in Figure 1. Though all the approaches except Calib T outperform MaxProb in most cases, the magnitude of improvement is very small. For instance, MCD achieves an average improvement of just on AUC value across all NLI datasets.
Calib C and Calib R achieve the highest improvement on DNLI: We find that they benefit from using the predicted label as a feature for calibration. Specifically, the model’s prediction accuracy varies greatly across labels (, , and for entailment, contradiction, and neutral labels respectively). This implies that when the model’s prediction is neutral, it is relatively less likely to be correct (at least in the IID setting). Calib C and R approaches leverage this signal and tune the confidence estimator using a held-out dataset and thus achieve superior SP performance.
4.2 Negligible Improvement / Degradation in OOD and ADV
Figure 2(a), 2(b) compare the SP performance in OOD and ADV setting respectively. The results have been averaged over all the task-specific OOD/ADV datasets mentioned in Section 3 to observe the general trend.111Refer appendix for more details In the OOD setting, we find that the approaches lead to a negligible improvement in AUC. Notable improvement is achieved only by MCD in the case of QQP dataset.
In ADV setting, all approaches degrade SP performance: Surprisingly, MCD that performed relatively well in IID and OOD settings, degrades more (by AUC) in comparison to other approaches (except Calib T which does not perform well in all three settings). This is because ensembling degrades the overall confidence estimate as the individual models of the ensemble achieve poor prediction accuracy in the ADV setting.
4.3 Calib T Degrades Performance
Calib C and Calib R slightly outperform MaxProb in most IID and OOD cases. However, Calib T considerably degrades the performance in nearly all the cases. We hypothesize that associating correctness directly with input text embeddings could be a harder challenge for the model as embeddings of correct and incorrect instances usually do not differ significantly. In contrast, as discussed before, providing features such as predicted label and softmax probabilities explicitly may help Calib C and R approaches in finding some distinguishing patterns that improve the selective prediction performance.
4.4 Existing Approaches Require Additional Resources
Unlike typical ensembling, MCD does not require training or storing multiple models but, it requires making multiple inferences and can still become practically infeasible for large models such as BERT as their inference cost is high. Calibration-based approaches need additional held-out data and careful feature engineering to train the calibrator. Despite being computationally expensive, these approaches fail to consistently outperform MaxProb that does not require any such additional resources.
4.5 Effect of Increasing Dropout Masks in MCD
With the increase in number of dropout masks used in MCD, the SP performance improves (from MCD lite with 10 masks MCD with 30 masks). We hypothesize that combining more predictions on the same input results in a more accurate overall output due to the ensembling effect. However, we note that both MCD lite and MCD degrade SP performance in the ADV setting as previously explained.
4.6 No Clear Winner
None of the approaches consistently and considerably outperforms MaxProb in all three settings. Most approaches do not fare well in OOD and ADV settings. Furthermore, a single approach does not achieve the highest performance across all tasks. For instance, MCD outperforms all other approaches on Duplicate Detection datasets but does not perform well on NLI datasets (as Calib C beats MCD, especially in the OOD setting). This indicates that these approaches do not translate well across tasks.
5 Conclusion
Selective prediction ability is crucial for NLP systems to be reliably deployed in real-world applications and we presented the most systematic study of existing selective prediction methods. Our study involves datasets across several NLP tasks and evaluation of existing selective prediction approaches in IID, OOD, and ADV settings. We showed that despite leveraging additional resources (held-out data/computation), they fail to consistently and considerably outperform the simplest baseline (MaxProb) in all three settings. Furthermore, we demonstrated that these approaches do not translate well across tasks as a single approach does not achieve the highest performance across all tasks. Overall, our results highlight that there is a need to develop stronger selective prediction approaches that perform well across multiple tasks (QA, NLI, etc.) and settings (IID, OOD, and ADV) while being computationally efficient.
References
- Bowman et al. (2015) Samuel R. Bowman, Gabor Angeli, Christopher Potts, and Christopher D. Manning. 2015. A large annotated corpus for learning natural language inference. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pages 632–642, Lisbon, Portugal. Association for Computational Linguistics.
- Chow (1957) Chi-Keung Chow. 1957. An optimum character recognition system using decision functions. IRE Transactions on Electronic Computers, (4):247–254.
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 4171–4186, Minneapolis, Minnesota. Association for Computational Linguistics.
- Dolan and Brockett (2005) William B Dolan and Chris Brockett. 2005. Automatically constructing a corpus of sentential paraphrases. In Proceedings of the Third International Workshop on Paraphrasing (IWP2005).
- Dunn et al. (2017) Matthew Dunn, Levent Sagun, Mike Higgins, V Ugur Guney, Volkan Cirik, and Kyunghyun Cho. 2017. Searchqa: A new q&a dataset augmented with context from a search engine. arXiv preprint arXiv:1704.05179.
- El-Yaniv et al. (2010) Ran El-Yaniv et al. 2010. On the foundations of noise-free selective classification. Journal of Machine Learning Research, 11(5).
- Elsahar and Gallé (2019) Hady Elsahar and Matthias Gallé. 2019. To annotate or not? predicting performance drop under domain shift. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pages 2163–2173, Hong Kong, China. Association for Computational Linguistics.
- Gal and Ghahramani (2016) Yarin Gal and Zoubin Ghahramani. 2016. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In international conference on machine learning, pages 1050–1059. PMLR.
- Garg and Moschitti (2021) Siddhant Garg and Alessandro Moschitti. 2021. Will this question be answered? question filtering via answer model distillation for efficient question answering. arXiv preprint arXiv:2109.07009.
- Geifman and El-Yaniv (2017) Yonatan Geifman and Ran El-Yaniv. 2017. Selective classification for deep neural networks. In NIPS.
- Geifman and El-Yaniv (2019) Yonatan Geifman and Ran El-Yaniv. 2019. Selectivenet: A deep neural network with an integrated reject option. In ICML.
- Glockner et al. (2018) Max Glockner, Vered Shwartz, and Yoav Goldberg. 2018. Breaking NLI systems with sentences that require simple lexical inferences. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), pages 650–655, Melbourne, Australia. Association for Computational Linguistics.
- Hendrycks and Gimpel (2017) Dan Hendrycks and Kevin Gimpel. 2017. A baseline for detecting misclassified and out-of-distribution examples in neural networks. Proceedings of International Conference on Learning Representations.
- Hendrycks et al. (2020) Dan Hendrycks, Xiaoyuan Liu, Eric Wallace, Adam Dziedzic, Rishabh Krishnan, and Dawn Song. 2020. Pretrained transformers improve out-of-distribution robustness. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 2744–2751, Online. Association for Computational Linguistics.
- Iyer et al. (2017) Shankar Iyer, Nikhil Dandekar, and Kornél Csernai. 2017. First quora dataset release: Question pairs. data. quora. com.
- Jiang et al. (2021) Zhengbao Jiang, Jun Araki, Haibo Ding, and Graham Neubig. 2021. How Can We Know When Language Models Know? On the Calibration of Language Models for Question Answering. Transactions of the Association for Computational Linguistics, 9:962–977.
- Joshi et al. (2017) Mandar Joshi, Eunsol Choi, Daniel Weld, and Luke Zettlemoyer. 2017. TriviaQA: A large scale distantly supervised challenge dataset for reading comprehension. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 1601–1611, Vancouver, Canada. Association for Computational Linguistics.
- Kamath et al. (2020) Amita Kamath, Robin Jia, and Percy Liang. 2020. Selective question answering under domain shift. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 5684–5696, Online. Association for Computational Linguistics.
- Koh et al. (2021) Pang Wei Koh, Shiori Sagawa, Henrik Marklund, Sang Michael Xie, Marvin Zhang, Akshay Balsubramani, Weihua Hu, Michihiro Yasunaga, Richard Lanas Phillips, Irena Gao, Tony Lee, Etienne David, Ian Stavness, Wei Guo, Berton Earnshaw, Imran Haque, Sara M Beery, Jure Leskovec, Anshul Kundaje, Emma Pierson, Sergey Levine, Chelsea Finn, and Percy Liang. 2021. Wilds: A benchmark of in-the-wild distribution shifts. In Proceedings of the 38th International Conference on Machine Learning, volume 139 of Proceedings of Machine Learning Research, pages 5637–5664. PMLR.
- Kwiatkowski et al. (2019) Tom Kwiatkowski, Jennimaria Palomaki, Olivia Redfield, Michael Collins, Ankur Parikh, Chris Alberti, Danielle Epstein, Illia Polosukhin, Jacob Devlin, Kenton Lee, Kristina Toutanova, Llion Jones, Matthew Kelcey, Ming-Wei Chang, Andrew M. Dai, Jakob Uszkoreit, Quoc Le, and Slav Petrov. 2019. Natural questions: A benchmark for question answering research. Transactions of the Association for Computational Linguistics, 7:452–466.
- McCoy et al. (2019) Tom McCoy, Ellie Pavlick, and Tal Linzen. 2019. Right for the wrong reasons: Diagnosing syntactic heuristics in natural language inference. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 3428–3448, Florence, Italy. Association for Computational Linguistics.
- Miller et al. (2020) John Miller, Karl Krauth, Benjamin Recht, and Ludwig Schmidt. 2020. The effect of natural distribution shift on question answering models. In International Conference on Machine Learning, pages 6905–6916. PMLR.
- Mishra et al. (2020) Swaroop Mishra, A. Arunkumar, Chris Bryan, and Chitta Baral. 2020. Our evaluation metric needs an update to encourage generalization. ArXiv, abs/2007.06898.
- Naik et al. (2018) Aakanksha Naik, Abhilasha Ravichander, Norman Sadeh, Carolyn Rose, and Graham Neubig. 2018. Stress test evaluation for natural language inference. arXiv preprint arXiv:1806.00692.
- Pedregosa et al. (2011) Fabian Pedregosa, Gaël Varoquaux, Alexandre Gramfort, Vincent Michel, Bertrand Thirion, Olivier Grisel, Mathieu Blondel, Peter Prettenhofer, Ron Weiss, Vincent Dubourg, et al. 2011. Scikit-learn: Machine learning in python. the Journal of machine Learning research, 12:2825–2830.
- Platt et al. (1999) John Platt et al. 1999. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Advances in large margin classifiers, 10(3):61–74.
- Rajpurkar et al. (2016) Pranav Rajpurkar, Jian Zhang, Konstantin Lopyrev, and Percy Liang. 2016. SQuAD: 100,000+ questions for machine comprehension of text. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, pages 2383–2392, Austin, Texas. Association for Computational Linguistics.
- Szegedy et al. (2016) Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jonathon Shlens, and Zbigniew Wojna. 2016. Rethinking the inception architecture for computer vision. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 2818–2826.
- Talmor and Berant (2019) Alon Talmor and Jonathan Berant. 2019. MultiQA: An empirical investigation of generalization and transfer in reading comprehension. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 4911–4921, Florence, Italy. Association for Computational Linguistics.
- Trischler et al. (2017) Adam Trischler, Tong Wang, Xingdi Yuan, Justin Harris, Alessandro Sordoni, Philip Bachman, and Kaheer Suleman. 2017. NewsQA: A machine comprehension dataset. In Proceedings of the 2nd Workshop on Representation Learning for NLP, pages 191–200, Vancouver, Canada. Association for Computational Linguistics.
- Wang et al. (2018) Alex Wang, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel Bowman. 2018. GLUE: A multi-task benchmark and analysis platform for natural language understanding. In Proceedings of the 2018 EMNLP Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP, pages 353–355, Brussels, Belgium. Association for Computational Linguistics.
- Welleck et al. (2019) Sean Welleck, Jason Weston, Arthur Szlam, and Kyunghyun Cho. 2019. Dialogue natural language inference. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 3731–3741, Florence, Italy. Association for Computational Linguistics.
- Williams et al. (2018) Adina Williams, Nikita Nangia, and Samuel Bowman. 2018. A broad-coverage challenge corpus for sentence understanding through inference. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers), pages 1112–1122, New Orleans, Louisiana. Association for Computational Linguistics.
- Yang et al. (2018) Zhilin Yang, Peng Qi, Saizheng Zhang, Yoshua Bengio, William Cohen, Ruslan Salakhutdinov, and Christopher D. Manning. 2018. HotpotQA: A dataset for diverse, explainable multi-hop question answering. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pages 2369–2380, Brussels, Belgium. Association for Computational Linguistics.
- Zhang et al. (2019) Yuan Zhang, Jason Baldridge, and Luheng He. 2019. PAWS: Paraphrase adversaries from word scrambling. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 1298–1308, Minneapolis, Minnesota. Association for Computational Linguistics.
Appendix A Related Tasks
A.1 Confidence Calibration
Selective Prediction is closely related to confidence calibration Platt et al. (1999) i.e aligning model’s output probability with the true probability of its predictions. Calibration focuses on adjusting the overall confidence level of a model, while selective prediction is based on relative confidence among the examples i.e systems are judged on their ability to rank correct predictions higher than incorrect predictions.
A.2 Out-of-Domain Detection
Using OOD Detection systems for selective prediction (abstain on all detected OOD instances) would be too conservative as it has been shown that models are able to correctly answer a significant fraction of OOD instances Talmor and Berant (2019); Hendrycks et al. (2020); Mishra et al. (2020).


Appendix B Why Lower AUC is Better?
Small magnitude values of area under curve (AUC) are preferred as they represent low average risk across all confidence thresholds.
Appendix C Comparing SP Approaches
Table 1 compares SP performance (AUC of risk-coverage curve) of various approaches for Duplicate Detection datasets. Table 2 compares SP performance (AUC of risk-coverage curve) of various approaches for QA datasets. Table 3 compares SP performance (AUC of risk-coverage curve) of various approaches for NLI datasets.
| Train On | Method | IID | OOD avg. | ADV avg. |
|---|---|---|---|---|
| QQP | MaxProb | 2.0 | 31.72 | 60.9 |
| MCD lite | 1.85 | 23.83 | 62.53 | |
| MCD | 1.8 | 23.61 | 62.52 | |
| LS | 2.08 | 27.92 | 61.92 | |
| Calib C | 2.04 | 31.09 | 61.22 | |
| Calib R | 2.07 | 28.53 | 60.68 | |
| Calib T | 4.21 | 38.25 | 60.25 | |
| MRPC | MaxProb | 6.13 | 40.46 | 63.88 |
| MCD lite | 5.48 | 38.23 | 65.76 | |
| MCD( | 5.35 | 38.21 | 65.62 | |
| LS | 6.08 | 39.05 | 64.99 | |
| Calib C | 6.17 | 39.82 | 64.99 | |
| Calib R | 6.52 | 39.99 | 65.13 | |
| Calib T | 13.35 | 39.75 | 64.22 |
| Train On | Method | IID | OOD avg. | ADV avg. |
|---|---|---|---|---|
| SQuAD | MaxProb | 6.71 | 46.73 | 33.69 |
| MCD lite | 6.06 | 44.56 | 33.34 | |
| MCD | 6.00 | 44.35 | 33.05 | |
| Calib C | 6.15 | 45.93 | 33.27 | |
| Calib R | 6.25 | 45.94 | 33.18 | |
| Calib T | 14.72 | 60.31 | 47.87 |
| Train On | Method | IID | OOD avg. | ADV avg. |
|---|---|---|---|---|
| SNLI | MaxProb | 2.78 | 23.34 | 32.4 |
| MCD(K=10) | 2.52 | 23.96 | 32.61 | |
| MCD(K=30) | 2.47 | 23.81 | 32.47 | |
| LS | 2.7 | 22.42 | 31.7 | |
| Calib C | 2.57 | 22.47 | 33.0 | |
| Calib R | 2.61 | 23.12 | 33.95 | |
| Calib T | 7.02 | 34.74 | 40.68 | |
| MNLI | MaxProb | 5.47 | 16.48 | 28.39 |
| MCD(K=10) | 5.07 | 16.29 | 29.42 | |
| MCD(K=30) | 4.92 | 16.18 | 29.18 | |
| LS | 5.18 | 16.94 | 28.55 | |
| Calib C | 5.16 | 14.16 | 29.57 | |
| Calib R | 5.28 | 14.84 | 29.67 | |
| Calib T | 13.51 | 26.12 | 35.79 | |
| DNLI | MaxProb | 7.36 | 53.59 | 51.85 |
| MCD(K=10) | 7.17 | 53.77 | 53.23 | |
| MCD(K=30) | 6.69 | 53.67 | 53.24 | |
| LS | 5.13 | 53.04 | 53.67 | |
| Calib C | 3.88 | 52.35 | 52.91 | |
| Calib R | 3.9 | 53.08 | 52.83 | |
| Calib T | 5.46 | 53.58 | 58.13 |
Appendix D MaxProb for Selective Prediction
Figure 3(a) shows the trend of accuracy against maxProb for various models in the IID setting. It can be observed that with the increase in MaxProb the accuracy usually increases. This implies that a higher value of MaxProb corresponds to more likelihood of the model’s prediction being correct. Hence, MaxProb can be directly used as the confidence estimator for selective prediction. We plot the risk-coverage curves using MaxProb as the SP technique in Figure 3(b). As expected, the risk increases with the increase in coverage for all the models. We plot such curves for all techniques and compute area under them to compare their SP performance. This shows that MaxProb is a simple yet strong baseline for selective prediction.
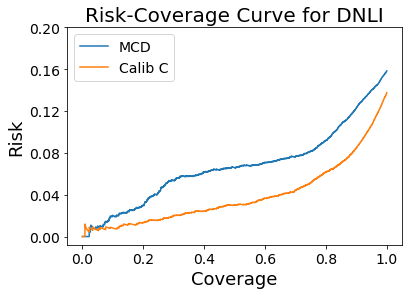
Appendix E Comparing Risk-Coverage Curves of MCD and Calib C for DNLI Dataset in IID Setting
We compare the risk-coverage curves of MCD and Calib C approaches on DNLI in Figure 4. We observe that at all coverage points, Calib C achieves lower risk than MCD and hence is a better SP technique. We find that they benefit from using the predicted label as a feature for calibration. Specifically, the model’s prediction accuracy varies greatly across labels (, , and for entailment, contradiction, and neutral labels respectively). This implies that when the model’s prediction is neutral, it is relatively less likely to be correct (at least in the IID setting). Calib C and R approaches leverage this signal and tune the confidence estimator using a held-out dataset and thus achieve superior SP performance.
Appendix F Composite SP Approach:
We note that calibration techniques can be used in combination with Monte-Carlo dropout to further improve the SP performance. However, it would require even more additional resources i.e held-out datasets in addition to multiple inferences.