Diverse Transient Chiral Dynamics in Evolutionary distinct Photosynthetic Reaction Centers

The protein structures and pigment arrangements of the PSII RC from cyanobacteria T. vulcanus and BRC from simpler anoxygenic bacteria T. tepidum are depicted inFig. 1(a) and (b), respectively. Pigments and their symmetrical partners are labeled using identical colors. In Fig. 1(a), the special pair (${P_{D1}}$ and $P_{D2}$) is highlighted in red, while the other pigments are represented in green and blue. The absorption and CD spectra for the PSII RC are computed and illustrated in Fig. 1(c) and (e), respectively. The excitonic energy levels of the PSII RC are presented as stick spectra in these figures. The broadened absorption and CD spectra are shown as blue solid lines. Excitonic models have been constructed and parameters refined to match these spectra, with detailed model descriptions and parameter values provided in the Methods section. Fig. 1(e) illustrates the CD spectrum, characterized by pronounced positive and negative peaks at the first and fifth sticks ($Ex_{1}$ and $Ex_{5}$), closely linked to the chiral configuration of the pigments. To further elucidate the relationship between excitons and pigments, we calculated and plotted the contributions of each excitonic stick to the PSII RC in Fig. 1(g). This analysis allows us to disentangle the primary contributors to the chiral signals observed in the CD spectrum. Notably, Fig. 1(g) reveals that the $Ex_{1}$ and $Ex_{5}$ are predominantly centered to $Chl_{D1}$ and $Chl_{D2}$, respectively, both of which are symmetrically positioned within the PSII RC protein structure. Moreover, $Chl_{D1}$ exhibits the lowest site energy within the protein complex, making it the initial trapping site for population transfer following photoexcitation. Tracking the temporal evolution of the first and fifth excitonic peaks in the CD spectrum can thus provide insights into the time-resolved chiral dynamics associated with energy and charge transfer in the PSII RC.

Using a similar approach, we present the pigment configuration of the BRC in Fig. 1(b). The corresponding calculated absorption and CD spectra are shown in Fig. 1(d) and (f). The stick spectra are depicted as black solid bars, while the broadened calculated absorption spectra are shown as blue solid lines. Contributions from each stick are illustrated in Fig. 1(h), enabling us to identify the major contributors to the CD spectrum. For example, the second and third sticks ($Ex_{2}$ and $Ex_{3}$), which exhibit the highest amplitudes in Fig. 1(h), are primarily associated with $BCh_{M}$, with the third stick ($Ex_{3}$) involving a more complex combination of pigments, including $P_{M}$, $BCh_{L}$, and $BPh_{L}$. Analyzing the time-resolved dynamics of these sticks in the CD spectra and their roles in downhill energy transfer can be further investigated using 2DCD spectroscopy, which will be discussed in the next section.

In this section, we present the calculated 2DES and 2DCD spectra of PSII RC at selected waiting times of 0, 100, 500, and 1500 femtoseconds (fs). Fig. 2(a), (c), (e), and (g) show the 2DES results, with solid crosses marking the positions of eigenstates in the PSII RC to provide better resolution of the dynamics. Population dynamics calculations were carried out using the Redfield quantum master equation[38, 39], while the 2DES and 2DCD spectra were computed using response function theory[40]. The specific calculation details are described in the previous section and in the Supplementary Information (SI).

Fig. 2(a) illustrates the 2DES of the PSII RC, displaying diagonal peaks labeled A through F. Cross peaks with both positive and negative magnitudes are also observed and marked as G, H, X, and Y, respectively. Notably, the blue peak G exhibits a strong negative value, indicating the presence of excited-state absorption (ESA). This ESA peak decays within 400 fs. As time progresses, downhill energy transfer becomes evident, highlighted by the increasing intensity of cross peaks (H, Y) and other peaks located in the bottom-right region. In contrast, the 2DCD spectra, shown in Fig. 2(b), (d), (f), and (h) for the same waiting times, reveal different characteristics. Solid crosses again indicate excitonic energy levels, with main and cross peaks labeled A through H. Peaks A and B exhibit both positive and negative magnitudes, corresponding to the main peaks in the CD spectrum shown in Fig. 1(e). Interestingly, other excitonic states do not produce strong signals in the CD and 2DCD spectra. Analyzing the contributions from the stick spectrum in Fig. 1(g) allows us to correlate the 2DCD spectral signals with the chiral arrangement of pigments within the PSII RC. Notably, peaks A and B, which are the most prominent in the 2DCD spectra, correspond to the first and fifth excitonic states ($Ex_{1}$ and $Ex_{5}$) and are primarily influenced by the pigments $Chl_{D1}$ and $Chl_{D2}$. These pigments exhibit a symmetric arrangement along the central axis of the PSII RC, underscoring the strong relationship between these main peaks and the cofactors $Chl_{D1}$ and $Chl_{D2}$. Furthermore, cross peaks are observed between A and C in the 2DCD spectra, with their magnitudes (X and Y) changing over time (as detailed in the next section). The upper-left cross peak X initially shows weak intensity, which increases over time. Previous studies indicate that population transfer to the lowest excitonic state, $Chl_{D1}$, occurs over time, leading to an imbalance between the symmetric pigments $Chl_{D2}$ and $Chl_{D1}$, thereby causing a significant increase in the magnitude of cross peak X. Although the bottom-right peak Y could also provide this spectroscopic information, it is affected by downhill energy transfer from other pigments.

Next, we analyze the transient chiral dynamics between the special pair $P_{D1}$ and $P_{D2}$ in the PSII RC. The close proximity of these pigments (3 $\AA$) results in strong excitonic coupling, approximately 150 cm^-1, leading to significant mixing in the excitonic basis. As indicated in Fig. 1(g), the third and eighth excitonic states ($Ex_{3}$ and $Ex_{8}$) are predominantly contributed by this special pair. Despite the strong excitonic interaction, cross peaks and associated electronic coherence between these states are absent in the 2DCD spectra and appear weak in the 2DES, possibly due to the large excitonic energy gap. This suggests that main and cross peaks in the 2DCD spectra are not directly related to excitonic coupling between pigments at the site basis but are more closely associated with the chiral arrangement of pigments.

We further investigate the population dynamics and transient chiral signals between the two Pheophytins, $Pheo_{D1}$ and $Pheo_{D2}$. Analyzing their contributions in the excitonic stick spectrum reveals that the second and fourth excitonic states ($Ex_{2}$ and $Ex_{4}$) are involved. However, these states do not generate significant main or cross peaks in the 2DCD spectra. Additionally, we explore the chiral dynamics between the side pigments, $Chlz_{D1}$ and $Chlz_{D2}$. The substantial distance between these pigments makes strong excitonic coupling unlikely, resulting in monomer-like absorption behavior, as evidenced by their contributions to the excitonic states in the stick spectrum. The sixth and seventh excitonic energy levels ($Ex_{6}$ and $Ex_{7}$) are mainly associated with these side pigments, yet no prominent main or cross peaks are observed between these levels in the 2DCD spectra. These findings demonstrate that 2DCD spectroscopy is not significantly influenced by strong excitonic coupling between pigments. Moreover, electronic transitions of pigments do not play a dominant role in shaping the 2DCD spectra. Instead, the chiral arrangement of pigments, in conjunction with other cofactors, primarily determines the spectroscopic signals observed in the 2DCD spectra.

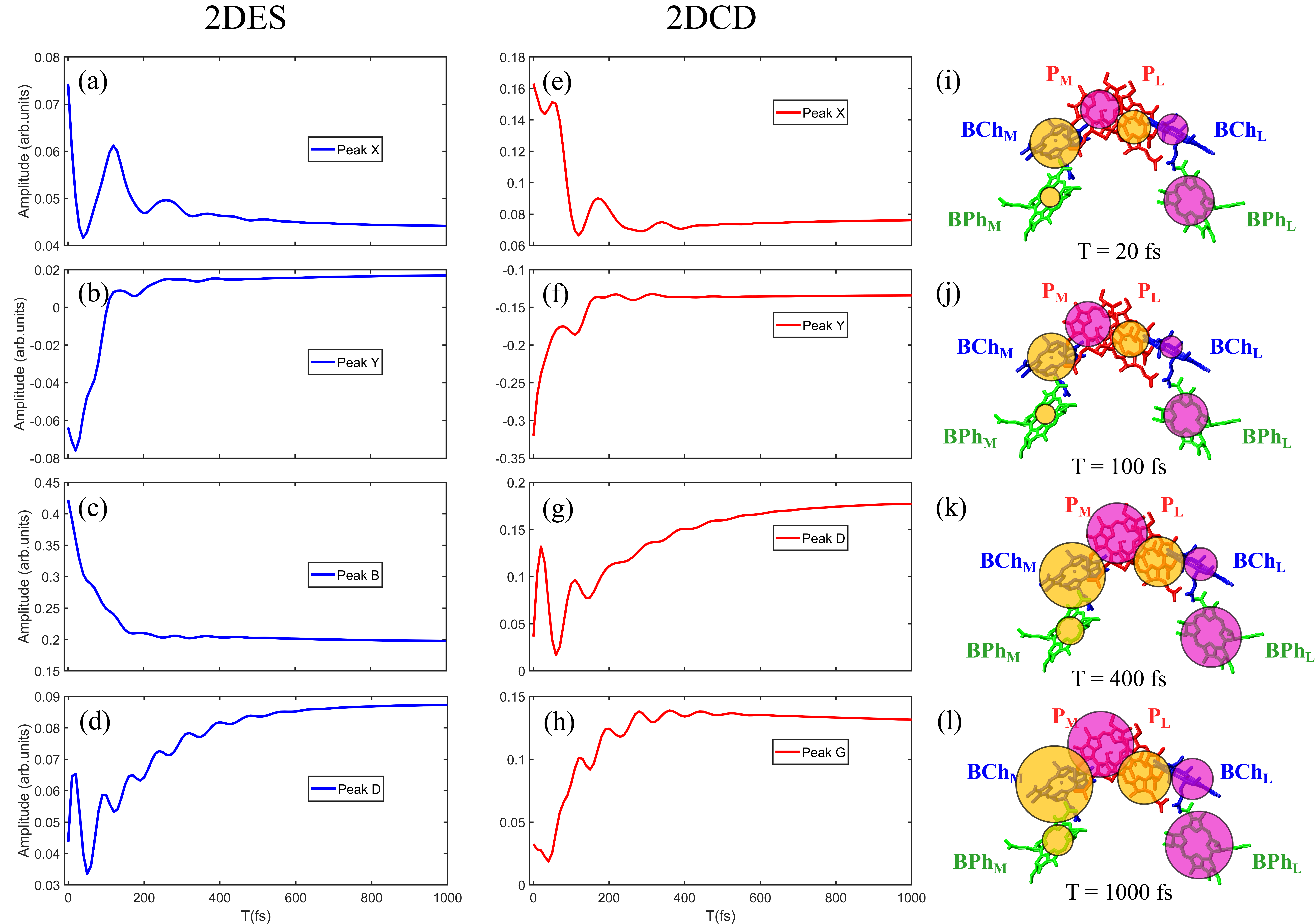
In this section, we present the traces and kinetics of selected diagonal and cross peaks in the 2DES, as illustrated in Fig. 3. The positions of these peaks are marked in Fig. 2. We begin by analyzing the cross peaks ’X’ and ’Y’, which correspond to the interactions between the first and fifth excitonic states ($Ex_{1}$ and $Ex_{5}$). To investigate these dynamics, we extract the amplitude of these peaks and plot their time-resolved behavior in Fig. 3. Notably, as the ESA decays, the magnitude of the X peak significantly increases over time, reaching its maximum at approximately 1000 fs. In contrast, the Y peak exhibits a rapid decay in magnitude, stabilizing at equilibrium after T $>$ 200 fs. We also depict the time-resolved magnitudes for peaks A and G in Fig. 3, with additional traces for other selected peaks available in the SI. Evidence of electronic coherence is clearly observed in the peaks labeled (d) and (e) presented in the SI. Compared to the 2DES, the kinetics of peaks in the 2DCD spectra exhibit slightly different behavior. The traces for cross peaks X and Y are plotted, revealing distinct kinetics compared to their 2DES counterparts. Specifically, the peak X shows an initial rapid decay in magnitude, followed by a subsequent increase with waiting time, continuing even beyond 1 ps. Additionally, the kinetic trace of Y peak display a rise in magnitude, peaking at around 1 ps. As discussed in the previous section, the cross peaks X and Y are predominantly influenced by the pigments $Chl_{D1}$ and $Chl_{D2}$. Based on the long-term calculations of the 2DCD spectra, we observe a decay in chirality-related signals, which is closely associated with the structural arrangement of $Chl_{D1}$ and $Chl_{D2}$ relative to other pigments within the PSII RC. Interestingly, the peak magnitudes do not rapidly decay within 1 ps and may persist for an extended duration, even though the population predominantly resides in the lowest energy site of $Chl_{D1}$. Moreover, oscillatory dynamics are evident in the traces of the X and Y peaks. It is noteworthy that the kinetics of peak Y appears to be less affected by energy transfer processes. However, the traces of peaks in Fig. 3(g) and (h) show no distinct evidence of electronic coherence compared to the 2DES, with further details provided in the SI.

The transient chiral dynamics of excitons can be revealed by an asymmetric population distribution between two pigments, such as the radical pair ($P_{D1}$ and $P_{D2}$). An increase in the population difference between these pigments leads to an enhancement of transient chiral signals in the 2DCD spectrum. Initially, it is assumed that the population is evenly distributed across the pigments following photoexcitation. Consequently, the population difference between symmetrically arranged pigments is minimal, resulting in a relatively weak chiral signal in the 2DCD spectrum at T = 0 fs, as depicted in Fig. 3(i). As time progresses, cross peaks emerge between the first and fifth excitonic states ($Ex_{1}$ and $Ex_{5}$), indicating an increasing asymmetry in population distribution between these excitons over time. This suggests that the chiral signal, driven by population differences, is becoming more pronounced among the delocalized wave packets. To illustrate the chirality-related dynamics from population difference, we further extract the magnitude of related cross peaks in 2DCD spectra and plot the chirality-related population difference from Fig. 3(i) to (l). We use the diameter of circles to present the strengths of chiral signal, which relates to the population difference. Moreover, we use the amplitudes of initial 2DCD spectrum (T = 0 fs) as a benchmark and plot the positive (negative) magnitude as magenta (yellow) circles. The details of this analysis process have been described in the SI. Through this exciton-site transformation analysis, it is evident that the delocalized wave packet predominantly resides in $Chl_{D1}$ and $Pheo_{D1}$. As time evolves (T $>$ 600 fs), the transient chiral signals stabilize between the first and fifth excitonic states, indicating that this persistent chiral dynamic primarily originates from the interaction between $Chl_{D1}$ and $Chl_{D2}$. This behavior is attributed to the population difference between these two pigments, with $Chl_{D1}$ having the lowest site energy, thereby sustaining the observed chiral signal.

In this section, we present the calculated 2DES and 2DCD spectra of the BRC, as illustrated in Fig. 4. The 2DES spectra are shown in Fig. 4(a), (c), (e), and (g) for waiting times of 0, 100, 500, and 1500 fs, respectively. The digonal and cross peaks in the BRC spectra are more distinctly separated compared to those in the PSII RC spectra shown in Fig. 2, despite the structural similarities between BRC and PSII RC proteins. Excitonic energy levels are marked with crosses on the 2DES spectra. The diagonal peaks are marked as A, F, B, and C, alongside cross peaks E, G, H and D in the 2DES spectra. Notably, peak E, characterized by a strong negative (blue) signal, is an ESA feature. The temporal evolution of these peaks will be further analyzed in the subsequent section using time-resolved traces.

For comparative analysis, we have also calculated the 2DCD spectra, displayed in Fig. 4(b), (d), (f), and (h) at the same waiting times (0, 100, 500, and 1500 fs). The 2DCD spectra exhibit well-separated diagonal and cross peaks, also labeled from A to H. Based on CD spectra and the pigment contributions to excitonic states, it is evident that two prominent CD signals predominantly originate from the second and third excitonic states ($Ex_{2}$ and $Ex_{3}$). Accordingly, we have marked the cross peaks between the second and third excitonic states ($Ex_{2}$ and $Ex_{3}$) as X and Y in both 2DES and 2DCD spectra. The 2DCD spectra, especially at extended waiting times (T $>$ 1 ps), provide clearer evidence of ESA peaks than the 2DES spectra. Analysis of pigment contributions shows that bar 2 ($Ex_{2}$) is mainly associated with $BCh_{M}$, whereas bar 3 ($Ex_{3}$) involves contributions from $BPh_{L}$, $BCh_{L}$ and $P_{M}$. This finding suggests that in the 2DCD spectra, peaks F and B are predominantly associated with $BCh_{M}$ and a combination of $BPh_{L}$, $BCh_{L}$ and $P_{M}$, respectively. The cross peaks X and Y reflect the chiral organization of these pigments relative to others within the BRC. Interestingly, peak D in the 2DCD spectra demonstrates a relatively stronger intensity than in the 2DES spectra, implying that the combined electronic and magnetic transition dipole moments bring a stronger influence than pure electronic transitions alone. This observation is rare in nature and likely results from the unique structural arrangement of pigments and proteins. Additionally, the increasing intensity of cross peak G provides evidence of downhill energy transfer within the BRC.

We proceed by examining the population dynamics in both 2DES and 2DCD spectra. For this purpose, we have extracted the magnitudes of selected peaks and plotted their time-resolved dynamics in Fig. 5. The kinetics of cross peaks X and Y are shown as blue solid lines. Peak X exhibits a pronounced oscillatory behavior, decaying within 600 fs, while peak Y shows a marked decrease in intensity, stabilizing around 200 fs. Fig. 5(c) to (d) depict the kinetics of other peaks, highlighting clear oscillatory signatures that underscore strong excitonic coupling among the pigments in BRC. Additional peak dynamics are presented in the SI. The time-resolved amplitudes of the 2DCD spectra are also plotted in Fig. 5, with peaks X and Y shown in (e) and (f), respectively. These traces indicate that aside from oscillatory dynamics, the peak magnitudes reach their maximum at approximately 200 fs, corresponding to the timescale observed in the population dynamics of 2DES peaks X and Y in Fig. 5(a) and (b), respectively. Beyond the coherent dynamics represented by oscillatory traces, it is predicted that the chiral arrangement involving $BCh_{M}$ and ($BPh_{L}$, $BCh_{L}$ and $P_{M}$) can be distinctly identified during the temporal evolution, with these signals persisting for extended periods ($>$ 1 ps). Moreover, we analyzed the kinetics of selected peak D and compared it with the 2DES results, showing its trace in Fig. 5(d). The oscillatory nature of the trace highlights the role of excitonic coupling and resultant electronic coherence. The increasing intensity of this trace suggests a significant rise in chiral interactions involving populations between the first and fourth excitonic states ($Ex_{1}$ and $Ex_{4}$). Calculations indicate that these states are mainly associated with contributions from $P_{M}$, $P_{L}$, and $BCh_{L}$. Finally, Fig. 5(h) presents the kinetics of peak G, which also exhibit oscillatory dynamics. The information of time-evolved chiral population of BRC is depicted in Fig. 5(i) to (l) with selected waiting times of 20, 100, 400 and 1000 fs. It is interesting to note that, in BRC, the chirality-related population difference rapidly increases even at early waiting time (T = 20 fs in Fig. 5(i)). Also, the chirality-related population difference shows significant larger values (depicted by larger diameter of circles), which is due to the strong excitonic couplings between pigments in the BRC. Compare to the results in PSII RC (as shown in Fig. 3(i-l)), we observe dramatic difference of this population-transfer-induced chiral dynamics.

In the open quantum system, the total Hamiltonian can be written as four parts

$$H=H_{S}+H_{B}+H_{SB}+H_{Ren},$$

(1)

where $H_{S}$, $H_{B}$ and $H_{SB}$ are the system, bath and system-bath interaction terms, respectively. The $H_{Ren}$ is the reorganization energy. The system and bath Hamiltonian can be written as

$$H_{S}=\sum\limits_{m=1}^{N}\epsilon_{m}\ket{m}\bra{m}+\sum\limits_{m=1}^{N}\sum\limits_{n<m}J_{n,m}(\ket{m}\bra{n}+\ket{n}\bra{m}),$$

(2)

$$H_{B}=\sum\limits_{m=1}^{N}\sum\limits_{j=1}^{N_{b}^{m}}\left(\frac{p_{mj}^{2}}{2}+\frac{1}{2}\omega_{mj}x_{mj}^{2}\right),$$

(3)

Where $\epsilon_{m}$ and $J_{n,m}$ is the m-th site energy and the excitonic coupling between n- and m-th pigments, respectively. $N$ is the total number of pigments. $N^{m}_{b}$ is the total number of bath modes coupled to the m-th molecule. $x_{mj}$ and $p_{mj}$ are the mass weighted position and momentum of j-th harmonic oscillator bath mode with frequency $\omega_{mj}$ in $H_{B}$. $H_{SB}=\sum_{m}K_{m}\Phi_{m}(x)$ is the interaction term and it describes the coupling between system and bath. It is assumed that $K_{m}$ only acts on system subspace and $\Phi_{m}(x)$ only on the bath degrees of freedom. In the following, we further assume a linear relation between bath coordinates and the system. The system-bath interaction is then given by

$$H_{SB}=\sum\limits_{m}K_{m}\sum\limits_{j}c_{mj}x_{mj}.$$

(4)

We further restrict our considerations to pure electronic dephasing only, i.e. $K_{m}=a_{m}^{\dagger}a_{m}$. The reorganization energy is given as

$$H_{Ren}=\sum\limits_{m}\sum\limits_{j}K_{m}^{2}\frac{c_{mj}^{2}}{m_{mj}\omega_{mj}^{2}}.$$

(5)

This term compensates for artificial shifts of the system frequencies due to the system-bath interaction. The influence of the bath can be fully described by the spectral density, which show the form

$$J_{m}(\omega)=\pi\sum\limits_{j}\frac{c_{mj}}{2m_{mj}\omega_{mj}}\delta(\omega-\omega_{mj})=2\lambda\frac{\omega\gamma}{\omega^{2}+\gamma^{2}},$$

(6)

where $\lambda$ is the reorganization energy and $\gamma$ is the high-frequency cutoff. In this paper, we take the Lorentzian type of spectral density with Drude cutoff frequency. We assume the bath at each monomer to be independent but with identical spectra, i,e., $J_{n}(\omega)=J_{m}(\omega)$.

The Redfield equation describes the time evolution of the density matrix of a system coupled to its environment. Under the Markov approximation, they provide a set of coupled master equations for the reduced density matrix of the system. In this form, we can accurately describe the dynamics of a dissipative system if the noise-inducing environment is weakly coupled and has short correlation times.The exact dynamics of the reduced density matrix $\sigma(t)$ of the system is given by the Nakajima-Zwanzig equation (simplified below with $\hbar$ = 1).

$$\frac{\partial\sigma(t)}{\partial t}=-i\mathcal{L}\sigma(t)-\int_{0}^{t}d\tau\mathcal{G}(\tau)\sigma(t-\tau),$$

(7)

and

$$\mathcal{G}(\tau)=\text{tr}_{B}\{\mathcal{L}_{SB}e^{-i\mathcal{L}(1-P)\tau}\mathcal{L}_{SB}\rho_{B}\}.$$

(8)

The Nakajima-Zwanzig equation is formally exact. However, since ${G}(\tau)$ is difficult to obtain, the Nakajima-Zwanzig equation has little practical use and can only serve as the basis for a more approximate theory. In order to obtain an equation that is easier to understand numerically, Redfield employs two approximations, the “Born approximation”[48] and “Markov approximation”[49], which gives the form

$$\mathcal{G}(\tau)\simeq\text{tr}_{B}\{\mathcal{L}_{SB}e^{-i(\mathcal{L}_{S}+\mathcal{L}_{B})\tau}\mathcal{L}_{SB}\rho_{B}\}.$$

(9)

$$\sigma(t-\tau)\simeq e^{i\mathcal{L}_{S}\tau}\sigma(t),$$

(10)

Using Eqs. 9 and 10, we obtain the local-time motion equation of the reduced density matrix, which show the form

$$\frac{\partial\sigma(t)}{\partial t}=-i[H_{S},\sigma(t)]-\int_{0}^{t}d\tau\text{tr}_{B}\{[H_{SB},[H_{SB}(\tau),\sigma(t)\rho_{B}]]\},$$

(11)

Then, by introducing the eigenstates of the system $H_{S}\ket{a}=E_{a}\ket{a}$. The original form of the Redfield equation can be obtained

$$\quad\quad\frac{\partial\sigma_{\mu\nu}(t)}{\sigma t}=-i\omega_{\mu\nu}\sigma_{\mu\nu}(t)+\sum_{\kappa\lambda}R_{\mu\nu\kappa\lambda}\sigma_{\kappa\lambda}(t).$$

(12)

$\sigma_{\mu\nu}(t)=\bra{\mu}\sigma(t)\ket{\nu}$ denotes the matrix elements of the reduced density matrix in the eigenstate representation, and $\omega_{\mu\nu}=E_{\mu}-E_{\nu}$ are the eigen-frequencies of the system.

The light-matter interaction Hamiltonian is given by

$$H_{int}=-\bm{\mu}\cdot\bm{E}(t)-\bm{m}\cdot\bm{B}(t)-\bm{q}\cdot\nabla\bm{E}(t)\,,$$

(13)

in this context, $\bm{\mu}$ denotes the transition electric dipole moment, $\bm{m}$ denotes the transition magnetic dipole moment, and $\bm{q}$ denotes the quadrupole moment. $\bm{E}(t)$ and $\bm{B}(t)$ represent the electric and magnetic fields, respectively, while $\nabla$ indicates the gradient operator.

We utilize the first-order response function to compute the absorption and circular dichroism spectra. Based on the field-matter interaction from Eq. 13, the linear signal can be expressed as follows

$$\begin{split}S^{(1)}(\Gamma)=\int dtdt_{1}(&R^{(1)}_{\mu\mu}(t_{1})\cdot(\bm{E}_{S}(t)\otimes\bm{E}_{1}(t-t_{1}))+R^{(1)}_{m\mu}(t_{1})\cdot(\bm{B}_{S}(t)\otimes\bm{E}_{1}(t-t_{1}))+\\ &R^{(1)}_{\mu m}(t_{1})\cdot(\bm{E}_{S}(t)\otimes\bm{B}_{1}(t-t_{1}))\,,\end{split}$$

(14)

and

$$\begin{split}R^{(1)}_{\mu\mu}(t_{1})=i\langle\bm{\mu}G(t_{1})\bm{\mu}^{\times}\rho(-\infty)\rangle\,,\end{split}$$

(15)

$$\begin{split}R^{(1)}_{m\mu}(t_{1})=i\langle\bm{m}G(t_{1})\bm{\mu}^{\times}\rho(-\infty)\rangle\,,\end{split}$$

(16)

respectively. Here, $\Gamma$ represents the set of parameters that govern the signal (including field-matter interaction, laser pulse polarization, wave vector configuration, central frequencies, and bandwidths). The symbols $\bm{E}_{1}$ and $\bm{B}_{1}$ denote the electric and magnetic fields of the incoming beams, while $\bm{E}_{S}$ and $\bm{B}_{S}$ denote the electric and magnetic fields of the probe beams. $G(t)$ indicates the time-evolution operator. For the electric dipole moment operator, we show $\mu=\mu_{+}+\mu_{-}$ with $\mu_{+}=\sum\limits_{n=1}^{N}\mu_{n}\ket{n}\bra{0}$ and $\mu_{-}=\sum\limits_{n=1}^{N}\mu_{n}\ket{0}\bra{n}$. For the magnetic dipole moment, it shows $m=m_{+}+m_{-}$, where $m_{+}=\sum\limits_{n=1}^{N}iM_{n}\ket{n}\bra{0}$ and $m_{-}=\sum\limits_{n=1}^{N}-iM_{n}\ket{0}\bra{n}$. The $\mu_{n}$ and $M_{n}$ are real values.

The linear absorption spectrum $I(\Omega)$ is obtained by Fourier transform of $S^{(1)}(\Gamma)$ over $t_{1}$ with the linearly polarized light. The circular dichroism (CD) spectrum, on the other hand, is expressed as the difference in signal between left and right circularly polarized light, and can be represented in the form

$$\begin{split}I(\omega)=&\int_{-\infty}^{\infty}dt_{1}e^{i\omega t_{1}}S^{(1)}(\uparrow,\Gamma)\,,\\ CD(\omega)=&\int_{-\infty}^{\infty}dt_{1}e^{i\omega t_{1}}S^{(1)}(\circlearrowleft,\Gamma)-\int_{-\infty}^{\infty}dt_{1}e^{i\omega t_{1}}S^{(1)}(\circlearrowright,\Gamma)\,,\end{split}$$

(17)

where $\uparrow$, $\circlearrowleft$ and $\circlearrowright$ denote the linearly, left and right circularly polarized light, separately.

We employ the third-order response function to calculate the nonlinear spectroscopy. The expression of nonlinear signal can be written as

$$\begin{split}S^{(3)}(\Gamma)=&\int dtdt_{3}dt_{2}dt_{1}(R^{(3)}_{\mu\mu\mu\mu}(t_{3},t_{2},t_{1})\cdot(\bm{E}_{S}(t)\otimes\bm{E}_{3}\otimes\bm{E}_{2}\otimes\bm{E}_{1})+\\ &R^{(3)}_{m\mu\mu\mu}\cdot(\bm{B}_{S}\otimes\bm{E}_{3}\otimes\bm{E}_{2}\otimes\bm{E}_{1})+R^{(3)}_{\mu m\mu\mu}\cdot(\bm{E}_{S}\otimes\bm{B}_{3}\otimes\bm{E}_{2}\otimes\bm{E}_{1})+\\ &R^{(3)}_{\mu\mu m\mu}\cdot(\bm{E}_{S}\otimes\bm{E}_{3}\otimes\bm{B}_{2}\otimes\bm{E}_{1})+R^{(3)}_{\mu\mu\mu m}\cdot(\bm{E}_{S}\otimes\bm{E}_{3}\otimes\bm{E}_{2}\otimes\bm{B}_{1}))\,,\end{split}$$

(18)

with

$$\begin{split}R^{(3)}_{\mu\mu\mu\mu}(t_{3},t_{2},t_{1})=-i\langle\bm{\mu}G(t_{3})\bm{\mu}^{\times}G(t_{2})\bm{\mu}^{\times}G(t_{1})\bm{\mu}^{\times}\rho(-\infty)\rangle\,,\end{split}$$

(19)

$$\begin{split}R^{(3)}_{\mu\mu\mu m}(t_{3},t_{2},t_{1})&=-i\langle\bm{\mu}G(t_{3})\bm{\mu}^{\times}G(t_{2})\bm{\mu}^{\times}G(t_{1})\bm{m}^{\times}\rho(-\infty)\rangle\,.\end{split}$$

(20)

$t_{1}$ is coherence time, $t_{2}$ is waiting time, and $t_{3}$ is detection time.

The 2DES is calculated by Fourier transform of $S^{(3)}(\Gamma)$ in Eq. 18 over the coherence time and the rephasing time.

$$\begin{split}S_{2DES}(\omega_{t},T,\omega_{\tau})=&\int_{-\infty}^{\infty}d\tau e^{i\omega_{\tau}\tau}\int_{-\infty}^{\infty}dte^{i\omega_{t}t}S^{(3)}(\uparrow,\Gamma),\end{split}$$

(21)

the 2DCD spectra is defined as the difference between two nonlinear signals from left- and right-circularly polarized pulses, which shows

$$\begin{split}S_{2DCD}(\omega_{t},T,\omega_{\tau})=&\int_{-\infty}^{\infty}d\tau e^{i\omega_{\tau}\tau}\int_{-\infty}^{\infty}dte^{i\omega_{t}t}S^{(3)}(\circlearrowleft,\Gamma)-\int_{-\infty}^{\infty}d\tau e^{i\omega_{\tau}\tau}\int_{-\infty}^{\infty}dte^{i\omega_{t}t}S^{(3)}(\circlearrowright,\Gamma)\,.\end{split}$$

(22)

The detailed model and method information is provided in the Supporting Information (SI).