Distinct topological Hall responses in CeCu₂-type EuZn₂ and EuCd₂ films

Transverse motion of carriers neither proportional to the magnetic field nor the magnetization has attracted broad interest both in fundamental and applied physics AHEreview . Such a nonmonotonic Hall response originates in a change in the real-space or momentum-space Berry curvature in the magnetization process. In particular, the Hall response reflecting a real-space spin texture is termed topological Hall effect (THE), where a noncoplanar spin texture with finite scalar spin chirality, defined by the solid angle spanned by three adjacent spins, generates an emergent magnetic field on charged carriers THE ; Nd2Mo2O7 . A magnetic skyrmion lattice is a typical example of the noncoplanar spin texture. Recently, the range of skyrmion host compounds has been expanded from noncentrosymmetric chiral to centrosymmetric frustrated magnets MnSi ; MnGe ; FeGe ; GdPdSi ; EuAl4 .

As centrosymmetric magnets which can host a skyrmion lattice, AlB₂-type compounds represented by Gd₂PdSi₃ have attracted growing attention GdPdSi . For example in Gd₂PdSi₃, a magnetic Gd triangular lattice layer and a Pd/Si honeycomb lattice layer are alternately stacked to form a two-dimensionally frustrated system, where a giant topological Hall response is observed with rather monotonic change in magnetization GdPdSi . The AlB₂-type structure is also famous for many lower-symmetry derivatives including the CeCu₂-type one AlB2_derivative . In rare-earth intermetallic compounds $RA_{2}$ ($R=$ La – Lu, $A=$ Zn, Cd, or Cu) with the CeCu₂-type structure, a distorted $R$ triangular lattice layer and a three-dimensionally buckled $A$ honeycomb lattice layer are alternately stacked CeCu2-type . Differences in distortion and buckling as well as magnetic anisotropy of rare-earth magnetic moments can bring about diverse frustrated magnetic structures and magnetotransport in $RA_{2}$. In addition to helical magnetic ordering with various propagation directions and rotation planes as observed in GdCu₂ and PrZn₂ GdCu2_mag ; PrZn2_mag ; DyZn2_mag , rich topological Hall responses have been recently found for EuCd₂ EuCd2_THE . However, comprehensive research on the magnetotransport in $RA_{2}$ is still lacking.

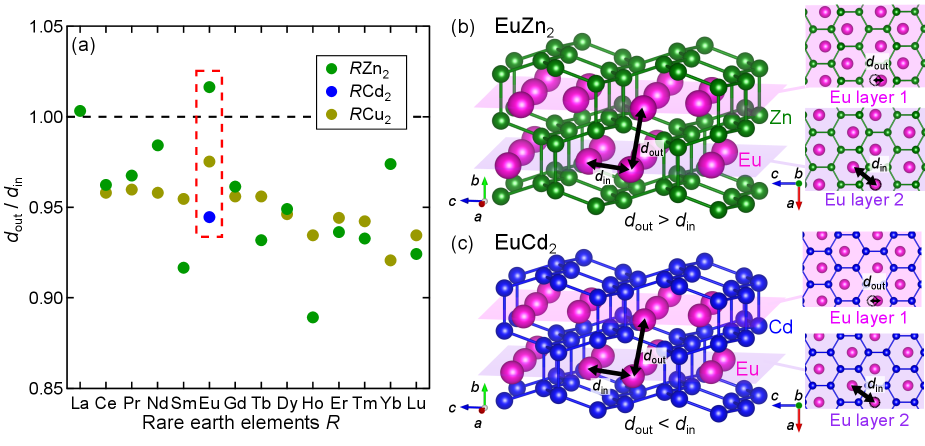
Figure 1(a) summarizes the ratio of out-of-plane and in-plane rare-earth atomic distances ($d_{\mathrm{out}}$ and $d_{\mathrm{in}}$) in CeCu₂-type intermetallic compounds EuCd2 ; EuZn2 ; CeZn2_mag ; PrZn2_mag ; NdZn2 ; NdZn2_mag ; DyZn2_mag ; HoZn2 ; YbZn2 ; CeCu2 ; GdCu2 ; NdCu2 ; EuCu2 ; DyCu2 ; HoCu2 ; ErCu2 ; TmCu2 ; YbCu2 . In most of them including EuCd₂, pairs of the nearest neighbor rare-earth atoms are formed between the adjacent triangular lattice layers ($d_{\mathrm{out}}<d_{\mathrm{in}}$). Actually, EuZn₂ is the only magnetic compound with such pairs within the triangular lattice layers ($d_{\mathrm{out}}>d_{\mathrm{in}}$), since LaZn₂ is nonmagnetic. Drastic changes in magnetotransport can be thus expected reflecting the different frustration arrangements of the Eu²⁺ isotropic magnetic moments EuCd2 ; EuZn2 , as compared in Figs. 1(b) and 1(c). In this paper, we report film growth of EuZn₂ by molecular beam epitaxy and observation of topological Hall responses highly contrastive to EuCd₂.

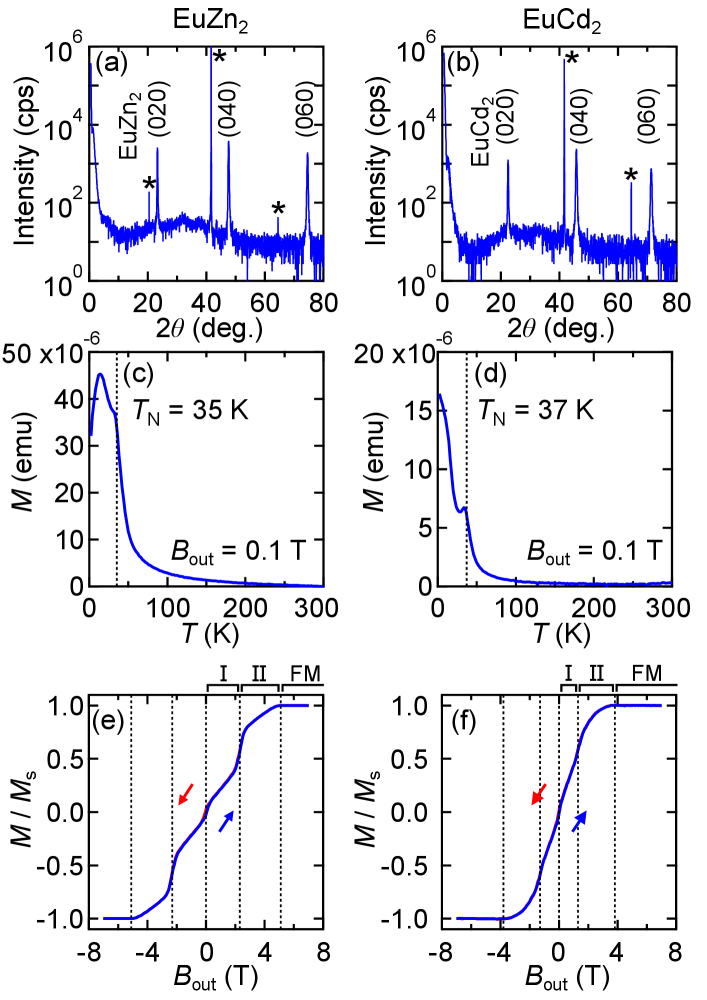
Thin films of EuZn₂ and EuCd₂ were grown on Al₂O₃ (0001) substrates using an Epiquest RC1100 II-V molecular beam epitaxy chamber EuAs ; EuCd2_THE ; EuCd2Sb2_film ; EuCd2As2_film ; EuCdSb2_film ; EuSb2_film . The growth temperature for EuZn₂ films was typically set to 400 ^∘C. Eu and Zn were supplied by an effusion cell with a Zn-rich flux ratio ($P_{\mathrm{Zn}}/P_{\mathrm{Eu}}=6$). This flux ratio is lower than in the growth of EuCd₂ films ($P_{\mathrm{Cd}}/P_{\mathrm{Eu}}=15-44$) EuCd2_THE , consistent with the less volatile nature of Zn compared to Cd. The film thickness is designed at 65 nm. As confirmed in Figs. 2(a) and 2(b), x-ray diffraction $2\theta$-$\omega$ scans for both EuZn₂ and EuCd₂ films exhibit sharp peaks from the (020) lattice plane without any impurity peaks, indicating that the distorted Eu triangular lattice layers are stacked on the Al₂O₃ (0001) plane.

Figures 2(c) – 2(f) compare fundamental magnetic properties taken for EuZn₂ and EuCd₂ films. The temperature dependence of the magnetization $M$ exhibits a cusp at the Néel temperature $T_{\text{N}}$ = 35 K for EuZn₂ and 37 K for EuCd₂, almost consistent with previous reports in polycrystalline bulks EuZn2 ; EuCd2 . Both in the EuZn₂ and EuCd₂ films, $M$ keeps increasing below $T_{\text{N}}$, suggesting that their magnetic ground states are not a simple collinear antiferromagnetic ordering. Magnetization curves, taken with sweeping the out-of-plane field $B_{\text{out}}$ at 2 K, are rather monotonic and also quite similar between EuZn₂ and EuCd₂. A transition from phase I to II occurs at the metamagnetic transition field $B_{\text{m}}$ = 2.3 T for EuZn₂ and 1.3 T for EuCd₂ with tiny hysteresis, and then the Eu²⁺ magnetic moments are forcedly aligned along the out-of-plane direction above the saturation field $B_{\text{s}}$ = 5.1 T for EuZn₂ and 3.8 T for EuCd₂. Another small hysteresis loop is confirmed centered at 0 T, indicating that there is a weak ferromagnetic component at the ground state of EuZn₂ as well as EuCd₂.

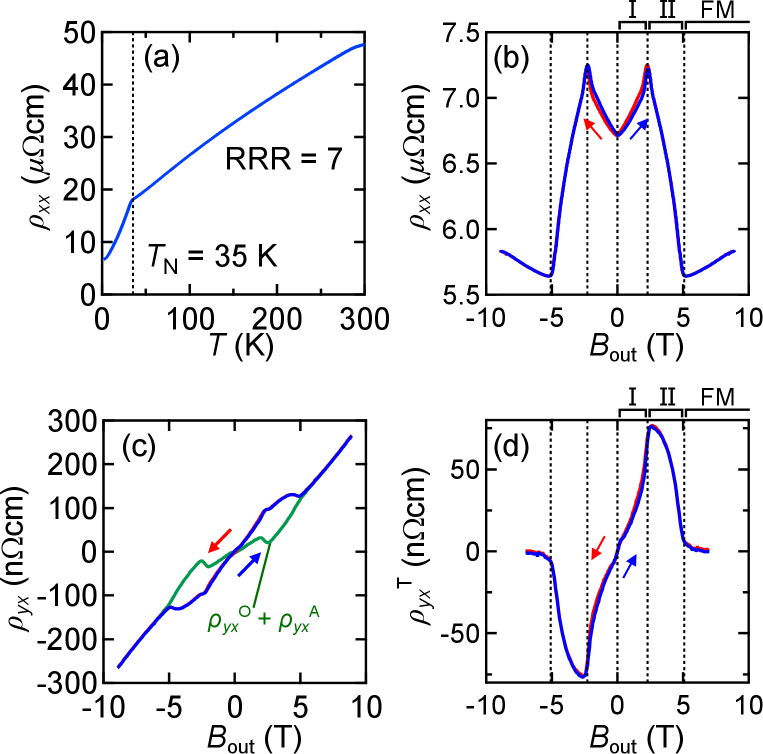
Figure 3 summarizes magnetotransport observed for the EuZn₂ film. As shown in Fig. 3(a), the temperature dependence of the longitudinal resistivity $\rho_{xx}$ is metallic with a residual resistivity ratio (RRR) of 7. It exhibits a clear kink at $T_{\text{N}}$, reflecting strong coupling between the itinerant carriers and the localized Eu²⁺ magnetic moments. In the out-of-plane field dependence shown in Fig. 3(b), $\rho_{xx}$ exhibits a peak at $B_{\text{m}}$ and then negative magnetoresistance up to $B_{\text{s}}$. Figure 3(c) shows the Hall resistivity $\rho_{yx}$ measured with sweeping the out-of-plane field $B_{\text{out}}$ at 2 K. The hole density estimated by fitting the $\rho_{yx}$ curve above the saturation field at 2 K is $1.7\times 10^{22}$ cm^-3, which is similar to that of EuCd₂EuCd2_THE . It is clear that there is a nonmonotnic Hall component in addition to the ordinary Hall resistivity $\rho_{yx}^{\text{O}}$ and the anomalous Hall resistivity $\rho_{yx}^{\text{A}}$. Here $\rho_{yx}^{\text{O}}$ is expressed by $\rho_{yx}^{\text{O}}$ = $R_{0}$$B_{\text{out}}$ with the Hall coefficient $R_{0}$, and $\rho_{yx}^{\text{A}}$ is extracted by $\rho_{yx}^{\text{A}}$ = $r_{s}$$\rho_{xx}$${}^{2}M$ with $r_{s}$ determined as a fitting parameter, since the longitudinal conductivity converted from $\rho_{xx}$ is located in the so-called intrinsic region of the conventional scaling plot AHE_scaling . Figure 3(d) displays the additional component obtained by subtracting $\rho_{yx}^{\text{O}}$ and $\rho_{yx}^{\text{A}}$ from the measured Hall resistivity. Hereafter we call this $\rho_{yx}^{\text{T}}$, which is ascribed to the topological Hall component originating in frustrated spin configuration, as discussed below.

$\rho_{yx}^{\text{T}}$ appears below $T_{\mathrm{N}}$, indicating that it is related to the magnetic ordering. As reported for some magnetic compounds, $\rho_{yx}$ may be affected by the change in $\rho_{xx}$ through a field dependence of the scattering time. In ErB₄, for example, a nonmonotonic Hall component has been explained by a modified two-band model incorporating this effect ErB4 . In the present case, however, the fitting curve of $\rho_{yx}^{\text{O}}$+$\rho_{yx}^{\text{A}}$ swells rather in the direction opposite to the hump around 2.5 T, and thus the change in the scattering time would not be the cause.

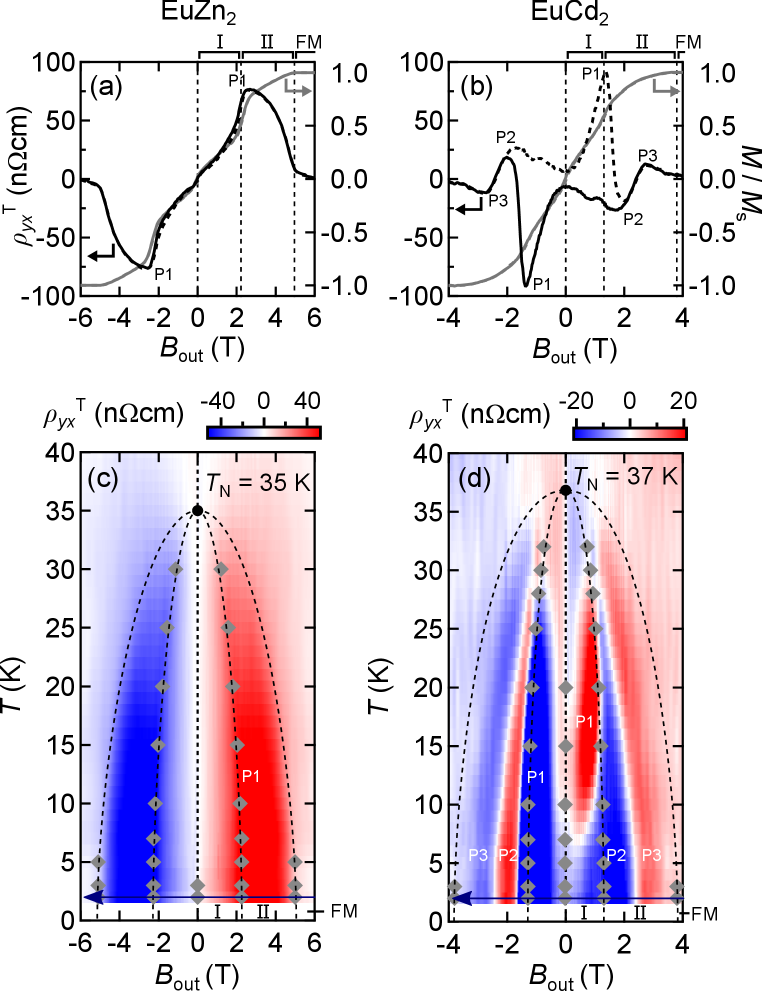
Here comparison with EuCd₂ is helpful for discussion. Figures 4(a) and 4(b) compare $\rho_{yx}^{\text{T}}$ taken for EuZn₂ and EuCd₂ at 2 K. In EuZn₂, only the peak P1 appears centered at $B_{\text{s}}$ between phase I and II. In EuCd₂, on the other hand, $\rho_{yx}^{\text{T}}$ is characterized by three peaks P1-P3, and among them, peak P1 similarly appears centered at $B_{\text{s}}$ as in EuZn₂. Another difference is that a large hysteresis loop is observed in EuCd₂ accompanied with a sharp enhancement of P1 at low temperatures. The origin of THE in EuCd₂ has been understood the real-space spin Berry curvature, or noncoplanar spin textures realized on the distorted $Eu^{2+}$ triangular lattice layers EuCd2_THE . It has been clarified based on the temperature dependence measurements that the sign of the THE peaks P1-P3 originating from the real-space spin Berry curvature remain unchanged, while $\rho_{yx}^{\text{A}}$ reflecting the momentum-space Berry curvature exhibits a sign change at 20 K. Although the sign change of $\rho_{yx}^{\text{A}}$ does not occur in EuZn₂ at elevated temperatures, it is reasonable to suggest that THE in EuZn₂ also originates in noncoplanar spin textures in the magnetization process, considering the similarity of the magnetization properties between the two materials. In fact, the distorted Eu triangular lattice in the $ac$-plane of CeCu₂-type structure can host uncanceled local Dzyaloshinskii-Moriya interaction which favors spin configuration canted from the $ac$-plane to the out-of-plane $b$-axis, possibly leading to a noncoplanar ordering.

Figures 4(c) and 4(d) compare a color-map of $\rho_{yx}^{\text{T}}$ taken in the downward field sweep on the $B_{\text{out}}$-$T$ phase diagram. In EuZn₂, $\rho_{yx}^{\text{T}}$ consisting only of the peak P1 appears antisymmetric to the magnetic field and continues to reach a maximum value at the magnetic transition field between phases I and II even upon increasing temperature. In EuCd₂, the appearance of $\rho_{yx}^{\text{T}}$ is more complex and not antisymmetric to the field due to the large hysteresis at low temperatures, but the enhancement of P1 at the magnetic transition field is commonly confirmed in the negative field region. As the peak P1 is enhanced not within a specific phase but at a phase boundary, it is naturally ascribed to the magnetic domain boundary formed between the two phases. In evidence, it has been demonstrated that P1 in EuCd₂ strongly depends on the field cooling processes, which can effectively modulate the domain boundary density EuCd2_THE . On the other hand, the differences in the appearance of THE between EuZn₂ and EuCd₂ are probably derived from different pairs of the nearest neighbor Eu atoms and dominant magnetic interactions as illustrated in Fig. 4(c). While spin modulation propagating along the $c$-axis has been reported for other intermetallic compounds $R$Zn₂ with $d_{\mathrm{out}}<d_{\mathrm{in}}$ CeZn2_mag ; PrZn2_mag ; NdZn2_mag ; DyZn2_mag , distinctive magnetic structures are realized in EuZn₂ with $d_{\mathrm{out}}>d_{\mathrm{in}}$, which deserve clarification in future studies. The appearance of a simple single-component THE also suggests that EuZn₂ is potentially a unique system for further studying the magnetic domain boundary effect on THE among the CeCu₂-type rare-earth intermetallic compounds.

In summary, we have grown EuZn₂ thin films by molecular beam epitaxy and revealed topological Hall responses which are in sharp contrast to EuCd₂. While their magnetization curves in the magnetization process are rather similar, the topological Hall effect observed in EuZn₂ is simpler, with the only one component enhanced at the metamagnetic transition field. Hence, we propose EuZn₂ as a unique system for further studying the magnetic domain boundary effect on THE among the CeCu₂-type rare-earth intermetallic compounds.