Distance and the Goeritz groups of bridge decompositions
Abstract.
We prove that if the distance of a bridge decomposition of a link with respect to a Heegaard splitting of a -manifold is at least , then the Goeritz group is a finite group.
Introduction
It is well known that any closed orientable -manifold is obtained by gluing two handlebodies and of the same genus along their boundaries. Such a decomposition of is called a Heegaard splitting, and the common boundary of and is called the Heegaarrd surface of the splitting. The distance of a Heegaard splitting is a measure of complexity introduced by Hempel [5]. It is defined to be the distance between the sets of meridian disks of and in the curve graph of . The distance has successfully provided a way of describing the topology and geometry of -manifolds.
A bridge decomposition of a link in a closed orientable -manifold is a Heegaard splitting such that intersects each of and in properly embedded trivial arcs. When the genus of the surface , called a bridge surface, is , and the number of components of is , we particularly call such a decomposition a -decomposition of . The distance is also defined for a bridge decomposition in the same way as in the case of a Heegaard splitting, and many results about Heegaard splittings have been extended to bridge decompositions. For example, Bachman-Schleimer [1] showed that the distance of a bridge decomposition of a knot is bounded above by the Euler characteristic of an essential surface in the complement of the knot, which is a generalization of a result of Hartshorn [4]. The arguments in [1] apply to the case of links as well, and their results, in particular, imply that if the distance of a link in a -manifold is at least , then the complement of the link admits a complete hyperbolic structure of finite volume. (The definition of the distance in this paper is slightly different from that in [1], see Section 1.3.) As another example, Tomova [17] gave a sufficient condition for uniqueness of bridge decompositions of knots in terms of the distances and the Euler characteristics of bridge surfaces, which is a generalization of a result of Sharlemann-Tomova [16].
In this paper, we are interested in the Goeritz group of a bridge decomposition. The Goeritz group (or the mapping class group) of a Heegaard splitting is defined to be the group of isotopy classes of self-diffeomorphisms of the ambient -manifold that preserve the splitting setwize. Namazi [14] showed that for each topological type of Heegaard surface there exists a constant such that if the distance is at least , then the Goeritz group is a finite group. Johnson [9] had refined this result by showing the constant can be taken to be at most independently of the genus of the Heegaard surface. The concept of Goeritz group has also been extended for bridge decompositions in [6]. In that paper, a variation of Namazi and Johnson’s result for the case of bridge decomposition was obtained: it was shown that the constant for the finiteness of the Goeritz group can be taken uniformly to be at most . The main result of the paper is the following, which improves the above mentioned result of [6].
Theorem 0.1.
Let , and . Let be a -decomposition of a link in a -manifold . If the distance of is at least , then the Goeritz group is a finite group. Further, for a -decomposition of a link in the -sphere , where , if the distance of is at least , then the Goeritz group is a finite group.
Theorems 0.1 is proved by extending the argument of [9] to the case of bridge decompositions. In fact, the major part of the proof is devoted to show the following.
Theorem 3.1.
Let be a link in a -manifold and a bridge decomposition. If the distance between the sets of disks and once-punctured disks in and in the curve graph of are at least , then the natural homomorphism is injective.
The key tool for the proof is the double sweep-out technique involving the theory of graphics introduced by Rubinstein-Scharlemann [15]. As noted above, if the distance of the bridge decomposition is at least , then the complement admits a hyperbolic structure, and hence the mapping class is a finite group. Theorem 0.1 thus follows from Theorem 3.1 and these facts.
The paper is organized as follows. In Section 1, we review basic definitions and properties of the distance and the Goeritz group of a bridge decomposition. In Section 2, we review the theory of sweep-outs, which is the main tool of the paper. In Section 3, we give the proof of Theorem 3.1. Finally, in Section 4, we give the proof of Theorem 0.1.
1. Preliminaries
We work in the smooth category. Throughout the paper, we will use the following notations and conventions:
-
•
Given two sets and , we denote by or the relative complement of in .
-
•
For a topological space , we denote by the number of connected components of . For a subset , we denote by or the closure of in .
-
•
For simplicity, we will not distinguish notationally between simple closed curves in a surface and their isotopy classes throughout.
1.1. Bridge decompositions
Let and . Let be a handleboby of genus . The union of properly embedded, mutually disjoint arcs in is called an -tangle. An -tangle in is said to be trivial if the arcs can be isotoped into simultaneously. Let be a link in a closed orientable -manifold . Let be a genus- Heegaard splitting of . A decomposition is called a -decomposition of if and are trivial -tangles in and , respectively. We sometimes denote such a decomposition by . The surface here is called the bridge surface of . Two bridge decompositions of are said to be equivalent if their bridge surfaces are isotopic through bridge surfaces of .
1.2. Curve graphs
Let and . Let be a closed orientable surface of genus with marked points . Set . A simple closed curve in is said to be essential if it does not bound a disk or a once-punctured disk in . We say that an open arc in is essential if it satisfies the following:
-
•
; and
-
•
If is a simple closed curve bounding a disk in , then the interior of contains at least one point of .
The curve graph of is the graph whose vertices are isotopy classes of essential simple closed curves in , and the edges are pairs of vertices with . Similarly, the arc and curve graph of is the graph whose vertices are isotopy classes of essential simple closed curves and essential open arcs in , and the edges are pairs of vertices with . By abuse of notation, we denote the underlying space of the curve graph (the arc and curve graph, respectively) by the same symbol (, respectively). The graph (, respectively) can be viewed as a geodesic metric space with the simplicial metric (, respectively). We note that the curve graph is non-empty and connected if and only if .
1.3. Distances
In this subsection, we give the definition of the distance of a bridge decomposition and its variations, and summarize their basic properties.
Let be a -decomposition of a link in a closed orientable -manifold , where . We denote by the set of vertices of that are represented by simple closed curves bounding disks in .
Definition.
The distance of the bridge decomposition is defined by .
There are other variations, and , of the distance. The first one, , is defined as follows. Let denote the set of all vertices of that are represented by simple closed curves bounding disks in that intersect at most once. Then is defined by . It is easily checked that the following inequality holds:
| (1) |
Furthermore, for a -decomposition the following holds.
Proposition 1.1 (Jang [8, Proposition ]).
Suppose that and the genus of is zero. Then,
-
•
if , and
-
•
or if .
We next define , which was introduced by Bachman-Schleimer [1]. For trivial -tangles , we denote by the set of all vertices of such that
-
•
, or
-
•
is an open arc in such that and cobounds a disk in with an arc of .
We define by the distance between two set and in the arc and curve graph . By the argument of the proof of the inequality in p.480 of Korkmaz-Papadopoulos [13], we have
| (2) |
See also [2]. We summarize a few facts needed in Sections 3 and 4. The following lemma is an extension of Haken’s lemma [3].
Lemma 1.2 ([1, Lemma ]).
Let be a bridge decomposition of a link in a closed orientable -manifold . If contains an essential -sphere, or if there exists a -sphere in that intersects transversely at a single point, then .
Remark.
[1, Lemma 4.1] is stated only for knots, but their arguments hold for links.
Corollary of Bachman-Schleimer [1] says that if , the complement of admits a complete hyperbolic structure of finite volume. (Again, [1, Corollary 6.2] is stated for knots, but their arguments are valid even for links.) Combining this fact and the inequality (2), we have the following.
Theorem 1.3.
Let be a bridge decomposition of a link in a closed orientable -manifold . If , then admits a complete hyperbolic structure of finite volume.
Remark.
Here is a subtle remark on the various notion of distances introduced above. In [8], two notions of distance of bridge decompositions are discussed. One is , which is denoted by in [8], and the other is , which is denoted by in the same paper. The important thing to note is that the definition of in [8] is different from the original one by Bachman-Schleimer [1]. Then, in [7, Theorem 5.1], it is claimed that if is a -decomposition of a link in , where , then the complement of admits a complete hyperbolic structure of finite volume. The proof in that paper bases on two results. One is [1, Corollary 6.2]. The other is, however, not a relationship between and but Proposition 1.1 above (literally this is described as a relationship between and in [8]). Thus, we do not have a reasonable explanation of [7, Theorem 5.1]. If [7, Theorem 5.1] is still valid, then we can improve the distance estimation of Theorem 0.1 for -decompositions of links in .
1.4. Goeritz groups
Let be an orientable manifold, and (possibly empty) subsets of . Let denote the group of orientation-preserving self-diffeomorphisms of that send to itself for . The mapping class group of the -tuple is defined to be the group of connected components of .
Definition.
For a bridge decomposition , the mapping class group is called the Goeritz group, and it is denoted by .
Let be a bridge decomposition of a link in a closed orientable -manifold . Since the natural map obtained by restricting the maps of concern to is injective, the Goeritz group can be thought of a subgroup of . Thus, we can write as
2. Sweep-outs
We review the basic theory of sweep-outs. The main references of this section are Kobayashi-Saeki [12] and Johnson [10]. In the following, let be a closed orientable -manifold, a link in , and a -decomposition of throughout.
Definition.
A function is said to be a sweep-out of associated with the decomposition if
-
•
for all , is a bridge surface of and the bridge decomposition is equivalent to ; and
-
•
and are finite graphs, which are called spines, embedded in .
We note that any bridge decomposition admits a sweep-out. For simplicity, we shall always assume further that the spines are uni-trivalent graphs, and the intersection of the spines and is exactly the set of vertices whose valency is one. See Figure 1.

A smooth map from a -manifold into is said to be stable if there exists a neighborhood of in the space of smooth maps with the following property: for any , there exist diffeomorphisms and satisfying . The image of the set of singular points of the stable map is called the discriminant set.
Let and be sweep-outs of . Due to Kobayashi-Saeki [12], the map can be perturbed so that is stable in the complement of spines of and . In the following, whenever we consider the product of sweep-outs, we slightly perturb it to be stable. Let be the closure in of the union of the discriminant set of and the image of under the map . Then is naturally equipped with a structure of a finite graph of valency at most four. Such a finite graph is called the (Rubinstein-Scharlemann) graphic defined by .
Each point in the interior of the square corresponds to the intersection of two level surfaces and . We note that the surfaces and always intersect transversely by definition. If the point lies in the complementary region of the graphic , then the surfaces and intersect transversely and . If lies in the interior of an edge of , then either

If is at a -valent vertex of , then either
-
•
and share exactly two tangent points, and those points are non-degenerate critical points of both and ;
-
•
and share a single tangent point, and that point is a non-degenerate critical point of both and . Further, intersects at a point where and intersect transversely; or
-
•
and intersect transversely, and consists of exactly two points.
If is at a -valent vertex of , then and share a single tangent point, and that point is a degenerate critical point of both and . See Figure 3.

Each - or -valent vertex is in the boundary of the square, and it corresponds to the point where the level surface of one of the two sweep-outs is tangent to the spine of the other sweep-out.
Definition.
The graphic defined by is said to be generic if is stable in the complement of the spines, and any vertical or horizontal arc in contains at most one vertex of the graphic.
The following is Lemma of Johnson [10].
Lemma 2.1.
Let and be sweep-outs associated to the bridge decomposition . Let be an ambient isotopy such that and for all . Set for . Then we can perturb slightly, if necessary, so that the graphic defined by is generic for all but finitely many . At each non-generic , the graphic fails to be generic due to one of the following two reasons:
-
•
there exists a single vertical or horizontal arc in containing two vertices of the graphic, or
-
•
the map is not stable in the complement of their spines. This case corresponds to the six types of local moves shown in Figure of [11].
Let and be sweep-outs associated to . Let . Set , , , , and .
Definition.
We say that is mostly above (mostly below, respectively) if each component of (, respectively) is contained in a disk with at most one puncture in .
Let (, respectively) denote the set of all points such that is mostly above (mostly below, respectively) . The regions and are bounded by the edges of the graphic. Note that a point near is labeled by because lies within a small neighborhood the spine of , and the all intersections of and must consist of disks. Similarly, a point near is labeled by . Also, by definition, both regions and are vertically convex, that is, if a point is in (, respectively), then so is for any (, respectively).
Lemma 2.2.
Suppose that . Then the closure of the regions and are disjoint.
Proof.
We first suppose that . Let . Then there exists a component of such that bounds once-punctured disks in in both sides of . Thus is a twice-punctured sphere and .
Next, suppose that and share an edge of the graphic. Let be a point in the (interior of the) common edge of and . A small neighborhood in of the component of containing a critical point of or a point of is either a pair of pants or a once-punctured annulus, see Figure 4.

By the assumption, each component of is inessential in . Therefore must be a twice-punctured sphere, and thus, we have .
Finally, suppose that and do not share any edge, but they share a vertex of the graphic. Let be points near the vertex shown in Figure 5.

There are exactly two critical points of between and : one is on and the other is on . As in the above case, a small neighborhood in of the component of each of concern is a pair of pants or a once-punctured annulus. In the surface , each component of either bounds a once-punctured disk or cobounds an annulus with another component of . Thus, we can check that is either a four-times punctured sphere or a once-punctured torus, which implies . ∎
In what follows, we assume that . We say that spans if there there exists such that the horizontal arc intersects both and . Otherwise, we say that splits . See Figure 6.

We say that spans positively if there exist points and with .
Lemma 2.3 ([10, Lemma 14]).
Let be a sweep-out of , and the result of perturbing slightly so that the graphic defined by is generic. Then spans positively.
3. Upper bounds for the distance
Let be a -decomposition of a link in a closed orientable -manifold , and suppose that . Recall that . The goal of this section is to show the following.
Theorem 3.1.
If , then the natural homomorphism is injective.
Assumption: Any meridional loop of does not bound a disk in .
Lemma 3.2.
Let and be as above. Let be a closed connected surface in intersecting transversely. Let be a disk in such that , , and intersects transversely in at most one point. Let be a component of a surface obtained by compressing along . Then we have , where denotes the Euler characteristic.
Remark.
In the above lemma, we allow the case where is not a compression disk for , in other words, can be inessential in .
Proof.
Suppose that . Then the only possibility is that , bounds a disk in with , and . This contradicts our assumption stated right before the lemma. ∎
Lemma 3.3.
Let be a closed orientable surface, the union of vertical arcs in , and a surface in that intersects transversely. If separates from , then . Furthermore, the equality holds if and only if is isotopic to a horizontal surface keeping transverse to throughout the isotopy.
Proof.
Let be the result of repeatedly compressing so that is incompressible in . The surface still separates from , and it follows from Lemma 3.2 that . Since any incompressible surface in is isotopic to a horizontal surface, we have . ∎
Let be a sweep-out of with , and the result of perturbing slightly. Let be in the kernel of . Then, there exists an ambient isotopy such that , , and for all . We can assume that satisfies the conditions described in Lemma 2.1, that is, only a finitely many element in the -parameter family of sweep-outs of is non-generic.
Lemma 3.4.
If spans for all , then is isotopic in to the identity relative to the points .
Proof.
For each , set and , where denotes the projection onto the second coordinate. Since spans , and have non-empty intersection. Indeed, is a closed interval in because and are vertically convex subsets of . Fix . We define the map from the surface to that sends the points to as follows.
Let be an interior point of the closed interval . There are points and in such that and , respectively. Set , and . Since is mostly above while is mostly below , we obtain a surface lying within the product region between and by repeatedly compressing along the innermost disks intersecting at most once in as long as possible. By the construction, the surface separates from . See Figure 7.

We argue that is canonically isotopic to a level surface of the sweep-out keeping transverse to the link throughout the isotopy. By Lemma 3.2 we have . On the other hand, since separates from , we have by Lemma 3.3. Thus, we have . Again, by Lemma 3.3, is isotopic to a level surface of the sweep-out with keeping the surfaces transverse to throughout.
By the argument above, it follows that coincides with away from some disks, each of which intersects at most once. Thus, there is a canonical identification of with . Therefore, we have the following map:
Note that all maps are uniquely defined up to isotopy (with fixing the intersection points between the surface of concern and ). It is clear that the composition map can be chosen so that it sends to . Define the map by such a composition map.
We shall now show that is isotopic to the identity relative to . There is the canonical identification of with because is the result of perturbing slightly. Under this identification, it holds that and . It is clear that the values of can be chosen so that it varies continuously. Although perhaps the points and do not vary continuously at some finitely many values of , the deformation of remains to be continuous even around such values: it is easily seen that the choice of or does not affect the definition of the map in the above argument modulo isotopy. Thus, we conclude that for any , and are isotopic fixing , which shows the proof. ∎
Lemma 3.5.
If there exists such that splits , then .
Proof.
We denote by the natural projection from the preimage of the open interval to that maps to . By Lemma 2.3, spans positively. Thus, there exists a time such that
-
•
spans positively for all , and
-
•
.
In the following, we consider the graphic defined by . By Lemma 2.1, the arc must intersect the region in exactly two vertices of the graphic. Let and be coordinates of such vertices. We note that . Let us consider the points near these vertices shown in Figure 8: their coordinates are , , and .
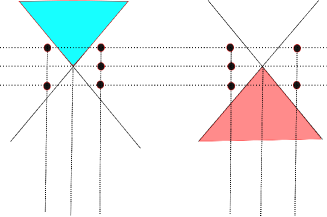
We set , as before. Set and . Note that the functions are Morse away from the preimages of .
We think about the function . Let be the set of simple closed curves of that are essential in . Similarly, let be the set of simple closed curves of that are essential in . We note that (, respectively) because (, respectively) does not lie in . Let and be arbitrary simple closed curves in and , respectively.
By the choice of , the same argument of the proof of Lemma 3.4 shows that we can find a natural map that extends to a homeomorphism from the whole surface to with . Since both and are level loops of , they are disjoint. Therefore, the images and in are also disjoint. In other words, we have
| (3) |
where we regard and as vertices of . The projection also takes and to simple closed curves in , which may have non-empty intersection. However, we see from the definition of that and ( and , respectively) are homotopic, hence, isotopic. Therefore, if we regard and as vertices of , we can write
| (4) |
We next show the following inequality:
| (5) |
We note that any level loop of can also be regard as loops of each of since the points and are in the same component of the complementary region of the graphic. In the following, for simplicity, we shall not distinguish between a level loop of and the corresponding loops of in their notations. Let . Let us first consider the function . Since the point lies within , as we pass from the level to the level , the simple closed curve turns into one or two inessential simple closed curves in . Therefore, in the surface , either
-
•
The simple closed curve bounds a twice-punctured disk, see Figure 9 (i) and (ii); or
-
•
The simple closed curve cobounds with another essential simple closed curve an annulus that intersects in at most one point, see Figure 9 (iii),
and the other simple closed curves of are inessential in .

As explained above, the natural map can be extended to the map defined on the whole surface. The same thing still holds for the natural map from to . Due to the existence of an extension of the natural map we see that, in the surface , either
-
•
The simple closed curve bounds a twice-punctured disk; or
-
•
The simple closed curve cobounds with another simple closed curve an annulus that intersects in at most one point,
according to which of the above two cases of the configuration of in occurs. The other simple closed curves of are inessential even in .
Let us next consider the function . Recall that we denote the simple closed curve in corresponding to by the same symbol .
Case A: The simple closed curve bounds a twice-punctured disk in (and hence in ).
Let be the twice-punctured disk in bounded by (note that such a subsurface is unique because ). We note that, in this case, . As we pass from the level to the level , there are the following four cases to consider.
Case A1: One or two new simple closed curves are created away from (Figure 10).

We first see that at least one of the two new simple closed curves is essential in . Suppose, contrary to our claim, that both of them are inessential in . As we pass from the level to the level , the simple closed curve turns into one or two inessential simple closed curves in . Thus, all of the simple closed curves in are inessential in . However, this contradicts the fact that the point lies in the complement in of .
Let be one of the new simple closed curves that is essential in . Since each simple closed curve of is inessential in except for , the curve is contained in a disk with at most one puncture in . Thus, is also inessential in . Let be a disk with at most one puncture bounded by . By repeatedly compressing along the innermost disk with at most one puncture in as long as possible, we finally obtain a disk in the handlebody such that and . Thus, is a vertex of . As shown in Figure 10, the inequality holds. In consequence, we have .
Case A2: The simple closed curve and another simple closed curve in are pinched together to produce a new simple closed curve (Figure 11).
Since the point is in the complement in of , the simple closed curve is essential in . We also see that bounds a once-punctured disk in . Suppose, contrary to our claim, that bounds a disk in . Hence is isotopic to in . As we pass from the level to the level , the simple closed curve turns into one or two inessential simple closed curves in , but this is impossible because the point lies in the complement of .
By the assumption, any meridional loop of does not bound a disk in . Thus, bounds no disk in . The possible configuration in of , and is shown in Figure 11. In particular, bounds a once-punctured disk in . By repeatedly compressing along the innermost disk with at most one puncture in as long as possible, we finally obtain a disk in the handlebody such that and . As the points and can be connected by a path that intersects the graphic once, holds. Therefore, it follows that .

Case A3: The simple closed curve passes through a puncture and turns into a new simple closed curve (Figure 12).
Since the point is in the complement in of , is essential in . As shown in Figure 12, bounds a once-punctured disk in . By repeatedly compressing along the innermost disk with at most one puncture in as long as possible, we finally obtain a disk in the handlebody such that and . As , it follows that .
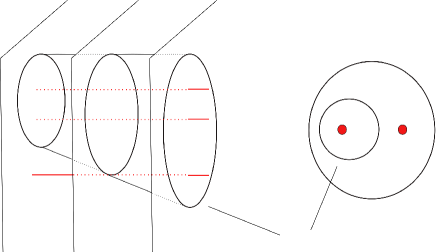
Case A4: The simple closed curve is pinched to produce two simple closed curves and (Figure 13).
There are two possible configurations of , and in . See Figure 13.

First, suppose that both of the two simple closed curves and bound once-punctured disks, which are mutually disjoint, in . Since the point is in the complement in of , one of and is essential in . We may assume that is essential in . Let be the disk such that and . By repeatedly compressing along the innermost disk with at most one puncture in as long as possible, we finally obtain a disk in the handlebody such that and . Thus, we have .
Next, suppose that bounds a disk in . It suffices to show that must be essential in . Indeed, if is essential in , a similar argument as above shows that there exists a disk in such that . Thus, we have .
Suppose, for the sake of contradiction, is inessential in . By the assumption, any meridional loop of does not bound a disk in . Hence, must bound a disk in . As we pass from the level to the level , the simple closed curve turns into one or two simple closed curves, which bound once-punctured disks in . Note that is isotopic to in because bounds a disk in . It follows that as we pass from the level to the level , the simple closed curve turns into one or two simple closed curves that is inessential in , and thus all of the simple closed curves of are inessential in . This contradicts the fact that the point does not lie in . This completes the proof of the inequality (5) in Case A.
Case B: The simple closed curve cobounds with another essential simple closed curve an annulus in (and hence in ) that intersects in at most one point.
Let be the annulus in bounded by and (note that such an annulus is unique because ). We note that . There are five cases to consider as we pass from the level to the level .
Case B1: A new simple closed curve is created away from and .
This case is same as Case A1.
Case B2: The simple closed curve and another simple closed curve of are pinched together to produce a single simple closed curve (Figure 14).
We see that bounds a once-punctured disk in . Suppose, contrary to our claim, that bounds a disk in . Then, it follows that is isotopic to in . As we pass from the level to the level , the simple closed curves and are pinched together to produce an inessential simple closed curve in . This contradicts the fact that the point does not lie in .
By the assumption, any meridional loop of does not bound a disk in . Thus, it follows that and bounds a once-punctured disk in . The possible configuration of , , and in the annulus is shown in Figure 14.

As we pass from the level to the level , the simple closed curves and are pinched together to produce a new single curve . The simple closed curve is essential in because the point lies in the complement of . On the other hand, bounds a disk in . By repeatedly compressing along the innermost disk in , we obtain a disk in such that . As , it follows that .
Case B3: The simple closed curve passes through a puncture and turns into a new simple closed curve (Figure 15).
In the annulus , cobounds with an annulus. See Figure 15.

As we pass from the level to the level , the simple closed curves and are pinched together to produce a new single curve . The simple closed curve is essential in because the point lies in the complement of . On the other hand, bounds a disk in . By repeatedly compressing along the innermost disk in , we obtain a disk in such that . Therefore, we have .
Case B4: The simple closed curve is pinched to produce two simple closed curves and (Figure 16).
There are two possible configurations of , , and in the annulus . See Figure 16.

First, suppose that bounds a disk in . By the assumption, any meridional loop of does not bound a disk in its complement. Thus, the curve does not bound a once-punctured disk in . We claim that does not bound a disk in . Suppose, contrary to our claim, that bounds a disk in . Then, is isotopic to in . As we pass from the level to the level , the simple closed curves and are pinched together to produce a single simple closed curve that is inessential in . This contradicts the fact that the point does not lie in . Therefore, we conclude that must be essential in .
By repeatedly compressing along the innermost disk with at most one puncture in as long as possible, we finally obtain a disk in such that . Since , we have .
Next, suppose that bounds a once-punctured disk in . If is essential in , by repeatedly compressing along the innermost disk with at most one puncture in as long as possible, we finally obtain a disk in the handlebody such that and . Since , it follows that . Thus, in the following, we shall assume that is inessential in .
The simple closed curve cobounds an annulus with in . As we pass from the level to the level , the simple closed curves and are pinched together to produce a new single simple closed curve . The curve is essential in because the point lies in the complement of . On the other hand, bounds a disk in . By repeatedly compressing along the innermost disk in as long as possible, we finally obtain a disk in such that . Since , it follows that .
Case B5: The simple closed curves and are pinched together to produce a single simple closed curve (Figure 17).
Since the point is in the complement in of , is essential in . In , bounds a disk with at most one puncture. See Figure 17.

By repeatedly compressing along the innermost disk with at most one puncture in as long as possible, we finally obtain a disk in the handlebody such that and . Therefore, we have , which completes the proof of the inequality (5) in Case B.
4. Proof of Theorem 0.1
We are now in position to prove Theorem 0.1.
Proof of Theorem 0.1..
Let be a bridge decomposition of with the distance at least , where is a link in a -manifold . By Theorem 1.3, admits a complete and finite volume hyperbolic structure. In this case it is well known that its mapping class group is a finite group, hence so is . The first assertion now follows from Theorem 3.1 and the inequality (1). The second assertion can be shown by the same argument using Proposition 1.1 instead of the inequality (1). ∎
Acknowledgements.
The authors would like to thank Kazuhiro Ichihara and Yeonhee Jang for their helpful comments on the remark at the end of Section 1.3. The authors would like to thank the anonymous referee for carefully reading the manuscript. D. I. is supported by JSPS KAKENHI Grant Number JP21J10249. Y. K. is supported by JSPS KAKENHI Grant Numbers JP20K03588, JP20K03614 and JP21H00978.
References
- [1] D. Bachman and S. Schleimer, Distance and bridge position. Pacific J. Math. 219 (2005), no. 2, 221–235.
- [2] R. Blair, M. Campisi, J. Johnson, S. A. Taylor and M. Tomova, Exceptional and cosmetic surgeries on knots, Math. Ann. 367 (2017), no. 1-2, 581–622.
- [3] W. Haken, Some results on surfaces in -manifolds, Studies in Modern Topology pp. 39–98 Math. Assoc. Amer. (distributed by Prentice-Hall, Englewood Cliffs, N.J.) 1968.
- [4] K. Hartshorn, Heegaard splittings of Haken manifolds have bounded distance. Pacific J. Math. 204 (2002), no. 1, 61–75.
- [5] J. Hempel, -manifolds as viewed from the curve complex, Topology 40 (2001), no. 3, 631–657.
- [6] S. Hirose, D. Iguchi, E. Kin and Y. Koda, Goeritz groups of bridge decompositions, to appear in Int. Math. Res. Not.
- [7] K. Ichihara and J. Ma, A random link via bridge position is hyperbolic, Topology Appl. 230 (2017), 131–138.
- [8] Y. Jang, Distance of bridge surfaces for links with essential meridional spheres. Pacific J. Math. 267 (2014), no. 1, 121–130.
- [9] J. Johnson, Mapping class groups of medium distance Heegaard splittings, Proc. Amer. Math. Soc. 138 (2010), no. 12, 4529–4535.
- [10] J. Johnson, Bounding the stable genera of Heegaard splittings from below. J. Topol. 3 (2010), no. 3, 668–690.
- [11] J. Johnson, Automorphisms of the three-torus preserving a genus-three Heegaard splitting. Pacific J. Math. 253 (2011), no. 1, 75–94.
- [12] T. Kobayashi and O. Saeki, The Rubinstein-Scharlemann graphic of a 3-manifold as the discriminant set of a stable map. Pacific J. Math. 195 (2000), no. 1, 101–156.
- [13] M. Korkmaz and A. Papadopoulos, On the arc and curve complex of a surface. Math. Proc. Cambridge Philos. Soc. 148 (2010), no. 3, 473–483.
- [14] H. Namazi, Big Heegaard distance implies finite mapping class group, Topology Appl. 154 (2007), 2939–2949.
- [15] H. Rubinstein and M. Scharlemann, Comparing Heegaard splittings of non-Haken -manifolds, Topology 35 (1996), 1005–1026.
- [16] M. Scharlemann and M. Tomova, Alternate Heegaard genus bounds distance. Geom. Topol. 10 (2006), 593–617.
- [17] M. Tomova, Multiple bridge surfaces restrict knot distance. Algebr. Geom. Topol. 7 (2007), 957–1006.