Dissipation-induced bound states as a two-level system
Abstract
Potential wells are employed to constrain quantum particles into forming discrete energy levels, acting as artificial few-level systems. In contrast, an anti-parity-time () symmetric system can have a single pair of real energy levels, while all the remaining levels are unstable due to the negative imaginary part of the energy. In this work, we investigate the formation of bound states in a tight-binding chain induced by a harmonic imaginary potential. Exact solutions show that the real parts of energy levels are equidistant, while the imaginary parts are semi-negative definite and equidistant. This allows for the formation of an effective two-level system. For a given initial state with a wide range of profiles, the evolved state always converges to a superposition of two stable eigenstates. In addition, these two states are orthogonal under the Dirac inner product and can be mutually switched by applying a pulse of a linear field. Our finding provides an alternative method for fabricating quantum devices through dissipation.
I Introduction
The bound state concept pervades various branches of physics, including optics and condensed matter. A bound state refers to a particle confined within a localized region by a real-valued potential, often due to interactions with other particles, within the framework of the Hartree-Fock approximation. Throughout the field of physics, phenomena that are stable or in equilibrium can be elucidated by the concept of bound states, which applies to both quantum and classical systems. Experimentally, bound states can be engineered by introducing artificial defects into photonic crystals. These defects, arranged in an array, form what are known as coupled-resonator optical waveguides (CROWs), which enable nearly lossless guidance and manipulation of wave packets, including their bending Johnson et al. (2001); John (1987); Yablonovitch (1987); Skorobogatiy et al. (2005); Engelen et al. (2008); Hughes et al. (2005); Kuramochi et al. (2005); Le Thomas et al. (2008); Mazoyer et al. (2009, 2010); O’Faolain et al. (2007).
In contemporary physics, the presence of a complex potential is now permissible, as non-Hermitian quantum mechanics has become a versatile framework for developing functional devices that operate within the non-Hermitian domain. The fundamental mechanism underlying non-Hermitian systems with parity-time () symmetry hinges on the concept of an imaginary potential Bender and Boettcher (1998); Dorey et al. (2001); Mostafazadeh (2002); Znojil (1999); Jones (2005); El-Ganainy et al. (2007); Musslimani et al. (2008); Makris et al. (2008); Joglekar et al. (2010); Scott and Joglekar (2011); Chong et al. (2010); Jing et al. (2014). This concept has been both theoretically explored and experimentally realized Guo et al. (2009); Rüter et al. (2010); Wan et al. (2011); Sun et al. (2014); Feng et al. (2012); Peng et al. (2014); Chang et al. (2014); Feng et al. (2014); Hodaei et al. (2014); Wimmer et al. (2015), serving as an essential building block for constructing such systems.
A non-Hermitian Hamiltonian exhibits unique characteristics that set it apart from its Hermitian counterpart in three distinct aspects. (i) Asymmetry hopping term can result in skin effect, a typical bound state Zhang and Song (2013); Kunst et al. (2018); Yao and Wang (2018); Gong et al. (2018); Jin and Song (2019). (ii) Adding a pseudo-Hermitian term to a non-Hermitian Hamiltonian consistently reduces the level spacing. Conversely, a nontrivial Hermitian perturbation invariably results in level repulsion. The phenomenon of shrinking level spacing is analogous to the impact of a real potential on a quantum system Zhang et al. (2019). (iii) In a system with energy levels featuring semi-negative imaginary components, only those eigenstates with real-valued energies are considered stable.
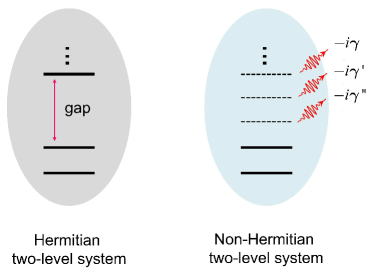
In this work, we explore the formation of two-level system through the mechanism associated with the characteristic mentioned as feature (iii) (see fig. 1). We investigate the formation of bound states in a tight-binding chain induced by a harmonic imaginary potential. It is an anti- symmetric system. Unlike -symmetry accompanied by real eigenvalues, an anti- symmetric system can have a single pair of real energy levels, while all the remaining levels are unstable due to the negative imaginary part of the energy. The phenomenon of dissipation gives rise to bound states that can be effectively described as a two-level system. We consider a tight-binding chain induced by a harmonic imaginary potential to demonstrate this feature. Exact solutions show that the real parts of energy levels are equidistant, while the imaginary parts are semi-negative definite and equidistant. This allows for the formation of an effective two-level system. For a given initial state with a wide range of profiles, the evolved state always converges to a superposition of two stable eigenstates. We also find that these two states are orthogonal under the Dirac inner product, and thus a superposition state obeys the Dirac probability-preserving dynamics. Therefore, although the two-level system is engineered by non-Hermitian terms, it acts as a conditional Hermitian device. In addition, it is shown that two states can be mutually switched by applying a pulse of a linear field. We demonstrate the conclusions by numerical simulations. Our finding provides an alternative method for fabricating quantum devices through dissipation.
This paper is organized as follows. In Sec. II, we introduce the non-Hermitian model and present approximate solutions for low energy levels. In Sec. III and IV, we show that two-level quantum states can be dynamically prepared and operated. Finally, our conclusion is given in Sec. V.
II Hamiltonian and symmetry
We start with the tight-binding model with the Hamiltonian
| (1) |
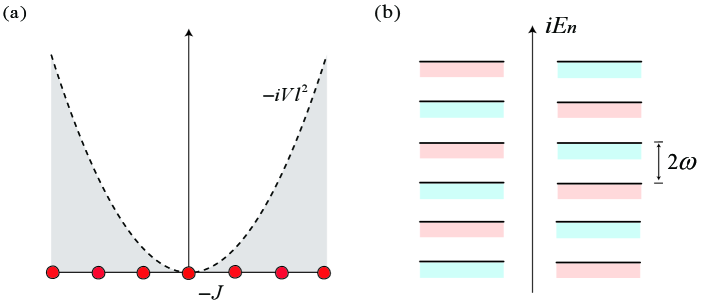
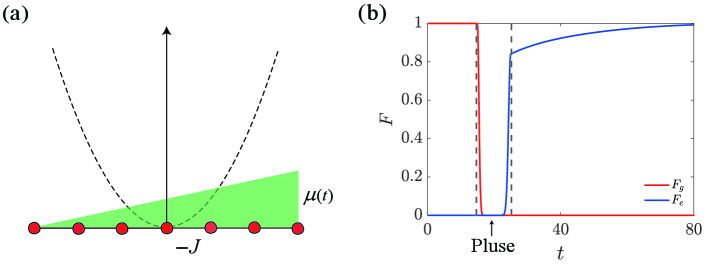
where denotes a site state describing the Wannier state localized on the th period of the potential. Here, is the tunneling strength, and is the strength of the harmonic potential. The system is schematically illustrated in fig. 2(a). In previous work, it has been shown that the lower energy levels are equidistant when the system is Hermitian by taking Shi et al. (2005); Tao et al. (2005). In this work, we take , , and constant . We note that the Hamiltonian has anti- symmetry, satisfying
| (2) |
where the linear operator and antilinear operator are defined as
| (3) |
The eigenstate , satisfying the Schrodinger equation
| (4) |
can be written in the form
| (5) |
According to the non-Hermitian quantum mechanics Scholtz et al. (1992), is a pseudo-Hermitian operator, and then can be real or come in complex conjugate pairs.
Specifically, we expect the solution for the wave function to be connected to a continuous function, . In the following, we aim to obtian the approximate expression of the function , under certain conditions. The Schrodinger equation (4) shows that function can be determined by the equation
| (6) |
We propose two types of functions as the Bethe ansatz wave function, which are defined as
| (7) |
and
| (8) |
with coefficients and . Obviously, are eigen functions of quantum oscillator system, satisfying the differential equation
| (9) |
with , , ,. As known that function is smooth and slowly varying for small and (or ), where is the Hermite polynomials. This allows the approximation
| (10) |
resulting in the eigen energy levels
| (11) |
in association with Eqs. (6) and (9). Similarly, we have
| (12) |
It accords with the prediction with the relations
| (13) |
and
| (14) |
i.e., the real parts of the levels are paired with opposite signs. The additional feature of the energy levels is that their imaginary parts are semi-negative finite and equally distant, which is schematically illustrated in fig. 2(b).
Remarkably, there are only two eigenstates have real energy, with wave function and eigen energy
| (15) | |||||
| (16) |
where the normalization factor . All the rest eigenstates decay as time increases. In this sense, such a system only supports two stable eigenstates, the ground state
| (17) |
and the excited state
| (18) |
In general, two different eigenstates are biorthogonal for non-Hermitian system, which satisfy the relationship, i.e., Brody (2013). It accords with the fact that we have
| (19) |
in the limit (or ), where satisfies
| (20) |
Meanwhile, we also have
| (21) |
in such a limit, which indicates that the Dirac orthogonality still holds. Therefore, such a non-Hermitian system can be regarded as a Hermitian two-level system.
III Two-level dynamics
In quantum physics, two-level atoms are simple yet rich quantum systems that are fundamental to our understanding of quantum mechanics and are essential for the development of quantum technologies. The ability to control and manipulate these systems is at the heart of many advances in quantum science.
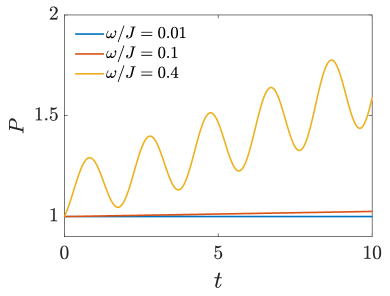
In a Hermitian system, an effective two-level system can be formed when the ground state and the excited state have relative large energy gap from the high excited states. In contrast, a distinguishing characteristic of the non-Hermitian two-level system is that the all other eigenstates are unstable in dynamics or short lived (see fig. 1). This enables the system to exhibit the following dynamical behaviors.
We start with the time evolution for an arbitrary initial state , which can always be expressed as the form
| (22) |
in the framework of the above approximation approach. Thus, the time evolved state is
| (23) |
which tends to
| (24) |
after a long time.
Specifically, for an initial state with the wave function varying slowly as changes, we have and . Then, the ground state can be dynamically generated from a variety of initial states. Note that the analytical expressions of and from are approximate. In practice, such two states can be obtained from numerical simulations. To verify and demonstrate the above results, numerical simulations of the dynamic process are performed using a uniform mesh for the time discretization.
We calculate the fidelity
| (25) |
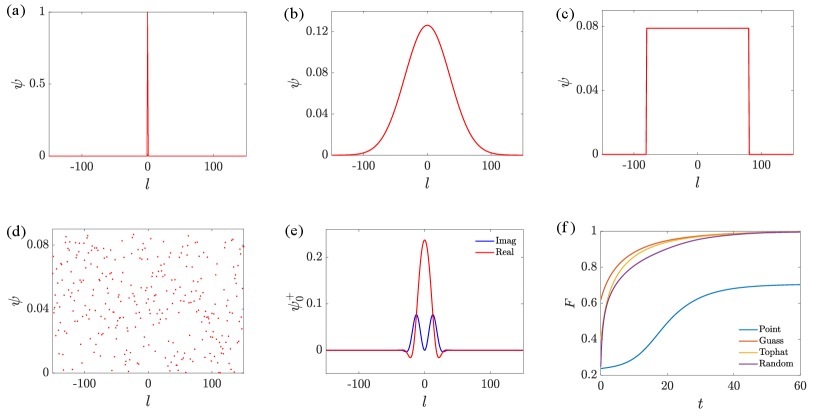
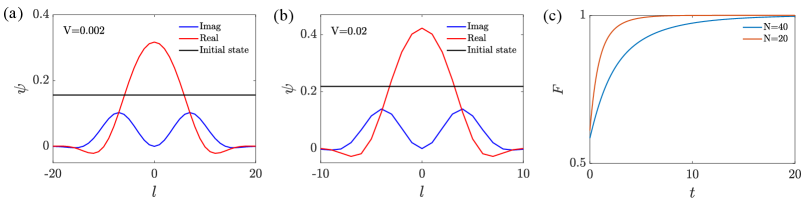
to measure the distance between the evolved state and the target state. We plot several typical initial states and in fig. 3. These numerical results are consistent with our previous analysis, which showed that the evolved states converge to the state for several selected initial states. Therefore, we conclude that a harmonic imaginary potential can support the stable bound state , which can also be prepared dynamically. We also investigate the small size systems by numerical simulation. We plot the profiles of ground states and of evolving from a uniform initial state in fig. 4. It indicates that a small system size requires a small width of the wavefunction profile, which requires a large (or ), resulting in faster convergence. The small size and the faster convergence of the fidelity make the scheme experimentally feasible.
In general, the dynamics of a non-Hermitian two-level system are not Dirac probability-preserving. However, as mentioned above, we have eg in the limit (or ). This indicates that a superposition state obeys the Dirac probability-preserving dynamics. We demonstrate this point by computing the probability
| (26) |
for initial state
| (27) |
where and are obtained by the numerical simulation for the systems with different values of . The plots of the function in fig. 5 conform to the theoretical predictions we established.
IV Transition between two levels
In parallel, one can dynamically generate the excited state from initial states with . In this section, we focus on a scheme designed to facilitate the transition between the two states and . Based on the above analysis, a possible clue is provided by the relation . We start with the dynamic realization of operator .
We consider to realize the action of operator by the time evolution under a quenching Hamiltonian
| (28) |
where
| (29) |
describes the action of an extra time-dependent uniform field. Here the coefficient is defined as
| (30) |
with which acts as a pulse. In general, the time evolution of a given initial state is governed by the time propagator
| (31) |
Under the condition , we can have
| (32) | |||||
It indicates that the time evolution of the initial state is
| (33) |
which tends to after a long time. Inversely, we can also realize the operation
| (34) |
To verify this result, we perform numerical simulation for such a quenching process for two different initial states and , which are obtained by exact diagonalization of the pre-quench Hamiltonian . We compute the two fidelities
| (35) | |||||
| (36) |
to evaluate the efficiency of the scheme. It is expected that the fidelities obey and (or and ). The numerical results are presented in fig. 6(b), which are in accord with our analysis. Here the form of is the simplest one for a pulse. Other types of could also have the same effect.
V Conclusion and Discussion
In summary, we have studied the formation of two-level bound states induced by imaginary potential in a Hermitian tight-binding system. We have shown that the real parts of energy levels are equidistant, while the imaginary parts are semi-negative definite and equidistant. This allows for the formation of an effective two-level system. The existence of bound states in a system with an imaginary potential is fundamentally due to the fact that the corresponding Hermitian system has a discrete spatial coordinates, which arises from the presence of a periodic real potential. The similar phenomenon occurs in another non-Hermitian system. It has been shown in Ref. Zhang et al. (2024) that bound states can form in a tight-binding chain in the presence of a linear imaginary potential. This allows for the formation of an effective two-level system. In contrast to a Hermitian two-level system, a non-Hermitian system can have a single pair of real energy levels, while the remaining levels are unstable due to their negative imaginary components. This feature enables the dynamic preparation and operation of two-level quantum states. Our findings reveal that the phenomenon of dissipation gives rise to bound states that can effectively be described as a two-level system.
Acknowledgements.
This work was supported by National Natural Science Foundation of China (under Grant No. 12374461).References
- Johnson et al. (2001) S.G. Johnson, A. Mekis, S. Fan, and J.D. Joannopoulos, “Molding the flow of light,” Computing in Science amp; Engineering 3, 38–47 (2001).
- John (1987) Sajeev John, “Strong localization of photons in certain disordered dielectric superlattices,” Physical Review Letters 58, 2486–2489 (1987).
- Yablonovitch (1987) Eli Yablonovitch, “Inhibited Spontaneous Emission in Solid-State Physics and Electronics,” Physical Review Letters 58, 2059–2062 (1987).
- Skorobogatiy et al. (2005) Maksim Skorobogatiy, Guillaume Begin, and Anne Talneau, “Statistical analysis of geometrical imperfections from the images of 2d photonic crystals,” Optics Express 13, 2487 (2005).
- Engelen et al. (2008) R. J. P. Engelen, D. Mori, T. Baba, and L. Kuipers, “Two Regimes of Slow-Light Losses Revealed by Adiabatic Reduction of Group Velocity,” Physical Review Letters 101, 103901 (2008).
- Hughes et al. (2005) S. Hughes, L. Ramunno, Jeff F. Young, and J. E. Sipe, “Extrinsic Optical Scattering Loss in Photonic Crystal Waveguides: Role of Fabrication Disorder and Photon Group Velocity,” Physical Review Letters 94, 033903 (2005).
- Kuramochi et al. (2005) E. Kuramochi, M. Notomi, S. Hughes, A. Shinya, T. Watanabe, and L. Ramunno, “Disorder-induced scattering loss of line-defect waveguides in photonic crystal slabs,” Physical Review B 72, 161318 (2005).
- Le Thomas et al. (2008) N. Le Thomas, V. Zabelin, R. Houdré, M. V. Kotlyar, and T. F. Krauss, “Influence of residual disorder on the anticrossing of Bloch modes probed in k space,” Physical Review B 78, 125301 (2008).
- Mazoyer et al. (2009) S. Mazoyer, J. P. Hugonin, and P. Lalanne, “Disorder-Induced Multiple Scattering in Photonic-Crystal Waveguides,” Physical Review Letters 103, 063903 (2009).
- Mazoyer et al. (2010) S. Mazoyer, P. Lalanne, J.C. Rodier, J.P. Hugonin, M. Spasenović, L. Kuipers, D.M. Beggs, and T.F. Krauss, “Statistical fluctuations of transmission in slow light photonic-crystal waveguides,” Optics Express 18, 14654 (2010).
- O’Faolain et al. (2007) Liam O’Faolain, Thomas P. White, David O’Brien, Xiadong Yuan, Michael D. Settle, and Thomas F. Krauss, “Dependence of extrinsic loss on group velocity in photonic crystal waveguides,” Optics Express 15, 13129 (2007).
- Bender and Boettcher (1998) Carl M. Bender and Stefan Boettcher, “Real Spectra in Non-Hermitian Hamiltonians Having Symmetry,” Physical Review Letters 80, 5243–5246 (1998).
- Dorey et al. (2001) Patrick Dorey, Clare Dunning, and Roberto Tateo, “Spectral equivalences, bethe ansatz equations, and reality properties in -symmetric quantum mechanics,” Journal of Physics A: Mathematical and General 34, 5679–5704 (2001).
- Mostafazadeh (2002) Ali Mostafazadeh, “Pseudo-Hermiticity versus PT symmetry: the necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian,” Journal of Mathematical Physics 43, 205–214 (2002).
- Znojil (1999) Miloslav Znojil, “PT-symmetric harmonic oscillators,” Physics Letters A 259, 220–223 (1999).
- Jones (2005) H F Jones, “On pseudo-Hermitian Hamiltonians and their Hermitian counterparts,” Journal of Physics A: Mathematical and General 38, 1741–1746 (2005).
- El-Ganainy et al. (2007) R. El-Ganainy, K. G. Makris, D. N. Christodoulides, and Ziad H. Musslimani, “Theory of coupled optical PT-symmetric structures,” Optics Letters 32, 2632 (2007).
- Musslimani et al. (2008) Z. H. Musslimani, K. G. Makris, R. El-Ganainy, and D. N. Christodoulides, “Optical Solitons in Periodic Potentials,” Physical Review Letters 100, 030402 (2008).
- Makris et al. (2008) K. G. Makris, R. El-Ganainy, D. N. Christodoulides, and Z. H. Musslimani, “Beam Dynamics in Symmetric Optical Lattices,” Physical Review Letters 100, 103904 (2008).
- Joglekar et al. (2010) Yogesh N. Joglekar, Derek Scott, Mark Babbey, and Avadh Saxena, “Robust and fragile -symmetric phases in a tight-binding chain,” Physical Review A 82, 030103 (2010).
- Scott and Joglekar (2011) Derek D. Scott and Yogesh N. Joglekar, “Degrees and signatures of broken symmetry in nonuniform lattices,” Physical Review A 83, 050102 (2011).
- Chong et al. (2010) Y. D. Chong, Li Ge, Hui Cao, and A. D. Stone, “Coherent Perfect Absorbers: Time-Reversed Lasers,” Physical Review Letters 105, 053901 (2010).
- Jing et al. (2014) Hui Jing, S.K. Özdemir, Xin-You Lü, Jing Zhang, Lan Yang, and Franco Nori, “-Symmetric Phonon Laser,” Physical Review Letters 113, 053604 (2014).
- Guo et al. (2009) A. Guo, G. J. Salamo, D. Duchesne, R. Morandotti, M. Volatier-Ravat, V. Aimez, G. A. Siviloglou, and D. N. Christodoulides, “Observation of -Symmetry Breaking in Complex Optical Potentials,” Physical Review Letters 103, 093902 (2009).
- Rüter et al. (2010) Christian E. Rüter, Konstantinos G. Makris, Ramy El-Ganainy, Demetrios N. Christodoulides, Mordechai Segev, and Detlef Kip, “Observation of parity–time symmetry in optics,” Nature Physics 6, 192–195 (2010).
- Wan et al. (2011) Wenjie Wan, Yidong Chong, Li Ge, Heeso Noh, A. Douglas Stone, and Hui Cao, “Time-Reversed Lasing and Interferometric Control of Absorption,” Science 331, 889–892 (2011).
- Sun et al. (2014) Yong Sun, Wei Tan, Hong-qiang Li, Jensen Li, and Hong Chen, “Experimental Demonstration of a Coherent Perfect Absorber with PT Phase Transition,” Physical Review Letters 112, 143903 (2014).
- Feng et al. (2012) Liang Feng, Ye-Long Xu, William S. Fegadolli, Ming-Hui Lu, José E. B. Oliveira, Vilson R. Almeida, Yan-Feng Chen, and Axel Scherer, “Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies,” Nature Materials 12, 108–113 (2012).
- Peng et al. (2014) Bo Peng, Şahin Kaya Özdemir, Fuchuan Lei, Faraz Monifi, Mariagiovanna Gianfreda, Gui Lu Long, Shanhui Fan, Franco Nori, Carl M. Bender, and Lan Yang, “Parity–time-symmetric whispering-gallery microcavities,” Nature Physics 10, 394–398 (2014).
- Chang et al. (2014) Long Chang, Xiaoshun Jiang, Shiyue Hua, Chao Yang, Jianming Wen, Liang Jiang, Guanyu Li, Guanzhong Wang, and Min Xiao, “Parity–time symmetry and variable optical isolation in active–passive-coupled microresonators,” Nature Photonics 8, 524–529 (2014).
- Feng et al. (2014) Liang Feng, Zi Jing Wong, Ren-Min Ma, Yuan Wang, and Xiang Zhang, “Single-mode laser by parity-time symmetry breaking,” Science 346, 972–975 (2014).
- Hodaei et al. (2014) Hossein Hodaei, Mohammad-Ali Miri, Matthias Heinrich, Demetrios N. Christodoulides, and Mercedeh Khajavikhan, “Parity-time–symmetric microring lasers,” Science 346, 975–978 (2014).
- Wimmer et al. (2015) Martin Wimmer, Alois Regensburger, Mohammad-Ali Miri, Christoph Bersch, Demetrios N. Christodoulides, and Ulf Peschel, “Observation of optical solitons in pt-symmetric lattices,” Nature Communications 6 (2015), 10.1038/ncomms8782.
- Zhang and Song (2013) X.Z. Zhang and Z. Song, “Momentum-independent reflectionless transmission in the non-Hermitian time-reversal symmetric system,” Annals of Physics 339, 109–121 (2013).
- Kunst et al. (2018) Flore K. Kunst, Elisabet Edvardsson, Jan Carl Budich, and Emil J. Bergholtz, “Biorthogonal Bulk-Boundary Correspondence in Non-Hermitian Systems,” Physical Review Letters 121, 026808 (2018).
- Yao and Wang (2018) Shunyu Yao and Zhong Wang, “Edge States and Topological Invariants of Non-Hermitian Systems,” Physical Review Letters 121, 086803 (2018).
- Gong et al. (2018) Zongping Gong, Yuto Ashida, Kohei Kawabata, Kazuaki Takasan, Sho Higashikawa, and Masahito Ueda, “Topological Phases of Non-Hermitian Systems,” Physical Review X 8, 031079 (2018).
- Jin and Song (2019) L. Jin and Z. Song, “Bulk-boundary correspondence in a non-Hermitian system in one dimension with chiral inversion symmetry,” Physical Review B 99, 081103 (2019).
- Zhang et al. (2019) K. L. Zhang, P. Wang, and Z. Song, “Exceptional-point-induced lasing dynamics in a non-Hermitian Su-Schrieffer-Heeger model,” Physical Review A 99, 042111 (2019).
- Shi et al. (2005) Tao Shi, Ying Li, Zhi Song, and Chang-Pu Sun, “Quantum-state transfer via the ferromagnetic chain in a spatially modulated field,” Physical Review A 71, 032309 (2005).
- Tao et al. (2005) Shi Tao, Chen Bing, and Song Zhi, “On Harmonic Approximation for Large Josephson Junction Coupling Charge Qubits,” Communications in Theoretical Physics 43, 795–798 (2005).
- Scholtz et al. (1992) F.G. Scholtz, H.B. Geyer, and F.J.W. Hahne, “Quasi-Hermitian operators in quantum mechanics and the variational principle,” Annals of Physics 213, 74–101 (1992).
- Brody (2013) Dorje C Brody, “Biorthogonal quantum mechanics,” Journal of Physics A: Mathematical and Theoretical 47, 035305 (2013).
- Zhang et al. (2024) H. P. Zhang, K. L. Zhang, and Z. Song, “Dynamics of non-Hermitian Floquet Wannier-Stark system,” (2024), arXiv:2401.13286 [quant-ph] .