Dissipation-accelerated entanglement generation

One of the most fundamental postulations of quantum mechanics is that the state of an isolated quantum system is described by a wavefunction, whose evolution is governed by a Hermitian Hamiltonian according to the Schrödinger equation. However, any quantum system is inevitably coupled to its surrounding environment, which acts as a meter that continuously acquires information about the system [1]. At the zero temperature, the environment can be regarded as a reservoir, composed of infinitely many bosonic modes, each initially in its vacuum state [2-4]. The system’s information is gradually leaked into the reservoir by exchanging energy quanta. The most remarkable feature of this process is that the system’s state evolution trajectory is significantly modified even if no quanta are leaked into the environment, as a consequence of measurement backaction.

For the no-jump trajectory, the system’s evolution still can be described by the Schrödinger equation with a non-Hermitian (NH) Hamiltonian, featuring the competition between Hermitian and dissipative terms [5]. Such environment-induced non-Hermiticity endows the Hamiltonian’s eigenstates and eigenenergies with striking features that are otherwise inaccessible, such as real-to-complex spectral phase transitions and NH topology [6-9]. So far, these NH effects have been experimentally demonstrated in distinct physical systems [10-30]. Recently, exceptional entanglement phenomena have been investigated in both theory and experiment in a NH spin-boson system [31]. In a very recent work [32], it was demonstrated that the entanglement between two interacting NH qubits can be generated within a time significantly shorter than that for two Hermitian ones. In the scheme, the two-qubit entanglement appears as a consequence of the competition between the intra-qubit coupling and individual driving of the qubits, and the entanglement speedup is enabled by proximity to a higher-order exceptional point. Each NH qubit is realized with a three-level natural or artificial atom, where the highest and intermediate levels are used to encode the quantum information, and the non-Hermiticity is manifested by the decay from the intermediate to the lowest levels. This scheme is valid only when the decaying channel from the highest to intermediate levels is neglected. However, such a condition cannot be satisfied for general systems. For example, the decaying rate of the levels of a normal transmon linearly scales with the quantum number.

We here propose an alternative scheme for exploiting non-Hermiticity to speed up entanglement generation speedup between two qubits. The theoretical model involves a Hermitian qubit interacting with a decaying one by swapping coupling, which conserves the total excitation number. The entanglement is generated in the single-excitation subspace. The excitation, initiall possessed by the NH qubit, is distributed between the two qubits by energy exchange. The maximal entanglement is attained when the two qubits are equally populated. We find that the non-Hermiticity significantly accelerate this excitation distribution process in a broad regime, enabling the two qubits to be entangled within a time much shorter than the dynamical timescale of the inter-qubit interaction. In distinct contrast with the scheme of Ref. [32], our approach does not require to encode the qubits in the highest and intermediate levels of a three-level system; the non-Hermiticity is manifested by the decay from the higher to lower levels of a two-level system. Futhermore, our scheme does not require individual driving of the qubits. Due to these simplications, our scheme is not subjected to the errors coming from the decay of the third level and from the fluctuations of individual drives, which are inherent in the previous scheme [33]. The idea can be directly extended to the three-qubit system, where a NH qubit is symmetrically coupled to two Hermitian ones. The dissipation of the NH qubit helps to speed up the generation of the three-qubit W-type maximally entangled state in a probabilistic manner.

We here consider the system involving two qubits with the same frequency interacting with each other by swapping coupling, as shown in Fig. 1a. The non-Hermiticity of the system is manifested by the non-negligible dissipative rate of the first qubit, denoted as $\kappa$. The decaying rate of the second qubit is much smaller than the inter-qubit swapping rate $\lambda$, thereby negligible. The system dynamics is described by the master equation

$$\frac{d\stackrel{{\scriptstyle\char 94\relax}}{{\rho}}}{dt}=-i[\stackrel{{\scriptstyle\char 94\relax}}{{{\cal H}}}_{NH},\rho]+\kappa\stackrel{{\scriptstyle\char 94\relax}}{{\sigma}}_{1}^{-}\rho\stackrel{{\scriptstyle\char 94\relax}}{{\sigma}}_{1}^{+},$$

(1)

where $\stackrel{{\scriptstyle\char 94\relax}}{{{\cal H}}}_{NH}$ represents the two-qubit NH Hamiltonian, defined as

$$\stackrel{{\scriptstyle\char 94\relax}}{{{\cal H}}}_{NH}=\lambda(\stackrel{{\scriptstyle\char 94\relax}}{{\sigma}}_{1}^{+}\stackrel{{\scriptstyle\char 94\relax}}{{\sigma}}_{2}^{-}+\stackrel{{\scriptstyle\char 94\relax}}{{\sigma}}_{1}^{-}\stackrel{{\scriptstyle\char 94\relax}}{{\sigma}}_{2}^{+})-i\frac{\kappa}{2}\left|1\right\rangle_{1}\left\langle 1\right|.$$

(2)

Here $\stackrel{{\scriptstyle\char 94\relax}}{{\sigma}}_{j}^{+}=\left|1\right\rangle_{j}\left\langle 0\right|$ and $\stackrel{{\scriptstyle\char 94\relax}}{{\sigma}}_{j}^{-}=\left|0\right\rangle_{j}\left\langle 1\right|$ with $\left|1\right\rangle_{j}$ ($\left|0\right\rangle_{j}$) denoting the upper (lower) level of the jth qubit, and $\lambda$ is inter-qubit coupling strength. The system evolution is a weighted mixture of infinitely many trajectories governed by the NH Hermiltonian but interrupted by randomly-occurring quantum jumps. For the trajectory without quantum jump, the system state evolution is governed by $\stackrel{{\scriptstyle\char 94\relax}}{{{\cal H}}}_{NH}$.

Under the NH Hamiltonian, the total excitation number of the qubits is conserved. Consequently, the qubit Hilbert space can be devided into three uncoupled subspaces ${\cal S}_{0}=\left\{\left|0_{1},0_{2}\right\rangle\right\}$, ${\cal S}_{1}=\left\{\left|1,0\right\rangle,\left|0,1\right\rangle\right\}$, and ${\cal S}_{2}=\left\{\left|1,1\right\rangle\right\}$. In ${\cal S}_{1}$, the system has a pair of eigenenergies, given by

$$E_{\pm}=-i\kappa/4\pm\Omega.$$

(3)

where $\Omega=\sqrt{\lambda^{2}-\kappa^{2}/16}$. The corresponding eigenstates are

$$\left|\Phi_{\pm}\right\rangle={\cal N}_{\pm}(E_{\pm}\left|1_{1},0_{2}\right\rangle+\lambda\left|0_{1},1_{2}\right\rangle),$$

(4)

where ${\cal N}_{\pm}=(\left|E_{\pm}\right|^{2}+\lambda^{2})^{-1/2}$. Suppose that the system is initially in the state $\left|\psi(0)\right\rangle=\left|1_{1},0_{2}\right\rangle$. Then the quantum state evolution associated with the no-jump trajectory can be rewritten as

$$\left|\psi(t)\right\rangle={\cal N}({\cal A}\left|1,0\right\rangle-i{\cal B}\left|0,1\right\rangle),$$

(5)

where ${\cal N}=({\cal A}^{2}+{\cal B}^{2})^{-1/2}$. When $R=\kappa/(4\lambda)<1$, the coefficients ${\cal A}$ and ${\cal B}$ are given by

	$\displaystyle{\cal A}$	$\displaystyle=$	$\displaystyle\cos(\Omega t)-\frac{\kappa}{4\Omega}\sin(\Omega t),$
	$\displaystyle{\cal B}$	$\displaystyle=$	$\displaystyle\frac{\lambda}{\Omega}\sin(\Omega t).$

For $R>1$, the trigonometric functions are replaced by the corresponding hyperbolic functions, with $\Omega=\sqrt{\kappa^{2}/16-\lambda^{2}}$. The two-qubit entanglement is quantified by the concurrence, given by [33]

$${\cal E}=2{\cal N}^{2}{\cal AB}\text{.}$$

(6)

To quantify to what extent the entanglement generation is speeded up by the non-Hermiticity, we define the rescaled entangling time, $T_{rs}=T/\tau$, where $T$ is the shortest time needed to conditionally produce the two-qubit maximally entangled state for the NH system, and $\tau=\pi/4\lambda$ is the corresponding time for the Hermitian system. For $R<1$, the rescaled entangling time is given by

$$T_{rs}=\frac{4}{\pi}\frac{1}{\sqrt{1-R^{2}}}\arctan\sqrt{\frac{1-R}{1+R}}.$$

(7)

When $R>1$, $T_{rs}$ is

$$T_{rs}=\frac{4}{\pi}\frac{1}{\sqrt{R^{2}-1}}arc\tanh\sqrt{\frac{R-1}{R+1}},$$

(8)

To quantitatively confirm the non-Hermiticity-enabled entanglement speedup, in Fig. 1b we present the two-qubit concurrence, associated with the no-jump trajectory, as a function of $\lambda t$ and $R$. The result clearly shows that the concurrence ${\cal E}$ exhibits a non-monotonous behavior, and can reach the maximum 1 no matter when $R<1$ or $R>1$. The time needed to reach the maximal entanglement (${\cal E}=1$) is monotonously decreased with the increase of $\kappa$. When $R>1$, after reaching the maximum ${\cal E}$ drops to zero at the time $t=G^{-1}arc\tanh(4G/\kappa)$, and then monotonously tends towards ${\cal E}_{t\rightarrow\infty}=2x/(1+x^{2})$, where $x=(G-\kappa/4)/\lambda$. For $R\gg 1$, ${\cal E}_{t\rightarrow\infty}\simeq 1/(2R)$. Fig. 1c display the rescaled entangling time $T_{sc}$ versus the ratio $R$. The results clearly show that the entanglement generation is indeed speeded up by the non-Hermiticity, and $T_{sc}^{2q}$ has a maximum $1$ when $\kappa=0$. The result can be interpreted as follows. The maximal entanglement is reached when the populations of $\left|1,0\right\rangle$ and $\left|0,1\right\rangle$, $P_{1,0}$ and $P_{0,1}$, are balanced. For the unitary evolution, this is achieved by coherent excitation transfer. When the excitation is initially populated in the NH qubit, the leakage of its population from the NH qubit to the environment help to increase the ratio $P_{0,1}/P_{1,0}$ from 0 to 1.

This entanglement dynamics is in stark contrast with that presented in Re. [32], where the system starts with the initial state $\left|0,1\right\rangle$. For such an initial state, the system evolution associated with the no-jump trajectory is given by [32]

$$\left|\psi^{\prime}(t)\right\rangle={\cal N}^{\prime}({\cal A}^{\prime}\left|0,1\right\rangle-i{\cal B}\left|1,0\right\rangle),$$

(9)

where ${\cal A}^{\prime}=\cos(\Omega t)+\frac{\kappa}{4\Omega}\sin(\Omega t)$ and $\cosh(Gt)+\frac{\kappa}{4G}\sinh(Gt)$ for $R<1$ and $R>1$, respectively. The two-qubit entanglement is ${\cal E}^{\prime}=2{\cal N}^{\prime 2}{\cal A}^{\prime}{\cal B}$. For $R<1$, the rescaled entangling time is

$$T_{rs}^{\prime}=\frac{4}{\pi}\frac{1}{\sqrt{1-R^{2}}}\arctan\sqrt{\frac{1+R}{1-R}}.$$

(10)

Contrary to the case with the initial state $\left|1,0\right\rangle$, $T_{rs}^{\prime}$ increases with $R$. This is due to the fact that the dissipation plays a negative role in the transfer of the excitation from the Hermitian qubit to the NH qubit, so that it takes a longer time to balance $P_{1,0}$ and $P_{0,1}$. When $R>1$, ${\cal E}$ is monotonously increased, tending to a fixed value, which is smaller than 1 and is decreased when R increases. The results imply that the dissipation can speed up entanglement only when excitation is initially held by the NH qubit.

It is worthwhile to investigate to what extent the success probability of producing the maximally entangled state is reduced with the increase of the dissipation rate. When $R<1$, this probability is

$${\cal P}=2\frac{1}{1-R^{2}}e^{-\kappa T/2}\sin^{2}\left(\Omega T\right).$$

(11)

For $R>1$, ${\cal P}$ is

$${\cal P}=2\frac{1}{R^{2}-1}e^{-\kappa T/2}\sinh^{2}\left(\Omega T\right).$$

(12)

Fig. 1d presents this probability as a function of $R$. The result implies that, for a given inter-qubit coupling strength, the time needed to achieve the maximal entanglement is shortened at the price of the decrease of the success probability.

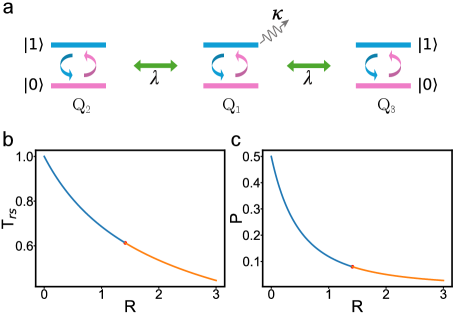
We note that the scheme can be directly generalized to realize dissipation-based three-qubit entanglement accelaration. The system involves two Hermitian qubits, each of which is coupled to a NH qubit with the coupling strength $\Omega$, as shown in Fig. 2a. For the no-jump evolution trajectory, the system dynamics is governed by the NH Hamiltonian

$$\stackrel{{\scriptstyle\char 94\relax}}{{{\cal H}}}_{NH}=\lambda[\stackrel{{\scriptstyle\char 94\relax}}{{\sigma}}_{1}^{+}(\stackrel{{\scriptstyle\char 94\relax}}{{\sigma}}_{2}^{-}+\stackrel{{\scriptstyle\char 94\relax}}{{\sigma}}_{3}^{-})+H.c.]-i\frac{\kappa}{2}\left|1\right\rangle_{1}\left\langle 1\right|.$$

(13)

In the single-excitation subspace $\left\{\left|1,0,0\right\rangle,\left|0,1,0\right\rangle,\left|0,0,1\right\rangle\right\}$, the system has three eigenenergies, given by

	$\displaystyle E_{0}$	$\displaystyle=$	$\displaystyle 0,$		(14)
	$\displaystyle E_{\pm}$	$\displaystyle=$	$\displaystyle-i\kappa/4\pm\Lambda,$

where $\Lambda=\sqrt{2\lambda^{2}-\kappa^{2}/16}$. The corresponding eigenstates are

	$\displaystyle\left|\Phi_{0}\right\rangle$	$\displaystyle=$	$\displaystyle\frac{1}{\sqrt{2}}(\left|0,1,0\right\rangle-\left|0,0,1\right\rangle),$		(15)
	$\displaystyle\left|\Phi_{j}\right\rangle$	$\displaystyle=$	$\displaystyle{\cal N}_{\pm}(E_{\pm}\left|1,0,0\right\rangle+\sqrt{2}\lambda\left|\phi_{b}\right\rangle,$

where $\left|\phi_{b}\right\rangle=\frac{1}{\sqrt{2}}(\left|0,1,0\right\rangle+\left|0,0,1\right\rangle)$. When the system is initially in the state $\left|\psi(0)\right\rangle=\left|1,0,0\right\rangle$, the state evolution associated to the no-jump trajectory is

$$\left|\Psi(t)\right\rangle={\cal M}({\cal C}\left|1,0,0\right\rangle-i{\cal D}\left|\phi_{b}\right\rangle),$$

(16)

where ${\cal M}=\sqrt{{\cal C}^{2}+{\cal D}^{2}}$. When $R<\sqrt{2}$, the coefficients ${\cal C}$ and ${\cal D}$ are given by

	$\displaystyle{\cal C}$	$\displaystyle=$	$\displaystyle\cos(\Lambda t)-\frac{\kappa}{4\Lambda}\sin(\Lambda t),$		(17)
	$\displaystyle{\cal D}$	$\displaystyle=$	$\displaystyle\frac{\lambda}{\Lambda}\sin(\Lambda t).$

For $R>\sqrt{2}$, the trigonometric functions are replaced by the corresponding hyperbolic functions, with $\Lambda=\sqrt{\kappa^{2}/16-2\lambda^{2}}$.

When $\left|{\cal C}\right|=\left|{\cal D}\right|/\sqrt{2}$, $\left|\Psi(t)\right\rangle$ corresponds to the three-qubit W-type maximally entangled state [34]

$$\left|\Psi_{w}\right\rangle=(e^{i\phi}\left|1,0,0\right\rangle\ +\left|0,1,0\right\rangle+\left|0,0,1\right\rangle)/\sqrt{3}.$$

(18)

For such a W state, any two qubits have a concurrence of $2/3$. When $R<\sqrt{2}$, the rescaled three-qubit W-state entangling time is given by

$$T_{rs}=\frac{\sqrt{2}}{\sqrt{2-R^{2}}\arccos(1/\sqrt{3})}\arctan\frac{\sqrt{2-R^{2}}}{1+R}.$$

(19)

Here $T_{rs}$ is defined as the ratio between the W-state generation times for the NH and Hermitian systems, $T_{rs}=T/\tau$, where $\tau=\frac{1}{\sqrt{2}\lambda}\arccos(1/\sqrt{3})$. For $R>\sqrt{2}$, the rescaled W-state entangling time is

$$T_{rs}=\frac{\sqrt{2}}{\sqrt{R^{2}-2}arc\cosh(1/\sqrt{3})}arc\tanh\frac{\sqrt{R^{2}-1}}{1+R}.$$

(20)

The rescaled W-state generation time $T_{sc}$, as a function of $R$, is presented in Fig. 2b, which confirms that $T_{sc}$ is smaller than 1 when $\kappa\neq 0$, verifying the non-Hermiticity-enabled acceleration of the W state generation. The result demonstrates that the time needed to reach the W-type maximally entangled state monotonously decreases with the increase of $\kappa$ for $\lambda<\kappa/4\sqrt{2}$. When $R<\sqrt{2}$, the success propability for producing the W-type maximally entangled state is

$${\cal P}=\frac{3}{2(2-R^{2})}e^{-\kappa T/2}\sin^{2}(\Lambda T).$$

(21)

For $R>\sqrt{2}$, ${\cal P}$ is given by

$${\cal P}=\frac{3}{2(R^{2}-2)}e^{-\kappa T/2}\sinh^{2}(\Lambda T).$$

(22)

which decreases with the increase of $R$, as shown in Fig. 2c.

In conclusion, we have presented a scheme for exploiting dissipation to speed up entanglement evolution for one NH qubit and one Hermitian qubit, interacting with each other via swapping a single excitation. When the excitation is initially possessed by the NH qubit, the system can conditionally evolve to a maximally entangled state within a time shorter than that needed for the Hermitian system with the same inter-qubit coupling strength. Neither does the three-level configuration nor individual driving of the qubits are required. The time needed to achieve the maximal entanglement monotonously decreases with the increase of the dissipation rate at the price of decreasing success probability. We further show that scheme can be extended to the three-qubit case, where one NH qubit initially in its excited state is coupled to two Hermitian qubits initially in their ground states. For the no-jump evolution trajectory, the time required to produce the W state is reduced by the dissipation of the NH qubit.

This work was supported by the National Natural Science Foundation of China under Grant No. 12474356.