Disparity Driven Heterogeneous Nucleation in Finite-Size Adaptive Networks

Introduction. Complex systems  [1, 2, 3], characterized by their intricate interconnections, often exhibit transitions from incoherence to coherence  [4, 5, 6]. Phase transitions are observed in several physical phenomena including crystallization and ferromagnetic transition. Beyond the physical systems, phase transitions in complex networks can shed more light on intriguing biological, ecological, and social problems such as population collapse and species extinction [7], polarization in society [8], and crashes in financial markets [9]. Particularly, transitions from incoherence to synchronization have been extensively studied employing various network topologies of real-world relevance [10, 11, 12]. Traditionally, most studies have been primarily concentrated on static networks. However, a large class of real-world networks co-evolve with their dynamical states and adapt to the prevailing environments. For instance, from intricate dynamics of human brain [13, 14, 15], technological systems [16, 17, 18], and biological networks [19, 20, 21] to social dynamics [22, 23, 24] adaptability manifests in the entire spectrum of complex networks across disciplines.

Recent interest in adaptive dynamical networks has surged due to their potential significance in addressing complex systems  [25, 26]. Adaptively coupled phase oscillator models are paradigms for describing the interplay of function and structure in complex systems [27]. Dynamical features such as frequency clusters [28, 29], solitary states [30], recurrent synchronization [31], and heterogeneous nucleation [32] are specific to adaptive dynamical networks [33]. In addition to adaptivity, large-scale systems consist of multiple populations exhibiting diverse and multi-scale behavior [34, 35, 36]. Examples include dynamics of distinct brain regions spanning multiple time scales [37], ecological communities exhibiting different time scales in response to infectious diseases [38, 39, 40], and time scales of social ties formation also vary across communities [41, 42]. These investigations also reveal that time scale disparity plays a nontrivial role in shaping their collective dynamics. Studies have shown that depending on various factors, a system may opt for different routes during phase transition. For instance, multiple nucleation pathways can unfold in crystal formation, each involving distinct intermediate states  [43, 44]. Similarly, in the opinion formation dynamics on social networks, individuals can form a cohesive community with consensus or can form fragmented structures known as echo chambers [45, 46]. The ability to manipulate the transition pathways holds immense importance as it allows to steer the system through the appropriate intermediate states under favorable conditions.

In this work, we consider a finite-size adaptive network comprised of two populations with time scale adaptation disparity and coupling strength disparity without any quenched disorder. We observe two distinct nucleation. In the first scenario, we find a single large interpopulation frequency cluster emerges at the population interface due to the coalescence of small intrapopulation clusters. The single large inter-frequency-cluster eventually enlarges to the system size as a function of the coupling strength facilitating a multi-step transition to global synchronization. In sharp contrast, intrapopulation clusters nucleate and coalesce together to manifest two completely entrained intrapopulation clusters as a function of the coupling strength for a strong intrapopulation adaptation rate. Finally, the two intraclusters merge together for a large coupling strength resulting in a single-step transition to synchronization. Recently, similar heterogeneous nucleation resulting in multi- and single-step transitions are reported to be facilitated by distinct quenched disorders [32]. A strong interpopulation coupling strength always favors nucleation of inter-frequency-clusters leading to multi-step transition even with a strong intrapopulation adaptation rate. Similarly, a strong intrapopulation coupling strength always favors nucleation of intra-frequency-clusters facilitating single-step transition even with a strong interpopulation adaptation rate. These results reveal that the disparity in the coupling strength determines the nature of nucleation leading to distinct synchronization transition. We analytically deduce the macroscopic evolution equations for the cluster dynamics using the collective coordinates framework [47] and show that the latter corroborates the simulation results. Further, we also deduce the upper bound for the coupling strength for the existence of two intraclusters explicitly, at which the abrupt single-step transition manifests, in terms of adaptation and coupling strength disparity parameters.
The Model. We consider a system of $N$ globally coupled phase oscillators with adaptive coupling represented as

where $\omega_{i}^{\eta}$ and $\phi_{i}^{\eta}(t)$ are the natural frequency and the phase of the $i^{th}$ oscillator ($i=1,2,\ldots,N_{\eta}$) in the $\eta^{th}$ population, respectively. Here, we consider two populations $\eta=\{A,B\}$. The coupling weights $\kappa_{ij}^{\eta\eta^{\prime}}(t)\in[-1,1]$ co-evolve with the phases of the oscillators, $\sigma_{\eta\eta^{\prime}}$ is the coupling strength, $\varepsilon_{\eta\eta^{\prime}}$ is the time-scale parameter determining the adaptation rate of the coupling weights, and the parameter $\beta$ accounts for different adaptation rules [48, 49]. We have fixed $\beta=-0.53\pi$, close to the symmetric rule [32], which is also referred to as Hebbian adaptation rule.

In this model, Eq. (1a) governs the phase dynamics, which is a generalized version of the Kuramoto model with adaptive coupling. The coupling matrix $\kappa(t)$ characterizes the network topology, and the dynamics of coupling weights is governed by Eq. (1b). To investigate the nontrivial effect of disparities among populations, we consider equally sized populations with homogeneous(heterogeneous) coupling strength and time scale adaptation among intra-(inter-) population. Further, the interactions are chosen to be symmetric with $(\sigma,\varepsilon)_{AB}=(\sigma,\varepsilon)_{BA}$ and $(\sigma,\varepsilon)_{AA}=(\sigma,\varepsilon)_{BB}$. The disparity between intra- and interpopulations coupling strengths is governed by $\sigma_{AA}=\sigma(1+\Lambda_{\sigma})$ and $\sigma_{AB}=\sigma(1-\Lambda_{\sigma})$, where $\Lambda_{\sigma}$ is the coupling strength disparity parameter, and $\sigma$ is the control parameter. Analogously, the disparity in time scales is governed by $\varepsilon_{AA}=\varepsilon(1+\Lambda_{\varepsilon})$ and $\varepsilon_{AB}=\varepsilon(1-\Lambda_{\varepsilon})$, where $\Lambda_{\varepsilon}$ is the adapation disparity parameter and $\varepsilon$ is set to $0.01$. When $\Lambda_{\sigma}=\Lambda_{\varepsilon}=0$, there is neither coupling disparity nor adaptation disparity between $A$ and $B$. Intrapopulation coupling strengths and adapations are larger for $(\Lambda_{\sigma},\Lambda_{\varepsilon})>0$ and smaller for $(\Lambda_{\sigma},\Lambda_{\varepsilon})<0$. Note that rescaling of time $t$ with the transformations $\omega_{i}\rightarrow\omega^{\prime}_{i}/\tau$, $\sigma\rightarrow\sigma^{\prime}/\tau$, and $\varepsilon\rightarrow\varepsilon^{\prime}/\tau$ recovers the dynamics of the model, where $\tau$ is a constant factor.

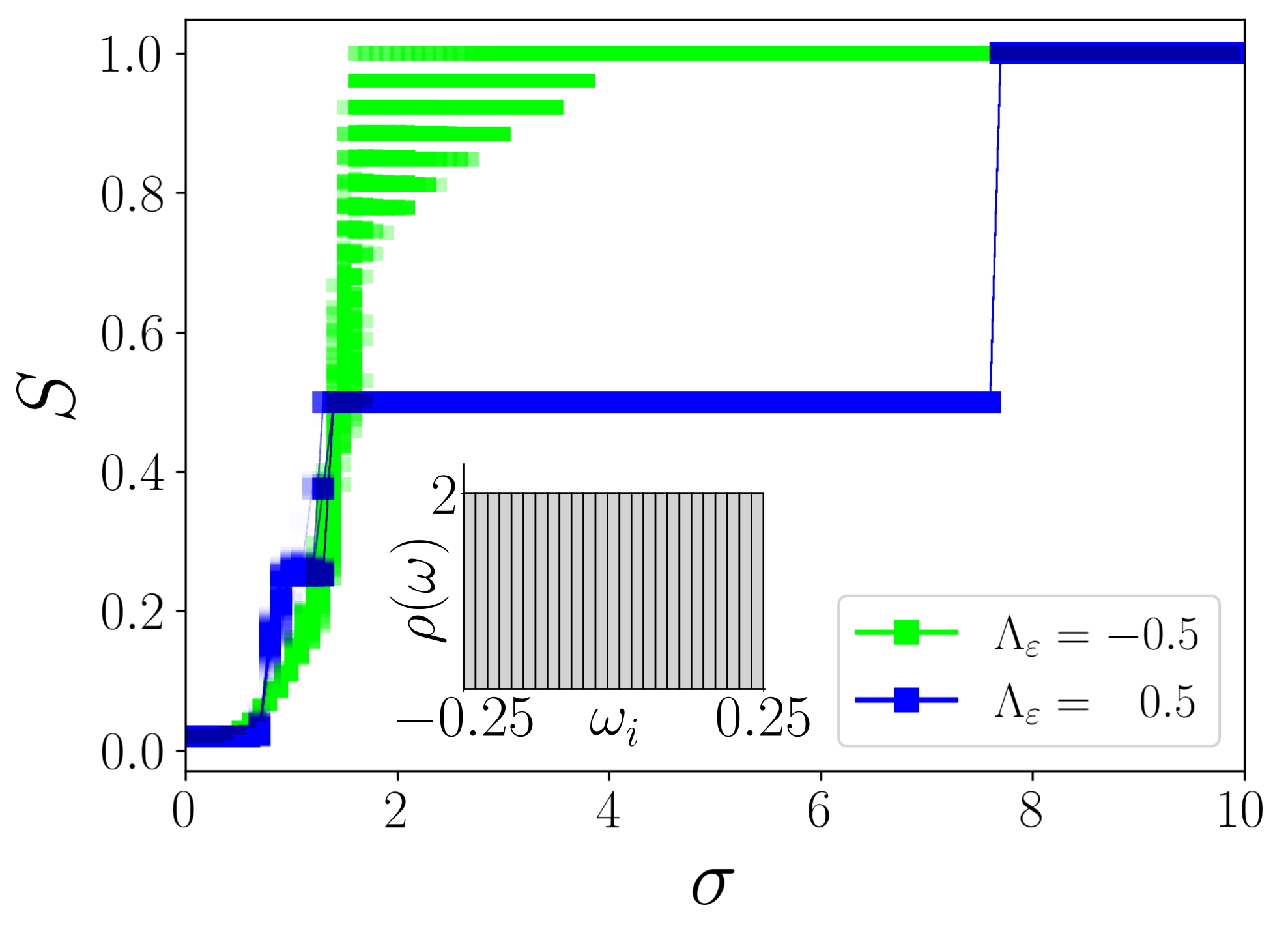
Results. The system of $N=50$ adaptively coupled phase oscillators (1) are numerically solved using the Runge-Kutta 4th order integration scheme. We assign oscillators in the range $i=1,\ldots,N/2$ to the first population, and oscillators in the range $N/2+1,\ldots,N$ are assigned to the second population. The oscillators in each population are sorted in the increasing order of their natural frequencies. $\phi_{i}^{\eta}$’s are chosen randomly from the interval $[0,2\pi)$. We have fixed $\kappa_{ij}^{\eta\eta^{\prime}}(0)=0~{}\forall~{}i,j$, $\varepsilon=0.01$ and $\beta=-0.53\pi$.

Initially, the system is in an incoherent state for $\sigma=0$, and small coupling strengths. As the coupling strength increases, the oscillators self-organize to global synchronization. The oscillators with larger $\kappa_{ij}^{\eta\eta^{\prime}}$ tend to synchronize more quickly than that with smaller $\kappa_{ij}^{\eta\eta^{\prime}}$. In the following, we show that the system undergoes qualitatively two distinct routes to synchrony as governed by the disparities among the populations.

We employ the synchronization index $S$ [32], that quantify the degree of coherence in the network, represented as

where $s_{ij}^{\eta\eta^{\prime}}$ measures the pairwise frequency synchronization between $i^{th}$ and $j^{th}$ oscillator defined as

where $\delta$ is a predefined threshold and $\langle\dot{\phi}_{i}^{\eta}\rangle=\lim_{T\to\infty}(1/T)\int_{T_{0}}^{T_{0}+T}\dot{\phi}_{i}^{\eta}dt$ is the mean phase velocity of the $i^{th}$ oscillator calculated after a large transient $T_{0}$. For $S=1$, the system is completely synchronized, whereas $S=1/N$ indicates complete incoherence.

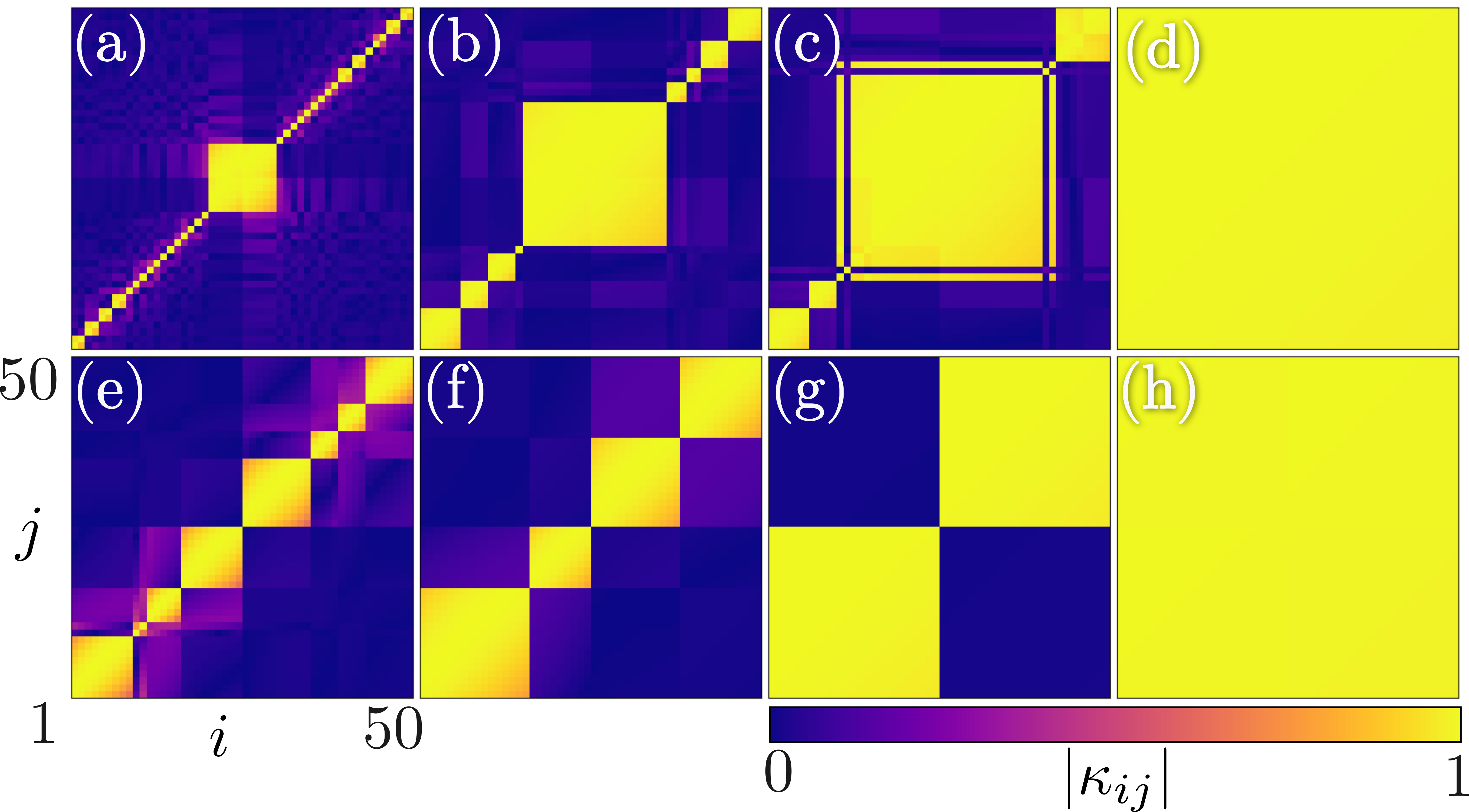
First, we discuss the phase transition facilitated solely by adaptation disparity $\Lambda_{\varepsilon}$ for $\Lambda_{\sigma}=0$. The network (1) exhibits a multi-step transition to global synchronization as a function of $\sigma$ for $\Lambda_{\varepsilon}=-0.5$ as depicted in Fig. 1 (green/light grey squares). The dynamics of the coupling weights $\kappa_{ij}^{\eta\eta^{\prime}}(t)$ unveil crucial insights on the underlying mechanism for such a transition as they co-evolve with the phases of the oscillators. The snapshots of $\kappa_{ij}^{\eta\eta^{\prime}}(t)$ are plotted in Figs. 2(a)-(d) for $\Lambda_{\varepsilon}=-0.5$. It is evident that a single frequency cluster, entrained by oscillators from both populations, emerges at the interface of the populations, which grows with an increase in the coupling strength due to the subsequent entrainment of smaller intrapopulation clusters. This process of continuous integration of smaller clusters (compare Figs. 2(a)-(c)), as a function of $\sigma$, leads to a staggered rise in the degree of synchronization $S$ (see Fig. 1) and eventually results in global synchronization (see Fig. 2(d)). Note that, for $\Lambda_{\varepsilon}<0$, the interpopulation adaptation rate is larger than intrapopulation adaptation, that is $\varepsilon_{AB}>\varepsilon_{AA}$, and hence oscillators from different populations rapidly entrained to form nucleations, which grow as a single cluster as observed in Figs. 2(a)-(d).

In stark contrast, for $\Lambda_{\varepsilon}>0$, the network exhibits a single-step transition to global synchronization as corroborated by $S$ in Fig. 1 for $\Lambda_{\varepsilon}=0.5$ (blue/dark grey squares). Again, $\kappa_{ij}^{\eta\eta^{\prime}}(t)$ uncover the underlying mechanism for such an abrupt synchronization transition. The snapshots of $\kappa_{ij}^{\eta\eta^{\prime}}(t)$ for $\Lambda_{\varepsilon}=0.5$ are depicted in Figs. 2(e)-(h). Coexisting intrapopulation clusters emerge and subsequently enlarge by the entrainment of smaller intrapopulation clusters (see Figs. 2(e) and (f)) manifesting entrained subpopulations for a large $\sigma$ (see Fig. 2(g)). Finally, the completely entrained intrapopulation clusters coalesce together resulting in global synchronization (Fig. 2(h)) as corroborated by an abrupt jump in the synchronization index to $S=1$ (see Fig. 1 for $\Lambda_{\varepsilon}=0.5$). Note that the intrapopulation adaptation is larger than interpopulation adaptation for $\Lambda_{\varepsilon}>0$, that is $\varepsilon_{AA}>\varepsilon_{AB}$, and consequently, nucleations are formed within the populations resulting in coexisting intrapopulation clusters. Thus, one can reinforce a particular route to the phase transition by tuning the time scale of adaptation.
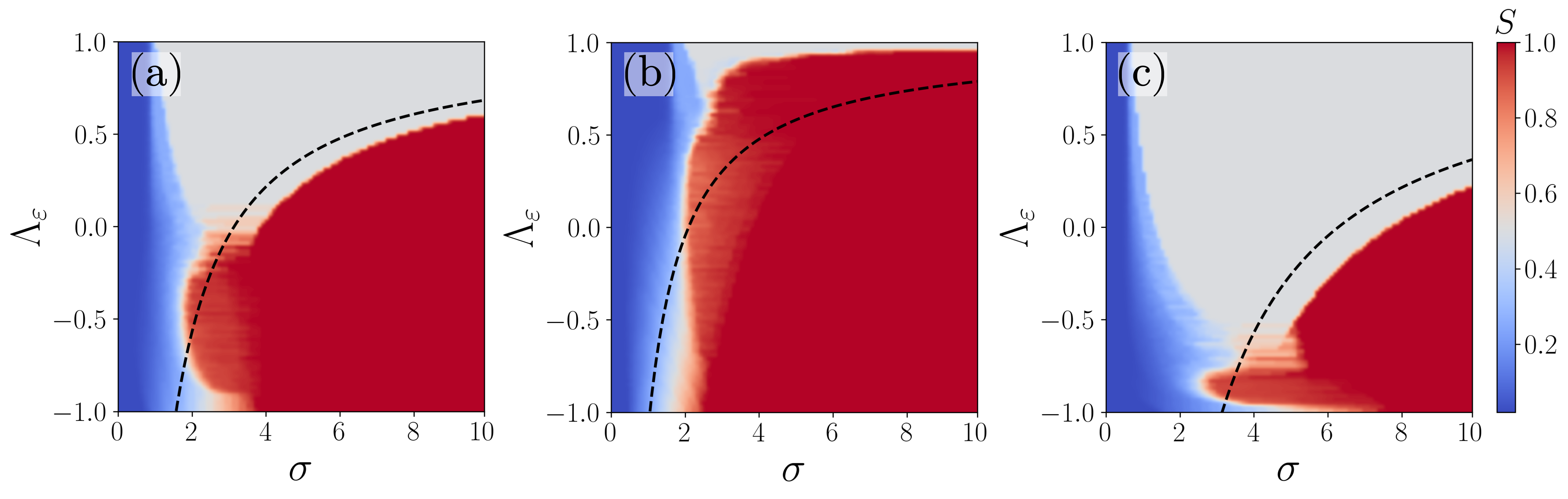
Heat maps of $S$ are depicted in the $(\sigma,\Lambda_{\varepsilon})$ parameter space in Figs. 3(a)-(c) for three distinct $\Lambda_{\sigma}$. For $\Lambda_{\sigma}=0$, clearly, there is a single-step(multi-step) transition for $\Lambda_{\varepsilon}>0(<0)$ (see Fig. 3(a)) as discussed above. Nevertheless, the effect of trade-off between $\Lambda_{\sigma}$ and $\Lambda_{\varepsilon}$ is evident from Figs. 3(b) and (c) depicted for $\Lambda_{\sigma}=-0.5$ and $0.5$, respectively. interpopulation coupling strength ($\sigma_{AB}$) is larger than that of intrapopulation ($\sigma_{AA}$) in Fig. 3(b) for $\Lambda_{\sigma}=-0.5$. interpopulation adaption ($\varepsilon_{AB}$) is also larger in the range of $\Lambda_{\varepsilon}\in[-1,0.0)$ resulting in a multi-step transition. Despite the intrapopulation adaption ($\varepsilon_{AA}$) is larger than $\varepsilon_{AB}$, a strong $\sigma_{AA}$ facilitates multi-step transition in the range of $\Lambda_{\varepsilon}\in(0,0.7)$ in Fig. 3(b). This elucidates that the coupling disparity ($\Lambda_{\sigma}$) dominates the adaptation disparity ($\Lambda_{\varepsilon}$) in facilitating phase transitions. However, when $\Lambda_{\varepsilon}\rightarrow 1$ $\varepsilon_{AB}\rightarrow 0$, and hence a large $\varepsilon_{AA}$ facilitates nucleation of clusters within populations resulting in entrained intrapopulations and eventually a single-step transition despite a large $\sigma_{AB}$ in the range of $\Lambda_{\varepsilon}\in(0.7,0.9)$. Further, $\varepsilon_{AB}\approx 0$ when $\Lambda_{\varepsilon}\approx 1$ and consequently only two-cluster state manifest without any global synchronization. Both $(\varepsilon,\sigma)_{AA}>(\varepsilon,\sigma)_{AB}$ facilitate distinct nucleation within intrapopulations and a single-step transition in the range of $\Lambda_{\varepsilon}\in(0,1)$ in Fig. 3(c) for $\Lambda_{\sigma}=0.5$. Now, again a large $\sigma_{AA}$ leads to a single-step transition even in the range of $\Lambda_{\varepsilon}\in(0,-0.5)$ (see Fig. 3(c)), where interpopulation adaptation is larger, which reinforces that the coupling disparity ($\Lambda_{\sigma}$) dominates the adaptation disparity. However, $\varepsilon_{AB}>>\varepsilon_{AA}$ for $\Lambda_{\varepsilon}\in(-0.5,-1)$ and hence a single large nucleation manifests at the population interface leading to a multi-step transition.

We consider there are $N_{c}^{\eta}$ number of clusters in the $\eta$-th population, and clusters are described by indices $\mu,\nu$. The term $\Theta_{\mu}^{\eta}(\omega_{i}^{\eta}-\Omega_{\mu}^{\eta})$ describes the frequency drift of $i^{th}$ oscillator within $\mu^{th}$ cluster in the population $\eta$, $\Omega_{\mu}^{\eta}$ is its mean natural frequency and $f_{\mu}^{\eta}$ describes its collective phase. The intercluster ($\kappa_{\mu\nu}^{\eta\eta^{\prime}}$) coupling weights evolve in time. The errors arising in describing the evolution of the phase and coupling weights in terms of collective coordinates can be defined as $E_{\phi_{i}^{\eta}}=\dot{\phi}_{i,\mu}^{\eta}-\dot{\phi}_{i}^{\eta}$ and $E_{\kappa_{ij}^{\eta\eta^{\prime}}}=\dot{\kappa}_{\mu\nu}^{\eta\eta^{\prime}}-\dot{\kappa}_{ij}^{\eta\eta^{\prime}}$, respectively. The evolution equations for the collective coordinates $(\Theta_{\mu}^{\eta},f_{\mu}^{\eta},\kappa_{\mu\nu}^{\eta\eta^{\prime}})$ are obtained by requiring the error $\bm{E}=(E_{\phi_{1}^{\eta}},\ldots,E_{\phi_{N_{\eta}}^{\eta}},E_{\phi_{1}^{\eta^{\prime}}},\ldots,E_{\phi_{N_{\eta^{\prime}}}^{\eta^{\prime}}},\ldots,E_{\kappa_{11}^{\eta\eta}},\ldots,E_{\kappa_{N_{\eta}N_{\eta}}^{\eta\eta}},\\ E_{\kappa_{11}^{\eta^{\prime}\eta^{\prime}}},\ldots,E_{\kappa_{N_{\eta^{\prime}}N_{\eta^{\prime}}}^{\eta^{\prime}\eta^{\prime}}},\ldots)$ to be orthogonal to the manifold of the ansatz. The frequency distribution corresponding to $\mu^{th}$ cluster of $\eta^{th}$ population can be expressed as $\rho_{\mu}^{\eta}(\omega)=2/n_{\mu}^{\eta}\text{ for }(\Omega_{\mu}^{\eta}-0.25n_{\mu}^{\eta}\leq\omega\leq\Omega_{\mu}^{\eta}+0.25n_{\mu}^{\eta}),\text{and }0\text{ otherwise}$. Here $n_{\mu}^{\eta}$ is the ratio ($N_{\mu}^{\eta}/N$) of oscillators. In the continuum limit, the cluster order parameter $r_{\mu}^{\eta}=1/N_{\mu}^{\eta}\left|\sum_{i\in C_{\mu}}e^{i\phi_{i,\mu}^{\eta}}\right|$ becomes $r_{\mu}^{\eta}=(4/{n_{\mu}^{\eta}\Theta_{\mu}^{\eta}})\sin{(n_{\mu}^{\eta}\Theta_{\mu}^{\eta}/4)}$ with the variance of natural frequencies of the cluster as $\xi_{\mu}^{\eta}=(n_{\mu}^{\eta})^{2}/48$. Consequently, the dynamics of the collective coordinates is governed by

In the context of mesoscopic description, the synchronization index (2) can be redefined to characterize the synchronization of frequency clusters as

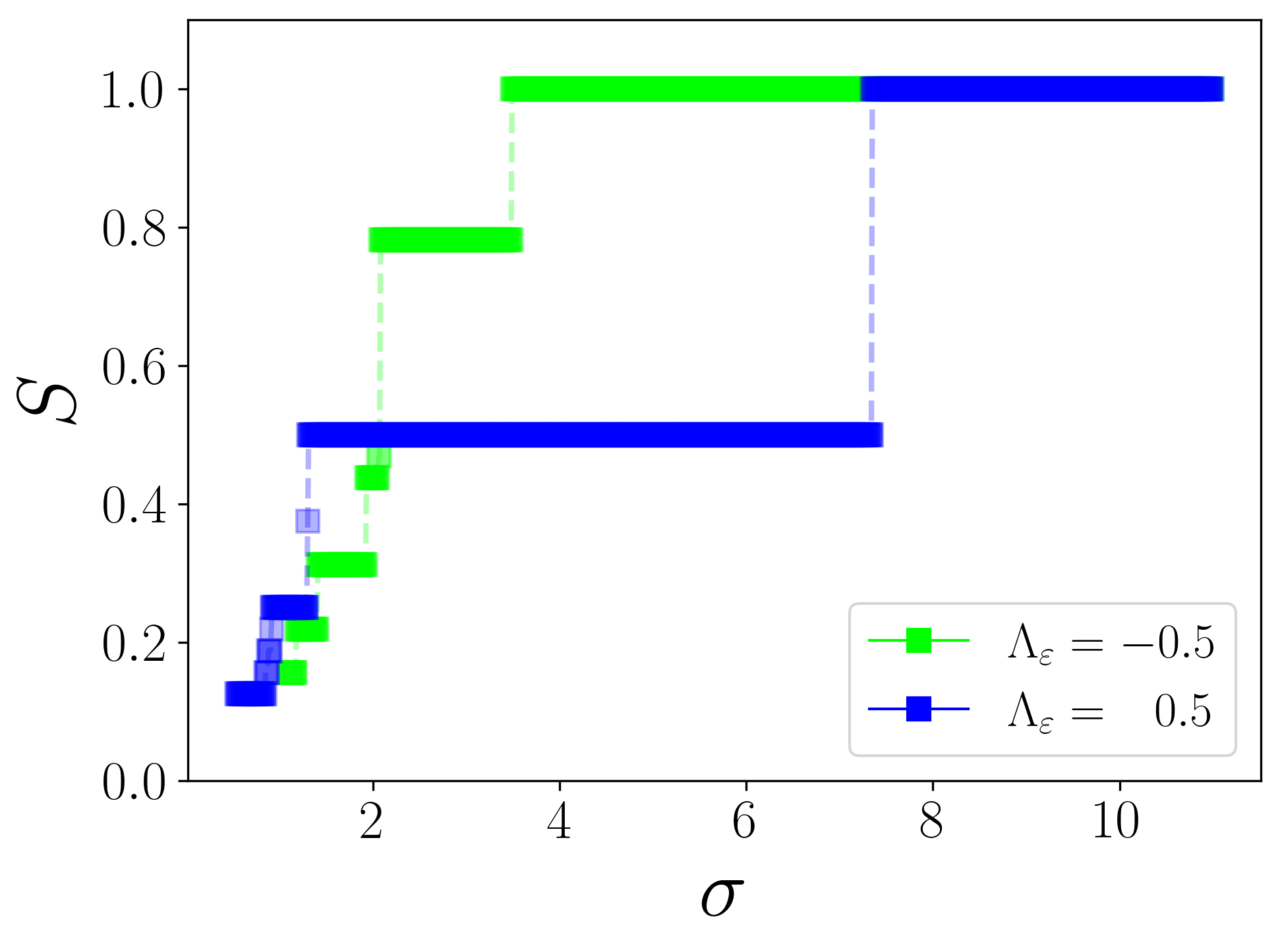
Akin to microscopic context (3), $s_{\mu\nu}^{\eta\eta^{\prime}}=1$, if $\langle\dot{f}_{\mu}^{\eta}\rangle=\langle\dot{f}_{\nu}^{\eta^{\prime}}\rangle$ otherwise $s_{\mu\nu}^{\eta\eta^{\prime}}=0$. Although the single-step transition can be described by a minimum of two clusters, the multi-step transition requires a larger number of clusters to describe it. The phase transition displayed by $S$ (6), estimated from the evolution equations for the collective coordinates, corresponding to two populations, each having 4 clusters, for two values of $\Lambda_{\varepsilon}$ is depicted in Fig. 4. It is evident from the figure that the collective coordinates approach clearly displays single-step and multi-step transitions for $\Lambda_{\varepsilon}=0.5$ and $-0.5$, respectively, in agreement with the simulation results in Fig. 1.

Now, an analytical estimate of the upper bound for the coupling strength corresponding to the completely entrained clusters of intrapopulations (Fig. 2(g)) during the single-step transition can be obtained using the perturbative approach in the weak coupling limit [32]. Assuming the intracluster phase difference ($f=f_{\mu}-f_{\nu}$) grows linearly in time with the relative phase velocity $\Omega^{\prime}$, the collective coordinates can be expressed in the orders of $\alpha$ as

Substituting the perturbed equations in (5) leads to the quadratic equation in $\Omega^{\prime}$

The condition for the existence of real solution of (8) requires $(\Omega_{\mu}-\Omega_{\nu})^{2}\geq-2\varepsilon_{\mu\nu}\sigma_{\mu\nu}(r_{\mu}^{(0)}r_{\nu}^{(0)})^{2}\sin{\beta}$. Now, the upper bound for the coupling strength for the existence of the two-cluster state can be obtained as

It is evident that $\sigma_{c}$ depends explicitly on the adaptation and the coupling disparity parameters. For a rough estimate of $\sigma_{c}$, one can consider $r_{\mu}^{(0)}\approx r_{\nu}^{(0)}\approx 1$. For the values of the parameters in Fig. 1, the upper bound can be obtained as $\sigma_{c}=6.28$ with $\Omega_{\mu}-\Omega_{\nu}=-0.25$, which almost agrees with the single-step transitions in Figs. 1 and  4. Now, the critical curve corresponding to the upper bound can be written as $\Lambda_{\varepsilon}=1-\left[(\Omega_{\mu}-\Omega_{\nu})^{2}/\left(2\varepsilon\sigma_{c}(1-\Lambda_{\sigma})(r_{\mu}^{(0)}r_{\nu}^{(0)})^{2}\sin{(-\beta)}\right)\right]$, which is depicted as a dashed curve in Figs. 3(a)-3(c) across which the single-step transition takes place. The finite size effect and the first order approximation for the order parameters $r_{\mu}^{(0)}$ and $r_{\nu}^{(0)}$ contribute to the error between the analytical curve and the numerical results in Figs. 3.

Discussion and Conclusion. We have considered a globally coupled finite-size adaptive network, wherein the subpopulations are distinguished by different degrees of time scale adaptation $(\Lambda_{\varepsilon})$ and coupling strength $(\Lambda_{\sigma})$ but with uniform distribution of natural frequencies. We have found that nucleations of intrapopulation frequency clusters coalesce at the interface of the two populations facilitating the manifestation of a single large interpopulation frequency cluster for a strong interpopulation adaptation rate, $\Lambda_{\varepsilon}<0$, without any coupling strength disparity. Eventually, the single large inter-frequency-cluster grows to the system size as the coupling strength is increased facilitating a multi-step transition to global synchronization. In contrast, nucleations of intrapopulation frequency clusters coalesce among themselves to manifest completely entrained two intrapopulation frequency clusters as a function of the coupling strength for a strong intrapopulation adaptation rate $\Lambda_{\varepsilon}>0$, without any coupling strength disparity. Finally, the two intra-frequency-clusters coalesce together facilitating a single-step transition to global synchronization. Synchronization index $S$ clearly displays the two distinct transitions for two distinct values of $\Lambda_{\varepsilon}$ when $\Lambda_{\sigma}=0$.
Further, we found that a strong interpopulation coupling strength, $\Lambda_{\sigma}<0$, always favors nucleation of inter-frequency-clusters leading to multi-step transition even for a strong intrapopulation adaptation rate ($\Lambda_{\varepsilon}>0$). Furthermore, we found that a strong intrapopulation coupling strength, $\Lambda_{\sigma}>0$, always favors nucleation of intra-frequency-clusters facilitating single-step transition even with a strong interpopulation adaptation rate ($\Lambda_{\varepsilon}<0$). These results corroborate that the degree of disparity in the coupling strength strongly determines the nature of nucleation leading to distinct synchronization transition. We have analytically deduced the macroscopic evolution equations for the cluster dynamics using the framework of collective coordinates [47]. The synchronization transitions obtained using the collective coordinates are found to agree with the simulation results. Further, we have also deduced the upper bound for the coupling strength for the existence of two intraclusters explicitly in terms of adaptation and coupling strength disparity parameters, which is found to almost match the coupling strength at the onset of abrupt single-step transition. It is also evident that the mesoscopic description brilliantly captures the multicluster dynamics.

Note that similar heterogeneous nucleation resulting in multi- and single-step transitions are reported to be facilitated by distinct quenched disorders [32], wherein the nucleations emerge at the site of the disorder(s) resulting in multi-(single-)step transitions. However, in our case with uniform distribution of natural frequencies, small intracluster nucleations coalesce either at the population interface or within the populations resulting in multi- and single-step synchronization transitions depending on the trade-off between the adaptation and coupling disparities. Understanding the mechanism of nucleations corresponding to distinct transition due to the inherent disparities of complex real-world systems is of paramount importance as they shed more light on the role of disparities among different regions of the brain in synchronization in unraveling brain functions and neurological disorders [52], segregation and polarization dynamics in social networks [46], etc. Moreover, our findings hold significance in the network control theory, offering strategies to optimize adaptive networks.

Acknowledgments. AK acknowledges the financial support from IISER-TVM. JF acknowledges funding by the Austrian Science Fund (FWF): I 5985-N. The work of V.K.C. is supported by DST-CRG Project under Grant No. CRG/2020/004353 and VKC wish to thank DST, New Delhi for computational facilities under the DST-FIST programme (SR/FST/PS- 1/2020/135) to the Department of Physics. DVS is supported by the DST-SERB-CRG Project under Grant No. CRG/2021/000816.