Disordered Parity Anomalous Semimetal

The anomalous Hall effect and its quantized version are well-known phenomena in ferromagnets, arising from the spin-orbit coupling [1, 2, 3]. In metallic ferromagnets, the Hall conductivity is typically non-quantized and can be expressed as an integral of the Berry curvature over the occupied electron states [4]. Recent studies have proposed the possible realziation of one half quantization of the Hall conductivity in systems with gapless Wilson fermions, which can be regarded as a topological invariant for a parity anomalous semimetal (PAS) [5]. It was reported that the measured Hall conductivity approaches one-half in a semi-magnetic structure of Cr-doped topological insulator $\mathrm{(Bi,Sb)_{2}\mathrm{Te}_{3}}$ [6]. The system exhibits a band structure with a single gapless surface Dirac cone of electrons in the first Brillouin zone, which gives rise to the half quantization of the Hall conductivity [7, 8, 9]. This phenomenon bears a similarity to the parity anomaly of massless Dirac fermions in quantum field theory [10, 11, 12, 13]. Due to existence of a finite Fermi surface and nonzero longitudinal conductivity, the PAS is apparently distinct from the quantum anomalous Hall effect and fractional quantum anomalous Hall effect observed in an insulating phase, which are characterized by the Chern numbers and emergence of the chiral edge states [14, 15, 16, 17, 18, 19, 20, 21, 22]. Consequently, there has been a significant research effort to comprehend the origins of this effect, with numerous studies focusing on topics such as the realization, robustness, and dissipative properties of the half quantized Hall effect [23, 24, 25, 9, 26, 27].

The stability and robustness of this new topological phase in the presence of disorder pose significant challenges. Strong electron scattering near a finite Fermi surface, combined with the broken time-reversal symmetry in metallic ferromagnets, can have a profound impact [28]. Disorder in two dimensions is known to give rise to remarkable phenomena, including the metal-insulator transition [29, 30, 31], quantum Hall effect [32], and topological Anderson insulator [33, 34]. In addition to causing the metal-insulator transition, disorder also plays a crucial role in the creation of chiral edge states in topological phases [33, 34, 35, 36, 37, 38, 39, 40, 41, 42]. Therefore, understanding the effects of disorder on the stability and formation of the PAS is of utmost importance. In this Letter, we investigate the disorder-driven topological phase transition in a semi-magnetic structure of topological and narrow-gap band insulator (as depicted in Fig. 1(a)) to explore the fate and the formation of of the PAS in the presence of disorder. The phase diagram is established by calculating the Hall conductivity on a real space lattice and the arithmetical and geometric mean density of states (DOS) numerically. It is found that strong disorder not only drives a topological transition from the PAS to a diffusive metallic (DM) phase, but also strikingly induces the topological phase from an ordinary band insulating (BI) phase, as exhibited in Fig. 1(b). The half quantized Hall conductance is attributed to the emergence of a single gapless Dirac cone even in the presence of disturbing disorder, provided that the energy broadening does not smear the gap between the gapless and massive Dirac cone. Furthermore, an effective medium theory is developed to understand the formation and breaking down of the PAS.

Consider a semi-magnetic structure of topological insulator as shown in Fig. 1(a), in which the magnetic ions are doped on the top layer of the film to form a ferromagnetic layer. The tight-binding model was introduced for topological insulator and studied extensively [43, 44, 17],

where $\mathcal{T_{\alpha}}=t_{\alpha}\tau_{z}\sigma_{0}-\frac{\mathrm{i}\lambda_{\alpha}}{2}\tau_{x}\sigma_{\alpha}$ and $M_{0}=\left(m_{0}-4t_{\parallel}-2t_{z}\right)\tau_{z}\sigma_{0}+V_{z}(i_{z})\tau_{0}\sigma_{z}$. $\Psi_{{\bf r}_{i}}^{\dagger}$ and $\Psi_{{\bf r}_{i}}$ are creation and annihilation operators of an electron at site $i$. $\tau_{\alpha}$ and $\sigma_{\alpha}$’s are Pauli matrices acting on the orbital and spin spaces, respectively. The magnetic doping is modeled by introducing a Zeeman potential $V_{z}(i_{z})$. $V_{z}(i_{z})=V_{0}$ for the top layer $i_{z}\leqslant L_{z}^{\mathrm{Mag}}$, and 0 otherwise. The model in Eq. (1) incorporating four orbitals, $|P1_{-}^{+},\pm\frac{1}{2}\rangle$ and $|P2_{+}^{-},\frac{1}{2}\rangle$, was proposed to describe the topological nature of strong topological insulator $\mathrm{Bi_{2}Se_{3}}$ and $\mathrm{Bi_{2}Te_{3}}$ by taking $m_{0}=0.28$ eV [43, 44]. For the topologically trivial insulator, we propose the transition-metal pentatelluride $\mathrm{ZrTe}_{5}$ as a possible candidate, which is commonly regarded as a weak topological insulator nearing the critical points for a transition to a strong topological insulator [45]. Notably, the low-energy states consist of four $p_{y}$ orbitals from two Te atoms per unit cell, specifically $|\mathrm{Te}_{1/2}p_{y}\uparrow\rangle$ and $|\mathrm{Te}_{1/2}p_{y}\downarrow\rangle$ [46]. This case can also be effectively modeled in Eq. 1 by taking $m_{0}=-0.02$eV,.

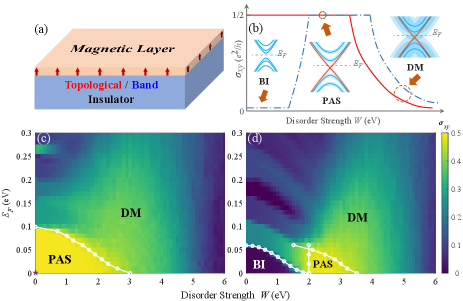
We then study the impact of disorder on the electrical Hall conductivity of the semi-magnetic structure of topological insulator thin film. For this purpose, we follow the common practice in the study of Anderson localization and introduce disorder through random on-site energy $u_{{\bf r}_{i}}$ that is uniformly distributed in $\left[-W/2,+W/2\right]$, and the impurity Hamiltonian is given by $H_{\mathrm{imp}}=\sum_{\mathbf{r}_{i}}\Psi_{{\bf r}_{i}}^{\dagger}u_{{\bf r}_{i}}\tau_{0}\sigma_{0}\Psi_{{\bf r}_{i}}$. The phase diagrams of the electrical Hall conductivity in the disorder strength $W$ and the chemical potential $E_{F}$ plane are presented in Fig. 1(c) and (d) for the topological insulator and narrow-gap band insulator, respectively. The Hall conductivity is numerically calculated by utilizing the real space noncommuative Kubo formula [47],

where $P$ denotes the projector onto the occupied states, and $x$ and $y$ are the coordinate operators. $\left\langle\cdots\right\rangle_{\mathrm{imp}}$ denotes the disorder-average. We take periodic boundary condition in the $x$ and $y$ directions, and open boundary condition in the $z$ direction. The yellow area indicates the PAS with one half quantum Hall conductivity $\frac{e^{2}}{2h}$. For the topologically nontrivial case, the PAS phase appears from the pristine state and exhibits a gradual departure for a finite disorder $W$. The deviation of Hall conductivity from the half-quantized value defines the phase boundary between PAS and DM, while a finite chemical potential can also modulate the transition disorder strength. For the topologically trivial case, with weak disorder, the system remains in the BI phase with negligible Hall conductivity, indicated by the dark-purple region in the lower left corner. With increasing disorder strength, the PAS phase emerges strikingly and persist over a finite range, distinctively signifying the existence of the metallic ferromagnetic phase. When the disorder strength is even stronger, the half-quantized Hall plateau tends to diminish, and the system eventually evolves into the DM phase. The finite-size effect analysis categorically supports the robustness of the emergent half-quantized Hall phase. For details refer to Ref. [48].

The quasiparticle picture is valid when the disorder strength is far from reaching the Anderson transition point from DM to Anderson insulator. In this situation, the disorder only renormalizes the energy spectrum of the quasiparticles and introduces a finite lifetime. Hence, by examining the evolution of the spectral function with varying the disorder strength, we can clearly observe the changes occurring during the phase transitions. The spectral function $A(\epsilon,\mathbf{k})$ is defined by $A(\epsilon,{\bf k})=\sum_{n}\left\langle\psi_{n{\bf k}}\right|\delta\left(\epsilon-H\right)\left|\psi_{n{\bf k}}\right\rangle$, where $\left|\psi_{n{\bf k}}\right\rangle=\frac{1}{\sqrt{S}}\left|u_{n{\bf k}}\right\rangle\mathrm{e}^{\mathrm{i}{\bf k}\cdot{\bf r}}$ are the Bloch states for the clean system with $H_{\mathrm{0}}\left|u_{n{\bf k}}\right\rangle=\epsilon_{n}\left|u_{n{\bf k}}\right\rangle$. For a disordered system, $A(\epsilon,\mathbf{k})$ can be numerically evaluated using the standard kernel polynomial method [52, 53], where the Wannier wavefunctions in DOS calculations are replaced by the Bloch eigenstates.

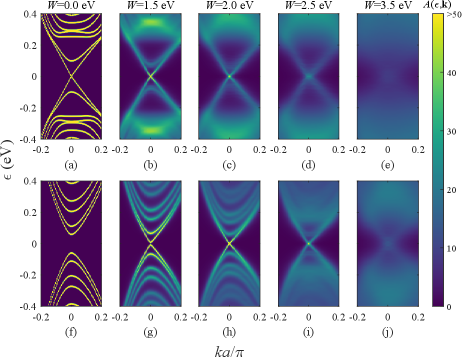
The spectral functions for different disorder strengths are clearly displaced in Fig. 2. Fig 2(a) shows the band structure of topologically nontrivial case in the absence of disorder $W=0$. A gapless Dirac cone appears at the $\Gamma$ point while a series of gapped Dirac cones also accompanies. We can identify the gap of one massive Dirac cone is manipulated by the Zeeman field $V_{z}$ in the magnetic layer. Thus the gapless Dirac cone is the surface states located at the bottom layer, and the gapped Dirac cone is the surface state located at the top layer of the sample. This is a straightforward evidence to illustrate the band structure is topologically nontrivial. Recent studies [5] reveal that the gapless Dirac cone of fermions gives rise to PAS as a signature of parity anomaly of gapless Dirac fermions. This is consistent with the fact that the Hall conductivity is one half as shown in Fig. 1(c). With increasing the disorder strength in PAS phase (from Fig. 2(a) to 2(c)), we notice that the gapless Dirac cone exhibits remarkable resilience to disorder, persisting even as other gapped energy dispersions are smeared. However, the broadening of these dispersions is still smaller than their respective band gap, and the Hall condcuctivity remains half-quantized. At PAS-DM transition point (Fig. 2(d)), the broadening induced by impurities reaches one half of the band gap in the gapped bands. With further increases in disorder strength, the chemical potential inevitably lies within the broadened gapped bands. Subsequently, the Hall conductivity derivates from $\frac{e^{2}}{2h}$.

On the contrary, Fig. 2(f) shows the trivial band structure has a finite gap at the $\Gamma$ point, and is a topologically trivial band insulator in the absence of disorder. With increasing the disorder strength, the band gap progressively shrinks and ultimately closes near $W=2.0$ eV, giving rise to a single, gapless Dirac cone. Correspondingly, the Hall conductivity is close to $\frac{e^{2}}{2h}$ as demonstrated in Fig. 1(d). The formation of the gapless Dirac cone is the signature of the disorder-induced PAS, which is consistent with the calculated Hall conductivity. For even stronger disorder in Fig. 2(e) or (j), the gapless Dirac cone collapses as anticipated, and the Hall conductivity deviates from half-quantization, giving rise to the DM. From the quasiparticle perspective, our core finding in this calculation can be summarized in Fig. 1(b), where in a disordered semi-magnetic topological insulator/band insulator film, the PAS phase occurs when the chemical potential solely intersects the gapless Dirac cone (despite broadening) within the broadened gapped bands.

These phase transitions can be characterized by analyzing the two types of means of the local density of states (DOS): the arithmetic mean $\rho_{\mathrm{a}}$ and the geometric mean $\rho_{\mathrm{t}}$. The local DOS, $\rho_{{\bf r},\alpha}(\epsilon)=\left\langle{\bf r},\alpha\right|\delta\left(\epsilon-H\right)\left|{\bf r},\alpha\right\rangle$, quantifies the amplitude of the wave function at site ${\bf r}$ for a given energy $\epsilon$, where $\left|{\bf r},\alpha\right\rangle$ denotes an $\alpha$-orbital electron wave function at that site. The spatial distribution of $\rho_{{\bf r},\alpha}(\epsilon)$ contains direct information about the localization properties, which are closely intertwined with the topology of the quantum system [54, 55, 56]. The arithmetic and geometric mean DOS for a disordered system are defined as $\rho_{\mathrm{a}}(\epsilon)=\left\langle\frac{1}{V}\sum_{i=1}^{V}\sum_{\alpha=1}^{4}\rho_{{\bf r}_{i},\alpha}(\epsilon)\right\rangle_{\mathrm{imp}}$ and $\rho_{\mathrm{t}}(\epsilon)=\exp\left[\frac{1}{N_{s}}\sum_{i=1}^{N_{s}}\left\langle\ln\sum_{\alpha=1}^{4}\rho_{{\bf r}_{i},\alpha}(\epsilon)\right\rangle_{\mathrm{imp}}\right]$, respectively [57, 58]. Here we randomly choose a finite number of lattice sites $N_{s}\ll V=L_{x}L_{y}L_{z}$ to improve the statistics of $\rho_{\mathrm{t}}$ [59]. A zero value of arithmetic mean DOS $\rho_{{\rm a}}(\epsilon)$ at a finite interval defines an energy gap, such as a band insulator, while a nonzero value of $\rho_{{\rm a}}(\epsilon)$ means that there exists the states at the energy $\epsilon$, which can be either localized or delocalized. The geometric mean DOS $\rho_{{\rm t}}(\epsilon)$ may reveal more information for the localization of the states. For energy $\epsilon$ where all states are extended, local DOS are uniformly distributed throughout the system, and we have $\rho_{{\rm t}}\simeq\rho_{{\rm a}}$. However, for the states whose wave-functions are localized in real space, there is no contribution to $\rho_{{\rm t}}$ [52]. Generally, comparison of $\rho_{\mathrm{a}}(\epsilon)$ to $\rho_{\mathrm{t}}(\epsilon)$ can investigate the localization properties of particle states. In the case of quasi-2D topological insulator films featuring surface states, the analysis of these properties becomes more complex. Further study shows that since the surface states are localized near the top or bottom surface in $z$ direction and extended in $x$ and $y$ direction, these states do not contribute to the value of $\rho_{{\rm t}}$, but do to $\rho_{{\rm a}}$. For a non-vanishing $\rho_{{\rm a}}$, if the ratio $\rho_{\mathrm{t}}/\rho_{\mathrm{a}}$ is 0, it can define two different phases: one is that all states are localized in real space in all directions, i.e., Anderson insulator, and another one is that the states are only localized at the top or bottom surface, i.e., the surface states. For a finite ratio of $\rho_{\mathrm{t}}/\rho_{\mathrm{a}}$ it indicates the existence of the delocalized states, defining a DM.

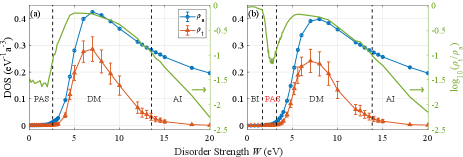
$\rho_{\mathrm{a}}$ and $\rho_{\mathrm{t}}$ can be calculated by using the standard kernel polynomial method. As illustrated in Fig. 3(a) and (b), by analyzing $\rho_{\mathrm{a}}$ and $\rho_{\mathrm{t}}$ at $E_{F}=0.01$ eV , we establish that the topologically nontrivial case undergoes two distinct quantum phase transitions: PAS$\to$DM$\to$AI (Anderson insulator) with varying disorder strength and the topologically trivial case exhibits three quantum phase transitions: BI$\to$PAS$\to$DM$\to$AI. For nontrivial case, when disorder strength is small ($W<W_{c}\approx 2.60$ eV), the gapless Dirac cone on the bottom surface experiences broadening as a result of self-scattering by impurities present on the same surface. Consequently, we observe that $\rho_{{\rm a}}\neq 0$ and $\rho_{{\rm t}}\simeq 0$, leading to a vanishingly small ratio $\rho_{{\rm t}}/\rho_{{\rm a}}$ (approximately $10^{-1}\sim 10^{-2}$ as calculated), which defines the PAS phase. Unlike in conventional metals, where $\rho_{{\rm t}}$ and $\rho_{{\rm a}}$ typically track each other, the absence of $\rho_{{\rm t}}$ provides the numerical evidence for the stability of the PAS phase under weak disorder. As disorder increases ($W_{c}<W<W_{l}\approx 13.55$ eV), both $\rho_{{\rm t}}$ and $\rho_{{\rm a}}$ are finite, defining the DM phase. With further increasing the disorder ($W>W_{l}$), all the states are expected to be Anderson localized, characterized by a vanishing $\rho_{t}$ and a finite $\rho_{{\rm a}}$ over the whole range of the spectrum. Starting from topologically trivial case and considering weak disorder ($W<1.70$ eV), the presence of a finite band gap results in no states within this gap, leading to $\rho_{{\rm t}}=\rho_{{\rm a}}=0$, which we refer as BI phase. Nevertheless, the numerical calculation inevitably introduce a vanishingly small broadening parameter, which effectively introduces a uniformly distributed nonzero local DOS in BI phase. This results in a ratio of $\rho_{{\rm t}}/\rho_{{\rm a}}\simeq$1 in this regime. As disorder increases, a phase transition from BI to PAS occurs at $W_{c,1}=2.0$ eV, characterized by a strongly suppressed $\rho_{{\rm t}}/\rho_{{\rm a}}$. Continuing to increase the disorder strength leads to encountering two more quantum phase transitions, analogous to those observed in the topologically nontrivial case.

To understand the origin of the phase transitions between PAS to DM, and BI to DM, we can employ the effective medium theory in conjunction with the Kubo formula for electrical conductivities [60, 61]. The self-consistent Born approximation is a very powerful tool and applied extensively to investigate the physics in topological Anderson insulator [33, 34, 62, 63, 64, 65, 66, 37, 67, 68, 69]. In the semi-magnetic structure with multiple layers, the electron wave function has an additional layer degree of freedom, which lead to a matrix structure of the Green’s function and self-energy. We extend the self-consistent Born approximation to the layered structure, in which the retarded self energy is diagonal in the layer degree of freedom subspace and can be expressed as

where $i_{z}$ is the layer number, $G^{R}(\mathbf{k}^{\prime},E_{F})=\left[E_{F}-H_{\mathrm{0}}(\mathbf{k}^{\prime})-\Sigma^{R}\right]^{-1}$ is the dressed Green’s function. Despite the translational symmetry breaking in the $z$ direction, our scheme is applicable to any layer number and doping. The self-consistent equation for self-energy can be solved numerically [68]. With the self-energy, the Hall conductivity can be calculated by means of the Kubo-Bastin formula . For technique details refer to Ref.[48].

Numerical solution shows the renormalized mass $\widetilde{m}_{0}\left(i_{z}\right)=m_{0}+\frac{1}{4}\mathrm{Tr}\left[\Sigma_{i_{z}i_{z}}^{R}(E_{F})\sigma_{0}\tau_{z}\right]$ exhibits weak layer dependence and is remarkably enhanced by disorder irrespective of its initial values. The evolution of the quasiparticle band structure shown in Fig. 2 is primarily due to this effect. For the trivial case, $\widetilde{m}_{0}\left(i_{z}\right)$ increases with increasing the disorder strength, and change its sign at a critical value, which causes a topological transition from the bulk insulating phase into a topological insulating phase, leading to the emergence of the Dirac cone of the surface states. This represents the disorder-induced topological Anderson insulator phase transition [33, 34, 62, 63, 64, 65, 66, 37, 67, 68, 69]. As shown in Fig. 4, the green circles indicate the band gap between the conduction and valence bands, extracted from the spectral function in Fig. 2. The green solid line, representing results from the effective medium theory, demonstrates good consistency with these findings. When the gap closes at $W_{c,1}$, a half-quantized Hall plateau emerges (indicated by the vertical green dashed line).

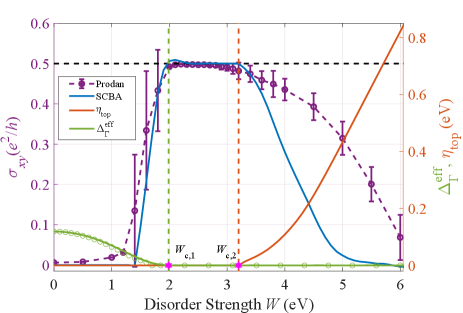
Another important result of the effective medium theory is the imaginary part of the self-energy, $\eta(i_{z})=-\frac{1}{4}\mathrm{Im}\mathrm{Tr}\left[\Sigma_{i_{z}i_{z}}^{R}(E_{F})\right]$, which is responsible for energy level broadening and serves as an order parameter for describing the phase transition from PAS to DM. Numerical results show that imaginary part $\eta$ slightly depends on the layer index $i_{z}$. The $\eta_{\mathrm{bottom}}$ on the bottom surface is always present, regardless of disorder strength, while the $\eta_{\mathrm{top}}$ on the top (the orange line in Fig. 4) surges at a critical value $W_{c,2}\approx 3.22$ eV of the disorder strength. It is observed that breaking down of the quantized Hall conductivity accompanies with the emergence of the band broadening near the top layer $\eta_{\mathrm{top}}$ as indicated by the vertical orange dashed line. As the wave functions of the surface states near the crossing point mainly reside at the bottom surface, the tiny energy broadening $\eta_{\mathrm{bottom}}$ has no impact to the Hall conductivity. The band broadening $\eta_{\mathrm{top}}$ on the top mains affects the higher energy states of the Dirac cone, which are mainly distributed in the whole bulk, and the are the key source to the nonzero Hall conductivity [8]. The phase boundary for the PAS-DM transition, indicated by the white dot-line in Fig. 1, is given by the emergence of $\eta_{\mathrm{top}}$, which shows good agreements with the independent numerical results of the real-space Hall conductivity. Therefore, the nonzero $\eta_{\mathrm{top}}$ causes the breaking down of the PAS to DM. In the DM region, the longitudinal conductivity is finite while the Hall conductivity decays to vanish.

To conclude, the PAS appears in the disordered semi-magnetic structure based on numerical calculation of the Hall conductivity and local DOS, and can be understood very well in the framework of the effective medium theory. We demonstrate that strong disorder not only leads to a topological transition from the PAS to DM phase, but also drives a BI into the PAS phase. Our findings unequivocally illuminate the genesis of half-quantized Hall phase in both topologically trivial and non-trivial cases, substantiates the paradigm of disorder-driven topological phase transition, and provide a sturdy foundation for the exploration and development of half-quantized Hall effects in quantum materials and devices.