Discriminating between Higgs Production Mechanisms via Jet Charge at the LHC

However, to date, all the knowledge of the Higgs couplings is inferred from the global analysis of the Higgs data under the narrow width approximation for the Higgs production and decay. As a result, the measurements of the Higgs properties are strongly depending on the assumption of the Higgs width, which is difficult to be directly measured at the LHC [19, 20]. Therefore, probing the Higgs couplings with the fewest possible theoretical assumptions (e.g., Higgs width) plays a crucial role to verify the nature of the EWSB. One of the approaches to overcome the shortness of the current global analysis is to measure the off-shell Higgs signal strengths [21, 22, 23, 24]. Unfortunately, the Higgs cross sections decrease so fast in off-shell Higgs phase space region that it would be a challenge to measure the Higgs couplings with a high accuracy [25, 26]. Moreover, generally, the determination of the Higgs couplings also depends on other theoretical assumptions made in the analysis [23, 27, 28, 29, 30, 31, 32].

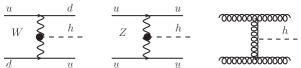
For the purpose of determining the $hVV$ couplings, the mechanism of Higgs production via vector boson fusion (VBF) plays an essential role at the LHC. The representative Feynman diagrams at the leading order are shown in Fig. 1. Since the Higgs+2 jets production through the gluon-gluon fusion (GGF) process is the dominant background for the VBF Higgs production at the LHC, the attempt of separating the VBF from the GGF production has been widely discussed [33, 34, 35, 36, 37, 38, 39, 40, 41]. It shows that the contribution from the GGF process can be largely suppressed by requiring a large rapidity gap and a large invariant mass of the two hardest jets in the Higgs+2 jets events [33, 34, 35]. We can also utilize the different features of soft gluon radiations between the VBF and GGF processes to suppress the contribution from the GGF, e.g., the difference in the jet energy profiles [36] and the azimuthal angle correlation between the Higgs and two-jet system [37, 40]. But, none of them could distinguish $WW$ and $ZZ$-boson fusion processes. Separating the $W$ boson’s contribution from the VBF Higgs production is an important task for determining $\kappa_{W}$ and $\kappa_{Z}$, separately, at the LHC.

To suppress the contributions from the $Z$-boson fusion and the GGF processes, we define a novel observable called jet charge asymmetry between the two leading jets in the Higgs+2 jets production. For the first time, we demonstrate that the jet charge correlations in Higgs+2 jets production can be used to separate the $W$-boson fusion from the $Z$-boson fusion and GGF processes; the electric charges of the two leading jets in $W$-boson fusion are opposite, while they could be the same or opposite for the $Z$-boson fusion and the GGF processes. We argue that one could determine the $\kappa_{W,Z}$ without making an assumption on the Higgs width and the other possible new physics effects from Higgs decay. Moreover, the correlation between $\kappa_{W}$ and $\kappa_{Z}$, obtained from the jet charges measurement, would be different from other experimental observable (e.g., the Higgs signal strength measurement) in the VBF processes. Therefore, the jet charge correlation in the production of Higgs+2 jets could play an important, and complementary, role in determining the $hVV$ couplings.

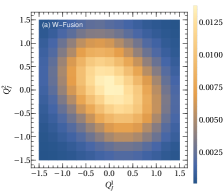
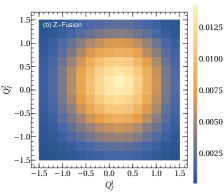
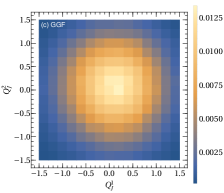
On average the sign of the jet charge is consistent with the charge of the parton which evolves into the jet from the measurements at the LHC [58, 59]. Therefore, the charge correlations for different VBF channels indicate the charge correlations of the parton in the hard process. Figure 2 shows the jet charge correlations between the leading and subleading jets from the $W$-fusion, $Z$-fusion and GGF processes after the kinematic cuts (see Eq. (3)) with the benchmark jet charge parameter $\kappa=0.3$. It clearly shows that the opposite sign of the two leading jet charges is favored in $W$-fusion process due to the partonic nature of the hard scattering at the leading order. However, this feature is disappeared in $Z$-fusion and GGF processes. It arises from the fact that both the opposite and same sign electric charges of the two leading jets in $Z$-fusion could be generated with a comparable production rate, while the sign of the jet charges in the GGF process is arbitrary. Motivated by this, we define the jet charge asymmetry of the two leading jets in Higgs+2 jets production by

$$A_{Q}=\left|\frac{Q_{J}^{1}-Q_{J}^{2}}{Q_{J}^{1}+Q_{J}^{2}}\right|,$$

(4)

where $Q_{J}^{1,2}$ is the jet charge of the leading and subleading jets, respectively. The advantage of this observable is that the systematic uncertainties, which are the dominant errors in jet charge measurements at the ATLAS and CMS Collaborations [58, 59], are expected to be canceled. This conclusion has been verified by the previous studies of other track-based observable in the HERA measurement [66]. On the other hand, the jet charge distributions are sensitive only to the weight of the jet flavor of final states in the hard scattering but not to the Higgs decay information (i.e., the Higgs width and the other possible new physics effects in Higgs decay). However, the jet charge asymmetry in Eq. (4) may be unstable since it can be much enhanced for the events with $Q_{J}^{1}+Q_{J}^{2}\sim 0$, therefore, we will utilize the average values of the jet charges to define this asymmetry in this paper, i.e.,

$$\overline{A}_{Q}\equiv\frac{\langle\left|Q_{J}^{1}-Q_{J}^{2}\right|\rangle}{\langle\left|Q_{J}^{1}+Q_{J}^{2}\right|\rangle}\equiv\frac{\langle Q^{(-)}\rangle}{\langle Q^{(+)}\rangle},$$

(5)

where $\langle Q\rangle$ denotes the average value of the quantity $Q$ and $Q^{(\pm)}=|Q_{J}^{1}\pm Q_{J}^{2}|$. From the definition, if the charges have the opposite sign such as the partonic process for $W$-fusion case, the asymmetry is expected to be $\overline{A}_{Q}>1$. However, if the charges have the same sign, e.g., the $Z$-fusion process $uu\to uuh$, $\overline{A}_{Q}<1$. For the GGF process the charges are fully uncorrelated so that $\overline{A}_{Q}\sim 1$.

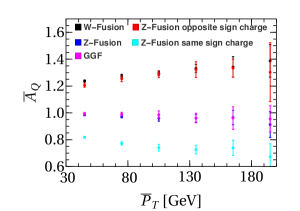
Figure 3 shows the jet charge asymmetry $\overline{A}_{Q}$ as a function of the average transverse momentum of the two leading jets ($\overline{p}_{T}\equiv(p_{T}^{1}+p_{T}^{2})/2$) in Higgs+2 jets production at the 14 TeV LHC with the integrated luminosity $\mathcal{L}=300~{}{\rm fb}^{-1}$. The statistical uncertainties are estimated from the Pythia simulation by generating a large number of pseudo experiments. We assume that the statistical errors follow the Gaussian distribution and could be rescaled to any integrated luminosity by the event numbers. We have checked that $\overline{A}_{Q}$ does not noticeably depend on the choice of $\kappa$ value, when varying from 0.3 to 0.7. As expected we find $\overline{A}_{Q}>1$ for the $W$-fusion (black points) since the sign of the jet charges are opposite. However, the asymmetry is close to one for the $Z$-fusion as shown with blue points in Fig. 3. To further understand the behavior of the $Z$-fusion, we also show $\overline{A}_{Q}$ for the $Z$-fusion with opposite (red points) and same sign jet charges (cyan points) in the same figure and the results are consistent with the argument before. When we combine all possible channels, this asymmetry would be close to one for the $Z$-fusion process since the opposite and same sign jet charge configurations could give a comparable contribution. The dominant contributions for the GGF process come from the $qg$ and $gg$ initial states, in result, we could expect that $\overline{A}_{Q}\sim 1$ due to the uncorrelated nature of the jet charges in this process.

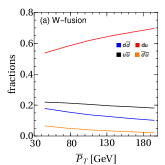
We also notice that the jet charge asymmetry is not very sensitive to $\overline{p}_{T}$ for the $Z$-fusion and the GGF processes. In particular, it exhibits a weak $\overline{p}_{T}$ dependence for the $W$-fusion and the $Z$-fusion with opposite or same sign jet charges. To be clear about the $\overline{p}_{T}$ dependence for the $W$ and the $Z$-fusion processes, we calculate various initial state ($qq^{\prime}$) fraction distributions $f_{qq^{\prime}}$ for the $W$-fusion and the $Z$-fusion after the kinematic cuts in Eq. (3) at the leading order; see Fig. 4. It shows that the $du$ quark initial state dominates the cross section in $W$-fusion (see Fig. 4(a)) and it will induce a weak $\overline{p}_{T}$ dependence for the charge asymmetry in Fig. 3 (black points). For the $Z$-fusion process, we only show the fractions of the dominated channels in Fig. 4(b). The weak $\overline{p}_{T}$ dependence for the charge asymmetry of the $Z$-fusion with opposite (red points in Fig. 3) and same sign (cyan points in Fig. 3) jet charges can also be understood from the behavior of the dominated fractions $f_{ud}$ and $f_{uu}$. As a consequence, the jet charge asymmetry of the $Z$-fusion will not be sensitive to the $\overline{p}_{T}$ after we combine all the subprocesses.

Next, we utilize the $\overline{A}_{Q}$ information to constrain the $hVV$ couplings. After combing the $W$-fusion, $Z$-fusion and GGF cross sections, the jet charge asymmetry in Higgs+2 jets process reads as

$\displaystyle\overline{A}_{Q}^{\rm tot}=$

$\displaystyle\frac{f_{W}\langle Q^{(-)}\rangle_{W}+f_{Z}\langle Q^{(-)}\rangle_{Z}+f_{G}\langle Q^{(-)}\rangle_{G}}{f_{W}\langle Q^{(+)}\rangle_{W}+f_{Z}\langle Q^{(+)}\rangle_{Z}+f_{G}\langle Q^{(+)}\rangle_{G}}\;,$

(6)

where the subscripts $W$, $Z$ and $G$ represent the contribution from different channels accordingly. The fractions $f_{i}(\overline{p}_{T},\kappa_{W/Z})$ is defined as $\sigma_{i}/(\sigma_{W}+\sigma_{Z}+\sigma_{G})$ with $i=W,Z,G$. It shows that the $W$-boson fusion dominates the cross section after applying the kinematic cuts in Eq. (3). The contamination from GGF can be further suppressed with boosted decision trees analysis, as shown in Fig. 2 of Ref. [67]. To estimate the impact of the jet charge asymmetry on constraining the $hVV$ couplings, we consider $h\to WW^{*}(\to 2\ell 2\nu_{\ell}){\,\rm and\,}ZZ^{*}(\to 4\ell)$, with $\ell=e,\mu,\tau$, as our benchmark decay processes in this work. The dominant background with these decay products is the GGF process [68]. But we emphasize that the correlations between $\kappa_{W}$ and $\kappa_{Z}$ measured from jet charges would not be sensitive to the Higgs decay information, which has been canceled in the definition of fractions. It can only change the statistical uncertainties in each $\overline{p}_{T}$ bin through the event numbers. The result could potentially be improved if we combine more decay modes of the Higgs boson, which is however beyond the scope of this work. Performing the pseudo experiments, we conduct a combined $\chi^{2}$ analysis as

$$\chi^{2}=\sum_{i}\left[\frac{\overline{A}_{Q}^{i,\rm tot}-\overline{A}_{Q}^{i,\rm tot,0}}{\delta\overline{A}_{Q}^{i,\rm tot}}\right]^{2},$$

(7)

where $\overline{A}_{Q}^{i,\rm tot,0}$ and $\delta\overline{A}_{Q}^{i,\rm tot}$ are the jet charge asymmetry in the SM (i.e., $\kappa_{W}=\kappa_{Z}=1$) and the statistical uncertainty of the $i$-th bin, respectively. For simplicity, we have assumed that the experimental values of jet charges agree with the SM predictions. Note that we have rescaled the statistical uncertainties to include the branching ratio ${\rm BR}(h\to 2\ell 2\nu_{\ell}/4\ell)$ in each bin in our $\chi^{2}$ analysis. The kinematic cuts for the decay products of Higgs boson can also change the total event numbers. However, such effects should not significantly change the conclusions of this paper and will be ignored in the following analysis. It shows that the typical error of $\overline{A}_{Q}^{\rm tot}$ is around $\mathcal{O}(1\%)$, which strongly depends on the average jet $\overline{p}_{T}$.

In Fig. 5, we show the expected limits on the $hVV$ couplings at the 68% confidence level (C.L.) for the integrated luminosity $3000~{}{\rm fb}^{-1}$, obtained from the jet charge asymmetries (red band) at the 14 TeV LHC (HL-LHC). It is evident that $\kappa_{W}$ and $\kappa_{Z}$ cannot be uniquely determined by the measurement of jet charge asymmetry alone. In order to further reduce the error band in the parameter space of $\kappa_{W}$ and $\kappa_{Z}$, without making any assumption on the total decay width ($\Gamma_{h}$) of the Higgs boson, we consider the following ratio of the Higgs signal strength measurements,

$$R_{h}\equiv\frac{\mu(gg\to h\to WW^{*})}{\mu(gg\to h\to ZZ^{*})}=\frac{\kappa_{W}^{2}}{\kappa_{Z}^{2}}\,,$$

(8)

where the signal strength modifier $\mu(gg\to h\to VV^{*})$ is defined as the measured cross section relative to the SM expectation. Hence, any new physics contributions to $gg\to h$ production cross section would cancel in $R_{h}$. Its constraint on $\kappa_{W}$ and $\kappa_{Z}$ at the HL-LHC is shown as the blue band in Fig. 5, where the error of $R_{h}$ is taken to be 5.7% [69]. It is evident that the combined analysis of the $\overline{A}_{Q}^{\rm tot}$ and $R_{h}$ data can further constrain the allowed $\kappa_{W}$ and $\kappa_{Z}$ values at the HL-LHC. We note that the correlation between $\kappa_{W}$ and $\kappa_{Z}$, extracted from $\overline{A}_{Q}^{\rm tot}$, is dependent of the fraction ($f_{W,Z}$) of production cross section contributed by various subprocesses, which is sensitive to the kinematic selection of the VBF events. Hence, it is possible to apply some advanced technologies, such as Boosted Decision Tree or Machine Learning, to further improve the constraints on $\kappa_{W}$ and $\kappa_{Z}$, which is however beyond the scope of this work.

For completeness, we also show in Fig. 5 the expected limits from the Higgs signal strength measurements of the VBF Higgs production with $h\to WW^{*}$ (denoted by $\mu_{\rm VBF}^{WW}$ in the figure, brown region) and $h\to ZZ^{*}$ (denoted by $\mu_{\rm VBF}^{ZZ}$ in the figure, gray region) at the HL-LHC [69]. Here, the error of the signal strength of the VBF production with $h\to WW^{*}$ and $h\to ZZ^{*}$ is taken to be 5.5% and 9.5%, respectively [69]. We note that while the constraints imposed by the $\overline{A}_{Q}^{\rm tot}$ and $R_{h}$ data are independent of $\Gamma_{h}$, those imposed by $\mu_{\rm VBF}^{WW}$ and $\mu_{\rm VBF}^{ZZ}$ are dependent of the assumption made in the calculation of $\Gamma_{h}$. Here, we assumed that $\Gamma_{h}$ is only modified by the values of $\kappa_{W}$ and $\kappa_{Z}$.