Directional direct detection of light dark matter up-scattered by cosmic rays from direction of the Galactic center
Abstract
Dark matter with MeV scale mass is difficult to detect with standard direct search detectors. However, they can be searched for by considering the up-scattering of kinetic energies by cosmic rays. Because the dark matter density is higher in the central region of the Galaxy, the up-scattered dark matter will arrive at Earth from the direction of the Galactic center. Once the dark matter is detected, we can expect to recognize this feature by directional direct detection experiments. In this study, we simulate the nuclear recoils of the up-scattered dark matter and quantitatively reveal that a large amount of this type of dark matter is arriving from the direction of the Galactic center. Also, we have shown that the characteristic signatures of the up-scattered dark matter can be verified with more than 5 confidence levels for the assumed target atoms and future upgrades to directional detectors.
1 Introduction
The identity of dark matter (DM) is a highly significant question in cosmology and particle physics. In the past a few decades, weakly interacting massive particles (WIMPs) have been expected to be the identity of DM. Many attempts have been made to detect WIMPs directly and indirectly, and to produce them in collider experiments. However, despite advances in the sensitivity of direct detection experiments, no obvious detection of DM has been achieved so far. Particularly, direct detection experiments have placed very stringent limits on the magnitude of the interaction cross section for WIMP particles of GeV-scale mass, i.e., cm2 and cm2, where represents spin-independent (SI) and spin-dependent (SD) cross sections of the DM and proton scattering, respectively [1, 2]. On the other hand, for DM having mass lighter than the GeV-scale, it is not easy to obtain high sensitivity through DM-nucleon scatterings. It has recently been proposed that even in such light DM cases, unavoidable scattering between DM and a cosmic ray produces substantial and very energetic DM that can be detected in neutrino detectors and direct detection experiments of DM [3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]. As well as the up-scattering of DM by cosmic rays, its effect on cosmic ray propagation in the Earth [6] has also been investigated. The cosmic ray scattered dark matter (CR-DM) flux has a substantial contribution from the direction of the Galactic center [6, 9, 18]. In some direct searches such as PandaX and CDEX, constraints for CR-DM have already been placed using real data [16, 17].
Directional direct detection of DM is expected to be very well suited to detect the characteristic events of CR-DM coming from the Galactic center. Using directional information to understand the DM nature has been investigated in both directional and non-directional direct searches [24, 25, 26, 27, 28, 29, 30]. Also, verifications of CR-DM using directional information through diurnal modulation in the ordinary direct detection experiments [6, 16], and directional search in the neutrino detector [19] are already studied. In this study, we simulate the CR-DM signals in directional searches and reveals its potential for validation of CR-DM. In directional detection, gas detectors are sensitive to the SD interactions between DM particles and nucleons [31, 32]. The gases used in the experiments are CF4 and SF6, and in most cases, the nucleon target for scattering with DM is fluorine (F). We also simulate a solid detector NEWSdm [33, 34], which is a nuclear emulsion detector and is sensitive to SI interactions. Nuclear emulsion detectors contain multiple targets, thus in the numerical calculations we employ hydrogen (), which is sensitive to light DM, and silver (Ag), which is sensitive to heavy DM.
2 CR-DM and the density profile
To simulate the scattering of CR-DM and the targets in direct detection experiments, first a parametrization of the incoming flux of CR-DM to the Earth is required. In this section, we follow the methods of reference [4] to calculate the incoming flux of CR-DM from all directions in space. The calculation procedure is listed below.
-
1.
If we assume the DM mass , the interaction cross section between DM and the nucleus , density profile , and cosmic ray flux in the Galaxy, the incoming CR-DM flux can be obtained by
(2.1) where is the length of the line-of-sight (l.o.s) integral, is the distance from the Galactic center. and are the kinetic energies of the CR-DM and nucleus, respectively. Minimum kinetic energy is defined as
where () corresponds to the case for (). Additionally, we use Hydrogen, which is the most abundant element in space, to be the cosmic ray particle , i.e., we assume for simplicity in this paper.
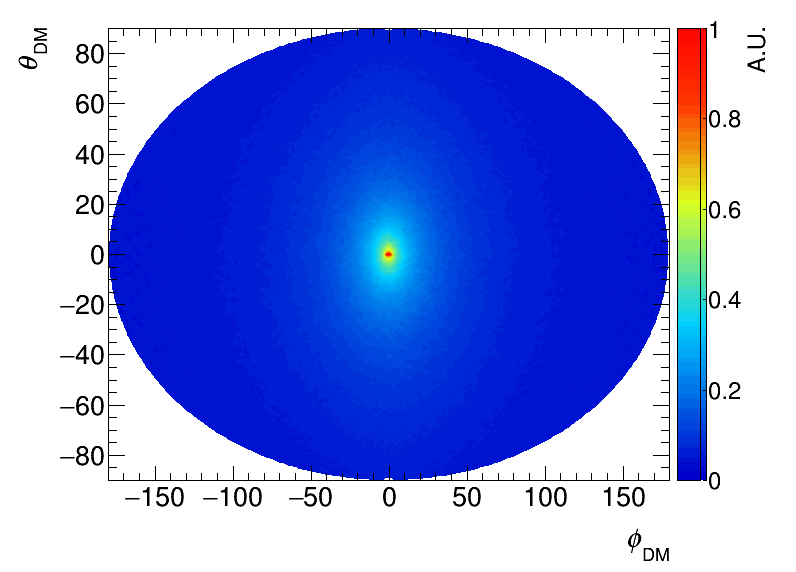
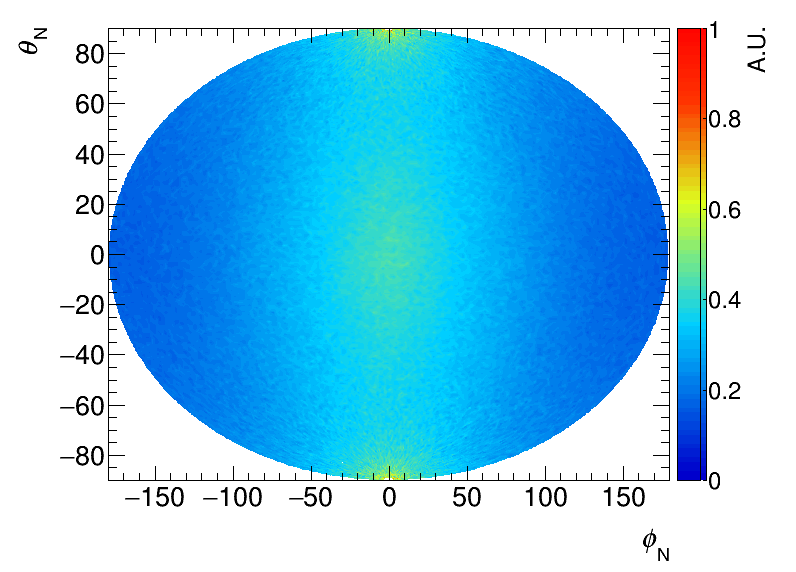
To define the direction of the incoming CR-DM and the nuclear recoils, we adopt the coordinate system shown in Figure 1. We define the direction of the incoming CR-DM with and , and the direction of the nuclear recoils as and . In this coordinate system, corresponds to events coming from the direction of the Galactic center. The scattering angle is the angle from the line connecting the Galactic center to the observer. There is a relation between and . To include contributions near the Galactic center in the integration of , we take the limits of integration up to the distance between the solar system and the Galactic center and take kpc [35]111Although the integration volume might be larger for a more realistic estimation, we limited the range of the l.o.s. integration to 8.122 kpc as a first step of the study. This can be justified as a conservative estimation by having confirmed the DM flux from the Galactic center increase of 40% (80%) if we change the range of the line-of-sight integration to 10 kpc (38 kpc)..
For the numerical calculation, we use the cosmic ray flux data from the Galprop codebase [36]. Both the cosmic ray sources and the DM profile would be denser in the vicinity of the Galactic center in a realistic scenario; however, following reference [4] we assume the flux of cosmic rays is uniform throughout the Galaxy. The dependence of CR-DM flux on cosmic ray profiles near the Galactic Center will be the scope of our future study.

Figure 1: Coordinate system used in the figures showing the numerical results. -
2.
The obtained CR-DM incoming flux in the Galactic rest frame is transformed to the laboratory frame in the Solar system.
-
3.
DM-nucleon scattering caused by the CR-DM in the Solar system is simulated using the CR-DM flux derived in step 2. Then we obtain the nuclear recoil energy and its scattering angle .
We assume three typical density profiles for . The first is the frequently used Navarro–Frenk–White (NFW) profile suggested by N-body simulations [37],
| (2.2) |
The second is the Einasto profile which gives a better fit to the N-body simulation data than the NFW profile [38, 39]. It is given by
| (2.3) |
Because both the NFW and Einasto profiles are cuspy in the Galactic center, we also investigate a cored profile to see the profile dependence clearly. The third profile is the pseudo-isothermal profile (PIT) [40]
| (2.4) |
Parameters used in the numerical calculation are shown in Table 1, which are taken from [35] for the NFW and the Esnasto profiles, and [41] for the PIT profile. In the table, the local DM density is represented as , and is normalized to reproduce that value of .
| [GeV/cm3] | [GeV/cm3] | [kpc] | ||
|---|---|---|---|---|
| NFW | 0.38 | 0.83 | 11.0 | - |
| Einasto | 0.38 | 0.30 | 9.2 | 0.18 |
| PIT | 0.35 | 3.56 | 2.7 | - |
3 Numerical Result and discussion
In direct detection experiments with directional sensitivity, the energy and angle of nuclear recoils are expected to be detected. We will discuss the results obtained from simulations in this section.
3.1 Angular distribution of CR-DM and nuclear recoil
Figure 2 shows the sky maps for the incoming distributions of the CR-DMs of 10 MeV mass expected in the Solar system for the three density profiles assumed. The left, middle, and right columns correspond to the NFW, the Einasto, and the PIT profiles, respectively. In the NFW and Einasto profiles, the incoming flux of CR-DM is highly concentrated in the direction of the Galactic center. Whereas in the PIT profile, the incoming flux of CR-DM is found over a wide area centered at the Galactic center. There is almost no difference in the directional distributions of the CR-DM in the mass range of 1 GeV to 1 MeV.
Next, we move to the directional distributions of nuclear recoils by the CR-DMs. In Figures 3-5, the angular distributions of the recoiled nuclei are shown in whole sky map density plots for the following reference cases:
-
•
the targets are , F, and Ag,
-
•
the DM profiles are NFW, Einasto, and PIT,
-
•
the DM masses are 100 MeV, 10 MeV, and 1 MeV.
These figures are intended to illustrate an ideal situation without any consideration of detector response (energy threshold, energy resolution, quenching factor and others) and any types of background. The center of the figures corresponds to the arrival from the direction of the Galactic center, thus in all simulations, the CR-DM flux from the Galactic center is significantly higher than the contribution from other directions. In the whole sky map density plots, there is no noticeable difference between the simulations using the NFW and Einasto profiles. However, there is a distinct difference between the simulations using the PIT profile and the other two profiles. The different appears because, the NFW and Einasto profiles in the Galactic center are cuspy, but it is cored in the PIT profile. This cuspy vs cored property is reflected in the fact that events are less dense in the Galactic center for simulations using the PIT profile than the other simulations using the NFW and Einasto profiles.
3.2 Energy dependence of the angular distribution
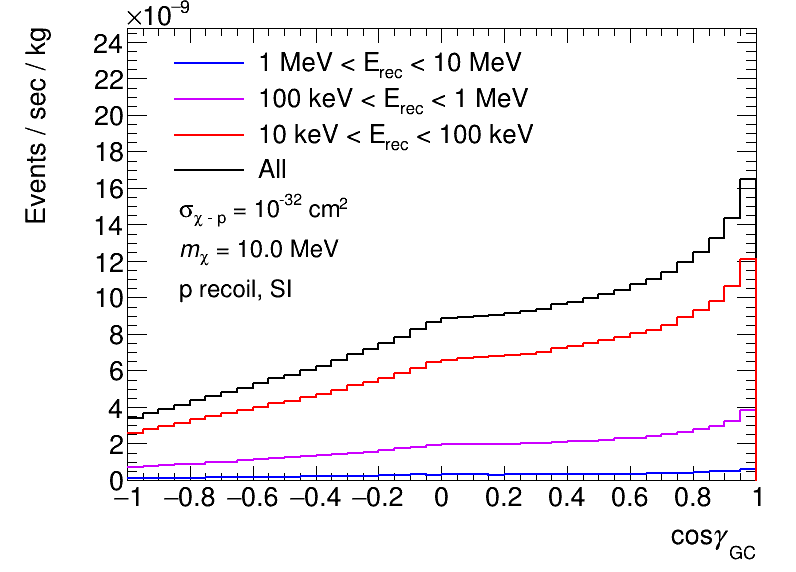
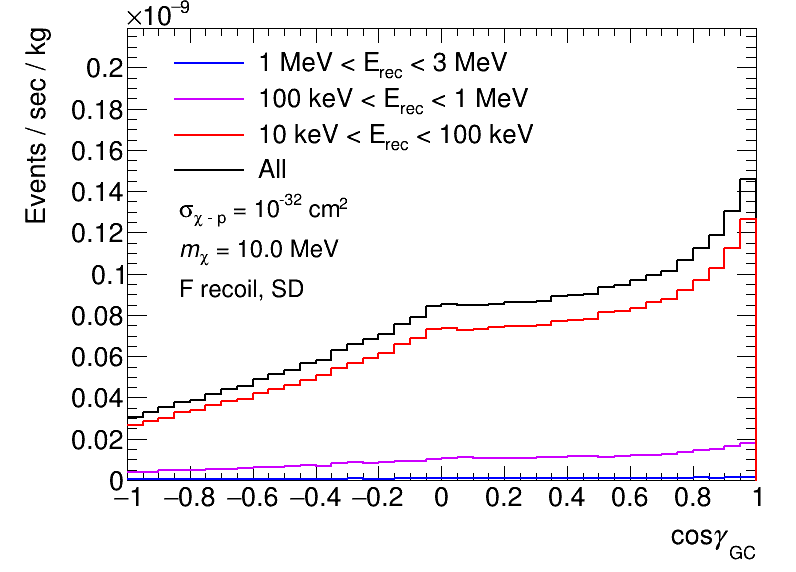
We now discuss the distributions of the nuclear recoil energies and scattering angles to see the dependence of the CR-DM mass, which is not visualized in the sky maps in subsection 3.1. The differential angular distributions expected with the , F, and Ag targets are shown in Figure 6, 7, and 8, respectively. The rate of detection is shown in units of event number per second per kilogram. NFW, Einasto and PIT profile simulations are shown in the left, center, and right columns of each figure. Simulations with a CR-DM mass of 100 MeV, 10 MeV, and 1 MeV are shown in the top, center, and bottom rows of each figure. SI interactions with the DM particles are assumed for the and Ag targets, while SD interactions are assumed for the F target. See Appendix A for the sensitivity with the F target for SI interactions. We assume the cross section of the DM and the proton interaction is cm2, which is currently not experimentally constrained for SI or SD interactions with GeV [4].
A detector energy threshold of keV is assumed for the and F targets, and threshold of keV for the Ag target is assumed. The event rates expected in the energy range greater than the detector energy threshold and which elastic scattering occurs are shown in the figures [42]. The black histograms show the distribution over the whole energy range of interest, while colored ones show the distributions corresponding to the recoil energy ranges. We have discarded large momentum transfer events before making these angular distributions, i.e., events with energies greater than 10, 3, and 0.6 MeV are discarded for , F, and Ag targets, respectively. The reason large momentum transfer events are discarded is that inelastic scatterings are expected to dominate once the kinetic energy of the DM is large enough to see the internal structure of the nucleus. To discuss inelastic scatterings between the DM and target nuclei, we would need to introduce some assumptions depending on the type of DM and its interactions [43, 44, 45, 11]. In this paper, we prefer to discuss the properties of the CR-DM in general manners as much as possible, thus we focus only on the elastic scatterings. We assume that if the de Broglie wavelength of the DM is longer than that of the target nuclei, it can be treated as a perfect elastic scattering. For the sake of consistency and considering current detector setups, only such events are included here, thus we conservatively focus only on the elastic scatterings.
As can be easily expected, forward scattering events make peaks at , and some distributions have peaks in the center at . These central peaks are clearly visible in the distributions for heavy CR-DMs and disappear in ones for light CR-DMs. The central peaks correspond to the instance where the target and CR-DM do not change the direction of their motions from their initial ones in the center-of-mass frame through scattering. This kind of scattering, in which the target and CR-DM graze each other in the center-of-mass frame, becomes less visible in the laboratory frame as the CR-DM mass decreases. For light CR-DM, in the center-of-mass frame, the CR-DM hits a light target and both the CR-DM and the target are bounced away in opposite directions from its initial state. As a result, a prominent peak is produced at , which is the direction expected to be naively scattered from the Galactic center.
The energy dependence is similar for the simulations of NFW and Einasto profiles. On the other hand, in the figures there is a difference between the simulations using the PIT profile and the other two profiles, because of the different treatment of structures in the center of the galaxy. Now we will take a closer look at the simulations using the PIT profile. The central peak near is moderate and less noticeable than in the NFW and Einasto profiles. This is because the PIT profile has a core at the Galactic center. It is clear from Figures 3-5 that the CR-DM signal comes from a wider range than that in the simulations using the other two profiles, in which the CR-DM comes from a narrow range near the Galactic center.
3.3 Asymmetry and sensitivity


|

|


|

|
To quantify the forward-backward asymmetries of the recoil direction distributions, a parameter is defined as
| (3.1) |
where and are the number of events for and , respectively.
Figure 9 shows the asymmetry parameters and their statistical errors obtained by the simulation. The colors represent the three density profiles and the errors are statistical ones. The number of events is normalized as 5.0 kg-yr exposure of the nano imaging tracker (NIT) for the target and Ag, and 1550 kg-yr exposure of SF6 gas. The latter is based on the assumption of the exposure 10k m3 SF6 gas at 20 Torr and six years, which is equivalent to 10 times the exposure envisioned for the Cygnus-1000 project [32]. The weight ratios of and Ag in the NIT are set at 1.6% and 44.5%, respectively [46]. For light CR-DMs less than MeV mass, enough statistics clearly confirm the directionality originated by signals coming from the Galactic center direction. Because the number of events discarded for the light CR-DM instance, is smaller than for the heavy CR-DM instance and the central peak disappears. As already mentioned, events with large recoil energy, which often occur in heavy CR-DM cases, are discarded because they are not elastic scattering, thus the number of events available for the analysis is reduced and the error is significant. The CR-DM generally can have a larger scattering cross section than WIMPs with masses around O(1 - 100) MeV. The large cross section often results in attenuation of flux before reaching underground detectors [4, 5, 6]. In the plots, we assume that the CR-DM descends from the upper atmosphere and reaches the underground detectors and neglect the attenuation effect. Due to their large scattering cross section, the component reaching the detector from the opposite side of the Earth experiences significant attenuation, thus it is not effective to use this component. Data selection is feasible for the time intervals when the detector is oriented towards the central region of the Galaxy, as gas detectors such as the NEWAGE offer time resolution, and in the NEWSdm, in principle it is possible to deactivate the nuclear emulsion by temperature adjustment [47]. Thus, if such an event selection by time is performed, the net exposure would need to be doubled.
Figure 10 shows the evolution of the null-rejection significance of the asymmetry parameter with each target, where the range of the exposure corresponds up to six years for the same configuration as that in Figure 9. The CR-DM masses are assumed to be 10 MeV (dotted lines) and 100 MeV (solid lines). As can be inferred from Figure 9, assuming elastic scattering, all targets investigated have sufficient potential for the null-rejection of the asymmetry parameter within the scope of the envisioned future upgrades. With enough exposure, the asymmetry can be confirmed with more than 5 confidence level for 10 MeV (100 MeV) mass CR-DM except for , at most 8 (7.6 ) and 2.6 (5.2 ) for F and Ag, respectively. For SD interactions using the fluorine target, the NEWAGE experiment is developing a 1 m3 scale detector filled with SF6 gas. Furthermore, an update is planned to the CYGNUS-1000 experiment [32], which has 1000 m3 scale gaseous time projection chamber (TPC). It is planned to achieve 5 sensitivity for the 10 MeV CR-DM mass after 2.6 (2.4) years’ of measurement for Einasto (NFW) profile. For the NEWSdm experiment, the device production system at the Gran Sasso National Laboratory (LNGS) has been operated successfully, and it is possible to produce the 10 kg scale target using the current system. In addition, new scanning systems with a 0.5 kg/year/machine are being developed, and several kg-scale scanning will be achieved by using the same upgrades on five existing machines. Furthermore, a high scanning speed machine with a 5 kg/year/machine has already been designed that uses a wide field of view with multi-camera imaging and optimal driving motion system. From the high scanning machine, several 10 kg scale experiment will be achieved. Low energy threshold tracking will be achieved by the finer grain nuclear emulsions [46] and super-resolution techniques [48]. Therefore, taking into account the possibility of future upgrades, both NEWAGE and NEWSdm would have the potential to verify the light CR-DM arriving from the direction of the Galactic center.
4 Conclusion
Up-scattering of DM by cosmic rays is an undeniable key phenomenon that can allow the search for light DMs, which are not easy to reach by standard nuclear recoil methods. The CR-DMs are expected to arrive mostly from the direction of the Galactic center, where the density of the DM is large, and thus can be examined with direction-sensitive detectors. In this paper, we study the detection possibilities of CR-DMs with directional detectors and investigate the expected energy and angular distributions.
We find that almost independent of the DM density profiles, CR-DM tends to come from the direction of the Galactic center, and the targets in the detector are scattered towards the forward direction. Assuming elastic scattering of DM and target, we also investigate the sensitivity of directional detectors to verify the existence of CR-DM. Our study showed that the asymmetry of nuclear recoil is expected to hold the characteristic signature of the CR-DM. It is shown that the feature can be verified by directional detectors, especially for light DM with mass less than MeV. With scattering cross section of DM and proton as cm2 and MeV ( MeV), the asymmetry can be evaluated at 0.7, 8, and 2.6 (0.2, 7.6, and 5.2) at most for the target (the SI interaction), for the F target (the SD interaction), and for the Ag target (the SI interaction), respectively. For the evaluation, exposures 0.48 kg-yr, 7200 kg-yr, and 13.2 kg-yr are assumed for , F, and Ag targets, respectively. These large exposures can be achieved with future large detectors like CYGNUS and NEWSdm.


|



|



|



|



|


|



|



|



|



|



|


|



|



|


|



|



|



|



|
Acknowledgments
It is a pleasure to thank S. Matsumoto, K. Hata, K. Hayashi, C. Cappiello and H. Oshima for helpful discussions. KIN is also grateful to S. Kime, T. Tomiya and N. Ikeda for discussion on the early stages of this work. This work was supported by JSPS KAKENHI Grant Number 19H05806, 26104005, (A) 16H02189, (A) 18H03699, (C) 21K03562, (C) 21K03583, 21K13943, 22H04574 and Wesco Scientific Promotion Foundation.
References
- [1] E. Aprile, et al. Dark Matter Search Results from a One Ton-Year Exposure of XENON1T. Phys. Rev. Lett., Vol. 121, No. 11, p. 111302, 2018.
- [2] J. Aalbers, et al. First Dark Matter Search Results from the LUX-ZEPLIN (LZ) Experiment. 7 2022.
- [3] Wen Yin. Highly-boosted dark matter and cutoff for cosmic-ray neutrinos through neutrino portal. EPJ Web Conf., Vol. 208, p. 04003, 2019.
- [4] Torsten Bringmann and Maxim Pospelov. Novel direct detection constraints on light dark matter. Phys. Rev. Lett., Vol. 122, No. 17, p. 171801, 2019.
- [5] Yohei Ema, Filippo Sala, and Ryosuke Sato. Light Dark Matter at Neutrino Experiments. Phys. Rev. Lett., Vol. 122, No. 18, p. 181802, 2019.
- [6] Christopher V. Cappiello and John F. Beacom. Strong New Limits on Light Dark Matter from Neutrino Experiments. Phys. Rev. D, Vol. 100, No. 10, p. 103011, 2019. [Erratum: Phys.Rev.D 104, 069901 (2021)].
- [7] James B. Dent, Bhaskar Dutta, Jayden L. Newstead, and Ian M. Shoemaker. Bounds on Cosmic Ray-Boosted Dark Matter in Simplified Models and its Corresponding Neutrino-Floor. Phys. Rev. D, Vol. 101, No. 11, p. 116007, 2020.
- [8] Gang Guo, Yue-Lin Sming Tsai, and Meng-Ru Wu. Probing cosmic-ray accelerated light dark matter with IceCube. JCAP, Vol. 10, p. 049, 2020.
- [9] Shao-Feng Ge, Jianglai Liu, Qiang Yuan, and Ning Zhou. Diurnal Effect of Sub-GeV Dark Matter Boosted by Cosmic Rays. Phys. Rev. Lett., Vol. 126, No. 9, p. 091804, 2021.
- [10] Joerg Jaeckel and Wen Yin. Boosted Neutrinos and Relativistic Dark Particles as Messengers from Reheating. JCAP, Vol. 02, p. 044, 2021.
- [11] Gang Guo, Yue-Lin Sming Tsai, Meng-Ru Wu, and Qiang Yuan. Elastic and Inelastic Scattering of Cosmic-Rays on Sub-GeV Dark Matter. Phys. Rev. D, Vol. 102, No. 10, p. 103004, 2020.
- [12] Nicole F. Bell, James B. Dent, Bhaskar Dutta, Sumit Ghosh, Jason Kumar, Jayden L. Newstead, and Ian M. Shoemaker. Cosmic-ray upscattered inelastic dark matter. Phys. Rev. D, Vol. 104, p. 076020, 2021.
- [13] Keiko I. Nagao and Hiroshi Okada. Modular A4 symmetry and light dark matter with gauged U(1)BL. Phys. Dark Univ., Vol. 36, p. 101039, 2022.
- [14] Jie-Cheng Feng, Xian-Wei Kang, Chih-Ting Lu, Yue-Lin Sming Tsai, and Feng-Shou Zhang. Revising inelastic dark matter direct detection by including the cosmic ray acceleration. JHEP, Vol. 04, p. 080, 2022.
- [15] Chen Xia, Yan-Hao Xu, and Yu-Feng Zhou. Production and attenuation of cosmic-ray boosted dark matter. JCAP, Vol. 02, No. 02, p. 028, 2022.
- [16] Xiangyi Cui, et al. Search for Cosmic-Ray Boosted Sub-GeV Dark Matter at the PandaX-II Experiment. Phys. Rev. Lett., Vol. 128, No. 17, p. 171801, 2022.
- [17] R. Xu, et al. Constraints on sub-GeV dark matter boosted by cosmic rays from the CDEX-10 experiment at the China Jinping Underground Laboratory. Phys. Rev. D, Vol. 106, No. 5, p. 052008, 2022.
- [18] Chen Xia, Yan-Hao Xu, and Yu-Feng Zhou. Azimuthal asymmetry in cosmic-ray boosted dark matter flux. 6 2022.
- [19] K. Abe, et al. Search for Cosmic-ray Boosted Sub-GeV Dark Matter using Recoil Protons at Super-Kamiokande. 9 2022.
- [20] Gilly Elor, Robert McGehee, and Aaron Pierce. Maximizing Direct Detection with HYPER Dark Matter. 12 2021.
- [21] Debjyoti Bardhan, Supritha Bhowmick, Diptimoy Ghosh, Atanu Guha, and Divya Sachdeva. Boosting through the Darkness : Bounds on boosted dark matter from direct detection. 8 2022.
- [22] James Alvey, Torsten Bringmann, and Helena Kolesova. No room to hide: implications of cosmic-ray upscattering for GeV-scale dark matter. 9 2022.
- [23] Tarak Nath Maity and Ranjan Laha. Cosmic-ray boosted dark matter in Xe-based direct detection experiments. 10 2022.
- [24] Moqbil S. Alenazi and Paolo Gondolo. Directional recoil rates for WIMP direct detection. Phys. Rev. D, Vol. 77, p. 043532, 2008.
- [25] Ciaran A. J. O’Hare and Anne M. Green. Directional detection of dark matter streams. Phys. Rev. D, Vol. 90, No. 12, p. 123511, 2014.
- [26] Bradley J. Kavanagh. Discretising the velocity distribution for directional dark matter experiments. JCAP, Vol. 07, p. 019, 2015.
- [27] Bradley J. Kavanagh and Ciaran A. J. O’Hare. Reconstructing the three-dimensional local dark matter velocity distribution. Phys. Rev. D, Vol. 94, No. 12, p. 123009, 2016.
- [28] Riccardo Catena, Jan Conrad, Christian Döring, Alfredo Davide Ferella, and Martin B. Krauss. Dark matter spin determination with directional direct detection experiments. Phys. Rev. D, Vol. 97, No. 2, p. 023007, 2018.
- [29] Keiko I. Nagao, Tomonori Ikeda, Ryota Yakabe, Tatsuhiro Naka, and Kentaro Miuchi. Discrimination of anisotropy in dark matter velocity distribution with directional detectors. Phys. Dark Univ., Vol. 27, p. 100426, 2020.
- [30] M. Andriamirado, et al. Limits on sub-GeV dark matter from the PROSPECT reactor antineutrino experiment. Phys. Rev. D, Vol. 104, No. 1, p. 012009, 2021.
- [31] F. Mayet, et al. A review of the discovery reach of directional Dark Matter detection. Phys. Rept., Vol. 627, pp. 1–49, 2016.
- [32] S. E. Vahsen, et al. CYGNUS: Feasibility of a nuclear recoil observatory with directional sensitivity to dark matter and neutrinos, arXiv:2008.12587. 8 2020.
- [33] A. Aleksandrov, et al. NEWS: Nuclear Emulsions for WIMP Search. 4 2016.
- [34] N. Agafonova, et al. Discovery potential for directional Dark Matter detection with nuclear emulsions. Eur. Phys. J. C, Vol. 78, No. 7, p. 578, 2018.
- [35] P.F. de Salas, K. Malhan, K. Freese, K. Hattori, and M. Valluri. On the estimation of the local dark matter density using the rotation curve of the milky way. Journal of Cosmology and Astroparticle Physics, Vol. 2019, No. 10, pp. 037–037, oct 2019.
- [36] A.E. Vladimirov, S.W. Digel, G. Jóhannesson, P.F. Michelson, I.V. Moskalenko, P.L. Nolan, E. Orlando, T.A. Porter, and A.W. Strong. Galprop webrun: An internet-based service for calculating galactic cosmic ray propagation and associated photon emissions. Computer Physics Communications, Vol. 182, No. 5, p. 1156â1161, May 2011.
- [37] Julio F. Navarro, Carlos S. Frenk, and Simon D. M. White. A Universal density profile from hierarchical clustering. Astrophys. J., Vol. 490, pp. 493–508, 1997.
- [38] J. F. Navarro, E. Hayashi, C. Power, A. R. Jenkins, C. S. Frenk, S. D. M. White, V. Springel, J. Stadel, and T. R. Quinn. The inner structure of cdm haloes - iii. universality and asymptotic slopes. Monthly Notices of the Royal Astronomical Society, Vol. 349, No. 3, p. 1039â1051, Apr 2004.
- [39] Alister W. Graham, David Merritt, Ben Moore, Jürg Diemand, and BalÅ¡a TerziÄ. Empirical models for dark matter halos. ii. inner profile slopes, dynamical profiles, and rho/sigma3. The Astronomical Journal, Vol. 132, No. 6, p. 2701â2710, Jan 2006.
- [40] Raul Jimenez, Licia Verde, and S. Peng Oh. Dark halo properties from rotation curves. Mon. Not. Roy. Astron. Soc., Vol. 339, p. 243, 2003.
- [41] Christopher Wegg, Ortwin Gerhard, and Marie Bieth. The gravitational force field of the galaxy measured from the kinematics of RR lyrae in gaia. Monthly Notices of the Royal Astronomical Society, Vol. 485, No. 3, pp. 3296–3316, feb 2019.
- [42] T. Ikeda, T. Shimada, H. Ishiura, K.D. Nakamura, T. Nakamura, and K. Miuchi. Development of a negative ion micro tpc detector with sf6 gas for the directional dark matter search. Journal of Instrumentation, Vol. 15, No. 07, p. P07015, jul 2020.
- [43] John R. Ellis, R. A. Flores, and J. D. Lewin. Rates for Inelastic Nuclear Excitation by Dark Matter Particles. Phys. Lett. B, Vol. 212, pp. 375–380, 1988.
- [44] J. Engel and P. Vogel. Neutralino inelastic scattering with subsequent detection of nuclear gamma-rays. Phys. Rev. D, Vol. 61, p. 063503, 2000.
- [45] G. Arcadi, C. Döring, C. Hasterok, and S. Vogl. Inelastic dark matter nucleus scattering. JCAP, Vol. 12, p. 053, 2019.
- [46] Takashi Asada, Tatsuhiro Naka, Ken-ichi Kuwabara, and Masahiro Yoshimoto. The development of a super-fine-grained nuclear emulsion. PTEP, Vol. 2017, No. 6, p. 063H01, 2017.
- [47] M. Kimura, T. Naka, S. Furuya, T. Asada, T. Katsuragawa, M. Yoshimoto, A. Umemoto, S. Machii, H. Ichiki, O. Sato, and Y. Hoshino. WIMP tracking with cryogenic nuclear emulsion. Nucl. Inst. Meth. A, Vol. 845, pp. 373–377, 2017.
- [48] Andrey Alexandrov, Takashi Asada, Di Crescenzo Antonia De Lellis, Giovanni, Valerio Gentile Gentile, Tatsuhiro Naka, Valeri Tioukov, and Atsuhiro Umemoto. Super-resolution high-speed optical microscopy for fully automated readout of metallic nanoparticles and nanostructures. Sci. Rep., Vol. 10, No. 18773, 2020.
Appendix A The SI and SD cross sections
Fluorine is the target assumed in the directional direct detection through SD interactions. The sensitivity to SI and SD cross sections varies by a factor . By evaluating the factor, the sensitivity to SD interactions in Section 3.2 can be scaled to that to SI interactions. The cross sections of DM and nucleus scattering for the SI and SD interactions are
| (A.1) | ||||
| (A.2) |
respectively, where is the DM and proton scattering cross section, is the reduced mass of CR-DM and nucleus (proton), is mass number, and for F. Therefore, the ratio of event number required to reach the same cross section , which is also denoted as , is estimated as
| (A.3) |