2023 \Page1\Endpage4
Direct triple- process in non-adiabatic approach
Abstract
Triple- reaction rates have been determined well with the sequential process via the narrow resonances.
However, the direct triple- process at off-resonant energies still remains in unsolved problems.
In the present report, the direct triple- contribution is estimated with a non-adiabatic method, and it is found to be 10-15–10-3 pb order in photodisintegration cross sections of 12C(2 0+) for MeV.
This is far below the values predicted by the recent adiabatic models.
In spite of the large difference, the derived rates are found to be concordant with NACRE at the helium burning temperatures.
Keywords: Triple- reaction; Reaction rates; Helium burning.
1 INTRODUCTION
The triple- reaction plays an important role in nucleosynthesis heavier than 12C, because no stable nuclei exist in mass number and [1]. This reaction, followed by 12C(,)16O [2], controls C/O ratio at the end of helium burning phase in stars, and it affects up to the nucleosynthesis in supernova explosion. In contrast to 12C(,)16O, the triple- reaction is currently well-understood through the experimental studies of the 0 state in 12C ( MeV) (e.g. [3, 4]), i.e., the reaction rates have been determined well with the sequential process via the narrow resonances: Be(0), +8BeC(0). Pioneering works of the reaction rates have been performed by [5, 6], and their experimental upgrade has been given by NACRE [4].
Apart from the sequential process, the triple- reaction from 3 continuum states is referred to as the direct triple- process: C. This process is generally expected to be very slow, because three -particles almost simultaneously collide and fuse into a 12C nucleus. So, this process is neglected or is treated in some approximations. For the theoretical studies, formulae in hyper-spherical coordinates have been applied to tackle the 3 continuum problem (e.g. [7]), and their adiabatic approaches have paved the way for a non-adiabatic approach of [8]. The Coulomb modified Faddeev (CMF) [9] and adiabatic channel function (ACF) expansion method [10] may have also achieved the successful progress quantitatively. However, non-adiabatic quantum-mechanical description at off-resonant energies still seem to remain in unsolved problems. In the present report, the contribution of the direct 3 process is estimated with a non-adiabatic Faddeev hyper-spherical harmonics and -matrix (HHR∗) expansion method [11, 12]. At the same time, the difference between the non-adiabatic and adiabatic calculations is discussed.
2 FADDEEV HHR∗ EXPANSION METHOD
Before discussing the calculated results, let me describe HHR∗, briefly. The triple- system satisfies the three-body Schrödinger equation, . is three-body Hamiltonian; is the center-of-mass energy to the 3 threshold in 12C; is spin of the states in 12C; is the projection of . This equation is expressed as the so-called Faddeev equations, consisting of three components. Due to the symmetric 3 system, three identical sets of equations are found, and they are expressed in a similar form of ordinary coupled-channel (CC) equations for inelastic scattering, (e.g. [13, 14]), after translating Jacobi coordinates () into hyper-spherical coordinates (), . The deduced CC equations of the hyper-radial waves, , are given in
| (1) |
where ; are the coupling potentials; ; is nucleon mass; is hyper-angular momentum; is a label of channels. are calculated from and 3 potentials, and they are the same as [8] except that the strength of 3 potentials are MeV ( MeV [8]) for 0+ and MeV ( MeV [8]) for 2+. Using the hyper-harmonic function [11, 12], the basis functions are defined by
| (2) |
where are harmonic oscillator wavefunctions in hyper-spherical coordinates, . The results are independent of , if a large number of basis are used. The CC equations (1), briefly rewritten as , are solved by the matrix diagonalization. The matrix size of the present calculation is (8,8008,800) for 0+ in 12C. In the -matrix expansion method, the continuum states with scattering boundary condition are expanded by the resultant eigenfunctions,
| (3) |
| (4) |
where and are the eigenfunctions and eigen-energy, respectively. and are the channel labels. are the incoming () and outgoing () Coulomb wavefunctions; is the Sommerfeld parameter; is the hyper-momentum, ; is the channel radius. is the -matrix, defined by the derived -matrix at .
To include the long-range Coulomb couplings, the CC equations in the external region are solved numerically from to by using the -matrix propagation technique [8]. The external wavefunctions are expanded by the resulting linearly-independent solutions , and the coefficients of expansion are obtained by matching to the asymptotic form,
| (5) |
where and are the coupled-Coulomb waves [14], . In the present report, the global back propagation [8] from to is not used. If the screening potential [8] is adopted to reduce the strength of Coulomb couplings at large , can be used. This is effective if the off-diagonal part of coupling potentials is relatively small at , compared with , (e.g. [13]). Multiplying eq. (3) by , I obtain the interior scattering waves including the long-range Coulomb couplings, .
The photodisintegration cross sections of 12C(2) are calculated from
| (6) |
where is the -ray energy, . is speed of light, and . are the factors stemming from the hyper-angle part. and are the internal and external components of the hyper-radial part. To execute stable calculations, quadruple precision is required. The energy-averaged reaction rates are calculated from the resultant .

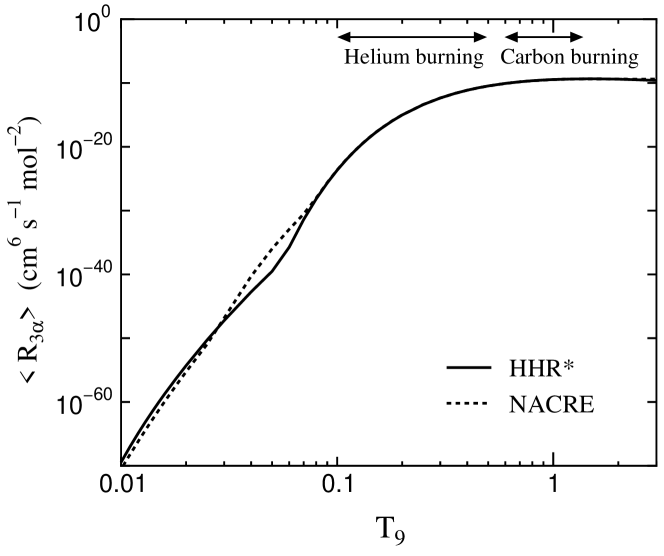
3 RESULTS
The calculated photodisintegration of 12C(2) is shown by the solid curve in Fig. 2. The prominent narrow resonance of 0 is found at MeV, and the smoothly varying non-resonant cross sections are obtained at off-resonant energies. The calculated - and -widths are eV and meV, comparable to the experimental data [4]: eV and meV. For MeV, I find – pb order of cross sections. This result is almost identical to the dotted curve of [8]. The result below MeV seems similar to CMF (dashed curve) and ACF (gray curve). On the other hand, the present result above MeV is much smaller than the values predicted by CMF and ACF. CMF has been developed below the three-body threshold, e.g. low-energy p+d reactions. The internal motion of 8Be in break-up channels is assumed to be localized within a certain range. ACF has the feature of +8Be for fm and 3 for large , and the resonance and bound states are expanded with the adiabatic basis. Judging from their theoretical approaches, most of the differences above MeV seem to stem from the internal adiabatic feature. The adiabatic approach to 8Be continuum states makes the assumed long resonant tail of 0, leading to the sequential decay process at off-resonant energies, and it might have enhanced the photodisintegration cross sections unexpectedly. The enhancement of [8] for MeV seems to be caused by the redundant propagation.
In spite of the large difference, the derived rates are found to be consistent with NACRE for , including the helium burning temperatures (see Fig. 2). In contrast, the present result is reduced by 10-4 at , because are reduced from CMF and ACF with the sequential process at MeV. Due to the strong influence of 0, the difference in for MeV cannot be found in the rates.
4 CONCLUSION
From the present calculation, I have found that the direct triple- contribution is 10-15–10-3 pb order in the photodisintegration cross sections of 12C (2) for MeV. This is far below the values predicted by CMF and ACF that include the assumed long resonant tail of 0, i.e. the sequential process. In spite of the large difference between the non-adiabatic and adiabatic cross sections, the derived reaction rates are concordant with NACRE at the helium burning temperatures. Due to the strong influence of 0 in 12C, astrophysical impact of the direct triple- process seems to be small. It would have been, however, important for theoretical nuclear physicists to understand the off-resonant cross sections, non-adiabatically, and to examine how slow the direct process is at the temperatures relevant to stellar evolution.
I thank M. Arnould and Y. Sakuragi for drawing my attention to the present subject and for their hospitality during my stay at Université Libre de Bruxelles and Osaka City University.
References
- [1] F. Hoyle, Astrophys. J. Suppl. Ser. 1 (1954) 121; E.E. Salpeter, Astrophys. J. 115 (1952) 326.
- [2] M. Katsuma, Phys. Rev. C 78 (2008) 034606; Astrophys. J. 745 (2012) 192; JPS Conf. Proc. 31 (2020) 011060.
- [3] D. Dell’Aquila et al., Phys. Rev. Lett. 119 (2017) 132501; R. Smith et al., Phys. Rev. Lett. 119 (2017) 132502.
- [4] C. Angulo, M. Arnould, M. Rayet, P. Descouvemont, D. Baye et al., Nucl. Phys. A 656 (1999) 3.
- [5] G.R. Caughlan and W.A. Fowler, Atom. Data and Nucl. Data Tables 40 (1988) 283.
- [6] K. Nomoto, F.-K. Thielemann and S. Miyaji, Astron. Astrophys. 149 (1985) 239.
- [7] D.V. Fedorov and A.S. Jensen, Phys. Lett. B 389 (1996) 631.
- [8] N.B. Nguyen, F.M. Nunes and I.J. Thompson, Phys. Rev. C 87 (2013) 054615.
- [9] S. Ishikawa, Phys. Rev. C 90 (2014) 061604; ibid. 87 (2013) 055804.
- [10] H. Suno, Y. Suzuki and P. Descouvemont, Phys. Rev. C 94 (2016) 054607.
- [11] I.J. Thompson and F. Nunes, Nuclear Reactions for Astrophysics. Cambridge Univ. Press (Cambridge), 2009.
- [12] P. Descouvemont, Theoretical Models for Nuclear Astrophysics. Nova Science Publishers (New York), 2003.
- [13] M. Katsuma, Y. Sakuragi, S. Okabe and Y. Kondō, Prog. Theor. Phys. 107 (2002) 377.
- [14] G.R. Satchler, Direct Nuclear Reactions. Oxford University Press (New York), 1983.