Direct evidence of electron-hole compensation for XMR in topologically trivial YBi
Abstract
The prediction of topological states in rare earth monopnictide compounds has attracted renewed interest. Extreme magnetoresistance (XMR) has also been observed in several nonmagnetic rare earth monopnictide compounds. The origin of XMR in these compounds could be attributed to several mechanisms, such as topologically nontrivial electronic structures and electron-hole carrier balance. YBi is a typical rare earth monopnictide exhibiting XMR, and expected to have a nontrivial electronic structure. In this work, we performed a direct investigation of the electronic structure of YBi by combining angle resolved photoemission spectroscopy and theoretical calculations. Our results show that YBi is topologically trivial without the expected band inversion, and they rule out the topological effect as the cause of XMR in YBi. Furthermore, we directly observed perfect electron-hole compensation in the electronic structure of YBi, which could be the primary mechanism accounting for the XMR.
I INTRODUCTION
Magnetoresistance (MR) is the effect of a material changing its electrical resistance when an external magnetic field is applied to it. MR in typical nonmagnetic material usually increases quadratically with the magnetic field in a low field, and saturates in a high field. In recent decade, intensive researches of topological materials has led to the discovery of numerous nonmagnetic semimetals that exhibit very large nonsaturating MRNature-2014-Ali ; PRL-2014-Pletikosic ; NC-2017-Kumar ; PRB-2016-Chen ; Science-2015-Xiong ; NP-2015-Shekhar ; NM-2015-Liang ; PRX-2015-Huang ; NP-2016-Tafti ; PNAS-2016-Tafti ; PRL-2016-Zeng ; PRL-2016-He ; PRB-2016-Kumar ; PNAS-2018-Leahy , known as extreme magnetoresistance (XMR), which has stimulated significant research interest in its underlying physical mechanisms and potential applications in electronics. While multiple mechanisms have been proposed, the origin of the XMR is still under debate. In some topological semimetals, e.g., Na3BiScience-2015-Xiong and Cd3As2NM-2015-Liang , XMR exhibiting linear field dependence is attributed to their topologically nontrivial electronic structures. On the other hand, in some Type-II Weyl semimetalsNature-2014-Ali ; PRL-2014-Pletikosic ; NC-2017-Kumar ; PRB-2016-Chen and topologically trivial semimetalsPRL-2016-Zeng ; PRL-2016-He , the compensation between electron and hole charge carriers (carrier compensation) is reported to play an important role in the origin of XMR with quadratic field dependence. Many other mechanisms have also been proposed, such as field-induced change of the Fermi surfaceSC-2014-Wang , field-induced metal-insulator transitionPRB-2016-Li , and open-orbit Fermi surface topologyPRB-2017-LouR ; PRL-2015-Jiang ; PRL-2015-Wu .
Rare earth monopnictides, i.e., RPn (R = rare earth element Sc, Y, La, Ce …; Pn = group VI element N, P, As, Sb, Bi) with rock salt crystal structure, also exhibit quadratic field-dependent XMR behaviorNP-2016-Tafti ; PNAS-2016-Tafti ; PRL-2016-Zeng ; PRL-2016-He ; PRB-2016-Kumar ; PRB-2018-Pavlosiuk ; JMCC-2018-Qian ; PRB-2019-Xu ; SR-2016-Pavlosiuk ; PRB-2017-Wu ; PRB-2018-Wang ; PRB-2019-Wu ; PRB-2017-Yang . The topological properties of the RPn family are interesting, and the origin of XMR in RPn is multiplex. A previous theoretical workarXiv-2015-Zeng , which rekindled significant research interest in RPn, predicted that lanthanum monopnictides, LaPn (Pn = N, P, As, Sb, Bi), could be topological semimetals or topological insulators as a consequence of band inversion around the X point of the bulk fcc Brillouin zone. However, later studiesPRL-2016-Zeng ; PRB-2016-Guo indicated that the band inversion was often overestimated in the calculations of the LaPn family, and only LaBi is topologically nontrivial among them. Because angle resolved photoemission spectroscopy (ARPES) has the ability to directly reveal the band structures of materials, the band topologies of numerous RPn compounds have been experimentally studiedPRL-2016-He ; PRL-2016-Zeng ; PRB-2016-Kumar ; PRB-2018-Wang ; PRB-2019-Wu ; PRB-2017-Yang ; PRB-2016-Niu ; PRB-2017-Lou ; NC-2017-Nayak ; PRM-2018-Jiang ; PRB-2017-Oinuma ; npjQM-2018-Nummy ; PRB-2018-Li-CeBi ; PRL-2018-Kuroda ; PRB-2019-Li-CeBi . Topological band inversion and nontrivial surface states were observed in compounds with group VI element Bi, such as LaBiPRB-2016-Kumar ; PRB-2016-Niu ; PRB-2017-Lou ; NC-2017-Nayak ; PRM-2018-Jiang , SmBiPRB-2019-Wu ; PRB-2018-Li-CeBi , and CeBiPRB-2018-Li-CeBi ; PRL-2018-Kuroda ; PRB-2019-Li-CeBi , while compounds with other group VI elements were confirmed to be topologically trivial without band inversionPRL-2016-He ; PRL-2016-Zeng ; PRB-2018-Wang ; PRB-2019-Wu ; PRB-2017-Yang ; PRB-2017-Oinuma ; npjQM-2018-Nummy ; PRL-2018-Kuroda . In those topologically trivial compounds, XMR behaviours are widely attributed to the classical electron-hole carrier compensation scenarioPRL-2016-He ; PRL-2016-Zeng .
Yttrium monopnictide YBi, belonging to the RPn family, has been reported to also exhibit XMR effectPRB-2018-Pavlosiuk ; JMCC-2018-Qian ; PRB-2019-Xu . Magnetotransport investigations and first-principle calculations attribute the XMR in YBi mainly to the electron-hole compensationPRB-2018-Pavlosiuk ; JMCC-2018-Qian ; PRB-2019-Xu . However, there is no direct measurement of its electronic structure to confirm electron-hole compensation in YBi. Moreover, one can not rule out the presence of the role of topology in the origin of XMR in YBi because several calculations have predicted that YBi is topologically nontrivialPRB-2018-Pavlosiuk ; JMCC-2018-Qian ; PRB-2019-Xu . In this work, we have employed ARPES to directly probe the band structure of YBi. There is no band inversions observed in the ARPES results. The combination of an ARPES experiment and first-principle calculation directly revealed that the electron and hole carriers in YBi are nearly compensated, which could be responsible for the XMR in topologically trivial YBi.
II EXPERIMENTAL
Single crystals of YBi were grown out of In flux. High-purity materials Y, Bi, and In were mixed in a molar ratio of Y : Bi : In = 1 : 1 : 20. And they were loaded into an alumina crucible in a highly-purified argon atmosphere glove box. The crucible was sealed in an evacuated quartz tube, heated to 1373 K and then cooled down to 973 K at a rate of 2 K/h. The crystals were separated from the In flux by centrifugation.
ARPES measurements were performed on beamline 9A NIMA-Matsui-BL9A ; SRL-Arita-BL9A of the Hiroshima Synchrotron Radiation Center (HiSOR), with a total energy resolution of 25 meV and a base pressure better than 5 10-9 Pa. The YBi samples for ARPES measurements were prepared in a highly-purified argon atmosphere glove-box to avoid degradation of YBi during the curing process of silver glue. Fresh surfaces for ARPES measurements were obtained by cleaving the samples in situ along the (001) plane at approximately 20 K. During ARPES measurements, the sample temperature was kept at approximately 20 K.
The band structure calculations were performed based on the density-functional theory (DFT), using an all-electron full potential WIEN2K code Blaha . The exchange correlation energy was treated using Perdew-Burke-Ernzerhof(PBE)PRL-1996-Perdew and modified Becke-Johnson (mBJ)PRL-2009-Tran functionals. The spin-orbit coupling (SOC) effect was included in all calculations. The mBJ method could overcome the band gap underestimation and band inversion overestimation using the PBE methodPRL-2016-He ; PRB-2016-Guo ; PRL-2016-Zeng ; PRB-2017-Oinuma ; SR-2018-Dey ; CP-2018-Duan-LnPn ; PRB-2018-Li-CeBi ; PRB-2019-Li-CeBi , which was also verified by our experimental results. Therefore, unless specifically indicated, the calculation results in this work were obtained using the mBJ method. During the calculations, the plane-wave cutoff parameter was selected as = 7 (product of muffin-tin radius vector and wave vector in a reciprocal lattice within the Brillouin zone). The spherical harmonic inside the muffin-tin spheres was = 10 and the Fourier expanded charge density was = 12. A set of 101010 special k-points was used for integration over the Brillouin zone of a unit cell.
III RESULTS AND DISCUSSION
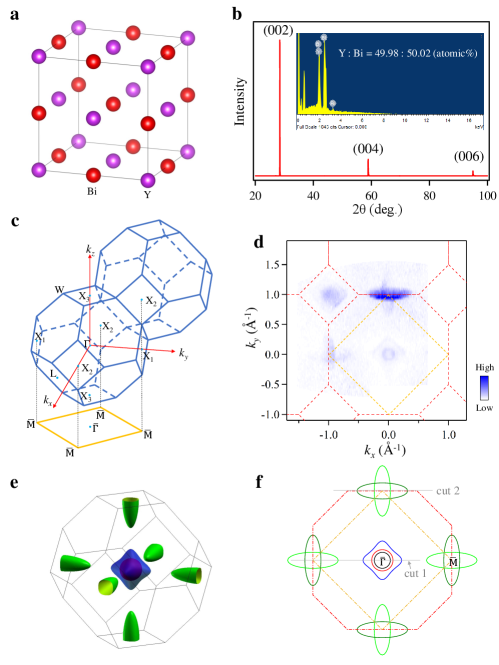
YBi crystallizes in a NaCl-type face-centered cubic (FCC) structure (space group ), as illustrated in Fig. 1(a). The x-ray diffraction (XRD) pattern on the cleaved surface of YBi after ARPES measurements is shown in Fig. 1(b). Only peaks of YBi were observed without any impurity derived ones, confirming the crystalline quality of YBi and that the cleaved surface was the (001) surface. The stoichiometry of the YBi sample was also verified by energy dispersive x-ray spectroscopy (EDX), as shown in the inset of Fig. 1(b).
Fig. 1(c) plots the three-dimensional (3D) bulk Brillouin zone and the projected (001) surface Brillouin zone of YBi. Considering the projection onto the (001) surface Brillouin zone, there are three inequivalent X points in the 3D bulk Brillouin zone. The X1 and X2 points are projected onto the surface point, while the and X3 points are projected onto the surface point. Figs. 1(d)-1(f) show the Fermi surface of YBi measured by ARPES, the calculated 3D bulk Fermi surface and its projection on the (001) surface Brillouin zone, respectively. As shown in Fig. 1(e), the bulk Fermi surface of YBi consists of two hole pockets (red inside and blue outside) at the point and one electron pocket (green) at each X point, which is a common feature in RPn materials, e.g., LaSb, YSb, and LaBiPNAS-2016-Tafti ; PRL-2016-Zeng ; PRL-2016-He ; PRB-2016-Kumar . We now consider the ARPES measured Fermi surface of YBi in Fig. 1(d), which agrees well with the projected Fermi surface by calculation in Fig. 1(f). Around the surface point, there are three hole-like pockets, where the outer two (red and blue) are projected from the point and the inner black one from the X3 point. Around the surface point, there are two intersecting ellipse-shaped electron-like pockets. The one (light green) with its long-axis along the - direction is projected from the X1 point and the other one (dark green) from the X2 point.

Fermi surface features of YBi at different coexist in one ARPES measured Fermi surface, as discussed above and shown in Fig. 1. This can be attributed to the broadening effect, which is common in the RPn compoundsPRB-2018-Wang ; PRB-2019-Wu ; PRB-2016-Niu ; PRM-2018-Jiang ; PRB-2017-Oinuma ; PRB-2018-Li-CeBi . As a result of short escape depth of photoelectrons excited by the ultraviolet photons (e.g., eV in this work), i.e. SIA-1979-Seah , corresponding uncertainty of becomes larger than , which is nearly the distance between and X points, . To further verify this, we conducted photon energy-dependent ARPES measurements on YBi. The band dispersions of YBi along the - direction obtained with various photon energies are shown in Figs. 2(a)-2(l). Except the spectral weight, the band dispersions show little change with photon energy. Fig. 2(m) shows the projected bulk band structure of YBi on the (001) surface obtained from the calculations, comprising bulk band dispersions along - over the entire range. The red curves indicate the band dispersions on , and the blue curves indicate the band dispersions on . The band dispersions from other fill the space between those from and , as shown in grey.
While the ARPES spectral intensity is clearly modulated depending on the incident photon energies as shown in Figs. 2(a)-2(l), we cannot see a systematic dependent energy shift due to the broadening effect. One can see, however, weighted spectral features, which are not contradictory to the theoretical projected results as shown in Fig. 2(m). In the ARPES image obtained using eV, as shown in Fig. 2(g), the major features with the largest spectral weights are two cone-like structures at the point, which is consistent with the blue curves in Fig. 2(m). This suggests that, if considering the photon energy vs correspondence, a photon energy of 25 eV is close to . On the one hand, the broadening effect mixes the bulk state and surface state features during the photon-energy dependent ARPES experiments, making the data analyses much more complicated. On the other hand, the sizeable broadening collects bulk state features from a broad range in one fixed ARPES photon energy measurement, making some ARPES analyses feasible without changing the photon energy. We assume that the ARPES spectral features for the corresponding to the high symmetry points should have stronger intensity because the energy bands should have the stationary points at these points. Thus, in the following, we use the ARPES spectra obtained with a fixed photon energy to analyse the band topology of YBi.

Figs. 3(a) and 3(b) show the band structures of YBi measured by ARPES along the high-symmetry directions of -- [cut 1 grey line in Fig. 1(f)] and -- [cut 2 grey line in Fig. 1(f)], respectively, where the calculated band structures are superimposed on top of them. For clarity, the calculated bulk band structures of YBi along high-symmetry lines are shown in Fig. 3(e). The ARPES spectrum shown in Fig. 3(a) agrees well with the calculation, especially the projected bulk band structures shown in Fig. 2(m). The good agreement between the ARPES measurement and the calculation can also be clearly seen from the second derivative image of Fig. 3(a), as shown in Fig. 3(c). As discussed earlier, the broadening effect in YBi allows ARPES measurements to cover the band structures across the entire range even with one photon energy. Therefore, the bands indicated by the red dashed curves of , , and are likely projected from the bulk bands along - on the plane, and the bands indicated by the yellow (purple) dashed curves of and are projected from the bulk bands along -- (--) on the plane. Similarly, for the ARPES spectrum shown in Fig. 3(b), and are projected from the bulk bands along -- on the plane, and and are projected from those along - in the second bulk Brillouin zone. For RPn compounds, the DFT calculations using the PBE functional usually result in the overestimation of band anti-crossing, and result in a misleading prediction of nontrivial topologyPRL-2016-He ; PRB-2016-Guo ; PRL-2016-Zeng ; PRB-2017-Oinuma ; SR-2018-Dey ; CP-2018-Duan-LnPn ; PRB-2018-Li-CeBi ; PRB-2019-Li-CeBi , which is also the case for YBiPRB-2018-Pavlosiuk ; JMCC-2018-Qian ; PRB-2019-Xu , as shown in Fig. 3(f). In contrast, calculations using the mBJ functional agree well with the experimental results. Thus, by combining the ARPES experimental and theoretical calculation results, one can conclude that no anti-crossing of bands and no band inversion exist along the bulk - direction.
| Type | Theoretical calculation |
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||||
| hole | 0.0479 | 3.86 | 0.0445 | 3.59 | |||||||
| hole | 0.0165 | 1.33 | 0.0156 | 1.25 | |||||||
| 111Note: There are three pockets in one Brillouin zone, so the volume and corresponding carrier density of the pocket was multiplied by 3. | electron | 0.0647 | 5.22 | 0.0597 | 4.82 | ||||||
As the band inversion is absent, YBi is topologically trivial, and hence the XMR of YBi could be a result of electron-hole compensation, which resembles that in LaSbPRL-2016-Zeng and YSbPRL-2016-He . To verify this, we calculated the electron and hole carrier densities. For convenience, we hereafter label the two hole pockets located around the point [see Fig. 1(e)] as and (for outer and inner, respetively), and the electron pocket located around the point as . The carrier densities were calculated based on the calculation of the enclosed volumes of the corresponding Fermi surface pockets, and the results are shown in Table 1. From pure theoretical calculation, the enclosed volumes of the , , and Fermi surface pockets in one Brillouin zone are 0.0479, 0.0165, and 0.0647 Å-3, corresponding to carrier densities of , , and cm-3, respectively, suggesting a perfect electron-hole compensation. In order to improve the carrier density calculation accuracy, we modified the theoretical calculations using the ARPES measured Fermi momenta at high-symmetry lines. The corrected volumes of , , and are 0.0445, 0.0156, and 0.0597 Å-3, corresponding to carrier densities of , , and cm-3, respectively, and the ratio of electron-to-hole carrier density is . Therefore, YBi is a compensated semimetal with nearly perfect electron-hole carrier balance, which could be the origin of the XMR in YBi.

Finally, to further study the origin of the bands and and further support the previous discussion that they are projected from the bulk bands along --, we conducted polarization-dependent ARPES experiments on YBi. Fig. 4(a) shows the experimental setup of the polarization-dependent ARPES. Figs. 4(b) and 4(c) show the band structures of YBi along -- measured by -polarization and -polarization photons, respectively. Based on the matrix element effect of ARPES, the even orbitals, which are even with respect to the mirror plane ( plane), could only be probed by -polarization photons, while the odd orbitals could only be probed by -polarization photons. Therefore, the bands with contributions from the Bi orbitals and and the Y orbitals , , and could only be observed by -polarization photons, while the bands with contributions from the Bi orbital and Y orbitals and could only be observed by -polarization photons. As shown in Figs. 4(d)-4(k), the band is mainly contributed by the odd orbital Y , and could mainly be probed by the -polarization photons. In contrast, the band is contributed by both even and odd orbitals, and could be probed by both types of polarization. These results are consistent with the ARPES spectra shown in Figs. 4(b) and 4(c), supporting that the bands and are projected from the bulk bands along -- and are not the features of surface states.
IV CONCLUSION
In summary, the electronic structures of YBi were comprehensively investigated by means of ARPES in combination with the theoretical DFT calculations. The broadening effect in YBi is sizeable, and it collects bulk band features across over the entire range in a fixed-photon-energy ARPES spectra. Combining the ARPES experimental and theoretical calculation results, we find that band inversions are absent in YBi, leading to a topologically trivial electronic structure. The electron and hole carrier densities in YBi are almost perfectly balanced, indicating that YBi is a compensated semimetal, which could be the origin of the XMR in YBi.
V ACKNOWLEDGMENTS
This work is supported by the National Key Research and Development Program of China (No. 2016YFA0300600, No. 2017YFA0303600, and 2017YFA0302901 ), the National Natural Science Foundation of China (Grant Nos. 11674367,11974364, U2032207, and U2032204), the Natural Science Foundation of Zhejiang, China (Grant No. LZ18A040002), the Ningbo Science and Technology Bureau (Grant No. 2018B10060). S.L.H. would like also to acknowledge the Ningbo 3315 program. Y.G.S. would like also to acknowledge the Strategic Priority Research Program (B) of the Chinese Academy of Sciences (No. XDB33000000), the K. C. Wong Education Foundation (GJTD-2018-01). We thank the Hiroshima Synchrotron Radiation Center for providing beamtime ( project No. 19BG025).
Author contributions
S.L.H. and S.Z.X conceived the project. Y.L. and Y.G.S. grew the samples. S.Z.X., X.F.Y., S.J. Z., and W.L. carried out the ARPES measurements. Y.X.L., X.X.W. and B.L. performed the theoretical calculations. S.L.H. and S.Z.X. analyzed the data and wrote the paper. All authors discussed the results and commented on the manuscript.
References
- (1) M. N. Ali, J. Xiong, S. Flynn, J. Tao, Q. D. Gibson, L. M. Schoop, T. Liang, N. Haldolaarachchige, M. Hirschberger, N. P. Ong, and R. J. Cava, Large, non-saturating magnetoresistance in WTe2, Nature 514, 205 (2014).
- (2) I. Pletikosić, M. N. Ali, A. V. Fedorov, R. J. Cava, and T. Valla, Electronic Structure Basis for the Extraordinary Magnetoresistance in WTe2, Phys. Rev. Lett. 113, 216601 (2014).
- (3) N. Kumar, Y. Sun, N. Xu, K. Manna, M. Yao, V. Süss, I. Leermakers, O. Young, T. Förster, M. Schmidt, H. Borrmann, B. Yan, U. Zeitler, M. Shi, C. Felser, C. Shekhar, Extremely high magnetoresistance and conductivity in the type-II Weyl semimetals WP2 and MoP2, Nature Communications 8, 1642 (2017).
- (4) F. C. Chen, H. Y. Lv, X. Luo, W. J. Lu, Q. L. Pei, G. T. Lin, Y. Y. Han, X. B. Zhu, W. H. Song, Y. P. Sun, Extremely large magnetoresistance in the type-II Weyl semimetal MoTe2, Phys. Rev. B. 94, 235154 (2016).
- (5) J. Xiong, S. K. Kushwaha, T. Liang, J. W. Krizan, M. Hirschberger, W. Wang, R. J. Cava, and N. P. Ong, Evidence for the chiral anomaly in the Dirac semimetal Na3Bi, Science 350 413 (2015).
- (6) C. Shekhar, A. K. Nayak, Y. Sun, M. Schmidt, M. Nicklas, I. Leermakers, U. Zeitler, Y. Skourski, J. Wosnitza, Z. Liu, Y. Chen, W. Schnelle, H. Borrmann, Y. Grin, C. Felser, and B. Yan, Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP, Nature Physics 11, 645 (2015).
- (7) T. Liang, Q. Gibson, M. N. Ali, M. Liu, R. J. Cava, and N. P. Ong, Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2, Nature Materials 14, 280 (2015).
- (8) X. Huang, L. Zhao, Y. Long, P. Wang, D. Chen, Z. Yang, H. Liang, M. Xue, H. Weng, Z. Fang, X. Dai, and G. Chen, Observation of the Chiral-Anomaly-Induced Negative Magnetoresistance in 3D Weyl Semimetal TaAs, Phys. Rev. X 5, 031023 (2015).
- (9) F. F. Tafti, Q. D. Gibson, S. K. Kushwaha, N. Haldolaarachchige, and R. J. Cava, Resistivity plateau and extreme magnetoresistance in LaSb, Nature Physics 12, 272 (2016).
- (10) F. F. Tafti, Q. Gibson, S. Kushwaha, J. W. Krizan, N. Haldolaarachchige, and R. J. Cava, Temperature–field phase diagram of extreme magnetoresistance, PNAS 113, E3475 (2016).
- (11) L.-K. Zeng, R. Lou, D.-S. Wu, Q. N. Xu, P.-J. Guo, L.-Y. Kong, Y.-G. Zhong, J.-Z. Ma, B.-B. Fu, P. Richard, P. Wang, G. T. Liu, L. Lu, Y.-B. Huang, C. Fang, S.-S. Sun, Q. Wang, L. Wang, Y.-G. Shi, H. M. Weng, H.-C. Lei, K. Liu, S.-C. Wang, T. Qian, J.-L. Luo, and H. Ding, Compensated Semimetal LaSb with Unsaturated Magnetoresistance, Phys. Rev. Lett. 117, 127204 (2016).
- (12) J. He, C. Zhang, N. J. Ghimire, T. Liang, C. Jia, J. Jiang, S. Tang, S. Chen, Y. He, S.-K. Mo, C. C. Hwang, M. Hashimoto, D. H. Lu, B. Moritz, T. P. Devereaux, Y. L. Chen, J. F. Mitchell, and Z.-X. Shen, Distinct Electronic Structure for the Extreme Magnetoresistance in YSb, Phys. Rev. Lett. 117, 267201 (2016).
- (13) N. Kumar, C. Shekhar, S.-C. Wu, I. Leermakers, O. Young, U. Zeitler, B. Yan, and C. Felser, Observation of pseudo-two-dimensional electron transport in the rock salt-type topological semimetal LaBi, Phys. Rev. B 93, 241106 (2016).
- (14) I. A. Leahy, Y.-P. Lin, P. E. Siegfried, A. C. Treglia, J. C. W. Song, R. M. Nandkishore, and M. Lee, Nonsaturating large magnetoresistance in semimetals, PNAS 115, 10570 (2018).
- (15) K. Wang, D. Graf, L. Li, L. Wang, and C. Petrovic, Anisotropic giant magnetoresistance in NbSb2, Scientific Reports, 4, 7328 (2014).
- (16) Y. Li, L. Li, J. Wang, T. Wang, X. Xu, C. Xi, C. Cao, and J. Dai, Resistivity plateau and negative magnetoresistance in the topological semimetal TaSb2, Phys. Rev. B 94, 121115 (2016).
- (17) R. Lou, Y. F. Xu, L.-X. Zhao, Z.-Q. Han, P.-J. Guo, M. Li, J.-C. Wang, B.-B. Fu, Z.-H. Liu, Y.-B. Huang, P. Richard, T. Qian, K. Liu, G.-F. Chen, H. M. Weng, H. Ding, and S.-C. Wang, Observation of open-orbit Fermi surface topology in the extremely large magnetoresistance semimetal MoAs2, Phys. Rev. B 96, 241106 (2017).
- (18) J. Jiang, F. Tang, X. C. Pan, H. M. Liu, X. H. Niu, Y. X. Wang, D. F. Xu, H. F. Yang, B. P. Xie, F. Q. Song, P. Dudin, T. K. Kim, M. Hoesch, P. K. Das, I. Vobornik, X. G. Wan, and D. L. Feng, Signature of Strong Spin-Orbital Coupling in the Large Nonsaturating Magnetoresistance Material WTe2, Phys. Rev. Lett. 115, 166601 (2015).
- (19) Y. Wu, N. H. Jo, M. Ochi, L. Huang, D. Mou, S. L. Bud’ko, P. C. Canfield, N. Trivedi, R. Arita, A. Kaminski, Temperature-Induced Lifshitz Transition in WTe2. Phys. Rev. Lett. 115, 166602 (2015).
- (20) O. Pavlosiuk, P. Swatek, P. Wiśniewski, Giant magnetoresistance, three-dimensional Fermi surface and origin of resistivity plateau in YSb semimetal, Scientific Reports 6, 1 (2016).
- (21) F. Wu, C. Y. Guo, M. Smidman, J. L. Zhang, H. Q. Yuan, Large magnetoresistance and Fermi surface topology of PrSb, Phys. Rev. B. 96, 125122 (2017).
- (22) O. Pavlosiuk, P. Swatek, D. Kaczorowski, P. Wiśniewski, Magnetoresistance in LuBi and YBi semimetals due to nearly perfect carrier compensation, Phys. Rev. B. 97, 235132 (2018).
- (23) B. Qian, F. Tang, Y. R. Ruan, Y. Fang, Z. D. Han, X. F. Jiang, J.-M. Zhang, S. Y. Chen, D. H. Wang, Extremely large magnetoresistance in the nonmagnetic semimetal YBi, J. Mater. Chem. C. 6, 10020 (2018).
- (24) C. Q. Xu, B. Li, M. R. van Delft, W. H. Jiao, W. Zhou, B. Qian, N. D. Zhigadlo, D. Qian, R. Sankar, N. E. Hussey, X. Xu, Extreme magnetoresistance and pressure-induced superconductivity in the topological semimetal candidate YBi, Phys. Rev. B. 99, 024110 (2019).
- (25) Y.-Y. Wang, H. Zhang, X.-Q. Lu, L.-L. Sun, S. Xu, Z.-Y. Lu, K. Liu, S. Zhou, T.-L. Xia, Extremely large magnetoresistance and electronic structure of TmSb, Phys. Rev. B. 97, 085137 (2018).
- (26) Z. Wu, F. Wu, P. Li, C. Guo, Y. Liu, Z. Sun, C.-M. Cheng, T.-C. Chiang, C. Cao, H. Yuan, Y. Liu, Probing the origin of extreme magnetoresistance in Pr/Sm mono-antimonides/bismuthides, Phys. Rev. B. 99, 035158 (2019).
- (27) H.-Y. Yang, T. Nummy, H. Li, S. Jaszewski, M. Abramchuk, D. S. Dessau, F. Tafti, Extreme magnetoresistance in the topologically trivial lanthanum monopnictide LaAs, Phys. Rev. B. 96, 235128 (2017).
- (28) M. Zeng, C.Fang, G. Chang, Y.-A. Chen, T. Hsieh, A. Bansil, H. Lin, and L. Fu, Topological semimetals and topological insulators in rare earth monopnictides, arXiv:1504.03492.
- (29) P.-J. Guo, H.-C. Yang, B.-J. Zhang, K. Liu, and Z.-Y. Lu, Charge compensation in extremely large magnetoresistance materials LaSb and LaBi revealed by first-principles calculations, Phys. Rev. B 93, 235142 (2016).
- (30) X. H. Niu, D. F. Xu, Y. H. Bai, Q. Song, X. P. Shen, B. P. Xie, Z. Sun, Y. B. Huang, D. C. Peets, and D. L. Feng, Presence of exotic electronic surface states in LaBi and LaSb, Phys. Rev. B 94, 165163 (2016).
- (31) R. Lou, B.-B. Fu, Q. N. Xu, P.-J. Guo, L.-Y. Kong, L.-K. Zeng, J.-Z. Ma, P. Richard, C. Fang, Y.-B. Huang, S.-S. Sun, Q. Wang, L. Wang, Y.-G. Shi, H. C. Lei, K. Liu, H. M. Weng, T. Qian, H. Ding, and S.-C. Wang, Evidence of topological insulator state in the semimetal LaBi, Phys. Rev. B 95, 115140 (2017).
- (32) J. Nayak, S.-C. Wu, N. Kumar, C. Shekhar, S. Singh, J. Fink, E. E. D. Rienks, G. H. Fecher, S. S. P. Parkin, B. Yan, and C. Felser, Multiple Dirac cones at the surface of the topological metal LaBi, Nature Communications 8, 1 (2017).
- (33) J. Jiang, N. B. M. Schröter, S.-C. Wu, N. Kumar, C. Shekhar, H. Peng, X. Xu, C. Chen, H. F. Yang, C.-C. Hwang, S.-K. Mo, C. Felser, B. H. Yan, Z. K. Liu, L. X. Yang, and Y. L. Chen, Observation of topological surface states and strong electron/hole imbalance in extreme magnetoresistance compound LaBi, Phys. Rev. Materials 2, 024201 (2018).
- (34) H. Oinuma, S. Souma, D. Takane, T. Nakamura, K. Nakayama, T. Mitsuhashi, K. Horiba, H. Kumigashira, M. Yoshida, A. Ochiai, T. Takahashi, and T. Sato, Three-dimensional band structure of LaSb and CeSb: Absence of band inversion, Phys. Rev. B 96, 041120 (2017).
- (35) T. J. Nummy, J. A. Waugh, S. P. Parham, Q. Liu, H.-Y. Yang, H. Li, X. Zhou, N. C. Plumb, F. F. Tafti, D. S. Dessau, Measurement of the atomic orbital composition of the near-fermi-level electronic states in the lanthanum monopnictides LaBi, LaSb, and LaAs, npj Quantum Materials 3, 1 (2018).
- (36) P. Li, Z. Wu, F. Wu, C. Cao, C. Guo, Y. Wu, Y. Liu, Z. Sun, C.-M. Cheng, D.-S. Lin, F. Steglich, H. Yuan, T.-C. Chiang, and Y. Liu, Tunable electronic structure and surface states in rare-earth monobismuthides with partially filled shell, Phys. Rev. B 98, 085103 (2018).
- (37) K. Kuroda, M. Ochi, H. S. Suzuki, M. Hirayama, M. Nakayama, R. Noguchi, C. Bareille, S. Akebi, S. Kunisada, T. Muro, M. D. Watson, H. Kitazawa, Y. Haga, T. K. Kim, M. Hoesch, S. Shin, R. Arita, T. Kondo, Experimental Determination of the Topological Phase Diagram in Cerium Monopnictides, Phys. Rev. Lett. 120, 086402 (2018).
- (38) P. Li, Z. Wu, F. Wu, C. Guo, Y. Liu, H. Liu, Z. Sun, M. Shi, F. Rodolakis, J. L. McChesney, C. Cao, H. Yuan, F. Steglich, and Y. Liu, Large Fermi surface expansion through anisotropic mixing of conduction and electrons in the semimetallic Kondo lattice CeBi, Phys. Rev. B 100, 155110 (2019).
- (39) T. Matsui, H. Sato, K. Shimada, M. Arita, S. Senba, H. Yoshida, K. Shirasawa, M. Morita, A. Hiraya, H. Namatame, and M. Taniguchi, 3m Off-Plane Eagle Monochromator at the Helical Undulator Beamline of HiSOR, Nucl. Instr. Meth. A 467-468, 537-540 (2001).
- (40) M. Arita, K. Shimada, H. Namatame, and M. Taniguchi, High-Resolution and Low-Temperature Photoemission Spectroscopy at the HiSOR Helical-Undulator Beamline, Surf. Rev. Lett. 9, 535 (2002).
- (41) P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, and J. Luitz, WIEN2k: An Augmented Plane Wave Local Orbitals Program for Calculating Crystal Properties (Technische Universitt Wien, 2001).
- (42) J. P. Perdew, S. Burke, and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996).
- (43) F. Tran, and P. Blaha, Phys. Rev. Lett. 102, 226401 (2009).
- (44) U. Dey, M. Chakraborty, A. Taraphder, and S. Tewari, Bulk band inversion and surface Dirac cones in LaSb and LaBi: Prediction of a new topological heterostructure, Scientific Reports 8, 1 (2018).
- (45) X. Duan, F. Wu, J. Chen, P. Zhang, Y. Liu, H. Yuan, and C. Cao, Tunable electronic structure and topological properties of LnPn (Ln=Ce, Pr, Sm, Gd, Yb; Pn=Sb, Bi), Commun. Phys. 1, 71 (2018).
- (46) M. P. Seah and W. A. Dench, Quantitative Electron Spectroscopy of Surfaces: A Standard Data Base for Electron Inelastic Mean Free Paths in Solids, Surf. Interface Anal. 1, 2 (1979).