Direct and ultrafast probing of quantum many-body interaction and Mott-insulator transition through coherent two-dimensional spectroscopy

Introduction– Important physical systems and materials often consist of a macroscopically large number of atoms, molecules, and electrons. The interaction between constituent particles can dictate various physical properties of the system, including, for example, the electrical and thermal transports and the magnetic and optical properties. However, in some metals and semiconductors, owing to the screening of the Coulomb interaction between electrons, their low-energy behaviors are similar to those of a system of non-interacting particles. These systems can be described by Landau’s Fermi liquid theory Landau56 . In contrast, there also exist strongly correlated electronic systems beyond the Fermi liquid theory, in which the interaction between electrons cannot be ignored. Examples include the Luttinger liquid in one dimension Tomonaga50 ; Luttinger63 , heavy fermionic systems Stewart01 , and systems near critical points such as the Mott-insulator phase transition Mott68 ; Imada98 . The interparticle interaction can also result in exotic phenomena such as superfluidity and superconductivity Leggett-book .

Meanwhile, continual progress in the development of laser-pulse techniques has enabled a faster manipulation and measurement of the physical and chemical properties of electronic, atomic, and molecular systems Krausz09 . This allowed us to observe intriguing nonequilibrium phenomena, such as light-induced superconductivity Fausti11 ; Cavalleri18 , ultrafast spintronics Kimel05 ; Kirilyuk10 , and the Floquet engineering of electronic band topology Wang13 ; McIver20 . In this Letter, we propose a method to investigate the interaction between particles directly in quantum many-body systems on an ultrafast timescale using coherent two-dimensional (2D) spectroscopy. Coherent multi-dimensional, especially 2D, spectroscopy has been widely used to study electronic excitation (exciton) and vibration dynamics in molecular and semiconductor systems Mukamel-book ; Mukamel00 ; Jonas03 ; Cho08 ; Cho-book ; Abramavicius09 ; Hamm-book ; Cundiff09 ; Cohen11 . More recently, intersubband electronic excitations in quantum wells Kuehn11 , carrier dynamics in graphene Woerner13 , spin-wave Lu17 and fractional excitations Wan19 ; Choi20 in magnetic materials, marginal Fermi glass Mahmood20 , and high-temperature superconductors Novelli20 have been studied.

Here, we calculate the coherent 2D spectrum of an interacting quantum many-body system of spin-1/2 fermions (see Figs. 1a,b), which can be, for example, electrons moving in a crystal lattice or ultracold atoms/molecules moving in an artificial lattice. We observe that a system of non-interacting particles would display a 2D spectrum with only peaks lying on the diagonal axis. This is attributed to the fact that the quasimomentum of the particles is a good quantum number in the absence of interparticle interaction. Moreover, because of the conservation of momentum in the light-matter interaction, two optical transitions with different quasi-momenta are not coupled to each other. In contrast, if the interaction between particles is sufficiently strong, off-diagonal peaks emerge in the 2D spectrum. Thus, this can be used as a direct probe of a nonnegligible interparticle interaction. In an interacting quantum many-body system, quasimomentum states are no longer energy eigenstates of the system. Consequently, two transitions with different optical excitation and emission frequencies can be effectively coupled to each other, leading to the emergence of off-diagonal peaks. However, if the interaction strength is increased further, when the system approaches the Mott-insulating phase, in which exactly one particle is localized at each lattice site as the hopping of particles between neighboring sites becomes energetically unfavorable, all the peaks in the 2D spectrum coalesce into a single diagonal peak at the frequency of the excitation band. Consequently, coherent 2D spectroscopy can be used to investigate the entire range of interaction strength from weak to moderate and strong interaction regimes. We also investigate the coherent 2D spectrum of the system when the interaction energy relative to the kinetic energy varies with time. The evolution of the 2D spectrum as a function of the time delay $t_{2}$ between the second and third pulses can provide us with important information on the ultrafast time variation of the interaction.

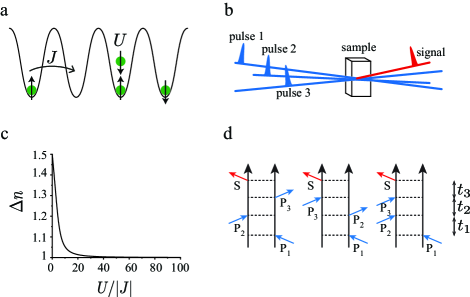
System– Consider the Hubbard model of a system of spin-1/2 fermionic particles moving in a lattice, whose Hamiltonian for the ground-state band is given by

where $\hat{c}_{j,\sigma}$ denotes the annihilation operator of a particle with spin $\sigma$ located at the $j$th site, and $\hat{n}_{j,\sigma}=\hat{c}_{j,\sigma}^{\dagger}\hat{c}_{j,\sigma}$ is the particle number operator. The parameters $J$ and $U$ represent the hopping amplitude of the particle between neighboring sites and the on-site interaction between two particles located at the same site, respectively. Here, $\langle...\rangle$ denotes a pair of nearest neighboring sites, and h.c. stands for Hermitian conjugate. Here, we restrict our consideration to the case of the half-filling factor, i.e., the number of particles is equal to the number of lattice sites. Furthermore, the total magnetization of the system is zero, i.e., the number of particles with spin-up is equal to that of particles with spin-down.

For a weakly interacting system with $|J|\gg U$, the motions of particles are almost independent of one another (except for the Pauli exclusive principle) and their wavefunctions are delocalized over different sites in the lattice. In contrast, in the strongly interacting limit $|J|\ll U$, the system would be in the Mott insulating phase, where each lattice site is occupied by exactly one particle as the hopping of particles between neighboring sites is energetically unfavorable. This transition is reflected by the change in the variance $\Delta n=\langle\psi_{0}|\hat{n}_{j}^{2}|\psi_{0}\rangle$ of the number of particles per site for the quantum many-body ground state $|\psi_{0}\rangle$. This is shown in Fig. 1c as a function of $U/|J|$ for a system of $N=6$ particles in a one-dimensional lattice. Here, $\hat{n}_{j}=\hat{n}_{j,\uparrow}+\hat{n}_{j,\downarrow}$. The variance is maximum for $U=0$, at which $\Delta n=1.5$; it decreases with increasing interaction strength and approaches $\Delta n=1$ for a sufficiently strong interaction.

We consider a one-dimensional system with the periodic boundary condition. As for the optical transitions caused by the light-matter interactions with the laser pulses in coherent 2D spectroscopy, we consider a Hubbard model with two energy bands: the ground-state and first excited bands. The total Hamiltonian of the system is given by

where $\alpha,\beta=(\mathrm{g/e};\uparrow/\downarrow)$. Here, $J_{\mathrm{g}}$ and $J_{\mathrm{e}}$ denote the hopping amplitudes of particles between neighboring sites in the ground and excited bands, respectively. Owing to the difference in the spatial confinement of the wavefunction of the particle at the lattice sites between the two bands, $J_{\mathrm{g}}\not=J_{\mathrm{e}}$. In general, the on-site interaction should also depend on the spins of the particles and on whether they are in the ground or excited band; however, for simplicity, we assume that the on-site interaction is characterized by a single variable parameter, namely $U_{\alpha\beta}=U$. By shifting the origin of the 2D spectrum by an amount equal to the excitation energy $\epsilon_{\mathrm{eg}}$, we can set $\epsilon_{\mathrm{eg}}=0$ without loss of generality. The periodic boundary condition indicates that $j=N$ is equivalent to $j=0$.

The optical signal measured via coherent 2D spectroscopy is proportional to $iP^{(3)}(t)$, where $P^{(3)}(t)$ is the time-dependent third-order polarization of the system. It can be expressed as a convolution of the third-order response function $R^{(3)}(t_{1},t_{2},t_{3})$ and the electric fields of the lasers Mukamel-book ; Hamm-book

As the wavelength of the laser is typically much larger than the lattice constant of the crystal lattice for electrons, the electric field can be considered homogeneous over a large number of lattice sites. A similar nanoscale artificial lattice for ultracold atoms can be realized by using nanoplasmonic systems Gullans12 , photonic crystals Tudela15 , time-periodic modulations Nascimbene15 , and superconductors Isart13 .

In the impulsive limit of the laser pulses, where the electric field is given by a sum of three Dirac’s delta functions, the polarization is proportional to the nonlinear response function $R^{(3)}(t_{1},t_{2},t_{3})$ , where $t_{1}$, $t_{2}$, and $t_{3}$ are the time intervals between the laser pulses and the emitted signal (see Fig. 1). The nonlinear response function and emitted signal are generated by various processes, each of which involves four interactions between light and matter. These processes can be grouped into three categories according to the direction of the emitted signal: rephasing, non-rephasing, and double quantum coherence. The three types of signals can generally provide different types of information about the energy levels and dynamics of the system. In this study, either rephasing or non-rephasing signals can be used as we concentrate on the interaction-induced emergence of off-diagonal peaks. The rephasing or photon-echo signal is detected in the direction given by the vector $\mathbf{k}_{\mathrm{r}}=-\mathbf{k}_{1}+\mathbf{k}_{2}+\mathbf{k}_{3}$. The light-matter interactions for the processes included in the rephasing signal are illustrated by the double-sided Feynman diagram (Fig. 1d). The corresponding rephasing third-order response function $R_{\mathrm{r}}^{(3)}(t_{1},t_{2},t_{3})$ can be expressed in terms of the Liouville-space operators as Mukamel-book

where $\hat{\rho}_{0}=|\psi_{0}\rangle\langle\psi_{0}|$ is the density operator for the quantum many-body ground state of the system, and the transition dipole moment operators $\hat{\mu}_{\leftarrow/\rightarrow}$ are given by

Here, $\mu_{\mathrm{eg}}$ is the transition dipole moment between the ground and excited bands, and $\mu_{\mathrm{ge}}=\mu_{\mathrm{eg}}^{*}$. The superoperators in Liouville space are defined as $\hat{\mu}^{\times}\hat{\rho}=\hat{\mu}\hat{\rho}-\hat{\rho}\hat{\mu}$ and $\mathcal{G}(t)\hat{\rho}=e^{-i\hat{H}t/\hbar}\hat{\rho}e^{i\hat{H}t/\hbar}$, where $\hat{H}$ is the quantum many-body Hamiltonian of the system given in Eq. (2). A small dephasing rate $\kappa$ is introduced to account for the dephasing of the quantum coherence between the ground and an excited states during the time intervals $t_{1}$ and $t_{3}$. The coherent 2D rephasing spectrum is obtained by making a Fourier transformation of the emitted signal $S(t_{1},t_{2},t_{3})$ with respect to the time intervals $t_{1}$ and $t_{3}$,

In the following 2D spectra, the real part of $S(\omega_{1},t_{2},\omega_{3})$ is plotted as a function of $-\omega_{1}$ and $\omega_{3}$.

We first consider a system of noninteracting particles, namely $U=0$. The coherent 2D rephasing spectrum for $N=18$ is shown in Fig. 2. Here, the system’s parameters were considered as follows: $J_{\mathrm{e}}/J_{\mathrm{g}}=2$ and $\hbar\kappa/|J_{\mathrm{g}}|=0.01$. The time delay was set to $t_{2}=0$. It is evident that all the peaks lie on the diagonal axis $\omega_{3}=-\omega_{1}$. The number of peaks increases with the lattice size. In the thermodynamic limit ($N\to\infty$), the peaks are distributed on the segment $0\leq\hbar\omega_{1}\leq 2(J_{\mathrm{e}}-J_{\mathrm{g}})$ of the diagonal axis. Note that the origin of the 2D spectrum was shifted by the excitation energy between the ground and excited bands, namely $\tilde{\omega}_{1}=\omega_{1}+\epsilon_{\mathrm{eg}}$ and $\tilde{\omega}_{3}=\omega_{3}-\epsilon_{\mathrm{eg}}$. Thus, the origin $\tilde{\omega}_{1}=\tilde{\omega}_{3}=0$ of the 2D spectrum corresponds to $\omega_{3}=-\omega_{1}=\epsilon_{\mathrm{eg}}$.

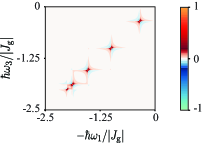
In the absence of interaction between particles, quasi-momentum is a good quantum number. The single-particle energy eigenstates in the ground and excited bands are characterized by a wavevector $k$ (within the Brillouin zone) with the corresponding energy eigenvalues given by $\epsilon_{k}^{\mathrm{g}}=-2J_{\mathrm{g}}\cos\left(2\pi k/N\right)$ and $\epsilon_{k}^{\mathrm{e}}=\epsilon_{eg}-2J_{\mathrm{e}}\cos\left(2\pi k/N\right)$ with $k=-N/2,\cdots,N/2$. Owing to the conservation of momentum in the light-matter interaction, optical transitions can only occur between pairs of single-particle energy eigenstates in the ground and excited bands with the same wavevector. As these transitions are not coupled to one another, only diagonal peaks appear in the coherent 2D rephasing spectrum. With the half-filling factor, the quantum many-body ground state of the system contains all the single-particle energy eigenstates of $\hat{H}_{\mathrm{g}}$ with the wavevectors $-N/4\leq k\leq N/4$ (for $J_{\mathrm{g}}>0$). The corresponding transition energy satisfies $\epsilon_{eg}-2(|J_{\mathrm{e}}|-|J_{\mathrm{g}}|)\leq\epsilon_{k}^{\mathrm{e}}-\epsilon_{k}^{\mathrm{g}}\leq\epsilon_{eg}$.

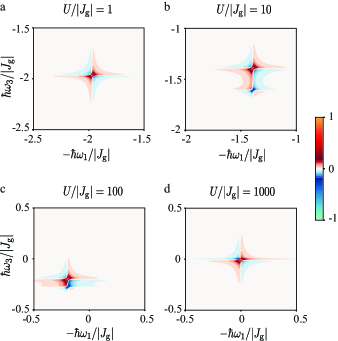
Next, we consider a system of interacting particles, namely $U>0$ (repulsive interaction). As the computational cost increases exponentially with the system size, we restrict the computation to a small system of $N=2$ lattice sites. The coherent 2D rephasing spectra for different interaction strengths (normalized by the hopping amplitude $|J_{\mathrm{g}}|$) are shown in Fig. 3. The other parameters of the system are the same as in the case of noninteracting particles. As the interparticle interaction becomes stronger, an off-diagonal peak starts to emerge in addition to the diagonal peak. The off-diagonal peak persists up to an interaction of $U/|J_{\mathrm{g}}|\simeq 100$. Finally, at the strongly interacting limit $U/|J_{\mathrm{g}}|\simeq 1000$, all the peaks coalesce into a single diagonal peak at the origin of the 2D spectrum. In the presence of the interparticle interaction, the quantum many-body ground state cannot be expressed by a collection of single-particle states. Consequently, the optical transitions become effectively coupled to one another, leading to the emergence of off-diagonal peaks. In the strongly interacting limit, the quantum many-body ground state is in the Mott insulating phase with each lattice site being occupied by exactly one particle. The optical excitation of each particle occurs locally with an excitation energy equal to $\epsilon_{\mathrm{eg}}$. This results in a single diagonal peak at the origin of the 2D spectrum.

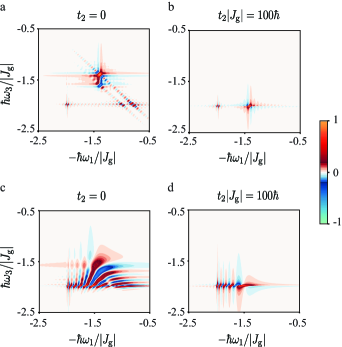
Finally, we consider the case of a time-varying interaction $U(t)$ and investigate the coherent 2D spectrum as a function of the time delay $t_{2}$. If the interaction is switched off abruptly at time $\tau$ after the incidence of the first laser pulse, i.e., $U(t)=U_{0}$ for $t\leq\tau$ and $U(t)=0$ for $t>\tau$, the coherent 2D spectra for different time delays are shown in Figs. 4a, b. Here, the initial interaction strength is $U_{0}/|J_{\mathrm{g}}|=10$, the switching time is $\tau|J_{\mathrm{g}}|=100\hbar$, and the other parameters of the system are the same as in the case of a time-independent interaction. The 2D spectrum is observed to change from $t_{2}=0$ to $t_{2}=\tau$, and subsequently, it remains almost unchanged. It can be observed that, at $t_{2}=0$, the pair of a diagonal peak at $\hbar\omega_{1}=-\hbar\omega_{3}\simeq 1.4|J_{\mathrm{g}}|$ and an off-diagonal peak at $\hbar\omega_{1}\simeq 1.4|J_{\mathrm{g}}|,\hbar\omega_{3}\simeq-1.6|J_{\mathrm{g}}|$, which is the 2D spectrum for constant $U/|J_{\mathrm{g}}|=10$, is extended along the diagonal direction of $\omega_{1}=\omega_{3}$ to $\hbar\omega_{3}=-2|J_{\mathrm{g}}|$. The spectrum also contains a small diagonal peak at $\hbar\omega_{1}=-\hbar\omega_{3}=2|J_{\mathrm{g}}|$, which is the 2D spectrum for a constant $U=0$. The 2D spectrum changes with the variable time delay. At $t_{2}=\tau$, it is composed of a small diagonal peak at $\hbar\omega_{1}=-\hbar\omega_{3}=2|J_{\mathrm{g}}|$, an off-diagonal peak at $\hbar\omega_{1}\simeq 1.4|J_{\mathrm{g}}|,\hbar\omega_{3}=-2|J_{\mathrm{g}}|$, and a connection between them.

If the interaction is switched off steadily over a time period of $\tau$ after the incidence of the first laser pulse, i.e., $U(t)=U_{0}(1-t/\tau)$ for $t\leq\tau$ and $U(t)=0$ for $t>\tau$, the coherent 2D spectra for different time delays are shown in Figs. 4c, d. A fringe pattern emerges in the 2D spectrum, which should be attributed to the continuous time variation of the interaction strength. The spectrum changes gradually with a variable time delay. At $t_{2}=\tau$, it consists of an array of peaks distributed on the segment between $\hbar\omega_{1}\simeq 1.4|J_{\mathrm{g}}|$ and $\hbar\omega_{1}=2|J_{\mathrm{g}}|$ of the horizontal line $\hbar\omega_{3}=-2|J_{\mathrm{g}}|$.

Conclusion– We investigated the coherent 2D spectrum of an interacting quantum many-body system of spin-1/2 fermions moving in a lattice, for example, electronic and ultracold atomic systems. In the weakly interacting limit, the 2D rephasing spectrum contains only diagonal peaks because different optical transitions are not coupled to one another. In contrast, if the interaction between particles is sufficiently strong, off-diagonal peaks emerge, which can be used as a direct probe of a non-negligible interaction. This is attributed to the fact that different optical transitions can be coupled to one another in the presence of interparticle interaction. Notably, effective coupling is induced by the quantum many-body interaction between particles as opposed to the conventional coupling between two transitions at the level of single-body physics. As the interaction strength is increased further, when the system approaches the Mott insulating phase in the strongly interacting limit, all the peaks coalesce into a single peak at the origin of the 2D spectrum, i.e., at the transition frequency between the ground and excited bands. Moreover, when the interaction is time-dependent, the information of its time variation can be obtained from the evolution of the coherent 2D spectrum as a function of the time delay between the second and third pulses. The results of this study demonstrate the potential of coherent multidimensional spectroscopy for studying quantum many-body interaction and ultrafast dynamics in various kinds of strongly correlated systems.