Dirac points for the honeycomb lattice with impenetrable obstacles

Inspired from the discovery of the quantum Hall effects and topological insulators in condensed matter, there has been increasing interest in the exploration of topological photonic/phononic materials recently to manipulate photons/phonons the same way as solids modulating electrons [HR-08, Khanikaev-12, Lu-14, Ozawa-19, Rechtsman-13, Yang-15]. These topological materials allow for the propagation of robust waveguide modes (or so-called edge modes) along the material interfaces without backscattering and even at the presence of large disorder, which could provide revolutionary applications for the design of novel optical/acoustic devices.

Typically the topological photonic/phononic materials are periodic band-gap media with the topological phases associated with the band structures of the underlying differential operators. The band gap is opened at certain special conical vertex of the band structure by breaking the time-reversal symmetry or the space-inversion symmetry of the periodic media [Fefferman-Thorp-Weinsein-16, Fefferman-Lee-Thorp-Weinsein-17, Lee-Thorp-Weinstein-Zhu-19, LZ21-2, ma-shvets, makwana-19, wang-08, wu-hu-15]. Such vertices in the dispersion relation are called Dirac points, which emerge from the touching of two bands of the spectrum in a linear conical fashion, and their investigations play an important role in the design of novel topological materials.

The mathematical analysis of Dirac point dates back to the study of the tight-binding approximation model for graphene in [slonczewski-weiss-58, wallace-47] by Wallace, Slonczewski and Weiss, and more recently for a more generalized quantum graph model with potential on the edges of the honeycomb lattice in [Kuchment-Post-07] by Kuchment and Post. Dirac points for the Schrödinger equation model of graphene were considered in [grushin-09] by Grushin over the honeycomb lattice with a weak potential and later thoroughly studied in [Fefferman-Weinsein-12] by Fefferman and Weinstein for potentials that are not necessarily weak; See also [berkokaiko-comech] for an alternative proof of the existence and stability of Dirac points for the Schrödinger operator. These results are then generalized to a broad class of elliptic operator defined over the honeycomb lattice, including the configurations with point scatterers, high-contrast medium, resonant bubbles, etc [ammari-20-4, Cassier-Weinstein-21, Fefferman-Thorp-Weinsein-18, Lee-16, Lee-Thorp-Weinstein-Zhu-19]. We also refer the readers to [ochiai-09, torrent-12, wang-08] for the numerical and experimental investigation of Dirac points in other acoustic and electromagnetic media.

In this paper we study the Dirac points for the honeycomb lattice with impenetrable obstacles embedded in a homogeneous medium. The setup arises naturally in photonic/phononic materials when the inhomogeneities are sound soft/hard in acoustic media or perfect electric/magnetic conducting in electromagnetic media. More precisely, we consider the honeycomb lattice in $\mathbb{R}^{2}$ given by

where the lattice vectors $\mathbf{e}_{1}=a\left(\frac{\sqrt{3}}{2},\frac{1}{2}\right)^{T}$, $\mathbf{e}_{2}=a\left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right)^{T}$, and the lattice constant is $a$. Let $Y:=\{t_{1}\mathbf{e}_{1}+t_{2}\mathbf{e}_{2}\,|\,0\leq t_{1},t_{2}\leq 1\}$ be the fundamental cell of the lattice, which contains a circular shape impenetrable obstacle $D_{\varepsilon}$ with radius $\varepsilon$ centered at $x_{c}=\frac{1}{2}(\mathbf{e}_{1}+\mathbf{e}_{2})$ (see Figure 1, left). $Y_{\varepsilon}:=Y\backslash D_{\varepsilon}$ denotes the domain exterior to the obstacle in the fundamental cell. The reciprocal lattice vectors ${\boldsymbol{\kappa}}_{1}$ and ${\boldsymbol{\kappa}}_{2}$ are ${\boldsymbol{\kappa}}_{1}=\frac{2\pi}{a}\left(\frac{\sqrt{3}}{3},1\right)^{T}$ and ${\boldsymbol{\kappa}}_{2}=\frac{2\pi}{a}\left(\frac{\sqrt{3}}{3},-1\right)^{T}$, which satisfy $\mathbf{e}_{i}\cdot{\boldsymbol{\kappa}}_{j}=2\pi\delta_{ij}$ for $i,j=1,2$. The reciprocal lattice is given by

The hexagon shape of the fundamental cell in $\Lambda^{*}$, or the Brillouin zone, is denoted by $\mathcal{B}$ and shown in Figure 1 (right).

For each Bloch wave vector ${\boldsymbol{\kappa}}\in\mathcal{B}$, we consider the following eigenvalue problem with the frequency $\omega\in\mathbb{R}$:

The eigenfunction $\psi$ is called the Bloch mode, which can be written as $\psi=e^{i{\boldsymbol{\kappa}}\cdot\mathbf{x}}u(\mathbf{x})$, wherein $u$ is a periodic function satisfying $u(\mathbf{x}+\mathbf{e})=u(\mathbf{x})$ for any $\mathbf{e}\in\Lambda$. Along the boundary of the obstacles, we impose the Dirichlet boundary condition

or the Neumann boundary condition

Here $\nu$ denotes the unit normal direction pointing to the exterior of the obstacle. We call (1)(2) and (1)(3) the Dirichlet and Neumann eigenvalue problem respectively.

Let $K=\frac{2}{3}{\boldsymbol{\kappa}}_{1}+\frac{1}{3}{\boldsymbol{\kappa}}_{2}=\frac{2\pi}{a}(\frac{1}{\sqrt{3}},\frac{1}{3})^{T}\in\mathcal{B}$ and $K^{\prime}=-K$ be two vertices of the Brillouin zone shown in Figure 1 (right). The matrix

is a rotation matrix such that $R\mathbf{x}$ rotates the vector $\mathbf{x}$ by $2\pi/3$ clockwise on the plane. Then all vertices of the Brillouin zone $\mathcal{B}$ are given by $\{K,RK,R^{2}K,K^{\prime},RK^{\prime}R^{2}K^{\prime}\}$. In addition, the following relations hold for the reciprocal lattice vectors:

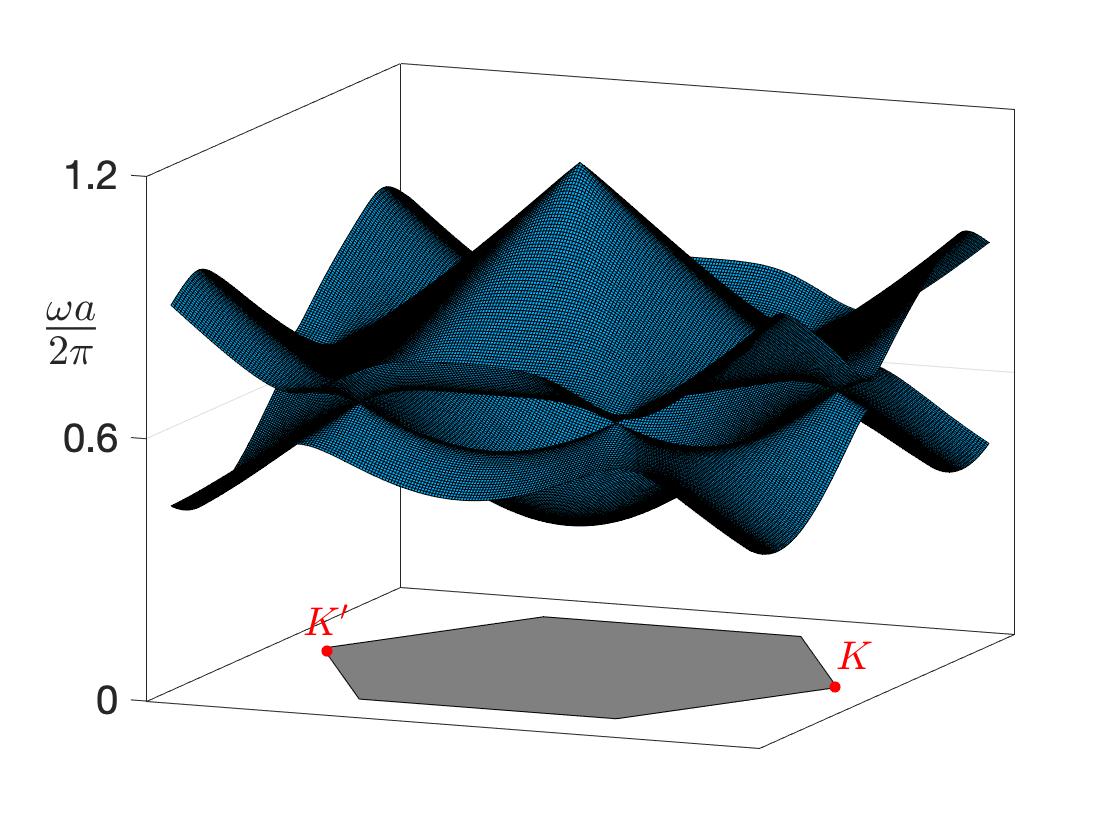
In the sequel, we set the Bloch wave vector ${\boldsymbol{\kappa}}^{*}=K$ and investigate Dirac points at ${\boldsymbol{\kappa}}^{*}$. Dirac points located at other Bloch wave vectors are reported in Section 5, but their mathematical studies will be our future endeavors. Figure 2 shows the occurrence of the Dirac points formed by the first and second, and the fourth and fifth band surfaces respectively for the Dirichlet eigenvalue problem. Note that due to the symmetry of the honeycomb structure, the same Dirac points also appear at other vertices of the Brillouin zone $\mathcal{B}$. In this paper we prove the existence of Dirac points $({\boldsymbol{\kappa}}^{*},\omega^{*})$ for both Dirichlet and Neumann eigenvalue problems and show that Dirac points appear at the crossing of lower band surfaces as well as higher band surfaces. In addition, we carry out quantitative analysis for the eigenvalues and the slopes of the conical dispersion surfaces near each Dirac point. It is shown that each eigenvalue $\omega^{*}$ is near a singular frequency associated with the Green’s function for the honeycomb lattice. These singular frequencies also correspond to the eigenvalues of the homogeneous medium over the honeycomb lattice when the obstacles are absent. In addition, the slopes of the dispersion surfaces are reciprocal to the eigenvalue $\omega^{*}$. We apply the layer potential technique to formulate the eigenvalue problem and reduce the integral equation to a set of characteristic equations at ${\boldsymbol{\kappa}}^{*}$ from the symmetry of the integral kernel and by the asymptotic analysis for the integral operator. The eigenvalues are roots of the nonlinear characteristic equations and we derive their asymptotic expansions with respect to the size of the obstacles $\varepsilon$. We would like to point out that our work is closely related to [ammari-20-4, Cassier-Weinstein-21] in the sense that the limit of the high-contrast elliptic operators considered in [ammari-20-4, Cassier-Weinstein-21] are related to the Neumann problem investigated in Section 6, although the arrangements of inclusions considered here are different.

The rest of the paper is organized as follows. Sections 2-5 are devoted to the study of Dirac points for the Dirichlet eigenvalue problem and Section 6 discusses the Neumann eigenvalue problem. In Section 2 we formulate the eigenvalue problem by using the layer potential and set up an infinite linear system for the expansion coefficients of the density function over the obstacle boundary. The existence of the Dirac point at low frequency bands is proved and the asymptotic expansion of the corresponding eigenvalue is derived in Section 3. We establish the conical singularity of the Dirac point in Section 4 and carry out quantitative analysis for the slopes of the dispersion surfaces near this Dirac point. Finally, the Dirac points located at higher frequency bands are investigated in Section 5.

In this section, we formulate the Dirichlet eigenvalue problem by an integral equation over the obstacle boundary and set up an infinite linear system for the expansion coefficients of the density function. The Dirichlet eigenvalues reduce to the characteristic values of the infinite linear system.

In this section, we focus on the lowest eigenvalue to the eigenvalue problem (1)-(2) when ${\boldsymbol{\kappa}}={\boldsymbol{\kappa}}^{*}$. Based on the decomposition of the quasi-periodic Green’s function $G({\boldsymbol{\kappa}},\omega,\mathbf{x})$ and the integral operator $\mathcal{S}_{\varepsilon}^{{\boldsymbol{\kappa}},\omega}$, we decompose the matrix $\mathcal{A}$ as $\mathcal{A}=\mathcal{D}+\varepsilon\,\mathcal{E}$, wherein $\mathcal{D}$ is a diagonal matrix. Such decomposition allows for reducing the subsystems (18)-(20) to three scalar nonlinear equations (characteristic equations). The eigenvalues are the roots of the characteristic equations and can be obtained by the asymptotic analysis.