Dineutron-dineutron correlation in 8He
Abstract
- Background
-
The four-neutron correlation has been attracting much attention for decades. In addition to the study on the tetra-neutron system, it is worthwhile to investigate the correlation in bound systems.
- Purpose
-
The 8He nucleus is a system where four neutrons are weakly bound around the 4He core. The dineutron () correlation has been long discussed in various weakly-bound neutron-rich nuclei such as 6He and 11Li, whereas the 8He nucleus gives us an opportunity to investigate the - type four-neutron correlation.
- Methods
-
We introduce a microscopic 4He+ model and describe the ground-state structure of 8He. The mixing of the two- component in the ground state is examined. The ground-state wave function is verified by investigating various observables including high-energy scattering cross sections.
- Results
-
Our model reasonably reproduces the available experimental data, the binding energy, charge radius, total reaction cross section, and proton-nucleus elastic scattering cross section data. We find that the significant mixing of the two- cluster configurations around 4He in the ground state of 8He: The ground state has a squared overlap of about 45% with a -4He- configuration with the 4He- distance of 3 fm and opening angle of 80∘.
- Conclusions
-
The ground state of 8He contains a certain amount of the two- cluster component, indicating the strong nuclear deformation, which was experimentally observed recently.
The existence of proton deficient nuclear systems has been a subject of debate in nuclear physics. In this context, the tetra-neutron system, comprising four neutrons, has garnered significant interest for decades [1, 2, 3, 4, 5, 6]. A crucial characteristic of the tetra-neutron system is that in the lowest energy configuration, one of the two-neutron pairs, known as dineutron (), occupies the state, while the other pair must occupy the state due to the Pauli exclusion principle. Consequently, the four-neutron correlation may be weakened in a vacuum as the two- systems should occupy distinctly different orbits with each other.
The two- correlations may be enhanced when a core nucleus, such as a 4He nucleus, is introduced into the four-neutron system. This is because, in the 8He nucleus, four neutrons are bound around the 4He core nucleus, and all four can occupy the state as their lowest energy configuration. As a result, the four-neutron correlation could emerge under a democratic situation, in contrast to the tetra-neutron system in a vacuum. It is important to note that in the 7H () system, the four neutrons are no longer bound, although numerous experimental and theoretical investigations have focused on exploring the resonance states of 7H [7, 8, 9, 10, 11, 12, 13, 14].
The correlations in the 8He nucleus have been theoretically discussed in Refs. [15, 16, 17], even though the neutron number of six in 7H and 8He corresponds to the subclosure of the orbits in the nuclear shell model, where the spin-orbit interaction acts attractively. The spin-orbit interaction serves as a driving force for promoting the independent particle motion of each nucleon with good total angular momentum [18] and leads to the breaking of the spin-singlet clusters. However, if the four valence neutrons in the shell have extended spatial distributions outside the interaction region of the spin-orbit force, it would be possible to form the clusters there. Recent experimental results support such spatially extended four-neutron wave functions: The four neutrons in the 8He nucleus are bound only by 3.11 MeV from the threshold energy [19], and the matter radius is evaluated as 2.53(2) fm with a neutron skin thickness of 0.82(2) fm, implying an extended four-neutron distribution [20].
We note that the - correlation has not been investigated sufficiently, although the correlations are extremely important in weakly bound systems and have been widely discussed in neutron-rich nuclei [21, 22, 23]. In Refs. [15, 17], the squared overlap between the ground-state wave function of 8He and two cluster configurations was examined. In those studies, two clusters were isotopically distributed around 8He by means of the Tohsaki-Horiuchi-Schuck-Röpke (THSR) wave function [24]. A similar approach was adopted in Ref. [25]. Several ab initio calculations were performed for the 8He nucleus. Many physical properties can be interpreted in connection with the realistic interactions but unfortunately the - correlation was not discussed there [26, 27, 28, 29]. Ref. [16] conducted the Hartree-Fock-Bogoliubov calculations with the Wood-Saxon potential, where the four-body density of the valence neutrons and the - correlation were discussed but that obtained nuclear radius is unrealistically larger than the experimental value. An investigation using a realistic wave function is needed to extract an amount of the - correlation quantitatively.
The recent experiment posited that the ground state of 8He is strongly deformed [30]. This suggests that the 8He configuration is not a simple subclosure configuration of . Instead, it may exhibit enhanced four-neutron correlations. Moreover, the possibility of the so-called soft dipole mode in 8He was recently pointed out in Ref. [31], implying the formation of a four-neutron cluster around the 4He core.
The purpose of this paper is to investigate the - correlation in the 8He nucleus. We perform microscopic cluster model calculations that explicitly include various geometric configurations of two- clusters. We remark that a strong dineutron correlation was implied within a 4He core plus picture [32]. We take special care to describe the valence four-neutron wave functions around the 4He core by superposing numerous configurations. To verify our wave function, we calculate the proton-8He elastic scattering and total reaction cross sections and compare them with available experimental data. Finally, we discuss whether the four neutrons occupying the states can favorably form two clusters under a democratic condition and the relationship between the two- correlations and nuclear deformation.
Here, we introduce a microscopic 4He+ model, wherein the wave function is fully antisymmetrized. We construct basis states with different neutron configurations and superpose them based on the generator coordinate method (GCM) after the angular momentum projection [33]. The coefficients of each basis state are determined by diagonalizing the norm and Hamiltonian matrices. Using the obtained ground-state wave function of 8He, we calculate the one-body density distributions for the cross-section calculations with the Glauber model [34].
The Hamiltonian consists of kinetic energy and potential energy () terms as
| (1) |
where the center-of-mass kinetic energy is subtracted to guarantee the translation-invariance of the wave functions. For the potential part, the interaction consists of the central, spin-orbit, and Coulomb terms. We employ the Volkov No.2 [35] effective nucleon-nucleon interaction with the Majorana exchange parameter of , which is known to reproduce the low-energy scattering phase shift of He [36]. The original Volkov interaction does not have the Heisenberg and Bartlett exchange terms, but we introduce just as in Ref. [13] to remove the spurious bound state of the two-neutron system. For the spin-orbit part, we use the spin-orbit term of the G3RS interaction [37], which is a realistic interaction originally developed to reproduce the nucleon-nucleon scattering phase shifts. The strength of the spin-orbit interaction is set to 2000 MeV, reproducing the low-energy scattering phase shift of He [37].
The wave function of 8He is described by a superposition of fully antisymmetrized () wave function as
| (2) |
where the and wave functions, and , are expressed by the product of the single-particle wave function with a Gaussian form as used in many other cluster models, including the Brink model [33]
| (3) |
where is a Gaussian center parameter related to the expectation value for the position of the nucleon, and are the spin and isospin parts of the wave function. For the size parameter , we here use fm-2, slightly smaller than the value for the free 4He nucleus, which is reasonable, as the 4He core swells due to the interaction and Pauli principle from the valence neutrons [38, 39]. The cluster as the core nucleus can be expressed by four nucleons with the spin and isospin saturated configuration sharing the same value. Similarly, the cluster can also be expressed by two neutrons with spin-up and spin-down with and .
Each Slater determinant is projected to the eigenstates of parity and angular momentum by using the projection operator
| (4) |
Here is the Wigner -function and is the rotation operator acting on the spatial and spin parts of the wave function. This integration over the Euler angle is numerically performed. The operator is for the parity projection. Here we take for the positive-parity states, where is the parity-inversion operator.
The generated many different Slater determinants () are superposed based on GCM [33]. After normalizing each basis state, the total wave function is written as
| (5) |
The coefficients for a linear combination of the Slater determinants are obtained together with the energy eigenvalue when we diagonalize the norm and Hamiltonian matrices, namely by solving the Hill-Wheeler equation [40]
| (6) |
In this study, we prepare wave functions with various isosceles triangle configurations and randomly generated (the core + four free neutrons) wave functions.
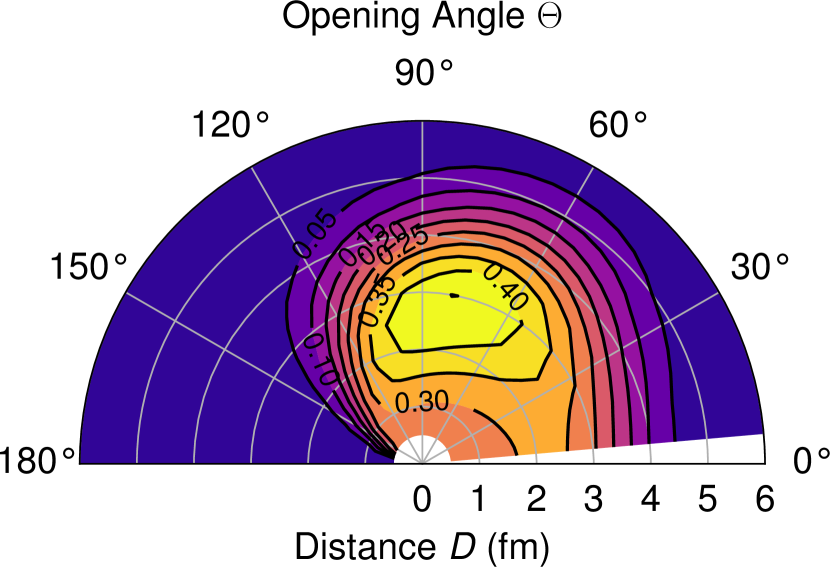
The geometric configurations of the wave functions are the isosceles triangles where the two sides of the 4He- distance are taken as , 2, 3, 4, 5, and 6 fm, and its opening angle is taken as , 60∘, , , and with the spin saturated configuration. Figure 1 shows the calculated potential energy surface of for the configuration as a function of and . We can see a local energy minimum of MeV at around fm and . Note that the rms distance of the two neutrons in the cluster is 2.43 fm, which implies developed clusters in the surface region in the ground state of 8He. Large positive values of the potential energy surface come from the Pauli principle.
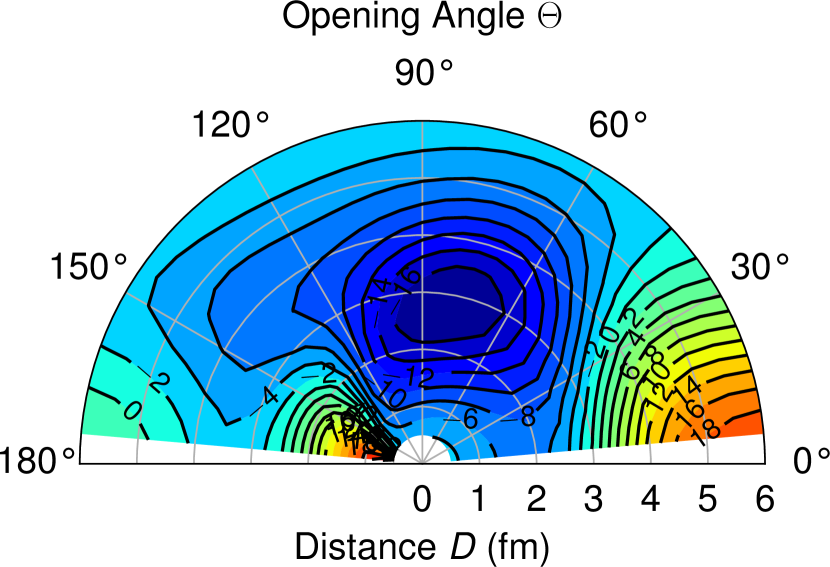
For the configurations, we randomly generate the Gaussian center parameters , and of the four neutrons, where two of them are spin-up and the remaining two are spin-down. To accelerate the energy convergence, these random numbers are generated by following an exponential distribution having a width of 1.4 fm for the distance between neutrons with the up and down spins and the distance between their center position and the core. The center of mass of each Slater determinant is shifted to the origin before the superposition.
Before discussing the ground state of 8He, we calculate 6He by randomly generated two-neutron configurations around an cluster to verify our choice of the model Hamiltonian. The binding energy is found to be MeV from the threshold with 200 basis states. The value is slightly overbinding compared with the experimental data of MeV [41] but is within the acceptable range because the calculated total reaction cross section on a carbon target is 719 mb at 800 MeV/nucleon, which is in good agreement with the experimental interaction cross section at 790 MeV/nucleon, 722 mb [42]. The details of the cross-section calculation will be described for a 8He case later. The root-mean-square (rms) matter radius is calculated as 2.44 fm, which is slightly smaller than the empirical value 2.480.03 fm [43].
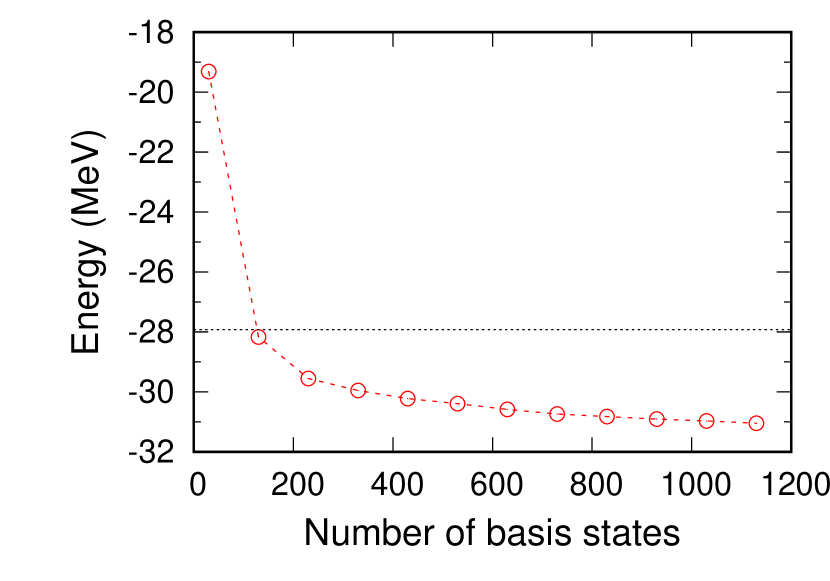
Figure 2 draws the energy convergence of the state of 8He as a function of the number of basis states superposed. The first 30 basis states correspond to the basis states, and the subsequent 1,100 basis states represent the 4He+ basis states. To achieve convergence, more than 1,000 basis states are required.
The calculated energy of the 8He nucleus is found to be MeV from the threshold, which is in reasonable agreement with experimental data, MeV [41]. This result demonstrates that the wave function used in this study provides a good description of the four-valence neutrons of the 8He nucleus.
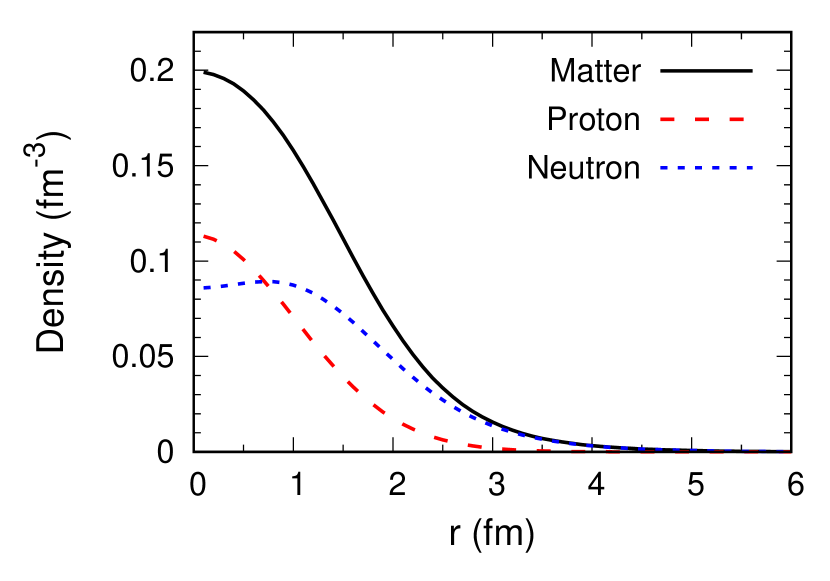
Figure 3 displays the point-matter, proton, and neutron density distribution of 8He. We see more extended neutron density distribution than proton one, indicating a thick neutron skin. The rms point-proton and matter radii of these density distributions are calculated as 1.82 fm and 2.50 fm, respectively. The calculated point-proton radius is in good agreement with the experimental ones deduced from the charge radius, 1.80(3) fm [44] and 1.81(3) fm [45].
To further verify our wave function, we calculate the total interaction cross sections on a carbon target as well as proton-nucleus elastic scattering cross sections. These calculations are performed based on the Glauber model [34] with the optical limit approximation [34, 46]. The nucleon-target formalism [47] is employed for the total reaction cross section calculation on a carbon target. The inputs to the theory are the one-body density distributions and the profile function which describes the nucleon-nucleon scattering properties. The profile function [48] has been well tested as shown in many examples of proton-nucleus [49, 50, 51] and nucleus-nucleus reactions [52, 53, 49, 54, 55, 56, 57]. For more details, see, for example, Refs. [58, 59] and references therein, showing the most recent application of this model. The essential input for the cross-section calculations, the one-body density distribution of the ground state of 8He, is obtained after solving the Hill-Wheeler equation (Eq. (6)). The density distribution is calculated in the angular momentum projected space, which is free from the center of mass motion, and the detail is described in Ref. [60].
Using these density distributions, the total reaction cross section on a carbon target at an incident energy of 800 MeV/nucleon is calculated as 798 mb. This value is slightly smaller than the experimental cross section of 817(6) mb at 790 MeV/nucleon [42] but still within the acceptable range considering the uncertainties of previous observations [45].
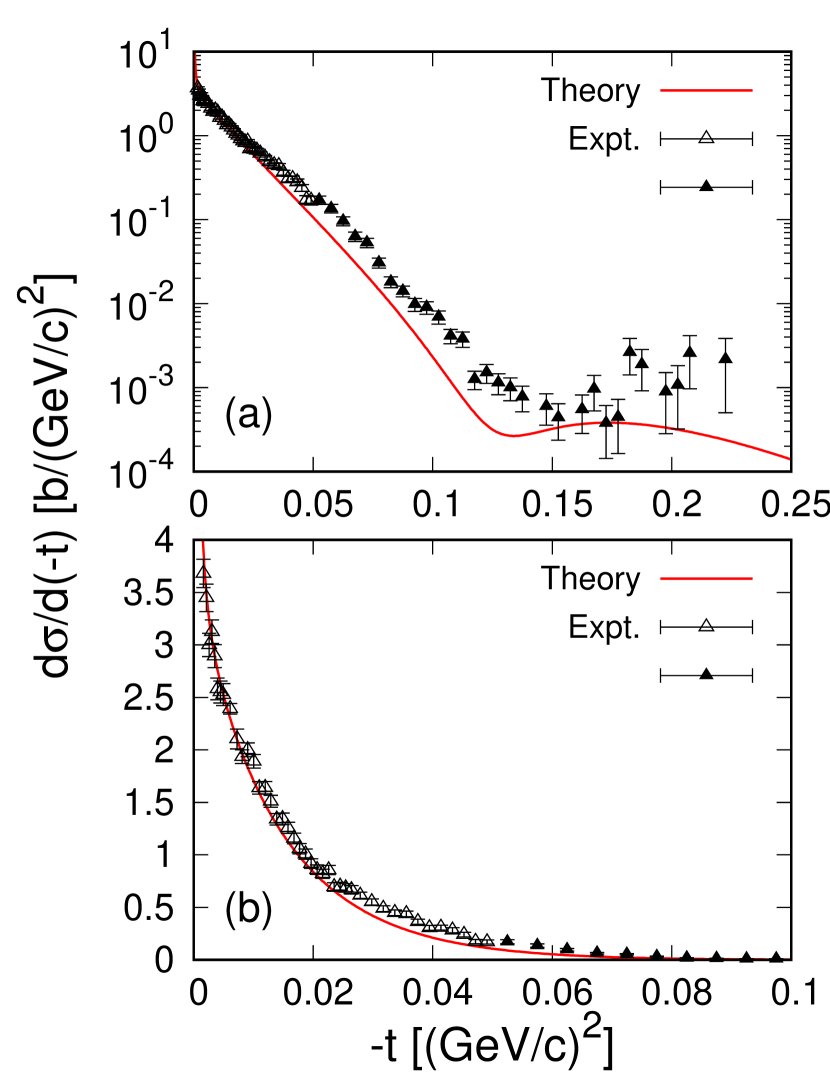
Figure 4 compares the calculated differential cross section for proton-8He scattering at an incident proton energy of 680 MeV with available experimental data at low [61] and high [62] four momentum transfer regions. Although there are some deviations at intermediate momentum transfer regions, the overall agreement between theory and experiment is achieved. To see it more quantitatively at low four momentum transfer regions, in Fig. 4 (b), we also plot the cross sections in a linear scale. This good agreement confirms the validity of the wave function used in this study.
Using the realistic wave function obtained in this way, the two- correlation in 8He is investigated by analyzing the wave function components. The squared overlap between the ground state of 8He and the 4He++ cluster configuration with isosceles triangular configurations is evaluated. Figure 5 displays the squared overlap results, showing that a 4He- distance of fm gives the largest squared overlap and a peak structure is found around the -4He- opening angle of . This large overlap area corresponds to a deep pocket in the potential energy surface coming from the triangular cluster configuration (Fig. 1).
The value of squared overlap at the peak position is about 0.45, indicating that 8He contains a significant amount of the two- component with a large 4He- distance. Despite the neutron number 6 corresponding to the closure of in the -coupling shell model, the spin-orbit interaction does not completely break the clusters due to the weakly bound nature of the system; neutrons also stay beyond the interaction range of the spin-orbit interaction, fm [37]. The rapid drop of the squared overlap beyond indicates that obtuse triangular shapes are not favored, which also suggests the correlation between the two clusters. We also compute the squared overlap between the harmonic-oscillator configuration [] and the ground state wave function. This overlap value is 0.40, which is comparable to the two- component. We remark that the coupling with the continuum states significantly enhances the component of the continuum orbits [63].
To relate the two- component with the nuclear shape, it is instructive to quantify the degree of deformation for each basis. The parameters is given by [64]
| (7) |
where the dimensionless deformation parameter is defined by
| (8) |
with fm and the quadrupole deformation parameters
| (9) | ||||
| (10) |
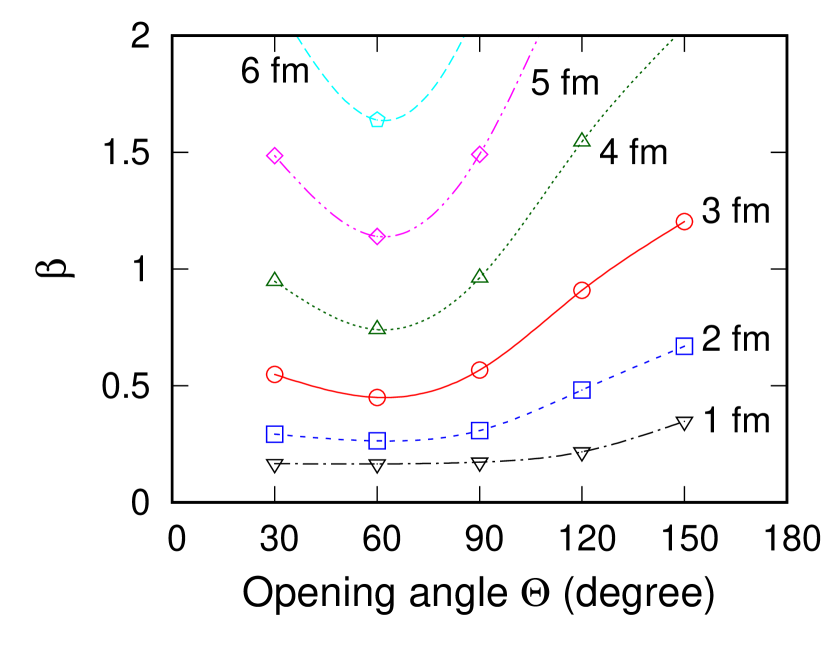
Figure 6 displays the calculated of the 4He+2+2 configuration, showing that the value rapidly increases with increasing 4He- distance. The mixing of such components could explain the large deformation of 8He discussed in the literature ( [30]). The large experimental value is consistent with the large distance between 4He and s; however, it is not necessarily direct evidence of - correlation with smaller opening angles. As shown in Fig. 6, large opening angles can also give large values.
To conclude, the four-neutron correlation has been a disputable topic in nuclear physics for decades. This study has investigated for the first time dineutron-dineutron (-) correlations in 8He using a reliable wave function obtained from a microscopic cluster model. To construct a 8He wave function, explicit two- configurations were superposed along with many configurations. The agreement between the theory and experiment is satisfactory. Overall, this study provides insights into the two- correlation in 8He and its effects on the nuclear structure. The results show that a significant amount of the two- components in the ground state of 8He could explain the strong nuclear deformation observed in recent studies. However, it should be noted that the strong deformation is not necessarily a direct evidence of - correlations with small opening angles, as it can also be interpreted as configurations locating s at large distances.
Further experimental studies are needed to clarify the existence of the two- correlations. Exploring the possibility of such - correlations in other neutron-rich nuclei near the neutron dripline is also an interesting topic for the universal understanding of the emergence of the - correlation.
This work was in part supported by JSPS KAKENHI Grants Nos. 18K03635, 22H01214, and 22K03618. The numerical calculations were performed using the computer facility of Yukawa Institute for Theoretical Physics, Kyoto University (Yukawa-21).
References
- Marqués et al. [2002] F. M. Marqués, M. Labiche, N. A. Orr, J. C. Angélique, L. Axelsson, B. Benoit, U. C. Bergmann, M. J. G. Borge, W. N. Catford, S. P. G. Chappell, N. M. Clarke, G. Costa, N. Curtis, A. D’Arrigo, E. de Góes Brennand, F. de Oliveira Santos, O. Dorvaux, G. Fazio, M. Freer, B. R. Fulton, G. Giardina, S. Grévy, D. Guillemaud-Mueller, F. Hanappe, B. Heusch, B. Jonson, C. Le Brun, S. Leenhardt, M. Lewitowicz, M. J. López, K. Markenroth, A. C. Mueller, T. Nilsson, A. Ninane, G. Nyman, I. Piqueras, K. Riisager, M. G. S. Laurent, F. Sarazin, S. M. Singer, O. Sorlin, and L. Stuttgé, Detection of neutron clusters, Phys. Rev. C 65, 044006 (2002).
- Kisamori et al. [2016] K. Kisamori, S. Shimoura, H. Miya, S. Michimasa, S. Ota, M. Assie, H. Baba, T. Baba, D. Beaumel, M. Dozono, T. Fujii, N. Fukuda, S. Go, F. Hammache, E. Ideguchi, N. Inabe, M. Itoh, D. Kameda, S. Kawase, T. Kawabata, M. Kobayashi, Y. Kondo, T. Kubo, Y. Kubota, M. Kurata-Nishimura, C. S. Lee, Y. Maeda, H. Matsubara, K. Miki, T. Nishi, S. Noji, S. Sakaguchi, H. Sakai, Y. Sasamoto, M. Sasano, H. Sato, Y. Shimizu, A. Stolz, H. Suzuki, M. Takaki, H. Takeda, S. Takeuchi, A. Tamii, L. Tang, H. Tokieda, M. Tsumura, T. Uesaka, K. Yako, Y. Yanagisawa, R. Yokoyama, and K. Yoshida, Candidate resonant tetraneutron state populated by the reaction, Phys. Rev. Lett. 116, 052501 (2016).
- Duer et al. [2022] M. Duer, T. Aumann, and R. Gernhäuser et al., Observation of a correlated free four-neutron system, Nature 606, 678–682 (2022).
- Hiyama et al. [2016] E. Hiyama, R. Lazauskas, J. Carbonell, and M. Kamimura, Possibility of generating a 4-neutron resonance with a isospin 3-neutron force, Phys. Rev. C 93, 044004 (2016).
- Shirokov et al. [2016] A. M. Shirokov, G. Papadimitriou, A. I. Mazur, I. A. Mazur, R. Roth, and J. P. Vary, Prediction for a four-neutron resonance, Phys. Rev. Lett. 117, 182502 (2016).
- Deltuva [2018] A. Deltuva, Tetraneutron: Rigorous continuum calculation, Physics Letters B 782, 238 (2018).
- Korsheninnikov et al. [2003] A. A. Korsheninnikov, E. Y. Nikolskii, E. A. Kuzmin, A. Ozawa, K. Morimoto, F. Tokanai, R. Kanungo, I. Tanihata, N. K. Timofeyuk, M. S. Golovkov, A. S. Fomichev, A. M. Rodin, M. L. Chelnokov, G. M. Ter-Akopian, W. Mittig, P. Roussel-Chomaz, H. Savajols, E. Pollacco, A. A. Ogloblin, and M. V. Zhukov, Experimental evidence for the existence of and for a specific structure of , Phys. Rev. Lett. 90, 082501 (2003).
- Caamaño et al. [2007] M. Caamaño, D. Cortina-Gil, W. Mittig, H. Savajols, M. Chartier, C. E. Demonchy, B. Fernández, M. B. Gómez Hornillos, A. Gillibert, B. Jurado, O. Kiselev, R. Lemmon, A. Obertelli, F. Rejmund, M. Rejmund, P. Roussel-Chomaz, and R. Wolski, Resonance state in , Phys. Rev. Lett. 99, 062502 (2007).
- Muzalevskii et al. [2021] I. A. Muzalevskii, A. A. Bezbakh, E. Y. Nikolskii, V. Chudoba, S. A. Krupko, S. G. Belogurov, D. Biare, A. S. Fomichev, E. M. Gazeeva, A. V. Gorshkov, L. V. Grigorenko, G. Kaminski, O. Kiselev, D. A. Kostyleva, M. Y. Kozlov, B. Mauyey, I. Mukha, Y. L. Parfenova, W. Piatek, A. M. Quynh, V. N. Schetinin, A. Serikov, S. I. Sidorchuk, P. G. Sharov, N. B. Shulgina, R. S. Slepnev, S. V. Stepantsov, A. Swiercz, P. Szymkiewicz, G. M. Ter-Akopian, R. Wolski, B. Zalewski, and M. V. Zhukov, Resonant states in : Experimental studies of the reaction, Phys. Rev. C 103, 044313 (2021).
- Caamaño et al. [2022] M. Caamaño, T. Roger, A. Moro, G. Grinyer, J. Pancin, S. Bagchi, S. Sambi, J. Gibelin, B. Fernández–Domínguez, N. Itagaki, J. Benlliure, D. Cortina–Gil, F. Farget, B. Jacquot, D. Pérez–Loureiro, B. Pietras, R. Raabe, D. Ramos, C. Rodríguez Tajes, H. Savajols, and M. Vandebrouck, Experimental investigation of ground-state properties of with transfer reactions, Physics Letters B 829, 137067 (2022).
- Golovkov et al. [2004] M. Golovkov, L. Grigorenko, A. Fomichev, Y. Oganessian, Y. Orlov, A. Rodin, S. Sidorchuk, R. Slepnev, S. Stepantsov, G. Ter-Akopian, and R. Wolski, Estimates of the width and lower decay energy limit, Physics Letters B 588, 163 (2004).
- Timofeyuk [2004] N. K. Timofeyuk, Hyperspherical harmonics with orthogonal symmetry in the shell model approach and its application to light nuclei, Phys. Rev. C 69, 034336 (2004).
- Aoyama and Itagaki [2009] S. Aoyama and N. Itagaki, Di-neutron correlations in , Phys. Rev. C 80, 021304 (2009).
- Hiyama et al. [2022] E. Hiyama, R. Lazauskas, and J. Carbonell, ground state as a +4n resonance, Physics Letters B 833, 137367 (2022).
- Kanada-En’yo [2007] Y. Kanada-En’yo, Dineutron structure in , Phys. Rev. C 76, 044323 (2007).
- Hagino et al. [2008] K. Hagino, N. Takahashi, and H. Sagawa, Strong dineutron correlation in and , Phys. Rev. C 77, 054317 (2008).
- Itagaki et al. [2008] N. Itagaki, M. Ito, K. Arai, S. Aoyama, and T. Kokalova, Mixing of di-neutron components in , Phys. Rev. C 78, 017306 (2008).
- Itagaki et al. [2011] N. Itagaki, J. Cseh, and M. Płoszajczak, Simplified modeling of cluster-shell competition in and , Phys. Rev. C 83, 014302 (2011).
- Tilley et al. [2004] D. Tilley, J. Kelley, J. Godwin, D. Millener, J. Purcell, C. Sheu, and H. Weller, Energy levels of light nuclei , Nuclear Physics A 745, 155 (2004).
- Wakasa et al. [2022] T. Wakasa, M. Takechi, S. Tagami, and M. Yahiro, Matter radii and skins of from reaction cross section of proton+ scattering based on the love-franey t-matrix model, Results in Physics 35, 105329 (2022).
- Bertsch and Esbensen [1991] G. Bertsch and H. Esbensen, Pair correlations near the neutron drip line, Annals of Physics 209, 327 (1991).
- Matsuo et al. [2005] M. Matsuo, K. Mizuyama, and Y. Serizawa, Di-neutron correlation and soft dipole excitation in medium mass neutron-rich nuclei near drip line, Phys. Rev. C 71, 064326 (2005).
- Cook et al. [2020] K. J. Cook, T. Nakamura, Y. Kondo, K. Hagino, K. Ogata, A. T. Saito, N. L. Achouri, T. Aumann, H. Baba, F. Delaunay, Q. Deshayes, P. Doornenbal, N. Fukuda, J. Gibelin, J. W. Hwang, N. Inabe, T. Isobe, D. Kameda, D. Kanno, S. Kim, N. Kobayashi, T. Kobayashi, T. Kubo, S. Leblond, J. Lee, F. M. Marqués, R. Minakata, T. Motobayashi, K. Muto, T. Murakami, D. Murai, T. Nakashima, N. Nakatsuka, A. Navin, S. Nishi, S. Ogoshi, N. A. Orr, H. Otsu, H. Sato, Y. Satou, Y. Shimizu, H. Suzuki, K. Takahashi, H. Takeda, S. Takeuchi, R. Tanaka, Y. Togano, J. Tsubota, A. G. Tuff, M. Vandebrouck, and K. Yoneda, Halo structure of the neutron-dripline nucleus , Phys. Rev. Lett. 124, 212503 (2020).
- Tohsaki et al. [2001] A. Tohsaki, H. Horiuchi, P. Schuck, and G. Röpke, Alpha Cluster Condensation in 12C and 16O, Phys. Rev. Lett. 87, 192501 (2001).
- Kobayashi and Kanada-En’yo [2013] F. Kobayashi and Y. Kanada-En’yo, Dineutron formation and breaking in , Phys. Rev. C 88, 034321 (2013).
- Pieper et al. [2001] S. C. Pieper, V. R. Pandharipande, R. B. Wiringa, and J. Carlson, Realistic models of pion-exchange three-nucleon interactions, Phys. Rev. C 64, 014001 (2001).
- Caurier and Navrátil [2006] E. Caurier and P. Navrátil, Proton radii of isotopes from high-precision nucleon-nucleon interactions, Phys. Rev. C 73, 021302 (2006).
- Maris et al. [2009] P. Maris, J. P. Vary, and A. M. Shirokov, Ab initio no-core full configuration calculations of light nuclei, Phys. Rev. C 79, 014308 (2009).
- Bonaiti et al. [2022] F. Bonaiti, S. Bacca, and G. Hagen, Ab initio coupled-cluster calculations of ground and dipole excited states in , Phys. Rev. C 105, 034313 (2022).
- Holl et al. [2021] M. Holl, R. Kanungo, Z. Sun, G. Hagen, J. Lay, A. Moro, P. Navratil, T. Papenbrock, M. Alcorta, D. Connolly, B. Davids, A. Diaz Varela, M. Gennari, G. Hackman, J. Henderson, S. Ishimoto, A. Kilic, R. Krucken, A. Lennarz, J. Liang, J. Measures, W. Mittig, O. Paetkau, A. Psaltis, S. Quaglioni, J. Randhawa, J. Smallcombe, I. Thompson, M. Vorabbi, and M. Williams, Proton inelastic scattering reveals deformation in , Physics Letters B 822, 136710 (2021).
- Myo et al. [2022] T. Myo, M. Odsuren, and K. Kiyoshi, Soft dipole resonance in neutron-rich 8He, Progress of Theoretical and Experimental Physics 2022, 10.1093/ptep/ptac130 (2022), 103D01, https://academic.oup.com/ptep/article-pdf/2022/10/103D01/46532952/ptac130.pdf .
- Fossez et al. [2018] K. Fossez, J. Rotureau, and W. Nazarewicz, Energy spectrum of neutron-rich helium isotopes: Complex made simple, Phys. Rev. C 98, 061302 (2018).
- Brink [1966] D. M. Brink, The alpha-particle model of light nuclei, Proc. Int. School Phys.“Enrico Fermi” XXXVI, 247 (1966).
- Glauber [1959] R. J. Glauber, High-energy collision theory, Lectures on Theoretical Physics 1, 315 (1959).
- Volkov [1965] A. Volkov, Equilibrium deformation calculations of the ground state energies of 1p shell nuclei, Nucl. Phys. 74, 33 (1965).
- Okabe and Abe [1979] S. Okabe and Y. Abe, The Structure of 9Be by a Molecular Model. II, Prog. Theor. Phys. 61, 1049 (1979).
- Tamagaki [1968] R. Tamagaki, Potential Models of Nuclear Forces at Small Distances, Prog. Theor. Phys. 39, 91 (1968).
- Arai et al. [1999] K. Arai, Y. Suzuki, and R. G. Lovas, Structure of with an extended three-cluster model, Phys. Rev. C 59, 1432 (1999).
- Mikami et al. [2014] D. Mikami, W. Horiuchi, and Y. Suzuki, Electric dipole response of : Halo-neutron and core excitations, Phys. Rev. C 89, 064303 (2014).
- Hill and Wheeler [1953] D. L. Hill and J. A. Wheeler, Nuclear constitution and the interpretation of fission phenomena, Phys. Rev. 89, 1102 (1953).
- Wang et al. [2021] M. Wang, W. Huang, F. Kondev, G. Audi, and S. Naimi, The ame 2020 atomic mass evaluation (ii). tables, graphs and references*, Chinese Physics C 45, 030003 (2021).
- Tanihata et al. [1985] I. Tanihata, H. Hamagaki, O. Hashimoto, S. Nagamiya, Y. Shida, N. Yoshikawa, O. Yamakawa, K. Sugimoto, T. Kobayashi, D. Greiner, N. Takahashi, and Y. Nojiri, Measurements of interaction cross sections and radii of he isotopes, Physics Letters B 160, 380 (1985).
- Tanihata et al. [1988] I. Tanihata, T. Kobayashi, O. Yamakawa, S. Shimoura, K. Ekuni, K. Sugimoto, N. Takahashi, T. Shimoda, and H. Sato, Measurement of interaction cross sections using isotope beams of be and b and isospin dependence of the nuclear radii, Physics Letters B 206, 592 (1988).
- Angeli and Marinova [2013] I. Angeli and K. Marinova, Table of experimental nuclear ground state charge radii: An update, Atomic Data and Nuclear Data Tables 99, 69 (2013).
- Mueller et al. [2007] P. Mueller, I. A. Sulai, A. C. C. Villari, J. A. Alcántara-Núñez, R. Alves-Condé, K. Bailey, G. W. F. Drake, M. Dubois, C. Eléon, G. Gaubert, R. J. Holt, R. V. F. Janssens, N. Lecesne, Z.-T. Lu, T. P. O’Connor, M.-G. Saint-Laurent, J.-C. Thomas, and L.-B. Wang, Nuclear charge radius of , Phys. Rev. Lett. 99, 252501 (2007).
- Suzuki et al. [2003] Y. Suzuki, R. G. Lovas, K. Yabana, and K. Varga, Structure and reactions of light exotic nuclei, (Taylor and Francis, London) (2003).
- Abu-Ibrahim and Suzuki [2000] B. Abu-Ibrahim and Y. Suzuki, Utility of nucleon-target profile function in cross section calculations, Phys. Rev. C 61, 051601 (2000).
- Abu-Ibrahim et al. [2008] B. Abu-Ibrahim, W. Horiuchi, A. Kohama, and Y. Suzuki, Reaction cross sections of carbon isotopes incident on a proton, Phys. Rev. C 77, 034607 (2008).
- Abu-Ibrahim et al. [2009] B. Abu-Ibrahim, S. Iwasaki, W. Horiuchi, A. Kohama, and Y. Suzuki, Elastic and total reaction cross sections of oxygen isotopes in glauber theory, Journal of the Physical Society of Japan 78, 044201 (2009).
- Horiuchi et al. [2016] W. Horiuchi, S. Hatakeyama, S. Ebata, and Y. Suzuki, Extracting nuclear sizes of medium to heavy nuclei from total reaction cross sections, Phys. Rev. C 93, 044611 (2016).
- Hatakeyama and Horiuchi [2019] S. Hatakeyama and W. Horiuchi, Complete glauber calculations for proton-nucleus inelastic cross sections, Nuclear Physics A 985, 20 (2019).
- Horiuchi and Suzuki [2006] W. Horiuchi and Y. Suzuki, : An -wave two-neutron halo nucleus, Phys. Rev. C 74, 034311 (2006).
- Horiuchi et al. [2007] W. Horiuchi, Y. Suzuki, B. Abu-Ibrahim, and A. Kohama, Systematic analysis of reaction cross sections of carbon isotopes, Phys. Rev. C 75, 044607 (2007).
- Horiuchi et al. [2010] W. Horiuchi, Y. Suzuki, P. Capel, and D. Baye, Probing the weakly-bound neutron orbit of with total reaction and one-neutron removal cross sections, Phys. Rev. C 81, 024606 (2010).
- Horiuchi et al. [2012] W. Horiuchi, T. Inakura, T. Nakatsukasa, and Y. Suzuki, Glauber-model analysis of total reaction cross sections for ne, mg, si, and s isotopes with skyrme-hartree-fock densities, Phys. Rev. C 86, 024614 (2012).
- Horiuchi et al. [2015] W. Horiuchi, T. Inakura, T. Nakatsukasa, and Y. Suzuki, Systematic analysis of total reaction cross sections of unstable nuclei with glauber theory, Proceedings of the Conference on Advances in Radioactive Isotope Science (ARIS2014), JPS Conf. Proc. 6, 030079 (2015).
- Nagahisa and Horiuchi [2018] T. Nagahisa and W. Horiuchi, Examination of the radius determination with interaction cross sections, Phys. Rev. C 97, 054614 (2018).
- Horiuchi and Itagaki [2022] W. Horiuchi and N. Itagaki, Density profiles near the nuclear surface of : An indication of clustering, Phys. Rev. C 106, 044330 (2022).
- Horiuchi and Itagaki [2023] W. Horiuchi and N. Itagaki, Imprints of clustering in the density profiles of and , Phys. Rev. C 107, L021304 (2023).
- Baye et al. [1994] D. Baye, P. Descouvemont, and N. Timofeyuk, Matter densities of and in a microscopic cluster model and the proton-halo problem of 8b, Nuclear Physics A 577, 624 (1994).
- Neumaier et al. [2002] S. Neumaier, G. Alkhazov, M. Andronenko, A. Dobrovolsky, P. Egelhof, G. Gavrilov, H. Geissel, H. Irnich, A. Khanzadeev, G. Korolev, A. Lobodenko, G. Munzenberg, M. Mutterer, W. Schwab, D. Seliverstov, T. Suzuki, N. Timofeev, A. Vorobyov, and V. Yatsoura, Small-angle proton elastic scattering from the neutron-rich isotopes 6he and 8he, and from 4he, at 0.7 gev in inverse kinematics, Nuclear Physics A 712, 247 (2002).
- Kiselev et al. [2011] O. Kiselev, F. Aksouh, A. Bleile, O. Bochkarev, L. Chulkov, D. Cortina-Gil, A. Dobrovolsky, P. Egelhof, H. Geissel, M. Hellstrm, N. Isaev, B. Komkov, M. Mato, F. Moroz, G. Mnzenberg, M. Mutterer, V. Mylnikov, S. Neumaier, V. Pribora, D. Seliverstov, L. Sergueev, A. Shrivastava, K. Smmerer, H. Weick, M. Winkler, and V. Yatsoura, A new experimental approach to investigate intermediate-energy proton elastic scattering and breakup reactions on exotic nuclei in inverse kinematics, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 641, 72 (2011).
- Myo et al. [2012] T. Myo, Y. Kikuchi, and K. Katō, Five-body resonances of 8c using the complex scaling method, Phys. Rev. C 85, 034338 (2012).
- Bohr and Mottelson [1975] A. Bohr and B. Mottelson, Nuclear Structure, Vol.2, Nuclear Deformations, edited by W.A.Benjamin (Advanced Book Program, 1975).