DIMIX: DIminishing MIXing for Sloppy Agents
Abstract
We study non-convex distributed optimization problems where a set of agents collaboratively solve a separable optimization problem that is distributed over a time-varying network. The existing methods to solve these problems rely on (at most) one time-scale algorithms, where each agent performs a diminishing or constant step-size gradient descent at the average estimate of the agents in the network. However, if possible at all, exchanging exact information, that is required to evaluate these average estimates, potentially introduces a massive communication overhead. Therefore, a reasonable practical assumption to be made is that agents only receive a rough approximation of the neighboring agents’ information. To address this, we introduce and study a two time-scale decentralized algorithm with a broad class of lossy information sharing methods (that includes noisy, quantized, and/or compressed information sharing) over time-varying networks. In our method, one time-scale suppresses the (imperfect) incoming information from the neighboring agents, and one time-scale operates on local cost functions’ gradients. We show that with a proper choices for the step-sizes’ parameters, the algorithm achieves a convergence rate of for non-convex distributed optimization problems over time-varying networks, for any . Our simulation results support the theoretical results of the paper.
1 Introduction
Distributed learning serves as a learning framework where a set of computing nodes/agents are interested in collaboratively solving an optimization problem. In this paradigm, in the absence of a central node, the learning task solely depends on on-device computation and local communication among the neighboring agents. With the appearance of modern computation architectures and the decentralized nature of storage, large-scale distributed computation frameworks have received significant attention due to data locality, privacy, data ownership, and scalability to larger datasets and systems. These features of distributed learning have led to applications in several domains including distributed deep networks [1, 2, 3], distributed sensor networks [4, 5, 6], and network resource allocation [7, 8]. In the context of Machine Learning, a prototypical application of distributed learning and optimization is the empirical risk minimization (ERM) problem. In ERM problems, each server in a network of data centers has access to a number of independent data points (realizations) sampled from an underlying distribution, and the objective is to minimize an additive and separable cost function (of the data points) over the underlying network [9, 10, 11].
Related Works. Decentralized consensus or averaging-based optimization algorithms have been studied extensively over the past few years [12, 13, 14, 15, 16, 17]. It has been shown that when a fixed step-size is utilized, the loss function decreases with the rate of until the estimates reach a neighborhood of the (local) minimum of the objective cost function [12]. However, with a fixed step-size, the local estimates may not converge to an optimal point [16]. To remedy this, the diminishing step-size variation of the algorithm is introduced and studied for convex [18, 17, 19] and non-convex problems [20, 21, 22].
A majority of the existing works in this area suffer from requiring large communication overhead, as a (potentially) massive amount of local information is needed to be exchanged among the agents throughout the learning algorithm. In addition, such communication load can lead to a major delay in the convergence of the algorithm, and become a severe bottleneck when the dimension of the model is large. To mitigate the communication overhead, several compression techniques are introduced to reduce the size of the exchanged information. In particular, this is used in the context of distributed averaging/consensus problem [23, 12, 24], where each node has an initial numerical value and aims at evaluating the average of all initial values using exchange of quantized information, over a fixed or a time-varying network. In the context of distributed optimization, various compression approaches have been introduced to mitigate the communication overhead [25, 26, 27, 28, 29].
An inexact proximal gradient method with a fixed step-size over a fixed network for strongly convex loss functions is proposed in [25]. In this algorithm, each node applies an adaptive deterministic quantizer on its model and gradient before sending them to its neighbors. It is shown that under certain conditions, the algorithm provides a linear convergence rate. In another related work [26], authors proposed a decentralized gradient descent method, named ‘QuanTimed-DSGD’, with fixed step-sizes. In this algorithm, agents exchange a quantized version of their models/estimates in order to reduce the communication load. It is shown that for strongly convex loss functions and a given termination time , constant step-size parameters for the algorithm can be chosen so that the average distance between the model of the agents and the global optimum is bounded by for some and any . In this algorithm not only the step sizes depend on , but also the results only hold for the exact termination iteration , which further needs to satisfy , where itself depends on as well as non-local parameters of the fixed underlying network. For smooth non-convex cost functions, there it is shown that the temporal average (up to time ) of the expected norm of the gradients at average models does not exceed . However, similar to the strongly convex case, the choice of parameters (i.e., the step-sizes) for QuanTimed-DSGD depend on the termination time , and need to be re-evaluated when the target termination time varies. To compensate the quantization error, a decentralized (diminishing) gradient descent algorithm is proposed in in [27, 30] using error-feedback. The proposed algorithm achieve the convergence rate of and for strongly and non convex objective functions, respectively. However, the nature of the algorithm restricts its use to time-invariant networks and in addition, the feedback mechanism cannot compensate communication noise between the nodes. In [31], a two-time-scale gradient descent algorithm was presented for distributed constrained and convex optimization problems over an i.i.d. communication graph with noisy communication links, and sub-gradient errors. It is shown that if the random communication satisfies certain conditions, proper choices of the time-scale parameters result in the almost sure convergence of the local states to an optimal point. Another interesting approach to address exact convergence for distributed optimization with fixed gradient step-sizes under a noiseless communication model is to use gradient tracking methods [32, 33].
Our Contributions. We introduce and study a two time-scale decentralized gradient descent algorithm for a broad class of imperfect sharing of information over time-varying communication networks for distributed optimization problems with smooth non-convex local cost functions. In this work, one time-scale addresses the convergence of the local estimates to an stationary point while the (newly introduced) second time-scale is introduced to suppress the noisy effect of the imperfect incoming information from the neighbors.
Our main result shows that with a proper choice of the parameters for the two diminishing step-size sequences, the temporal average of the expected norm of the gradients decreases with the rate of . To prove this result, we have established new techniques to analyze the interplay between the two time-scales, in particular, in the presence of underlying time-varying networks. To validate our theoretical results, we numerically evaluate the algorithm for optimizing a regulized logistic regression on benchmark dataset MNIST. To assess the efficiency of our algorithm over time-varying networks, we also implement a linear regression model (convex) over synthetic data and a CNN (non-convex) over CIFAR-10. Our simulation results also confirm that introducing a time-shift in our step-sizes improves the finite-time performance of our algorithm leading to a faster decay of the loss function.
Paper Organization. After introducing some notations, we present the problem formulation, the algorithm, the main result, and some of its practical implications in Section 2. Our theoretical results are corroborated by simulation results in Section 3. To prove the main result, we first provide some auxiliary lemmas in Section 4 whose proofs are presented in Appendix A. In Sections 5, we present the proof of the main result. Finally, we conclude the paper in Section 7.
Notation and Basic Terminology. Throughout this paper, we use to denote the set of integers . In this paper, we are dealing with agents that are minimizing a function in . For notational convenience, throughout this paper, we assume that the underlying functions are acting on row vectors, and hence, we view vectors in as row vectors. The rest of the vectors, i.e., the vectors in , are assumed to be column vectors. The -norm of a vector is defined as . The Frobenius norm of a matrix is defined as . A vector is called stochastic if and . Similarly, a non-negative matrix is called (row) stochastic if for every . For a matrix , we denote its -th row and -th column by and , respectively. Note that we deal with two types of vector throughout the paper. For an matrix and a strictly positive stochastic vector , we define the -norm of by . It can be verified that is a norm on the space of matrices. Finally, we write if (is well-defined and) has non-negative entries.
2 Problem Setup and Main Result
In this section, first we formulate non-convex distributed optimization problems over time-varying networks and introduce some standard assumptions on the underlying problem. After proposing our algorithm, we state our main result. Finally, we discuss the implications of our result on various important practical settings with imperfect information sharing.
2.1 Problem Setup
This paper is motivated by stochastic learning problems in which the goal is to solve
| (1) |
where is a loss function, is the decision/optimization row vector, and is a random vector taking values in that is drawn from an unknown underlying distribution . One of the key practical considerations that renders (1) as a challenging task is that the underlying distribution is often unknown. Instead, we have access to independent realizations of and focus on solving the corresponding ERM problem which is given by
| (2) |
where is the empirical risk with respect to the data points . We assume that is a non-convex loss function, which potentially results in a non-convex function .
In distributed optimization, we have a network consisting of computing nodes (agents, or workers), where each node observes a non-overlapping subset of data points, denoted by , where . Here, represents the fraction of the data that is processed at node . Note that the vector is a strictly positive stochastic vector, i.e., and . Thus, the ERM problem in (2) can be written as the minimization of the weighted average of local empirical risk functions for all nodes in the network, i.e.,
| (3) |
where . We can rewrite the ERM problem in (3) as a distributed consensus optimization problem, given by
| (4) |
Consider an agents that are connected through a time-varying network. We represent this network at time by the directed graph , where the vertex set represents the set of agents and the edge set represents the set of links at time . At each discrete time , agent can only send information to its (out-) neighbors in , i.e., all with .
To discuss our algorithm (DIMIX) for solving (4) distributively, let us first discuss its general structure and the required information at each node for its execution. In this algorithm, at each iteration , agent updates its estimate of an optimizer of (3). To this end, it utilizes the gradient information of its own local cost function as well as a noisy/lossy average of its current neighbors estimates, denoted by . Here, is a row-stochastic matrix that is consistent with the underlying connectivity network (i.e., only if ) and is a random noise vector. Later, in Section 2.4 we discuss several noisy and lossy information sharing architectures (quantization and noisy communication) that fit in this broad information structure. Now we are ready to discuss the DIMIX algorithm. In this algorithm, using the information available to agent at time , agent updates its current estimate by computing a diminishing weighted average of its own state and the noisy average of its neighbors’ estimates, and moves along its local gradient. More formally, the update rule at node is given by
| (5) |
where and for some are the diminishing step-sizes of the algorithm, and is an arbitrary shift, that is introduced to accelerate the finite-time performance of the algorithm. The description of DIMIX is summarized in Algorithm 1. For notational simplicity, let
| (6) |
Since , we can rewrite the update rule in (5) in the matrix format
| (7) |
Let us discuss some important aspects of the above update rule. Note that both and are diminishing step-sizes. If and are both constants, then the dynamics in (7) reduces to the algorithm proposed in [26] for both convex and non-convex cost functions. Alternatively, if is a constant sequence and for all , (7) would be reduced to the averaging-based distributed optimization with diminishing steps-sizes (for gradients), which is introduced and studied in [18] for local convex cost functions . The newly introduced time-scale/step-size suppresses the incoming noise from the neighboring agents. However, also suppresses the incoming signal level at each node . This casts a major technical challenge for establishing convergence-to-consensus guarantees for the algorithm over time-varying networks.
On the other hand, the diminishing step-size for the gradient update is . We chose to represent our algorithm in this way to ensure that the local mixing (consensus) scheme is operated on a faster time-scale than the gradient descent.
2.2 Assumptions
In order to provide performance guarantees for DIMIX, we need to assume certain regularity conditions on (i) the statistics of the (neighbors’ averaging) noise process , (ii) the mixing properties of the weight sequence , and (iii) the loss function .
First, we discuss our main assumption on the noise sequence .
Assumption 1 (Neighbors State Estimate Assumption)
Suppose that is adapted to a filtration on the underlying probability space (see e.g. Section 5.2 in [34]). We assume that there exists some such that for all and all , the noise sequence satisfies
| (8) | ||||
| (9) |
Note that the natural filtration of the random process is one choice for . In this case, (8) reduces to and
Next, we discuss the main assumption on the network connectivity, or more precisely, the mixing of information over the time-varying network.
Assumption 2 (Connectivity Assumption)
We assume that the weight matrix sequence in (7) satisfies the following properties
-
(a)
Stochastic with Common Stationary Distribution: is non-negative and and for all , where is the all-one vector, and is the weight vector.
-
(b)
Bounded Nonzero Elements: There exists some such that if for some and we have , then .
-
(c)
-Connected: For a fixed integer , the graph is strongly connected for all , where .
Finally for the loss function , we make the following assumption.
Assumption 3 (Stochastic Loss Function Assumption)
We assume that:
-
(a)
The function is -smooth with respect to its first argument, i.e., for any and we have that .
-
(b)
Stochastic gradient is unbiased and variance bounded, i.e.,
Note that Assumption 3-b implies a homogeneous sampling, i.e., each agent draws i.i.d. sample points from a data batch. In a related work [35], a stronger assumption has been considered which allows for heterogeneous data samples.
Remark 1
Recall that local function is defined as . Then the conditions of Assumption 3 on the function can be directly translated to conditions on given by
.
2.3 Main Result
Here, we characterize the convergence rates of our algorithm for the -smooth non-convex loss functions. More precisely, we establish a rate for the temporal average of the expected norm of the gradients for various choice of the time-scale parameters .
Theorem 1
Suppose that Assumptions 1–3 hold and let , where , , and are arbitrary constants with and . Then the weighted average estimates generated by Algorithm 1 satisfy
| (10) |
where is an arbitrary constant.
Furthermore, for we get the optimal rate of
| (11) |
Remark 2
Note that the expectation operator is over the randomness of the dataset and the compression/communication noise. Moreover, note that the theorem above shows that the gradient of (which depends of the choice of ) at the average state of (which also depends on ) vanishes at a certain rate. It is worth mentioning that this is not the performance of the average trajectory for the average function.
Remark 3
Proposition 1
Remark 4
We should comment that almost universally, all the existing results and algorithms on distributed optimization algorithms for time-varying graphs assume a uniform positive lower bound on non-zero elements of the (effective) weight matrices [36, 12, 37, 38, 39, 16, 21, 40]. Absence of such an assumption significantly increases the complexity of the convergence analysis of the algorithm. In our work, even though the stochastic matrix sequence is assumed to be -connected, the effective averaging weight sequence, that is given by , has vanishing (non-self) weights. One of the major theoretical contributions of this work is to introduce tools and techniques to study distributed optimization with diminishing weight sequences.
Remark 5
In a related work [26] on distributed optimization with compressed information sharing among the nodes, authors considered a fixed step-size (zero time-scale) version of Algorithm 1 with a fixed averaging matrix . It is shown that for a given termination time , the algorithm’s step-sizes can be chosen (depending on ) such that the temporal average (up to iteration ) of the expected norm of the gradient (i.e., defined in (12)) does not exceed (where is a constant). However, the step-sizes should be re-evaluated and the algorithm needs to be re-executed if one targets another termination time . In this work, we use vanishing step-sizes and (which do not depend on the termination time) and show that the same temporal average vanishes at the rate of for every iteration and any arbitrarily small .
2.4 Examples for Stochastic Noisy State Estimation

The noisy information in (5) is very general, and captures several models of imperfect data used in practice and/or theoretical studies. A rather general architecture that leads to such noisy/lossy estimates is demonstrated in Figure 1: Once the estimate of node at iteration is evaluated, node may apply an operation (such as compression/sparsification or quantization) on its own model to generate . This data will be sent over a potentially noisy communication channel, and a neighbor will receive a corrupted version of , say from every neighbor node . Upon receiving such channel outputs from all its neighbors, node computes their weighted average . This can be decoded to the approximate average model . In the following we describe three popular frameworks, in which each node can only use an imperfect neighbors’ average to update its estimate. It is worth emphasizing that these are just some examples that lie under the general model in (5).
Example 1
(Unbiased Random Sparsification). Let be the set of all subsets of of size for a parameter . We define the operator as
| (16) |
For a given time, with being drawn uniformly at random from independent of the input vector , iteration, and other agents, is an unbiased version of the random sparisification introduced in [41]. It can be verified that, when , we have
Then, we can get
where . From the properties of , we can verify that and
which fulfills the conditions of Assumption 1. With respect to the architecture of Figure 1, we have . Moreover, the noisy channel is perfect, and the decoder is just an identity function, i.e., and .
Example 2
(Stochastic Quantizer with bounded trajectory). The stochastic quantizer with a number of quantization levels maps a vector to a random vector , where its th entry is given by
| (17) |
and is a random variable taking values
| (20) |
Note that, random variables are independent, across the coordinates, agents, and time steps. Thus, in this case, the relationship between and in Figure 1 would be . Furthermore, the noisy channel is perfect, and the decoder component is just an identity function, i.e., and . It is shown in [42] that applying this quantizer on with a bounded norm satisfies and . Therefore, the neighbors estimate for node will be
where satisfies and
provided that for every and every . Therefore, the conditions of Assumption 1 are satisfied.
Note that in both examples above and might be correlated, especially when nodes and have common neighbor(s). However, this does not violate the conditions of Assumption 3.
Example 3
(Noisy Communication). The noisy neighbor estimate model may arise due to imperfect communication between the agents. Consider a wireless network, in which the computing nodes communicate with their neighbors over a Gaussian channel, i.e., when node sends its state (without compression, i.e., ) to its neighbor , the signal received at node is where is a zero-mean Gaussian noise with variance , independent across , and . Applying an identity map decoder at node (i.e., ) we have
Thus, we get implying
. Hence, the conditions of Assumption 1 are satisfied.
3 Experimental Results
In the following, we discuss two sets of simulations to verify our theoretical results. First, we perform Algorithm 1 for a fixed network to compare fixed step-sizes [26] versus diminishing step-sizes (this work). Then, we compare the performance of our algorithm on fixed versus time-varying graph. Throughout this section, we use the unbiased stochastic quantizer in (17) with various total number of quantization levels . For CNN experiments over CIFAR-10 and regularized logistic regression problem over MNIST dataset, the mini-batch size is set to be and , respectively, the loss function is the cross-entropy function, we use data points which are distributed across agents. Moreover, for each set of experiments, we distribute the data points across the nodes according to , where is drawn uniformly at random from the interval . Our codes are implemented using Python and tested on a 2017 MacBook Pro with 16 GB memory and a 2.5 GHz Intel Core i7 processor.
3.1 DIMIX vs. QuanTimed-DSGD over Fixed Network
We use regularized logistic regression to validation our algorithm on the benchmark dataset MNIST. Data and Experimental Setup. In this experiments we train a regularized logistic regression to classify the MNIST dataset over a fixed network. First, we generate a random (connected) undirected Erdös-Renyi graph with the edge probability , which is fixed throughout this experiment. We also generate a doubly stochastic weight matrix where is the Laplacian matrix and is the maximum degree of the graph. Finally, we use the time-invariant weight sequence , where , , and is a diagonal matrix with as its th diagonal element. It can be verified that satisfies the conditions of Assumption 2, i.e., it is row-stochastic and satisfies . We implemented our algorithm with quantizer parameter and tuned the step-size parameters , , with . For the fixed step-sizes, we used the termination time , which results in and for all .

Results. The plot in Figure 2 shows network variance defined by for fixed and diminishing step-sizes. It can be observed that with a fixed step-sizes algorithm we can only reach a neighborhood of the average model, but a consensus is not necessarily achieved. However, using diminishing step-sizes guarantees that each node’s state converges to the average model.
3.2 Diminishing Step-sizes over Time-varying vs. Fixed Network
Here, we provide simulation results to demonstrate the performance of DIMIX on time-varying networks. For this, we conduct simulations on non-convex (CNN) and convex (linear regression) problems. For the sake of comparison, we apply our algorithm on a corresponding fixed network.
Data and Experimental Setup. For the non-convex setting, we study the problem of learning the parameters of the LeNet-5 CNN [43] for CIFAR-10 dataset. The LeNet-5 CNN architecture consists of two convolutional layers, two sub-sampling (pooling) layers, and three fully connected layers, with the ReLU activation function. As before we have nodes and data points, which are distributed among the agents according to some stochastic vector . For the convex setting, we consider a -dimensional linear regression problem. We generate data points , where , with , and for all . In order to generate the data, we uniformly and independently draw the entries of each and each from and , respectively. Similarly, entries of are sampled uniformly and independently from . The goal is to estimate the unknown coefficient vector , which leads to solving the minimum mean square error problem, i.e.,
.
Experiments with Fixed Graph. We consider a fixed undirected cyclic graph , where , and . For these experiments, the stochastic matrix sequence for any is given by
| (21) |
Experiments with Time-varying Graph. To evaluate Algorithm 1 for a time-varying network, we use cyclic gossip [44, 45, 6, 46, 47] iterations. Here, the algorithm goes through the cycle graph (described above), and a pair of neighbors (on the cycle) exchange their information at a time. More precisely, at time , the averaging graph only consists of a single edge . For , we let
| (22) |
Note that each edge in will be visited periodically, and hence, the sequence of stochastic matrices in (22) is -connected with .


Results. In Figure 3, the plot on the left demonstrates the training loss of LeNet-5 for CIFAR-10 dataset and the plot on the right shows the training loss of the linear regression. Here, ‘Fixed network’ refers to the full cycle with stochastic matrix in (21) and ‘Time-varying network’ refers to the network with stochastic matrix sequence in (22). For the CNN, the parameters of the dynamics in (5) are fine-tuned to , , , and is the parameter of the stochastic quantizer for both networks. For the linear regression model, the parameter are adjusted to , , and with the quantizer parameter . It can be observed that the algorithm works for both fixed and time-varying networks. However, the performance of the algorithm over the time-varying network naturally suffers from a slower convergence, which is due to a slower mixing of information over the network.
4 Auxiliary Lemmas
The following lemmas are used to facilitate the proof of the main result of the paper. We present the proofs of Lemmas 1–5 in Section A.
Lemma 1
For any pair of vectors , , and any scalar , we have
| (23) |
Similarly, for matrices and and any scalar , their -norm satisfy
| (24) |
Lemma 2
Let be a sequence in and be a positive scalar. Then the following identities hold
| (25) | ||||
| (26) |
As a result, for any sequence in and , we have
and
Lemma 3
For any , , and , we have
| (27) |
Lemma 4
For an matrix and matrix , we have:
As we discussed in Remark 4, we cannot use the conventional results (e.g., in [48, 36, 12, 37, 38, 39, 16, 21, 40]) to bound the norm of a vector after averaging with matrices with diminishing weights. The following lemma provides a new bounding techniques, which we will use in the proof of the main result of this work.
Lemma 5
Let satisfy the Connectivity Assumption 2 with parameters , and let be given by where for all and is a non-increasing sequence. Then, for any matrix , parameter , and all , we have
where and .
5 Proof of Theorem 1
For our analysis, first we obtain an expression for the average reduction of the objective function at the average of the states, i.e., . Recall that for all . Hence, multiplying both sides of (7) by , we get
From Assumption 3-(a) Lemma 3.4 in [49] we can conclude
or equivalently,
Then, since is adapted to the filtration and using Assumption 1, we arrive at
| (28) | ||||
| (29) |
Let us focus on the second term in (28). Using the identity , we can write
| (30) |
Moreover, we have
where the last inequality holds as is a convex function and the is a stochastic vector. Therefore, using the above inequality and Assumption 3-(a), we get
| (31) | ||||
| (32) |
Next, we analyze the last term in (28). From Assumption 1 we have , which leads to
| (33) |
For the first term in (33), we again exploit Assumption 1 which implies
| (34) |
where we used the fact that and the inequality holds since
for all . Thus, the last term in (28) is upper bounded as
| (35) |
Therefore, replacing (30), (31), and (35) in (28) we get
Taking the expectation of both sides lead to
| (36) | ||||
| (37) | ||||
| (38) |
5.1 State Deviations from the Average State:
Note that the dynamics in (7) can be viewed as the linear time-varying system
| (39) |
with
The solution of (39) is given by
| (40) |
where with is the transition matrix of the linear system (39). For the simplicity of notations, let us define
As a result of Lemma 5, we have
where is defined by
| (41) |
Now consider the dynamic in (40). Assuming , we get
| (42) |
Moreover, multiplying both sides of (42) from the left by and using , we get
| (43) |
Then, subtracting (43) from (42), and plugging the definition of we have
Therefore, using Lemma 1 with , we get
By expanding , we get
| (44) | ||||
| (45) |
Recall from Assumption 1 that . Moreover, since is measurable with respect to for , we have
Using a similar argument for and conditioning on , we conclude that the above relation holds for all . Therefore, taking the expectation of both sides of (44) and noting that the average of the second and the forth terms are zero, we get
| (46) |
We continue with bounding the first term in (46). First note that Assumption 1 implies
| (47) |
This together with Lemma 5 leads to
| (48) | ||||
| (49) |
To bound the second term in (46), we use the triangle inequality for the norm , and write
| (50) | ||||
Using Lemma 5 and , we can upper-bound this expression as
| (51) | ||||
| (52) | ||||
| (53) | ||||
| (54) | ||||
| (55) | ||||
| (56) |
where is given by (41). Next, the fact that and Lemma 2 imply
| (57) | ||||
| (58) | ||||
| (59) |
Using this inequality in (56), we get
| (60) |
Finally, using the bounds obtained in (48) and (60) in (46) we arrive at
| (61) | ||||
| (62) |
5.2 Analysis of the overall deviation:
Our goal here is to bound the overall weighted deviation of the states from their average. First recall the bound for , derived in Section 5.1 for each . Our goal here is to bound
| (63) | ||||
Focusing on the first term in (63), we can write
| (64) | ||||
| (65) | ||||
| (66) |
where the first inequality is due to the fact that for , and the second one follows from Lemma 2. Similarly, using the fact that for , for the second term in (63), we have
| (67) | |||
| (68) | |||
| (69) |
Recall that . Then, using the fact that , we can write
| (70) | ||||
| (71) |
where the last inequality follows from Lemma 2. Therefore, from (69) and (71) we have
| (72) |
Therefore, from (64) and (72) we can conclude
| (73) |
5.3 Bounding
In this part, we study , to provide an upper bound for it. Following [26], we can rewrite as
Then, since is a convex function, we have
| (74) |
Next, we bound each term in (5.3). Recall from (6) that the th row of is given by , where is the th row of matrix . Thus, from Assumption 3-(a) we have
| (75) | ||||
| (76) | ||||
| (77) |
Similarly, using the convexity of function , for the second term in (5.3) we have
| (78) | |||
| (79) | |||
| (80) | |||
| (81) | |||
| (82) | |||
| (83) | |||
| (84) | |||
| (85) | |||
| (86) |
where in (a) we replaced the definitions of and from (3) and (2), respectively, the equality in (b) holds since s are independent samples from the underlying distribution, and (c) follows from Assumption 3-(b) and the fact that for . Finally, for the third term in (5.3), we have
| (87) |
Plugging (77)–(87) in (5.3), we get
| (88) |
Next, replacing this bound in (73), we arrive at
| (89) | ||||
| (90) | ||||
| (91) | ||||
| (92) |
Now, let us define .
Then, and , where and .
Furthermore, we
set such that . Then, for we can rewrite (89) as
where the second inequality holds since is a non-increasing sequence, and
| (93) |
does not grow with . Therefore, we have
| (94) | ||||
| (95) | ||||
| (96) |
5.4 Back to the Main Dynamics
Recall the dynamics in (36), that is,
Summing (36) for , and using (94) we get
| (97) | ||||
| (98) | ||||
| (99) | ||||
| (100) | ||||
| (101) | ||||
| (102) | ||||
| (103) |
where . Recall that for . Moreover, for and defined in Lemma 5 we have and . Therefore, for we have
This allows us to lower bound the second summation in (97) for as
| (104) | ||||
| (105) | ||||
| (106) | ||||
| (107) |
where does not grow with , and the inequality holds since for . Similarly, for , we have . Therefore, for , the last summation in (97) can be upper bounded by
| (108) | ||||
| (109) | ||||
| (110) | ||||
| (111) |
where
| (112) |
does not depend on . Plugging (104) and (108) in (97), for , we get
Hence,
| (113) | |||
| (114) | |||
| (115) | |||
| (116) | |||
| (117) |
where
is constant (does not depend on ), and the last inequality in (117) follows from the fact that
| (118) |
5.5 Bound on the Moments of and
The inequality in (117) provides us with an upper bound on the temporal average of sequence . However, our goal is to derive a bound on the temporal average of . To this end, for any given , we define the measure of convergence as
Note that by Hölder’s inequality [50, Theorem 6.2] for any with , and non-negative sequences and , we have
or equivalently,
| (119) |
Let so that . Furthermore, let
| (120) | ||||
Then, applying Hölder’s inequality (119), we arrive at
| (121) |
It remains to upper bound the terms in the right hand side of (121). First, using Lemma 3 we get
Therefore,
| (122) |
Next, continuing from (117), for we can write
| (123) | ||||
| (124) | ||||
| (125) |
where the last inequality follows from the fact that . Next, we can use Lemma 3 to bound , as
| (126) |
where we used the fact that for . Similarly, applying Lemma 3 on , we get
| (127) | ||||
| (128) |
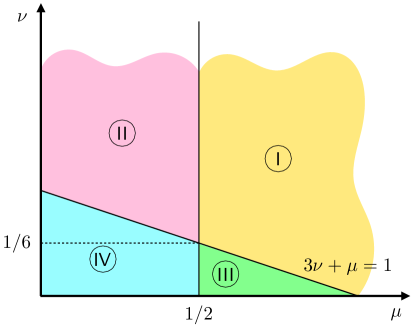
in which we have upper bounded by by , for . Note that the upper bound in (123) is the maximum of a constant, and two functions. Moreover, depending on the values of and , each can be upper bounded by a constant, a logarithmic function, or a polynomial (in ). Figure 4 illustrates the four regions of . In the following we first, analyze the interior of the four regions shown in Figure 4, and then study the boundary cases.
Region : and
Recall from (126) and (127) that both and are upper bounded by constant functions, which grows faster than a constant. Hence, from (123) in this regime we have
| (129) | ||||
| (130) | ||||
| (131) |
Note that does not depend on . Plugging (122) and (129) in (121), we arrive at
| (132) |
Region : and
From (126) and (127), we can see that and the upper bounded by a polynomial and a constant function of , respectively. Noting that for sufficiently large , a polynomial function beats any constant, we can write
| (133) | ||||
| (134) | ||||
| (135) |
This together with (121) and (122) implies
| (136) |
Region : and
Recall from (126) and (127) that and are upper bounded by a constant and a polynomial function of , respectively. Therefore, for sufficiently large , we get
| (137) | ||||
| (138) | ||||
| (139) |
Therefore, plugging (137) and (122) to (121), we get
| (140) |
Region : and
In this region, we can use (126) and (127) to upper bound both and by polynomial functions. Thus, for sufficiently large , we get
| (141) | ||||
| (142) | ||||
| (143) |
Then, we can plug (141) and (122) to (121), to conclude
| (144) | ||||
| (145) |
Summarizing the result of the four cases above, we get
| (146) | ||||
| (147) |
which concludes the first claim of Theorem 1.
Recall that our goal is to optimize over to achieve the best convergence rate. This is equivalent to maximizing the exponent of in each of the four regions, i.e.,
Interestingly, it turns out that the respective supremum value in all four regions is , which corresponds to the boundary point . However, this point does not belong to any of the corresponding open sets, which motivates the convergence analysis of for .
6 Proof of Proposition 1
First note that we cannot directly conclude the proposition from Theorem 1, since the theorem only holds for , and not . In order to show the claim, for a vector and some we define222Note that for is not a norm, since it is not a subadditive function for . . Then we have since
where the inequality holds since we have , and .
Now, for the vector with we have
Then, from Theorem 1 for and , we get
| (155) |
where the last equality holds since for any . Similarly, for the vector with and any we have
| (156) |
We need to bound the RHS of (6). Let and . Then, using the Hölder’s inequality in (119) for we can write
| (157) |
Note that is bounded in (122). Moreover, for we can write
| (158) |
where follows from (94), holds since , the inequality in follows from (117) and (118), we have used a bounds in (126) and (127) for in , and holds since the constant term is upper bounded by for large enough . Plugging (122) for and (158) into (157) and (6), and setting we arrive at
| (159) |
where the last equality holds since for any . Finally, combining (12), (13), and using Assumption 3 and Lemma 1 (for ) we have
for every . This concludes the proof of Proposition 1.
7 Conclusion
We have studied non-convex distributed optimization over time-varying networks with lossy information sharing. Inspired by the original averaging-based distributed optimization algorithm, we proposed and studied a two-time scale decentralized algorithm including a damping mechanism for incoming information from the neighboring agents as well as local cost functions’ gradients. We presented the convergence rate for various choices of the diminishing step-size parameters. By optimizing the achieved rate over all feasible choices for parameters, the algorithm obtains a convergence rate of for non-convex distributed optimization problems over time-varying networks, for any . Our theoretical results are corroborated by numerical simulations.
References
- [1] J. Dean, G. Corrado, R. Monga, K. Chen, M. Devin, M. Mao, M. Ranzato, A. Senior, P. Tucker, K. Yang, et al., “Large scale distributed deep networks,” in Advances in neural information processing systems, pp. 1223–1231, 2012.
- [2] M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis, J. Dean, M. Devin, S. Ghemawat, G. Irving, M. Isard, et al., “Tensorflow: A system for large-scale machine learning,” in 12th USENIX Symposium on OSDI, pp. 265–283, 2016.
- [3] P. H. Jin, Q. Yuan, F. Iandola, and K. Keutzer, “How to scale distributed deep learning?,” in NIPS Workshop MLSystems, 2016.
- [4] D. Li, K. D. Wong, Y. H. Hu, and A. M. Sayeed, “Detection, classification, and tracking of targets,” IEEE signal processing magazine, vol. 19, no. 2, pp. 17–29, 2002.
- [5] M. Rabbat and R. Nowak, “Distributed optimization in sensor networks,” in Proceedings of the 3rd International Symp. on Information processing in Sensor Networks, pp. 20–27, 2004.
- [6] S. Kar and J. M. Moura, “Distributed consensus algorithms in sensor networks with imperfect communication: Link failures and channel noise,” IEEE Trans. Signal Process., vol. 57, no. 1, pp. 355–369, 2008.
- [7] A. Ribeiro, “Ergodic stochastic optimization algorithms for wireless communication and networking,” IEEE Transactions on Signal Processing, vol. 58, no. 12, pp. 6369–6386, 2010.
- [8] T. Chen, Q. Ling, and G. B. Giannakis, “An online convex optimization approach to proactive network resource allocation,” IEEE Trans. Signal Process., vol. 65, no. 24, pp. 6350–6364, 2017.
- [9] A. Nedić, S. Lee, and M. Raginsky, “Decentralized online optimization with global objectives and local communication,” in 2015 American Control Conference (ACC), pp. 4497–4503, IEEE, 2015.
- [10] R. Xin, A. K. Sahu, S. Kar, and U. A. Khan, “Distributed empirical risk minimization over directed graphs,” in 2019 53rd Asilomar Conference on Signals, Systems, and Computers, pp. 189–193, IEEE, 2019.
- [11] H. Zhang, M. Cisse, Y. N. Dauphin, and D. Lopez-Paz, “mixup: Beyond empirical risk minimization,” arXiv preprint arXiv:1710.09412, 2017.
- [12] A. Nedić and A. Ozdaglar, “Distributed subgradient methods for multi-agent optimization,” IEEE Trans. Automat. Contr., vol. 54, no. 1, pp. 48–61, 2009.
- [13] I. Lobel and A. Ozdaglar, “Distributed subgradient methods for convex optimization over random networks,” IEEE Trans. Automat. Contr., vol. 56, no. 6, pp. 1291–1306, 2010.
- [14] I. Lobel, A. Ozdaglar, and D. Feijer, “Distributed multi-agent optimization with state-dependent communication,” Mathematical programming, vol. 129, no. 2, pp. 255–284, 2011.
- [15] J. Chen and A. H. Sayed, “Diffusion adaptation strategies for distributed optimization and learning over networks,” IEEE Trans. Signal Process., vol. 60, no. 8, pp. 4289–4305, 2012.
- [16] K. Yuan, Q. Ling, and W. Yin, “On the convergence of decentralized gradient descent,” SIAM Journal on Optimization, vol. 26, no. 3, pp. 1835–1854, 2016.
- [17] D. Jakovetić, J. Xavier, and J. M. Moura, “Fast distributed gradient methods,” IEEE Trans. Automat. Contr., vol. 59, no. 5, pp. 1131–1146, 2014.
- [18] A. Nedić, A. Ozdaglar, and P. A. Parrilo, “Constrained consensus and optimization in multi-agent networks,” IEEE Trans. Automat. Contr., vol. 55, no. 4, pp. 922–938, 2010.
- [19] A. Nedić and A. Olshevsky, “Distributed optimization over time-varying directed graphs,” IEEE Trans. Automat. Contr., vol. 60, no. 3, pp. 601–615, 2014.
- [20] Y. Sun, G. Scutari, and D. Palomar, “Distributed nonconvex multiagent optimization over time-varying networks,” in IEEE Asilomar Conf. Signals Syst. Comput., pp. 788–794, 2016.
- [21] T. Tatarenko and B. Touri, “Non-convex distributed optimization,” IEEE Trans. Automat. Contr., vol. 62, no. 8, pp. 3744–3757, 2017.
- [22] J. Zeng and W. Yin, “On nonconvex decentralized gradient descent,” IEEE Transactions on signal processing, vol. 66, no. 11, pp. 2834–2848, 2018.
- [23] A. Kashyap, T. Başar, and R. Srikant, “Quantized consensus,” Automatica, vol. 43, no. 7, pp. 1192–1203, 2007.
- [24] K. Cai and H. Ishii, “Quantized consensus and averaging on gossip digraphs,” IEEE Trans. Automat. Contr., vol. 56, no. 9, pp. 2087–2100, 2011.
- [25] Y. Pu, M. N. Zeilinger, and C. N. Jones, “Quantization design for distributed optimization,” IEEE Trans. Automat. Contr., vol. 62, no. 5, pp. 2107–2120, 2016.
- [26] A. Reisizadeh, H. Taheri, A. Mokhtari, H. Hassani, and R. Pedarsani, “Robust and communication-efficient collaborative learning,” in Advances in Neural Information Processing Systems, pp. 8388–8399, 2019.
- [27] A. Koloskova, S. Stich, and M. Jaggi, “Decentralized stochastic optimization and gossip algorithms with compressed communication,” in International Conference on Machine Learning, pp. 3478–3487, PMLR, 2019.
- [28] H. Reisizadeh, B. Touri, and S. Mohajer, “Distributed optimization over time-varying graphs with imperfect sharing of information,” arXiv preprint arXiv:2106.08469, 2021.
- [29] H. Reisizadeh, B. Touri, and S. Mohajer, “Adaptive bit allocation for communication-efficient distributed optimization,” in 2021 60th IEEE Conference on Decision and Control (CDC), pp. 1994–2001, IEEE, 2021.
- [30] A. Koloskova, T. Lin, S. U. Stich, and M. Jaggi, “Decentralized deep learning with arbitrary communication compression,” arXiv preprint arXiv:1907.09356, 2019.
- [31] K. Srivastava and A. Nedic, “Distributed asynchronous constrained stochastic optimization,” IEEE journal of selected topics in signal processing, vol. 5, no. 4, pp. 772–790, 2011.
- [32] S. Pu and A. Nedić, “A distributed stochastic gradient tracking method,” in 2018 IEEE Conference on Decision and Control (CDC), pp. 963–968, IEEE, 2018.
- [33] J. Zhang and K. You, “Decentralized stochastic gradient tracking for non-convex empirical risk minimization,” arXiv preprint arXiv:1909.02712, 2019.
- [34] R. Durrett, Probability: theory and examples. Cambridge University Press, 2010.
- [35] X. Lian, C. Zhang, H. Zhang, C.-J. Hsieh, W. Zhang, and J. Liu, “Can decentralized algorithms outperform centralized algorithms? a case study for decentralized parallel stochastic gradient descent,” arXiv preprint arXiv:1705.09056, 2017.
- [36] A. Nedić, A. Olshevsky, A. Ozdaglar, and J. N. Tsitsiklis, “On distributed averaging algorithms and quantization effects,” IEEE Trans. Automat. Contr., vol. 54, no. 11, pp. 2506–2517, 2009.
- [37] A. Nedić and A. Olshevsky, “Distributed optimization of strongly convex functions on directed time-varying graphs,” in IEEE Glob. Conf. Signal Inf. Process. Proc., pp. 329–332, 2013.
- [38] B. Touri and A. Nedić, “Product of random stochastic matrices,” IEEE Trans. Automat. Contr., vol. 59, no. 2, pp. 437–448, 2013.
- [39] B. Touri and C. Langbort, “On endogenous random consensus and averaging dynamics,” IEEE Transactions on Control of Network Systems, vol. 1, no. 3, pp. 241–248, 2014.
- [40] A. Aghajan and B. Touri, “Distributed optimization over dependent random networks,” arXiv preprint arXiv:2010.01956, 2020.
- [41] S. U. Stich, J.-B. Cordonnier, and M. Jaggi, “Sparsified sgd with memory,” arXiv preprint arXiv:1809.07599, 2018.
- [42] D. Alistarh, D. Grubic, J. Li, R. Tomioka, and M. Vojnovic, “Qsgd: Communication-efficient sgd via gradient quantization and encoding,” in Advances in Neural Information Processing Systems, pp. 1709–1720, 2017.
- [43] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, “Gradient-based learning applied to document recognition,” Proceedings of the IEEE, vol. 86, no. 11, pp. 2278–2324, 1998.
- [44] S. Boyd, A. Ghosh, B. Prabhakar, and D. Shah, “Randomized gossip algorithms,” IEEE transactions on information theory, vol. 52, no. 6, pp. 2508–2530, 2006.
- [45] A. G. Dimakis, S. Kar, J. M. Moura, M. G. Rabbat, and A. Scaglione, “Gossip algorithms for distributed signal processing,” Proceedings of the IEEE, vol. 98, no. 11, pp. 1847–1864, 2010.
- [46] S. S. Ram, A. Nedić, and V. V. Veeravalli, “Asynchronous gossip algorithm for stochastic optimization: Constant stepsize analysis,” in Recent Advances in Optimization and its Applications in Engineering, pp. 51–60, Springer, 2010.
- [47] S. Lee and A. Nedić, “Asynchronous gossip-based random projection algorithms over networks,” IEEE Trans. Automat. Contr., vol. 61, no. 4, pp. 953–968, 2015.
- [48] P. M. DeMarzo, D. Vayanos, and J. Zwiebel, “Persuasion bias, social influence, and unidimensional opinions,” The Quarterly journal of economics, vol. 118, no. 3, pp. 909–968, 2003.
- [49] S. Bubeck, “Convex optimization: Algorithms and complexity,” Foundations and Trends in Machine Learning, vol. 8, no. 3-4, pp. 231–357, 2015.
- [50] G. B. Folland, Real analysis: modern techniques and their applications, vol. 40. John Wiley & Sons, 1999.
- [51] B. Touri and A. Nedić, “On existence of a quadratic comparison function for random weighted averaging dynamics and its implications,” in 2011 50th IEEE Conference on Decision and Control and European Control Conference, pp. 3806–3811, IEEE, 2011.
Appendix A Proof of Auxiliary Lemmas
In this section, we provide the proofs of auxiliary lemmas.
Proof of Lemma 1: For two vectors and (with identical dimension) and any scalar , we have
where follows from the Cauchy–Schwarz inequality and we used the geometric-arithmetic inequality in .
Now, recall that for a matrix we have . Therefore, for matrices and we have
This completes the proof of the lemma.
Proof of Lemma 2: To prove (25), let . Then, we have
Note that the last summation is a telescopic sum, we have
Dividing both sides by we arrive at (25). To show (26), we utilize the same idea by letting , we can write
Dividing both sides by , results in (26).
Proof of Lemma 3: In order to prove the lemma, we separately analyze the cases , , , and . Note that for , the function is a decreasing function, and thus we have . In the following we upper bound the latter integral for each regime of . When we have
| (160) |
which does not grow with . For , we get
| (161) |
When we arrive at
| (162) |
where the last inequality holds since .
Finally, for , the function is an increasing function. Hence, we can write
| (163) |
Note that the last inequality follows from which holds for any and .
Proof of Lemma 4: Recall that the th entry of the matrix product is the inner product between the th row of and the th column of . Thus, using the Cauchy-Schwarz inequality, we have . Therefore,
Using this inequality and the definition of -norm, we get
Proof of Lemma 5: Due to the separable nature of , i.e., , without loss of generality, we may assume that . Thus, let . Define by
| (164) |
For notational simplicity, let , and . Also with a slight abuse of notation, we denote by for .
Using Theorem 1 in [51], we have
| (165) |
where . Note that is a non-negative matrix, and hence we have , for . Also, note that since , then Assumption 2-(b) implies that the minimum non-zero elements of are bounded bellow by . Therefore, since is non-increasing, on the window , the minimum non-zero elements of for in this window are lower bounded by . Without loss of generality assume that the entries of are sorted, i.e., , otherwise, we can relabel the agents (rows and columns of s and to achieve this). Therefore, by Lemma 8 in [36], for (165), we have
| (166) |
We may comment here that although Lemma 8 in [36] is written for doubly stochastic matrices, and its statement is about the decrease of for the special case of , but in fact, it is a result on bounding for a sequence of -connected stochastic matrices in terms of the minimum non-zero entries of stochastic matrices .
Next, we will show that . This argument adapts a similar argument used in the proof of Theorem 18 in [36] to the general .
For a with , define the quotient
| (167) |
Note that is invariant under scaling and translations by all-one vector, i.e., for all non-zero and for all . Therefore,
| (168) | ||||
| (169) |
Since is a stochastic vector, then for a vector with and , we would have . On the other hand, the fact that would imply . Let us consider the difference sequence for , for which we have . Therefore, the optimization problem (168) can be rewritten as
| (170) | ||||
| (171) |
Using the Cauchy-Schwarz inequality, we get . Hence,
| (172) |
This implies that for , we have (note that this inequality also holds for with ). Using this fact in (A) implies
| (173) |
Applying (173) for steps recursively, we get
Using the fact that and since is a non-increasing sequence, we have
Recall from (165) that is non-increasing. Therefore, for we have
| (174) |
Next, since is a non-increasing sequence, we have . Thus,
| (175) |
Therefore, combining (A) and (A), we get
| (176) |
Now, we define
for with . Note that Assumption 2-(a) and the fact imply . Then, setting and , we can write
Therefore, using (A) we have
where the second inequality follows form the the fact that . This completes the proof of the lemma.