Digital Twin Earth - Coasts: Developing a fast and physics-informed surrogate model for coastal floods via neural operators

Peishi Jiang¹, Nis Meinert², Helga Jordão³, Constantin Weisser⁴
Simon Holgate⁵, Alexander Lavin,⁶ Björn Lütjens,^4,5, Dava Newman, ⁴
Haruko Wainwright⁷, Catherine Walker^8,9, Patrick Barnard¹⁰
1. Pacific Northwest National Laboratory, USA
2. German Aerospace Center (DLR), Germany
3. CERENA, Universidade de Lisboa, Portugal
4. Massachusetts Institute of Technology, USA
5. IBM Research, UK
6. Institute for Simulation Intelligence, USA
7. Lawrence Berkeley National Laboratory, USA
8. NASA Headquarters, USA
9. Woods Hole Oceanographic Institution, USA
10. United States Geological Survey, USA

Abstract

Developing fast and accurate surrogates for physics-based coastal and ocean models is an urgent need due to the coastal flood risk under accelerating sea level rise, and the computational expense of deterministic numerical models. For this purpose, we develop the first digital twin of Earth coastlines with new physics-informed machine learning techniques extending the state-of-art Neural Operator. As a proof-of-concept study, we built Fourier Neural Operator (FNO) surrogates on the simulations of an industry-standard flood and ocean model (NEMO). The resulting FNO surrogate accurately predicts the sea surface height in most regions while achieving upwards of 45x acceleration of NEMO. We delivered an open-source CoastalTwin platform in an end-to-end and modular way, to enable easy extensions to other simulations and ML-based surrogate methods. Our results and deliverable provide a promising approach to massively accelerate coastal dynamics simulators, which can enable scientists to efficiently execute many simulations for decision-making, uncertainty quantification, and other research activities.

1 Introduction

Refer to caption — Figure 1: Snapshots of NEMO simulation and FNO emulation for present time estimation using present atmospheric forcings (i.e., Case 1 in Table 1).

Coastal flooding is considered one of the most significant impacts of climate change, potentially threatening lives and damaging infrastructure with rising sea levels [1]. Increasingly into the future, coastal flooding effects on society will be exacerbated due to the increasing coastal populations and the accelerating rate of sea level rise and the severity of extreme climate events [2, 3]. Physics-based numerical models, such as Nucleus for European Modelling of the Ocean (NEMO) [4], have been developed to simulate and predict coastal and ocean dynamics. These physical models – driven by wind speed and mean sea level atmospheric pressure – simulate the dynamics of water velocity and sea surface height by solving the mass and momentum conservation equations. Yet running these physics-based models can be extremely computationally expensive (>1 day per run), due to the need to numerically resolve multi-physics and multi-scale dynamics represented through coupled nonlinear equations in large spatial domains [5]. In particular, these complex simulators are not fast enough for reliable risk estimation, uncertainty quantification, hypothesis testing, or real-time predictions [5], and are replaced by models with physical approximations that sacrifice accuracy for runtime [6].

Machine learning (ML) methods have received much attention in the Earth Science community due to their success at providing fast data-driven models with high accuracy [7, 8]. In particular, surrogate modeling approaches replace expensive forward simulations by statistical representations through regression [9]. A recent focus has been on coupling ML and physical models (such as partial differential equations (PDEs)), such that the solutions not only honor data sets but also physical constraints [10, 11]. However, training classical physics-informed neural networks is difficult due to the need to resolve the discretized PDE in the loss function [12]. Indeed, researchers found that these approaches are unable to represent dynamics of simple cases such as a one-dimensional two-phase flow model [13]. On the other hand, the recently proposed Fourier Neural Operator (FNO) [14] shows a promising alternative by learning the dynamics in the frequency domain. In doing so, FNO is more amenable to training and directly learns the PDE-based operator which makes it mesh-independent [14].

Here, we propose the first “coastal digital twin”, an emulator built on state-of-art physics-informed ML techniques to produce computationally lightweight surrogate models that provide fast and accurate predictions of sea surface heights in coastal regions. As a proof-of-concept experiment, we developed a digital twin for the NEMO simulations in northwestern Europe using an improved version of FNO.

Our results show: (1) the extension of FNO to learn multivariate dynamics (note that FNO was used for univariate cases in its original development [14]); (2) the overall superior performance of FNO over the baseline model UNet [15] in emulating sea surface height; (3) the adverse impact of masked land boundaries in training FNO; and (4) a 45x acceleration achieved by FNO compared with NEMO simulation. We deliver the code and data to reproduce these results with our open-source platform CoastalTwin, including tools to extend our initial experiments.¹¹1Repository will be open-sourced upon publication at the following address: gitlab.com/frontierdevelopmentlab/fdl-2021-digital-twin-coasts/coastaltwin

2 Method

We first summarize the NEMO simulations and environment for this coastal climate setting, the FNO surrogate methods, and the specifications of our open-source platform CoastalTwin.

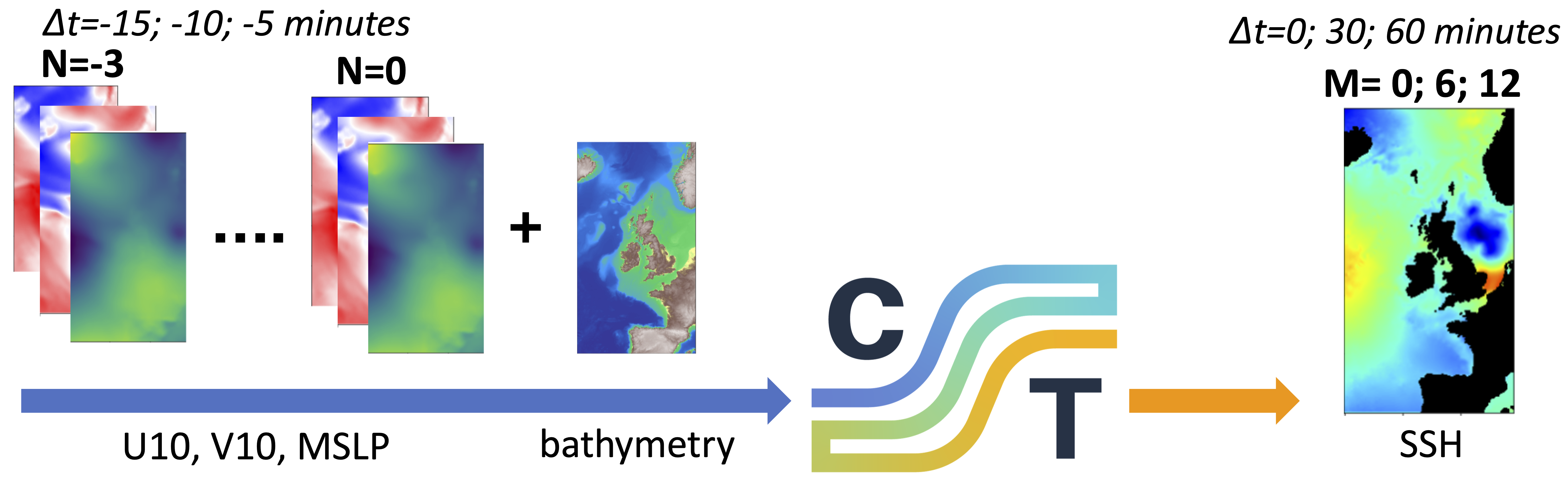
2.1 NEMO simulation

NEMO was set up at 7-km regular grids in northwestern Europe, composing overall 520x292 grids. The atmospheric forcings of NEMO include mean sea level pressure (MSLP), U-direction wind speed (U10), and V-direction wind speed (V10) averaged on the top 10m above the sea surface from the downscaled product of ECMWF Reanalysis 5th Generation [16]. The bathymetry profile was from the General Bathymetric Chart of the Oceans product [17]. The simulation of two-dimensional (2D) sea surface height (SSH) was performed for all of 2020 at every 5min. In this experiment, we normalized the dynamic forcings and simulations (i.e., U10/V10/MSLP/SSH) to mean zero and unit variance, and implemented a special scaling for bathymetry such that $B^{\prime}=\frac{\ln(B+50)-\ln(50))}{\ln(100)}$ , where $B$ is the ocean depth. This special scaling results in the local topological features that are sensitive to small bathymetry changes around zero, but insensitive to moderate changes at large bathymetry. We then splitted the normalized dataset into test (April 2020) and training (the remaining 11 months) datasets. More information on NEMO can be found at [4].

2.2 Fourier Neural Operator

Physics-informed ML methods integrate mathematical physics models with data-driven learning, namely with neural networks (NNs) [10]. A promising direction in spatiotemporal use-cases is neural operator learning: using NNs to learn mesh-independent, resolution-invariant solution operators for PDEs [18, 19]. To achieve this, Li et al. [14] use a Fourier layer that implements a Fourier transform, then a linear transform, and an inverse Fourier transform for a convolution-like operation in a NN.

2.3 CoastalTwin

For implementing FNO and other ML-based surrogates with NEMO, we developed CoastalTwin, a modular and extensible platform to integrate simulations from physical models, such as NEMO, with ML models, to produce reliable, accelerated emulation of coastal dynamics.

Using CoastalTwin, we developed the surrogate models of NEMO to predict SSH at time $t_{M}$ based on both atmospheric forcings (i.e., U10, V10, and MSLP) at preceding times $t_{N},...,t_{0}$ and the bathymetry, where $t_{0}$ is the present time, $N\in\mathds{I}$ the history and $M\in\mathds{I}$ the lookahead, and $\Delta t=5$ min the FNO time step. FNO is compared to a baseline UNet-based model [15]. The model was trained on various timescales constituting cases $C_{i}=\{N{=}0,M{=}0\}_{1},\{N{=}-3,M{=}0\}_{2},\{N{=}-3,M{=}6\}_{3},\{N{=}-3,M{=}12\}_{4}$ (Fig. 2). While case 1 predicts the present SSH using the present forcings, cases 2-4 use forcings at purely historical time steps, $t_{N:{-1}}$ , to estimate SSH at a single present or future time, $\{t_{0},t_{6},t_{12}\}={0,15,30}$ min. Our work is the first to use FNO to represent the complexity of real-world dynamics, including multivariate, multi-scale, and coupled phenomena. Here, we simulate a coupled system of nonlinear equations including 2D momentum balance for water velocity, mass balance, and boundary conditions between ocean/sea floor/sea surface [4].

Modeling and experiment specs

Each FNO was developed by sequentially stacking a linear layer outputting 20 channels, 5 Fourier layers, and a final linear layer outputting 1 channel. Each Fourier layer contains 20 channels and a maximum of 40 frequency modes in both spatial dimensions, followed by a batch normalization and ReLU activation. Each UNet adopted three blocks of convolution in both contracting and expansive paths with the remaining architecture equivalent to [15]. We used the Adam optimization and a step-wise decreased learning scheduler with an initial rate 0.01, step size 20 epochs, and decay rate 0.1. We trained each model using MSE as the loss function over 50 epochs and batch size 32, on one Tesla A100 Graphics Processing Unit (GPU). We masked the land simulation in the loss to alleviate the adverse impact of land, where SSH is supposed to be zero. In addition to MSE as a performance metric, we computed the Structural Similarity Index (SSIM) [20] and the correlation (CORR) between times series of prediction and true at each grid point.

3 Results

	MSE/1-SSIM
	Case 1: $N$ =0, $M$ =0	Case 2: $N$ =-3, $M$ =0	Case 3: $N$ =-3, $M$ =6	Case 4: $N$ =-3, $M$ =12
FNO	0.0011/0.2283	0.0018/0.2549	0.0011/0.2369	0.0011/0.2323
UNet	0.0025/0.4178	0.0033/0.4180	0.0025/0.4232	0.0025/0.4263

Table 1: FNO and UNet training result of the four cases on the test dataset.

Table 1 summarizes the experiment results. Our FNO approach outperforms UNet for all the four cases with respect to MSE and 1-SSIM. This illustrates that FNO can better capture the PDE-based simulations than the baseline model, particularly in this multivariate scenario. Snapshots of FNO emulation of Case 1 on the test dataset shows its good agreement with the NEMO simulation (Fig. 1). In general a significant speed-up is achieved by using the FNO surrogate, which took $\sim$ 2min to emulate the 1-month test dataset while the NEMO simulation took $\sim$ 1.5hr on a single core of a 2.6 GHz CPU – we can expect GPU-parallelization and other optimizations to improve this speed-up another magnitude or more. Therefore, the FNO is well posed to be used as a fast and accurate surrogate for PDE-based simulation of NEMO.

For all the cases using FNO, the two metrics are similar to each other, with values of 0.001 $\sim$ 0.002 and 0.228 $\sim$ 0.255 for MSE and 1-SSIM, respectively. The close performances of Cases 1 and 2 indicates that including historical dynamics does not strictly improve the modeling performance. Meanwhile, when involving historical inputs (i.e., Cases 2-4), the results show that longer time prediction (1hr for Case 4) can be as reliable as the present prediction (Case 2). This is likely because the prediction at limited future time steps (up to 1hr) are well constrained by the PDE surrogates.

To explore the detailed estimation behavior of FNO and UNet, we plotted the spatial maps of the correlation and the 2D frequency differences between the two surrogates, based on Fast Fourier Transform (FFT). Case 1 is shown in the top panel of Fig. 3, where we observe higher spatially averaged correlation with FNO than with UNet. In fact, FNO predictions correlate with the NEMO simulation better in most regions than UNet except the east of France-Spain boundaries, where the SSH dynamics are severely constrained by the land surface surroundings. The worse prediction of FNO in land-surrounded areas reveals its potential inability to resolve local dynamics that are strongly affected by masked boundaries. Indeed, the impact of the masked boundaries is evidenced by the reduced correlations of FNO around the UK coastal region, although FNO still outperforms UNet. The 2D frequency plot in the bottom panel of Fig. 3 shows the temporally-averaged 2D spectra of NEMO simulation, and its difference with FNO and UNet in the frequency domain. Compared with UNet, FNO does a better job in resolving the dynamics to a great extent in the red center box where the maximum frequency cutoff of the Fourier layer is defined. Nevertheless, both models show a significant difference with the NEMO spectra in the other cross sign frequency, which likely signifies the inability to represent coastal dynamics around the masked region.

4 Conclusion and Outlook

For the first time, a digital twin was developed for physics-based multivariate coastal and ocean modeling by leveraging the state-of-the-art neural operator, and demonstrated on complex real-world Earth systems data. Through experiments with NEMO simulations, we demonstrated the efficiency and accuracy of FNO on the sea surface height predictions, given that the training was performed with a limited dataset (i.e., single run of one-year simulation). Future work will focus on a thorough hyperparameter tuning on FNO as well as addressing the adverse impact of masked land boundaries, which is a common issue in coastal modeling. Despite this potential limitation, it is important to note that emulation of digital twin is upwards of 45x faster than the NEMO simulation. For this reason, our coastal digital twin will be helpful for research and operation activities that require fast simulations, such as uncertainty quantification and real-time forecasting. It is nonetheless important to continue validation experiments in various settings prior to use for real-world decision making, and further investigation is suggested into downstream effects and ethical implications of such decisions.

Acknowledgments and Disclosure of Funding

This research was conducted at the Frontier Development Lab (FDL), US. The authors gratefully acknowledge support from the MIT Portugal Program, National Aeronautics and Space Administration (NASA), Google Cloud, and the Coastal Observations, Mechanisms, and Predictions Across Systems and Scales (COMPASS) Project of the U.S. Department of Energy (DOE).

The authors would like to thank Zongyi Li and Anima Anandkumar from California Institute of Technology and Kamyar Azizzadenesheli from Purdue University for their insightful suggestions on the development and usage of FNO.

References

[1] Ebru Kirezci, Ian R Young, Roshanka Ranasinghe, Sanne Muis, Robert J Nicholls, Daniel Lincke, and Jochen Hinkel. Projections of global-scale extreme sea levels and resulting episodic coastal flooding over the 21st century. Scientific reports, 10(1):1–12, 2020.
[2] IPCC. Global warming of 1.5c. an ipcc special report on the impacts of global warming of 1.5c above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty, 2018.
[3] Douglas A Edmonds, Rebecca L Caldwell, Eduardo S Brondizio, and Sacha MO Siani. Coastal flooding will disproportionately impact people on river deltas. Nature communications, 11(1):1–8, 2020.
[4] Gurvan Madec and NEMO System Team. NEMO ocean engine.
[5] Matthew J. Purvis, Paul D. Bates, and Christopher M. Hayes. A probabilistic methodology to estimate future coastal flood risk due to sea level rise. Coastal Engineering, 55(12):1062–1073, 2008.
[6] Paul D. Bates, Matthew S. Horritt, and Timothy J. Fewtrell. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. Journal of Hydrology, 387(1):33–45, 2010.
[7] Markus Reichstein, Gustau Camps-Valls, Bjorn Stevens, Martin Jung, Joachim Denzler, Nuno Carvalhais, et al. Deep learning and process understanding for data-driven earth system science. Nature, 566(7743):195–204, 2019.
[8] P. Gentine, M. Pritchard, S. Rasp, G. Reinaudi, and G. Yacalis. Could Machine Learning Break the Convection Parameterization Deadlock? Geophysical Research Letters, 45(11):5742–5751, jun 2018.
[9] Steven L. Brunton and J. Nathan Kutz. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control. Cambridge University Press, USA, 1st edition, 2019.
[10] George Em Karniadakis, Ioannis G. Kevrekidis, Lu Lu, Paris Perdikaris, Sifan Wang, and Liu Yang. Physics-informed machine learning. Nature Reviews Physics 2021 3:6, 3(6):422–440, may 2021.
[11] Björn Lütjens, Catherine H. Crawford, Mark Veillette, and Dava Newman. Pce-pinns: Physics-informed neural networks for uncertainty propagation in ocean modeling, 2021.
[12] M. Raissi, P. Perdikaris, and G.E. Karniadakis. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378:686–707, 2019.
[13] Olga Fuks and Hamdi A Tchelepi. Limitations of physics informed machine learning for nonlinear two-phase transport in porous media. Journal of Machine Learning for Modeling and Computing, 1(1), 2020.
[14] Zongyi Li, Nikola Borislavov Kovachki, Kamyar Azizzadenesheli, Burigede liu, Kaushik Bhattacharya, Andrew Stuart, and Anima Anandkumar. Fourier neural operator for parametric partial differential equations. In International Conference on Learning Representations, 2021.
[15] Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention, pages 234–241. Springer, 2015.
[16] Hans Hersbach, …, and Jean-Noël Thépaut. The era5 global reanalysis. Quarterly Journal of the Royal Meteorological Society, 146(730):1999–2049, 2020.
[17] Gebco gridded bathymetry data. https://www.gebco.net/data_and_products/gridded_bathymetry_data/. Accessed: 2021-09-20.
[18] Lu Lu, Pengzhan Jin, and George Em Karniadakis. Deeponet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators, 2020.
[19] Anima Anandkumar, Kamyar Azizzadenesheli, Kaushik Bhattacharya, Nikola Kovachki, Zongyi Li, Burigede Liu, and Andrew Stuart. Neural operator: Graph kernel network for partial differential equations. In ICLR 2020 Workshop on Integration of Deep Neural Models and Differential Equations, 2020.
[20] Zhou Wang, A.C. Bovik, H.R. Sheikh, and E.P. Simoncelli. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing, 13(4):600–612, 2004.