DiffusionPhase: Motion Diffusion in Frequency Domain
Abstract
In this study, we introduce a learning-based method for generating high-quality human motion sequences from text descriptions (e.g., “A person walks forward”). Existing techniques struggle with motion diversity and smooth transitions in generating arbitrary-length motion sequences, due to limited text-to-motion datasets and the pose representations used that often lack expressiveness or compactness. To address these issues, we propose the first method for text-conditioned human motion generation in the frequency domain of motions. We develop a network encoder that converts the motion space into a compact yet expressive parameterized phase space with high-frequency details encoded, capturing the local periodicity of motions in time and space with high accuracy. We also introduce a conditional diffusion model for predicting periodic motion parameters based on text descriptions and a start pose, efficiently achieving smooth transitions between motion sequences associated with different text descriptions. Experiments demonstrate that our approach outperforms current methods in generating a broader variety of high-quality motions, and synthesizing long sequences with natural transitions.
1 Introduction

Virtual human characters play a crucial role in various computer graphics and robotics applications, such as AR/VR, gaming, and simulation of human-robot interactions. Generating natural human motions with conventional computer graphics techniques involves a tedious and time-consuming process, requiring complex motion capture recordings, along with manual editing and synthesis of motions based on selected key frames by animation experts. To address these challenges and make the process more accessible to non-experts, recent studies [26, 31, 8] have introduced text-conditioned deep generative models to generate human motions based on text descriptions (e.g., keywords of actions like “walk” and “jump”, and short sentences like “A person rotates 360 degrees and walks forward”). While there has been significant progress, current methods still face challenges in generating diverse animations, ensuring smooth transitions between motion sequences associated with different text descriptions, and creating natural looping animations.
These challenges primarily stem from limited paired language-motion training data and the pose representations used which are often either lacking in expressiveness or inefficient in compactness for generating motion transitions through blending. In a distinct area of character animation generation, which is under the user’s specific locomotion control (e.g., trajectory direction), some studies [15, 29, 25] explore the idea of identifying smooth transitions in a transformed periodic phase space. However, these methods are only trained on a specific type of motion (e.g., walking) and their performance degrades significantly when training on diverse motions. Additionally, these methods often fail to capture high-frequency information in the synthesized motions. Furthermore, applying these methods to human motion generation with semantic text control is challenging due to the ambiguous mapping from text descriptions to the periodic phases.
In this work, we propose the first method for text-conditioned human motion generation in the frequency domain. Similar to DeepPhase [25], we presume that the full-body movements of interest inherently exhibit local periodicity in both time and space, and we learn a periodic parameterized phase space with an autoencoder to encode the local periodicity of each body part over time in motions. To tackle the aforementioned issues in DeepPhase [25], we introduce a designated frequency set that includes high frequencies to enhance the encoding capability for motion details. Next, to handle the ambiguity in text-to-motion mapping, we introduce a conditional diffusion model that predicts periodic phase parameters to generate motions conditioned on text descriptions and the start pose. Unlike previous approaches [25, 15], we eliminate the requirement for additional network modules to align the phases between two poses for smooth transitions. Instead, we can produce natural motion transitions efficiently by conditioning on the start pose. We have evaluated our approach using two large human motion datasets with text annotations. The results demonstrate the superiority of our approach over existing methods in terms of the quality and diversity of the generated motions, as well as in facilitating smooth and natural motion transitions.
In summary, our contributions are:
-
1.
We propose the first method for text-conditioned human motion generation in the frequency domain, which enables efficient synthesis of diverse and arbitrary-length human pose sequences with smooth and natural transitions.
-
2.
We introduce a novel motion encoding method that maps human motions into a compact yet expressive periodic parameterized space with high-frequency details encoded, thereby enhancing the capability to learn high-quality human motions from diverse motion datasets.
-
3.
We design a new conditional motion diffusion model conditioned on a start pose for parameterized phase prediction, effectively achieving seamless transitions between motion sequences associated with different text descriptions.
2 Related Work
2.1 Motion Generative Models
The stochastic nature of human motion has driven the application of generative models in motion generation tasks. Prior works have shown impressive results in leveraging generative adversarial networks (GANs) to sequentially generate human motion [4, 6]. Variational autoencoder (VAE) and transformer architectures have also been widely adapted for their capability of improving the diversity of generated motion sequences [12, 10, 11, 19, 3]. Most recently, [30] proposed T2M-GPT, a framework that learns a mapping between human motion and discrete codes in order to decode motion from token sequences generated by a Generative Pre-trained Transformer. Large Language Models have also been leveraged for text-to-motion tasks to boost zero-shot capabilities [33, 16, 17]. Diffusion models, with their strong ability to model complex distributions and generate high-fidelity results, have become increasingly popular for motion generation, especially for context-conditioned schemes [28, 31, 8, 18]. With a transformer-encoder backbone, [26] presented a light-weight diffusion model that predicts samples instead of noise for efficient text-to-motion generation. [32] enhanced the quality of generation for uncommon conditioning signals by integrating a retrieval mechanism into a diffusion-based framework for refined denoising. Although diffusion-based approaches for motion generation have achieved outstanding results, the synthesis of long, arbitrary-length sequences remains limited in quality and computationally expensive. Recently, [7] greatly improved the efficiency of the diffusion process by introducing a motion latent space, providing an avenue for addressing computational challenges. However, similar to prior approaches, limited data still restricts the capability of generating naturally aligned movements for arbitrary time sequences.

2.2 Phase in Motion Synthesis and Control
Previous works in the field of computer graphics have developed approaches using periodic signals to enhance movement alignment over time, incorporating phase variables that represent the progression of motion. Phase-functioned Neural Networks [15], a notable instance of such approaches, adjust network weights based on a phase variable, defined by interactions between the foot and the ground during leg movement. This principle has been expanded to include additional types of complex movements [29, 23], and for complex movements involving multiple contact points [24]. Periodic signal analysis of such complex movements have shown to be important in real-world motion control tasks, contributing to the optimization of complex movements for robotic systems [22, 9]. Building on the idea of periodic representations, [25] developed a neural network structure that is capable of learning periodic characteristics from unstructured motion datasets. However, this model can only be trained on one type of motion data at a time. In addition, the phase information obtained is not well aligned with semantic signals, such as textual descriptions, limiting intuitive motion generation. Inspired by these observations, we propose DiffusionPhase, a framework that incorporates periodic motion representations with diffusion models to achieve text-driven generation of a wide range of periodic natural movements of arbitrary lengths.
3 Method
Given input text descriptions as motion control indicators , our goal is to generate natural and expressive motion sequences of arbitrary lengths with smooth transitions between adjacent synthesized motion sequences.
To achieve this goal, our key idea is to transform the motion space into a learned phase manifold. The phase manifold is then used for motion synthesis and transition. Same as DeepPhase [25], we assume that full-body movements inherently exhibit local spatial-temporal periodicity and use a phase representation to encode the input motions. However, directly applying the motion encoding method in DeepPhase to our setting fails to produce high-quality results, due to three reasons: (1) DeepPhase is designed to train on a specific type of motion and its performance degrades when training on diverse motions; (2) DeepPhase tends to encode low-frequency components of the motion, leading to limited accuracy in motion encoding; (3) The severe ambiguity in text-to-motion generation.
To address these issues, we present a compact yet expressive phase encoding with high-frequency information encoded. We then propose a new motion diffusion model for predicting phase parameters from input text descriptions to address the ambiguity issue. Compared to two widely-used motion representations, i.e., full skeletal poses and an one-dimensional code, phase encoding has a good balance in expressiveness and compactness. As illustrated in Figure 2, we first learn a network encoder to map the motion space to a periodic parameterized phase space. The encoder is trained by minimizing the distances between the original motions and the motions reconstructed from periodic parameters using the Inverse FFT (Section 3.2). Next, we learn a conditional diffusion model to predict the periodic parameters, which is conditioned on the text prompt and the starting pose (Section 3.3).
3.1 Preprocessing: Isolating The Primary Movement in Motion Sequences
Most sequences in the dataset include separate segments at the beginning and end, showing the initiation and conclusion of the movement. These segments do not reflect the essence of the intended action itself. We enhance our method by excluding these segments from being encoded into the periodic phase manifold, while using the linear signals for encoding them. Hence, we focus on encoding the primary motion into periodic phase manifolds, and then proceed to extend them during the testing phase.
To efficiently and robustly detect main segments of motion, we first process the whole motion sequence from a motion dataset into a latent space, where each frame of the sequence has a feature vector that contains temporal and spatial features of the pose at the frame. We tested two choices of embedding the motions. Please refer to our Suppl. Materials for more detail. Then we are able to select the start pose and end pose through:
| (1) |
where is the actual length of this motion clip; , and are the coefficients. The first term encourages the poses at the selected start and end time to be similar, aiding us in encoding the primary motion as a motion circle. The second term ensures that the primary motion is of adequate length, while the third term excludes the separate segments.
Periodicity-Based Data Augmentation To increase the data size with various start and end poses for training the main diffusion network that is conditioned on the starting pose (See Section 3.3 for more detail), we select the top sets of and for each motion sequence from the dataset. This selection pool enables us to train the network with the same text prompt and on the same training sequence but with a different starting pose.
3.2 A Periodic Latent Representation For Motion Sequences
Now, we aim to train an encoder network that can encode the latent representation parameters from motion sequences and a convolution-based decoder network that is trained to reconstruct the input sequences from the encoded parameters. Our latent representation is itself the parameters of discrete periodic phases. In particular, encodes the input human motion sequence to the amplitudes , phase shifts , and offsets parameters of a frequency decomposition of this periodic latent representation. Then with frequencies provided, can be transformed to its time-domain phase signal via Inverse Fourier. Prior work [25] trained a periodic latent representation by extracting frequencies from motions, which were predominantly in the low-frequency range, and it specialized only in one activity type such as walking, dancing, or dribbling. Since we aim to generate a large variety of motion sequences for many different activities conditioned on unconstrained text descriptions, we need to process a training dataset with many types of actions. Hence we provide a set of positive integer frequencies and let an encoder network predict the , , and for each of the phases. Then the phase signal can be calculated as:
| (2) |
where is the value of time control.
We set the lowest frequency value to 1: this enables embedding the non-repeatable parts of the motion. Next, we set the highest frequency to be a common multiple of all frequencies in , so that the pattern of the signals can repeat smoothly forever as increases. This thus permits generating sequences of any desired length simply by setting . We can regard the encoded motion sequence as one motion circle, and can smoothly transition to a new extrapolated motion circle.
Our improved encoding design boasts two primary advantages: 1) it facilitates the synthesis of motions with lengths that exceed the scope of training motion distribution, thereby broadening the spectrum of possible motions; and 2) it fosters a continuous motion embedding in the temporal domain, promoting arbitrary-length motion synthesis and seamless motion transitions.
Encoding the Periodic Portion: For each motion sequence and a pair of its and , the encoder network produces . consists of an input convolution layer to reduce the dimension of , followed by fully connected layers. To calculate for all the frames in , we align to the , and to the and perform the calculation in Equation 2.
Encoding the Non-Periodic Portions: We separately represent the non-repeatable parts, i.e. using linear signals:
| (3) |
where we align to where is and ; and to where equals and . Finally, to combine the periodic and non-periodic portions of signals into one complete , we simply concatenate the signals in time in the correct order:
Auto-Encoder Training Objective: We reconstruct from by a 1-D convolution-based decoder network . The loss function for training this encoder-decoder setup for reconstruction is
| (4) |
where indicates the forwards kinematics for the joints, and is a hyper-parameter for adjusting the loss.
3.3 Text-Conditioned Diffusion for Parameterized Motion Synthesis
After training the encoder and the convolution decoder , we fix the weights of these two networks and use them as a foundation to train our diffusion module that produces from a text prompt and a conditional pose . Providing our DiffusionPhase model with a variety of conditional poses can improve comprehensive coverage of diverse character motions during training, and enhance its capability to generate human motion sequences from different starting pose. It also offers a clear and coherent starting point when concatenating motions. Facilitated by our periodicity-based data augmentation, we select a from the selection pool and use the pose at to help generate this periodic signal, and this conditional pose can be randomly masked during the training for performing prediction conditioned on only.
We denote as the periodic parameters at noising step . For each and a pair of its and in the training set, we derive . The diffusion noising step is a Markov process that follows:
| (5) |
where is a small constant that could approach to a standard Gaussian distribution. According to [14], this diffusion process can be formulated as:
| (6) |
where and . For the reverse step of this diffusion, we need to denoise from . We follow the idea in [21, 26] where we directly predict using our denoising network conditioned on pose , text prompt and noising step during training with the simple objective [14].
| (7) |
where is the total number of denoising steps.
To evaluate the quality of , we need to process it to achieve the time-domain signals , and then apply to reconstruct the motion sequences . We use the loss function to constrain and in training this part of the network.
3.4 Generating Composite and Extended Motions with DiffusionPhase
Having trained our DiffusionPhase model as above, we now discuss how to generate motion sequences. In the test stage, DiffusionPhase is given and hyper-parameter , . For generating the first period of signals, we can start with or a random pose as the conditional pose, and we can use the end pose of the last period for smooth transitions between the periods. The sample stage of diffusion is similar to the approach seen in [14, 26]. We start with iteratively execute the prediction , and then this is diffused back to during the noising step . The whole process iteratively decreases from to 1. Following [13], we apply classifier-free guidance, where we randomly mask out and during the training and then set a trade-off between and during sampling.
There are two operations for synthesizing new composited motions in our setting: (a) phase repetition; and (b) transition between two phases.
Phase repetition refers to extending the signals by allowing the time control value k to grow thus making the periodic part of repeat.
Transition between two phases refers to applying diffusion to synthesize a new set of parameters for extending motions. To ensure smooth transitions at conjunctions, the synthesis of control parameters is made to be conditioned on the initial pose, which can be set to the end human pose of the preceding period motion. This measure facilitates the alignment of the starting pose of the second phase with the ending position of the preceding phase. We also explore the ability of our framework to synthesize motions under different conditions to allow for concatenating actions with different semantic meanings.
4 Experiments
In this section, we evaluate our DiffusionPhase framework on the text-driven motion generation task and motion extension. In all the evaluated benchmarks, DiffusionPhase achieves SoTA performances. In particular, when generating human motion sequences with longer time lengths, our method produces better results than previous methods. Moreover, the quality of our results would not decrease as time increases.
4.1 Experimental Settings
Dataset We evaluate our approach on the two most widely used datasets for text-driven motion generation tasks: KIT Motion Language (KIT-ML) [20] and HumanML3D [11]. KIT-ML includes 3,911 unique human motion sequences alongside 6,278 distinct text annotations. The motion sequences are at the frame rate of 12.5 FPS.
HumanML3D is a more comprehensive dataset of 3D human motions and their corresponding text descriptions. It comprises 14,616 distinct human motion capture data alongside 44,970 corresponding textual descriptions. All the motion sequences in KIT-ML and HumanML3D are padded into 196 frames in length.
Metrics Following the settings used in previous works [11], we use the following five performance metrics: R-Precision and Multimodal distances (MM-DIST) measure the relevance of generated motion sequences to the given text prompt. Frechet Inception Distance (FID) assesses the similarity between generated motion sequences and real motion sequences. Diversity and Multimodality (MModality) quantify the variability present within the generated motions. For the details of these metrics. please refer to our Suppl. Materials.
Implementation The encoder network for generating periodic signals from motion is a 4-layered MLP with a convolution layer at the front. The decoder of the periodic signals is a 4-layered 1D convolutional network. Motions are encoded into 128 phases with the maximum frequency set to 30. We use a 512-dimension latent code to encode the conditioned pose and the text prompt, where the conditional pose is processed through an embedding layer, and the text feature is processed from a frozen CLIP-ViT-B/32 model. An 8-layered transformer is used for handling the denoising step. Our models were trained with batch size 128 and a learning rate that decayed from 1e-4 to 1e-6.
4.2 Qualitative Results
Motion Blending
As we have introduced in Section 3.4, our method is designed to produce smooth transitions among signals generated from different stages. We can also apply these techniques to generate motions from different conditions with different semantic meanings. With the conditioned pose and the decoder network with multiple layers of convolutional operations, we are able to query two sets of phases that can be blended to produce smooth transition movements. We show some examples in Figure 3 and include more results in the supplemental materials.
Motion Interpolation
Because phase signals are continuous, we can actually consider the generation of longer motions using phase repetition as a process of extrapolating the phase. Similarly, we can also use phase to interpolate motions. By generating additional frames within the period of a generated motion, we can increase the frame rate of the motion video. Please refer to our Suppl. Materials for more detail.

4.3 Comparisons
For this comparison experiment, we select 7 related state-of-the-art methods: Language2Pose [2], Text2Gestures [5], Dance2Music [1], MOCOGAN [27], Generating Diverse and Natural 3D Human Motions from Text [11], MDM, [26], MotionDiffuse [31], T2M-GPT [30] and MLD [7]. The quantitative comparison results on the HumanML3D test set and the KIT-ML test set are shown in Table 1. Please refer to Suppl. Materials for visual results.
| Length | Method | HumanML3D | KIT | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Top-3 R-Precision ↑ | FID ↓ | MM-DIST ↓ | Diversity → | MModality ↑ | Top-3 R-Precision ↑ | FID ↓ | MM-DIST ↓ | Diversity → | MModality ↑ | ||
| Default Length | Real | 0.797 | 0.002 | 2.974 | 9.503 | - | 0.779 | 0.031 | 2.788 | 11.08 | - |
| Language2Pose | 0.486 | 11.02 | 5.296 | 7.676 | - | 0.483 | 6.545 | 5.147 | 9.073 | - | |
| Text2Gesture | 0.345 | 5.012 | 6.03 | 6.409 | - | 0.338 | 12.12 | 6.964 | 9.334 | - | |
| Dance2Music | 0.097 | 66.98 | 8.116 | 0.725 | 0.043 | 0.086 | 115.4 | 10.40 | 0.241 | 0.062 | |
| MOCOGAN | 0.106 | 94.41 | 9.643 | 0.462 | 0.019 | 0.063 | 82.69 | 10.47 | 3.091 | 0.250 | |
| Guo et al. | 0.736 | 1.087 | 3.347 | 9.175 | 2.219 | 0.681 | 3.022 | 3.488 | 10.720 | 2.052 | |
| MDM | 0.611 | 0.544 | 5.566 | 9.559 | 2.799 | 0.396 | 0.497 | 9.191 | 10.847 | 1.907 | |
| MotionDiffuse | 0.782 | 0.630 | 3.113 | 9.410 | 1.553 | 0.739 | 1.954 | 2.958 | 11.100 | 0.730 | |
| T2M-GPT | 0.775 | 0.141 | 3.121 | 9.722 | 1.831 | 0.745 | 0.514 | 3.007 | 10.921 | 1.570 | |
| MLD | 0.772 | 0.473 | 3.196 | 9.724 | 2.413 | 0.734 | 0.404 | 3.204 | 10.800 | 2.192 | |
| Ours | 0.761 | 0.397 | 3.194 | 9.363 | 2.805 | 0.736 | 0.503 | 3.167 | 10.873 | 2.071 | |
| 3x Default Length | Guo et al. | 0.496 | 8.701 | 4.947 | 7.370 | - | 0.551 | 7.591 | 4.907 | 8.767 | - |
| MDM | 0.121 | 18.499 | 9.706 | 5.806 | - | 0.094 | 41.760 | 11.228 | 5.588 | - | |
| MotionDiffuse | 0.392 | 10.303 | 5.819 | 5.928 | - | 0.281 | 72.225 | 9.961 | 6.119 | - | |
| MLD | 0.546 | 7.842 | 4.976 | 7.938 | - | 0.495 | 7.681 | 5.335 | 9.235 | - | |
| Ours (Repetition) | 0.751 | 0.385 | 3.266 | 9.009 | 2.802 | 0.727 | 0.902 | 3.429 | 10.067 | 1.968 | |
| Ours (Generative) | 0.725 | 0.584 | 3.311 | 8.884 | 2.817 | 0.710 | 1.174 | 3.483 | 9.813 | 2.196 | |
In the Default Length experiments, the baseline methods easily result in random motion failure, thus, the MModality results become unreliable. Therefore, we only report the MModality of our method when generating default length.




| Method | Metrics | ||||
|---|---|---|---|---|---|
| Highest Freq | Representation | Num of Phases | Top-1 | Top-3 | FID |
| 8 | sin | 128 | 0.457 | 0.784 | 0.232 |
| 30 | sin | 128 | 0.499 | 0.789 | 0.106 |
| 30 | sin, cos | 128 | 0.506 | 0.791 | 0.082 |
| 30 | sin, cos | 256 | 0.507 | 0.792 | 0.080 |
| DeepPhase | 0.426 | 0.737 | 0.968 | ||
Our method is evaluated in two settings. Default Length: We consider the 196-frame motion length used in previous works as the default length setting. Default Length: To further evaluate the quality of generated motion for extended lengths, we generate motions of Default Length. Considering that the ground truth data is limited to a length of 196 frames, we select the last 196 frames of the extended motion sequence for evaluation. If a motion is extended effectively, the last 196 frames of the generated sequence should still exhibit similar motion to the ground truth.
In particular, we test two different operation modes for generating longer sequences using our method. For the Repetition mode, we apply our diffusion model once to produce one set of parameters that determine a repetition period and repeat the sequence to form an extended sequence with Default Length frames. For the Generative mode, we call our diffusion model multiple times until the length of the (accumulated) generated sequence reaches Default Length.
We compare our approach with the top performing methods in the Default Length setting that are capable of specifying the length of generated motion, i.e., [11], MDM [26], MotionDiffuse [31], and MLD [7]. From Table 1 , we can see that our method demonstrates comparable performance in the Default Length setting and a significant advantage over the baselines in the Default Length setting.
Furthermore, to better examine the effect of the generated sequence length on the generation quality, we conduct the same experiments on the HumanML3D test set for length settings from 1 to 5 times the default length setting and plot the Top-3 R-Precision, FID, MultiModal Distance, and Diversity scores as a function of motion length. As shown in Figure 4, compared to other methods that exhibit immediate performance deterioration once the length setting increases, the quality of the sequence generated by our method is nearly length-invariant. This indicates that our method can generate sequences of arbitrary lengths with stable quality.
Here we analyze why the baseline methods have difficulties in generating long sequences. For those methods that use diffusion directly, i.e. [26, 31], long motion sequences are outside of the training distribution, and the quality is impacted immediately since the denoising module must handle the whole sequences at once. Recurrent network-based methods, i.e. [11], have the ability to handle variable lengths using an auto-regressive approach, but typically fail for other reasons; for example, the quality of generated outputs deteriorates slowly over time. Our method generalizes much better to the generation of motion sequences with longer lengths which are far from the training motion distribution.
4.4 Ablation Studies
Motion Encoding
We conduct an ablation study on the parameterized phase representation used in DiffusionPhase. As shown in Table 2, we evaluated different combinations of the choices of phase signals concerning the highest frequency, the representation of the phases and the number of phases being used, and measure the quality of the reconstructed motions using our encoder and decoder .
The result shows that using both and functions and adding high frequency phases can help encode the high-frequency details of motions.

Pose Condition-based Phase Transitions We also present an ablation study on the different pose condition choices for translating between different phases, i.e., the choice for when using for generating new phases.
We choose a test batch that contains 32 different text prompts from HumanML3D [11]. For each text prompt, we first use it to produce the starting motion sequence, then we randomly choose another text prompt to generate the ending motion sequence. The generation of the ending sequences is tested under three different pose conditions: 1) the last poses of the starting sequences; 2) random poses; 3) zero masks.
To evaluate the quality of the transitions between these two motion segments, we use the encoder network and the decoder network to reconstruct the new motion from the transition frames. The networks should reconstruct a motion sequence with better quality if the two segments of the sequence are smoothly transitioned. To evaluate the quality of the transitions, we measure the L2 distance between the input and reconstructed motions among the frames centered at the transition moment. From Figure 5, we can see that if the phase parameters of the ending sequences are generated conditioned on the last pose of the starting segments, then the synthesized motion would have better quality.
5 Conclusions
In this paper, we proposed a new method for generating high-quality human motions in arbitrary lengths for text descriptions. We propose to encode repetitive motions using periodic signals and design a new diffusion model to predict the periodic signals given text inputs. Our method achieves natural motion generation with smooth transitions, especially for long-sequence generation, and significantly outperforms previous methods.
Limitation and future work At present, our method cannot directly extract and understand the quantitative vocabularies (e.g., “walk for 11 steps” and “turn left 30 degrees”) provided in text prompts but only treat them equivalently to regular descriptions, resulting in an inability to generate precise motions for these text commands. Therefore, a meaningful future direction would be to extract specific quantitative control commands from text, and directly use these commands to operate periodic signals and generate more controllable motions. It is also interesting to explore how to incorporate the environmental constraints (e.g., uneven terrain and large obstacles which require the character to respond accordingly) into our motion generation framework to enable its practical use in gaming and virtual simulation engines.
References
- Aggarwal and Parikh [2021] Gunjan Aggarwal and Devi Parikh. Dance2music: Automatic dance-driven music generation. arXiv preprint arXiv:2107.06252, 2021.
- Ahuja and Morency [2019] Chaitanya Ahuja and Louis-Philippe Morency. Language2pose: Natural language grounded pose forecasting. CoRR, abs/1907.01108, 2019.
- Athanasiou et al. [2022] Nikos Athanasiou, Mathis Petrovich, Michael J. Black, and Gül Varol. Teach: Temporal action compositions for 3d humans. In International Conference on 3D Vision (3DV), 2022.
- Barsoum et al. [2017] Emad Barsoum, John Kender, and Zicheng Liu. HP-GAN: probabilistic 3d human motion prediction via GAN. CoRR, 2017.
- Bhattacharya et al. [2021] Uttaran Bhattacharya, Nicholas Rewkowski, Abhishek Banerjee, Pooja Guhan, Aniket Bera, and Dinesh Manocha. Text2gestures: A transformer-based network for generating emotive body gestures for virtual agents. In 2021 IEEE Conference on Virtual Reality and 3D User Interfaces (IEEE VR). IEEE, 2021.
- Cai et al. [2018] Haoye Cai, Chunyan Bai, Yu-Wing Tai, and Chi-Keung Tang. Deep video generation, prediction and completion of human action sequences. In Proceedings of the European Conference on Computer Vision (ECCV), 2018.
- Chen et al. [2023] Xin Chen, Biao Jiang, Wen Liu, Zilong Huang, Bin Fu, Tao Chen, and Gang Yu. Executing your commands via motion diffusion in latent space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 18000–18010, 2023.
- Dabral et al. [2023] Rishabh Dabral, Muhammad Hamza Mughal, Vladislav Golyanik, and Christian Theobalt. Mofusion: A framework for denoising-diffusion-based motion synthesis. In Computer Vision and Pattern Recognition (CVPR), 2023.
- Feng et al. [2023] Gilbert Feng, Hongbo Zhang, Zhongyu Li, Xue Bin Peng, Bhuvan Basireddy, Linzhu Yue, Zhitao Song, Lizhi Yang, Yunhui Liu, Koushil Sreenath, et al. Genloco: Generalized locomotion controllers for quadrupedal robots. In Conference on Robot Learning, pages 1893–1903. PMLR, 2023.
- Guo et al. [2020] Chuan Guo, Xinxin Zuo, Sen Wang, Shihao Zou, Qingyao Sun, Annan Deng, Minglun Gong, and Li Cheng. Action2motion: Conditioned generation of 3d human motions. In Proceedings of the 28th ACM International Conference on Multimedia, pages 2021–2029, 2020.
- Guo et al. [2022] Chuan Guo, Shihao Zou, Xinxin Zuo, Sen Wang, Wei Ji, Xingyu Li, and Li Cheng. Generating diverse and natural 3d human motions from text. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 5152–5161, 2022.
- Habibie et al. [2017] Ikhsanul Habibie, Daniel Holden, Jonathan Schwarz, Joe Yearsley, and Taku Komura. A recurrent variational autoencoder for human motion synthesis. In Proceedings of the British Machine Vision Conference (BMVC), 2017.
- Ho and Salimans [2022] Jonathan Ho and Tim Salimans. Classifier-free diffusion guidance. arXiv preprint arXiv:2207.12598, 2022.
- Ho et al. [2020] Jonathan Ho, Ajay Jain, and Pieter Abbeel. Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems, 33:6840–6851, 2020.
- Holden et al. [2017] Daniel Holden, Taku Komura, and Jun Saito. Phase-functioned neural networks for character control. ACM Trans. Graph., 36(4), 2017.
- Jiang et al. [2023] Biao Jiang, Xin Chen, Wen Liu, Jingyi Yu, Gang Yu, and Tao Chen. Motiongpt: Human motion as a foreign language. arXiv preprint arXiv:2306.14795, 2023.
- Kalakonda et al. [2023] Sai Shashank Kalakonda, Shubh Maheshwari, and Ravi Kiran Sarvadevabhatla. Action-gpt: Leveraging large-scale language models for improved and generalized action generation, 2023.
- Kim et al. [2023] Jihoon Kim, Jiseob Kim, and Sungjoon Choi. Flame: Free-form language-based motion synthesis editing. In Proceedings of the Thirty-Seventh AAAI Conference on Artificial Intelligence and Thirty-Fifth Conference on Innovative Applications of Artificial Intelligence and Thirteenth Symposium on Educational Advances in Artificial Intelligence. AAAI Press, 2023.
- Petrovich et al. [2022] Mathis Petrovich, Michael J. Black, and Gül Varol. Temos: Generating diverse human motions from textual descriptions. In Computer Vision – ECCV 2022: 17th European Conference, Tel Aviv, Israel, October 23–27, 2022, Proceedings, Part XXII, page 480–497, Berlin, Heidelberg, 2022. Springer-Verlag.
- Plappert et al. [2016] Matthias Plappert, Christian Mandery, and Tamim Asfour. The kit motion-language dataset. Big data, 4(4):236–252, 2016.
- Ramesh et al. [2022] Aditya Ramesh, Prafulla Dhariwal, Alex Nichol, Casey Chu, and Mark Chen. Hierarchical text-conditional image generation with clip latents. arXiv preprint arXiv:2204.06125, 2022.
- Shao et al. [2021] Yecheng Shao, Yongbin Jin, Xianwei Liu, Weiyan He, Hongtao Wang, and Wei Yang. Learning free gait transition for quadruped robots via phase-guided controller. IEEE Robotics and Automation Letters, 7(2):1230–1237, 2021.
- Starke et al. [2019] Sebastian Starke, He Zhang, Taku Komura, and Jun Saito. Neural state machine for character-scene interactions. ACM Trans. Graph., 38(6):209–1, 2019.
- Starke et al. [2020] Sebastian Starke, Yiwei Zhao, Taku Komura, and Kazi Zaman. Local motion phases for learning multi-contact character movements. ACM Transactions on Graphics (TOG), 39(4):54–1, 2020.
- Starke et al. [2022] Sebastian Starke, Ian Mason, and Taku Komura. Deepphase: Periodic autoencoders for learning motion phase manifolds. ACM Transactions on Graphics (TOG), 41(4):1–13, 2022.
- Tevet et al. [2022] Guy Tevet, Sigal Raab, Brian Gordon, Yonatan Shafir, Daniel Cohen-Or, and Amit H Bermano. Human motion diffusion model. arXiv preprint arXiv:2209.14916, 2022.
- Tulyakov et al. [2018] Sergey Tulyakov, Ming-Yu Liu, Xiaodong Yang, and Jan Kautz. MoCoGAN: Decomposing motion and content for video generation. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 1526–1535, 2018.
- Yuan et al. [2022] Ye Yuan, Jiaming Song, Umar Iqbal, Arash Vahdat, and Jan Kautz. Physdiff: Physics-guided human motion diffusion model. arXiv preprint arXiv:2212.02500, 2022.
- Zhang et al. [2018] He Zhang, Sebastian Starke, Taku Komura, and Jun Saito. Mode-adaptive neural networks for quadruped motion control. ACM Transactions on Graphics (TOG), 37(4):1–11, 2018.
- Zhang et al. [2023a] Jianrong Zhang, Yangsong Zhang, Xiaodong Cun, Shaoli Huang, Yong Zhang, Hongwei Zhao, Hongtao Lu, and Xi Shen. T2m-gpt: Generating human motion from textual descriptions with discrete representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2023a.
- Zhang et al. [2022] Mingyuan Zhang, Zhongang Cai, Liang Pan, Fangzhou Hong, Xinying Guo, Lei Yang, and Ziwei Liu. Motiondiffuse: Text-driven human motion generation with diffusion model. arXiv preprint arXiv:2208.15001, 2022.
- Zhang et al. [2023b] Mingyuan Zhang, Xinying Guo, Liang Pan, Zhongang Cai, Fangzhou Hong, Huirong Li, Lei Yang, and Ziwei Liu. Remodiffuse: Retrieval-augmented motion diffusion model. arXiv preprint arXiv:2304.01116, 2023b.
- Zhang et al. [2023c] Yaqi Zhang, Di Huang, Bin Liu, Shixiang Tang, Yan Lu, Lu Chen, Lei Bai, Qi Chu, Nenghai Yu, and Wanli Ouyang. Motiongpt: Finetuned llms are general-purpose motion generators, 2023c.
Supplementary Material
1 Repetitive Period Detection
In the Section 3.1 of the main paper that discusses preprocessing, we introduce a method of locating the starting time and the ending time of the longest primary motion for each ground truth motion sequence. Specifically, we train an Auto-Encoder to encode the whole videos into a sequence of features, where for the pose of each frame there is a corresponding feature vector that encodes the temporal and spatial information. Then and can be determined via Equation 1 in the main paper. We evaluate two kinds of phase embedding when training the Auto-Encoder: the original DeepPhase and our novel configuration detailed in Section 3.2 of the main paper. Figures 2 and 2 present Euclidean loss matrices where both the horizontal and vertical axes represent time frames; the value at matrix(i, j) indicates the difference between frame i and frame j. Both embedding methods effectively highlight the primary movement segments. Nonetheless, with intentionally incorporated high-frequency components, Figure 2 exhibits clearer boundaries for areas of interest, facilitating the pinpointing of distinct and pairs. Here we show some cases of selected and in Figure 3 and Figure 4.


2 Interpolate the motions
To increase the frame rate of a motion video, we can utilize phase interpolation. When creating videos at the original frame rate, we extract samples from the time-domain signal . By multiplying the sample rate by a factor of , we can boost the video’s FPS. This process involves distributing the samples obtained from the high sample rate across distinct signal sets, each representing a full motion sequence in the original frame rate. Then we apply our decoder to each of these signal sets and subsequently rearrange the resulting frames in alignment with their initial sampling order. Through this method, we effectively interpolate a motion video from frames to frames. Please refer to our supplementary video for the visual result.
3 Evaluation metrics
Following the settings used in previous works [11], we use the following five performance metrics: R-Precision evaluates a motion sequence alongside 32 textual narratives, including 1 accurate one and 31 other arbitrary descriptions. This involves calculating the Euclidean distances between the embeddings between the motion and the textual content. We then report the accuracy of the motion-to-text retrieval at the top-3 level. Frechet Inception Distance (FID) is also used to evaluate the quality of motion generated by generative methods. It measures the distance between the real and generated distributions in the feature space of a pre-trained model. Multimodal distances (MM-DIST) quantify the distances between the text derived from the provided description and the generated motions. Diversity is measured by arbitrarily dividing all the created sequences from all testing texts into pairs, and the average combined differences within each pair are determined. Multimodality (MMmodality) is measured by generating 32 motion sequences in a single text description and calculating the differences within these consistently produced sequences. Same as previous works, we evaluate all the metrics by using the pre-trained network from [11] for gathering the text and motion embeddings.


4 Efficiency Analysis
Generating longer sequences leads the computation cost of attention operations to increase quadratically for methods using latent dependent to motion length since all pairwise interactions are calculated. While using compact frequency-domain parameters as our latent variables, DiffusionPhase can efficiently produce high-quality motion of any desired length. We test the average inference time for one sentence using an A6000 GPU with different motion length settings. The results are shown in Figure 5.

5 Classifier-free Guidance Parameters
In this work, we follow [26], [7] and [13] that use a hyperparameter to balance between and during sampling, where the adjusted is given by:
| (1) |
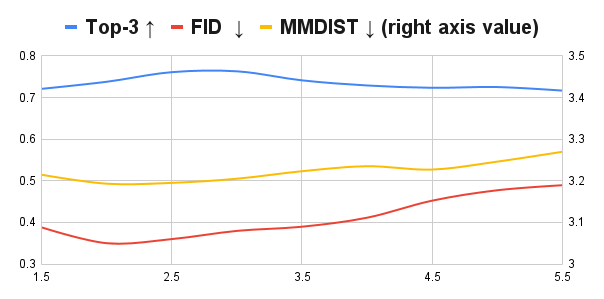
Then we scale from 1.5 to 5.5 and evaluate the sampling results in the test set of HumanML3D. The results in Figure 6 indicate that setting to the range between 2.5 to 3.5 would yield the most balanced performance across the indicators.
6 Additional Visual Results
Please refer to our supplemental video for more visual results. In the presented video, we illustrate a comparison between standard length generation and extended length generation; the transitions between various phases under both the same and different textual conditions; motion interpolation; and an instance of long motion generation.