DiffRef3D: A Diffusion-based Proposal Refinement Framework for 3D Object Detection
Abstract
Denoising diffusion models show remarkable performances in generative tasks, and their potential applications in perception tasks are gaining interest. In this paper, we introduce a novel framework named DiffRef3D which adopts the diffusion process on 3D object detection with point clouds for the first time. Specifically, we formulate the proposal refinement stage of two-stage 3D object detectors as a conditional diffusion process. During training, DiffRef3D gradually adds noise to the residuals between proposals and target objects, then applies the noisy residuals to proposals to generate hypotheses. The refinement module utilizes these hypotheses to denoise the noisy residuals and generate accurate box predictions. In the inference phase, DiffRef3D generates initial hypotheses by sampling noise from a Gaussian distribution as residuals and refines the hypotheses through iterative steps. DiffRef3D is a versatile proposal refinement framework that consistently improves the performance of existing 3D object detection models. We demonstrate the significance of DiffRef3D through extensive experiments on the KITTI benchmark. Code will be available.
1 Introduction
Denoising diffusion models have demonstrated remarkable performance in the field of image generation (Ho, Jain, and Abbeel 2020; Song, Meng, and Ermon 2020). Recently, the attempts to extend the use of the diffusion model to visual perception tasks (Wang et al. 2023; Lai et al. 2023; Gu et al. 2022; Shan et al. 2023; Chen et al. 2022) have exhibited notable success. However, these successes are limited to perception tasks in image data, while the application to perception tasks involving other modalities (e.g., LiDAR point clouds) remains unsolved. In this paper, we introduce DIffRef3D, a novel framework that utilizes the diffusion process for the task of LiDAR-based 3D object detection.
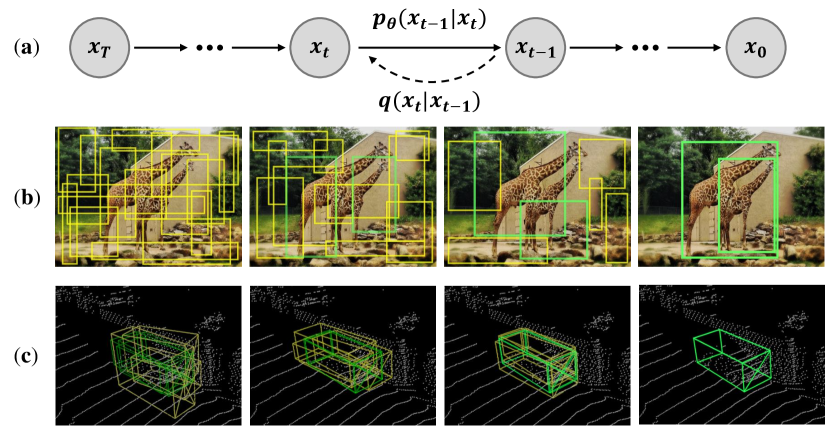
DiffRef3D is mostly inspired by DiffusionDet (Chen et al. 2022) which aims to solve 2D object detection by adopting the diffusion process to Sparse R-CNN (Sun et al. 2021). The key concept of DiffusionDet is to scatter random noisy boxes along the image scene and gradually refine the noisy boxes to the object bounding boxes by the reverse diffusion process. However, a straightforward extension of the DiffusionDet pipeline to the 3D domain encounters challenges attributed to the inherent dissimilarity between image and point cloud data. Firstly, since an image is consecutive grid-structured data, meaningful features can be extracted from a random location. In contrast, the random placement of boxes in 3D scenes often falls short of providing any information due to the sparsity of point cloud data caused by occlusion and the inherent limitation of LiDAR sensors. Secondly, while 2D objects have various sizes in an image frame due to perspective, objects in point cloud data are relatively small compared to the 3D scene. Given these characteristics of 3D scenes, scattering noisy boxes for object detection without any prior is akin to finding a needle in a haystack. Inevitably, the diffusion model on 3D point cloud space requires extended prerequisites such as coarse information about object sizes and displacements. Therefore, we design DiffRef3D to be a proposal refinement framework that enhances two-stage detectors, leveraging guidance of the region proposals generated from the first stage.
In DiffRef3D, we formulate the proposal refinement stage of two-stage detection models as a conditional diffusion process. For each proposal, our framework applies a noisy box residual and generates a hypothesis. The model is trained to denoise the residuals by the reverse diffusion process and predict object bounding boxes, using the knowledge of both the proposal and hypothesis regions. Figure 1 highlights conceptual differences between DiffusionDet and DiffRef3D, which are proposed for 2D and 3D object detection tasks, respectively. Specifically, DiffRef3D employs region proposals as the condition for both its forward and reverse diffusion process, as opposed to DiffusionDet, which is built upon an unconditional diffusion process. To this end, we introduce a hypothesis attention module (HAM), which treats features extracted from hypotheses to be conditioned on region proposals. During training, the noisy residuals are generated through the forward diffusion process from the true residuals between the proposals and target object bounding boxes. For inference, the residuals are sampled from a Gaussian distribution, and the model iteratively refines the prediction by denoising the hypotheses. We adopt the iterative sampling method from DDIM (Song, Meng, and Ermon 2020) to predict intermediate hypotheses during inference. DiffRef3D can be implemented with existing two-stage 3D object detectors and consistently improve performances compared to the baseline. We demonstrate the performance and scalability of DiffRef3D through extensive experiments held on the KITTI benchmark (Geiger, Lenz, and Urtasun 2012).
In summary, our main contributions are as follows:
-
•
DiffRef3D serves as a generalizable proposal refinement framework that can be applied to existing two-stage 3D object detectors, resulting in consistent performance improvements.
-
•
To the best of our knowledge, DiffRef3D represents the pioneering effort in employing the diffusion process for 3D object detection, interpreting the proposal refinement stage as a conditional diffusion process.
2 Related Works
2.1 LiDAR-based 3D Detection
3D object detectors can be broadly categorized into two methods: point-based methods and voxel-based methods. Point-based methods (Qi et al. 2017a, b) take the raw point clouds as inputs and employ permutation invariant operations to aggregate the point features. Voxel-based methods (Zhou and Tuzel 2018; Yan, Mao, and Li 2018) divide point clouds into a regularly structured grid and apply convolutional operations to extract features. Two-stage models employ the above methods to serve as a region proposal network (RPN), introducing the proposal refinement stage that further improves the prediction quality.
PointRCNN (Shi, Wang, and Li 2019) performs foreground segmentation and generates initial proposals using a PointNet++ (Qi et al. 2017b) backbone, and then extracts RoI features from the point clouds inside the proposals for refinement. PV-RCNN (Shi et al. 2020a) proposes a Voxel Set Abstraction module to encode the voxel-wise feature volumes into a small set of keypoints, then aggregates to the RoI-grid points to take advantage of both point-based and voxel-based methods to refine proposals. Voxel R-CNN (Deng et al. 2021) follows a typical pipeline of anchor-based two-stage models, using SECOND (Yan, Mao, and Li 2018) as RPN and refine proposals with the voxel features pooled for RoI. CenterPoint (Yin, Zhou, and Krahenbuhl 2021) predicts proposals from object centers computed from class-specific heatmap then point features are extracted from 3D centers of each face of the proposals for refinement. CT3D (Sheng et al. 2021) embeds and decodes proposals into effective proposal features based on neighboring point features for box prediction by channel-wise transformer.
There are special cases of two-stage models which utilize additional proposal refinement modules in order to adopt the cascade detection paradigm. 3D Cascade RCNN (Cai et al. 2022) iteratively refines proposals through cascade detection heads while considering point completeness score. CasA (Wu et al. 2022) progressively refines proposals by cascade refinement network while aggregating features from each stage by cascade attention module. The previous cascade detection paradigm boosts performance by leveraging the advantages of multiple predictions such as ensemble, however it lacks flexibility in sampling steps and increases memory usage for additional detection heads. In contrast, iterative sampling of diffusion-based models exploits advantages without increasing memory usage for each sampling step and sampling steps are adjustable without additional training.
2.2 Diffusion Framework on Perception Task
The diffusion framework (Dhariwal and Nichol 2021; Ho, Jain, and Abbeel 2020) has shown remarkable performance in the field of image generation. Notably, DDIM (Song, Meng, and Ermon 2020) expedites the sampling process through the utilization of a more efficient class of iterative implicit probabilistic models. Drawing attention to its denoising capabilities and performance, there have been exploding recent efforts to apply it to perception tasks (Shan et al. 2023; Zou et al. 2023) beyond generation tasks. DiffusionDet (Chen et al. 2022) first adopt the diffusion model to the 2D object detection problem by denoising random boxes to object bounding boxes via the diffusion process. DiffusionInst (Gu et al. 2022) utilizes additional mask branches and instance-aware filters upon DiffusionDet to address the instance segmentation task, and the following works (Lai et al. 2023; Wang et al. 2023) show competitive performance on semantic segmentation. However, diffusion-based perception models have been mostly explored in the image domain. Through DiffRef3D, we demonstrate the first application of the diffusion framework to a 3D perception task that involves point cloud input.
3 Preliminaries
3.1 Proposal Refinement Module
A proposal refinement module in two-stage 3D object detectors takes the initial proposals of the RPN as input and exploits the information of the RoIs to refine them. Formally, the refinement module takes a proposal and outputs the box residual and the confidence score :
| (1) | ||||
| (2) |
The RoI feature pooling operation extracts proposal feature from . represents the detection head, which consists of a regression branch producing and a classification branch producing . is supervised with the target residual between the proposal and its target object box , i.e., where represents box encoding functions (Yan, Mao, and Li 2018), and the target for is calculated with the intersection over union (IoU) between and .
3.2 Conditional Diffusion Model
During training, a small amount of Gaussian noise is gradually added to the data sample through a Markovian chain of the forward diffusion process. The forward diffusion process is formulated as:
| (3) |
where represents a noise variance schedule (Ho, Jain, and Abbeel 2020; Nichol and Dhariwal 2021). For brevity, let , , and a noisy sample at timestep is derived as follows:
| (4) |
| (5) |
The conditional diffusion model learns a reverse diffusion process, aiming to progressively refine back to with the guidance of the conditional input . The reverse diffusion process is formulated as follows:
| (6) |
4 DiffRef3D
In this section, we introduce DiffRef3D, a diffusion-based proposal refinement framework for 3D object detection. We formulate the refinement module of two-stage detectors as a conditional diffusion model that takes proposal as the conditional input and denoises the noisy residual sampled from timestep . DiffRef3D reconstructs the actual residual towards the object by the reverse diffusion process and also outputs the confidence score :
| (7) |
As shown in Fig. 2, DiffRef3D can be implemented on any existing refinement module that follows the general formulation of Eq. 1, 2 by adding a simple parallel module named the hypothesis attention module (HAM). Details of the HAM architecture, training, and inference procedures are described in the following subsections.
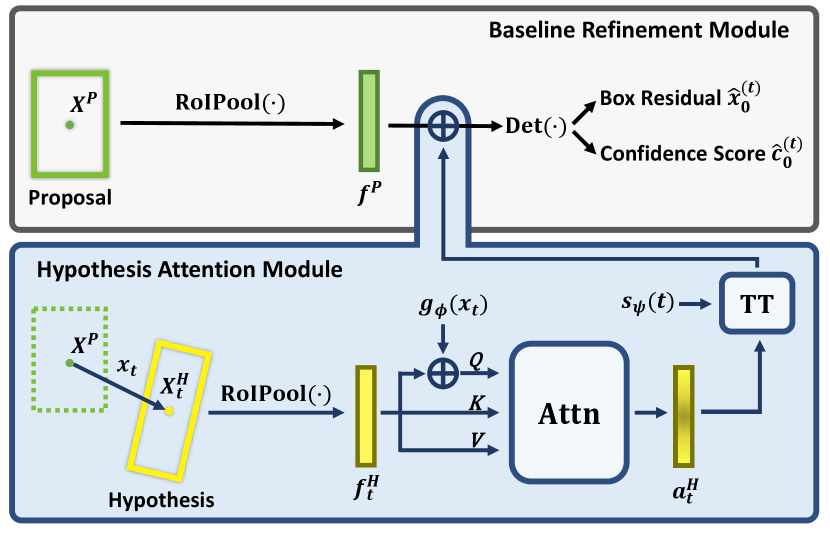
4.1 Hypothesis Attention Module
The hypothesis is a secondary inspection region derived by applying the given box residual to the proposal. i.e., . As the baseline refinement module extracts the proposal feature (Eq. 1), HAM also extracts the hypothesis feature using the same RoI feature pooling operation:
| (8) |
The hypothesis feature is further processed to incorporate the information of and by applying a self-attention block and a temporal transformation block .
The self-attention block is a common multi-head attention module (Vaswani et al. 2017) that takes as input for the query, key, and value. Except, we embed as a positional encoding to the query. We utilize a shallow MLP to convert as the same dimensional vector with . Formally, the attention feature of the hypothesis is computed as:
| (9) |
is a feature vector that represents the information of the hypothesis region with consideration of its relative displacement from the proposal.
The temporal transformation block reweights with respect to to adjust the effect of the noise signal which gets dominant as timestep increases. Specifically, the output of HAM is formulated as follows:
| (10) |
where are the scaling and shifting factors derived from an MLP :
| (11) |
Finally, is aggregated with the proposal feature for prediction:
| (12) |
4.2 Training
During the training stage, We set the reconstruction target and sample noisy residual by the forward diffusion process. The model is trained to perform the reverse diffusion process of reconstructing the true residual, which is identical to refining a hypothesis to the target object bounding box. We elucidate the methodology for generating hypotheses from proposals and present the overall training process of DiffRef3D in pseudo-code through Algorithm 1.
Hypothesis generation
From our attempts, spreading random boxes along the point cloud scene to detect objects fails to train 3D object detection by the diffusion process. Therefore, we propose hypothesis generation to map random signals into 3D boxes rather than mapping normalized values directly into a point cloud scene. Utilizing proposals as a reference frame to generate a hypothesis guarantees that random boxes start in close proximity to the potential object locations. Before we apply the forward diffusion process on the target residual , normalization is preceded since the range of the residual differs according to the size of each proposal. Details of the normalization process are provided in supplementary materials. Noise scaled by signal-to-noise ratio (SNR) is applied to according to Eq. 5 results in noisy residual . Finally, hypothesis is obtained by applying noisy residual on proposal .
Training objectives
Recent diffusion models (Ho, Jain, and Abbeel 2020) are trained with L2 loss between predicted noise and actual noise added to the data sample. However, noise prediction could be replaced by direct prediction of data samples. A number of diffusion-based approaches (Chen et al. 2022; Gu et al. 2022; Ji et al. 2023) on perception tasks report that it is better to predict data samples and train on task-specific losses. Following consensus from previous works, we also trained our model with task-specific losses, e.g., binary cross-entropy loss for classification, and smooth-L1 loss for regression.
4.3 Inference
During the inference stage, DiffRef3D refines the hypothesis generated from random Gaussian noise and follows iterative sampling steps from DDIM (Song, Meng, and Ermon 2020) for progressive refinement. Starting from a random Gaussian noise , DDIM progressively denoises Gaussian noise into data samples with step size , i.e., . The progressive refinement is formulated as follows:
| (13) |
| (14) | ||||
| (15) |
where represents noise term added to data sample and represents stochastic parameter, respectively. Algorithm 2 describes the inference procedure of DiffRef3D in pseudo-code.
Iterative sampling
| Method | Car 3D APR40 | Ped. 3D APR40 | Cyc. 3D APR40 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Easy | Mod. | Hard | Easy | Mod. | Hard | Easy | Mod. | Hard | |
| Voxel R-CNN (Deng et al. 2021) | 92.24 | 84.57 | 82.30 | 64.97 | 58.07 | 52.66 | 91.83 | 73.13 | 68.40 |
| DiffRef3D-V (1 step) | 92.53 | 84.98 | 82.55 | 67.32 | 60.45 | 55.28 | 89.13 | 71.80 | 67.60 |
| DiffRef3D-V (3 step) | 92.89 | 84.77 | 82.64 | 69.70 | 63.07 | 57.70 | 93.33 | 74.20 | 69.63 |
| PV-RCNN (Shi et al. 2020a) | 92.10 | 84.36 | 82.48 | 64.26 | 56.67 | 51.91 | 88.88 | 71.95 | 66.78 |
| DiffRef3D-PV (1 step) | 91.67 | 84.21 | 81.93 | 64.56 | 58.79 | 54.44 | 92.37 | 72.44 | 68.42 |
| DiffRef3D-PV (3 step) | 91.84 | 84.33 | 82.15 | 65.71 | 59.46 | 55.13 | 93.76 | 73.94 | 69.60 |
| CT3D (Sheng et al. 2021) | 92.34 | 84.97 | 82.91 | 61.05 | 55.57 | 51.10 | 89.01 | 71.88 | 67.91 |
| DiffRef3D-T (1 step) | 92.99 | 85.13 | 82.83 | 65.09 | 59.13 | 54.36 | 88.20 | 71.27 | 67.13 |
| DiffRef3D-T (3 step) | 93.28 | 85.13 | 82.97 | 67.49 | 61.29 | 56.17 | 90.92 | 72.61 | 68.52 |
DiffRef3D generates hypotheses in the first sampling step using residuals sampled from a Gaussian distribution. These hypotheses perform bounding box predictions in conjunction with proposal features, and the predicted outcomes serve two purposes: firstly, as the subsequent proposal in the next sampling step, and secondly, they contribute to inferring the next-step hypothesis according to Eq. 13. The iterative sampling steps share similarities with the cascade detection paradigm (Cai et al. 2022; Wu et al. 2022); however, in the case of cascade detection, distinct weights for each iteration’s detection head are required, limiting the number of iterations. In contrast, iterative sampling employs a single-weight detection head, minimizing memory consumption and allowing customizable sampling repetitions.
5 Experiments
In this section, we delve into the intricate implementation details and outline the evaluation setup adopted to assess the performance of DiffRef3D. Moreover, we conduct ablation studies to comprehensively examine each element of DiffRef3D and affirm the validity of our design choices.
5.1 Implementation Details
Architecture
We implement DiffRef3D on three popular two-stage 3D object detectors: Voxel R-CNN (Deng et al. 2021), PV-RCNN (Shi et al. 2020a), and CT3D (Sheng et al. 2021). The models enhanced with DiffRef3D framework are denoted as DiffRef3D-V, DiffRef3D-PV, and DiffRef3D-T, respectively. The model architectures mostly follow the original baseline, and only the HAM module is newly introduced. Given the output feature dimension , ( for Voxel R-CNN, 128 for PV-RCNN and CT3D), and are also -dimensional vectors. is a multi-head attention module with the head number of 8, and is a two-layer MLP with the hidden dimension of . is also a two-layer MLP, with the hidden dimension of .
Training
For consistency, training configurations for the 3D object detectors mirror those reported in the respective baseline works. In the context of the diffusion process, we set the maximum timestep to 1000 and we adopt a cosine noise schedule (Nichol and Dhariwal 2021) for the forward diffusion process. From our observations, SNR for signal scaling results in optimal performance at 2. During the training stage, only one hypothesis was generated for each proposal. All models were trained using 4 NVIDIA RTX 3090 GPUs, and the training duration was largely consistent with the baseline models due to the limited computational overhead introduced by the HAM.
Inference
In the inference phase, DiffRef3D can control the number of sampling steps and the number of hypothesis generation for each proposal. However, we observed that increasing the number of hypotheses yields only minimal performance improvement. Therefore, we fixed the number of hypothesis generation for each proposal as one. We also employ an ensemble method to make usage of the output of intermediate steps by averaging the predictions.
5.2 Results on KITTI Benchmark
| Method | Car 3D APR40 | Ped. 3D APR40 | Cyc. 3D APR40 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Easy | Mod. | Hard | Easy | Mod. | Hard | Easy | Mod. | Hard | |
| SECOND (Yan, Mao, and Li 2018) | 83.34 | 72.55 | 65.82 | 48.73 | 40.57 | 37.77 | 71.33 | 52.08 | 45.83 |
| PointPillars (Lang et al. 2019) | 82.58 | 74.31 | 68.99 | 51.45 | 41.92 | 38.89 | 77.10 | 58.65 | 51.92 |
| PointRCNN (Shi, Wang, and Li 2019) | 86.96 | 76.50 | 71.39 | 47.98 | 39.37 | 36.01 | 74.96 | 58.82 | 52.53 |
| STD (Yang et al. 2019) | 86.61 | 77.63 | 76.06 | 53.08 | 44.24 | 41.97 | 78.89 | 62.53 | 55.87 |
| Point-GNN (Shi and Rajkumar 2020) | 88.33 | 79.47 | 72.29 | 51.92 | 43.77 | 40.14 | 78.60 | 63.48 | 57.08 |
| 3DSSD (Yang et al. 2020) | 88.36 | 79.57 | 74.55 | 50.64 | 43.09 | 39.65 | 82.48 | 64.10 | 56.90 |
| SA-SSD (He et al. 2020) | 88.75 | 79.79 | 74.16 | ||||||
| PV-RCNN (Shi et al. 2020a) | 90.25 | 81.43 | 76.82 | 52.17 | 43.29 | 40.29 | 78.60 | 63.71 | 57.65 |
| Part-A2 (Shi et al. 2020b) | 87.81 | 78.49 | 73.51 | 53.10 | 43.35 | 40.06 | 79.17 | 63.52 | 56.93 |
| Voxel R-CNN (Deng et al. 2021) | 90.90 | 81.62 | 77.06 | ||||||
| VoTr (Mao et al. 2021) | 89.90 | 82.09 | 79.14 | ||||||
| SPG (Xu et al. 2021) | 90.64 | 82.66 | 77.91 | 80.21 | 66.96 | 63.61 | |||
| CT3D (Sheng et al. 2021) | 87.83 | 81.77 | 77.16 | ||||||
| BTCDet (Xu, Zhong, and Neumann 2022) | 90.64 | 82.86 | 78.09 | 82.81 | 68.68 | 61.81 | |||
| PDV (Hu, Kuai, and Waslander 2022) | 90.43 | 81.86 | 77.36 | 47.80 | 40.56 | 38.46 | 83.04 | 67.81 | 60.46 |
| 3D Cascade RCNN (Cai et al. 2022) | 90.46 | 82.16 | 77.06 | ||||||
| PG-RCNN (Koo et al. 2023) | 89.38 | 82.13 | 77.33 | 47.99 | 41.04 | 38.71 | 82.77 | 67.82 | 61.25 |
| DiffRef3D-V | 90.45 | 81.29 | 76.66 | 46.59 | 40.55 | 38.27 | 80.16 | 66.61 | 59.98 |
The KITTI benchmark (Geiger, Lenz, and Urtasun 2012) is one of the most popular benchmarks for 3D object detection evaluation. The dataset consists of 7,481 LiDAR samples for training and 7,518 LiDAR samples for testing. Training samples are divided into the train set with 3,712 samples and the val set with the remaining 3,769 samples. We present two performance evaluations for comparative analysis: For evaluation on KITTI val set, we compared DiffRef3D-V, DiffRef3D-PV, and DiffRef3D-T trained with the train set with their respective baselines. For KITTI test set, we trained a model with our framework using randomly selected 5,981 samples, validated with the remaining 1,500 samples, and evaluated the performance on the online test leaderboard. The performance were assessed across three classes: car, pedestrian, and cyclist on three different levels (easy, moderate, and hard). The results on both the val and test sets were evaluated using the mean average precision calculated at 40 recall positions.
Comparison with baseline models
Table 1 outlines the efficacy of DiffRef3D implementation across three baseline models on the KITTI val set. We present the performance of the baseline model by incorporating the officially released model weights from each study except Voxel R-CNN which is reported without pedestrian and cyclist classes results. Therefore we reproduced Voxel R-CNN detection results on three classes based on their open-source code. DiffRef3D improves detection performance for pedestrian and cyclist classes for all baseline models and difficulties, while performance remains consistent or decreases slightly in car class. We consider this is due to car class proposal boxes being sufficiently large to exploit local features which results DiffRef3D performs similar to baseline models on car class detection. DiffRef3D with sampling steps of 3 improves the baseline Voxel R-CNN, PV-RCNN, and CT3D with 5.00%, 2.79%, and 5.72% AP (R40), respectively, in the moderate pedestrian class. Moreover, DiffRef3D improves the cyclist detection performance by 1.07%, 1.99%, and 0.73%, respectively. The performance improvements primarily stem from the hypothesis generation, which contributes additional local features from individual proposals, consequently yielding greater enhancements in the pedestrian and cyclist classes. Notably, as the sampling step increases in DiffRef3D, detection performance increases in the trade-off of computation costs. Nevertheless, the performance improvement becomes less pronounced relative to the escalating computational demands as the sampling step is raised. Therefore, we present the results of the sampling steps of 1 and 3 in comparison with baseline models.
Comparison with state-of-the-art methods
To further comparisons with state-of-the-art methods, we report results of DiffRef3D-V on the KITTI test set since it shows the best overall performances among three baseline enhanced models. Therefore we trained DiffRef3D-V on a random split of training samples and reported results on the KITTI test set with a sampling step of 3. Table 2 summarizes the comparison with state-of-the-art methods. DiffRef3D-V shows comparable performance in car and cyclist with other models, while performance lags slightly on pedestrian. Nevertheless, as DiffRef3D is applicable to other two-stage 3D detectors published later, it can consistently show competitive performance with state-of-the-art models.
5.3 Ablation study
We conduct extensive ablation studies on the KITTI val set to verify our design choices of DiffRef3D.
Effectiveness of HAM and diffusion process
| HAM | D.P. | Sampling Steps | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| 59.62 | 61.01 | 61.38 | ||
| ✓ | 59.22 | 60.91 | 61.50 | |
| ✓ | ✓ | 60.45 | 62.77 | 63.07 |
To investigate the effects of HAM and the diffusion process (denoted as D.P. in Table 3), we assessed performance by implementing HAM and D.P. with Voxel R-CNN as our baseline model. DiffRef3D-V refers to configuration with HAM and D.P. all enabled. During ablation study, box ensemble is applied as default in multiple sampling steps. Moreover, we also applied iterative update of box predictions on baseline either for fair comparison. Table 3 summarizes the result of the experiment. In the absence of the D.P., which implies that hypotheses are sampled from random Gaussian noise during both training and testing, AP (R40) decreased by 0.4% and 0.1% in sampling steps of 1 and 2, respectively. This suggests hypotheses generated by noise that does not follow the diffusion process distracts baseline refinement module. Integrating all of our proposed components results in AP (R40) improvements compared to baseline with 0.83%, 1.76%, and 2.69% for each sampling steps, respectively. Note that performance improvement introduced by iterative sampling steps is higher with D.P., baseline AP (R40) increased by 0.39% and DiffRef3D-V increased by 2.32% at sampling steps of 2 compared to sampling steps of 1.
Sampling steps
| Sampling Steps | Car | Ped. | Cyc. | Latency |
|---|---|---|---|---|
| (ms) | ||||
| 1 | 92.53 | 69.15 | 89.19 | 72 |
| 2 | 92.86 | 69.50 | 93.05 | 113 |
| 3 | 92.89 | 69.70 | 93.33 | 152 |
| 4 | 92.91 | 70.04 | 94.18 | 185 |
| 5 | 93.02 | 70.00 | 92.43 | 232 |
We also conduct experiments to investigate the impacts of increasing the number of sampling steps on performance and inference time. As a baseline model, DiffRef3D-V trained in the KITTI train set is employed. Results of the ablation study are summarized in Table 4. Increasing the sampling steps from 1 to 5 provides an AP (R40) gain of 0.49%, 0.85%, and 2.24% in car, cyclist, and pedestrian, respectively. However, AP gain introduced by increasing the number of sampling steps become insignificant compared to increase of latency after sampling steps of 3. Therefore, we select 3 as an optimal number of sampling steps throughout the other experiments.
5.4 Qualitative Analysis
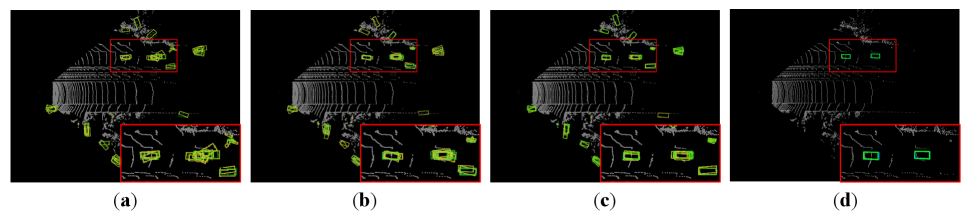
We visualize the hypothesis-driven box prediction process facilitated by the proposal refinement process of DiffRef3D. Figure 3 illustrates iterative sampling steps of DiffRef3D in each timestep. Visualization result implies the necessity of proposals as conditional inputs due to point cloud sparsity and relatively small object size compared to point cloud scenes. Figure 3 (a) shows hypotheses generated around proposal centers tend to prioritize regions with higher object presence, while hypotheses exhibit less realistic box forms since generated from random Gaussian noise. During the iterative sampling, DiffRef3D progressively refines proposals and hypotheses toward object boxes, as demonstrated in Fig. 3 (b) and (c). This result highlights DiffRef3D successfully employing the diffusion process to iteratively denoise hypotheses and refine proposals.
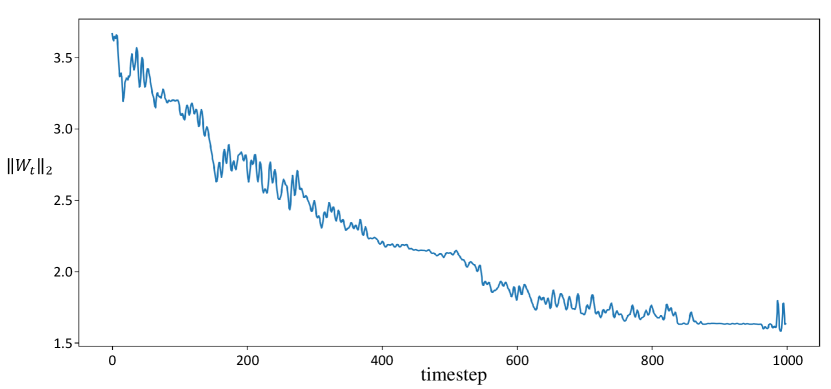
To verify the temporal transformation block considers the effect of the noise signal, we visualize the norm of the scaling factor along every timestep. Results are illustrated in Fig. 4. We affirm that the norm of the scaling factor is larger at a smaller timestep, implying that the refinement module takes more attention to the hypothesis feature at the later refinement process. Therefore, the temporal transformation block controls the importance of hypothesis features before aggregating it with proposal features.
6 Conclusion
In this article, we propose a novel framework, DiffRef3D, that utilizes the diffusion process for the task of 3D object detection with point clouds. The HAM and hypothesis generation scheme we proposed demonstrated consistent performance improvements across different models by integrating the proposal refinement of a two-stage 3D object detector into the diffusion process. Experiments on the KITTI benchmark show that DiffRef3D can serve as a generalizable proposal refinement framework that can be applied to other two-stage 3D object detectors with simple implementation but effective performance improvement.
References
- Cai et al. (2022) Cai, Q.; Pan, Y.; Yao, T.; and Mei, T. 2022. 3D Cascade RCNN: High Quality Object Detection in Point Clouds. IEEE Transactions on Image Processing.
- Chen et al. (2022) Chen, S.; Sun, P.; Song, Y.; and Luo, P. 2022. Diffusiondet: Diffusion model for object detection. arXiv preprint arXiv:2211.09788.
- Deng et al. (2021) Deng, J.; Shi, S.; Li, P.; Zhou, W.; Zhang, Y.; and Li, H. 2021. Voxel r-cnn: Towards high performance voxel-based 3d object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 35, 1201–1209.
- Dhariwal and Nichol (2021) Dhariwal, P.; and Nichol, A. 2021. Diffusion models beat gans on image synthesis. Advances in neural information processing systems, 34: 8780–8794.
- Geiger, Lenz, and Urtasun (2012) Geiger, A.; Lenz, P.; and Urtasun, R. 2012. Are we ready for autonomous driving? the kitti vision benchmark suite. In 2012 IEEE conference on computer vision and pattern recognition, 3354–3361. IEEE.
- Gu et al. (2022) Gu, Z.; Chen, H.; Xu, Z.; Lan, J.; Meng, C.; and Wang, W. 2022. Diffusioninst: Diffusion model for instance segmentation. arXiv preprint arXiv:2212.02773.
- He et al. (2020) He, C.; Zeng, H.; Huang, J.; Hua, X.-S.; and Zhang, L. 2020. Structure aware single-stage 3d object detection from point cloud. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 11873–11882.
- Ho, Jain, and Abbeel (2020) Ho, J.; Jain, A.; and Abbeel, P. 2020. Denoising diffusion probabilistic models. Advances in neural information processing systems, 33: 6840–6851.
- Hu, Kuai, and Waslander (2022) Hu, J. S.; Kuai, T.; and Waslander, S. L. 2022. Point density-aware voxels for lidar 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8469–8478.
- Ji et al. (2023) Ji, Y.; Chen, Z.; Xie, E.; Hong, L.; Liu, X.; Liu, Z.; Lu, T.; Li, Z.; and Luo, P. 2023. Ddp: Diffusion model for dense visual prediction. arXiv preprint arXiv:2303.17559.
- Koo et al. (2023) Koo, I.; Lee, I.; Kim, S.-H.; Kim, H.-S.; Jeon, W.-j.; and Kim, C. 2023. PG-RCNN: Semantic Surface Point Generation for 3D Object Detection. arXiv preprint arXiv:2307.12637.
- Lai et al. (2023) Lai, Z.; Duan, Y.; Dai, J.; Li, Z.; Fu, Y.; Li, H.; Qiao, Y.; and Wang, W. 2023. Denoising Diffusion Semantic Segmentation with Mask Prior Modeling. arXiv preprint arXiv:2306.01721.
- Lang et al. (2019) Lang, A. H.; Vora, S.; Caesar, H.; Zhou, L.; Yang, J.; and Beijbom, O. 2019. Pointpillars: Fast encoders for object detection from point clouds. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 12697–12705.
- Mao et al. (2021) Mao, J.; Xue, Y.; Niu, M.; Bai, H.; Feng, J.; Liang, X.; Xu, H.; and Xu, C. 2021. Voxel transformer for 3d object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 3164–3173.
- Nichol and Dhariwal (2021) Nichol, A. Q.; and Dhariwal, P. 2021. Improved Denoising Diffusion Probabilistic Models.
- Qi et al. (2017a) Qi, C. R.; Su, H.; Mo, K.; and Guibas, L. J. 2017a. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition, 652–660.
- Qi et al. (2017b) Qi, C. R.; Yi, L.; Su, H.; and Guibas, L. J. 2017b. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Advances in neural information processing systems, 30.
- Shan et al. (2023) Shan, W.; Liu, Z.; Zhang, X.; Wang, Z.; Han, K.; Wang, S.; Ma, S.; and Gao, W. 2023. Diffusion-Based 3D Human Pose Estimation with Multi-Hypothesis Aggregation. arXiv preprint arXiv:2303.11579.
- Sheng et al. (2021) Sheng, H.; Cai, S.; Liu, Y.; Deng, B.; Huang, J.; Hua, X.-S.; and Zhao, M.-J. 2021. Improving 3d object detection with channel-wise transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 2743–2752.
- Shi et al. (2020a) Shi, S.; Guo, C.; Jiang, L.; Wang, Z.; Shi, J.; Wang, X.; and Li, H. 2020a. Pv-rcnn: Point-voxel feature set abstraction for 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 10529–10538.
- Shi, Wang, and Li (2019) Shi, S.; Wang, X.; and Li, H. 2019. Pointrcnn: 3d object proposal generation and detection from point cloud. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 770–779.
- Shi et al. (2020b) Shi, S.; Wang, Z.; Shi, J.; Wang, X.; and Li, H. 2020b. From points to parts: 3d object detection from point cloud with part-aware and part-aggregation network. IEEE transactions on pattern analysis and machine intelligence, 43(8): 2647–2664.
- Shi and Rajkumar (2020) Shi, W.; and Rajkumar, R. 2020. Point-gnn: Graph neural network for 3d object detection in a point cloud. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 1711–1719.
- Song, Meng, and Ermon (2020) Song, J.; Meng, C.; and Ermon, S. 2020. Denoising diffusion implicit models. arXiv preprint arXiv:2010.02502.
- Sun et al. (2021) Sun, P.; Zhang, R.; Jiang, Y.; Kong, T.; Xu, C.; Zhan, W.; Tomizuka, M.; Li, L.; Yuan, Z.; Wang, C.; et al. 2021. Sparse r-cnn: End-to-end object detection with learnable proposals. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 14454–14463.
- Vaswani et al. (2017) Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A. N.; Kaiser, Ł.; and Polosukhin, I. 2017. Attention is all you need. Advances in neural information processing systems, 30.
- Wang et al. (2023) Wang, H.; Cao, J.; Anwer, R. M.; Xie, J.; Khan, F. S.; and Pang, Y. 2023. DFormer: Diffusion-guided Transformer for Universal Image Segmentation. arXiv preprint arXiv:2306.03437.
- Wu et al. (2022) Wu, H.; Deng, J.; Wen, C.; Li, X.; and Wang, C. 2022. CasA: A Cascade Attention Network for 3D Object Detection from LiDAR point clouds. IEEE Transactions on Geoscience and Remote Sensing.
- Xu, Zhong, and Neumann (2022) Xu, Q.; Zhong, Y.; and Neumann, U. 2022. Behind the curtain: Learning occluded shapes for 3d object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 36, 2893–2901.
- Xu et al. (2021) Xu, Q.; Zhou, Y.; Wang, W.; Qi, C. R.; and Anguelov, D. 2021. Spg: Unsupervised domain adaptation for 3d object detection via semantic point generation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 15446–15456.
- Yan, Mao, and Li (2018) Yan, Y.; Mao, Y.; and Li, B. 2018. Second: Sparsely embedded convolutional detection. Sensors, 18(10): 3337.
- Yang et al. (2020) Yang, Z.; Sun, Y.; Liu, S.; and Jia, J. 2020. 3dssd: Point-based 3d single stage object detector. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 11040–11048.
- Yang et al. (2019) Yang, Z.; Sun, Y.; Liu, S.; Shen, X.; and Jia, J. 2019. Std: Sparse-to-dense 3d object detector for point cloud. In Proceedings of the IEEE/CVF international conference on computer vision, 1951–1960.
- Yin, Zhou, and Krahenbuhl (2021) Yin, T.; Zhou, X.; and Krahenbuhl, P. 2021. Center-Based 3D Object Detection and Tracking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 11784–11793.
- Zhou and Tuzel (2018) Zhou, Y.; and Tuzel, O. 2018. Voxelnet: End-to-end learning for point cloud based 3d object detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, 4490–4499.
- Zou et al. (2023) Zou, J.; Zhu, Z.; Ye, Y.; and Wang, X. 2023. DiffBEV: Conditional Diffusion Model for Bird’s Eye View Perception. arXiv preprint arXiv:2303.08333.