Device-Independent Quantum Key Distribution
Based on the Mermin-Peres Magic Square Game
Abstract
Device-independent quantum key distribution (DIQKD) is information-theoretically secure against adversaries who possess a scalable quantum computer and who have supplied malicious key-establishment systems; however, the DIQKD key rate is currently too low. Consequently, we devise a DIQKD scheme based on the quantum nonlocal Mermin-Peres magic square game: our scheme asymptotically delivers DIQKD against collective attacks, even with noise. Our scheme outperforms DIQKD using the Clauser-Horne-Shimony-Holt game with respect to the number of game rounds, albeit not number of entangled pairs, provided that both state visibility and detection efficiency are high enough.
Device-independent quantum key distribution (DIQKD) enables distant parties to achieve quantum key distribution even with untrusted apparatuses [1, 2, 3]. DIQKD provides information-theoretic security [4, 5, 6] against certain side-channel attacks that compromise the security of conventional quantum key distribution implementations [7, 8, 9]. To achieve this security, DIQKD treats all devices that prepare, transmit, and measure information carriers as black boxes that could have been created by an adversary. A nonlocality test [10] is typically executed by two communicating parties to estimate an adversary’s possible knowledge about the generated data. Based on the result of the test, the parties determine whether the data suffice to yield secure keys [4, 5, 6].
However, as a sacrifice for high-level security, DIQKD yields a low key rate, as confirmed by recent experimental demonstrations [11, 12, 13]. For the potential use of DIQKD in practice, a high key-rate DIQKD protocol is demanding. Here, we remedy this issue by employing the nonlocality test of a Mermin-Peres magic square game (MPG) [14, 15] in DIQKD. The MPG is a special nonlocal game whose quantum strategies allow two players to win with unit probability [16, 17], thereby exceeding the winning probability of other nonlocal games such as the Clauser-Horne-Shimony-Holt (CHSH) game [18]. These remarkable features enable the MPG to yield a distinct DIQKD protocol from conventional protocols [19, 20, 21, 22, 23, 24].
Here, we propose a DIQKD protocol based on the MPG and prove security in the asymptotic case subject to collective attacks. Adopting the technique proposed in Ref. [25], we numerically determine thresholds for state visibility and detection efficiency required by the protocol to generate secure keys. We show that our MPG-based protocol generates a higher key rate, defined as the average number of secret bits generated in each instance of the protocol (namely, preparation, distribution, and measurement), compared to CHSH-based DIQKD protocols for certain parameter regimes. Precisely, we show that our MPG-based protocol demonstrates advantages if the state visibility exceeds 0.978 (with perfect detection) or if the detection efficiency exceeds 0.982 (with a perfect source). Our results show the potential advantage of using more complex entangled states in implementing DIQKD.
MPG-based DIQKD protocol.—Alice and Bob play the MPG [14, 15, 16], which is depicted and explained in Fig. 1.
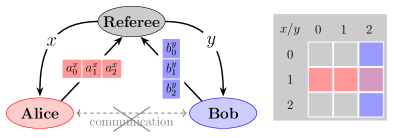
After the game, the referee decides whether Alice and Bob win or not according to the average winning probability
| (1) |
Here, is the probability of distributing index pair , and is the winning probability of Alice and Bob with respect to .
Throughout, we employ the unbiased MPG: . When using classical strategies (see one example in §IA of Supplemental Material 111See Supplemental Material for the classical and quantum strategies for the MPG, the security of MPG-based protocol beyond the ideal case, and the CHSH-based DIQKD protocols.), Alice and Bob’s average winning probability is at most [27, 17]. As classical strategies are equivalent to local hidden variables, is actually a Bell inequality; some quantum strategies violate this inequality [27, 17]. Here, we denote a quantum strategy as and its average winning probability as , where is the distributed quantum state and is the set of Alice’s and Bob’s quantum measurements used to generate the outputs. In particular, when the state is two pairs of maximally entangled qubits
| (2) |
a measurement set (details in §IB of Supplemental Material [26]) exists such that Alice and Bob will win the MPG: with optimal quantum strategy .
Crucially, the MPG certifies whether the outputs are correlated in every input pair. This feature allows us to design a DIQKD protocol, as introduced in Protocol 1. In this protocol, two communication parties, also termed Alice and Bob, initially generate data by playing the MPG. They announce their inputs and record the overlapped bits. To estimate parameters, Alice communicates with Bob which part of the bits serves as raw keys with the remaining part of the bits announced to play the MPG. If the average winning probability estimated from the announced data is less than an expected value , they abort the protocol; otherwise, they perform data reconciliation on raw keys to obtain the final keys.
- Input
-
—number of rounds,
—Alice’s final key, —Bob’s final key.
- Data generation
-
In each round , Alice and Bob independently pick , uniformly at random. They inject and to their devices and record the outputs for Alice and for Bob, respectively.
- Announcement
-
Alice and Bob announce their inputs and . They keep the bits and , respectively.
- Parameter estimation
-
Alice picks a random index subset with a length and communicates with Bob. They use the bits with indexes in as raw keys and , respectively, and announce the remaining bits, based on which they estimate the average winning probability of the MPG. If , they abort the protocol; otherwise, they proceed.
- Data reconciliation
-
Alice and Bob apply error correction and privacy amplification on the raw keys and to obtain final secure keys and , respectively.
Security analysis.—To prove security for a DIQKD protocol, one needs to consider general adversary attacks and finite-data effect [4, 5, 6]. On the other hand, one can also temporarily consider weak security where adversary attacks are independent identically distributed (i.i.d.) collective and where the number of rounds is infinite (asymptotic scenario), followed by extending the weak security to the general scenario [6, 28, 29]. Here, we analyze the weak security of Protocol 1.
Suppose that an MPG-based DIQKD protocol with a pre-determined is successfully implemented. We analyze if and how much secure key can be established for the case of i.i.d. collective attacks in the asymptotic scenario. Because DIQKD assumes the correctness and completeness of quantum theory, data generated in the protocol can be described by quantum measurements on a quantum state. As all quantum devices are untrusted, the precise quantum state and quantum measurements are unknown. Nevertheless, the assumption of i.i.d. collective attacks allows one to suppose that [19], in each round, the adversary Eve produces a quantum state [19, 6] and distributes it to Alice and Bob.
Measurements in the protocol, without losing generality, can always be described by the sets of projector-valued measures for Alice and for Bob, respectively. Here, and denote the inputs (i.e., measurement settings) while and are bits representing Alice’s and Bob’s outputs,
| (3) |
respectively. For
| (4) |
is evidently a quantum strategy for the MPG. The only constraint on is that the protocol is not aborted; i.e., .
An essential feature of the protocol is that raw keys are generated by all pairs of quantum measurements in on the state . For each input pair , whatever the precise forms of and are, the quantum state after the measurement can always be expressed as a classical-classical-quantum state.
| (5) |
where are the raw keys (bits from the overlapping grid of Alice’s row and Bob’s column) and is the unnormalized quantum state characterizing Eve’s knowledge of the raw keys.
An appropriate one-way data-reconciliation protocol always exists such that a certain amount of secure keys can be processed from the raw keys while eliminating Eve’s information [30]. As a result, for each input pair , at least a ratio of the raw keys will remain as final keys, where
| (6) |
Here, denotes the conditional von Neumann entropy, and the bold symbols and imply that Alice and Bob’s states are in classical states, representing the raw keys and , respectively.
Finally, the security of the protocol should take all possible into account, which implies that the final keys correspond to the worst case of all quantum strategies . We define the key rate of DIQKD as the ratio of the length of final keys and the number of all rounds. In the asymptotic limit , the key rate can be expressed as
| (7) |
subject to
| (8) |
Here, the coefficient comes from the fact that each input pair occurs with a probability while a ratio of the rounds is used as raw keys. The key rate defined here characterizes how many secure keys can be generated given the number of experimental rounds, which is different from the definition used in some literature where the test rounds are excluded [24].
To further prove that the protocol can produce correct and secure keys, we need to show that the key rate has positive values when implementing the protocol using certain quantum strategies. We first consider an ideal case, namely, implementing the protocol with the optimal quantum strategy and setting . As the inputs are unbiased and randomly picked, the test rounds and the key rounds have the same correlations, both of which yield , so the protocol will not be aborted. Meanwhile, Alice and Bob’s raw keys are uniformly distributed and perfectly correlated (see details in §IB of Supplemental Material [26]). We have for any . Furthermore, in the MPG can self-test two singlets [31]; i.e., the unknown quantum state must be locally isometric to two pairs of maximally entangled 2-qubit states. Such states cannot be correlated with a third party because of entanglement monogamy [32]. Combining with the fact that is uniformly random for all , we have , indicating that the adversary has no information on . As a result, we obtain for this ideal case, which shows that the protocol can indeed produce secure keys.
For non-ideal cases when general quantum strategies are adopted or when noises are involved, we can bound via the recently developed technique of quasi-relative entropy [25]. Precisely, a lower bound for in Eq. (6) can be derived as [25]
| (9) |
where and , with a set of nodes and weights of the Gauss-Radau quadrature, and is defined as
| (10) |
with an arbitrary operator and the projector-valued measure corresponding to Alice’s input and output . Combining with Eqs. (7) and (8), the minimization in Eq. (9) is taken over all possible pure states and measurement strategies subject to
| (11a) | ||||
| (11b) | ||||
| (11c) | ||||
| (11d) | ||||
| (11e) | ||||
| (11f) | ||||
This constrained minimization can be resolved via the Navascués-Pironio-Acín (NPA) hierarchy [33], which is numerically computable via solving a semidefinite program 222The code for obtaining the key-rate bound can be found in https://github.com/YizhengZhen/Code_DIQKD_MPG. In §II of Supplemental Material [26], we numerically show that has a positive lower bound if , which implies that the protocol can produce secure keys if, in the end, Eq. (7) has a positive value.
Noise tolerance.—Consider the case where the optimal quantum strategy is supposed to be used to implement the MPG-based protocol. Here, we characterize the performance of the protocol under two types of noise. For the first type, we consider the imprecise preparation of such that each qubit may be mixed with some white noise. The distributed state becomes before the detection, where and is the state visibility. For the second type, we consider the noise led by non-click events in measurements. Such non-click events are caused by the loss of the state in transmission or the inefficiency of the detector, and cannot be sifted out from the data (otherwise, it may open detection loopholes [10, 11, 12, 13]). Instead, Alice and Bob must assign an output to the non-click events. We consider the following procedure: in each round, unless Alice (or Bob) successfully measured her (or his) state, Alice (or Bob) will output values according to a deterministic strategy of the MPG (Table I in §IA of Supplemental Material [26]). The detection efficiency on each side is assumed identical and denoted as .
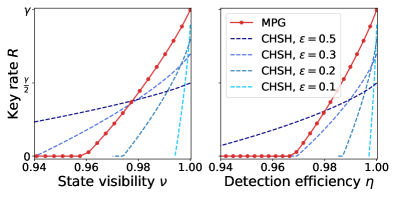
We consider two cases where only the white noise is involved and where only the detection inefficiency is involved. For each value of or , we select such that the produced data can pass the parameter estimation in the protocol. The results are shown in Fig. 2. In the figure, the red solid line is the key-rate lower bound of the MPG-based protocol, which is obtained by solving the semidefinite programming problem combining Eqs. (6)-(11). For the calculation, we set the NPA hierarchy as 2 and the number of nodes in the Gauss-Radau quadrature as 16. From the figure, we observe that the key rate decreases when the state visibility or detection efficiency becomes smaller. It shows that the MPG-based protocol can produce a positive key rate if the state visibility or if the detection efficiency .
Overcoming the key rate of CHSH-based protocols.—A prominent feature of the MPG-based protocol is that outputs of every input pair can be used to generate secure keys. As a result, all the outputs except that used in the estimation are collected as raw keys. This feature may enable the MPG-based protocol to yield a higher key rate than conventional DIQKD protocols. Particularly, if the optimal quantum strategy of the MPG can be faithfully implemented, the key rate . It is actually the maximal key rate that any DIQKD protocol can achieve. As we will show, the MPG-based protocol outperforms a variety of CHSH-based protocols for certain regions of noise parameters.
In a standard CHSH-based protocol [20, 19], Alice and Bob usually have inputs and , respectively. To generate the data, Alice picks uniformly at random while Bob picks according to probabilities , respectively, and they input and into their local device and record the outputs . After obtaining all the data, they announce the inputs and select the outputs corresponding to the input pair to play the CHSH game. If the average winning probability is above a certain threshold, they select the outputs corresponding to the input pair as the raw keys, followed by the data-reconciliation procedure to obtain the final keys. One can immediately see that the key rate cannot exceed , which is half of the optimal key rate of the MPG-based protocol.
To make a full comparison between the MPG-based protocol and protocols based on the CHSH game, we consider a variety of protocols based on biased CHSH games [35]. Suppose that in the CHSH-based protocol, Alice picks according to probabilities , respectively, while Bob’s probabilities of picking remain the same. Then, the optimal key rate of the protocol becomes , which is higher than that of the standard CHSH-based protocol and is approaching when . We provide the details of the biased CHSH game and its induced DIQKD protocols in §IIIA of Supplemental Material [26].
We compare the performance of MPG-based protocol and CHSH-based protocols with different input probabilities. We suppose that the optimal quantum strategy for the biased CHSH game is used to implement the CHSH-based protocol [35, 36]. It turns out that when introducing the white noise, it is equivalent to treating the distributed state as . When a non-click event occurs, Alice (or Bob) will output for any input (or ) such that a deterministic classical strategy is equivalently selected.
The results are shown again in Fig. 2, where the key-rate lower bounds of the CHSH-based protocols with different s are plotted with blue dashed lines. These key-rate lower bounds are obtained in a similar fashion to calculating the key-rate lower bound for the MPG-based protocol, as presented in §IIIB of Supplemental Material [26]. We observe that all key rates decrease when state visibility or detection efficiency decreases. As expected, decreasing can increase the optimal key rate of CHSH-based protocols. Nevertheless, these protocols cannot exceed the key rate of the MPG-based protocol in regions of and , showing the advantage of the MPG-based protocol in these regions.
Discussion.—We have shown that our MPG-based protocol generates more secret keys per instance of protocol than CHSH-based protocols, in regions where the state visibility and detection efficiency are high. This comparison is made on the basis that the costly resource is the number of nonlocal games executed in the experiment [23, 24]. Indeed, the secrecy of the keys in DIQKD is guaranteed by winning nonlocal games. Therefore, our result implies that a more complex nonlocal game may lead to a higher amount of secure keys per game round.
Nevertheless, the number of nonlocal games does not necessarily equal to the number of entangled states generated by the source, which is usually the considered resource in practice. In the case where the source generates a certain number of 2-qubit entangled states, the CHSH-based protocol is preferred. This is because the CHSH-based protocol can run twice as many rounds as that of a MPG-based protocol, and more keys could be produced. Also, the CHSH-based protocol is more robust against diminished state visibility and detection efficiency.
As for the realization of Protocol 1, the resource state can be produced using two identical preparation of entangled singlets, or using the hyper-entanglement technique to reduce the experimental overheads [37, 38, 39]. An obvious downside of the protocol is its high requirements for state visibility and detection efficiency. The selection of platforms is important to fulfill the desired requirements. For instance, the platform with remote matter-qubit entanglement can provide a higher detection efficiency. Meanwhile, theoretical improvements, including the use of on-maximally entangled states [21, 22], noisy-preprocessing procedures [40], and post-selection techniques [41], can be considered to reduce the requirements of the protocol on the experimental imperfections.
In addition, regarding the higher key rate of the MPG-based protocol over CHSH-based protocols, one may wonder if there are improvements on the CHSH-based protocol such that the key rate can be achieved. For instance, in the standard CHSH-based protocol, one can add a key-generation agreement after the state distribution but before the measurements. Such step allows Alice and Bob to do either key generation or CHSH test [i.e., the original rounds corresponding to do not exist], which theoretically enables the key rate to be as high as . However, the security of the modified protocol requires an additional assumption that no unwanted information is leaked during the key-generation agreement step 333Otherwise, the untrusted devices may communicate with the adversary in the agreement step of each round. We remark that the MPG-based protocol can achieve a key rate as high as without relying on the above additional assumption.
Conclusions.—We have proposed the DIQKD protocol based on the MPG and have provided the security analysis of the protocol against the collective attacks in the asymptotic scenario. We have numerically characterized the regions of two noise parameters, namely, state visibility and detection efficiency, when the MPG-based protocol can produce secure keys. We have further shown that, in certain regions, the MPG-based protocol has a higher key rate over a variety of protocols based on CHSH games. Our result shows the advantage of a sophisticated nonlocal game in DIQKD protocols and the potential usage of high-dimensional entanglement in device-independent quantum information tasks.
Acknowledgements.
We gratefully acknowledge valuable discussions with Nai-Le Liu, Kai Chen, Li Li, and Valerio Scarani. We also thank Enrique Cervero Martín and Marco Tomamichel for pointing out errors in a previous version of this paper and for drawing our attention to related works [43, 44, 45], which we had not known. This work was supported by National Natural Science Foundation of China (No. 62031024, No. 12005091, No. 12104444), National Key Research and Development Program of China (No. 2020YFA0309700), Shanghai Academic/Technology Research Leader (No. 21XD1403800), and Shanghai Science and Technology Development Funds (No. 22JC1402900). Y.M. acknowledges support from the China Postdoctoral Science Foundation (Grant No. 2021M693093). F.X. acknowledges the support from the Tencent Foundation.References
- Ekert [1991] A. K. Ekert, Quantum Cryptography Based on Bell’s Theorem, Phys. Rev. Lett. 67, 661 (1991).
- Mayers and Yao [1998] D. Mayers and A. Yao, Quantum Cryptography with Imperfect Apparatus, in Proceedings of the 39th Annual Symposium on Foundations of Computer Science (IEEE, 1998) pp. pp. 503–509.
- Barrett et al. [2005] J. Barrett, L. Hardy, and A. Kent, No Signaling and Quantum Key Distribution, Phys. Rev. Lett. 95, 010503 (2005).
- Vazirani and Vidick [2014] U. Vazirani and T. Vidick, Fully Device-Independent Quantum Key Distribution, Phys. Rev. Lett. 113, 140501 (2014).
- Miller and Shi [2016] C. A. Miller and Y. Shi, Robust Protocols for Securely Expanding Randomness and Distributing Keys Using Untrusted Quantum Devices, J. Assoc. Comput. Mach. 63, 33:1 (2016).
- Arnon-Friedman et al. [2018] R. Arnon-Friedman, F. Dupuis, O. Fawzi, R. Renner, and T. Vidick, Practical Device-Independent Quantum Cryptography via Entropy Accumulation, Nat. Commun. 9, 459 (2018).
- Gisin et al. [2002] N. Gisin, G. Ribordy, W. Tittel, and H. Zbinden, Quantum Cryptography, Rev. Mod. Phys. 74, 145 (2002).
- Xu et al. [2020] F. Xu, X. Ma, Q. Zhang, H.-K. Lo, and J.-W. Pan, Secure Quantum Key Distribution with Realistic Devices, Rev. Mod. Phys. 92, 025002 (2020).
- Portmann and Renner [2022] C. Portmann and R. Renner, Security in Quantum Cryptography, Rev. Mod. Phys. 94, 025008 (2022).
- Brunner et al. [2014] N. Brunner, D. Cavalcanti, S. Pironio, V. Scarani, and S. Wehner, Bell Nonlocality, Rev. Mod. Phys. 86, 419 (2014).
- Nadlinger et al. [2022] D. P. Nadlinger, P. Drmota, B. C. Nichol, G. Araneda, D. Main, R. Srinivas, D. M. Lucas, C. J. Ballance, K. Ivanov, E. Y.-Z. Tan, P. Sekatski, R. L. Urbanke, R. Renner, N. Sangouard, and J.-D. Bancal, Experimental Quantum Key Distribution Certified by Bell’s Theorem, Nature (London) 607, 682 (2022).
- Zhang et al. [2022] W. Zhang, T. van Leent, K. Redeker, R. Garthoff, R. Schwonnek, F. Fertig, S. Eppelt, W. Rosenfeld, V. Scarani, C. C.-W. Lim, and H. Weinfurter, A Device-Independent Quantum Key Distribution System for Distant Users, Nature (London) 607, 687 (2022).
- Liu et al. [2022] W.-Z. Liu, Y.-Z. Zhang, Y.-Z. Zhen, M.-H. Li, Y. Liu, J. Fan, F. Xu, Q. Zhang, and J.-W. Pan, Toward a Photonic Demonstration of Device-Independent Quantum Key Distribution, Phys. Rev. Lett. 129, 050502 (2022).
- Mermin [1990] N. D. Mermin, Simple Unified Form for the Major No-Hidden-Variables Theorems, Phys. Rev. Lett. 65, 3373 (1990).
- Peres [1990] A. Peres, Incompatible Results of Quantum Measurements, Phys. Lett. A 151, 107 (1990).
- Brassard et al. [2005] G. Brassard, A. Broadbent, and A. Tapp, Quantum Pseudo-Telepathy, Found. Phys. 35, 1877 (2005).
- Gisin et al. [2007] N. Gisin, A. A. Méthot, and V. Scarani, Pseudo-Telepathy: Input Cardinality and Bell-Type Inequalities, Int. J. Quantum Inf. 05, 525 (2007).
- Clauser et al. [1969] J. F. Clauser, M. A. Horne, A. Shimony, and R. A. Holt, Proposed Experiment to Test Local Hidden-Variable Theories, Phys. Rev. Lett. 23, 880 (1969).
- Pironio et al. [2009] S. Pironio, A. Acín, N. Brunner, N. Gisin, S. Massar, and V. Scarani, Device-Independent Quantum Key Distribution Secure against Collective Attacks, New J. Phys. 11, 045021 (2009).
- Acín et al. [2007] A. Acín, N. Brunner, N. Gisin, S. Massar, S. Pironio, and V. Scarani, Device-Independent Security of Quantum Cryptography against Collective Attacks, Phys. Rev. Lett. 98, 230501 (2007).
- Woodhead et al. [2021] E. Woodhead, A. Acín, and S. Pironio, Device-Independent Quantum Key Distribution with Asymmetric CHSH Inequalities, Quantum 5, 443 (2021).
- Sekatski et al. [2021] P. Sekatski, J.-D. Bancal, X. Valcarce, E. Y.-Z. Tan, R. Renner, and N. Sangouard, Device-Independent Quantum Key Distribution from Generalized CHSH Inequalities, Quantum 5, 444 (2021).
- Gonzales-Ureta et al. [2021] J. R. Gonzales-Ureta, A. Predojević, and A. Cabello, Device-Independent Quantum Key Distribution Based on Bell Inequalities with More than Two Inputs and Two Outputs, Phys. Rev. A 103, 052436 (2021).
- Primaatmaja et al. [2023] I. W. Primaatmaja, K. T. Goh, E. Y.-Z. Tan, J. T.-F. Khoo, S. Ghorai, and C. C.-W. Lim, Security of Device-Independent Quantum Key Distribution Protocols: A Review, Quantum 7, 932 (2023).
- Brown et al. [2021] P. Brown, H. Fawzi, and O. Fawzi, Device-Independent Lower Bounds on the Conditional von Neumann Entropy (2021), arXiv:2106.13692 [quant-ph] .
- Note [1] See Supplemental Material for the classical and quantum strategies for the MPG, the security of MPG-based protocol beyond the ideal case, and the CHSH-based DIQKD protocols.
- Cabello [2001] A. Cabello, “All versus Nothing” Inseparability for Two Observers, Phys. Rev. Lett. 87, 010403 (2001).
- Arnon-Friedman et al. [2019] R. Arnon-Friedman, R. Renner, and T. Vidick, Simple and Tight Device-Independent Security Proofs, SIAM J. Comput. 48, 181 (2019).
- Tan et al. [2022] E. Y.-Z. Tan, P. Sekatski, J.-D. Bancal, R. Schwonnek, R. Renner, N. Sangouard, and C. C.-W. Lim, Improved DIQKD Protocols with Finite-Size Analysis (2022).
- Devetak and Winter [2005] I. Devetak and A. Winter, Distillation of Secret Key and Entanglement from Quantum States, Proc. R. Soc. A 461, 207 (2005).
- Wu et al. [2016] X. Wu, J.-D. Bancal, M. McKague, and V. Scarani, Device-Independent Parallel Self-Testing of Two Singlets, Phys. Rev. A 93, 062121 (2016).
- Terhal [2004] B. M. Terhal, Is Entanglement Monogamous?, IBM J. Res. Dev. 48, 71 (2004).
- Navascués et al. [2007] M. Navascués, S. Pironio, and A. Acín, Bounding the Set of Quantum Correlations, Phys. Rev. Lett. 98, 010401 (2007).
- Note [2] The code for obtaining the key-rate bound can be found in https://github.com/YizhengZhen/Code_DIQKD_MPG.
- Lawson et al. [2010] T. Lawson, N. Linden, and S. Popescu, Biased Nonlocal Quantum Games (2010), arXiv:1011.6245 [quant-ph] .
- Acín et al. [2012] A. Acín, S. Massar, and S. Pironio, Randomness versus Nonlocality and Entanglement, Phys. Rev. Lett. 108, 100402 (2012).
- Xu et al. [2022a] J.-M. Xu, Y.-Z. Zhen, Y.-X. Yang, Z.-M. Cheng, Z.-C. Ren, K. Chen, X.-L. Wang, and H.-T. Wang, Experimental Demonstration of Quantum Pseudotelepathy, Phys. Rev. Lett. 129, 050402 (2022a).
- Yang et al. [2005] T. Yang, Q. Zhang, J. Zhang, J. Yin, Z. Zhao, M. Żukowski, Z.-B. Chen, and J.-W. Pan, All-Versus-Nothing Violation of Local Realism by Two-Photon, Four-Dimensional Entanglement, Phys. Rev. Lett. 95, 240406 (2005).
- Aolita et al. [2012] L. Aolita, R. Gallego, A. Acín, A. Chiuri, G. Vallone, P. Mataloni, and A. Cabello, Fully Nonlocal Quantum Correlations, Phys. Rev. A 85, 032107 (2012).
- Ho et al. [2020] M. Ho, P. Sekatski, E. Y.-Z. Tan, R. Renner, J.-D. Bancal, and N. Sangouard, Noisy Preprocessing Facilitates a Photonic Realization of Device-Independent Quantum Key Distribution, Phys. Rev. Lett. 124, 230502 (2020).
- Xu et al. [2022b] F. Xu, Y.-Z. Zhang, Q. Zhang, and J.-W. Pan, Device-Independent Quantum Key Distribution with Random Postselection, Phys. Rev. Lett. 128, 110506 (2022b).
- Note [3] Otherwise, the untrusted devices may communicate with the adversary in the agreement step of each round.
- Vidick [2017] T. Vidick, Parallel DIQKD from parallel repetition (2017), arxiv:1703.08508 [quant-ph] .
- Jain et al. [2020] R. Jain, C. A. Miller, and Y. Shi, Parallel Device-Independent Quantum Key Distribution, IEEE Transactions on Information Theory 66, 5567 (2020).
- Jain and Kundu [2023] R. Jain and S. Kundu, A direct product theorem for quantum communication complexity with applications to device-independent cryptography (2023), arxiv:2106.04299 [quant-ph] .