Development of long-range phase coherence on the Kondo lattice

Heavy fermion systems are featured with correlated phenomena such as unconventional superconductivity, quantum criticality, and non-Fermi liquid Sigrist1991RMP ; Stewart2001RMP ; Gegenwart2008NatPhys ; Yang2012PNAS . Underlying all these exotic properties is the interplay of inter-site magnetic correlations and spin screening as described by the Kondo lattice model Hewson1997 ; Coleman2015 ; Yang2017PNAS . It differs from the single-impurity Kondo physics in that the many-body spin-entangled state between local moments and conduction electrons can extend and propagate on the lattice as dispersive heavy electrons. But how this state emerges, develops and eventually extends in space remains less understood despite many theoretical efforts Lonzarich2017RPP . In particular, recent angle-resolved photoemission spectroscopy (ARPES) experiment reported the onset of hybridization well above the coherence temperature in transport measurements Chen2017PRB ; Yang2016RPP . Later pump probe experiment revealed a two-stage process for the heavy electron development on the lattice Hu2019PRB ; Liu2020PRL . This two-stage scenario seems quite universal Pei2021PRB , but still awaits a microscopic explanation. Its theoretical formulation will necessarily deepen our understanding of the Kondo lattice physics.

Phase fluctuations play an indispensable role in modern strongly correlated physics and have been extensively studied in past decades. Notable examples include deconfined phases in lattice gauge theories Kogut1979RMP ; Gazit2017NatPhys ; Xu2019PRX , phase-fluctuation scenario in high-$T_{c}$ cuprates Dagotto2005PRL ; Dagotto2008PRL ; Dubi2007Nature ; TaoLi2010PRB , and flux phases in quantum spin liquids Wen2004 ; Zhou2017RMP ; Wang2021PRL . In Kondo lattice systems, phase fluctuations appear when some slave particles or auxiliary fields are introduced to describe local spins and their entanglement with conduction electrons, but were often ignored in prevailing mean-field calculations, causing artificial finite-temperature phase transitions Auerbach1986PRL ; Newns1987AdvPhys ; Zhang2000PRB ; Coqblin2003PRB ; Pepin2011PRL ; Zhang2018PRB . Phase fluctuations can convert these artificial transitions into a crossover Senthil2003PRL ; Senthil2004PRB , and may be a key controlling the development of heavy electron state beyond usual mean-field or local approximations Coleman2005PRB ; Pepin2007PRL ; Pepin2008PRB ; Ohara2007PRB ; Ohara2013JPSJ ; Ohara2014JPSJ ; Jiang2017PRB ; Jiang2020PRB ; Hu2020PRR ; Han2021PRB , but a proper description is not yet available.

In this work, we address this issue by proposing a novel theoretical framework to describe heavy electron emergence based on phase coherence. We employ a recently-proposed static auxiliary field approach for Kondo systems Dong2021PRB and introduce a gauge-invariant bond phase to characterize spatial correlation of the hybridization fields. This bond phase combines the onsite hybridization fields and inter-site magnetic correlation fields between two spatially separated lattice sites, so its probabilistic distribution tracks directly the spatial development of heavy electron state. Our calculations show a logarithmic temperature dependence of its characteristic length scale and reveal a precursor short-range phase-correlated pseudogap state before the long-range phase coherence is developed to form the Kondo insulating or heavy electron state at lower temperatures. Our theory provides a general scheme to describe the phase coherence and other phase-related physics in Kondo lattice systems.

For simplicity, we consider the two-dimensional Kondo-Heisenberg model on a square lattice,

$$H=-t\sum_{\left\langle ij\right\rangle\sigma}\left(c_{i\sigma}^{{\dagger}}c_{j\sigma}+\text{H.c.}\right)+J_{\text{K}}\sum_{i}\mathbf{s}_{i}\cdot\mathbf{S}_{i}+J_{\text{H}}\sum_{\left\langle ij\right\rangle}\mathbf{S}_{i}\cdot\mathbf{S}_{j},$$

(1)

where $t$ is the hopping integral of conduction electrons between nearest-neighbor sites, $\mathbf{s}_{i}=\sum_{a\beta}c_{i\alpha}^{{\dagger}}\frac{\bm{\sigma}_{\alpha\beta}}{2}c_{i\beta}$ is the conduction electron spin localized at $\mathbf{r}_{i}$, and $\mathbf{S}_{i}$ denotes the local spins. $J_{\text{K}}$ and $J_{\text{H}}$ describe the Kondo and Heisenberg exchange interactions. Under the Abrikosov pseudofermion representation $\mathbf{S}_{i}=\sum_{\eta\gamma}f_{i\eta}^{{\dagger}}\frac{\bm{\sigma}_{\eta\gamma}}{2}f_{i\gamma}$, both terms can be decoupled using the Hubbard-Stratonovich transformation: $2\mathbf{s}_{i}\cdot\mathbf{S}_{i}\rightarrow\sum_{\sigma}(V_{i}c_{i\sigma}^{{\dagger}}f_{i\sigma}+\text{H.c.})+\left|V_{i}\right|^{2}$ and $2\mathbf{S}_{i}\cdot\mathbf{S}_{j}\rightarrow\sum_{\sigma}(\chi_{ij}f_{i\sigma}^{{\dagger}}f_{j\sigma}+\text{H.c.})+\left|\chi_{ij}\right|^{2}$, where $V_{i}$ and $\chi_{ij}$ are two fluctuating auxiliary fields describing the hybridization and inter-site magnetic correlation, respectively. This gives the action SM :

	$\displaystyle S$	$\displaystyle=\sum_{i,l}\frac{\beta J_{\text{K}}\left|V_{i,l}\right|^{2}}{2}+\sum_{\left\langle ij\right\rangle,l}\frac{\beta J_{\text{H}}\left|\chi_{ij,l}\right|^{2}}{2}-\sum_{i}\beta\lambda_{i}$
		$\displaystyle\quad+\sum_{nm\sigma}\Psi_{n\sigma}^{{\dagger}}\left(O_{nm}-\operatorname*{i}\omega_{n}\delta_{nm}\right)\Psi_{m\sigma},$		(2)

where $\Psi_{n\sigma}=\left[c_{1\sigma n},\cdots,c_{N_{0}\sigma n},f_{1\sigma n},\cdots,f_{N_{0}\sigma n}\right]^{T}$, $N_{0}$ is the number of lattice sites, and the subscripts $l$ ($n/m$) denote bosonic (fermionic) Matsubara frequency. $\lambda_{i}$ is the Lagrange multiplier for the constraint $\sum_{\sigma}f_{i\sigma}^{{\dagger}}f_{i\sigma}=1$ and takes a real value after Wick rotation Zhou2017RMP .

The above action is generally impossible to solve. To proceed, we adopt a static approximation, $V_{i,n-m}=V_{i}\delta_{nm}$, $\chi_{ij,n-m}=\chi_{ij}\delta_{nm}$ such that $O_{nm}=O\delta_{nm}$. This ignores temporal fluctuations of the auxiliary fields but takes full account of their spatial fluctuations and statistical distribution Mukherjee2014PRB ; Pradhan2015PRB ; Karmakar2016PRA ; Patel2017PRL . The fermions can be integrated out, giving an effective action only of the auxiliary fields:

	$\displaystyle S_{\text{eff}}$	$\displaystyle=\sum_{i}\frac{\beta J_{\text{K}}\left|V_{i}\right|^{2}}{2}+\sum_{\left\langle ij\right\rangle}\frac{\beta J_{\text{H}}\left|\chi_{ij}\right|^{2}}{2}-\sum_{i}\beta\lambda_{i}$
		$\displaystyle\quad-2\sum_{n}\ln\det\left(O-\operatorname*{i}\omega_{n}\right).$		(3)

The matrix $O$ has a block form $O=\left[\begin{array}[c]{cc}T^{c}&M\\ M^{{\dagger}}&T^{f}\end{array}\right]$, where $T^{c}$ ($T^{f}$) is the $N_{0}\times N_{0}$ hopping matrix of conduction electrons (pseudofermions), and $M_{ij}=\delta_{ij}J_{\text{K}}V_{i}/2$ is a diagonal matrix for their onsite hybridization. The summation over Matsubara frequency can be evaluated using $\sum_{n}\ln\det\left(O-\operatorname*{i}\omega_{n}\right)=\sum_{l}\ln\left(1+\operatorname{e}^{-\beta\xi_{l}}\right)$, where $\xi_{l}$ is the eigenvalues of $O$ and always real because $O$ is Hermitian. The probabilistic distribution of the auxiliary fields is then simply, $p(V_{i},\chi_{ij})=Z^{-1}\operatorname{e}^{-S_{\text{eff}}}$, where $Z$ is the partition function serving as the normalization factor. It can be simulated using the Monte Carlo and Metropolis algorithm on $3N_{0}$ complex random variables without sign problem Ishizuka2012PRL ; Yang2019PRB ; Maska2020PRB . This is different from the (non-uniform) mean-field method where the auxiliary variables take fixed values determined by the saddle-point approximation. For simplicity, we set the half conduction bandwidth to unity ($t=1/4$), fix $J_{\text{H}}=0.2$, and consider only the particle-hole symmetric model on a $N_{0}=8\times 8$ lattice where the Lagrangian multipliers are approximated by their saddle-point value $\lambda_{i}=0$ Saremi2011PRB . Other choices of parameters or a larger lattice have been examined and the conclusions are qualitatively unchanged.

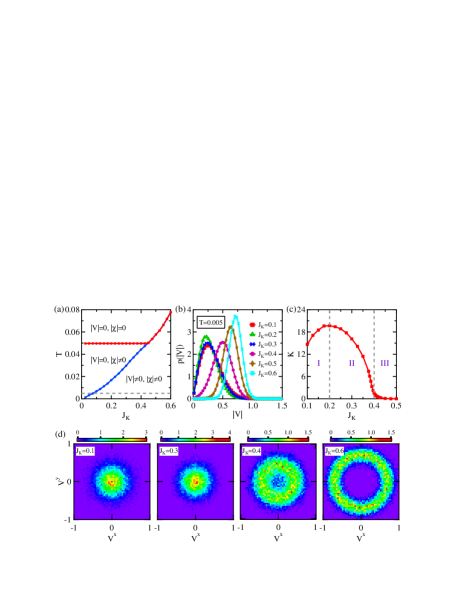
For comparison, we first show the usual mean-field phase diagram in Fig. 1(a), where the auxiliary fields are assumed to be uniform and real: $V_{i}=\overline{V}_{i}=V$, $\chi_{ij}=\overline{\chi}_{ij}=\chi$. The solution can be obtained by minimizing the free energy $F=S_{\text{eff}}/\beta$ SM . With lowering temperature, we see a second-order phase transition from $\chi=0$ to $\chi\neq 0$ at $T=J_{\text{H}}/4$, below which there is a weakly coupled state of conduction electrons and spin liquid Senthil2003PRL . Increasing $J_{\text{K}}$ drives the system into a Kondo insulating state with nonzero $V$.

We may examine this mean-field picture by considering the probabilistic distribution of the complex hybridization fields, $p(V)\equiv p(V_{i})$, which is the same on all sites due to translational symmetry and can be evaluated using the Metropolis algorithm for importance sampling of the effective action Eq. (3) SM . Figure 1(b) plots the marginal distribution of its amplitude, $p(|V|)$, at a low temperature after integrating out all other variables. The maximum of $p(|V|)$ is seen to vary nonmonotonically with increasing $J_{\text{K}}$. As shown in Fig. 1(c), we may identify three regions according to the slope $K=dp(\left|V\right|)/d\left|V\right|$ at $\left|V\right|=0$. Figure 1(d) plots the distribution $p(V)$ on the complex plane $V=\left(V^{x},V^{y}\right)$. As expected, the data cluster around $(0,0)$ at small $J_{\text{K}}$ and turn into a ring at large $J_{\text{K}}$. The distribution is therefore dominated by the bare fluctuation term $\beta J_{K}|V|^{2}/2$ in region I and the coupling with conduction electrons in region III, while region II marks a crossover in between.

The difference from the mean-field solution can be revealed by studying phase fluctuations of the auxiliary fields. Since the effective action (3) is invariant under the gauge transformation $V_{i}\rightarrow V_{i}\operatorname{e}^{\operatorname*{i}\beta_{i}}$, $\chi_{ij}\rightarrow\operatorname{e}^{-\operatorname*{i}\left(\beta_{i}-\beta_{j}\right)}$, we may define two gauge-invariant phases from

	$\displaystyle F_{i}$	$\displaystyle\equiv\chi_{ij}\chi_{jk}\chi_{kl}\chi_{li}=\left|F_{i}\right|\operatorname{e}^{\operatorname*{i}\phi_{i}},$
	$\displaystyle B_{ij}$	$\displaystyle\equiv V_{i}\chi_{ij}\overline{V}_{j}=\left|B_{ij}\right|\operatorname{e}^{\operatorname*{i}\theta_{ij}},$		(4)

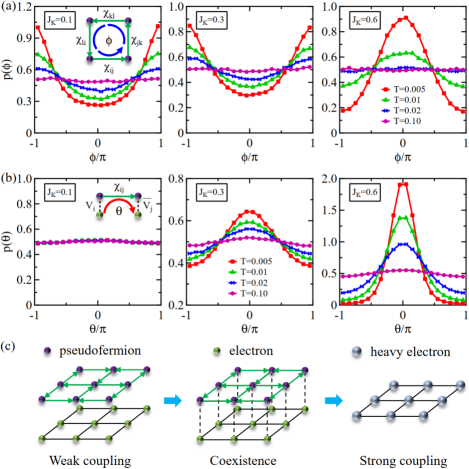
where $\phi_{i}$ denotes the flux in a plaquette $ijkl\in\Box$ and $\theta_{ij}$ reflects the phase of the hybridization bond $B_{ij}$ between nearest-neighbor sites $ij$ as illustrated in the insets of Fig. 2. The bond phase $\theta_{ij}$ reflects the correlation of two onsite hybridization fields $V_{i}$ and $V_{j}$ mediated by their inter-site magnetic correlation $\chi_{ij}$. It by definition contains spatial correlation information and is a key quantity introduced in this work to distinguish the Kondo lattice physics from the single-impurity Kondo physics Nakatsuji2002PRL ; Yang2008Nature ; Wang2021PRB ; Wang2022SCPMA .

Figures 2(a) and 2(b) plot their probabilistic distributions for three typical values of $J_{\text{K}}$. Again, due to translational symmetry, we drop the site subscript and use $p(\phi)\equiv p(\phi_{i})$ and $p(\theta)\equiv p(\theta_{ij})$. For weak coupling $J_{\text{K}}=0.1$, the local spins and conduction electrons are almost decoupled. The bond phase $p(\theta)$ distributes uniformly at all temperatures, while the flux distribution $p(\phi)$ becomes peaked at $\phi=\pi$ below certain temperature. The latter indicates a $\pi$-flux state Affleck1988PRB ; Hsu1990PRB ; Wen2002PRB ; Coleman2021PRR , which is a special feature of the pseudofermion representation of the Heisenberg model on the two-dimensional lattice and might be realized if the spin interaction is highly frustrated or on an optical lattice. Our results are in accordance with Lieb’s theorem Lieb1994PRL , which states that the saddle point for a half-filled band of fermions hopping on a planar lattice is $\pi$ per plaquette. This implies that our approach can capture the correct saddle point beyond the ad hoc uniform mean-field approximation. The $\pi$-flux state may not be stable in general situations, giving rise to confined states like antiferromagnetic order or magnon excitations. For simplicity, we ignore all these complications and take it as our starting point in order to focus on the Kondo aspect of the model. For an intermediate $J_{\text{K}}=0.3$, we still have $\pi$-flux, but the bond phase distribution becomes non-uniform at low temperatures with a peak around $\theta=0$, indicating the onset of phase correlation between nearest-neighbor hybridization fields. It therefore marks a coexisting state of flux and hybridization correlation. For strong coupling $J_{\text{K}}=0.6$, the location of maximal $p(\phi)$ changes from $\phi=\pi$ to $\phi=0$, indicating that the $\pi$-flux is completely suppressed and the system enters the Kondo insulating (or heavy electron) state. Figure 2(c) gives an illustration of all three low-temperature states. For completeness, the probabilistic distributions of $|F_{i}|$ and $|B_{ij}|$ are also given in the Supplemental Material SM .

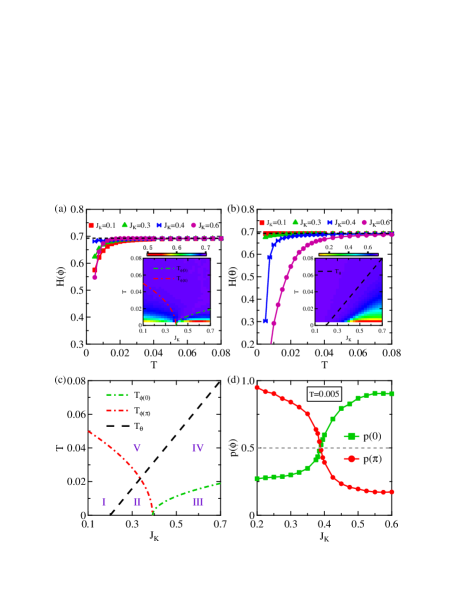
The variation of the probabilistic distributions may be reflected also in their Shannon entropy defined as $H(x)\equiv-\int p(x)\ln p(x)dx$ for a continuous random variable $x$ with the probabilistic distribution $p(x)$. The results are plotted in Figs. 3(a) and 3(b). As expected, the Shannon entropies for both $\phi/\pi$ and $\theta/\pi$ approach their uniform limit $\ln 2$ at high temperatures. Deviation from $\ln 2$ defines a crossover temperature scale for the onset of non-uniform probabilistic distribution due to either flux or bond phase correlation. A tentative phase diagram can then be constructed based on the intensity plots in the insets and the amplitude analysis in Fig. 1(c). As shown in Fig. 3(c), the dashed line $T_{\theta}$ marks a crossover to the region with non-uniform $p(\theta)$, while the dash-dotted lines, $T_{\phi(\pi)}$ and $T_{\phi(0)}$, mark the crossover to $\pi$ or 0-flux dominated regions, respectively. Note that these lines are not phase transitions but only serve as a tentative guide to the eye. Approaching zero temperature, as shown in Fig. 3(d), the curves of $p(\phi)$ at $\phi=\pi$ and $\phi=0$ as a function of $J_{\text{K}}$ cross each other exactly at the transition between regions II and III, indicating that the flux phase $\phi$ distributes uniformly and restores its full symmetry at this point. The phase diagram is therefore divided tentatively into five regions: region I is dominated by $\pi$-flux; region II is a crossover with coexisting $\pi$-flux and hybridization (bond phase) correlation; regions III and IV are dominated mostly by hybridization; region V contains weakly coupled local spins and almost decoupled conduction electrons. To exclude possible finite size effect, we have performed calculations on a $24\times 24$ lattice using the traveling cluster approximation method Kumar2006EPJB , and the results confirmed all five regions.

To clarify the hybridization properties in regions II-IV, we extend the definition of the bond phase to

	$\displaystyle\theta_{R}$	$\displaystyle\equiv\theta_{i_{0}i_{1}}+\theta_{i_{1}i_{2}}+\cdots+\theta_{i_{R-1}i_{R}}\,\,\text{mod}\,\,2\pi$
		$\displaystyle=\operatorname*{Im}\ln\left(V_{i_{0}}\chi_{i_{0}i_{1}}\overline{V}_{i_{1}}V_{i_{1}}\chi_{i_{1}i_{2}}\cdots\chi_{i_{R-1}i_{R}}\overline{V}_{i_{R}}\right),$		(5)

where $i_{0}i_{1}i_{2}...i_{R}$ denotes a path of length $R$ linking two end sites at $\textbf{r}_{i_{0}}$ and $\textbf{r}_{i_{R}}\equiv\textbf{r}_{i_{0}}+\textbf{R}$. Since $\overline{V}_{j}V_{j}=|V_{j}|^{2}$ do not contribute a phase, we have also $\theta_{R}=\operatorname*{Im}\log(V_{i_{0}}\chi_{i_{0}i_{1}}\chi_{i_{1}i_{2}}\cdots\chi_{i_{R-1}i_{R}}\overline{V}_{i_{R}})$, which is a gauge-invariant quantity describing phase correlation of the hybridization fields on two end sites mediated by inter-site magnetic correlations along the path. Figures 4(a)-4(c) compare the distribution $p(\theta_{R})$ for different $R$ in regions II, III, and IV, respectively. We find it rapidly decays to uniform distribution with increasing $R$ in II and IV but remains peaked at $\theta_{R}=0$ in region III.

To quantify this decay, we plot in Fig. 4(d) the probability $p(\theta_{R}=0)$ at $J_{\text{K}}=0.6$ as a function of the length $R$ for the shortest path linking two sites and fit the curves with an exponential function $p(\theta_{R}=0)=A\operatorname{e}^{-R/\xi}+B$ (dashed lines). This allows us to extract a characteristic correlation length $\xi$ which reflects an effective spatial extension of the influence of the hybridization at one site to reach other sites on the Kondo lattice. As shown in Fig. 4(e), $\xi$ is less than $1$ (in the unit of lattice parameter) at high temperatures but increases logarithmically (dashed line) with lowering temperature. The latter seems to be consistent with the phenomenological two-fluid model Nakatsuji2004PRL ; Curro2004PRB ; Yang2008PRL . Remarkably, the temperature where $\xi\approx 1$ agrees roughly with $T_{\phi(0)}$, the crossover between regions III and IV estimated from the Shannon entropy. Thus, region IV (and II) represents a state where the phase correlation is developed only on short range between nearest-neighbor sites, while in region III, the hybridization fields start to extend their influence in space and build a long-range phase coherence on the lattice.

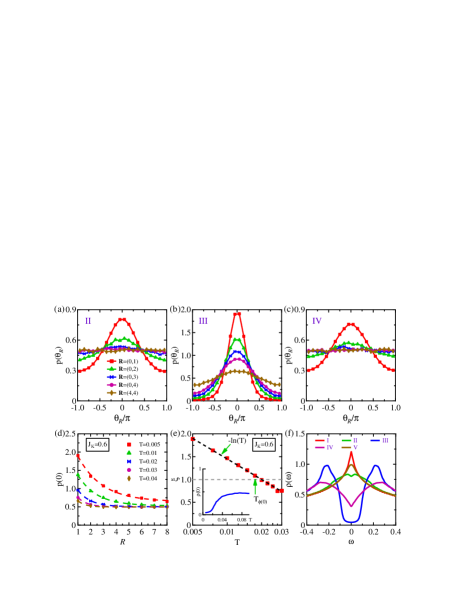
A direct consequence of the phase correlation may be found on the conduction electron density of states $\rho(\omega)$ calculated using Eq. (2). A twisted boundary condition $c_{j}^{{\dagger}}\rightarrow c_{j}^{{\dagger}}\operatorname{e}^{\operatorname*{i}\bm{\psi}\cdot\mathbf{r}_{j}}$ was used to reduce the finite size effect and obtain a smooth curve Gros1996PRB ; Li2018PRL . The results are presented in Fig. 4(f) after being averaged over $20\times 20$ twisted boundary configurations of $\bm{\psi}=\left(\psi_{x},\psi_{y}\right)$ with both $\psi_{x}$ and $\psi_{y}$ regularly spaced in $\left[0,\frac{2\pi}{\sqrt{N_{0}}}\right)$. We find that the conduction electron spectra are barely affected in regions I and V, while a pseudogap is developed in regions II and IV where the hybridization bond phase is short-range correlated. This is associated with the ARPES band bending due to the opening of direct hybridization gap Chen2017PRB . Only in region III, we see a fully opened (indirect hybridization) gap with a small remaining spectral weight around $\omega\approx 0$ due to Lorentzian broadening ($\delta=0.01$) used in the calculations. The full gap opening temperature is in rough accordance with the growth of $\xi$ in the bond phase distribution, as compared in the inset of Fig. 4(e) for $J_{\text{K}}=0.6$. Thus, the heavy electron emergence or Kondo insulating state is closely related to the development of long-range phase coherence of hybridization fields mediated by inter-site magnetic correlations, suggesting the importance of our defined bond phase in describing heavy fermion physics beyond the usual mean-field picture and local approximations. The distinction of short- and long-range phase correlations provides a potential microscopic explanation of the two-stage scenario for the pump-probe experiment Liu2020PRL ; Pei2021PRB and lays a theoretical basis for resolving the conflict between ARPES and transport data Chen2017PRB .

To summarize, we propose a novel scheme to study the hybridization physics of Kondo lattice systems based on static auxiliary field approximation. A gauge-invariant hybridization bond phase is introduced to investigate the spatial phase correlation of the hybridization fields. Its probabilistic distribution allows us to define a characteristic length scale which diverges logarithmically with lowering temperature. A precursor pseudogap state with short-range phase correlation is revealed, before the Kondo insulating (or heavy electron) state emerges when a long-range phase coherence starts to develop. This provides a possible microscopic support of the two-stage hybridization scenario suggested by recent experiment. Our work proposes a novel framework based on spatial phase correlation beyond conventional mean-field and local pictures, and offers a useful tool to explore phase-related physics in Kondo lattice systems.

We acknowledge useful discussions with Yin Zhong. This work was supported by the National Natural Science Foundation of China (NSFC Grants No. 12204075, No. 11974397, No. 12174429, and No. 12147102), the National Key Research and Development Program of MOST of China (Grant No. 2017YFA0303103), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB33010100).