Deuteron EDM induced by CP violating couplings of pseudoscalar mesons

Study of nature of CP-violation is one of the most important tasks in particle physics. Here the main puzzle consists in disagreement of predictions of Standard Model (SM) and existing data on CP-violating effects like, e.g., electric dipole moments (EDMs) of electron, nucleons, and more composite system like deuteron and nuclei. SM gives more stringent upper limits than experiments. It calls for search for a New Physics (new particles or mechanisms) contributing to CP-violating effects. In particular, data bounds on the hadron and lepton EDMs are very useful for derivation of more stringent limits on parameters of new particles Kirpichnikov:2020tcf ; Kirpichnikov:2020new . In QCD the source of the CP-violation is encoded in the so-called QCD vacuum angle $\bar{\theta}$, which is very small quantity ($\bar{\theta}\sim 10^{-10}$) due to Peccei-Quinn mechanism Peccei:1977hh . As it was shown in QCD sum rules Crewther:1979pi ; Shifman:1979if , this angle is related to the effective CP-violating hadronic couplings, which, e.g., define the EDMs of baryons. E.g., the expressions for the CP-violating $\eta(\eta^{\prime})\pi\pi$ couplings derived in Refs. Crewther:1979pi ; Shifman:1979if read:

where $g_{\eta}=\sqrt{1/3}$, $g_{\eta^{\prime}}=\sqrt{2/3}$, $R=m_{u}/m_{d}$ is the ratio of the $u$ and $d$ current quark masses, $F_{\pi}=92.4$ MeV is the pion decay constant, $M_{\pi}=139.57$ MeV, $M_{\eta}=547.862$ MeV, and $M_{\eta^{\prime}}=957.78$ MeV are the masses of the charged pion, $\eta$, and $\eta^{\prime}$ mesons, respectively.

In series of papers Gutsche:2016jap -Zhevlakov:2019ymi we developed phenomenological Lagrangian approach involving nucleons, pseudoscalar mesons $P=\pi,\eta,\eta^{\prime}$, and photon for analysis of nucleon EDM and deriving upper limits for the CP-violating couplings between hadrons and $\bar{\theta}$ angle. In particular, using existing upper limit on neutron EDM (nEDM) Tanabashi:2018oca

which corresponds to the following boundary for the QCD angle $|\bar{\theta}|<10^{-10}$, we derived more stringent upper limits for the CP-violating $\eta\pi\pi$ and $\eta^{\prime}\pi\pi$ couplings $f_{\eta\pi\pi}<4.4\times 10^{-11}$ and $f_{\eta^{\prime}\pi\pi}<3.8\times 10^{-11}$ than the ones deduced from experiment by the LHCb Collaboration Aaij:2016jaa : $f_{\eta\pi\pi}<6.7\times 10^{-4}$ and $f_{\eta^{\prime}\pi\pi}<2.2\times 10^{-4}$. Using limits for these coupling one can estimate other hadronic EDMs where these couplings contribute. The proposed experiments for measurement of EDMs of charge particles (proton, deuteron, and possibly helium-3) with a sensitivity of $10^{-29}e\cdot{\rm cm}$ by several Collaborations (the Storage Ring EDM at BNL Anastassopoulos:2015ura , the JEDI at JülichEversmann:2015jnk ; Abusaif:2019gry ) call for more accurate theoretical analysis of EDMs.

In this paper we extend our analysis to the deuteron, which is considered as proton-neutron bound state. In addition to the deuteron EDM (dEDM) we estimate the slope of the EDM form factor, which is known as the Schiff moment. We will take into account the contributions of one- and two-body forces to the dEDM. One-body forces correspond to a picture there proton and neutron are quasi free constituents of deuteron and their contribution to the dEDM is simply the sum of proton and neutron EDMs. Two-body forces in deuteron are induced by one-meson ($\pi$, $\eta$, and $\eta^{\prime}$) exchange between nucleons. They produce a contribution to the dEDM, which is estimated using potential approach proposed in Ref. Khriplovich:1999qr . From numerical analysis of nucleon and deuteron EDMs we derive stringent limits on the CP-violating hadronic couplings and $\bar{\theta}$ parameter. We show that proposed measurements of proton and deuteron EDMs at level of $\sim 10^{-29}$ by the Store Ring EDM and JEDI Collaborations will provide more stringent upper limits on the CP-violation parameters.

The paper is organized as follows. In Sec. II we briefly discuss our formalism and results for EDM and Schiff moments of nucleons. In Sec. III we extend our formalism to the dEDM. In Sec. IV we present our numerical results for the dEDM and discuss it in connection with planned experiments. In Appendix A we present the results for the $K$- mesons contributions to the pseudoscalar meson and baryon CP-violating couplings relevant for the $|\Delta T|=0,1$ isospin transition.

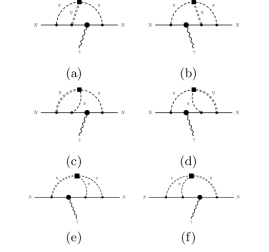
In this section we briefly review our formalism, which is based on phenomenological Lagrangians formulated in terms of nucleons $N=(p,n)$, pseudoscalar mesons [pions $\pi=(\pi^{\pm},\pi^{0})$ and etas $H=(\eta,\eta^{\prime})$], and photon $A_{\mu}$ (see details in Ref. Zhevlakov:2018rwo ). The full Lagrangian needed for the analysis of nucleon EDMs is conventionally divided on free ${\cal L}_{0}$ and interaction ${\cal L}_{\rm int}$ parts  Zhevlakov:2018rwo . In particular, the interaction part ${\cal L}_{\rm int}$ is given a sum of CP-even and CP-odd strong interactions terms ${\cal L}_{S}$ and ${\cal L}_{S}^{\rm CP}$ and electromagnetic terms describing coupling of charged pions and nucleons with photon. In case of nucleons we take into account non-minimal coupling with photon induced by anomalous magnetic moment $k_{N}$:

where $g_{\pi NN}=(g_{A}/F_{\pi})\,m_{N}$, $g_{HNN}$, and $f_{H\pi\pi}$ are corresponding coupling constants, $\gamma^{\mu}$, $\gamma^{5}$ are the Dirac matrices, $\sigma^{\mu\nu}=\frac{i}{2}[\gamma^{\mu},\gamma^{\nu}]$. Here $g_{A}=1.275$ is the axial nucleon charge, For the constants $g_{\eta NN}$ and $g_{\eta^{\prime}NN}$ we use the values deduced from recent analysis of photoproduction on nucleons in Ref. Tiator:2018heh : $g_{\eta NN}=g_{\eta^{\prime}NN}=~{}0.9$.

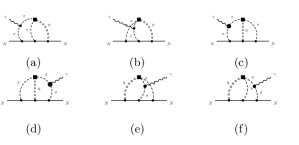
Nucleon EDM is extracted from the electromagnetic vertex function, which is expanded in terms of four relativistic form factors $F_{E}(Q^{2})$ (electric), $F_{M}(Q^{2})$ (magnetic), $F_{D}(Q^{2})$ (electric dipole), and $F_{A}(Q^{2})$ (anapole) as EDM_PCQM ; EDM_SUSY :

where $p_{1}$ and $p_{2}$ are momenta of initial and final nucleon states, $Q^{2}=(p_{2}-p_{1})^{2}$ is the transfer momentum squared. The nucleon EDM is defined as $d_{N}^{E}=-F_{D}(0)/(2m_{N})$.

In preceding papers Gutsche:2016jap -Zhevlakov:2019ymi we analyzed the neutron EDM (nEDM), which is evaluated by taking into account the two-loop diagrams. E.g., in Figs. 1 and 2 we display the diagrams induced by minimal couplings of charged hadrons with photon (see details in Ref. Zhevlakov:2018rwo ). The contributions to the nEDM induced by non-minimal coupling of proton and neutron to the electromagnetic field have been analyzed in Ref. Zhevlakov:2019ymi . We showed that non-minimal contributions are of the same order of magnitude as the ones induced by minimal $\gamma$-proton coupling, but separate non-minimal contributions induced by anomalous magnetic moments of proton and neutron compensate each other due to their opposite sign. The total numerical contribution of the non-minimal couplings of the nucleon is relatively suppressed (by one order of magnitude) compared to the total contribution of the minimal coupling. Our final numerical results for the nEDM including minimal and non-minimal electromagnetic couplings of nucleons are Zhevlakov:2019ymi :

in terms of the CP-violating $\eta\pi\pi$ and $\eta^{\prime}\pi\pi$ couplings and in terms of the QCD $\bar{\theta}$ angle:

using the ratio of $u$- and $d-$ quarks $R=0.556$ from ChPT at 1 GeV scale Gasser:1982ap and

for the $R=0.468$ taken from lattice QCD at scale of 2 GeV Tanabashi:2018oca . Then using data on the nEDM we deduced Zhevlakov:2019ymi the following upper limits on the QCD angle: $|\bar{\theta}|<4.4\times 10^{-10}$ (ChPT) and $|\bar{\theta}|<4.7\times 10^{-10}$ (lattice QCD).

In this paper we first do an extension of our formalism to the proton EDM (pEDM), which is straightforward. Our numerical results for the pEDM in terms of the CP-violating $\eta\pi\pi$ and $\eta^{\prime}\pi\pi$ couplings are

Using relations of the $\eta\pi\pi$ and $\eta^{\prime}\pi\pi$ couplings with $\bar{\theta}$ we express the pEDM in terms of the $\bar{\theta}$ as:

for $R=0.556$ from ChPT and same

for $R=0.468$ from lattice QCD. The magnitude of pEDM is less then the one for nEDM because in case of pEDM the contributions from diagrams in Fig. 1 and Fig. 2 have different sign in comparison with their contribution to the nEDM. Due to the leading diagrams to the pEDM and nEDM are induced by the coupling of photon with charged pions with opposite charge, i.e. with $\pi^{-}$ and $\pi^{+}$, respectively, the nucleon EDMs should have different signs.

After substitution of upper limits for the $\bar{\theta}$ derived in the neutron case we get the following upper limits for the pEDM: $|d^{E}_{p}|\simeq 0.72\times 10^{-26}\,\text{e}\cdot\text{cm}$ (ChPT) and $|d^{E}_{p}|\simeq 0.68\times 10^{-26}\,\text{e}\cdot\text{cm}$ (lattice QCD). These limits are more stringent than existing limit $|d^{E}_{p}|<2.5\times 10^{-25}$ obtained in indirect way from analysis of the Hg atoms Griffith:2009zz ; Sahoo:2016zvr ; Dmitriev:2003sc and have the same order of magnitude as the nEDM.

We go further and estimate the Schiff moments (SFMs) of nucleons. The nucleon SFM is defined as the slope of its EDM form factor Faessler:2005gd :

Our numerical results for the nucleon SFMs are:

in terms of the CP-violating $\eta\pi\pi$ and $\eta^{\prime}\pi\pi$ couplings and in terms of the QCD vacuum angle

for the ChPT set and

for the lattice QCD set. Main contribution to the nucleon SFMs comes from the diagram describing the coupling of photon with charged pions (see Fig. 2), while the contribution of the graphs in Fig. 1 is suppressed. It is different from the nucleon EDMs, which are generated by both sets of diagrams in Figs. 1 and 2 with equal contribution on magnitude.

Note that our result for the neutron SFM is in good agreement with prediction of ChPT at the leading-order in the chiral expansion Thomas:1994wi :

and perturbative chiral quark model EDM_PCQM :

The CP-violating $HNN$, $H=\eta,\eta^{\prime}$ couplings have been calculated in ChPT in Ref. Gutsche:2016jap . It is defined by pion-loop diagram and its value at the leading order in chiral expansion reads:

Here, by analogy we also calculate the CP-violating $\pi NN$ coupling, which is generated by similar loop diagram in Fig. 3a:

where

As it is seen, that the CP-violating $\eta NN$ coupling dominates over the $\pi NN$ one. It is why it makes sense to take into account the $\eta$ exchange in the evaluation of the dEDM. Note that our CP-violating couplings have microscopic (loop) origin. Therefore, it is interesting to compare our loop results for the CP-violating meson-nucleon couplings with the results for these couplings derived using chiral techniques. In particular, the CP-violating $\pi NN$ coupling at the leading order in chiral expansion was obtained in Ref. Crewther:1979pi in terms of current quark masses and $m_{\Xi}-m_{N}$ baryon mass difference:

where $R_{s}=m_{s}/m_{d}$ and $m_{\Xi}=1321.71$ MeV is the mass of the $\Xi(1321)^{-}$ hyperon. Both $g_{\pi NN}^{\rm CP}$ and $g_{\eta NN}^{\rm CP}$ couplings can be presented in terms of matrix elements of quark operators projected over nucleon states (nucleon condensates) Crewther:1979pi :

for $R$ from lattice data at scale 2 GeV Tanabashi:2018oca . Matrix elements $\langle N|\bar{q}\tau^{3}q|N\rangle$ and $\langle N|\bar{q}q|N\rangle$ can be related to the nucleon axial charge $g_{A}$ Faessler:2007pp and pion-nucleon sigma-term $\sigma_{\pi N}$ Gasser:1990ce ; Lyubovitskij:2000sf :

where $\bar{m}=(m_{u}+m_{d})/2=7$ MeV Gasser:1982ap . For the $\sigma_{\pi N}$ we use the latest update 58 MeV derived in Ref. RuizdeElvira:2017stg .

Our numerical results for the CP-violating constants in terms of the $\bar{\theta}$ parameter are:

including contribution of all pseudoscalar mesons in the loop diagrams (see details in Appendix A) and

when we restrict to the contribution of pion and $\eta$ meson in the loop diagrams. One can see, that our prediction for the full $g_{\pi NN}^{\rm CP}$ coupling (33) is close to the prediction $0.027\bar{\theta}$ of Ref. Crewther:1979pi and in agreement with central value of Ref. Bsaisou:2012rg : $(-0.018\pm 0.007)\,\bar{\theta}$. On the other hand, the CP-violating constants $g_{\eta NN}^{\rm CP}$ and $g_{\eta^{\prime}NN}^{\rm CP}$ dominate over $g_{\pi NN}^{\rm CP}$ by a one order of magnitude. They are so-called isospin $|\Delta T|=0$ CP-violating couplings Khriplovich:1999qr ; Bsaisou:2012rg .

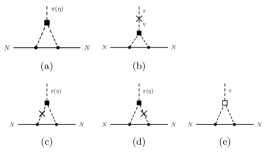
In this section we discuss calculation of the dEDM $d_{D}^{E}$, which is defined as the coupling of the external electric field $\vec{E}$ with deuteron spin $\vec{S}$: $H=-d_{D}^{E}\,(\vec{S}\cdot\vec{E})$. The contributions to the dEDM comes from one-body forces (additive sum of the pEDM and nEDM) and from two-body forces due one-meson exchanges between nucleons. The two-body contribution to the dEDM is induced by the CP-violating meson-nucleon coupling. Therefore, the dEDM is defined as:

where $d_{D}^{\pi NN}$ is the two-body contribution due to pion meson exchange generated by $\pi^{0}-\eta$ and $\pi^{0}-\eta^{\prime}$ mixing.

The two-body contributions can be estimated using potential approach proposed and developed in Ref. Khriplovich:1999qr . In case of the pion exchange it was shown that the dominant contribution comes due to the isospin triplet coupling Khriplovich:1999qr :

where

Here $P=\pi,\eta,\eta^{\prime}$ and $\epsilon_{D}=2.23$ MeV is the deuteron binding energy, $g^{\rm CP(1)}_{\pi NN}$ is the CP-violating $\pi NN$ isospin-breaking coupling constant Khriplovich:1999qr ; Lebedev:2004va ; Bsaisou:2012rg including the $\eta-\pi$ and $\eta^{\prime}-\pi$ mixing

where

where $SU_{f}(3)$ flavor breaking coefficients $\epsilon$ and $\epsilon^{\prime}$ Leutwyler:1996np ; Kroll:2004rs ; Gardner:1998gz defined as

with parameter $\epsilon_{0}$ encoding the isospin breaking effects:

and $\chi=1+(4M_{K}^{2}-3M_{\eta}^{2}-M_{\pi}^{2})/(M_{\eta^{\prime}}^{2}-M_{\eta}^{2})\simeq 1.23$. Here $\varphi\simeq-21.6^{0}$ is mixing angle between $\eta$ and $\eta^{\prime}$ mesons which is fixed from relation $\sin 2\varphi=-(4\sqrt{2}/3)(M_{K}^{2}-M_{\pi}^{2})/(M_{\eta^{\prime}}^{2}-M_{\eta}^{2})$ Leutwyler:1996np ; Kroll:2004rs ; Gardner:1998gz . Resulting values are $\epsilon=0.017$ and $\epsilon^{\prime}=0.004$.

First term in Eq. (44) is induced by the $\pi^{0}-\eta$ mixing in the triangle loop diagrams in Figs. 3c and  3d. Second term in Eq. (44) is induced by $\pi^{0}-\eta$ mixing in the external meson leg (see Fig. 3b). Therefore, one can denote two mechanisms of isospin violation due to the $\pi^{0}-\eta$ mixing as internal mechanism (depicted in Figs. 3c and 3d) and as external mechanism (depicted in Fig. 3b). One should note that the internal mechanism is strongly suppressed in comparison with external mechanism by a factor $10^{-2}$ . We get the following numerical results for the CP-violating $g^{\rm CP(1)}_{\pi NN}$ coupling:

due to $\pi-\eta$ mixing and

due to $\pi-\eta^{\prime}$ mixing without $K$-mesons contribution. The total result with taking into account $K$-mesons contribution (see details in Appendix A) for the isospin breaking $|\Delta T|=1$ CP-violating pion-nucleon coupling is $g^{\rm CP(1)}_{\pi NN}=0.0025\,\bar{\theta}$, which is in good agreement with prediction of Refs. Bsaisou:2012rg ; Dekens:2014jka : $\bar{g}^{1}=(0.003\pm 0.002)\,\bar{\theta}$.

The ratio of the full CP-violating $\pi NN$ coupling constants corresponding to the $|\Delta T|=1$ and $|\Delta T|=0$ is:

The latter expression also gives the prediction for the ratio of the couplings $\bar{g}^{1}$ and $\bar{g}^{0}$. One can see that our result for the $R_{\pi NN}$ is close to the lower boundary of the prediction of Ref. Bsaisou:2012rg : $R_{\pi NN}\sim-0.2\pm 0.1$.

Finally, resulting contribution from one-meson exchange is:

which is in good agreement with data (see Ref. Bsaisou:2012rg ).

The dEDM is contributed by the EDMs of constituent nucleons and correction due to one-meson exchange in the isospin channel $|\Delta T|=1$. The latter is induced due to isospin breaking effects ($\eta-\pi$ and $\eta^{\prime}-\pi$ mixing) and, therefore, it is relatively suppressed. Our final prediction for the dEDM in terms of the $\bar{\theta}$ angle reads:

Next using the upper limit for the $\bar{\theta}$ Zhevlakov:2019ymi we get

Here we take into account that proton and neutron EDMs have different signs.

In prospects of future experiments an observation that the dEDM is proportional to the nucleon EDM and the other contributions are suppressed has big importance. A comparison between our theoretical prediction and sensitivity of future experimental measurements of the dEDM at the level of accuracy $\sim 10^{-29}$ from the EDM Collaboration Anastassopoulos:2015ura gives more stringent limit on the CP-violating parameter $\bar{\theta}$:

The same order of magnitude for the $\bar{\theta}$ has been obtained in framework of supersymmetric approach MSSM Lebedev:2004va . These limits on the dEDM and $\bar{\theta}$ allow to derive new bounds on nucleon EDMs at level $10^{-29}$ and more stringent limits on the decay rates of the CP-violation processes $\eta\to\pi\pi$ and $\eta^{\prime}\to\pi\pi$. In connection with planned EDM experiments one can derive the limits for the branching ratios of these rare processes decays at level $\sim 10^{-21}$ and $\sim 10^{-23}$ for $\eta$ and $\eta^{\prime}$ mesons, respectively. Direct observation of these decays at a such level of accuracy is impossible. There is the same situation in case of future experiment on measurement of the proton EDM by the JEDI Collaboration Eversmann:2015jnk ; Abusaif:2019gry . We would like to stress that direct measurement of the decay rates of the CP-violation processes $\eta\to\pi\pi$ and $\eta^{\prime}\to\pi\pi$ at level higher than limitations from data on EDMs could potentially signal about manifestation of New Physics.

In conclusion, we derived limits on the proton EDM and nucleon SFMs from existing experimental data on neutron EDM. We calculated the dEDM with taking into account one- and two-body forces in deuteron. All these quantities were calculated using phenomenological Lagrangian approach involving the PS-coupling between baryons and pseudoscalar mesons and the CP-violating couplings $3P$ couplings of pseudoscalar mesons. Note that these couplings are proportional to the QCD CP-violating parameter $\bar{\theta}$ and, therefore, encode a source of the strong CP-violation in our formalism. Complementary we also derived the dependence of the dEDM on $\bar{\theta}$. In future, we plan to continue our study of the EDMs of baryons and nuclei induced by strong CP-violating effects, e.g., by taking into account of the CP-violation three-pseudoscalar meson vertices involving all nonet states ($\pi$, $K$, $\eta$, and $\eta^{\prime}$) and all isospin transitions $|\Delta T|=0,1,2$.