Deterministic Rendezvous in Infinite Trees
Abstract
The rendezvous task calls for two mobile agents, starting from different nodes of a network modeled as a graph to meet at the same node. Agents have different labels which are integers from a set . They wake up at possibly different times and move in synchronous rounds. In each round, an agent can either stay idle or move to an adjacent node. We consider deterministic rendezvous algorithms. The time of such an algorithm is the number of rounds since the wakeup of the earlier agent till the meeting. In most of the literature concerning rendezvous in graphs, the graph is finite and the time of rendezvous depends on its size. This approach is impractical for very large graphs and impossible for infinite graphs. For such graphs it is natural to design rendezvous algorithms whose time depends on the initial distance between the agents. In this paper we adopt this approach and consider rendezvous in infinite trees. All our algorithms work in finite trees as well. Our main goal is to study the impact of orientation of a tree on the time of rendezvous.
We first design a rendezvous algorithm working for unoriented regular trees, whose time is in , where is the size of the ball of radius , i.e, the number of nodes at distance at most from a given node. The algorithm works for arbitrary delay between waking times of agents and does not require any initial information about parameters or . Its disadvantage is its complexity: is exponential in for any degree of the tree. We prove that this high complexity is inevitable: turns out to be a lower bound on rendezvous time in unoriented regular trees, even for simultaneous start and even when agents know and . Then we turn attention to oriented trees. While for arbitrary delay between waking times of agents the lower bound still holds, for simultaneous start the time of rendezvous can be dramatically shortened. We show that if agents know either a polynomial upper bound on or a linear upper bound on , then rendezvous can be accomplished in oriented trees in time , which is optimal. If no such extra knowledge is available, a significant speedup is still possible: in this case we design an algorithm working in time .
Keywords: algorithm, tree, rendezvous, mobile agent
1 Introduction
The rendezvous task calls for two mobile agents, starting from different nodes of a network modeled as a graph to meet at the same node. This task is ubiquitous in many applications. In the social context, people may want to meet in a city whose streets form a graph. In computer networks, software agents navigating in a network have to meet to share data collected from distributed databases. In robotics, mobile robots circulating in a network of corridors in a mine or a building may have to meet to coordinate maintenance tasks.
In most of the literature concerning rendezvous in graphs, the graph is finite and the time of rendezvous depends on its size. This approach is impractical for very large graphs and impossible for infinite graphs. For such graphs it is natural to design rendezvous algorithms whose time depends on the initial distance between the agents. In this paper we adopt this approach and consider rendezvous in infinite trees. All our algorithms work in finite trees as well. Our main goal is to study the impact of orientation of a tree on the time of rendezvous.
1.1 The model
We consider infinite trees. They can be either unoriented or oriented. An unoriented tree does not have labels of nodes and the port labelings at each node are arbitrary. In oriented trees, one node, called the root, has label , all other nodes do not have labels, and at each node different from the port 0 is on the simple path toward .
Agents have different labels which are integers from a set . They wake up at possibly different times and move in synchronous rounds. In each round, an agent can either stay idle or move to an adjacent node. An agent makes a move by choosing a port number at its current node. When entering the adjacent node corresponding to the chosen edge the agent learns the port of entry and the degree of this node. We assume that the memory of the agents is unlimited: from the computational point of view they are modeled as Turing machines. We consider deterministic rendezvous algorithms. Both agents execute the same algorithm, each agent starting in its wakeup round. Each agent knows its label which is a parameter of the algorithm but does not know the label of the other agent. The execution time of such an algorithm is the number of rounds since the wakeup of the earlier agent till the meeting. This time depends on values of the initial distance between the agents and of the size of the space of labels. These values may be known or unknown to the agents, depending on the scenario. By saying that the time of an algorithm is we mean that this is the worst case time of the execution of this algorithm, over all pairs of starting nodes of agents at distance , over all pairs of agents’ labels from , and over all possible delays between waking times of agents, if the algorithm works for arbitrary delay.
1.2 Our results
We first design a rendezvous algorithm working for unoriented regular***The discussion of the assumption of regularity is deferred to the Conclusion. trees of degree . These are infinite trees all of whose nodes have degree . (For this is the infinite line). The time of our algorithm is in , where is the size of the ball of radius , i.e, the number of nodes at distance at most from a given node. The algorithm works for arbitrary delay between waking times of agents and does not require any initial information about parameters or . Its disadvantage is its complexity: is exponential in for any degree . We prove that this high complexity is inevitable: turns out to be a lower bound on rendezvous time in unoriented regular trees, even for simultaneous start and even when agents know and . Then we turn attention to oriented trees. While for arbitrary delay between waking times of agents the lower bound still holds, for simultaneous start the time of rendezvous can be dramatically shortened. Our algorithms for oriented trees do not assume regularity of the tree. We show that if agents know either a polynomial upper bound on or a linear upper bound on , then rendezvous can be accomplished in oriented trees in time , which is optimal in view of [14]. If no such extra knowledge is available, a significant speedup is still possible: in this case we design an algorithm working in time .
1.3 Related Work
The task of rendezvous has been studied in the literature both in the randomized and deterministic settings. Randomized rendezvous is surveyed in [2], cf. also [1, 5]. Deterministic rendezvous in networks is surveyed in [23, 24]. Several authors considered geometric settings (rendezvous in an interval of the real line, e.g., [5, 6], or in the plane, e.g., [3, 8, 11]). Rendezvous of more than two agents, also called gathering, was studied, e.g., in [15, 17, 22].
In the deterministic setting, feasibility and time complexity of synchronous rendezvous in networks is one of the main topics of investigation. Deterministic rendezvous of agents equipped with tokens used to mark nodes was considered, e.g., in [21]. In most of the papers concerning rendezvous in networks, nodes of the network are assumed to be unlabeled and marking nodes by agents is not allowed. In this case, anonymous agents cannot meet in many highly symmetric networks, e.g., in oriented rings. Hence symmetry is usually broken by assigning the agents distinct labels and assuming that each agent knows its own label but not the label of the other agent. Deterministic rendezvous of labeled agents in rings was investigated, e.g., in [14, 19] and in arbitrary graphs in [14, 19, 25]. Gathering many anonymous agents in unlabeled networks was studied in [15]. In this weak scenario, not all initial configurations of agents are possible to gather, and the authors of [15] characterized all such configurations and provided universal gathering algorithms for them. In [10], the authors studied rendezvous under a very strong assumption that each agent has a map of the network and knows its position in it. Using this assumption they designed optimal algorithms for several classes of networks, including the infinite line and finite trees.
Another measure of efficiency of rendezvous algorithms is the amount of memory needed to execute this task. Memory of the agents required to achieve deterministic rendezvous was studied in [18] for trees and in [12] for arbitrary graphs. Memory needed for randomized rendezvous in the ring was investigated, e.g., in [20].
A scenario significantly differing from the above was discussed by several authors. The difference is in dropping the assumption that agents navigate in synchronous rounds. Asynchronous rendezvous and approach in the plane was studied in [7, 9, 17] and asynchronous rendezvous in networks modeled as graphs was investigated in [4, 13, 16]. In the latter scenario, the agent chooses the edge to traverse, but the adversary controls the speed of the agent. Under this assumption, rendezvous at a node cannot be guaranteed even in the two-node graph. Hence the rendezvous requirement is relaxed to permit the agents to meet inside an edge. In [4], the authors designed almost optimal algorithms for asynchronous rendezvous in infinite multidimensional grids, under a strong assumption that the agent knows its position in the grid. In [16], the authors designed a polynomial-cost algorithm for asynchronous rendezvous in arbitrary finite graphs, without this assumption.
2 Unoriented regular trees
In this section we design and analyze a rendezvous algorithm for agents operating in an unoriented infinite regular tree of degree . This is an infinite tree all of whose nodes have degree . (For this is the infinite line). Nodes do not have labels and ports at each node are arbitrarily numbered by integers . Note that each agent knows from the outset, as it sees the degree of its starting node. In any such tree, we define the ball of radius , centered at node , as the subtree induced by all nodes at distance at most from . Let be the number of nodes in any ball . Let . Note that is the number of edge traversals of a DFS exploration of any ball , starting and finishing at the same node.
Labels of agents are integers from the set . For any label we define the transformation of as follows. Lat be the binary representation of . is the sequence obtained from by replacing every bit 1 by the string and replacing every bit 0 by the string . Hence is of length and has the property that it does not contain a substring of three consecutive zeroes.
2.1 The algorithm
For any node and any positive integer , we define the following procedures.
Procedure
Explore the ball by DFS, in increasing order of port numbers at each node,
starting and finishing at node .
Procedure
Stay at node for rounds.
The following procedure takes as parameters the degree of the infinite regular tree, a bit of the transformed label, and a positive integer . For , i.e., for the infinite line, and for any integer , the procedure consists of two DFS explorations of the ball , if the bit is 1, and of staying at node for the duration of these two explorations, if the bit is 0. (Exploration of a ball of radius 0 takes time 0.) For , the procedure consists of two DFS explorations of the ball , if the bit is 1, and of staying at node for the duration of these two explorations, if the bit is 0.
Procedure
if then
else
if then
else
We first present the high-level idea of the rendezvous algorithm and its challenges. The algorithm exploits the fact that agents have different labels and guarantees that at some point one of the agents stays idle at its starting node while the other one fully explores a sufficiently large ball centered at its own starting node and thus meets the waiting agent. Exploration and waiting periods depend on bits of the transformed label of the agent. Since agents do not know the distance between them, the algorithm is divided into stages with increasing radii of explored balls and increasing waiting times. The main challenge is due to the fact that agents may start with some delay and that, due to possibly different label lengths, they complete the same stage at different speeds. Hence the whole process may become significantly desynchronized and the difficulty is to hold one agent idle at its starting node for a sufficiently long time to allow the other agent to meet it.
Now we are ready to succinctly describe Algorithm URT (for unoriented regular trees). The algorithm is executed by an agent with label , starting at a node of an infinite regular tree of degree . The algorithm works in stages . In a stage it “executes” consecutive bits of by performing procedure . Notice that for , explores balls if and instructs the agent to wait a corresponding time if , while for , explores balls if and instructs the agent to wait a corresponding time if . This is because for the size of a ball is linear in its radius, while for it is exponential in it. Stages are organized so that their durations telescope. For technical reasons we want the size of the balls treated in stage to be at least 4 times larger (and not only 2 times larger) than those in stage . The algorithm is interrupted as soon as the agents meet.
Algorithm URT
for do
for to do
2.2 Correctness and complexity
In this section we prove the correctness of Algorithm URT and analyze its time complexity. We start with the definition of the critical stage. Intuitively, it is the first stage such that the radius of the balls explored in this stage is at least the initial distance between the agents. Thus, more formally, the critical stage is the smallest integer such that:
-
•
, if
-
•
, if .
This smallest integer is denoted by . Hence is the radius of balls explored in the critical stage.
According to the algorithm, during an execution of bit in stage , an agent explores a ball of radius twice. We refer to each of these explorations as one activity cycle. Thus, during an execution of a single bit , an agent performs two activity cycles. Similarly, during an execution of a bit in stage , an agent waits for two consecutive periods each of duration of one such exploration. We refer to each of these waiting periods as one passivity cycle. Thus, during an execution of a single bit , an agent waits for two passivity cycles.
For a given , let be the duration of the execution of a bit in stage , using procedure . Let be the length of the transformed label of an agent. Let denote the duration of stage . The time taken by the agent to reach its critical stage is the sum of durations of all previous stages. Thus this time is .
In the following lemma we compute the duration of stage , depending on and .
Lemma 2.1
For ,
Proof. First consider the case when . In stage , an agent explores a ball of radius . We first compute , the number of nodes in the ball of radius . Since in this case the graph is a line, . Recall that, is the number of edge traversals of a DFS exploration of the ball , starting and finishing at the same node. Thus, . By definition, i.e., . Hence, .
Next suppose . In this case, in stage , an agent explores a ball of radius . The value of is as follows:
Thus, in this case, and . Hence, .
Lemma 2.2
For , we have
Proof. When , by Lemma 2.1, we have
Next suppose . In this case, by Lemma 2.1, we have,
The next lemma estimates the duration of any stage in terms of the duration of the preceding and of the following stage.
Lemma 2.3
For , we have
Proof. We consider two cases:
Lemma 2.3 implies
Corollary 2.1
In the next lemma we compute the value of the time taken by an agent to reach its critical stage.
Lemma 2.4
if , and if .
Proof. When , we have
Suppose . Then we have
Corollary 2.2
Denote by the agent that starts earlier, and by the agent that starts later. (In the case of simultaneous start, names and are given arbitrarily). Let denote the delay of the start of w.r.t the start of .
The next lemma shows that if the delay is sufficiently large then agents meet during the critical stage of the earlier agent.
Lemma 2.5
Let be the time in which agent reaches its critical stage. If , then agents meet during the critical stage of .
Proof. Agent takes time to reach its critical stage. Since each transformed label starts with bits 01, during its critical stage agent first executes two consecutive passivity cycles, i.e., for a time it does not moves and then it starts executing its two consecutive activity cycles and each activity cycle takes time . Hence, in time at most since its start agent reaches the node initially occupied by agent . Thus, if , i.e., if agent remains inactive till that time, agent meets at its initial position. This happens during the critical stage of .
2.2.1 Labels of equal length
In this section we assume that the transformed labels of the agents have the same length. This implies that the duration of each stage is the same for both agents. We denote by and the time when (resp. ) starts its stage .
Lemma 2.6
If then agent starts its critical stage before the end of the critical stage of .
Proof. Let be the length of the transformed labels of the agents. The time taken by agent to reach its critical stage is after the start of agent , and the time taken by agent to reach its stage is . We prove the lemma by contradiction. Suppose that agent starts its critical stage after the end of the critical stage of . Hence which implies , and thus because . Since and , we have and thus . This is a contradiction because .
Lemma 2.7
If agents have labels of equal length, then they meet before the end of stage of agent .
Proof. Let be the time taken by to reach its critical stage from its starting time. If , then by Lemma 2.4, agent meets agent in stage of , before starts its execution. Thus we may assume that . Let the transformed label of be and that of be . Our arguments to prove the lemma depend on the value of as follows:
-
•
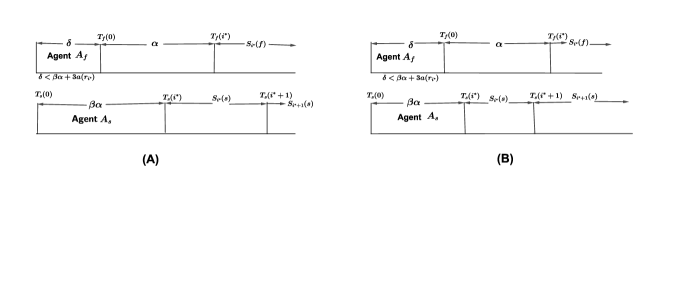
Consider the smallest such that and . (Since transformed labels of agents are different and have equal lengths, there are at least three such indices). Consider the execution of the critical stage by the agents (Figure 1(A)). Since , agent fully executes one activity cycle corresponding to within the two passivity cycles of corresponding to . Thus agent meets during the execution of the critical stage of .
-
•
The duration of execution of the first two bits 01 in the critical stage is for both agents (Figure 1(B)). Since , agent is idle while executing its bit during a complete activity cycle of corresponding to . Hence meets during the execution of the critical stage of .

Figure 1: An illustration for the proof of Lemma 2.7: (A) when , agent meets during the execution of the critical stage of , and (B) when , agent meets during the execution of the critical stage of . -
•
In this case at least a time segment of length of the critical stage of is executed during the execution of stage of (Figure 2(A)). The first time segment of length of stage of is devoted to the execution of the first bit of the transformed label, which is 0. Thus is idle during this time segment. The final time segment of length of the critical stage of contains exactly two activity cycles of (since among the last two bits of the transformed label of each agent there is one bit ). Since , at least one activity cycle of in its critical stage is completely executed during the first passivity period of in its stage . Thus agent meets during stage of the latter.
-
•
In this case, by Lemma 2.5, agent starts its critical stage before the the end of the critical stage of . Let be the initial time segment of length of stage of (Figure 2(B)). Since the duration of the execution of each bit in stage is at least (by Corollary 2.1), we know that during time segment , agent executes the first bit of its transformed label, i.e., bit 0. Hence during time segment , agent is idle. Since , during time segment agent still executes its critical stage. Since the duration of execution of each bit in the critical stage of the agents is , during time segment agent must perform complete executions of at least 3 consecutive bits of its transformed label. Among any three consecutive bits of any transformed label there must be at least one bit 1. Hence, during time segment in which agent is idle, agent performs two activity cycles of its critical stage. Thus it must meet agent before the end of stage of the latter.

2.2.2 Labels of different lengths
In this section we assume that the labels of the agents have different lengths. Let denote the length of the shorter transformed label. We refer to the agent having this label as the faster agent, and denote it by . Let , for , be the length of the longer transformed label. We refer to the agent having this label as the slower agent, and denote it by . These names are chosen due to the fact that, since the duration of any stage of an agent is proportional to the length of its transformed label, the agent with shorter transformed label completes its stages faster than the agent with longer transformed label. Since and , we have . Let and denote the lengths of stage of the faster and slower agents, respectively. Let agent start its critical stage during the stage of agent , where is an integer.
We will use the following technical lemma to estimate by which stage of the agents will meet.
Lemma 2.8
Let agent start its stage during the stage of where and . Let . If , then agent meets agent in stage at most of . Furthermore, during this meeting agent is in stage at most .
Proof. Let and denote the starting times of the stage of the agents and respectively. Since agent starts its stage during the stage of , we have . We consider the following two cases:
-
•
In this case agent completes its stage and starts its stage before the end of stage of agent (Figure 3(A)). Since , we have and hence the part of stage of executed after has length at least . Now since , we have and this implies that agent fully executes at least consecutive bits of stage during the execution of the first bit of stage of agent . The execution of any consecutive bits of an agent contains at least two activity cycles and during the execution of the first bit of any stage, an agent executes two passivity cycles. Thus, agent executes at least two activity cycles of stage during the first two consecutive passivity cycles of stage of agent . This implies that agent meets agent during the stage of the latter. During this meeting agent is in stage .

Figure 3: An illustration for the proof of Lemma 2.8: (A) , and (B) . In both cases, agent meets during the execution of stage of ; during this meeting agent is in stage . -
•
Here we consider the following two subcases:
-
–
Since , agent executes at least the first 4 bits of its stage during the execution of the first bit 0 of stage of agent (Figure 3(B)). This implies that agent meets agent during the execution of the first two passivity cycles of stage of agent corresponding to the execution of the first bit . The agent is in stage during this meeting.
-
–
In this case a portion of the stage of agent is executed during the stage of agent . Let and be the durations of the portions of the stages and of executed during the stage of . Note that is of length zero when . Let denote the time segment of stage of during which agent executes its first bit . Since , we have (by Corollary 2.1). The execution of the last two bits of stage is of duration and exactly one of these last two bits is 1. This implies that the time segment of length at the end of stage of agent contains at least one activity cycle. Thus, if (Figure 4(A)), then agent executes at least one activity cycle of stage during the time segment (since ). Since during the whole execution of agent remains idle, agent meets agent in stage of the latter. During this meeting agent is in stage at most . Next suppose (Figure 4(B)). Note that in this case, agent starts its stage during the execution of the first bit of stage of agent . Now,
This implies that agent fully executes at least the first 3 bits of stage during time segment . Since the execution of the first two bits in any stage contains exactly two activity cycles, agent executes two activity cycles of stage during and it meets agent in stage of the latter. During this meeting agent is in stage at most .

Figure 4: An illustration for the proof of Lemma 2.8: (A) , and (B) . In both cases, agent meets during the execution of stage of . In case (A), agent is in stage at most and in case (B) agent is in stage at most .
-
–
We now proceed to the proof that agents meet always by the end of stage of . The proof is split into two cases in Lemmas 2.9 and 2.11.
Lemma 2.9
If agent starts its execution before the start of agent , then the agents meet during stage at most of .
Proof. In this case, we have . We consider two cases.
-
•
In this case, agent starts its critical stage during the execution of the critical stage of (Figure ). We have and . Since , we have .
Since the execution of one bit of stage has duration , this implies that at least bits of stage of agent are fully executed during the initial part of the execution of stage of agent . Thus, since , agent fully executes at least consecutive bits of stage during the execution of the first bit of stage of agent . The execution of any consecutive bits of an agent contains at least two activity cycles and during the execution of the first bit of any stage, an agent executes two passivity cycles. Thus, agent executes at least two activity cycles of stage during the first two consecutive passivity cycles of stage of agent . This implies that agent meets agent during the stage of the latter.

Figure 5: An illustration for the proof of Lemma 2.9: (A) when , agent meets during the execution of stage of , and (B) when , agent meets during the execution of stage of . -
•
Let be the time in which agent reaches its critical stage. We assume (otherwise, by Lemma 2.5, agents meet in stage of agent ). Since agent starts its critical stage during the execution of stage of agent (Figure ), we have,
(3) Let . We compute a lower bound on as follows:
Hence the lemma is true in this case by Lemma 2.8 substituting and .
Lemma 2.10
If agent starts its execution before the start of agent then agent starts its stage after the start of stage of .
Proof. If , then the lemma is obvious by the definition of . Thus we assume . Hence the agent starts its critical stage before the start of the critical stage of agent (Figure ). We know that , where is the time in which agent reaches its critical stage (otherwise agent meets agent before the latter starts its execution).
Suppose for contradiction that agent starts its stage before the start of stage of (Figure ). Then we have the following inequalities:
This is a contradiction, since ). Hence the lemma is true.
Lemma 2.11
If agent starts its execution before the start of agent , then agents meet during stage at most of .
Proof. Let denote the delay of the start of w.r.t the start of , and let denote the time in which agent reaches its critical stage. We assume (otherwise agent meets agent during the stage of the former). Let agent start its critical stage during stage of , where is an integer. Note that in this case can assume either a non-negative or a negative value. We consider two cases.
-
•
In this case the proof of the lemma is similar to the proof of Lemma 2.9. Indeed, if , the proof is exactly the same (Figure ). Now consider the case when (Figure ). We only show that inequality also holds in this case and the rest of the proof is the same. Since the critical stage of starts during the stage of agent we have
Hence inequality holds in this case.

Figure 7: An illustration for the proof of Lemma 2.11 when and: (A) agent starts its stage during the stage stage of agent , and (B) agent starts its stage during the stage of agent for . -
•
In this case the critical stage of starts before the start of the critical stage of . By Lemma 2.10, agent starts its stage after the start of stage of . Let and denote the starting times of the stage of of the agents and respectively. We consider two subcases: and .
-
–
Let agent start its stage during the stage of agent for . First suppose that (Figure ). We have
This implies that agent fully executes at least bits of stage during the execution of stage of . Since , agent fully executes at least consecutive bits of stage during the execution of the first bit of stage of . At least one of those 3 bits is 1. Since during the execution of the first bit of any stage agents remains passive, agent meets agent during the execution of the stage of the latter.

Figure 8: An illustration for the proof of Lemma 2.11 when , and: (A) agent starts its stage during the stage of agent i.e., , and (B) agent starts its stage during the stage of agent for . Next consider the case when (Figure ). Let . Since agent starts its stage during the stage of agent we have
Thus,
Hence by Lemma 2.8 substituting and , we can conclude that agent meets agent during the stage at most of and moreover, during this meeting agent is in stage at most .
-
–
By Lemma 2.10, we have . Let . Since agent starts stage during the stage of , we have . Note that is the duration of the part of stage of agent that is executed during the execution of stage of . Now one of the last two bits of any transformed label is . Thus, if , then agent executes at least one complete activity cycle of its stage during the execution of the first two passivity cycles in stage of corresponding to the first of its transformed label (Figure ). Thus in this case agent meets agent during the stage of the latter. Now suppose (Figure ). Let . Then . The difference is the duration of the part of stage of executed during the stage of agent . Since , we have . This implies that during the execution of the first bit of the stage of agent , agent executes at least 3 consecutive bits of stage (since ). At least one of these bits must be 1. Hence while agent executes two passivity cycles of total length , agent executes at least two activity cycles of its stage and it meets agent during stage of .

Figure 9: An illustration for the proof of Lemma 2.11 when , and: (A) , and (B) .
-
–
2.2.3 Complexity of Algorithm URT
The correctness of Algorithm URT follows immediately from Lemmas 2.7, 2.9 and 2.11. Indeed, these three lemmas together imply that agents always meet. It remains to estimate the complexity of Algorithm URT. This is done in the following theorem.
Theorem 2.1
Consider two agents with different labels from the set , executing Algorithm URT in an unoriented infinite regular tree of constant degree , starting at an unknown distance . Let be the number of nodes in a ball of radius in this tree. Then the agents meet in time .
Proof. Recall that the execution time of the algorithm is counted since the start of the earlier agent. Let be any agent. In view of Lemma 2.1 and since the length of the transformed label of is in , we have that the duration of stage of is in for any . Hence each of , , are in , and hence in . Let be the length of time since the start of to the time when reaches its critical stage. By Corollary 2.2, we have , and hence is also in .
Let be the earlier agent or any of the agents if they start simultaneously. Let be the delay of the start of the later agent w.r.t the start of . By Lemma 2.5, if then agents meet during the critical stage of . In this case, and hence is in .
Hence we may assume that . Thus is in . If agents have labels of equal length then by Lemma 2.7 we have and hence is in . Suppose that agents have labels of different lengths and that is the faster agent and is the slower agent. By Lemma 2.9, if then . Hence in this case is in . Finally, by Lemma 2.11, if then . Hence in this case is in . This proves that in all cases is in , and hence concludes the proof.
2.3 The lower bound
Algorithm URT has the advantage of working without any extra assumptions: agents may start with arbitrary delay and do not need any knowledge of the parameters of the problem which are the initial distance between them and the size of the space of labels. However, the disadvantage of the algorithm is its complexity that has as a factor the number of nodes in a ball of radius in the underlying tree. For any degree of the tree, the value of is exponential in , thus making the time of the algorithm prohibitively large for large . Hence it is natural to ask if such a long time is actually needed for rendezvous. In this section we show that the answer is yes. In fact we prove that is a lower bound on the time of rendezvous, even in the most benign scenario, when the agents start simultaneously and know the exact values of and .
Theorem 2.2
For any there exists a port labeling of the infinite regular tree of degree , such that the time of any rendezvous algorithm is in , even if agents start simultaneously and know the exact values of and .
Proof. For the theorem is trivial because then . Hence we may assume that . Consider the port numbering of the infinite regular tree of degree in which port numbers at both ends of each edge are equal. For any , there is exactly one such tree, up to isomorphism. Notice that an agent executing any rendezvous algorithm in this tree cannot learn anything during the execution. Indeed, when the agent takes port at some node, it knows in advance that it will enter the adjacent node of the same degree by a port with the same number . Hence a rendezvous algorithm in this tree does not have any “if” statements. It is simply a sequence of terms from corresponding to ports taken at consecutive steps. This sequence may depend on the label of the agent, but for a given label it is fixed.
Consider any initial distance and any size of the space of labels. Suppose that there exists an algorithm guaranteeing rendezvous in time at most for any agents with different labels starting simultaneously at distance . Consider any labels and let and be the sequences of integers from corresponding to the executions of the algorithm by agents and with labels and , respectively. For any node and any sequence of port numbers, let denote the node which an agent reaches starting from node and taking consecutive ports .
Let and be the starting nodes of agents and , respectively, and let . If agents meet after time , then they are at the same node after steps, i.e, . This implies that . Thus, if agents meet after some time , then, for a fixed starting node of , the number of possible starting nodes of agent is at most . However, the number of nodes at distance exactly from is larger than half of the size of the ball of radius centered at . Hence there exists a node of at distance from such that agents and starting from nodes and , respectively, and executing algorithm do not meet after time at most . This is a contradiction and it proves that the time of algorithm is in .
Another lower bound on rendezvous time was proved in [14]. It was proved for agents operating in a ring with port numbers in clockwise order, even if agents start simultaneously and know the exact values of and . The same proof is valid for agents in the infinite line with the same port numbering. Hence this lower bound also holds for agents in any infinite regular tree of degree containing such an infinite line. This gives the following corollary.
Corollary 2.3
For any , any rendezvous algorithm working for all infinite regular trees of degree with arbitrary port numberings, must have time in , even if agents start simultaneously and know the exact values of and .
Notice that for , i.e., for the infinite line, where is in , the above corollary implies that Algorithm URT has optimal complexity.
3 Oriented trees
An oriented tree is a tree such that one node called the root has label , all other nodes do not have labels, and at each node different from the port 0 is on the simple path toward . In this section we investigate rendezvous in infinite oriented trees. First note that Algorithm URT designed for rendezvous in unoriented regular trees works for oriented regular trees with the same complexity. However, we will show that in many cases orientation allows us to significantly speed up rendezvous.
We start with the observation that if the delay between the starting times of agents can be arbitrary then there is a large lower bound on rendezvous time even in oriented regular trees. This lower bound holds even if agents know the exact values of the initial distance and of the size of the label space .
Proposition 3.1
For any , the time of any rendezvous algorithm working for agents with arbitrary delay in infinite oriented regular trees of degree is in , even if agents know the exact values of and .
Proof. Consider two agents at distance . The adversary starts one of the agents and delays the start of the other agent by . The earlier agent cannot visit all nodes at distance from its starting node by time . Let be any such node not visited by time . If the initial node of the later agent is then the execution time of algorithm is at least .
The lower bound from [14] holds for infinite oriented regular trees as well (this bound holds even for simultaneous start). Hence we get
Corollary 3.1
For any , any rendezvous algorithm working for agents with arbitrary delay in infinite oriented regular trees of degree , must have time in , even if agents know the exact values of and .
Thus for agents starting with arbitrary delay, rendezvous must be slow, even for oriented regular trees. It turns out that for simultaneous start, the situation changes dramatically. Recall that for unoriented trees, rendezvous must be slow even for simultaneous start. By contrast, we will show that orientation helps to speed up rendezvous significantly in this case. Indeed, we design three algorithms. All of them work for arbitrary oriented trees (regularity does not have to be assumed). Two of them work in the optimal time under assumption that agents know some upper bounds on the parameters or . The third algorithm works without any extra assumptions and has the complexity , hence it still avoids the extremely costly lower bound .
The main idea of these three rendezvous algorithms is the same. We have to avoid costly exploration of balls that was crucial in Algorithm URT. Here is where we use orientation. Agents go “up” (towards the root) in order to position themselves on the same branch and then make moves up and down on this branch, depending on bits of their transformed label. These moves play a role similar to ball exploration for unoriented trees but are much faster, and permit the agents to meet when the range of the moves is sufficiently large.
In all these algorithms we will use the following procedures that take a positive integer as parameter. Procedure consists of consecutive moves, each of them taking port 0, unless the root is visited on the way. In the latter case the agent stops at and stays there forever. Thus the procedure results in going steps towards the root or getting to the root. Procedure consists of an execution of Procedure followed by a backtrack to the node where Procedure started. Procedure lasts rounds and Procedure lasts rounds.
3.1 Known polynomial bound on label space size
In this section we assume that the agents know some common polynomial upper bound on the size of the label space. Let . Hence the length of the binary representation of all labels is at most and the agents know . Moreover, since is a polynomial upper bound on , we have that is in . For any label we define the padded label as follows. Let be the binary representation of . is the binary sequence of length obtained as follows. First concatenate a prefix of zeroes to to get a sequence of length , and then replace each bit 1 by 10 and each bit 0 by 01. All padded labels have equal length and the following property. If then there exists an index , such that the th bit of is 1 and the th bit of is 0.
Algorithm Known-Bound-on-L works in stages . In a stage the agent makes steps up and then “executes” consecutive bits of its padded label: if the bit is 1, the agent executes Procedure , and it stays idle for rounds if the bit is 0. There is an exception to this rule: if an agent visits the root , it stops executing moves and stays there forever. In view of the simultaneous start, the use of padded labels whose length is the same for both agents guarantees that both agents will start each stage simultaneously (unless one of them visits ). The algorithm is interrupted as soon as the agents meet.
Algorithm Known-Bound-on-L
for do
for to do
if then
else
stay idle for rounds
Theorem 3.1
Consider two agents with different labels from the set , executing Algorithm Known-Bound-on-L in an infinite oriented tree, starting simultaneously at an unknown distance . Suppose that agents know a common polynomial upper bound on the size of the label space. Then the agents meet in time , which is optimal.
Proof. Let be the smallest integer such that . First suppose that none of the agents visits the root before the end of stage . The duration of stage is , for each of the agents. Since agents start simultaneously, they also start each stage simultaneously. By induction on , after the first execution of Procedure of stage , agents are at distance at most and each agent ends stage at the same node at which it was after the first execution of Procedure in this stage. Consider the time immediately after the first execution of Procedure of stage . Both agents are on the same branch in the tree, at distance at most . Let be the lower agent and the upper agent (i.e., is on the simple path from the position of at time to the root). Let be the first index such that the th bit of the padded label of is 1 and the th bit of the padded label of is 0. Both agents execute this th bit simultaneously during rounds. Hence the upper agent stays idle at distance at most while the lower agent executes the first part of Procedure . In view of this guarantees that agent meets agent . This meeting occurs during stage , i.e., in time which is , by definition of and .
Next suppose that one of the agents visits root before the end of stage . Suppose that agent is the first to visit this node. Let and be the distance of the starting node of agent (resp. ) from the root. Hence . Hence, if agents do not meet before, agent must reach the root by the end of stage and stop. Hence the meeting must occur at the latest in time which is , by definition of and .
3.2 Known linear bound on the initial distance
In this section we assume that the agents know some common linear upper bound on the initial distance between them but they may have no knowledge about . For any label we first define the prefix-free label as follows. Let be the binary representation of . In order to obtain , replace each bit 1 by 10, each bit 0 by 01 and add bits 11 at the end. The obtained sequence is of length and has the property that if we start with two different labels then none of the obtained sequences can be a prefix of the other (cf. [14]). To get the adapted label , replace each 1 by 10 and each 0 by 01 in the string . The resulting sequence has length . Notice that since binary representations of labels may have different lengths, the same is true for the adapted labels. However, the adapted labels have the property that if then there exists an index , such that the th bit of is 1 and the th bit of is 0.
Algorithm Known-Bound-on-D has the same idea as Algorithm Known-Bound-on-L but now we do not need stages, as a linear bound on is known: agents know the appropriate search range from the outset.
Algorithm Known-Bound-on-D
for to do
if then
else
stay idle for rounds
if the current node is not then
Theorem 3.2
Consider two agents with different labels from the set , executing Algorithm Known-Bound-on-D in an infinite oriented tree, starting simultaneously at a distance . Suppose that agents know a common linear upper bound on . Then the agents meet in time .
Proof. First suppose that none of the agents visits the root by the end of the first execution of procedure . Consider the time immediately after the first execution of Procedure . Both agents are on the same branch in the tree, at distance at most . Let be the lower agent and the upper agent. Let be the first index such that the th bit of the adapted label of is 1 and the th bit of the adapted label of is 0. Both agents execute this th bit simultaneously during rounds. Hence the upper agent stays idle at distance at most while the lower agent executes the first part of Procedure . In vew of , this guarantees that agent meets agent . This meeting occurs in time which is , by definition of and .
Next suppose that one of the agents visits the root by the end of the first execution of procedure . Suppose that agent is the first to visit this node. Let and be the distance of the starting node of agent (resp. ) from the root. Hence . It follows that if agent did not visit root by the end of the first execution of procedure then it must visit it by the end of the second execution of procedure . Hence the meeting occurs in time which is , by definition of and .
3.3 No extra knowledge
We finally consider the situation when agents start simultaneously but do not have any extra knowledge about the parameters and . In this case we design a rendezvous algorithm which, although slower than the two previous ones, still avoids the exponential lower bound that was unavoidable for unoriented trees even with simultaneous start and also unavoidable for oriented trees with arbitrary delay.
First, for any label , define an infinite binary sequence . The sequence is defined as follows. Concatenate infinitely many copies of the prefix-free label (defined in the previous subsection) and denote the obtained sequence by . Then is defined by replacing each 1 by 10 and each 0 by 01 in . Note that an equivalent way of defining is to concatenate infinitely many copies of the adapted label , defined in the previous subsection.
The idea of Algorithm No-Extra-Knowledge is similar to that of Algorithms Known-Bound-on-L and Known-Bound-on-D but with two important differences. First, in each stage only one bit of is processed and second, in consecutive stages the ranges of agents’ moves are not doubled but increased by 1. The algorithm is interrupted as soon as the agents meet.
Algorithm No-Extra-Knowledge
for do
if then
else
stay idle for rounds
In the proof of correctness and the analysis of complexity of Algorithm No-Extra-Knowledge we will use the following lemma.
Lemma 3.1
Consider two distinct labels and . For any index there exists an integer , such that the th bit of is 1 and the th bit of is 0.
Proof. First consider the infinite sequences and . Let be the length of . Let be any even index. Let be the smallest index at which a copy of starts in . By definition of a prefix-free label, there exists an index such that the th bit is different in and . Let and be the pairs of bits in and respectively, corresponding to the th bit of and respectively. Hence, either and or vice-versa. In both cases, for one of the indices corresponding to these bits, the -th bit of is 1 and the -th bit of is 0.
Consider any index . Let . Hence we have and thus , which concludes the proof.
We are now ready to prove the correctness and analyze the complexity of Algorithm No-Extra-Knowledge.
Theorem 3.3
Consider two agents with different labels from the set , executing Algorithm No-Extra-Knowledge in an infinite oriented tree, starting simultaneously at a distance . Then the agents meet in time .
Proof. First assume that none of the agents visits the root before the meeting. Since agents start simultaneously, they execute each turn of the for loop (corresponding to the consecutive bits) precisely in the same time period. It is enough to prove the theorem for . Consider any index . After the execution of the -th bit both agents are on the same branch in the tree, at the same distance at most . Let be the label of the lower agent. By Lemma 3.1, there exists an integer , such that the th bit of is 1 and the th bit of is 0. During the execution of bit , first both agents execute procedure simultaneously, and then the upper agent stays idle for rounds, while the lower agent executes procedure . Since , the lower agent must meet the upper agent during the first half of the execution of this procedure. It follows that the agents meet at the latest after the execution of bit . Since the time of execution of any bit is , executing all bits until bit takes time .
Next assume that one of the agents visits the root before the meeting. Consider the first agent visiting . This must happen at some time before the end of the execution of bit . The other agent must reach by the time . Since is in , the meeting at must also happen in time .
Remark. It is important to explain why the ranges of agents processing consecutive bits are incremented by 1 and not doubled, as in the other algorithms. If the range in the processing of the -th bit was instead of , then processing bit would take time causing an exponential blow-up. Incrementing by 1 results in total cost quadratic in but not exponential. We have seen before that when some upper bound on or on is known, this problem can be avoided altogether, resulting in optimal complexity .
4 Conclusion
We studied deterministic rendezvous in unoriented and oriented infinite trees, showing the impact of orientation of the tree on the time of rendezvous. For unoriented regular trees, we designed an algorithm working in time and showed a lower bound of on the time of any such algorithm. While these bounds match for and are very close for if is not very large, there remains a gap whose filling is a natural open problem. For oriented regular trees with arbitrary delay between waking times of agents, the situation is identical: the above algorithm still works and the same lower bound is valid. However, for simultaneous start in oriented trees (not necessarily regular), the situation is different. Assuming either the knowledge of a polynomial upper bound on or of a linear upper bound on , we showed algorithms working in time , which is optimal. Without such extra knowledge, we showed an algorithm working in time , thus avoiding the exponential lower bound without additional assumptions. If and are of the same order of magnitude, this algorithm is still optimal. The problem whether there exists a rendezvous algorithm working in oriented trees in time for simultaneous start, without assuming any knowledge concerning and , remains open.
It remains to discuss our assumptions concerning the environment where the agents operate. First it is natural to ask if our results could be generalized for graphs which are not trees. Our main rendezvous algorithm for unoriented regular trees relies on exploration of balls of increasing radii, with the aim of meeting the other agent that stays idle at some node of such a ball during its exploration. It should be recalled that while in an anonymous tree a ball can be explored in time linear in its size, no such exploration algorithm is known in arbitrary anonymous graphs because of loops that the agent may not notice due to anonymity of the nodes. Hence most rendezvous algorithms known from the literature and working for anonymous graphs (cf. [14, 19, 25]) are restricted to finite graphs, rely on the exploration of the entire graph, and have complexity polynomial in its size. Efficient algorithms working for infinite graphs [4, 10] use additional assumptions, such as the knowledge of the position of the agent in the graph. It remains open to design efficient rendezvous algorithms working in arbitrary infinite graphs without such extra knowledge.
Restricting attention to trees, we should discuss the assumptions that they are infinite and, in case of unoriented trees, regular. The first assumption is for convenience of problem statement, in order to dismiss algorithms relying on the exploration of the entire tree. In [14], the authors give such an algorithm working in time , where is the size of the tree. In our case, the assumption that the tree is infinite can be easily removed. All our algorithms work for finite trees as well, without change of complexity. (In the case of finite trees, “regular” means that all internal nodes have the same degree.)
The discussion of the second assumption, that of regularity of the tree, is more subtle. In our algorithm for unoriented trees, we use it in order to guarantee that all balls of a given radius have equal size, and thus an agent can compute the periods of its idleness to match exploration periods of the other agent. This is not possible if the tree is arbitrary because then different balls of the same radius can have very different sizes. If agents knew a common upper bound on the size of any ball of radius then our algorithm for unoriented trees could be generalized to arbitrary (non-regular) trees with replaced by in the complexity. However, for arbitrary unoriented trees without any extra knowledge, designing a rendezvous algorithm with time close to optimal seems to be a challenging open problem. By contrast, all our algorithms with simultaneous start for oriented trees are efficient and work without assuming regularity, as these algorithms do not rely on exploring balls in the tree.
References
- [1] S. Alpern, The rendezvous search problem, SIAM J. on Control and Optimization 33 (1995), 673-683.
- [2] S. Alpern and S. Gal, The theory of search games and rendezvous. Int. Series in Operations research and Management Science, Kluwer Academic Publisher, 2002.
- [3] E. Anderson and S. Fekete, Two-dimensional rendezvous search, Operations Research 49 (2001), 107-118.
- [4] E. Bampas, J. Czyzowicz, L. Gasieniec, D. Ilcinkas, A. Labourel, Almost optimal asynchronous rendezvous in infinite multidimensional grids, Proc. 24th International Symposium on Distributed Computing (DISC 2010), 297-311.
- [5] V. Baston and S. Gal, Rendezvous on the line when the players’ initial distance is given by an unknown probability distribution, SIAM J. on Control and Opt. 36 (1998), 1880-1889.
- [6] V. Baston and S. Gal, Rendezvous search when marks are left at the starting points, Naval Reaserch Logistics 48 (2001), 722-731.
- [7] S. Bouchard, M. Bournat, Y. Dieudonné, S. Dubois, F. Petit, Asynchronous approach in the plane: a deterministic polynomial algorithm. Distributed Compuing. 32 (2019), 317-337.
- [8] S. Bouchard, Y. Dieudonné, A. Pelc, F. Petit, Almost universal anonymous rendezvous in the plane, Proc. 32nd ACM Symposium on Parallelism in Algorithms and Architectures (SPAA 2020), 117-127.
- [9] M. Cieliebak, P. Flocchini, G. Prencipe, N. Santoro, Distributed computing by mobile robots: Gathering, SIAM J. Comput. 41 (2012), 829-879.
- [10] A. Collins, J. Czyzowicz, L. Gasieniec, A. Kosowski, R. Martin, Synchronous rendezvous for local aware agents, Proc. 25th International Symposium on Distributed Computing (DISC 2011), 447-459.
- [11] J. Czyzowicz, L. Gasieniec, R. Killick, E. Kranakis, Symmetry breaking in the plane: Rendezvous by robots with unknown attributes, Proc. 38th ACM Symposium on Principles of Distributed Computing (PODC 2019 ), 4-13.
- [12] J. Czyzowicz, A. Kosowski, A. Pelc, How to meet when you forget: Log-space rendezvous in arbitrary graphs, Distributed Computing 25 (2012), 165-178.
- [13] G. De Marco, L. Gargano, E. Kranakis, D. Krizanc, A. Pelc, U. Vaccaro, Asynchronous deterministic rendezvous in graphs, Theoretical Computer Science 355 (2006), 315-326.
- [14] A. Dessmark, P. Fraigniaud, D. Kowalski, A. Pelc. Deterministic rendezvous in graphs. Algorithmica 46 (2006), 69-96.
- [15] Y. Dieudonné, A. Pelc, Anonymous meeting in networks, Algorithmica 74 (2016), 908-946.
- [16] Y. Dieudonné, A. Pelc, V. Villain, How to meet asynchronously at polynomial cost, SIAM Journal on Computing 44 (2015), 844-867.
- [17] P. Flocchini, G. Prencipe, N. Santoro, P. Widmayer, Gathering of asynchronous robots with limited visibility, Theoretical Computer Science 337 (2005), 147-168.
- [18] P. Fraigniaud, A. Pelc, Delays induce an exponential memory gap for rendezvous in trees, ACM Transactions on Algorithms 9 (2013), 17:1-17:24.
- [19] D. Kowalski, A. Malinowski, How to meet in anonymous network, Theoretical Computer Science 399 (2008), 141-156.
- [20] E. Kranakis, D. Krizanc, and P. Morin, Randomized Rendez-Vous with Limited Memory, Proc. 8th Latin American Theoretical Informatics (LATIN 2008), 605-616.
- [21] E. Kranakis, D. Krizanc, N. Santoro and C. Sawchuk, Mobile agent rendezvous in a ring, Proc. 23rd Int. Conference on Distributed Computing Systems (ICDCS 2003), 592-599.
- [22] W. Lim and S. Alpern, Minimax rendezvous on the line, SIAM J. on Control and Optimization 34 (1996), 1650-1665.
- [23] A. Pelc, Deterministic rendezvous in networks: A comprehensive survey, Networks 59 (2012), 331-347.
- [24] A. Pelc, Deterministic rendezvous algorithms, in: Distributed Computing by Mobile Entities, P. Flocchini, G. Prencipe, N. Santoro, Eds., Springer 2019, LNCS 11340.
- [25] A. Ta-Shma and U. Zwick. Deterministic rendezvous, treasure hunts and strongly universal exploration sequences, ACM Trans. Algorithms 10 (2014), 12:1-12:15.