Detection Prospects of Fast-merging Gravitational Wave Sources in M31
Abstract
It is widely accepted that quite a number of double compact objects (DCOs) in the Milky Way can be identified by future space-based gravitational wave (GW) detectors, while systematic investigations on the detection of the GW sources in nearby galaxies are still lacking. In this paper, we present calculations of potential populations of GW sources for all types of DCOs in the Local Group galaxy M31. For M31, we use an age-dependent model for the evolution of the metallicity and the star-formation rate. By varying assumptions of common-envelope ejection efficiencies and supernova-explosion mechanisms during binary evolution, we make predictions on the properties of DCOs that can be detected by the Laser Interferometer Space Antenna (LISA). Our calculations indicate that a few (a dozen) DCOs are likely to be observed by LISA during its 4 (10) yr mission. We expect that the sources with black-hole components are more likely to be firstly identified during a 4-yr mission since these binaries have relatively large chirp masses, while the systems with white-dwarf components dominate the overall population of detectable GW sources during a 10-yr mission. LISA can only detect very tight fast-merging systems in M31, corresponding to the peak of orbital period distribution from min for double white dwarfs to min for double black holes.
1 Introduction
The discovery of the first double black hole (BHBH) merger GW150914 (Abbott et al., 2016) opened the era of gravitational wave (GW) astrophysics. To date, there are nearly 100 double compact object (DCO) mergers detected by the ground-based GW detectors LIGO and Virgo (The LIGO Scientific Collaboration et al., 2021; Nitz et al., 2021; Abbott et al., 2023). The vast majority of them are identified as BHBH mergers with component masses , two are double neutron star (NSNS) mergers, four are BHNS mergers, and one event, GW190814 with a component, is either a BHNS or BHBH merger (Abbott et al., 2020). All these events involve DCO mergers with GW signals emitting at high frequencies of .
Before merger, tight DCO systems may emit GW signals in the band that are likely to be observed by future space-based detectors e.g., LISA (Amaro-Seoane et al., 2017), TianQin (Luo et al., 2016), and Taiji (Ruan et al., 2020). For inspiral DCOs in the Milky Way, it is expected that they can spend a typical duration of in the LISA band. Previous studies of binary population synthesis (BPS) have shown that LISA can identify a large number of resolved DCOs in the Milky Way (see Amaro-Seoane et al., 2023, for a review) including thousands of double white dwarf (WDWD) systems (e.g., Nelemans et al., 2001; Ruiter et al., 2010; Liu et al., 2010; Korol et al., 2017; Lamberts et al., 2019; Breivik et al., 2020), hundreds of NSWD systems (e.g., Tauris, 2018; Chen et al., 2020, 2021; Wang et al., 2021), and tens of other types of DCO systems with BH and/or NS components (e.g., Belczynski et al., 2010a; Liu & Zhang, 2014; Lamberts et al., 2018; Lau et al., 2020; Andrews et al., 2020; Sesana et al., 2020; Shao & Li, 2021; Wagg et al., 2022b; Gao et al., 2022; Qin et al., 2023; Feng et al., 2023).
Outside the Milky Way, it is predicted that a number of DCO systems in the Local Group galaxies are detectable by LISA (Korol et al., 2018; Seto, 2019; Andrews et al., 2020; Lau et al., 2020). Since these binaries have a typical distance of Mpc, they are expected to spend a relatively short duration of in the LISA band (Amaro-Seoane et al., 2023). Regarding M31 (the Andromeda galaxy), the largest galaxy in the Local Group, Seto (2019) estimated that LISA may detect NSNS systems with a 10-yr observation duration (see also Andrews et al., 2020). In addition, Korol et al. (2018) predicted that 1760 WDWD binaries in M31 can be identified by LISA for its mission duration of 410 yr.
According to the theory of binary star evolution, tight DCO systems originate from the primordial binaries with two zero-age main-sequence stars when both components have evolved to be compact stars (Tauris & van den Heuvel, 2023). During the evolution, common envelope (CE, Ivanova et al., 2013) phases play a vital role to shrink binary orbits probably leading to the formation of close DCO systems (e.g., Webbink, 1984). Recently, stable Roche lobe overflow has also been considered as a potentially important channel for the formation of close DCO binaries (e.g., Pavlovskii et al., 2017; van den Heuvel et al., 2017; Neijssel et al., 2019; Marchant et al., 2021; Shao & Li, 2021; Olejak et al., 2021; Gallegos-Garcia et al., 2022). At the end of stellar evolution, massive stars are expected to leave behind NSs or BHs via the process of supernova explosions. It is still unclear whether there exists a mass gap between NSs and BHs (see Shao, 2022, for a review). It is believed that the coalescence of DCO binaries can result in various kinds of astrophysical phenomena associating with intense electromagnetic emissions, e.g., type Ia supernovae for WDWD systems (Iben & Tutukov, 1984; Webbink, 1984), long-duration gamma-ray bursts for NSWD/BHWD systems (Fryer et al., 1999; Yang et al., 2022), short-duration gamma-ray bursts (Paczynski, 1986; Abbott et al., 2017; Gompertz et al., 2020) and kilonovae (Li & Paczyński, 1998; Zhu et al., 2021) for NSNS/BHNS systems. It is expected that the detection of tight DCO binaries emitting low-frequency GW signals can shed light on the physics of close binary interactions and the origin of DCO coalescence events.
In this paper, we aim to use a BPS method to assess the properties and the numbers of all types of LISA DCO sources in M31. Our calculations include different treatments of the input parameters related to CE phases and supernova-explosion processes. Furthermore, we adopt a recently reported star-formation history of the M31 disk (Williams et al., 2017), for which the metallicity and the star-formation rate are age-dependent.
2 Method
2.1 BPS Code
Except GW transients, no DCO systems have been reported outside the Milky Way. Here we present estimations on the potential population of LISA sources in M31 by adopting a BPS approach. Only the systems formed via isolated binary evolution are included in our calculations. We employ the BSE code originally developed by Hurley et al. (2002) and significantly modified by Shao & Li (2014) that has been used to predict the detection of Galactic LISA sources (Shao & Li, 2021). In this code, some important modifications are summarized as follows. During the evolution of primordial binaries, it is assumed that the accretion rate of the secondary stars is dependent on their rotational velocities. Under this assumption, small amount of transferred mass is accreted by rapidly rotating secondary stars. Mass accretion onto the secondary stars can cause them to expand and spin up. On the one hand, the significant expansion of the secondary stars due to rapid mass accretion may lead to the formation of contact binaries as the secondary stars fill their Roche lobes (Nelson & Eggleton, 2001). On the other hand, a small amount of accreted mass can spin up the secondary stars to near critical rotation (Packet, 1981). As a consequence, the secondary stars are likely to reach critical rotation at the early stage of mass transfer and then accrete at relatively low rates. In this situation, the maximal mass ratios between the primary stars and the secondary stars for avoiding the formation of contact binaries can reach as high as about 6 (Shao & Li, 2014). For stellar wind mass-loss rates, the prescription of Belczynski et al. (2010b) has been applied to various types of stars, except that for helium stars we use half of the Hamann et al. (1995) rates (Kiel & Hurley, 2006). When dealing with mass-transfer stability in the binaries with a BH accretor and a massive donor, the criteria of Shao & Li (2021) have been adopted to determinate whether such binaries experience CE evolution or stable mass transfer. These criteria are related to the masses of both components and the radii of donor stars, and show that the binaries with heavier BHs are more likely to undergo stable mass transfer. It’s worth noting that these criteria are not strongly dependent on metallicities, except for the systems with donors initially more massive than 111The stability of mass transfer is sensitive to the structure of the donor stars (Soberman et al., 1997). At solar metallicity, the donor stars with masses above never develop a fully convective envelope which can increase the stability of mass transfer (Pavlovskii et al., 2017; Klencki et al., 2021).. Since the massive donors with increasing metallicities are more likely to experience extensive wind mass loss before mass transfer, the mass transfer tends to be more stable. The use of these criteria allows the formation of tight DCO binaries via stable mass transfer rather than CE evolution (see also e.g., Pavlovskii et al., 2017; van den Heuvel et al., 2017; Marchant et al., 2021).
During a CE phase, we use the standard energy conservation equation (Webbink, 1984) to calculate the orbital evolution of a binary system, i.e.,
| (1) |
where
| (2) |
is the binding energy of the donor’s envelope at the onset of CE evolution. Here and respectively denote the donor’s and accretor’s masses, is the orbital separation of the binary system, is the mass of donor’s envelope that is ejected out of the binary, is the Roche lobe radius of the donor at the beginning of mass transfer, the subscripts and correspond to the initial and final stages of a CE phase, respectively. is the binding energy parameter that is determined by the mass distribution of the envelope (Xu & Li, 2010) and is the CE ejection efficiency with the orbital energy of the binary unbinding donor’s envelope. When CE evolution is triggered in binaries with Hertzsprung gap donors, we allow them to survive CE phases (see e.g., Dominik et al., 2012).
Equation (1) indicates that all of binary orbital energy is used to eject the envelop of engulfing star when . Generally, the larger the , the binaries more likely to survive CE evolution and the longer the separations of post-CE binaries. Recently, Scherbak & Fuller (2023) suggested that according to the analyses of Galactic WDWD binaries. This is consistent with the case of for the post-CE binaries with a WD and a main-sequence companion (Zorotovic et al., 2010). Note that seems to be required to account for the formation of some post-CE binaries such as IK Peg with a WD and a main-sequence star (Davis et al., 2010). Furthermore, investigations on NS binaries indicate higher CE ejection efficiencies varying from (Zuo & Li, 2014) to (Fragos et al., 2019; Yarza et al., 2022). In our calculations, we set three values for CE ejection efficiencies i.e., , and .
Following Shao & Li (2021), we apply three different mechanisms of supernova explosions. These mechanisms involve the rapid (Fryer et al., 2012), the delayed (Fryer et al., 2012) and the stochastic (Mandel & Müller, 2020) prescriptions. The rapid recipe allows the formation of a mass gap among which no compact remnants are formed, while the delayed and stochastic mechanisms do not. So whether existing such a mass gap can provide a clue to constrain the process of supernova explosions (see e.g., Shao, 2022). Both the rapid and the delayed mechanisms treat the remnant masses as a function of CO core masses prior to supernova and fallback-material masses during explosion. In these two mechanisms, it is assumed that the natal kicks of NSs and BHs obey a Maxwellian distribution. We adopt a dispersion velocity of (Hobbs et al., 2005) for NSs formed via core-collapse supernovae. For BHs, we use reduced kick velocities due to the fallback of some materials compared to the case of NS kicks. In the stochastic mechanism, the remnant masses and the natal kicks are assumed to be probabilistic rather than deterministic. It is assumed that the natal kicks of both NSs and BHs follow a Gaussian distribution and a part of BHs form without any kick (Mandel & Müller, 2020). In this case, we further apply the scaling pre-factor calibrated by Kapil et al. (2023) to deal with the velocity distribution of NS kicks. In our calculations, we also include the formation of NSs through electron-capture supernovae. It is assumed that these NSs have the mass of and their natal kicks follow a Maxwellian distribution with a relatively low dispersion velocity of (see also Shao & Li, 2014, 2018).
For primordial binaries we set a grid of initial parameters: the primary masses and the secondary masses are both limited in the range of , and the orbital separations in the range of . The fraction of binaries among all stars is taken to be unity and all initial binaries are assumed to have circular orbits. Following Shao & Li (2021), we calculate the birth rate of a specific DCO system as
| (3) |
where is the star formation rate of the M31 disk, is a combination parameter to weight the contribution of the system evolved from a specific primordial binary. Then represents the distribution of primary masses in logarithmic space and describes the initial mass function (IMF, Kroupa et al., 1993). Here we apply a modified IMF for M31 (Weisz et al., 2015), i.e.,
| (4) |
where is a normalized parameter. This IMF can slightly increase the fraction of stars with masses above compared to the Kroupa’s IMF. The secondary masses are assumed to have a uniform distribution (Kobulnicky & Fryer, 2007), then giving . It is assumed that the orbital separations follow a flat distribution in logarithmic space with , where is a normalized parameter. In addition, the size of each interval in logarithmic space is determined as . Here, represents the number of grid points for a specific parameter and is set to (where is the total number of primordial binary samples in the 3-dimensional parameter space mentioned above). Our calculations include 9 models with different supernova mechanisms and CE ejection efficiencies, and run primordial binaries for each evolutionary model.
2.2 Star Formation History of M31
The evolutionary history of SFR and stellar metallicity is an important factor that can make a considerable impact on the population of observable LISA sources in M31. We follow the work of Williams et al. (2017) which gives wide-area maps of the full star-formation history of the M31 disk by fitting resolved stellar photometry coming from the Panchromatic Hubble Andromeda Treasury survey. According to the result of PARSEC model (see Table 3 of Williams et al., 2017), we obtain the total SFR of M31 during different history stages. For the metallicity evolution we use the age-dependent model (Kemp et al., 2022) which linearly interpolates between (age (Gyr), ) coordinates of (0, 0.0002), (2, 0.008), (10, 0.02), (14, 0.022) approximately. The history distribution of and of M31 has been mapped by Kemp et al. (2022, see their Figure 4).

Since the metallicity changes over the age, we need to divide all binary stars into different sample spaces according to the metallicity or age. For convenience, we set 12 grids of metallicities as shown in Figure 1. The orange ladder-like curve gives the sample spaces separated by different metallicities. The metallicity of every primordial binary is randomly taken from the 12 individual values. For each metallicity grid, we know the age and the SFR. When calculating , the corresponding number of the primordial binaries in each grid is then set to be . In our calculations, we select the binary samples if the primordial binaries can evolve to be observable LISA sources at the present age of 14 Gyr. For one selected binary sample, its number as LISA sources can be calculated by multiplying the birthrate by the timespan spent in the LISA band. As a consequence, we can estimate the total number of detectable LISA DCOs in M31 by accumulating the contribution from all selected binary samples.
2.3 GW Signal
For GW signal detected over a mission duration (4 or 10 yr), the characteristic strain at the harmonic can be expressed as (Barack & Cutler, 2004),
| (5) |
Here is the power of the harmonic radiation (Peters & Mathews, 1963),
| (6) |
where is the chirp mass of a source and (depending on the harmonic order and the eccentricity ) is the Fourier decomposition of GW signal and gives the relative power of gravitational radiation at the nth harmonic. If binaries have eccentric orbits, they would emit most of their energy at higher harmonics and be detected in a higher frequency band (Nelemans et al., 2001).
The change rate of GW frequency can be written as
| (7) |
where gives the integrated enhancement factor of gravitational radiation from an eccentric source compared with an equivalent circular source. The luminosity distance of M31 is taken to be (Ribas et al., 2005), which reduces the characteristic strain amplitudes of tight DCO systems in M31 by over 30 times compared with those in the Milky Way.
2.4 Signal to Noise Ratio
In this work, we use the python package LEGWORK developed by Wagg et al. (2022a) to calculate signal-to-noise ratio (S/N) and identify the DCO systems as LISA sources with the condition of (e.g., Lamberts et al., 2018; Shao & Li, 2021). In the following, we briefly describe the method used in the LEGWORK.
The S/N calculation includes the response of detector to signal and the detector’s noise. For quasi-stationary sources we consider here, they evolve slowly during detector’s observation mission and their sky locations in the detector-based coordinate system are always changing. The averaged spectral power of GW signal is used to determine which sources can be detected and has the expression of
| (8) |
Here is sky and polarization averaged signal response function of the instrument. It has been numerically computed by Larson et al. (2000), and then fitted by Robson et al. (2019) as
| (9) |
The second term in right side of Equation (8) gives the spectral powers of plus and cross GW,
| (10) | ||||
where and represent the amplitude and phase of GW, respectively, describes the inclination of the orbital angular momentum of a binary with respect to the line of sight.
For sources with known positions, we should consider GW signal modulation to obtain more precise S/N. The orbital motion of LISA induces a power spreading effect, where the power spectrum of the GW signal exhibits sidebands with a bandwidth of around the GW frequency . As a result, the strain amplitude at the true frequency is diminished. This effect is more pronounced at higher frequencies due to the larger bandwidth. Consequently, WDWD binaries are particularly impacted due to their relatively higher detectable frequencies. We make the assumption that all sources detectable by LISA share the same sky location as M31, with the ecliptic coordinates (). Additionally, we consider their polarization and inclination to be uniformly distributed within the allowed range. In this study, we utilize the orbit-averaged amplitude modulation, originally defined by Cornish & Larson (2003) and subsequently revised by Wagg et al. (2022a), as
| (11) |
where is the intrinsic amplitude of the source and is the amplitude recorded in the detector. The amplitude modulation is given as
| (12) |
where the orbit-averaged detector responses and are the functions of sky location and polarization of sources in the ecliptic coordinates.
For the noise, we apply LISA’s sensitivity curve constructed by Robson et al. (2019). The effective power spectral density of the noise is expressed as
| (13) |
where is the power spectral density of the LISA noise, including the single-link optical metrology noise and the single test mass acceleration noise ,
| (14) |
where is the arm-length of LISA and is LISA transfer frequency. Actually, dominates when is below otherwise dominates. For convenience, we ignore the term in and the term in when calculating . In addition, is the effective noise source resulted from unresolved galactic binaries (Cornish & Robson, 2017; Babak et al., 2021) and can be alleviated by the increase of observation time. In our calculations, we apply the calculated by Cornish & Robson (2017).
After the analyses of signal and noise, we can calculate the sky, inclination and polarization averaged S/N (Wagg et al., 2022a)
| (15) |
The equation above for the is suitable whether the binary is circular or eccentric and stationary or non-stationary.
It is noted that the amplitude modulation derived by Cornish & Larson (2003) is just suitable for quasi-circular systems. For WDWD systems detected by LISA, it is proper to add the amplitude modulation when calculating S/N. While for eccentric binaries with BH and/or NS components, we take the averaged value of . After calculation, we find that the ratio of S/N with amplitude modulation to S/N without amplitude modulation is about for the same circular source.

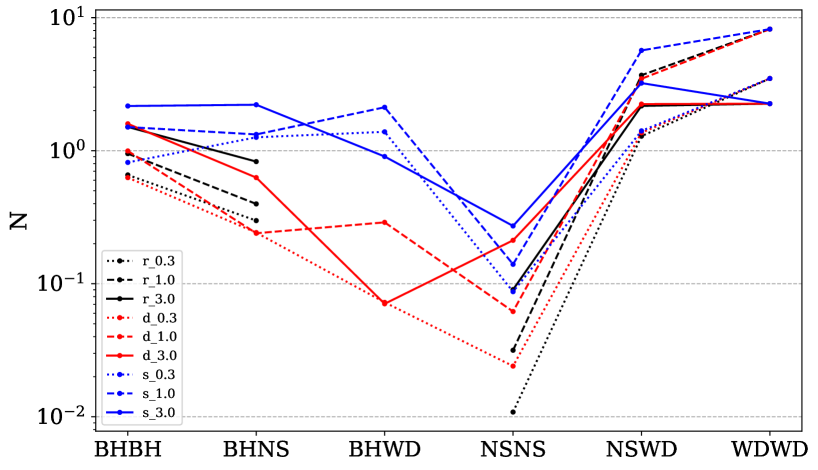
3 Result
3.1 Overall Populations
After analysing our obtained data, we find that the most common evolutionary path for the formation of LISA DCO binaries involves the canonical channel proposed by the reviews of Bhattacharya & van den Heuvel (1991) and Tauris & van den Heuvel (2023). Evolved from a primordial binary, the primary star firstly evolves to fill its Roche lobe and stably transfers its envelope to the secondary star. After mass transfer, the primary star becomes a helium star and then evolves to be the first compact object. When the secondary star also evolves to fill its own Roche lobe, the binary enters the X-ray binary phase. Since the mass ratio between the secondary star and the compact star is relatively large, the mass transfer is dynamically unstable leading to the CE phase. During CE evolution, the secondary star fully loses its hydrogen envelope to become another helium star and finally evolves to be the second compact object. This CE phase leads to significant orbit decay of the binary so that the formed DCO is able to appear as a GW source. In some cases, the formation of tight DCO binaries with BH components does not involve this CE phase and the mass transfer is stable during the X-ray binary stage (see also e.g., Pavlovskii et al., 2017; Shao & Li, 2021). According to our calculations, the formation of LISA BHBH and BHNS binaries can be dominated by the channel of stable Roche lobe overflow if one takes and . In the case, all kinds of LISA DCO systems are predominantly formed through the channel of CE evolution.
Figure 2 presents estimated numbers of various types of DCOs in M31 that can be detected by LISA for a mission duration of 4 (top panel) or 10 yr (bottom panel), by assuming different models related to CE ejection efficiencies and supernova-explosion mechanisms. These numbers are also given in the Appendix. We can see that, for a 4 yr observation duration, at most DCO systems are likely to be identified by LISA. In this case, the systems with BH components dominate overall GW sources albeit in small numbers. For a 10 yr observation duration, the total number of LISA sources significantly increases to nearly a dozen. The numbers of the LISA binaries with BH components show a slight increase, while the numbers of the systems with WD components (i.e. WDWDs and NSWDs) increase by a factor of . For the rapid supernova mechanism (indicated by black dots in the diagram), no BHWD binaries can form within the LISA band. As this mechanism is only able to produce BHs with masses of and the masses of WD’s progenitors are less than , the mass ratios of the WD’s progenitors to the BHs are so small that mass transfer occurs via stable Roche lobe overflow rather than CE evolution, eventually leading to the formation of long-period BHWD binaries (see also Shao & Li, 2021). Overall, the numbers of different types of LISA sources are affected by adopted CE ejection efficiencies and supernova-explosion mechanisms. There is a common feature that stochastic supernova mechanism tends to produce more LISA sources as relatively small natal kicks are imparted to NSs and BHs (Mandel & Müller, 2020).
Figure 3 shows the distribution of M31 LISA sources as a function of orbital periods and chirp masses for 4 (top panel) or 10 yr (bottom panel) observation duration. The black solid curve gives a boundary of , indicating that only the DCO systems located above this curve are considered detectable by LISA. The blue and red dashed lines correspond to the chirp masses of typical NSWD and WDWD systems, respectively. In the case with , the red dashed line is below the black solid curve, indicating a lack of detectability of WDWD binaries. In addition, the blue dashed line is very close to the black solid curve. This means that the maximal of merging NSWD binaries can just reach LISA’s detection threshold. In the case with , we see that the regions where WDWD and NSWD systems can be detected are obviously enlarged. By contrast, the detection of the systems with BH components is not sensitive to the options of instrument’s observation lifetime since these systems have relatively large chirp masses.

Considering that a number of GW sources are expected to be observed by LISA for a 10 yr mission lifetime, we will analyse their parameter distributions in the following.

3.2 The case of WDWD binaries
Figure 4 presents the probability density functions of M31 LISA WDWDs as a function of component masses and orbital periods. Since WDWD systems do not undergo supernova explosions during their formation, we discuss the calculated results with different CE ejection efficiencies. Our results show that almost all of these LISA sources consist of CO WDs and/or ONe WDs. Note that the Galactic WDWD sample identified via electromagnetic observations mostly include He WDs (Korol et al., 2022, and references therein). These binaries, characterized by small chirp masses, would not be detectable as M31 LISA sources. Under the assumption of different , the masses of the secondary WDs are distributed with a peak at and the masses of the primary WDs have a relatively flat distribution varying in the range of . Importantly, these WDWD systems possess total masses exceeding the Chandrasekhar limit, indicating they are promising progenitors of type Ia supernovae.
For , there is a remarkable subgroup of systems consisting of a ONe WD and a CO WD. These systems are evolved from the primordial binaries with both component masses of in d orbits. When or 3.0, the primordial binaries with similar parameters always evolve into wide WDWD systems that do not contribute to the population of LISA sources.

The orbital periods of WDWD binaries are always less than 6 min (see also Figure 3) and distributed with a peak at 2 min. Note that the scenario leads to a bulge at min in the curve of orbital period distribution, corresponding to the formation of very massive WDWD systems as mentioned above. The orbital period distributions of post-CE binaries are expected to be influenced by the CE ejection efficiencies. However, it should be noted that very close systems detectable by LISA have undergone significant orbital shrinkage due to GW radiation. Therefore, different assumptions of do not significantly alter the shape of the orbital period distributions. For other types of LISA DCO systems, we focus on the role of supernova-explosion mechanisms in their parameter distributions and take .

3.3 The case of NSWD binaries
In Figure 5, we show the probability density functions of M31 LISA NSWDs as a function of component masses and orbital periods under the assumption of . It can be clearly seen that different supernova mechanisms we adopted tend to produce similar parameter distributions for LISA NSWD systems. The NS masses are distributed with a sharp peak at , and the WD masses are mainly distributed in the range of with a peak at . The orbital periods of these binaries are narrowly distributed within the range of min with a peak at min, which are greatly lower than the minimal orbital period of d for Galactic WD binaries with a pulsar companion (Manchester et al., 2005).
For these LISA sources, almost all NSs are formed via electron-capture rather than core-collapse supernovae. For core-collapse NSs, the resulting NS binaries with main-sequence companions of intermediate mass () have orbital periods of d and most of them have orbital periods of less than a few days; while for electron-capture NSs, the corresponding systems possess orbital periods of d and the majority are relatively wide binaries (see Figure 2 of Shao & Li, 2015). It is possible that the former binaries with relatively close orbits undergo mergers in subsequent CE phases, avoiding the formation of tight NSWD binaries.
3.4 The case of BHNS/BHBH binaries
Figures 6 and 7 present the probability density functions of LISA BHNS and BHBH systems in M31, respectively, as a function of component masses and orbital periods. Here the CE ejection efficiency is taken to be 1.0. Since the rapid supernova mechanism allows the existence of a mass gap between NSs and BHs, it predicts that the BH masses in both BHNS and BHBH systems are always larger than and distributed with a peak at . On the contrary, the delayed and stochastic mechanisms are likely to form the systems with low-mass () BH components. Compared with the LISA sources with WD components, the BHNS (BHBH) systems have wider orbital period distributions in the range of min ( min) with peaks at min ( min).

4 Discussion
For LISA WDWD systems in M31, Korol et al. (2018) proposed that 17 (60) such sources with can be detected for 4 (10) yr observation lifetime, which are significantly larger than our obtained. A main reason for this discrepancy may be attributed to the calculation of . It is known that theoretical predictions for the detection of LISA WDWD binaries in M31 are very sensitive to the magnitude of (see Figure 3). Since the adopted values of (from Amaro-Seoane et al. (2017) and Robson et al. (2019), respectively) in the effective power spectral density of the noise differ from each other by a factor of 1.5, the S/N calculated by Korol et al. (2018) is significantly higher than ours. In addition, Korol et al. (2018) made some physical assumptions that differ from our model: e.g. they assumed the total stellar mass of M31 to be twice that of the Milky Way and extrapolated the properties of Galactic WDWD population to that of M31; they adopted the Kroupa’s IMF and set the binary fraction to be ; for CE evolution, they used a different prescription proposed by Nelemans et al. (2001) that the orbital evolution of a binary system is assumed to be caused by angular momentum loss due to mass outflow. Checking the influence of these different assumptions requires a more in-depth study of LISA WDWD sources, which is beyond the scope of this paper.
Among all LISA sources, we predict that the number of NSNS binaries is the smallest, indicating that it is difficult to detect NSNS systems in M31 even during a 10 yr observation mission. Using the inferred merger rate density of from the detection of GW170817 (Abbott et al., 2017) and combining it with a simple relation to estimate the merger rate of NSNS systems in M31, Seto (2019) suggested that LISA might identify NSNS binaries in M31 with . There is a significant difference between their predictions and ours. On the one hand, the recently estimated merger rate density of NSNS systems is between and (Abbott et al., 2023), which is still subject to a big uncertainty with probably a very low value. On the other hand, the overall distribution of orbital parameters for Galactic NSNS binaries implies that the small natal kicks are imparted to the second-born NSs (e.g., Tauris et al., 2017; Shao & Li, 2018), we do not include an additional assumption on the natal kicks of second-born NSs in our current work.
Our calculations show that NSWD systems in M31 are expected to be observed by LISA for 10 yr instrument’s lifetime. Among them, almost all NSs may originate from electron-capture supernovae, with corresponding masses of . Different from WDWD and NSWD systems, the LISA sources with BH components are more vulnerable to adopted supernova-explosion mechanisms. It is predicted that the stochastic mechanism can produce the largest population of these types of binaries, with likely being detected in M31 (see the Appendix). Furthermore, these GW sources are likely to host mass-gap () BHs.
Our estimations of the number of M31 LISA sources include some uncertainties and simplifications. For example, we allow the binaries with Hertzsprung gap donors to survive CE phases. However, it remains uncertain whether such binaries can survive CE phases or directly lead to mergers (e.g., Dominik et al., 2012), as Hertzsprung gap donors are not expected to have developed a steep density gradient between envelope and core (Ivanova & Taam, 2004). If assuming all binaries with Hertzsprung gap donors to merge during the CE evolution, we obtain that the total number of M31 DCO binaries detectable by LISA during its 10 yr observation mission will decrease by a factor of less than 2. In contrast to WDWD binaries, which have almost unchanged numbers, other types of binaries are obviously vulnerable to this assumption (especially in the case). Furthermore, we assume that all primordial binaries have circular orbits in our calculations. If we choose the orbital eccentricities from a thermal distribution between 0 and 1 (Heggie, 1975), the total number of M31 LISA sources will slightly increase (decrease) by a factor of ().
For the treatment of CE evolution with the energy balance method, we assume that has a fixed value for the calculation of a specific population. However, some authors (e.g., Davis et al., 2012) have tried to connect to the binary parameters such as component masses and orbital periods at the onset of CE evolution, and given some possible relations between the parameters of post-CE binaries. It is possible that these relations are extrapolated and incorporated in BPS codes to determine the values precisely.
Recently, Fryer et al. (2022) introduced a new treatment of supernova mechanisms by incorporating a convection mixing parameter, . Typically, ranges from to , where and approximately correspond to the delayed and the rapid mechanisms, respectively. This new method aims to mitigate the mass gap. Future observation of LISA sources can help settle a possible supernova mechanism and give a proper parameter in the remnant mass prescription.
In our calculations, we only consider the formation of DCO systems through isolated binary evolution in M31. As expected, LISA may detect GW sources originating from globular clusters and these sources are more likely to form through dynamical interactions.
5 Conclusion
In this work, we have investigated the prospects of detecting DCO GW sources in M31 with a BPS method, by considering the star-formation history of the M31 disk and a range of evolutionary models. For a 4-yr mission duration, we expect that LISA can resolve BHBHs, BHNSs, BHWDs, NSNSs, NSWDs, and WDWDs. For a 10-yr mission duration, LISA may detect BHBHs, BHNSs, BHWDs, NSNSs, NSWDs, and WDWDs. Since M31 has a distance of 780 kpc, only very tight DCOs can be observed by LISA. These binaries provide an important category of GW sources that are fast-merging.
We thank the anonymous referee for valuable suggestions that helped to improve our manuscript. This work was supported by the National Key Research and Development Program of China (2021YFA0718500), the Natural Science Foundation of China (Nos. 11973026, 12041301, 12121003), and the Project U1838201 supported by NSFC and CAS.
Appendix A Numbers of M31 LISA binaries
Table 1 shows the expected numbers for various types of DCO binaries in M31 that can be resolved by LISA during its mission duration of 4 or 10 yr, by assuming different models related to supernova-explosion mechanisms and CE ejection efficiencies.
| Models | ||||||
|---|---|---|---|---|---|---|
| 0.47 (0.66) | 0.20 (0.30) | 0 (0) | 0 (0.01) | 0.09 (1.28) | 0.17 (3.49) | |
| 0.68 (0.95) | 0.26 (0.40) | 0 (0) | 0.01 (0.03) | 0.17 (3.69) | 0.13 (8.20) | |
| 1.07 (1.51) | 0.55 (0.83) | 0 (0) | 0.01 (0.09) | 0.12 (2.17) | 0.01 (2.26) | |
| 0.44 (0.63) | 0.14 (0.24) | 0.03 (0.07) | 0 (0.02) | 0.13 (1.36) | 0.17 (3.49) | |
| 0.71 (1.00) | 0.15 (0.24) | 0.11 (0.29) | 0.01 (0.06) | 0.19 (3.47) | 0.13 (8.20) | |
| 1.13 (1.59) | 0.35 (0.63) | 0.03 (0.07) | 0.05 (0.21) | 0.20 (2.24) | 0.01 (2.26) | |
| 0.58 (0.82) | 0.64 (1.26) | 0.55 (1.39) | 0.03 (0.09) | 0.11 (1.41) | 0.17 (3.49) | |
| 1.06 (1.50) | 0.63 (1.32) | 0.74 (2.12) | 0.04 (0.14) | 0.29 (5.67) | 0.13 (8.20) | |
| 1.51 (2.17) | 1.12 (2.21) | 0.24 (0.90) | 0.06 (0.27) | 0.33 (3.22) | 0.01 (2.26) |
References
- Abbott et al. (2016) Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. Lett., 116, 061102, doi: 10.1103/PhysRevLett.116.061102
- Abbott et al. (2017) —. 2017, Phys. Rev. Lett., 119, 161101, doi: 10.1103/PhysRevLett.119.161101
- Abbott et al. (2020) Abbott, R., Abbott, T. D., Abraham, S., et al. 2020, ApJ, 896, L44, doi: 10.3847/2041-8213/ab960f
- Abbott et al. (2023) Abbott, R., Abbott, T. D., Acernese, F., et al. 2023, Physical Review X, 13, 011048, doi: 10.1103/PhysRevX.13.011048
- Amaro-Seoane et al. (2017) Amaro-Seoane, P., Audley, H., Babak, S., et al. 2017, arXiv e-prints, arXiv:1702.00786. https://arxiv.org/abs/1702.00786
- Amaro-Seoane et al. (2023) Amaro-Seoane, P., Andrews, J., Arca Sedda, M., et al. 2023, Living Reviews in Relativity, 26, 2, doi: 10.1007/s41114-022-00041-y
- Andrews et al. (2020) Andrews, J. J., Breivik, K., Pankow, C., D’Orazio, D. J., & Safarzadeh, M. 2020, ApJ, 892, L9, doi: 10.3847/2041-8213/ab5b9a
- Babak et al. (2021) Babak, S., Hewitson, M., & Petiteau, A. 2021, arXiv e-prints, arXiv:2108.01167. https://arxiv.org/abs/2108.01167
- Barack & Cutler (2004) Barack, L., & Cutler, C. 2004, Phys. Rev. D, 69, 082005, doi: 10.1103/PhysRevD.69.082005
- Belczynski et al. (2010a) Belczynski, K., Benacquista, M., & Bulik, T. 2010a, ApJ, 725, 816, doi: 10.1088/0004-637X/725/1/816
- Belczynski et al. (2010b) Belczynski, K., Bulik, T., Fryer, C. L., et al. 2010b, ApJ, 714, 1217, doi: 10.1088/0004-637X/714/2/1217
- Bhattacharya & van den Heuvel (1991) Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1, doi: 10.1016/0370-1573(91)90064-S
- Breivik et al. (2020) Breivik, K., Coughlin, S., Zevin, M., et al. 2020, ApJ, 898, 71, doi: 10.3847/1538-4357/ab9d85
- Chen et al. (2021) Chen, H.-L., Tauris, T. M., Han, Z., & Chen, X. 2021, MNRAS, 503, 3540, doi: 10.1093/mnras/stab670
- Chen et al. (2020) Chen, W.-C., Liu, D.-D., & Wang, B. 2020, ApJ, 900, L8, doi: 10.3847/2041-8213/abae66
- Cornish & Robson (2017) Cornish, N., & Robson, T. 2017, in Journal of Physics Conference Series, Vol. 840, Journal of Physics Conference Series, 012024, doi: 10.1088/1742-6596/840/1/012024
- Cornish & Larson (2003) Cornish, N. J., & Larson, S. L. 2003, Phys. Rev. D, 67, 103001, doi: 10.1103/PhysRevD.67.103001
- Davis et al. (2012) Davis, P. J., Kolb, U., & Knigge, C. 2012, MNRAS, 419, 287, doi: 10.1111/j.1365-2966.2011.19690.x
- Davis et al. (2010) Davis, P. J., Kolb, U., & Willems, B. 2010, MNRAS, 403, 179, doi: 10.1111/j.1365-2966.2009.16138.x
- Dominik et al. (2012) Dominik, M., Belczynski, K., Fryer, C., et al. 2012, ApJ, 759, 52, doi: 10.1088/0004-637X/759/1/52
- Feng et al. (2023) Feng, W.-F., Chen, J.-W., Wang, Y., Mohanty, S. D., & Shao, Y. 2023, Phys. Rev. D, 107, 103035, doi: 10.1103/PhysRevD.107.103035
- Fragos et al. (2019) Fragos, T., Andrews, J. J., Ramirez-Ruiz, E., et al. 2019, ApJ, 883, L45, doi: 10.3847/2041-8213/ab40d1
- Fryer et al. (2012) Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91, doi: 10.1088/0004-637X/749/1/91
- Fryer et al. (2022) Fryer, C. L., Olejak, A., & Belczynski, K. 2022, ApJ, 931, 94, doi: 10.3847/1538-4357/ac6ac9
- Fryer et al. (1999) Fryer, C. L., Woosley, S. E., Herant, M., & Davies, M. B. 1999, ApJ, 520, 650, doi: 10.1086/307467
- Gallegos-Garcia et al. (2022) Gallegos-Garcia, M., Berry, C. P. L., & Kalogera, V. 2022, arXiv e-prints, arXiv:2211.15693, doi: 10.48550/arXiv.2211.15693
- Gao et al. (2022) Gao, S.-J., Li, X.-D., & Shao, Y. 2022, MNRAS, 514, 1054, doi: 10.1093/mnras/stac1426
- Gompertz et al. (2020) Gompertz, B. P., Levan, A. J., & Tanvir, N. R. 2020, ApJ, 895, 58, doi: 10.3847/1538-4357/ab8d24
- Hamann et al. (1995) Hamann, W. R., Koesterke, L., & Wessolowski, U. 1995, A&A, 299, 151
- Heggie (1975) Heggie, D. C. 1975, MNRAS, 173, 729, doi: 10.1093/mnras/173.3.729
- Hobbs et al. (2005) Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974, doi: 10.1111/j.1365-2966.2005.09087.x
- Hurley et al. (2002) Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897, doi: 10.1046/j.1365-8711.2002.05038.x
- Iben & Tutukov (1984) Iben, I., J., & Tutukov, A. V. 1984, ApJS, 54, 335, doi: 10.1086/190932
- Ivanova & Taam (2004) Ivanova, N., & Taam, R. E. 2004, ApJ, 601, 1058, doi: 10.1086/380561
- Ivanova et al. (2013) Ivanova, N., Justham, S., Chen, X., et al. 2013, A&A Rev., 21, 59, doi: 10.1007/s00159-013-0059-2
- Kapil et al. (2023) Kapil, V., Mandel, I., Berti, E., & Müller, B. 2023, MNRAS, 519, 5893, doi: 10.1093/mnras/stad019
- Kemp et al. (2022) Kemp, A. J., Karakas, A. I., Casey, A. R., Kobayashi, C., & Izzard, R. G. 2022, MNRAS, 509, 1175, doi: 10.1093/mnras/stab3103
- Kiel & Hurley (2006) Kiel, P. D., & Hurley, J. R. 2006, MNRAS, 369, 1152, doi: 10.1111/j.1365-2966.2006.10400.x
- Klencki et al. (2021) Klencki, J., Nelemans, G., Istrate, A. G., & Chruslinska, M. 2021, A&A, 645, A54, doi: 10.1051/0004-6361/202038707
- Kobulnicky & Fryer (2007) Kobulnicky, H. A., & Fryer, C. L. 2007, ApJ, 670, 747, doi: 10.1086/522073
- Korol et al. (2022) Korol, V., Hallakoun, N., Toonen, S., & Karnesis, N. 2022, MNRAS, 511, 5936, doi: 10.1093/mnras/stac415
- Korol et al. (2018) Korol, V., Koop, O., & Rossi, E. M. 2018, ApJ, 866, L20, doi: 10.3847/2041-8213/aae587
- Korol et al. (2017) Korol, V., Rossi, E. M., Groot, P. J., et al. 2017, MNRAS, 470, 1894, doi: 10.1093/mnras/stx1285
- Kroupa et al. (1993) Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545, doi: 10.1093/mnras/262.3.545
- Lamberts et al. (2019) Lamberts, A., Blunt, S., Littenberg, T. B., et al. 2019, MNRAS, 490, 5888, doi: 10.1093/mnras/stz2834
- Lamberts et al. (2018) Lamberts, A., Garrison-Kimmel, S., Hopkins, P. F., et al. 2018, MNRAS, 480, 2704, doi: 10.1093/mnras/sty2035
- Larson et al. (2000) Larson, S. L., Hiscock, W. A., & Hellings, R. W. 2000, Phys. Rev. D, 62, 062001, doi: 10.1103/PhysRevD.62.062001
- Lau et al. (2020) Lau, M. Y. M., Mandel, I., Vigna-Gómez, A., et al. 2020, MNRAS, 492, 3061, doi: 10.1093/mnras/staa002
- Li & Paczyński (1998) Li, L.-X., & Paczyński, B. 1998, ApJ, 507, L59, doi: 10.1086/311680
- Liu et al. (2010) Liu, J., Han, Z., Zhang, F., & Zhang, Y. 2010, ApJ, 719, 1546, doi: 10.1088/0004-637X/719/2/1546
- Liu & Zhang (2014) Liu, J., & Zhang, Y. 2014, PASP, 126, 211, doi: 10.1086/675721
- Luo et al. (2016) Luo, J., Chen, L.-S., Duan, H.-Z., et al. 2016, Classical and Quantum Gravity, 33, 035010, doi: 10.1088/0264-9381/33/3/035010
- Manchester et al. (2005) Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993, doi: 10.1086/428488
- Mandel & Müller (2020) Mandel, I., & Müller, B. 2020, MNRAS, 499, 3214, doi: 10.1093/mnras/staa3043
- Marchant et al. (2021) Marchant, P., Pappas, K. M. W., Gallegos-Garcia, M., et al. 2021, A&A, 650, A107, doi: 10.1051/0004-6361/202039992
- Neijssel et al. (2019) Neijssel, C. J., Vigna-Gómez, A., Stevenson, S., et al. 2019, MNRAS, 490, 3740, doi: 10.1093/mnras/stz2840
- Nelemans et al. (2001) Nelemans, G., Yungelson, L. R., & Portegies Zwart, S. F. 2001, A&A, 375, 890, doi: 10.1051/0004-6361:20010683
- Nelson & Eggleton (2001) Nelson, C. A., & Eggleton, P. P. 2001, ApJ, 552, 664, doi: 10.1086/320560
- Nitz et al. (2021) Nitz, A. H., Kumar, S., Wang, Y.-F., et al. 2021, arXiv e-prints, arXiv:2112.06878. https://arxiv.org/abs/2112.06878
- Olejak et al. (2021) Olejak, A., Belczynski, K., & Ivanova, N. 2021, A&A, 651, A100, doi: 10.1051/0004-6361/202140520
- Packet (1981) Packet, W. 1981, A&A, 102, 17
- Paczynski (1986) Paczynski, B. 1986, ApJ, 308, L43, doi: 10.1086/184740
- Pavlovskii et al. (2017) Pavlovskii, K., Ivanova, N., Belczynski, K., & Van, K. X. 2017, MNRAS, 465, 2092, doi: 10.1093/mnras/stw2786
- Peters & Mathews (1963) Peters, P. C., & Mathews, J. 1963, Physical Review, 131, 435, doi: 10.1103/PhysRev.131.435
- Qin et al. (2023) Qin, K., Jiang, L., & Chen, W.-C. 2023, ApJ, 944, 83, doi: 10.3847/1538-4357/acb340
- Ribas et al. (2005) Ribas, I., Jordi, C., Vilardell, F., et al. 2005, ApJ, 635, L37, doi: 10.1086/499161
- Robson et al. (2019) Robson, T., Cornish, N. J., & Liu, C. 2019, Classical and Quantum Gravity, 36, 105011, doi: 10.1088/1361-6382/ab1101
- Ruan et al. (2020) Ruan, W.-H., Guo, Z.-K., Cai, R.-G., & Zhang, Y.-Z. 2020, International Journal of Modern Physics A, 35, 2050075, doi: 10.1142/S0217751X2050075X
- Ruiter et al. (2010) Ruiter, A. J., Belczynski, K., Benacquista, M., Larson, S. L., & Williams, G. 2010, ApJ, 717, 1006, doi: 10.1088/0004-637X/717/2/1006
- Scherbak & Fuller (2023) Scherbak, P., & Fuller, J. 2023, MNRAS, 518, 3966, doi: 10.1093/mnras/stac3313
- Sesana et al. (2020) Sesana, A., Lamberts, A., & Petiteau, A. 2020, MNRAS, 494, L75, doi: 10.1093/mnrasl/slaa039
- Seto (2019) Seto, N. 2019, MNRAS, 489, 4513, doi: 10.1093/mnras/stz2439
- Shao (2022) Shao, Y. 2022, Research in Astronomy and Astrophysics, 22, 122002, doi: 10.1088/1674-4527/ac995e
- Shao & Li (2014) Shao, Y., & Li, X.-D. 2014, ApJ, 796, 37, doi: 10.1088/0004-637X/796/1/37
- Shao & Li (2015) —. 2015, ApJ, 809, 99, doi: 10.1088/0004-637X/809/1/99
- Shao & Li (2018) —. 2018, ApJ, 867, 124, doi: 10.3847/1538-4357/aae648
- Shao & Li (2021) —. 2021, ApJ, 920, 81, doi: 10.3847/1538-4357/ac173e
- Soberman et al. (1997) Soberman, G. E., Phinney, E. S., & van den Heuvel, E. P. J. 1997, A&A, 327, 620, doi: 10.48550/arXiv.astro-ph/9703016
- Tauris (2018) Tauris, T. M. 2018, Phys. Rev. Lett., 121, 131105, doi: 10.1103/PhysRevLett.121.131105
- Tauris & van den Heuvel (2023) Tauris, T. M., & van den Heuvel, E. P. J. 2023, Physics of Binary Star Evolution. From Stars to X-ray Binaries and Gravitational Wave Sources
- Tauris et al. (2017) Tauris, T. M., Kramer, M., Freire, P. C. C., et al. 2017, ApJ, 846, 170, doi: 10.3847/1538-4357/aa7e89
- The LIGO Scientific Collaboration et al. (2021) The LIGO Scientific Collaboration, the Virgo Collaboration, the KAGRA Collaboration, et al. 2021, arXiv e-prints, arXiv:2111.03606, doi: 10.48550/arXiv.2111.03606
- van den Heuvel et al. (2017) van den Heuvel, E. P. J., Portegies Zwart, S. F., & de Mink, S. E. 2017, MNRAS, 471, 4256, doi: 10.1093/mnras/stx1430
- Wagg et al. (2022a) Wagg, T., Breivik, K., & de Mink, S. E. 2022a, ApJS, 260, 52, doi: 10.3847/1538-4365/ac5c52
- Wagg et al. (2022b) Wagg, T., Broekgaarden, F. S., de Mink, S. E., et al. 2022b, ApJ, 937, 118, doi: 10.3847/1538-4357/ac8675
- Wang et al. (2021) Wang, B., Chen, W.-C., Liu, D.-D., et al. 2021, MNRAS, 506, 4654, doi: 10.1093/mnras/stab2032
- Webbink (1984) Webbink, R. F. 1984, ApJ, 277, 355, doi: 10.1086/161701
- Weisz et al. (2015) Weisz, D. R., Johnson, L. C., Foreman-Mackey, D., et al. 2015, ApJ, 806, 198, doi: 10.1088/0004-637X/806/2/198
- Williams et al. (2017) Williams, B. F., Dolphin, A. E., Dalcanton, J. J., et al. 2017, ApJ, 846, 145, doi: 10.3847/1538-4357/aa862a
- Xu & Li (2010) Xu, X.-J., & Li, X.-D. 2010, ApJ, 716, 114, doi: 10.1088/0004-637X/716/1/114
- Yang et al. (2022) Yang, J., Ai, S., Zhang, B.-B., et al. 2022, Nature, 612, 232, doi: 10.1038/s41586-022-05403-8
- Yarza et al. (2022) Yarza, R., Everson, R. W., & Ramirez-Ruiz, E. 2022, arXiv e-prints, arXiv:2210.00010. https://arxiv.org/abs/2210.00010
- Zhu et al. (2021) Zhu, J.-P., Wu, S., Yang, Y.-P., et al. 2021, ApJ, 917, 24, doi: 10.3847/1538-4357/abfe5e
- Zorotovic et al. (2010) Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86, doi: 10.1051/0004-6361/200913658
- Zuo & Li (2014) Zuo, Z.-Y., & Li, X.-D. 2014, MNRAS, 442, 1980, doi: 10.1093/mnras/stu993